大学物理第2章力动量能量
合集下载
大学物理2-1第2章

F0的方向与非惯性系的加 速度反向。
说明
惯性力不是真实力,无施力物体,无反作用力。
2、非惯性系中的力学规律
F F0 ma
a 为物体相对非惯性系的加速度
物体相对惯性系的加速度 a a a0
常见的非惯性系 1、作直线运动的加速参考系 以恒定加速度 a0 作直线运动的车厢内吊一重物 m 。
g
GM地 球 R2
9.8m s 2
2 弹性力:发生形变的物体,有恢复原状的趋势,对与它接 触的物体产生的作用力。 ★绳或线对物体的拉力
绳或线对物体的拉力,是由绳发生形变而产生的,其大小取决于 绳被拉紧的程度。绳产生拉力时,绳的内部各段之间也有相互的 弹力作用,这种内部的弹力作用称为张力。 设绳子不可伸长,每段的质量为△mi 则:
s
2.4 惯性系和非惯性系
一、惯性系与非惯性系:
乙
甲
F m
a
l0
观察者甲: 有力 F和加速度 a即 F m a
牛顿定律在该参照系中适用 — 惯性系 牛顿运动定律适用的参考系称为惯性系。
观察者乙:有力 F 但没有加速度 a即 m a 0 , F 0
讨论结果的物理意义,判断其是否合理和正确。
选对象、分析力、看运动、建坐标系和列方程
例题2-1 光滑桌面上放置一固定圆环,半径为R ,一 物体贴着环带内侧运动,如图所示。物体与环带间的滑动磨 擦系数为μ。设 t = 0 时,质点经 A 点的速度为v0 。求此后 t 时刻物体的速率和从 A 点开始所经过的路程。 分析:已知初始条件求速率和路程,需先求出加速度。 结论:用牛顿运动定律求出加速度后,问题变成已知加速度 和初始条件求速度方程或运动方程的第二类运动学问题。 解:1)以桌面为参考系,建立自然坐标系 2)分析受力,设物体的质量为m 3) 应用牛顿第二定律
说明
惯性力不是真实力,无施力物体,无反作用力。
2、非惯性系中的力学规律
F F0 ma
a 为物体相对非惯性系的加速度
物体相对惯性系的加速度 a a a0
常见的非惯性系 1、作直线运动的加速参考系 以恒定加速度 a0 作直线运动的车厢内吊一重物 m 。
g
GM地 球 R2
9.8m s 2
2 弹性力:发生形变的物体,有恢复原状的趋势,对与它接 触的物体产生的作用力。 ★绳或线对物体的拉力
绳或线对物体的拉力,是由绳发生形变而产生的,其大小取决于 绳被拉紧的程度。绳产生拉力时,绳的内部各段之间也有相互的 弹力作用,这种内部的弹力作用称为张力。 设绳子不可伸长,每段的质量为△mi 则:
s
2.4 惯性系和非惯性系
一、惯性系与非惯性系:
乙
甲
F m
a
l0
观察者甲: 有力 F和加速度 a即 F m a
牛顿定律在该参照系中适用 — 惯性系 牛顿运动定律适用的参考系称为惯性系。
观察者乙:有力 F 但没有加速度 a即 m a 0 , F 0
讨论结果的物理意义,判断其是否合理和正确。
选对象、分析力、看运动、建坐标系和列方程
例题2-1 光滑桌面上放置一固定圆环,半径为R ,一 物体贴着环带内侧运动,如图所示。物体与环带间的滑动磨 擦系数为μ。设 t = 0 时,质点经 A 点的速度为v0 。求此后 t 时刻物体的速率和从 A 点开始所经过的路程。 分析:已知初始条件求速率和路程,需先求出加速度。 结论:用牛顿运动定律求出加速度后,问题变成已知加速度 和初始条件求速度方程或运动方程的第二类运动学问题。 解:1)以桌面为参考系,建立自然坐标系 2)分析受力,设物体的质量为m 3) 应用牛顿第二定律
大学物理:2-2 动量守恒定律

y P
rP
F
O
地球
r
C
Q
rQ x
7
3、保守力 (conservation force)
物体在某种力的作用下, 沿任意闭合路径绕行一周所 作的功恒等于零,即
Q
CD
E
F
P
F dl 0
具有这种特性的力,称为保守力;不具有这种特 性的力称为非保守力。
8
四、 机械能守恒定律
1、功能原理 由 n 个相互作用着的质点所组成的质点系。系统中
Q
A
Q Q
AaPdFv,d
r
P
dr
ma d r
vdt
F
Q
m
d
vdtv
d
t
P dt
Q P
mv
d
v
1 2
mvQ2
1 2
P
mvP2
vdPr
质点的动能(kinetic energy)定义:质点的质量与
其运动速率平方的乘积的一半。
用Ek表示,即
Ek
1 2
mv2
5
所以有 A Ek Q Ek P 动能定理:作用于质点的合力所作的功,等于质点
0
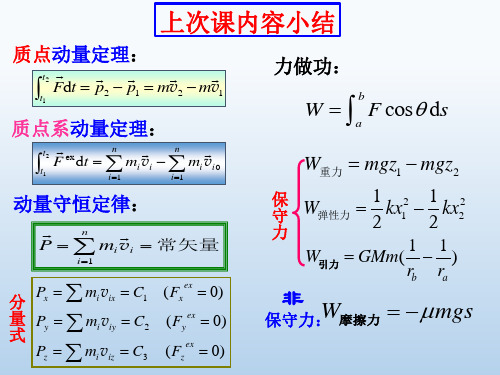
mivi 恒矢量
i 1
在外力的矢量和为零的情况下,质点系的总动量
不随时间变化——动量守恒定律。
其分量式
n
mi vix 恒量
i 1 n
mi viy 恒量
i 1 n
mi viz 恒量
i 1
n
(当 Fix 0 时)
i 1
n
(当 Fiy 0 时)
i 1
n
(当 Fiz 0 时)
i 1
大学物理动量守恒定律和能量守恒定律

04
动量守恒定律和能量守恒定 律的意义与影响
在物理学中的地位
基础定律
动量守恒定律和能量守恒定律是物理学中的两个基础定律,它们 在理论物理学和实验物理学中都占据着重要的地位。
理论基石
这两个定律为物理学理论体系提供了基石,许多物理理论和公式都 是基于这两个定律推导出来的。
验证实验
许多实验通过验证动量守恒定律和能量守恒定律的正确性,来检验 实验的准确性和可靠性。
适用条件
系统不受外力或外力合力为零
动量守恒定律只有在系统不受外力或外力合力为零的情况下才成立。如果系统受到外力作 用,则总动量将发生变化。
系统内力的作用相互抵消
系统内力的作用只会改变系统内各物体的速度,而不会改变系统的总动量。如果系统内力 的作用相互抵消,则总动量保持不变。
理想气体和刚体的动量守恒
未来能源利用的发展需要解决环 境问题和能源短缺问题,动量守 恒定律和能量守恒定律将在新能 源技术、节能技术等领域发挥关
键作用。
感谢您的观看
THANKS
在理想气体和刚体的研究中,由于气体分子之间的相互作用力和刚体之间的碰撞力都可以 忽略不计,因此它们的动量守恒。
实例分析
弹性碰撞
当两个小球发生弹性碰撞时,根据动量守恒定律,它们碰撞后 的速度满足m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'。由于弹性碰撞中能 量没有损失,因此碰撞前后两小球的速度变化量相等。
动量与能量的关系
动量是质量与速度的乘积,表 示物体的运动状态;能量是物 体运动状态的度量,包括动能
和势能。
动量和能量都是矢量,具有 方向性,遵循矢量合成法则。
动量和能量可以相互转化,但 总量保持不变,这是动量守恒 和能量守恒定律的内在联系。
大学物理第二章习题质点力学的基本规律 守恒定律

第2章 质点力学的基本规律 守恒定律
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题,理 解力学量的单位和量纲。掌握动量、冲量、动量定理,动量守恒定律。并 能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本 原理的适用范围。掌握功与功率、动能、势能(重力势能、弹性势能、引 力势能)概念,动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类: 第一类是已知质点的运动,求作用于质点的力; 第二类是已知作用于质点的力,求质点的运动.
2.基本定理 动量定理
动能定理
I
t2 t1
F (t )dt
mv
mv0
A12
2
F
(r)
dr
1
1 2
mv
2 2
1 2
解:根据牛顿第二定律
f
k x2
m dv dt
m dv d x dx dt
mv
dv dx
k x2
mv
dv dx
v
dv
k
dx mx2
v
v
0
dv
A/4
A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解:根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题,理 解力学量的单位和量纲。掌握动量、冲量、动量定理,动量守恒定律。并 能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本 原理的适用范围。掌握功与功率、动能、势能(重力势能、弹性势能、引 力势能)概念,动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类: 第一类是已知质点的运动,求作用于质点的力; 第二类是已知作用于质点的力,求质点的运动.
2.基本定理 动量定理
动能定理
I
t2 t1
F (t )dt
mv
mv0
A12
2
F
(r)
dr
1
1 2
mv
2 2
1 2
解:根据牛顿第二定律
f
k x2
m dv dt
m dv d x dx dt
mv
dv dx
k x2
mv
dv dx
v
dv
k
dx mx2
v
v
0
dv
A/4
A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解:根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量
大学物理-狭义相对论-相对论性动量和能量

我国于 1958 年建成的首座重水反应堆
我国已 建成的岭澳 核电站
我国在 建的单机容 量最大的田 湾核电站
原子弹核裂变
2 轻核聚变
氘核 氦核 质量亏损
释放能量
轻核聚变条件 温度要达到
有
的动能,足以克服两
力.
时,使 具 之间的库仑排斥
1967年6 月17日,中国 第一颗氢弹爆 炸成功
五 动量与能量的关系
而
,所以光速 C 为物体的极限速度 .
当
时
相对论动量守恒定律
当
时
常矢量
若
,则相对论动量守恒 经典动量守恒 .
常矢量
三 质量与能量的关系
相对论质能关系
静能
:物体静止时所具有的能量 .
质能关系预言:物质的质量就是能量的一种储藏 .
爱因斯坦认为(1905)
懒惰性
惯性 ( inertia )
活泼性
物理意义
惯性质量的增加和能量的增加相联系,质量的 大小应标志着能量的大小,这是相对论的又一极其 重要的推论 .
相对论的质能关系为开创原子能时代提供了理 论基础 , 这是一个具有划时代的意义的理论公式 .
质能关系预言:物质的质量就是能量的一种储藏.
例:
现有 100 座楼,每楼 200 套房,每套房用电功率
能量 ( energy )
物体的懒惰性就 是物体活泼性的度量 .
相对论能量和质量守恒是一个统一的物理规律.
一些微观粒子和轻核的静能量
粒子
符号
光子
电子(或正电子) e(或 +e
质子
)p
中子
n
氘
氚
氦( 粒子)
静能量 MeV 0 0.510
大学物理第二章动能定理
例题3. 如图,一轻绳跨过一定滑轮,两边分别拴有质量
为m及M的物体,M离地面的高度为h: (1)若滑轮质量及
摩擦力不计,m与桌面的摩擦也不计,开始时两物体均静
止,求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为,结果又如何?
解:
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理:
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得:
t2 t1
M外dt
L2
L1
注意:只有外力矩对质点系的角动量变化有贡献,
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
大学物理学习指导(第2章)

^
^!"自(!饥
1 6,1
(? !
在经典力学中,77^恒定不变,上式则为
在直角坐标系中,其分量5^为
凡 二
饥"I
二
1/
0
尺 二
1
尺 二
5?
对于平面曲线运动,常用自然坐标系,其分量式为
1^『^ 171(1^ ^
舰":
9
3^动量定理 微分形式 积分形式 ^
^1^1
^ 6(7^^ ^
二 ^ (!^ 171^ ^
的夹角为0,现沿斜面以恒力I拉杆,求杆内各部分间的相互作用〖张力)沿棒长方 向的变化规律。 解取杆V^为研究对象,设加速度为"则有 V
一
31X10
^
771^1
(!)
再取长为工的一段/10:为研究对象,设在0:点杆内张力为/,^(:段受力如图所
示,则有
第 页
山 # 、理工大学备课欽
^ 、 月
日
卞 习题2-2图
771^ ―
^
X;2。求跳伞员的运
2 二 6.1
分离变量两边积分
3。
、2一 解得 厂 2
,
V 」 瑝 "广"& 二 1 1 1 饥8
今
,
:
"
―
/ , 十
V
^
口 ( ? , / , " ) 十 丄 ] " 口 ( ; , 〃 。 ― 1〕
当,—①,极限速率为 1^
11
5 ?
2 - 8
一质量为7^
^
101^8的质点,在力7 ^ ^ 5111处,其速度^0
0.21
5,这力应在这物体上作用多少时间?试就一
^!"自(!饥
1 6,1
(? !
在经典力学中,77^恒定不变,上式则为
在直角坐标系中,其分量5^为
凡 二
饥"I
二
1/
0
尺 二
1
尺 二
5?
对于平面曲线运动,常用自然坐标系,其分量式为
1^『^ 171(1^ ^
舰":
9
3^动量定理 微分形式 积分形式 ^
^1^1
^ 6(7^^ ^
二 ^ (!^ 171^ ^
的夹角为0,现沿斜面以恒力I拉杆,求杆内各部分间的相互作用〖张力)沿棒长方 向的变化规律。 解取杆V^为研究对象,设加速度为"则有 V
一
31X10
^
771^1
(!)
再取长为工的一段/10:为研究对象,设在0:点杆内张力为/,^(:段受力如图所
示,则有
第 页
山 # 、理工大学备课欽
^ 、 月
日
卞 习题2-2图
771^ ―
^
X;2。求跳伞员的运
2 二 6.1
分离变量两边积分
3。
、2一 解得 厂 2
,
V 」 瑝 "广"& 二 1 1 1 饥8
今
,
:
"
―
/ , 十
V
^
口 ( ? , / , " ) 十 丄 ] " 口 ( ; , 〃 。 ― 1〕
当,—①,极限速率为 1^
11
5 ?
2 - 8
一质量为7^
^
101^8的质点,在力7 ^ ^ 5111处,其速度^0
0.21
5,这力应在这物体上作用多少时间?试就一
大学物理第2章-质点动力学基本定律

②保守力作功。
势能的绝对值没有意义,只关心势能的相对值。 势能是属于具有保守力相互作用的系统 计算势能时必须规定零势能参考点。但是势能差是一定的,与零点的选择无关。 如果把石头放在楼顶,并摇摇欲坠,你就不会不关心它。 一块石头放在地面你对它并不关心。
重力势能:以地面为势能零点
01
万有引力势能:以无限远处为势能零点
m
o
θ
设:t 时刻质点的位矢
质点的动量
运动质点相对于参考原点O的角动量定义为:
大小:
方向:右手螺旋定则判定
若质点作圆周运动,则对圆心的角动量:
质点对轴的角动量:
质点系的角动量:
设各质点对O点的位矢分别为
动量分别为
二.角动量定理
对质点:
---外力对参考点O 的力矩
力矩的大小:
力矩的方向:由右手螺旋关系确定
为质点系的动能,
令
---质点系的动能定理
讨论
内力和为零,内力功的和是否为零?
不一定为零
A
B
A
B
S
L
例:炸弹爆炸,过程内力和为零,但内力所做的功转化为弹片的动能。
内力做功可以改变系统的总动能
例 用铁锤将一只铁钉击入木板内,设木板对铁钉的阻力与铁钉进入木板之深度成正比,如果在击第一次时,能将钉击入木板内 1 cm, 再击第二次时(锤仍以第一次同样的速度击钉),能击入多深? 第一次的功 第二次的功 解:
(1)重力的功
重力做功仅取决于质点的始、末位置za和zb,与质点经过的具体路径无关。
(2) 万有引力的功
*
设质量M的质点固定,另一质量m的质点在M 的引力场中从a运动到b。
M
a
b
势能的绝对值没有意义,只关心势能的相对值。 势能是属于具有保守力相互作用的系统 计算势能时必须规定零势能参考点。但是势能差是一定的,与零点的选择无关。 如果把石头放在楼顶,并摇摇欲坠,你就不会不关心它。 一块石头放在地面你对它并不关心。
重力势能:以地面为势能零点
01
万有引力势能:以无限远处为势能零点
m
o
θ
设:t 时刻质点的位矢
质点的动量
运动质点相对于参考原点O的角动量定义为:
大小:
方向:右手螺旋定则判定
若质点作圆周运动,则对圆心的角动量:
质点对轴的角动量:
质点系的角动量:
设各质点对O点的位矢分别为
动量分别为
二.角动量定理
对质点:
---外力对参考点O 的力矩
力矩的大小:
力矩的方向:由右手螺旋关系确定
为质点系的动能,
令
---质点系的动能定理
讨论
内力和为零,内力功的和是否为零?
不一定为零
A
B
A
B
S
L
例:炸弹爆炸,过程内力和为零,但内力所做的功转化为弹片的动能。
内力做功可以改变系统的总动能
例 用铁锤将一只铁钉击入木板内,设木板对铁钉的阻力与铁钉进入木板之深度成正比,如果在击第一次时,能将钉击入木板内 1 cm, 再击第二次时(锤仍以第一次同样的速度击钉),能击入多深? 第一次的功 第二次的功 解:
(1)重力的功
重力做功仅取决于质点的始、末位置za和zb,与质点经过的具体路径无关。
(2) 万有引力的功
*
设质量M的质点固定,另一质量m的质点在M 的引力场中从a运动到b。
M
a
b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t1
t1
6
t2
t1
F d t p 2 p1 m v 2 m v1
动量定理 在给定的时间内,外力作用在质点 上的冲量,等于质点在此时间内动量的增量 . 分量形式
Ix Iy Iz
t2
t1 t2
F x d t m v 2 x m v1 x F y d t m v 2 y m v1 y F z d t m v 2 z m v1 z
yv d yv
1 3
gy
3
1
g y d y
2 0
y
yv
0
yv d yv
2 2 v gy 3
yv
1 2
2
第三节
一 功
功 动能
13
力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积 . (功是标量,过程量) d W F cos d r F cos d s d ri B * i dW F dr 0 90 , d W 0 dr Fi 90 180 , d W 0 1 F d r1 * A F1 90 F d r d W 0
t1
( F 2 F 21 ) d t m 2 v 2 m 2 v 20
F 21
F2
m2
t2
t1
( F1 F 2 ) d t ( m 1 v 1 m 2 v 2 ) ( m 1 v 10 m 2 v 20 )
质点系动量定理 作用于系统的合外力的冲量等于 系统动量的增量. n n t2 ex F dt mi vi mi vi0 I p p0
dr dxi dyj dzk
r
rB
W
F
x
dx
F
y
dy
F
z
dz
W Wx Wy Wz
15
功的大小与参照系有关
功的量纲和单位 dim W ML T
平均功率
P W t
2
2
1J 1 N m
瞬时功率
P lim
W t
t 0
W
Ft d s
1 2
1 2
Ft m
mv
2 2
dv dt
m v1
2
v2
v1
m
dv dt
ds
v2
v1
m vdv
Ek
1 2
p
2
动能(状态函数)
mv
2
动能定理 合外力对质点所作的功, 等于质点动能的增量 . 注意
2m
W E k2 E k1
功和动能都与 参考系有关;动能定理 仅适用于惯性系 .
22
2 ) 重力作功
P mg k dr dxi dyj dzk
W
z
zA
A
B A
P dr
B
zB
mg d z
A
zA
zB
mg
B
( mgz
W
mgz
)
o
y
x
mg d z 0
23
3 ) 弹性力作功
F
x
o
xA xB
O
则 F
ex
m 1 g yg
ex
m1
y
由质点系动量定理得
F
dt dp
y
12
F
又
ex
dt dp d p d( y v )
d yv dt
m2
O
yg d t d( y v )
则
yg
m1
y
y
两边同乘以 y d y 则
y gdy ydy
2
d yv dt
变力的功
W
dW F dr
14
F cos
B A
F dr
B A
F cos d r
o r dr 合力的功 = 分力的功的代数和 A W Fi d r Fi d r W i i F Fx i F y j Fz k
t1 i 1 i 1
8
注意
内力不改变质点系的动量
初始速度
v g 0 v b0 0
m b 2m g
则 则
Байду номын сангаас
推开后速度 v g 2 v b
且方向相反
推开前后系统动量不变
p p0
p0 0 p 0
9
动量定理常应用于碰撞问题 t2 Fdt t1 m v 2 m v1 F t 2 t1 t 2 t1 注意
三
摩擦力 滑动摩擦力 F滑 F N 静摩擦力 一般情况
F滑 F静
F静 0 F N
0
第二节 动量 一 冲量 质点的动量定理 动量
5
p mv
冲量 力对时间的积分(矢量) I
t2
Fdt
dp d (m v) F Fdt dp d (m v) dt dt t2 F d t p 2 p1 m v 2 m v1
0
d
mgl sin d
W mgl
0
sin d
v
FT
l
ds
mgl (cos cos 0 )
P
19
m 1 . 0 kg
l 1 .0 m
10
0 30
0
W mgl (cos cos 0 )
B
m
m'
O
A
r (t )
ds
r d s r d s cos r d r
W
r (t d t )
rA G
rB
m'm r
2
dr
r (t )
dr
B
ds
m'm m'm W (G ) (G ) rB rA
r (t d t )
W ( mgz
B
mgz
2
A
)
2
弹力功
W (
1 2
kx B
1 2
A
C
kx A )
D
F dr
ACB
F dr
ADB
B
25
l
F dr
ACB
F dr
ADB
A
C
F dr
F dr
ACB
F dr
m ' 对 m 的万有引力为
m'm F G r 3 r
m
m'
O
A
r (t )
ds
m 由 A 点移动到 B 点时 F 作功为
W
r (t d t )
F ds
m'm A G r 3 r d s
B
B
21
W
F ds
m'm A G r 3 r d s
Fx t mv2 x mv1x mv cos (mv cos )
x
m v1
2mv cos Fy t mv2 y mv1 y
mv2
y mv sin α mv sin 0 2mv cos F Fx 14.1 N 方向沿 x 轴反向 t
T' T m
P P'
m
地球
几种常见的力: 一 万有引力 m1m 2 F G 2 r 重力 P mg ,
二 弹性力
4
引力常量
G 6 . 67 10
11
N m kg
2
2
g
Gm R
2
E
9 . 80 m s
-2
(压力,张力,弹簧弹性力等) 弹簧弹性力
f kx
I I xi I y j I zk
t1 t2
t1
7
二 质点系的动量定理 t2 ( F1 F12 ) d t m 1 v 1 m 1 v 10
质点系
F1
F12
m1
因为内力 F12 F 21 0 ,故
t1 t2
18
例 2 一质量为1.0kg 的小球系在长为1.0m 细绳下 端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖直 线成 30 角处, 然后放手使小球沿圆弧下落 . 试求绳与 竖直线成 10 角时小球的速率 .
解 d W F d s FT d s P d s P d s mgl d cos
在 p 一定时
mv
m v1
F
mv2
F
Fm
F
t 越小,则 F 越大 .
例如人从高处跳下、飞 机与鸟相撞、打桩等碰 撞事件中,作用时间很 短,冲力很大 .
o
t
t1
t2
t1
6
t2
t1
F d t p 2 p1 m v 2 m v1
动量定理 在给定的时间内,外力作用在质点 上的冲量,等于质点在此时间内动量的增量 . 分量形式
Ix Iy Iz
t2
t1 t2
F x d t m v 2 x m v1 x F y d t m v 2 y m v1 y F z d t m v 2 z m v1 z
yv d yv
1 3
gy
3
1
g y d y
2 0
y
yv
0
yv d yv
2 2 v gy 3
yv
1 2
2
第三节
一 功
功 动能
13
力对质点所作的功为力在质点位移方向的分量与 位移大小的乘积 . (功是标量,过程量) d W F cos d r F cos d s d ri B * i dW F dr 0 90 , d W 0 dr Fi 90 180 , d W 0 1 F d r1 * A F1 90 F d r d W 0
t1
( F 2 F 21 ) d t m 2 v 2 m 2 v 20
F 21
F2
m2
t2
t1
( F1 F 2 ) d t ( m 1 v 1 m 2 v 2 ) ( m 1 v 10 m 2 v 20 )
质点系动量定理 作用于系统的合外力的冲量等于 系统动量的增量. n n t2 ex F dt mi vi mi vi0 I p p0
dr dxi dyj dzk
r
rB
W
F
x
dx
F
y
dy
F
z
dz
W Wx Wy Wz
15
功的大小与参照系有关
功的量纲和单位 dim W ML T
平均功率
P W t
2
2
1J 1 N m
瞬时功率
P lim
W t
t 0
W
Ft d s
1 2
1 2
Ft m
mv
2 2
dv dt
m v1
2
v2
v1
m
dv dt
ds
v2
v1
m vdv
Ek
1 2
p
2
动能(状态函数)
mv
2
动能定理 合外力对质点所作的功, 等于质点动能的增量 . 注意
2m
W E k2 E k1
功和动能都与 参考系有关;动能定理 仅适用于惯性系 .
22
2 ) 重力作功
P mg k dr dxi dyj dzk
W
z
zA
A
B A
P dr
B
zB
mg d z
A
zA
zB
mg
B
( mgz
W
mgz
)
o
y
x
mg d z 0
23
3 ) 弹性力作功
F
x
o
xA xB
O
则 F
ex
m 1 g yg
ex
m1
y
由质点系动量定理得
F
dt dp
y
12
F
又
ex
dt dp d p d( y v )
d yv dt
m2
O
yg d t d( y v )
则
yg
m1
y
y
两边同乘以 y d y 则
y gdy ydy
2
d yv dt
变力的功
W
dW F dr
14
F cos
B A
F dr
B A
F cos d r
o r dr 合力的功 = 分力的功的代数和 A W Fi d r Fi d r W i i F Fx i F y j Fz k
t1 i 1 i 1
8
注意
内力不改变质点系的动量
初始速度
v g 0 v b0 0
m b 2m g
则 则
Байду номын сангаас
推开后速度 v g 2 v b
且方向相反
推开前后系统动量不变
p p0
p0 0 p 0
9
动量定理常应用于碰撞问题 t2 Fdt t1 m v 2 m v1 F t 2 t1 t 2 t1 注意
三
摩擦力 滑动摩擦力 F滑 F N 静摩擦力 一般情况
F滑 F静
F静 0 F N
0
第二节 动量 一 冲量 质点的动量定理 动量
5
p mv
冲量 力对时间的积分(矢量) I
t2
Fdt
dp d (m v) F Fdt dp d (m v) dt dt t2 F d t p 2 p1 m v 2 m v1
0
d
mgl sin d
W mgl
0
sin d
v
FT
l
ds
mgl (cos cos 0 )
P
19
m 1 . 0 kg
l 1 .0 m
10
0 30
0
W mgl (cos cos 0 )
B
m
m'
O
A
r (t )
ds
r d s r d s cos r d r
W
r (t d t )
rA G
rB
m'm r
2
dr
r (t )
dr
B
ds
m'm m'm W (G ) (G ) rB rA
r (t d t )
W ( mgz
B
mgz
2
A
)
2
弹力功
W (
1 2
kx B
1 2
A
C
kx A )
D
F dr
ACB
F dr
ADB
B
25
l
F dr
ACB
F dr
ADB
A
C
F dr
F dr
ACB
F dr
m ' 对 m 的万有引力为
m'm F G r 3 r
m
m'
O
A
r (t )
ds
m 由 A 点移动到 B 点时 F 作功为
W
r (t d t )
F ds
m'm A G r 3 r d s
B
B
21
W
F ds
m'm A G r 3 r d s
Fx t mv2 x mv1x mv cos (mv cos )
x
m v1
2mv cos Fy t mv2 y mv1 y
mv2
y mv sin α mv sin 0 2mv cos F Fx 14.1 N 方向沿 x 轴反向 t
T' T m
P P'
m
地球
几种常见的力: 一 万有引力 m1m 2 F G 2 r 重力 P mg ,
二 弹性力
4
引力常量
G 6 . 67 10
11
N m kg
2
2
g
Gm R
2
E
9 . 80 m s
-2
(压力,张力,弹簧弹性力等) 弹簧弹性力
f kx
I I xi I y j I zk
t1 t2
t1
7
二 质点系的动量定理 t2 ( F1 F12 ) d t m 1 v 1 m 1 v 10
质点系
F1
F12
m1
因为内力 F12 F 21 0 ,故
t1 t2
18
例 2 一质量为1.0kg 的小球系在长为1.0m 细绳下 端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖直 线成 30 角处, 然后放手使小球沿圆弧下落 . 试求绳与 竖直线成 10 角时小球的速率 .
解 d W F d s FT d s P d s P d s mgl d cos
在 p 一定时
mv
m v1
F
mv2
F
Fm
F
t 越小,则 F 越大 .
例如人从高处跳下、飞 机与鸟相撞、打桩等碰 撞事件中,作用时间很 短,冲力很大 .
o
t
t1
t2
