第2章(3) 系统传递函数
第2章 2.3传递函数

i =1 i =1 l 1 ( m−l ) 2
G(s ) =
(
)
∏ (T s +1) ∏ (T
h j j =1 j =1
1 ( n −h ) 2
2 2 j
s + 2ξ jT j s + 1
)
注意!
K 传递系数或 静态增益,常 数项归一
C (s) (s G( s ) = R(s)
C(s) b0 s + b1s + ⋯ + bm−1s + bm = n n −1 R(s) a0 s + a1s + ⋯ + an−1s + an
m
m−1
2.3传递函数
一 定义与性质 [性质] (1)传递函数的概念只适用于线性定常 系统,它是在零初始条件下定义的。 (2)传递函数是复变量 S 的有理分式函 数,即: ≥ m;各系数均为实数。 n 是系统元件参 数的函数 物理系统的固有特性是因果性;若m>n, 则这是物理不可实现的系统。
C (s) 1 = 2 2 传递函数: G ( s ) = R ( s ) T s + 2ξ Ts + 1
ω n2 1/T 2 = = 2 2ξ 1 s + 2ξω n s + ω n2 2 s + s+ 2 T T
R(s)
ωn :无阻尼 无阻尼
ζ :阻尼比
22
1 T 2 s 2 + 2ξ Ts + 1
振荡环节方框图
C(s)
自然振荡频率
2.3传递函数
《自动控制原理》第2章 线性系统的传递函数

+
anc(t)
=
b0
dm dtm
r(t)
+
b1
d m−1 d t m −1
r(t)
++
bm−1
d dt
r(t)
+
bmr(t)
(m n)
设r(t), c(t)及各阶导数在t=0时的值均为零(零初始条件), 则对方程两端求拉氏变换,可得系统的传递函数
Ch2 控制系统的数学模型
◼ 传递函数的一般形式:
Ch2 控制系统的数学模型
第二章 控制系统的数学模型
Ch2 控制系统的数学模型
本章内容
❖ 引言 ❖ 物理系统的微分方程 ❖ 拉氏变换与拉氏反变换 ❖ 线性系统的传递函数 ❖ 方框图及其等效变换 ❖ 信号流图与Mason公式*
Ch2 控制系统的数学模型
2.3 线性系统的传递函数
一. 传递函数的定义
Ux(s) =
I
(s) − I2(s) sC1
(2)
I 2 (s)
=
Ux
(s) −Uo(s) R2
(3)
U o (s)
=
I 2 (s) sC2
(4)
Ch2 控制系统的数学模型
I (s) = Ui (s) −U x (s) (1) R1
Ui _
I
1/R1
Ux
Ux(s) =
I
(s) − I2(s) sC1
Uo (s)
Ui (s) (b)
I(s) Uo (s)
Ch2 控制系统的数学模型
I(s)
(c)
Uo (s)
Ui (s)
I(s)
- Uo (s) (d)
第二章习题解答

第二章2-3 设系统传递函数为342)(2++=s s s G 初始条件0/)0(,1)0(=-=dt dc c 。
求单位阶跃输入r (t)=1(t)时,系统的输出响应c (t)。
【解】系统传递函数与微分方程是一一对应的,故通过传递函数先求出微分方程,然后通过拉氏变换的方法求解微分方程。
系统对应的微分方程为 4()3()2()c c t c t r t ++= 在给定的非零初始条件下,进行拉氏变换22(43)()(0)(0)4(0)s s C s sc c c s++---=整理后2221()(43)(43)s C s s s s s s +=-++++部分分式展开后,拉氏反变换111223242/35/25/6()[()][][](43)(43)13255326t t s c t L C s L L s s s s s s s s e e -----+==-=-+++++++=-+2-4 在图2-48中,已知G (s) 和H (s)两方框对应的微分方程分别为()2()5()4()3()6()c t c t e t b t b t c t +=+=图2-48 习题2-4系统结构框图且初始条件为零,试求传递函数C (s)/R (s)。
【解】求出每个方框的传递函数,利用反馈等效的方法求C(s)/R(s)。
根据定义可得 5()2G s s =+,6()43H s s =+ 255()5()25(43)10075(2)56()1()()(2)(43)30411361(2)(43)C s G s s s s R s G s H s s s s s s s +++====+++++++++2-5 图2-49是由电阻、电容和运算法放大器组成的无源网络和有源网络,试列写以V in (t)为输入量,V out (t)为输出量的传递函数。
(a) (b )(c) (d)图2-49 习题2-5电路图【解】(a) 1211211,1RZ R Z C s RC s C s===+ 22112121211()1()11Z C s RC s G s R Z Z R C C s RC s C s +===+++++(b ) 21122211R Z R Z R Cs R Cs ===+ 2222111211()1R Z R Cs R G s Z R R R Cs +=-==-+ (c) 32321123232321()(1)1()1()1R R R R Cs Cs Z R Z R R Cs R R Cs R R Cs++==+==++++ 323232211132(1)()11()()1R R Cs R R Cs R Z R Cs G s Z R R R R Cs ++++=-=-=-++ (d)本题和(b)、(c)做法图通,因为反馈通路有接地的部分。
自动控制原理课后习题答案第二章

第 二 章2-3试证明图2-5(a)的电网络与(b)的机械系统有相同的数学模型。
分析 首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找出两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列出系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析,可得:o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得:2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出,电网络(a )和机械系统(b )两者参数的相似关系为1112221211,,,K f R K f R C C2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) ;)()(2t t x t x =+(2))。
控制工程基础第2章答案
第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
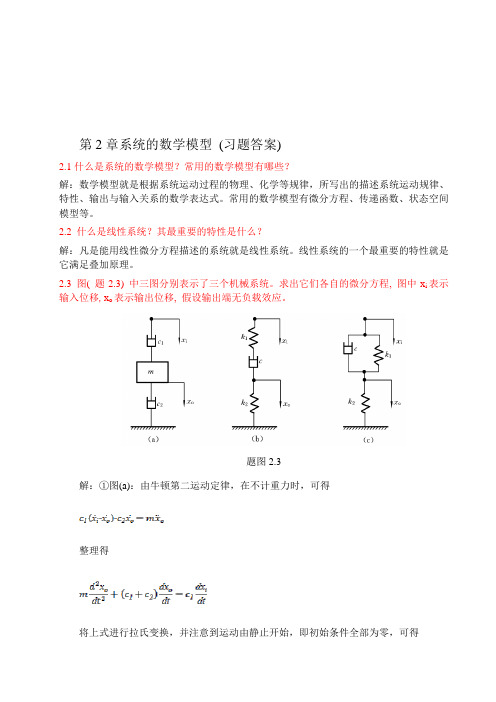
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
控制工程基础第2章答案
第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
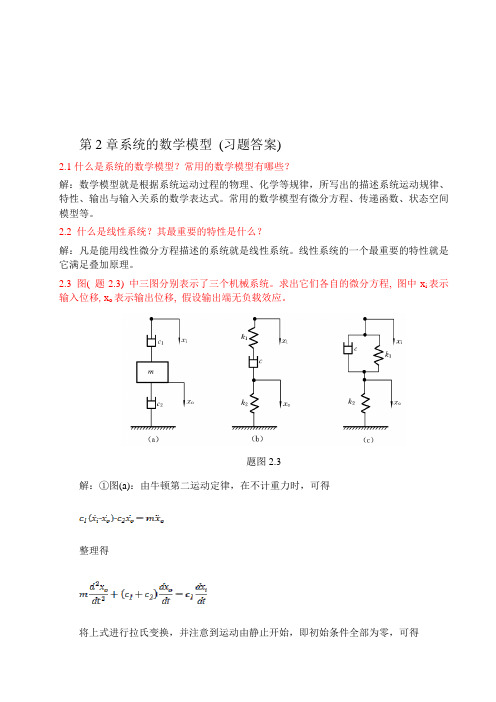
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-C)(t u r )(t u c )(t r )(t x c f1k 2k CR)(t u r )(u c +-+-f)(t r )(t x c )(a )(b )(c )(d R 2R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
第二章-3-系统传递函数的计算-非线性系统线性化

(a)原始结构图 (b) 等效结构图 图(3) 引出点后移的变换
挪动后的支路上的信号为:
R
1 G(s) R R G(s)
15
系统传递函数的计算
综合点与引出点的移动:
d. 相邻引出点之间的移动
若干个引出点相邻,引出点之间相互交换位置,完全不会改 变引出信号的性质。如图(4)所示。
图(4) 相邻引出点的移动
自动控制理论 自动控制
第二章 连续时间控制系统的数学模型
周立芳 徐正国
浙江大学控制科学与工程学系
第 章要点 第二章要点
引言 电路及组成 线性代数与状态的基本概念 传递函数及方块图 机械传递系统 其他的数学建模实例 系统传递函数的计算 非线性系统的线性化 系统整体传递函数的确定 仿真图 信号流图 从传 函数到状 从传递函数到状态空间模型的转换 间模 的转换
信息不变原理:变换前后信息不改变 E1=u+H2y;
H1 (s) H 2 (s) 1 G (s) H 2 (s) 1 H 1 (s) H 2 (s)
E2={u(1/H2)+y}H2=u+H2y
10
系统传递函数的计算
方块图简化
u1 u2
引出点
y
引出点后移
u1
H (s)
??
y
H (s)
1 R1C1s 1 GLOOP1 ( s ) 1 1 R1C1s 1 R1C1s
1 R2C2 s 1 GLOOP 2 ( s) 1 1 R2C2 s 1 R2C2 s
29
系统传递函数的计算
系统传递函数
例4: 推导如下图所示系统的传递函数
朱玉华自动控制原理第2章 数学模型2-3

G(s) C(s) ……① R(s)
若已知线性定常系统的微分方程为
a0
d nc(t) dt n
a1
d n1c(t) dt n1
an1
dc(t) dt
anc(t)
b0
d mr(t) dt m
b1
d m1r(t) dt m1
bm1
dr(t) dt
bmr(t)
式中,c(t)为输出量,r(t)为输入量。
§2.3 传 递 函 数
一、传递函数的基本概念
指导思想:在零初始条件下,通过拉氏变换,将微分 方程变为s域(复数域)内的代数方程,在s 域内研究系统 的运动规律。必要时,通过拉氏反变换转化为时域形式。
s域(复数域)内的代数方程(即数学模型),称为 传递函数。
1、传递函数的定义
在初始条件为零时,线性定常系统输出量的拉氏变换与 输入量的拉氏变换之比,定义为该系统的传递函数。
RC
du0 (t) dt
u0 (t)
RC
dui (t) dt
G(s) RCs Td s RCs 1 Td s 1
只有当Td<<1时,才有G(s)≈Tds,实际的微分环节趋 于理想微分环节
再如:RL网络,其电路方程为
du0 (t) dt
R L
u0 (t)
dui (t) dt
G(s) Ls Td s Ls 1 Td s 1
如
G(s)
C(s) R(s)
b1s a0s2
b2 a1s
a2
S的代数方程:
(a0s2 a1s a2 )C(s) (b1s b2 )R(s)
用 d 置换s后得相应的微分方程 dt
a0
d 2c(t) dt 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c1s c2 s ( 1)( 1) k1 k2 G( s ) c1s c2 s c1s ( 1)( 1) k1 k2 k2 1 对比:R1 c1 R2 c2 C1 k1
1 C2 k2
三、传递函数的表达形式
1.多项式分式形式 X o ( s ) bm s m b1s b0 G( s) X i ( s ) an s n a1s a0 2.零极点增益形式 分子、分母首一化,再分解因式
0
特点: (1)一般不能单独存 在; (2)反映输入的变化 趋势; (3)增加系统阻尼; (4)强化噪声。
iC du i (t ) dt
du i (t ) uo (t ) Ri RC dt U o ( s) G( s) RCs U i ( s)
4.惯性环节 微分方程: Tx o (t ) xo (t ) xi (t )
2
特征量——
时间常数: T
固有振荡频率: n 1T
阻尼比:
0 1 : 欠阻尼(振荡) 1: 临界阻尼 1 : 过阻尼
时间响应:
单位阶跃响应 欠阻尼 1 过阻尼 临界阻尼 t 0
例10:
特点: (1)0<ξ<1,输出存在 振荡,ξ越小,振荡越 剧烈 ; (2)ξ>1,输出无振荡, 由两一阶惯性环节组成。
例:求传递函数
k2 c1 k1
c2
xi
xo
k2
A
c2 c1
B
xi
xo
x2
k1
二、相似性原理 相似系统: 能用形式相同的数学模型来描述的两个系统; 相似量: 在微分方程或在传递函数中占有相同 位置的物理量。
ui (i2 i1 )R1 uo
1 (i2 i1 ) R1 i1dt C1 1 uo i2 R2 i2 dt C2
(3)一切物理系统都有n≥m 3.传递函数的物理意义 传递函数是系统单位脉冲响应的象函数
xi (t ) (t ) , X i (s) 1
X o ( s) G( s) X i ( s) G( s)
1 1
xo (t ) L1 [ X o ( s)] L1[G( s)] w(t ) G( s ) L[ w(t )]
实例:齿轮传动副 比例运算放大器
X o ( s) z1 G( s) K X i ( s) z2
ui(t) R1 ∑
xo(t) z2
uo(t)
R2 R2 u o (t ) u i (t ) G ( s ) K R1 R1
1 微分方程: xo (t ) xi (t )dt T X o ( s) 1 传递函数:
§2.2 系统的传递函数
一、传递函数
( n) ( n 1) an xo (t ) an1 xo (t ) a1 x o (t ) a0 xo (t )
( m) ( m1) bm xi (t ) bm1xi (t ) b1x i (t ) b0 xi (t )
K bm / a n 系统增益 零极点增益形式:
N ( s) ( s z1 )( s z2 )( s zm ) G( s ) K K D( s ) ( s p1 )( s p2 )( s pn )
K
( s zi ) (s p j )
j 1 i 1 n
m
( n m)
零点: s=-zi(i=1,2,…m) 极点: s=-zj(j=1,2,…n)
3.典型环节形式 分子、分母“末1化”,再分解因式
G( s) K (1s 1) s(T1s 1)(T 2 s 2 2Ts 1)
4.传递函数相互转换的MATLAB命令 (1)多项式形式的表达 num=[bm bm-1 … b1 b0]; den=[an an-1 … a1 a0]; g=tf(num,den) (2)零极点形式的表达 Z=[z1;z2];P=[p1;p2+j*p3; p2-j*p3];K=k; d=zpk(Z,P,K) (3)多项式与零极点形式的转换 [Z,P,K]=tf2zp(num,den) [num,den]=zp2tf(Z,P,K)
(t)
t
0 t
6.振荡环节
2 T x o (t ) 2Tx o (t ) xo (t ) xi (t ) 微分方程:
x o (t ) 2n x o (t ) n xo (t ) n xi (t )
2 2
传递函数:
n 1 G ( s) 2 2 2 T s 2Ts 1 s 2 n s n 2
U o ( s) 1 U i (s) LCs 2 L s 1 R
7.延迟环节
微 分 方 程 : x o (t ) x i (t )
X i ( s)e s 传递函数:G( s) e s X i ( s)
( L [ f (t )] F ( s)e s )
例 4:
U o ( s) RCs Ts G( s) U i (s) 1 RCs Ts 1
5.一阶超前环节 (一阶微分环节)
i (t ) xi (t ) xo (t ) 微分方程: Tx
传递函数: G( s) Ts 1 时间响应:
单位阶跃响应 1 0
单位斜坡响应 t
特点:输出滞后于输入,但不失真。
G( s)
2.积分环节
Xi ( s)
1 Ts
Xo ( s)
时间响应:
X i ( s)
Ts
T >1
单位脉冲响应 T 1 T` > 1 1 0 图 2.6.7 t
单位阶跃响应
特点: (1)输出累加; (2)输出滞后; (3)记忆功能。
t
例 8:
0
积分 环节的时间响应
ui (t ) du o (t ) C R dt
k2 ( xi xo ) c2 ( x i x o ) c1 ( x o x 2 ) k1 x2 k2 ( X i ( s) X o ( s)) c2 s( X i ( s) X o ( s)) c1s( X o ( s ) X 2 ( s )) k1 X 2 ( s ) c1sX o ( s ) X 2 ( s) c1s k1 X o ( s) (c1s k1 )(c2 s k2 ) G( s ) X i ( s ) (c1s k1 )(c2 s k2 ) c1k1s c1s c2 s ( 1)( 1) k1 k2 c1s c2 s c1s ( 1)( 1) k1 k2 k2
例:
dxo (t ) T xo (t ) kxi (t ) dt
L: TsX o ( s ) X o ( s) kX i ( s )
(Ts 1) X o ( s ) kX i ( s )
X o ( s) k G( s) X i ( s) Ts 1
2.讨论 (1)传递函数的分母是系统特征多项式,分子 反映系统与外界的关系。 G(s) Xi (s) X (2) X o (s) G(s) X i (s) o( s) 时域函数 xo (t ) L [ X o (s)] L [G(s) X i (s)]
传递函数: G ( s )
时间响应: 例 3:
ui i R
1 0.632 0 T
1 Ts 1
0.98 4T t 4T 3T 0 误差 T
4T t
特点: (1)存在储能元 件和耗能元件; (2)在阶跃输入 下,输出不能立 即达到稳态值。
C uo
1 ui (t ) idt iR C u o (t ) iR
k2 c1 k1 c2 xi
i2 i1
C1 R1
i2
xo
ui
C2 R2
uo
先做L变换,再消去I1(s)、I2(s)
U o ( s) ( R1C1s 1) ( R1C1s 1)( R2C2 s 1) R1C2 s
常用机电相似系统:力—电压相似系统, 力—电流相似系统
U o ( s) 1 G( s) U i ( s) RCs
3.微分环节
i ( t ) 微分方程: xo (t ) Tx
Xi ( s)
Ts
Xo ( s)
X o ( s) Ts 传递函数:G( s) X i ( s)
时间响应: 例 5:
(t) >1 1 0
t
>1 t
(n m) 作拉氏变换(在零初始条件下) n m (an s a1s a0 ) X o ( s) (bm s b1s b0 ) X i ( s) (n m) 1.定义:
m b s b1s b0 (n m) L[ xo (t )] X o ( s) m G( s) n a s a1s a0 L[ xi (t )] X i ( s) n
diL (t ) ui (t ) L uo (t ) dt 1 uo (t ) RiR (t ) iC (t ) dt C
iL (t ) iR (t ) iC (t )
LCuo (t ) L uo (t ) uo (t ) ui (t ) R
G( s)
四、典型环节
典型环节的微分方程、传递函数
微分方程:xo (t ) Kxi (t ) ;
传递函数: G( s) K
Xi ( s ) K
1.比例环节
Xo( s )
时间响应: K
1 0
K >1 t 0
K >1 t
