第2章 随机变量及其分布PPT课件
合集下载
概率论课件第二章
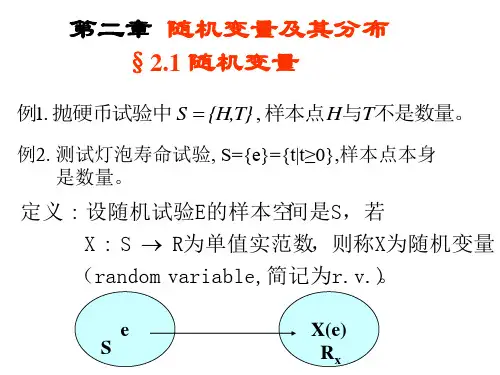
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
《概率论与数理统计》课件-第2章随机变量及其分布 (1)
则称X服从参数为λ的泊松分布, 记为 X ~ P() .
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数， 原子放射的粒子数，保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义： 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数， 原子放射的粒子数，保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义： 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
概率论与数理统计课件第2章
X0
1
pk 03.5
0.25
4
625
0.0625
X的分布函数为
2 0.125
0
x0
0.5
0 x1
F
(
x)
0.75 0.875
1 x 2 2 x3
0.9375 3 x 4
Байду номын сангаас
1
x4
0.0
分布函数 是累计概率
例3 有人对随机变量X的分布列表述如下:
X -1
0 12 3
P
a 0.16
a2 2a 0.3
第2章 随机变量及其分布
2.1 随机变量及其分布函数 2.2 离散型随机变量及其分布律 2.3 几种常见的离散型分布 2.4 连续型随机变量及其密度函数 2.5 正态分布 2.6 随机变量函数及其分布
2.1 随机变量及其分布函数
一、随机变量 二、随机变量的分布函数
信息管理学院 徐晔
一、随机变量
例
包含出现1点
包含出现1,2点
包含出现1,2,3点
包含出现1,2,3,4 点 包含出现1,2,3,4,5 点包含出现1,2,3,4,5,6 点
分布函数的性质
F(x) P(X x), （ x ）
(1) F x 在 , 上是一个不减函数 ,
即对 x1 , x2 , 且 x1 x2 ,都有 F x1 F x2 ;
样本点
1， 4， 5 2， 3， 4 2， 3， 5 2， 4， 5 3， 4， 5
黑球数 X
1 2 2 1 1
由上表可以看出，该随机试验的每一个结果都对应
着变量 X 的一个确定的取值，因此变量 X 是样本空
间Ω上的函数：
概率论与数理统计图文课件最新版-第2章-随机变量及其分布
一. 连续型随机变量的概率密度 1.定义 若对于随机变量 X 的分布函数，存在非负
函数 f ( x)，使得对于任意实数 x 有:
x
F ( x) f (t)dt ( P( X x))
则称 X 为连续型变量，f ( x)为 X 的概率密度函数 注 ▲ 连续型随机变量与离散型随机变量的区别
离散型： P( X xk ) 0 连续型：P( X xk ) 0
机
多，而且还不能一 一列
变 连续型随机变量 量
举，而是充满一个区间
例如，“电视机的寿命”，实际中
常 遇到的“测量误差”等等.
概率统计
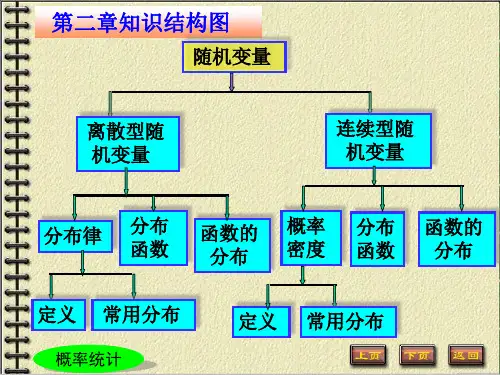
第二章知识结构图
随机变量
离散型随 机变量
连续型随 机变量
分布律
分布 函数
函数的 分布
概率 密度
分布 函数
函数的 分布
定义 常用分布
概率统计
定义 常用分布
第四节 连续型随机变量及其概率密度
0 x 0
则称 X 为服从参数 的指数分布.
概率统计
二 . 连续型随机变量的分布函数
定义: 若定义在 (, )上的可积函数 f ( x)
满足： (1). f ( x) 0
(2). f ( x)dx 1
f (x)确定了 分布函数F(x)，
则称 F ( x)
x
f ( x)dx
f (x)是F(x)的 导函数， F(x)是f (x)的一
(2) 某段时间内候车室的旅客数目为 X , 则它也是一个随机变量，它可以取 0 及一切 自然数。X 是定义在样本空间，则：
S e {人数 人数 0}
X X (e)的值域RX [0, )
概率统计
二. 随机变量的分类 离散型随机变量
函数 f ( x)，使得对于任意实数 x 有:
x
F ( x) f (t)dt ( P( X x))
则称 X 为连续型变量，f ( x)为 X 的概率密度函数 注 ▲ 连续型随机变量与离散型随机变量的区别
离散型： P( X xk ) 0 连续型：P( X xk ) 0
机
多，而且还不能一 一列
变 连续型随机变量 量
举，而是充满一个区间
例如，“电视机的寿命”，实际中
常 遇到的“测量误差”等等.
概率统计
第二章知识结构图
随机变量
离散型随 机变量
连续型随 机变量
分布律
分布 函数
函数的 分布
概率 密度
分布 函数
函数的 分布
定义 常用分布
概率统计
定义 常用分布
第四节 连续型随机变量及其概率密度
0 x 0
则称 X 为服从参数 的指数分布.
概率统计
二 . 连续型随机变量的分布函数
定义: 若定义在 (, )上的可积函数 f ( x)
满足： (1). f ( x) 0
(2). f ( x)dx 1
f (x)确定了 分布函数F(x)，
则称 F ( x)
x
f ( x)dx
f (x)是F(x)的 导函数， F(x)是f (x)的一
(2) 某段时间内候车室的旅客数目为 X , 则它也是一个随机变量，它可以取 0 及一切 自然数。X 是定义在样本空间，则：
S e {人数 人数 0}
X X (e)的值域RX [0, )
概率统计
二. 随机变量的分类 离散型随机变量
概率论与数理统计 第二章 随机变量及其分布
解：
6 6 X ~ ( ), 且 P X 0 e 即 e e 6
P { X 2 } 1 P { X 2 } 1 P { X 0 } P { X 1 }
6 6 1 e 6 e 0 . 9826
A={X=1}，B={X=2}，C={X=0}
② 设Y为进行5次试验中成功的次数，则 D={Y=1}，F={Y1},G={Y3}
随机变量的分类
离散型随机变量 随机变量 连续型 非离散型 奇异型（混合型）
§2 离散型随机变量的分布律(P27)
定义 若随机变量X取值x1, x2, …, xn, … ，且取这些 值的概率依次为p1, p2, …, pn, …, 则称 P{X=xk}=pk, (k=1, 2, … ) 为X的分布律。 可表为 X～ P{X=xk}=pk, (k=1, 2, … )， 或…
k k n
k 0 , 1 , , n
若以X表示n重贝努里试验中事件A发生的次数， P(A)=p, 则称X服从参数为n,p的二项分布。 记作X~b(n,p), 其分布律为：
P { X k } p ( 1 p ), ( k 0 , 1 ... n ) C n
kk
n k
例2 掷一颗骰子10次，求（1）双数点出现6次的概率？ （2）“3”点出现两次的概率？ 解：(1)设X表出现双数点的次数，则X~b(10，1/2） 6 6 10 6 6 10 1 1 1 所求概率： P ( X 6 ) C ( ) ( ) C ( ) 10 10 2 2 2 (2) 设Y表出现“3”点的次数，则Y~b(10，1/6） 2 1258 所求概率为： P ( Y 2 ) C () () 10
6 6 X ~ ( ), 且 P X 0 e 即 e e 6
P { X 2 } 1 P { X 2 } 1 P { X 0 } P { X 1 }
6 6 1 e 6 e 0 . 9826
A={X=1}，B={X=2}，C={X=0}
② 设Y为进行5次试验中成功的次数，则 D={Y=1}，F={Y1},G={Y3}
随机变量的分类
离散型随机变量 随机变量 连续型 非离散型 奇异型（混合型）
§2 离散型随机变量的分布律(P27)
定义 若随机变量X取值x1, x2, …, xn, … ，且取这些 值的概率依次为p1, p2, …, pn, …, 则称 P{X=xk}=pk, (k=1, 2, … ) 为X的分布律。 可表为 X～ P{X=xk}=pk, (k=1, 2, … )， 或…
k k n
k 0 , 1 , , n
若以X表示n重贝努里试验中事件A发生的次数， P(A)=p, 则称X服从参数为n,p的二项分布。 记作X~b(n,p), 其分布律为：
P { X k } p ( 1 p ), ( k 0 , 1 ... n ) C n
kk
n k
例2 掷一颗骰子10次，求（1）双数点出现6次的概率？ （2）“3”点出现两次的概率？ 解：(1)设X表出现双数点的次数，则X~b(10，1/2） 6 6 10 6 6 10 1 1 1 所求概率： P ( X 6 ) C ( ) ( ) C ( ) 10 10 2 2 2 (2) 设Y表出现“3”点的次数，则Y~b(10，1/6） 2 1258 所求概率为： P ( Y 2 ) C () () 10
“随机变量及其分布”简介PPT优秀课件
6. 教材内容的变化与特点
a. 知识的引入的变化: • 注重利用学生熟悉的实例和具体情景，以 引发学生的学习兴趣； • 通过思考或探究栏目提出问题，以调动学 生解决问题的积极性。 b. 具体内容的变化： • 以取有限值的离散型随机变量为载体； • 增加了超几何分布。 c. 知识的应用 • 体现概率统计的应用价值； • 利用思考、探究等栏目提高学生解决实际 问题能力。
发展要求
了解两点分布、二项分布的方差的计算公式。
§2.4正态分布
基本要求
1、初步了解正态分布的意义。 2、初步了解正态曲线的性质。 3、初步了解参数 、 对正态曲线的影响。
3. 课时分配与知识框图
随机变量及其分布 （16学时）
离 散 型 ︵随 3 机 变 课量 时及 ︶其 分 布 列
独立性的应用
例2.3 某商场推出二次开奖活动，凡购买一定价值 的商品可以获得一张奖券．奖券上有一个兑 奖号码，可以分别参加两次抽奖方式相同的 兑奖活动．如果两次兑奖活动的中奖概率都 是0．05，求 （1）两次抽奖都抽到某一指定号码的概率； （ 2 ）两次抽奖恰有一次抽到某一指定号码 的概率； （ 3 ）两次抽奖至少有一次抽到某一指定号 码的概率． 思考：二次开奖至少中一次奖的概率是不是一次 开奖中奖概率的两倍？为什么？
4．对教学安排的说明
(4)为了使学生更容易理解二项分布的产生背景,教 材通过简单实例的讨论,向学生展示从独立重复 试验到二项分布的推导过程. (5)对于离散型随机变量的均值与方差的含义及其 计算公式,重点是概念的理解,这也是难点.因此 教材中借助于很简单的离散型随机变量来介绍 均值与方差的概念，以避免复杂的计算冲淡概 念的理解. (6)关于正态分布模型，仅需学生了解正态分布密 度曲线的特征，密度曲线与相应的随机变量落 在某个区间的概率之间的关系,参数 和 的 含义,以及3 准则.
随机变量及分布PPT课件
P( y X y ) FX ( y ) FX ( y )
fY
(
y
)
dFY ( dy
y
)
1
2
y
0,
fX
(
y ) fX(
y ) , y 0 y0
y 1
fX (
y
)
2
0
y 1
0
y 1
fX (
y
)
2
1 y 0
其它
0
其它
则 Y=X2 的概率密度为：
1
fY
(
y)
2
( y
0
y 1 2
U 的概率密度
P{ X
u 1} 3
FX
{
u
3
1)
fU (u)
dFU (u) du
f
X
(
u
3
1
)
(
u
3
1
)u
fU
(u)
2.
u
3
1
.
1 3
0
即
fU
(u)
2 9
(u
1)
0
0 u1 1 3
其它
1 u 2 其它
例4(P62-例3) 设随机变量X的概率密度为fX(x)(x R),求:
z0
0
z0
（3）备用方式： 系统L的寿命 Z=X+Y
fZ (z) fX ( x) fY (z x)dx
积分区域
z
x
x
0
0
即0 x z
fZ (z)
z e x e (zx)dx e z
0
z e( ) xdx
《概率论与数理统计教程》课件
2-7
随机变量的分类
仅可能取得有限个或 可数无穷多个数值
离散型随机变量 随机变量 连续型随机变量
2-8
§2.2 离散随机变量
一. 概率分布
二. 概率函数及其性质 三. 几何分布 四. 频率分布表
2-9
概率分布
定义 随机变量X一切可能值为x1, x2, ... , xn, ... , 而取 得这些值的概率分别为p(x1), p(x2), ... , p(xn) , ... , 称为离散型随机变量的概率分布或分布律。 可以列出概率分布表如下：
1. 当一批产品总数 N很大，而抽取样品的个 数 n 远小于 N 时，可用二项分布来近似地 计算超几何分布的概率，即 m n m C M C N M M m m n m Cn p q , p n N CN
2. 实际应用中，当n/N10%时，不放回抽样（样品 中的次品数服从超几何分布）与放回抽样（样品 中的次品数服从二项分布）区别不大。
2 - 13
课堂练习
1. P{ X i } 2a i ,i 1,2 , , 求常数a. 2. 下面给出的数列能否成为某一随机变量的 分布列: 0.1,0.2,0.3,0.4.
3. 设随机变量X的概率分布为
X P 0 1/8 1 3/8 2 3/8 3 a
求:(1)a的值; (2)P(X≤1); (3)P(1≤X<3) 4. 某射手在相同条件下独立地进行5次射击,每 次击中目标的概率是0.6,求击中目标次数X的概 2 - 14 率分布.
P(X=n)=qn-1p, (n=1,2,...)
几何分布
2 - 15
频率分布表
频率分布表
X
f n ( xi )
x1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.16
例2.1.3
已知 X 的分布函数如下,求 X 的分布列.
0,
F
(x)
0.4, 0.8,
1,
x0 0 x1 1 x2 2 x
解：
X0 1 2 P 0.4 0.4 0.2
2.17
2.1.4 连续随机变量的密度函数
➢ 连续随机变量X的可能取值充满某个区间 (a, b). ➢ 因为对连续随机变量X，有P(X=x)=0，
(2) pi 1. (正则性)
i
2.11
注 意 点 (1)
求离散随机变量的分布列应注意： (1) 确定随机变量的所有可能取值; (2) 计算每个取值点的概率.
2.12
例2.1.1 从1～10这10个数字中随机取出5个数字，令
X：取出的5个数字中的最大值． 试求 X 的分布列．
解：X 的取值为5，6，7，8，9，10．
所以无法仿离散随机变量用 P(X=x) 来描述连续 随机变量X的分布.
➢ 注意离散随机变量与连续随机变量的差别.
2.18
定义2.1.4
设随机变量X 的分布函数为F(x),
若存在非负可积函数 p(x) ，满足：
F
(
x
)
x
p
(t
)dt
则称 X 为连续随机变量，
称 p(x)为概率密度函数，简称密度函数.
注意点
(3) 注意以下一些表达式： {X = k}= {X k}{X < k}； {a < X b} = {X b}{X a}； { X > b} = {X b}.
(4) 同一样本空间可以定义不同的随机变量.
2.5
实例
掷一枚骰子，令X ={出现的点数},则X 就是一个随机 变量,它的取值为1，2，3，4，5，6．
PX k C k 4 1C 1 5 0 k 5 ， 6 ， L ， 1 0
具体写出，即可得 X 的分布列：
X 5 6 7 8 9 10
P1
5
15 35 70 126
252 252 252 252 252 252
精选
13
2.13
例2.1.2 已知 X 的分布列如下：
X0 1 2 P 1/3 1/6 1/2
➢ 前例中的 X, Y, Z 为离散随机变量； 而 T 为连续随机变量.
2.7
2.1.2 随机变量的分布函数
定义2.1.2 设X为一个随机变量，对任意实数 x，
称 F(x)=P( X x) 为 X 的分布函数.
基本性质：
(1) F(x) 单调不降； (2) 有界：0F(x)1，F()=0，F(+)=1； (3) 右连续.
ቤተ መጻሕፍቲ ባይዱ2.8
用分布函数表示事件的概率
对 任 意 实 数 a与 b,有 P (a X b) F (b) F (a), P ( X a ) F (a ) F (a 0), P ( X b ) 1 F (b 0), P ( X b ) 1 F (b), P (a X b) F (b 0) F (a), P (a X b) F (b) F (a 0), P (a X b) F (b 0) F (a 0).
(2) n个产品中的不合格品个数 Y 0，1，2，…，n
(3) 某商场一天内来的顾客数 Z 0，1，2，…
(4) 某种型号电视机的寿命 T ： [0, +)
2.2
2.1.1 随机变量的定义
定义2.1.1 设 ={}为某随机现象的样本空间， 称定义在上的实值函数X=X()为随机变量.
2.3
注意点
我们还可以定义其它的随机变量，例如可以定义：
1 出现偶数点 Y 0 出现奇数点
Z
1 0
点数为6 点数不为6
等等． 精选
6
2.6
两类随机变量
➢ 若随机变量 X 可能取值的个数为有限个或 可列个，则称 X 为离散随机变量.
➢ 若随机变量 X 的可能取值充满某个区间 [a, b]，则称 X 为连续随机变量.
2.9
2.1.3 离散随机变量的分布列
➢ 设离散随机变量 X 的可能取值为： x1，x2，……，xn，……
称 pi=P(X=xi)， i =1, 2, …… 为 X 的分布列.
➢ 分布列也可用表格形式表示：
X x1 P p1
x2 …… xn …… p2 …… pn ……
2.10
分布列的基本性质 (1) pi 0， (非负性)
求X 的分布函数并画图.
解： 0, x0
F
(
x)
1/ 1/
3, 2,
0 x1 1 x2
1, 2 x
2.14
F(x) 1
1 2 1 3
•
•
o1
2
x
2.15
注 意 点 (2)
对离散随机变量的分布函数应注意： (1) F(x)是递增的阶梯函数; (2) 其间断点均为右连续的; (3) 其间断点即为X的可能取值点; (4) 其间断点的跳跃高度是对应的概率值.
2.21
注意点(2)
(4) P{a<X≤b} = P{a<X<b} = P{a≤X<b} = P{a≤X≤b} = F(b)F(a).
(5) 当F(x) 在x点可导时, p(x) = F (x)
当F(x) 在x点不可导时, 可令p(x) =0.
2.22
离散型
连续型
1. 分布列: pn = P(X=xn) ( 唯一 )
(1) 随机变量X()是样本点的函数， 其定义域为 ，其值域为R = (，) 若 X 表示掷一颗骰子出现的点数， 则 {X=1.5} 是不可能事件.
(2) 若X为随机变量，则 {X = k} 、 {a < X b} 、……
均为随机事件. 即 {a < X b} ={；a < X() b }
2.4
第二章 随机变量及其分布
§2.1 随机变量及其分布 §2.2 随机变量的数学期望 §2.3 随机变量的方差与标准差 §2.4 常用离散分布 §2.5 常用连续分布 §2.6 随机变量函数的分布 §2.7 分布的其他特征数
2.1
§2.1 随机变量及其分布
(1) 掷一颗骰子， 出现的点数 X 1，2，…，6.
2.19
密度函数的基本性质
(1) p(x) 0; (非负性)
(2)
p(
x)dx
1.
(正则性)
满足(1) (2)的函数都可以看成某个 连续随机变量的概率密度函数.
2.20
注意点(1)
(1) P(a X b) b p( x)dx. a
(2) F(x) 是 (∞, +∞) 上的连续函数; (3) P(X=x) = F(x)F(x0) = 0;
1. 密度函数 X ~ p(x) ( 不唯一 )
例2.1.3
已知 X 的分布函数如下,求 X 的分布列.
0,
F
(x)
0.4, 0.8,
1,
x0 0 x1 1 x2 2 x
解：
X0 1 2 P 0.4 0.4 0.2
2.17
2.1.4 连续随机变量的密度函数
➢ 连续随机变量X的可能取值充满某个区间 (a, b). ➢ 因为对连续随机变量X，有P(X=x)=0，
(2) pi 1. (正则性)
i
2.11
注 意 点 (1)
求离散随机变量的分布列应注意： (1) 确定随机变量的所有可能取值; (2) 计算每个取值点的概率.
2.12
例2.1.1 从1～10这10个数字中随机取出5个数字，令
X：取出的5个数字中的最大值． 试求 X 的分布列．
解：X 的取值为5，6，7，8，9，10．
所以无法仿离散随机变量用 P(X=x) 来描述连续 随机变量X的分布.
➢ 注意离散随机变量与连续随机变量的差别.
2.18
定义2.1.4
设随机变量X 的分布函数为F(x),
若存在非负可积函数 p(x) ，满足：
F
(
x
)
x
p
(t
)dt
则称 X 为连续随机变量，
称 p(x)为概率密度函数，简称密度函数.
注意点
(3) 注意以下一些表达式： {X = k}= {X k}{X < k}； {a < X b} = {X b}{X a}； { X > b} = {X b}.
(4) 同一样本空间可以定义不同的随机变量.
2.5
实例
掷一枚骰子，令X ={出现的点数},则X 就是一个随机 变量,它的取值为1，2，3，4，5，6．
PX k C k 4 1C 1 5 0 k 5 ， 6 ， L ， 1 0
具体写出，即可得 X 的分布列：
X 5 6 7 8 9 10
P1
5
15 35 70 126
252 252 252 252 252 252
精选
13
2.13
例2.1.2 已知 X 的分布列如下：
X0 1 2 P 1/3 1/6 1/2
➢ 前例中的 X, Y, Z 为离散随机变量； 而 T 为连续随机变量.
2.7
2.1.2 随机变量的分布函数
定义2.1.2 设X为一个随机变量，对任意实数 x，
称 F(x)=P( X x) 为 X 的分布函数.
基本性质：
(1) F(x) 单调不降； (2) 有界：0F(x)1，F()=0，F(+)=1； (3) 右连续.
ቤተ መጻሕፍቲ ባይዱ2.8
用分布函数表示事件的概率
对 任 意 实 数 a与 b,有 P (a X b) F (b) F (a), P ( X a ) F (a ) F (a 0), P ( X b ) 1 F (b 0), P ( X b ) 1 F (b), P (a X b) F (b 0) F (a), P (a X b) F (b) F (a 0), P (a X b) F (b 0) F (a 0).
(2) n个产品中的不合格品个数 Y 0，1，2，…，n
(3) 某商场一天内来的顾客数 Z 0，1，2，…
(4) 某种型号电视机的寿命 T ： [0, +)
2.2
2.1.1 随机变量的定义
定义2.1.1 设 ={}为某随机现象的样本空间， 称定义在上的实值函数X=X()为随机变量.
2.3
注意点
我们还可以定义其它的随机变量，例如可以定义：
1 出现偶数点 Y 0 出现奇数点
Z
1 0
点数为6 点数不为6
等等． 精选
6
2.6
两类随机变量
➢ 若随机变量 X 可能取值的个数为有限个或 可列个，则称 X 为离散随机变量.
➢ 若随机变量 X 的可能取值充满某个区间 [a, b]，则称 X 为连续随机变量.
2.9
2.1.3 离散随机变量的分布列
➢ 设离散随机变量 X 的可能取值为： x1，x2，……，xn，……
称 pi=P(X=xi)， i =1, 2, …… 为 X 的分布列.
➢ 分布列也可用表格形式表示：
X x1 P p1
x2 …… xn …… p2 …… pn ……
2.10
分布列的基本性质 (1) pi 0， (非负性)
求X 的分布函数并画图.
解： 0, x0
F
(
x)
1/ 1/
3, 2,
0 x1 1 x2
1, 2 x
2.14
F(x) 1
1 2 1 3
•
•
o1
2
x
2.15
注 意 点 (2)
对离散随机变量的分布函数应注意： (1) F(x)是递增的阶梯函数; (2) 其间断点均为右连续的; (3) 其间断点即为X的可能取值点; (4) 其间断点的跳跃高度是对应的概率值.
2.21
注意点(2)
(4) P{a<X≤b} = P{a<X<b} = P{a≤X<b} = P{a≤X≤b} = F(b)F(a).
(5) 当F(x) 在x点可导时, p(x) = F (x)
当F(x) 在x点不可导时, 可令p(x) =0.
2.22
离散型
连续型
1. 分布列: pn = P(X=xn) ( 唯一 )
(1) 随机变量X()是样本点的函数， 其定义域为 ，其值域为R = (，) 若 X 表示掷一颗骰子出现的点数， 则 {X=1.5} 是不可能事件.
(2) 若X为随机变量，则 {X = k} 、 {a < X b} 、……
均为随机事件. 即 {a < X b} ={；a < X() b }
2.4
第二章 随机变量及其分布
§2.1 随机变量及其分布 §2.2 随机变量的数学期望 §2.3 随机变量的方差与标准差 §2.4 常用离散分布 §2.5 常用连续分布 §2.6 随机变量函数的分布 §2.7 分布的其他特征数
2.1
§2.1 随机变量及其分布
(1) 掷一颗骰子， 出现的点数 X 1，2，…，6.
2.19
密度函数的基本性质
(1) p(x) 0; (非负性)
(2)
p(
x)dx
1.
(正则性)
满足(1) (2)的函数都可以看成某个 连续随机变量的概率密度函数.
2.20
注意点(1)
(1) P(a X b) b p( x)dx. a
(2) F(x) 是 (∞, +∞) 上的连续函数; (3) P(X=x) = F(x)F(x0) = 0;
1. 密度函数 X ~ p(x) ( 不唯一 )