随机变量及其分布PPT课件
合集下载
随机变量函数的分布课件

解
X ~ N 0,1
fX x
1
x2
e 2,
x ,
2
第一步 先求Y的分布函数.
FY ( y) P(Y y) P( X 2 y)
① 当 y 0 时,FY y 0,
② 当 y 0 时,FY ( y) P(Y y) P( y X y )
1
y x2
2
y x2
e 2 dx
fY
(
y
)
f
X
0,
[h(
y)]
|
h(
y
)
|,
y
其他,
,
其中 min(g(), g()), max(g(), g()),
h(y)是g(x)的反函数.
例4 设随机变量 X ~ N 0,1 , 试证明X的线性函数
Y aX b, a 0 也服从正态分布.
解 X的概率密度为
fX (x)
1
( x μ)2
P 0.3 0.3 0.4
二、连续型随机变量函数的分布
1. 分布函数法 设连续型随机变量X的分布函数为FX ( x), Y g( x) 的概率分布?
方法:根据X的分布先求随机变量Y 的分布函数,
FY ( y) P(Y y) P{g( X ) y},
利用不等式等价变形,将事件“g( X ) y”转化为X的 不等式,然后通过分布函数求Y = g(X)的概率密度.
8
0 y 1 2, 2
所以Y的概率密度
y1
fY ( y)
8
,
0,
1 y 5, 其他.
例2 设随机变量X具有概率密度
f
X
(
x)
x 2
,
第七章随机变量及其分布小结PPT课件(人教版)

,进一步体会概率模型的作用及概率思想和方法的特点.
第1课时 条件概率、乘法公式及全概率公式
条件概率公式:PA|B=
PAB
,
PB
加法公式:如事件 B,C 互斥,则有 P( B
C | A) P( B | A) P(C | A).
乘法公式:PAB=PBPA|B,
PAB
.
P ( A)
P ( A)
P ( B)
P ( B) 2
A产生,则B一定产生
P ( A)
由此可得, 若A B,则P ( B | A) 1,P ( A | B )
.
P ( B)
课本48页
夯实概念
2.下列说法正确的是(
)
P(B)
是可能的
P(A)
A.P(B|A)=P(AB)
B.P(B|A)=
C.0<P(B|A)<1
D.P(A|A)=0
P(AB)
1
解析:∵ P(B|A)=
,
≥1,
P(A) P(A)
∴P(B|A)≥P(AB),故 A 不正确;
当 P(A)=1 时,P(B)=P(AB),
P(B)
则 P(B|A)=P(B)=
,所以 B 正确;
P(A)
而 0≤P(B|A)≤1,P(A|A)=1,∴ C、D 不正确.
击落,求飞机被击落的概率.
解:设 A={飞机被击落},Bi={飞机被 i 人击中},i=1,2,3,则
P(A|B1)=0.2,P(A|B2)=0.6,P(A|B3)=1.
P(B1)=0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7=0.36,
P(B2)=0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7=0.41,
第1课时 条件概率、乘法公式及全概率公式
条件概率公式:PA|B=
PAB
,
PB
加法公式:如事件 B,C 互斥,则有 P( B
C | A) P( B | A) P(C | A).
乘法公式:PAB=PBPA|B,
PAB
.
P ( A)
P ( A)
P ( B)
P ( B) 2
A产生,则B一定产生
P ( A)
由此可得, 若A B,则P ( B | A) 1,P ( A | B )
.
P ( B)
课本48页
夯实概念
2.下列说法正确的是(
)
P(B)
是可能的
P(A)
A.P(B|A)=P(AB)
B.P(B|A)=
C.0<P(B|A)<1
D.P(A|A)=0
P(AB)
1
解析:∵ P(B|A)=
,
≥1,
P(A) P(A)
∴P(B|A)≥P(AB),故 A 不正确;
当 P(A)=1 时,P(B)=P(AB),
P(B)
则 P(B|A)=P(B)=
,所以 B 正确;
P(A)
而 0≤P(B|A)≤1,P(A|A)=1,∴ C、D 不正确.
击落,求飞机被击落的概率.
解:设 A={飞机被击落},Bi={飞机被 i 人击中},i=1,2,3,则
P(A|B1)=0.2,P(A|B2)=0.6,P(A|B3)=1.
P(B1)=0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7=0.36,
P(B2)=0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7=0.41,
《随机变量及分布》课件

应用
广泛应用于统计学和实证研究中的抽 样分布及模拟实验。
总结
• 随机变量与分布的概念 • 离散型随机变量及其分布 • 连续型随机变量及其分布 • 常见离散型与连续型随机变量分布 • 中心极限定理的应用
次数的概率分布。
3
几何分布
用于描述在成功与失败交替出现的是/
超几何分布
4
非试验中成功首次出现的概率分布。
用来描述无放回抽样实验中成功次数 的概率分布。
常见的连续型随机变量分布
均匀分布
在某个区间内取值的概率密度函数恒定的随 机变量。
指数分布
描述等待时间的概率分布。
正态分布
钟形曲线,广泛应用于自然科学和社会科学 中。
样本空间与事件
样本空间是所有可能的结果的集合,事件是样 本空间的子集。
离散型随机变量
概率分布函数
描述离散型随机变量的取值与可能取到的值与其概率乘积的 和。
概率质量函数
用来描述离散型随机变量分布的函数。
方差
测量随机变量离其期望值的平均距离。
连续型随机变量
概率密度函数
《随机变量及分布》PPT 课件
欢迎来到《随机变量及分布》PPT课件。本课程将带你深入了解随机变量的概 念、离散型和连续型随机变量的分布以及中心极限定理的应用。
随机变量
什么是随机变量
对随机试验结果的数值化描述,并依赖于试验 的具体情况。
离散型随机变量
取有限个或可数个数值的随机变量。
连续型随机变量
取连续数值的随机变量。
描述连续型随机变量在某个区间内取值的概率 密度。
累积分布函数
描述连续型随机变量在某个数值前取值的概率。
期望
随机变量每个可能取到的值与其概率密度乘积 的积分。
概率论课件第二章
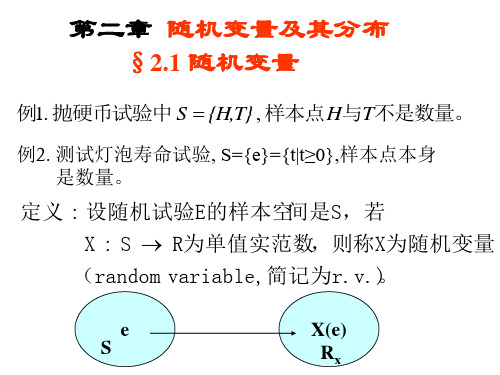
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
新教材选择性必修二8.2.1随机变量及其分布列课件(60张)

2.概率分布列 (1)定义 一般地,随机变量 X 有 n 个不同的取值,它们分别是 x1,x2,…,xn,且 P(X=xi)= pi,i=1,2,…,n,① 称①为随机变量 X 的概率分布列,简称 X 的分布列.①也可以用下表的形式来表示.
X x1 x2 … xn P p1 P2 … pn 我们将上表称为随机变量 X 的概率分布表.它和①都叫作随机变量 X 的概率分布.
三、解答题 11.设 S 是不等式 x2-x-6≤0 的解集,整数 m,n∈S. (1)记“使得 m+n=0 成立的有序数组(m,n)”为事件 A,试列举 A 包含的基本事件; (2)设 X=m2,求 X 的分布列.
【解析】(1)由 x2-x-6≤0,得-2≤x≤3,即 S={x|-2≤x≤3}.由于 m,n∈Z,m,n ∈S 且 m+n=0,所以 A 包含的基本事件为(-2,2),(2,-2),(-1,1),(1,-1), (0,0). (2)由于 m 的所有不同取值为-2,-1,0,1,2,3, 所以 X=m2 的所有不同取值为 0,1,4,9, 且有 P(X=0)=61 ,P(X=1)=26 =13 ,
【解析】选 BCD.抛掷两枚骰子,点数之差满足小于等于-4 的只有三种情况,故第 一枚为 1 点、第二枚为 6 点,第一枚为 1 点、第二枚为 5 点,第一枚为 2 点、第二枚 为 6 点.
8.(多选题)(2021·成都高二检测)已知随机变量 X 的分布列如表(其中 a 为常数):
X0 1 2 34 P 0.1 0.2 0.4 0.2 a 则下列计算结果正确的有( )
离散型随机变量及其分布列 随机变量及其分布列
基础认知·自主学习
1.随机变量 一般地,对于随机试验样本空间 Ω 中的每个样本点 ω 都有唯一的实数 X(ω)与之对应, 则称 X 为随机变量.通常用大写字母 X,Y,Z(或小写字母 ζ,η,ξ)等表示,而用小 写英文字母 x,y,z(加上适当下标)等表示随机变量的取值.
概率论与数理统计课件:随机变量及其分布

随机变量及其分布
首页 返回 退出
§2.2 离散型随机变量及其分布律
定义 设离散型随机变量 X 所有可能取的值为xk , k = 1, 2,
X 取各个可能值的概率,即事件{ X xk } 的概率,为
P{ X xk } pk , k 1, 2, .
称此为离散型随机变量 X 的分布律.
随机变量及其分布
首页 返回 退出
定义2.1 设随机试验E, 其样本空间S, 若对样本
空间每一个样本点e, 都有唯一一个实数X(e)与之对
应,那么就把这个定义域为S的单值实值函数X=X(e),
称为随机变量。
随机变量通常用大写字母X,Y,Z 或希腊字母 ξ,η等表示.
而表示随机变量所取的值时,一般采用小写字母x,y,z等.
量方面,如,投掷一枚均匀骰子,我们观察出现的点
数。
记X=“出现的点数”
则X的可能取1, 2, …, 6中任一个数,可见X是变量;
又X取那个值不能事先确定,故此X的取值又带有随机
性.
有了随机变量,有关事件的表示也方便了,如
{X=2}, {X≤2}, ……
随机变量及其分布
首页 返回 退出
这样的例子还有很多. 又如,研究手机的使用寿命
或写成
随机变量及其分布
5
P( X k )
6
k 1
1
, k 1, 2,
6
首页 返回 退出
常见离散型随机变量
(一)“0-1”分布
设随机变量 X 只可能取 0 和1 两个值,它的分布律
为
k
P X k p(
1 p)1k k 0,1
(0 p 1)
概率论与数理统计-第二章-随机变量及其分布函数ppt课件

表格: X
x1 x2
pk
p1 p2
概率分布图:
1P
xn
pn
0.5
x4 x3
x1
x2
X
.
由概率的性质易知离散型随机变量的分布列
pk
满足下列特征性质:
k 1
① pk 0(k 1,2,) [非负性]
②
pk 1 [规范性]用于确定待定参数
k 1
③ F( x) P( X x) P(X xi ). xi x
1. 2
.
【例2】设随机变量X的分布函数为
aex b, x 0
F(x)
0,
x0
解: 因为 F(x) 在 x=0 点右连续
求: 常数 a 和 b。
所以 lim F ( x) lim (ae x b) a b 0
x0
x0
又因为 F () lim (ae x b) b 1 x
1、两点分布 或(0 - 1)分布
two-point distribution
定义1 设离散型随机变量X的分布列为
X0 1 pk 1 p p
其中 0<p<1
则称 X 服从(0 - 1)分布,记作 X ~(0 - 1)分布
F(x)
(0 - 1)分布的分布函数
0 , x0 F ( x) 1 p, 0 x 1
X = “三次试验中 A 发生的次数”,
{ X 2} A1A2 A3 A1A2 A3 A1A2 A3 P{X 2} P(A1A2 A3 A1A2 A3 A1A2 A3 )
P(A1A2 A3 ) P(A1A2 A3 ) P(A1A2A3 ) P(A1)P(A2)P(A3) P(A1)P(A2)P(A3) P(A1)P(A2 )P(A3 ) C32 p2(1 p)32
随机变量及其分布PPT课件

35
例8. 某类灯泡使用时数在1000小时以上 的概率是0.2,求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯
泡数 . X ~ B (3, 0.8),
P(X k)C3k (0.8)k (0.把2)观3察k ,一个k 灯泡0,的1,2使,3用
随后单调减少.
..
0
n=13,p=0.5
..n
当(n+1)p为整数时,二项概率P(X=k) 在k=(n +1)p和k =(n+1)p-1处达到最大 值.
课下请自行证明上述结论.
31
例6. 将一枚均匀骰子抛掷3次, 令X 表示3次中出现“4”点的次数
不难求得,
X的概率分布列是:
P{
X
k}C3k
(
依题意x可取值0第i个路口遇红灯i123路口3路口2路口118x表示该汽车首次遇到红灯前已通过的路口的个数路口3路口2路口1路口3路口2路口1第i个路口遇红灯i123路口3路口2路口1第i个路口遇红灯i123某加油站替公共汽车站代营出租汽车业务每出租一辆汽车可从出租公司得到3因代营业务每天加油站要多付给职工服务费60元
一般地,我们给出如下定义:
定义1 :Байду номын сангаасxk(k=1,2, …)是离散型随 机变量X所取的一切可能值,称
P(X xk ) pk, k=1,2,… …
为离散型随机变量X的概率分布列
简称分布列, 又称分布律.
其中 pk (k=1,2, …) 满足:
(1) pk 0,
用这两条性质判断
k=1,2, … 一个函数是否是
P( X k) a k , k =0,1,2, …, 0
例8. 某类灯泡使用时数在1000小时以上 的概率是0.2,求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯
泡数 . X ~ B (3, 0.8),
P(X k)C3k (0.8)k (0.把2)观3察k ,一个k 灯泡0,的1,2使,3用
随后单调减少.
..
0
n=13,p=0.5
..n
当(n+1)p为整数时,二项概率P(X=k) 在k=(n +1)p和k =(n+1)p-1处达到最大 值.
课下请自行证明上述结论.
31
例6. 将一枚均匀骰子抛掷3次, 令X 表示3次中出现“4”点的次数
不难求得,
X的概率分布列是:
P{
X
k}C3k
(
依题意x可取值0第i个路口遇红灯i123路口3路口2路口118x表示该汽车首次遇到红灯前已通过的路口的个数路口3路口2路口1路口3路口2路口1第i个路口遇红灯i123路口3路口2路口1第i个路口遇红灯i123某加油站替公共汽车站代营出租汽车业务每出租一辆汽车可从出租公司得到3因代营业务每天加油站要多付给职工服务费60元
一般地,我们给出如下定义:
定义1 :Байду номын сангаасxk(k=1,2, …)是离散型随 机变量X所取的一切可能值,称
P(X xk ) pk, k=1,2,… …
为离散型随机变量X的概率分布列
简称分布列, 又称分布律.
其中 pk (k=1,2, …) 满足:
(1) pk 0,
用这两条性质判断
k=1,2, … 一个函数是否是
P( X k) a k , k =0,1,2, …, 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可由X的概率分布通过求和得到
20求离散型r.v.X的分布问题 核心是: 求出 (1)X的所有可能取值; (2)取各值的概率 .
例2 问下面给出的是不是某 r.v.的分布列?
X0 1 2 P 1/2 1/4 1/3
1 1 1 13 1 2 4 3 12
不是某 r.v.的分布列
例3 设离散型r.v.X的概率分布为:
X
1
:击中
0 :未击中
P{X 0}
P{500 X 1000}
2、在有些试验中,试验结果看来与数值无关,但可以
引进一个变量来表示它的各种结果.--把试验结果数值化.
办法是:将基本事件与一个实数对应 例如,掷一枚硬币,观察出现正、反面情况;
{H ,T } {1,0}
X
X ( )
1 , H
(2)规范性
f ( x)dx 1
这两条性质是判定一个函数 f(x)是否为 某连续型r.v的密度函数的充要条件
b
P{a X b} a f ( x)dx
20 事件的概率与密度函数的关系
P{a X b} P{a X b}
P{a X b} b
P{a X b} a f ( x)dx
一、随机变量的概念 1、有些试验结果本身与数值有关(本身就是一个数).
例如,掷一颗骰子出现的点数; {1,2,3,4,5,6} 记录某车站的等车人数; {0,1,2, } “无人等车”
检查某元件的寿命 [0,)
一个射手对目标进行射击“,元 击中 件得寿1命分在,5未00击 1中00得0小0分时. 之间”
10 X的分布列{ pi } 具有下述性质:
(1)非负性 pi 0, i 1,2,
用这两条性质判断 一个数列是否是某个
(2)规范性 pi 1
离散型r.v.的概率分布
i 1
(3)可加性 P{a X b} pi , P{ X B} pi
“数点求和”
a xi b
xiB
由性质(3)可见,事件的概率都
事件及事件的Leabharlann 率随机变量及其取值规律二、离散型r.v.的概率分布
引例 对于掷一粒骰子的试验,以X表示出现的点数,
X可能取的值是1,2,3,4,5,6 1
P{1
X
P{X i} 6 (i 1,2,3,4,5,6) 3} P{X 1} P{X 2} P{X 3}
1
“数点求和”
2
1.Def . 如果随机变量X只可能取有限个或可列个值,则称
用一个不同的实数 X 与之相对应,亦即可以定义不同的一个实
数 X 来表征试验的每一个结果.
Def . 在随机试验E中,随机试验结果取不同数值的量
X 称为随机变量,简记为X.
1.通常用字母 X、Y、Z 或 、、 表示随机变量.
用小写字母 x, y ,z等表示随机变量所取的值.
2. 随机变量X ,有时简记为 r.v. X (random variable X)
3. r.v.的分类: (1) 离散型r.v.;
()
所有取值可以 (2) 连续型r.v.;
()
逐个一一列举 (3) 非离散非连续型r.v..
例1 从一批产品中任抽取10件,若用X表示检测的10件中 的废品数. “少于两件废品”可表示成 {0 X 2}
“恰有一件废品”可表示成 {X 1}
“至少有一件废品” { 1 X 10 }
2 a (2)2a (2)3a
2 3
a
2a
33
3
1
2 3
a1 2
例4 袋中有5张卡片,其中标有数字1的有1张, 标有数字 2和3的各有2张. 从袋中一次随机地抽取3张,用X表示 取到的3张卡片上的最大数字, 写出X的概率分布.
例5 设离散型r.v.X的概率分布为:
X1 2 3
P
9 19
随机变量及其分布
Ch2 随机变量的分布与数字特征
密度函数
分布函数
概率分布
连续型 随机变量
三种重要的 连续型分布
随机变量 随机变量的数字特征
期
方
望
差
离散型 随机变量
三种重要的 离散型分布
随机变量函数的分布
§2.1 随机变量及其分布
本节知识要点:
1. 理解一维离散型随机变量的概念及性质;
2. 理解一维连续型随机变量的概率密度及其性质; 3. 熟练求解离散型随机变量的分布列和连续型随机变量的分布函数.
y f (x)
P{a X b}
30 P{ X c} 0,
0a
b
x
连续型r.v取任一指定值的概率为0.
X为离散型随机变量.
2.Def .设X为离散型r.v.它的一切可能取值为 x1, x2 , , xn , ,
记 pi P{ X xi }, i 1,2
称为X的概率分布.
X x1 x2 xn
为直观起见,习惯上把它们写成 P p1 p2 pn
pi P{ X xi },
X x1 x2 xn P p1 p2 pn
0
,
T
例如 袋内有1个红球,1个白球,1个黑球,从中任
取一个球,考察取得的球的颜色 .
设1=“球是红的”,2=“球是白 的”,3=“球是黑的” .
={ 1 ,2, 3 } {1,2,3}
X
X ( )
1 , 2 ,
1 2
3 , 3
P{ X
1}
1 3
P{ X
2}
1 3
对于任何一个试验E的每一个基本结果(即基本事件) 都可以
(1) P{ X i} a (2)i , i 1,2,3. 3
(2) P{ X i} a (2)i , i 1,2,
求a的值.
解
(1)
1
P{ X
3
1}
P{ X
2}
P{ X
3}
a 2 a 4 a 8 a 38 3 9 27 27
a 27 38
(2) 1 P{X 1} P{X 2}
6 19
4 19
P{X 1} 0
P{ X
1}
P{ X
1}
9 19
P{ X
2.5}
9 19
6 19
15 19
P{ X
4}
9 19
6 19
4 19
1
Ex1.袋内有5个黑球,3个白球,每次抽取一个,不放回,直到取得 黑球为止.记X为取到白球的数目,求随机变量X的概率分布.
三、连续型r.v.的密度函数
1.Def . 设X是一个r.v., 如果存在一个非负可积函数f(x),
使得对于任意的实数a < b, 都有
b
P{a X b} a f ( x)dx
则称 X为连续型 r.v. , f ( x)为X的概率密度函数, 记为 X ~ f (x)
10密度函数f ( x)的性质 (1)非负性 f ( x) 0
