随机变量及其分布教学课件
合集下载
概率论课件第二章
第二章 随机变量及其分布 §2.1 随机变量
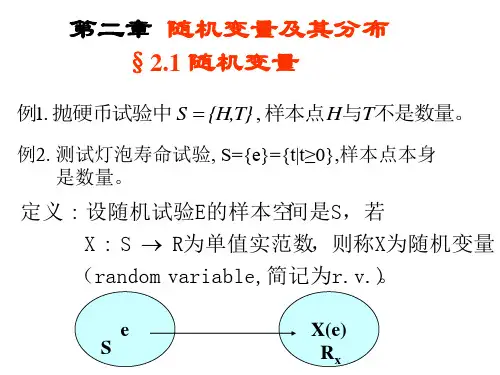
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
《概率论与数理统计》课件-第2章随机变量及其分布 (1)

则称X服从参数为λ的泊松分布, 记为 X ~ P() .
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数, 原子放射的粒子数,保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义: 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
泊松分布的应用
“稠密性”问题(一段时间内,电话交换中心接到的呼叫次 数,公共汽车车站候车的乘客数,售票窗口买票的人数, 原子放射的粒子数,保险公司在一定时期内被索赔的次 数等)都服从泊松分布.
随机变量的分布函数
1.定义: 设X为一随机变量, x为任意实数, 称函数 F(x)=P{X≤x}为X的分布函数.
注: ① F(x)是一普通函数, 其定义域为 ,; ② F x的值为事件X x的概率; ③ F x可以完全地描述随机变量取值的规律性.
例如: Pa X b PX b PX a
连续型随机变量及概率密度函数
1.定义: 设X ~ F(x), 若存在一个非负可积的函数 f (x),
使 x R, 有
F ( x)
PX
x
x
f
(t)dt
,
则称X为连续型随机变量, f (x) 称为X的概率密度函数或
分布密度函数.
2.几何意义:
HAINAN UNIVERSITY
概率论与数理统计
第二五章 基随本机极变限量定及理其分布
二、随机变量的概念
定义: 设试验E的样本空间为 , 若对于每个样本
点 , 均有一个实数 X ()与之对应, 这样就得
到一个定义在 上的单值函数 X X () , 称X为随
机变量.
X
样本空间
实数
注: ① 随机变量是一个定义在样本空间上的实函数, 它取值的随机性是由样本点的随机性引起的;
x 1
x0
0 x x
不是 (不满足规范性)
人教A版选择性必修第三册7.2离散型随机变量及其分布列课件

考察下列随机实验及其引入的变量:
实验1:从100个电子元件(至少含3个以上次品)中随机抽取三个 进行检验,变量X表示三个元件中的次品数
如果用0表示“元件为合格品”,1表示“元件为次品”.
用0和1构成的长度为3的字符串表示样本点,则
X=0, 1, 2, 3
样本空间为 Ω={000,001,010,011,100,101,110,111 }
为X的概率散布列,简称散布列,以表格的情势表示如下:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
上表称为离散型随机变量X的概率散布列,简称为X的散布列.
1.离散型随机变量的散布列不仅能清楚地反应随机变量的所有可能取值, 而且能清楚地看到取每一个值时的概率的大小,从而反应了随机变量在 随机实验中取值的散布情况. 2.离散型随机变量的散布列类似于函数,也有三种表示情势,即解析式、 表格和图象,但离散型随机变量的散布列多是用表格或解析式表示.
(2)ξ=3,表示取出123号球; ξ=4,表示取出124,134,234号球; ξ=5,表示取出125, 135, 145,235, 245,345号球;
若X是随机变量,则Y=aX+b(其中a、b是常数)也是随机变量.
三、离散型随机变量的概率散布列
抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,
(1)从箱中取2个球的情形有以下6种:
{2个白球},{1个白球,1个黄球},{1个白球,1个黑球},
{2个黄球},{1个黑球,1个黄球},{2个黑球}.
当取到2个白球时,随机变量X=-2;
当取到1个白球,1个黄球时,随机变量X=-1;
当取到1个白球,1个黑球时,随机变量X=1;
当取到2个黄球时,随机变量X=0; 当取到1个黑球,1个黄球时,随机变量X=2; 当取到2个黑球时,随机变量X=4. 所以随机变量X的可能取值为-2,-1,0,1,2,4.
7.2 离散型随机变量及其分布列 课件-2021-2022学年高二下学期数学人教A版(2019)选择

八、教学过程分析:
环节一、复习回顾:
1.随机试验的概念和特点; 2.样本点和样本空间,及有限样本空间; 3.随机事件的定义; 4.随机事件的概率定义; 5.古典概型的特征,及古典概型的概率 公式。
• 【设计意图】通过复习回顾随机事件、样本点和样 本空间的概念,古典概型的公式,为本节课学习分
布列打下基础。
【第二层】随机变量与离散型随机变量的概念
一般的,对于随机试验样本空间中的每个样本点, 都有唯一的实数X()与之对应,我们称X为随机变量。
可能取值为有限个或可以一一列举的随机变量,叫做 离散型随机变量。
例如,探究中的试验1随机变量X的可能取值为 0,1,2,3. 试验2中随机变量Y的可能取值为1,2,3,..., 有无限个,但可一一列举。
试验的样本点与实数的关 本节的考查主要为离散型随
系。
机变量的分布列的求法,分
2.通过具体实例,理解取有 布列的性质、服从两点分布
限个值的离散型随机变量 的随机变量的概率求法。
及其分布列的概念。
2.从考查形式看,常以选择
3.认识分布列对于刻画随机 题、填空题的形式考查分布
现象的重要性。
列的性质及两点分布,另外
如:1.掷一枚骰子时掷出的点数;样本空间 1,2,3,4,5,6
2.掷两枚骰子时,两枚骰子的点数之和。
样本空间 2,3,4,5,6,7,8,9,10,11,12
【第二类】随机试验的样本点与数值没有直接 关系,可以根据问题的需要为每个样本点指定 一个数值。 例如:随机抽取一件产品,有“抽到次品”和“抽到 正品”两种可能,它们与数值无关;
习统计学的理论基础。本节课不仅是“生活化” 数学的集中体现,也为学生在大学进一步的深入 学习打下理论基础,因此它起到了承前启后的核 心作用。教材是教学的主媒体。
随机变量及其分布优秀课件

1 20 3 20 3 10 1 2
C
6
C 11 C “ 5” 表示其中一个球号码等于“5”, ( 5 ) 3 ∴P 另两个都比“5”小 C6
2 4
C 11 C “ 6” 表示其中一个球号码等于“3”, ( 6 ) 3 ∴P 另两个都比“3”小 C6
2 5
∴ 随机变量 的分布列为:
思考2.将一枚骰子掷2次,求下列随机变量的概率分布. (1)两次掷出的最大点数ξ; (2)第一次掷出的点数减去第二次掷出的点数之差η .
研究性问题
设一部机器在一天发生故障的概率为0.2,机 器发生故障时全天停止工作,若一周5个工作日 里无故障可获利润10万元,发生一次故障可获利 5万元,若发生两次故障所获利润0万元,发生三 次或三次以上就亏损2万元.试写出一周所获利 润可能的取值及每个值的概率.
P
3
1 20
4
3 20
5
3 10
6
1 2
说明:在写出ξ的分布列后,要及时检查所有的概率之和是否为1.
课堂练习:
1、下列A、B、C、D四个表,其中能成为随机变量 分布列的是(B )
的
A
P
0
0.6
1
0.3
B
P
0
0.9025
1
0.095
2
0.0025
C
0
1 2 … n
1 4
1 8
D
P
0
1 3
1 p 36
2 36
3 36
4 36
5 36
6 36
5 36
4 36
3 36
2 36
随机事件与概率随机变量与概率分布PPT教学课件

天气系统,如高压、冷锋等
⑵锋是影响天气的重要天气系统,
冷暖空气的交界面叫锋面。
向 东 南 移 动
大风 降温 降雨
向东北移动
升温 降雨
如何从锋的图例 上知道它是向哪 个方向移动呢?
三角形或半圆凸 所指的方向
过境前 过境时 过境后
冷锋
气温高,气压低
出现较大风 雨雪天气
气温下降,气压 上升,天气转好
问题的引伸
随机事件的数量化—随机变量 多个事件的概率描述—概率分布
随机变量及其概率分布
随机变量的分类
离散变量(疗效分级、受教育程度) 计数变量(如单位时间或空间内检出细菌的
数量、发生某事件的数量)
连续变量 如血压、血脂、血糖等
判断:白色的程度越浓,表明云层越厚, 这种云区下面下雨往往就越大。
问题:
古代劳动人民并没有现代科技手段, 他们是如何预知未来的天气形势呢?
燕子低飞要下雨
天气谚语
一场秋雨凉一阵 •东虹日头西虹雨1
暖锋 气温低气压高
多连续性降水
气温上升,气压 下降,天气转晴
常见天气系统
高压 低压 冷锋 暖锋 台风
探 1、请分析当天的天气形势,并说明理由。 究 2、预测北京、上海、广州未来24小时天气形势,并说明理由
活
动
1012.5
1017.5
1007.5
低
1017.5
高
1007.5 1002.5
低
* *
1017.5 1012.5
定小概率事件选择大概率事件
多个随机事件的关系
任一事件发生:和事件 几个事件同时发生:积事件 一事件发生则另一事件不发生:互斥 当只有两种事件时,互斥即对立
⑵锋是影响天气的重要天气系统,
冷暖空气的交界面叫锋面。
向 东 南 移 动
大风 降温 降雨
向东北移动
升温 降雨
如何从锋的图例 上知道它是向哪 个方向移动呢?
三角形或半圆凸 所指的方向
过境前 过境时 过境后
冷锋
气温高,气压低
出现较大风 雨雪天气
气温下降,气压 上升,天气转好
问题的引伸
随机事件的数量化—随机变量 多个事件的概率描述—概率分布
随机变量及其概率分布
随机变量的分类
离散变量(疗效分级、受教育程度) 计数变量(如单位时间或空间内检出细菌的
数量、发生某事件的数量)
连续变量 如血压、血脂、血糖等
判断:白色的程度越浓,表明云层越厚, 这种云区下面下雨往往就越大。
问题:
古代劳动人民并没有现代科技手段, 他们是如何预知未来的天气形势呢?
燕子低飞要下雨
天气谚语
一场秋雨凉一阵 •东虹日头西虹雨1
暖锋 气温低气压高
多连续性降水
气温上升,气压 下降,天气转晴
常见天气系统
高压 低压 冷锋 暖锋 台风
探 1、请分析当天的天气形势,并说明理由。 究 2、预测北京、上海、广州未来24小时天气形势,并说明理由
活
动
1012.5
1017.5
1007.5
低
1017.5
高
1007.5 1002.5
低
* *
1017.5 1012.5
定小概率事件选择大概率事件
多个随机事件的关系
任一事件发生:和事件 几个事件同时发生:积事件 一事件发生则另一事件不发生:互斥 当只有两种事件时,互斥即对立
第七章 随机变量及其分布(章末小结课件)高二数学(人教A版2019选择性必修第三册)
(1)如图1,进行一次高尔顿板试验,求小球掉入5号球槽的概率.
(2)小红和小明在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板,付费6元可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .小明改进了高尔顿板(如图2),首先将小木块减少成5层,然后使小球在下落的过程中与小木块碰撞时,有 的概率向左, 的概率向右滚下,最后掉入编号为1, , , 的球槽内,改进高尔顿板后只需付费4元就可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .两位同学的高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小红和小明谁的盈利多?请说明理由.
方法总结 求离散型随机变量的均值、方差的步骤: 明确随机变量的取值,以及取每个值的试验结果; 求出随机变量取各个值的概率; 列出分布列; 用期望、方差公式求解; 标准差代入公式 求解.本题渗透了数据分析、数学运算的素养.
题型7 正态分布
例7 某物理量的测量结果服从正态分布 ,则下列结论中不正确的是( ).
方法总结 正态曲线的应用及求解策略:解答此类题目的关键在于将待求的问题向 , , 这三个区间进行转化,然后利用上述区间的概率求出相应的概率.解题过程渗透了直观想象、数学运算以及数据分析的素养.
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿( , —1911)是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟,虽然不像达尔文那样声名显赫,但也不是无名之辈.并且,高尔顿幼年是神童,长大是才子,九十年的人生丰富多彩,是个名副其实的博学家.他涉猎范围广泛,研究水平颇深,纵观科学史,在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等,还有与社会有关的人类学、民族学、教育学、宗教学,以及优生学、指纹学、照相术、登山术等等.
(2)小红和小明在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板,付费6元可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .小明改进了高尔顿板(如图2),首先将小木块减少成5层,然后使小球在下落的过程中与小木块碰撞时,有 的概率向左, 的概率向右滚下,最后掉入编号为1, , , 的球槽内,改进高尔顿板后只需付费4元就可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .两位同学的高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小红和小明谁的盈利多?请说明理由.
方法总结 求离散型随机变量的均值、方差的步骤: 明确随机变量的取值,以及取每个值的试验结果; 求出随机变量取各个值的概率; 列出分布列; 用期望、方差公式求解; 标准差代入公式 求解.本题渗透了数据分析、数学运算的素养.
题型7 正态分布
例7 某物理量的测量结果服从正态分布 ,则下列结论中不正确的是( ).
方法总结 正态曲线的应用及求解策略:解答此类题目的关键在于将待求的问题向 , , 这三个区间进行转化,然后利用上述区间的概率求出相应的概率.解题过程渗透了直观想象、数学运算以及数据分析的素养.
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿( , —1911)是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟,虽然不像达尔文那样声名显赫,但也不是无名之辈.并且,高尔顿幼年是神童,长大是才子,九十年的人生丰富多彩,是个名副其实的博学家.他涉猎范围广泛,研究水平颇深,纵观科学史,在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等,还有与社会有关的人类学、民族学、教育学、宗教学,以及优生学、指纹学、照相术、登山术等等.
随机变量的函数的分布ppt课件
布,且知一对夫妇有不超过1个孩子的概率为3e-2。求 任选一对夫妇,至少有3个孩子的概率。 解 由题意
X ~ p ( ) 且 P , X 1 P ( X 0 ) P ( X 1 ) 3 e 2
e e 3 e 2 2
P ( X 3 ) 1 P ( X 0 ) P ( X 1 ) P ( X 2 )
➢ k 阶中心矩:k = E[XE(X)]k , k = 1, 2, ….
注意: 2 = Var(X).
.
2.7.2 变异系数
方差(或标准差)反映了随机变量取值的 波动程度,但在比较两个随机变量大小时 会产生不合理的现象。 原因有二: (1)方差(或标准差)是有量纲的; (2)有一个相对性问题,取值较大的随机变量 的方差(或标准差)也允许大一些。
52051 60 2
.
例5 设有一项工程有甲、乙两家公司投标承包。甲公 司要求投资2.8亿元,但预算外开支波动较大,设实际 费用X~N(2.8,0.52)。乙公司要求投资3亿元,但预算外 开支波动较小,设实际费用Y~N(3,0.22)。现假定工程资 方掌握资金(1)3亿元,(2)3.4亿元,为了在这两种情况 下,不至造成资金赤字,选择哪家公司来承包较为合 理?
pY ( y)
pX [h( y)] | h( y) |
pX [ln
y]
1 y
1
y(1 ln 2 y)
由此得
pY ( y)
1 y(1 ln2
, y)
0,
y0 其它
.
正态变量的线性不变性
定理2.6.2 设 X ~N (, 2),则当a 0 时, Y = aX+b ~ N (a +b, a22).
习题
2、设随机变量 X 服从参数为的泊松分布,且 P{X 1} P{X 2},则 E(X)= ,D(X)=
X ~ p ( ) 且 P , X 1 P ( X 0 ) P ( X 1 ) 3 e 2
e e 3 e 2 2
P ( X 3 ) 1 P ( X 0 ) P ( X 1 ) P ( X 2 )
➢ k 阶中心矩:k = E[XE(X)]k , k = 1, 2, ….
注意: 2 = Var(X).
.
2.7.2 变异系数
方差(或标准差)反映了随机变量取值的 波动程度,但在比较两个随机变量大小时 会产生不合理的现象。 原因有二: (1)方差(或标准差)是有量纲的; (2)有一个相对性问题,取值较大的随机变量 的方差(或标准差)也允许大一些。
52051 60 2
.
例5 设有一项工程有甲、乙两家公司投标承包。甲公 司要求投资2.8亿元,但预算外开支波动较大,设实际 费用X~N(2.8,0.52)。乙公司要求投资3亿元,但预算外 开支波动较小,设实际费用Y~N(3,0.22)。现假定工程资 方掌握资金(1)3亿元,(2)3.4亿元,为了在这两种情况 下,不至造成资金赤字,选择哪家公司来承包较为合 理?
pY ( y)
pX [h( y)] | h( y) |
pX [ln
y]
1 y
1
y(1 ln 2 y)
由此得
pY ( y)
1 y(1 ln2
, y)
0,
y0 其它
.
正态变量的线性不变性
定理2.6.2 设 X ~N (, 2),则当a 0 时, Y = aX+b ~ N (a +b, a22).
习题
2、设随机变量 X 服从参数为的泊松分布,且 P{X 1} P{X 2},则 E(X)= ,D(X)=
概率论与数理统计课件:多维随机变量及其分布
多维随机变量及其分布
首页 返回 退出2
在实际问题中, 试验结果有时需要同时用两个或两
个以上的随机变量来描述.
如, 炮弹的弹着点的位置, (X, Y)是一个二维随
机变量.
又如,研究天气变化状况,令X, Y, Z分别表示
温度、湿度、风速,则(X, Y, Z)是一个三维随机变量.
研究多维随机变量有必要将多个变量作为一个整
二元函数
F ( x , y ) P{( X x ) (Y y )} P ( X x , Y y )
称为随机变量(X,Y)的联合分布函数。
一维随机变量X的联合分布
函数F ( x ) P ( X x ).
多维随机变量及其分布
首页 返回 退出
F(x,y)=P(X≤x,Y≤y)
y
F ( , y ) 0,
o
F ( x , ) 0,
F ( , ) 0, F ( , ) 1;
4 F ( x , y )关于x和y分别右连续;
x1
F ( x1 , y ) F ( x2 , y )
5 对于任意x1 x2 , y1 y2 , 有矩形公式
…
…
…
…
X
性质: 1 pij 0, i , j 1, 2, ;
2
p
i 1 j 1
多维随机变量及其分布
ij
1.
首页 返回 退出
例1 从1,2,3,4中任取一个数记为X、再从1,2, ⋯ ,
中任取一个数记为Y,求 ( X, Y ) 的联合分布律及P
( X=2Y ).
解:
可以证明,f(x,y)满足联合密度的性质。
人教版高中数学选修2-3课件:2.1 离散型随机变量及其分布列(共52张PPT)
预习探究
[探究] 以下随机变量是离散型随机变
量的是
.
①某部手机一小时内收到短信的次数
ξ;
②电灯泡的寿命ξ; ③某超市一天中的顾客量ξ; ④将一颗骰子掷两次出现的点数之和
ξ.
⑤连续不断地射击,首次命中目标所需
要的射击次数ξ.
④将一颗骰子掷两次出现点数之和ξ的取
值为2,3,…,12,是离散型随机变量;
三维目标
3.情感、态度与价值观 使学生感悟数学与生活的和谐之美,学会合作探讨,体验成功,提 高学习数学的兴趣.
重点难点
[重点] (1)随机变量、离散型随机变量的意义; (2)离散型随机变量的分布列的概念.
[难点] (1)随机变量、离散型随机变量的意义; (2)求简单的离散型随机变量的分布列.
教学建议
例1 指出下列变量中,哪些是随机变量, 哪些不是随机变量,并说明理由. (1)任意掷一枚质地均匀的硬币5次,出 现正面向上的次数; (2)投一颗质地均匀的骰子出现的点数 (最上面的数字); (3)某个人的属相随年龄的变化; (4)在标准状况下,水在0℃时结冰.
(3)属相是出生时便确定的,不随年龄的变化 而变化,不是随机变量. (4)标准状况下,水在0℃时结冰是必然事件, 不是随机变量.
P
分别求出随机变量η1=2ξ1,η2=ξ2的分布列.
当ξ取-1与1时,η2=ξ2取相同的值,故η2的分布 列为 η2 0 1 4 9
考点类析
例2 指出下列随机变量是不是离散型 随机变量,并说明理由. (1)从10张已编好号码的卡片(从1号到 10号)中任取1张,被取出的卡片的号数; (2)一个袋中装有5个白球和5个黑球,从 中任取3个,其中所含白球的个数; (3)某林场树木最高达30 m,则此林场中 树木的高度; (4)某加工厂加工的某种铜管的外径与 规定的外径尺寸之差.
