第二章 传输线理论
合集下载
电磁波第二章 传输线的基本理论

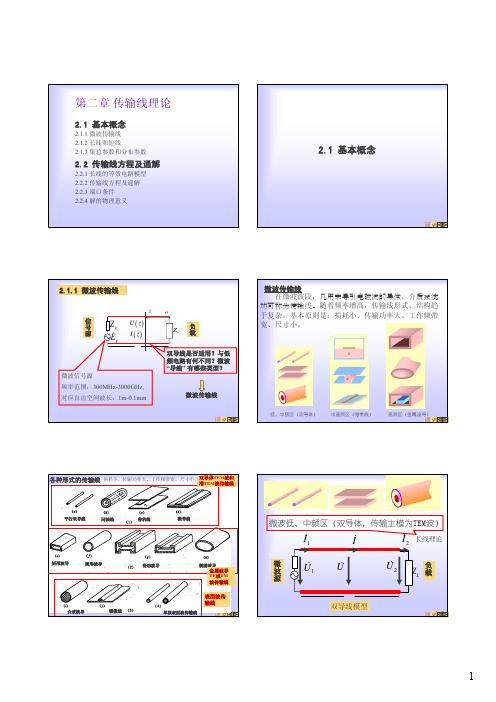
1 短线分布参数等效电路
短线分布参数可以用其集总的等效电路 表示。
z
iz, t
iz z, t
u z, t
L0 z R0 z
C 0 z G0 z
z
z
u z z, t
z z
一段传输线实际上就是由无穷多部分网络 链接的系统。
z
为什么高频条件下要考虑电路分布参数
1 2 L0 C 0 R0 G0 2 1 R0 G0 2 L0 C 0 2
解的具体形式
1 e l z 1 U Z I e l z U ( z ) U L Z 0 I L L 0 L 2 2 1 U L l z 1 U L ( z ) e l z I IL e Z0 I L 2 Z0 2 Z0
Z R 0 j L 0 Y G 0 jC 0
ZY (R0 jL0 )(G0 jC0 )
2
2 方程的通解
典型波动方程的解
U ( z ) A1e z A2 e z z z I ( z ) B1e B2 e 传播常数和波阻抗
f 0 50Hz
X L 2f 0 L0 2 50 0.99910
9
31410 / mm
3
BC 2f 0 C0 2 50 0.01111012 3.491012 S / mm
f 0 5000MHz
X L 2f 0 L0 2 5000106 0.999109 31.4 / mm
BC 2f 0 C0 2 5000106 0.01111012 3.49104 S / mm
第2章传输线理论

j z
1 2Z0
(U1
I1Z0 )e
j z
(2―2―14)
同样可以写成三角函数表达式
U (z)
U1 cos z
jZ0
sin z
I
(
z)
j
U1 Z0
sin
z
I1
cos
z
(2―2―15)
第2章 传输线理论
三、入射波和反射波的叠加 由式(2―2―5)和式(2―2―6)两式可以看出,传输线 上任意位置的复数电压和电流均有两部分组成,即有
U (z)
A1e j z
A2e j z
Ui(z) Ur(z)
I
(z)ຫໍສະໝຸດ 1 Z0A1e j z
1 Z0
A2e j z
Ii(z)
Ir(z)
(2―2―16)
第2章 传输线理论
根据复数值与瞬时值的关系,并假设A1、A2为实数, 则沿线电压的瞬时值为
u(z,t) Re[U (Z )e ji ] A1 cos(t z) A2 cos(t z)
式中v0为光速。由此可见,双线和同轴线上行波电
压和行波电流的相速度等于传输线周围介质中的光速,
它和频率无关,只决定周围介质特性参量ε,这种波称为
无色散波。
第2章 传输线理论
(三) 相波长λp
相波长λp是指同一个时刻传输线上电磁波的相位相 差2π的距离,即有
p
2
vp f
vpT
0 r
(2―3―5)
第2章 传输线理论
这种路的分析方法,又称为长线理论。事实上,“场” 的理论和“路”的理论既是紧密相关的,又是相互补充 的。有些传输线宜用“场”的理论去处理,而有些传输 线在满足一定条件下可以归结为“路”的问题来处理, 这样就可借用熟知的电路理论和现成方法,使问题的处 理大为简化。
第二章-传输线理论

第二章 传输线理论
根据传输线上的分布参数是否均匀分布,可将其分为 均匀传输线和不均匀传输线。我们可以把均匀传输线分割
成许多小的微元段dz (dz<<λ),这样每个微元段可看作集 中参数电路,用一个Γ型网络来等效。于是整个传输线可
等效成无穷多个Γ型网络的级联
第二章 传输线理论
2 - 2 无耗传输线方程及其解 一、传输线方程
即:
( ) I (z) = Ii2e jβ z + Ir2e- jβ z = Ii2 e jβ z + e- jβ z = 2Ii2 cos β z
( ) u(z,t) =
2Ui2
sin
β
z cos ω t
+
φ 2
+π
2
i(z,t) =
2
Ii2
cos β
z cos(ω t
+
φ) 2
第二章 传输线理论
=
-
Ur (z) Ir (z)
=
R0 + jωL1 G0 + jωC1
对于无耗传输线( R0 = 0, G0 = 0 ),则
Z0 =
L1 C1
对于微波传输线 ,也符合。
平行双线 同轴线 特性阻抗
在无耗或低耗情况下,传输线的特性阻抗为一实数, 它仅决定于分布参数L1和C1,与频率无关。
第二章 传输线理论
l = (2n +1) λ (n = 0,1,2,)
4
1.传输线上距负载为半波长整数倍的各点的输入阻抗等于负载阻抗;
2.距负载为四分之一波长奇数倍的各点的输入阻抗等于特性阻抗的
平方与负载阻抗的比值;
3.当Z0为实数,ZL为复数负载时,四分之一波长的传输线具有变换阻 抗性质的作用。
第二章 传输线理论总结

当Z0为实数时,电压入射波与电流入射波的相位 相同;电压反射波与电流反射波相位相反。
三、 传输线的特性参数
1、特性阻抗Z0
将传输线上导行波的电压与电流之比定义为传输线的 特性阻抗, 用Z0来表示, 其倒数称为特性导纳, 用Y0来表
示。
由定义得 Z 0
R1 jL1 G1 jC1
可见特性阻抗Z0通常是个复数, 且与工作频率有关。 它由传输 线自身分布参数决定而与负载及信源无关, 故称为特性阻抗。
或者
二、传输线方程
2. 时谐均匀传输线方程
a. 时谐传输线方程
对于时谐电压和电流, 可用复振幅表示为 v(z, t)=Re[V(z)e jωt] i(z, t)=Re[I(z)e jωt] 将上式代入(2.1-1)式, 即得时谐传输线方程:
dV ( z ) ( R1 jL1 ) I ( z ) Z1 I ( z ) dz (2.1-3) dI ( z ) (G1 jC1 )V ( z ) Y1V ( z ) dz Z1 R1 jL1 传输线单位长度的串联阻抗 式中 传输线单位长度的并联导纳 Y1 G1 jC1
(2.1-11)
二、传输线方程
2. 时谐均匀传输线方程
c. 电压、电流的定解
V (d ) VL chd I L Z 0 shd VL I (d ) shd I L chd Z0
写成矩阵形式:
(2.1-12)
chd V (d ) I (d ) shd Z0
无耗线 j L1C1
低耗线
0, L1C1
(2.1-22)
R1 G1Z 0 c d 2Z 0 2
(2.1-23)
传输线理论
u(z,t) → U (z) i(z,t) → I(z)
∂ → jω, ∂ → d
∂t
∂z dz
∂2 → ( jω )2 = −ω 2
∂t 2
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
∂u ∂z ∂i ∂z
= =
− R0 −G0
⋅
i
−
L0
⋅
∂i ∂t
⋅
u
−
C0dz
`
C0dz
G0dz
dz
z
z + dz
dz
,
t
)
dz → 0
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
∂u(z,
∂z
t
)
=
− R0
∂i(z,
∂z
t
)
=
−G0
⋅ i(z, t ) ⋅ u(z, t )
− −
L0 C0
⋅ ⋅
∂i(z, t
∂t
∂u(z,
∂t
)
t
)
称为时域传输线方程或电报方程
时域 → 频域
[ ] ⎪⎧u(z,t) = Re U (z)e jωt [ ] ⎪⎩⎨i(z,t) = Re I(z)e jωt
输送市电的电力传输线(f=50Hz, λ = 6000 km),长达6千 米, l /λ=0.001,为短线;对远距离电力传输线,线路可 能长达几百或几千千米时,则又应视为长线。
在微波技术中,所讨论的传输线都属于长线范畴。
长线和短线有何不同?
l < 0.05λ
“短线”是集总参数电路结构 l ≥ 0.05λ
u(z,t) → U (z), i(z,t) → I(z),∂ → jω, ∂ → d
∂t
《微波技术基础》第二章_传输线理论

i z, t z
3/1/2014
G1 ( z, t ) C1
z, t t
Sch.EIE Hefei Normal University
一般传输线方程、电报方程
13
i( z, t )
L1 z
R1 z
G1z
i(z z,t)
C1z (z z, t)
3/1/2014
9
Sch.EIE Hefei Normal University
二、传输线方程 1) 一般传输线方程或电报方程
i( z, t )
L1 z
R1 z
G1z
i(z z,t)
C1z (z z, t)
( z, t )
按泰勒级数展开, 忽略高次项
z
z, t z z i z z, t i z , t
D D2 d 2 / ln d 2 Rs d
C1 ( F / m)
W
d 2 Rs W W d
R1 ( / m)
2 2 D D d G1 ( S / m) / ln d 导体表面电阻 Rs 复介电常数 j
b 2 / ln a
换坐标:
d lz
VL I L Z 0 d VL I L Z 0 d V (d ) e e V (d ) V (d ) 2 2 VL I L Z 0 d VL I L Z 0 d I (d ) e e I (d ) I (d ) 2Z 0 2Z 0
3
Sch.EIE Hefei Normal University
第二章 传输线理论
2.1 传输线方程 2.2 分布参数阻抗 2.3 无耗线工作状态分析
第2章 传输线理论

第二章 传输线理论
五、反射系数
“路”的理 论
距终端z处的反射波电压U r (z)与入射波电压U i (z)之比 定义为该处的电压反射系数Γu(z),即
U r ( z ) A2 e − jβ z A2 − j 2 β z Γu ( z ) = = = e jβ z Ui ( z ) A1e A1
电流反射系数 终端反射系数
U i (z ) U r (z ) Z0 = == I i (z ) I r (z ) R1 + jωL1 G1 + jωC1
L1 对于无耗传输线( R1 = 0, G1 = 0 ),则 Z 0 = C1 对于微波传输线,也符合。
平行双线 同轴线 特性阻抗
在无耗或低耗情况下, 在无耗或低耗情况下,传输线的特性阻抗为一实数 它仅决定于分布参数L 它仅决定于分布参数 1和C1,与频率无关
β = 2πf L1C 1 量纲为1/m或者rad/m
第二章 传输线理论
二、相速度和相波长
“路”的理 论
相速度是指波的等相位面移动速度
dz ω = 一般:入射波的相速度为 v p = dt β 1 对于微波传输线 v p = L1C1
为TEM波(无色散波)
C 平行双线和同轴线:v p = εr
相波长定义为
“路”的理 论
根据复数振幅与瞬时值间的关系,可求得传输线上电压和电流的瞬时值表达式
= A1 cos ( ω t + β z ) + A2 cos ( ω t − β z ) = ui ( z,t ) + ur ( z,t )
i ( z,t ) = Re I ( z ) e jωt = A1 A cos ( ω t + β z ) − 2 cos ( ω t − β z ) = ii ( z,t ) + ir ( z,t ) Z0 Z0
第2.1章 传输线理论

——→与低频状态完全不同。
第二章 传输线理论
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。 其截面尺寸远小于线的长度, 而其轴向尺寸远比工作波长大 时,此时线上电压只沿传输线 方向变化。
一维分布参数电路理论
第二章 传输线理论
1)长线理论
传输线的电长度:传输线的几何长度 l 与其上 工作波长l的比值(l/l)。
当f =2GHz时
wLl = 2.3碬 3 / m > > Rl 10 wCl = 1.89S / m > > Gl
可忽略R和G的影响。——低耗线
第二章 传输线理论
P17表2.1-1给出了双导线、同轴线和平行板传输线的 分布参数与材料及尺寸的关系。
同轴线 a:内导体半径 b:外导体半径 m,e:填充介质 L(H/m)
①终端条件解:
边界条件: V (l ) = VL , I (l ) = I L
第二章 传输线理论
将上式代入解中: V = A e- g l + A e g l L 1 2
IL = 1 ( A1eZ0
gl
V ( z ) = A1e- g z + A2 eg z I ( z) = 1 ( A1e- g z - A2eg z ) Z0
第二章 传输线理论
2)时谐均匀传输线方程
a)时谐传输线方程 电压和电流随时间作正弦变化或时谐变化,则
电压电流的瞬时值可用复数来表示:
v ( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 e jwt e jy v ( z ) = Re 轾( z )e j wt V0 V 犏 犏 臌 臌 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾e jwt e jy I ( z ) = Re 轾 z )e j wt I0 I( 犏 犏 臌 臌
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
e j2 z
L
L
e j L 2 z
L
e j
第二章 传输线理论
输入阻抗与反射系数间的关系
Zin
z
Uz Iz
Ui z1 z Ii z1 z
Z0
1 1
z z
负载阻抗与终端反射系数的关系
ZL
Z0
Uz U1chz I1Z0shz
Iz U1 shz Z0 I1chz
第二章 传输线理论
三、入射波和反射波
根据复数振幅与瞬时值间的关系,可求得传输线上电压和电流的瞬时值表达式
uz,t Re U ze jt
A1ez cos t z A2ez cos t z = ui z,t ur z,t
当频率提高到微波波段时,这些分布效应不可忽 略,所以微波传输线是一种分布参数电路。这导致 传输线上的电压和电流是随时间和空间位置而变化 的二元函数。
第二章 传输线理论
根据传输线上的分布参数是否均匀分布,可将其分为 均匀传输线和不均匀传输线。我们可以把均匀传输线分割
成许多小的微元段dz (dz<<),这样每个微元段可看作集 中参数电路,用一个 型网络来等效。于是整个传输线可 等效成无穷多个 型网络的级联
U z A1e z A2e z
1
Iz Z0
A1e z A2 e z
将终端条件U (0)=U2, I (0)=I2代入上式可得
U 2 A1 A2
I2
1 Z0
A1
A2
解得
,。A1
1 2
U2
Z0I2
U K min
I min
1
1
U
I
1
max
max
第二章 传输线理论
传输线上反射波的大小,可用反射系数的模、驻波比 和行波系数三个参量来描述。
反射系数模的变化范围为 0 1
驻波比的变化范围为
1
,,
行波系数的变化范围为
0 K1
传输线的工作状态一般分为三种:
四、输入阻抗
定义:传输线终端接负载阻抗ZL时,距离终端z处向负载方向 看去的输入阻抗定义为该处的电压U (z)与电流I (z)之比,即
Zin
z
Uz Iz
均匀无耗传输线
传输线的输入阻抗
Zin z
U 2cos z sin z
jU 2 Z0
jI2 Z0sin z I2cos z
(2)当压振幅恒为最大值,即
U max 2 Ui2 而电流振幅恒为零, 这些点称之为电压的波腹点 和电流的波节点;
当 z n 2, n 0,1, 时,
电流振幅恒为最大值,而电压 振幅恒为零,这些点称之为电 流的波腹点和电压的波节点。
2 Ui2 Z0
2Ii2
Ii2
Ir2
复数表达式为
U z Ui2e j z Ur2e j z Ui2 e j z e j z j2Ui2 sin z
I z Ii2e j z Ir2e j z Ii2 e j z e j z 2Ii2 cos z
(1)行波状态
0, 1, K 1
(2)行驻波状态 (3)驻波状态
0 1 1 0 K 1
1, , K 0
第二章 传输线理论
七、传输功率
传输功率为
Pz
1 2 Re
UzI z
1 2
Re
Ui z
(3)传输线终端短路时,输入
阻抗为
Zin z
iz,t Re Ize jt
A1 ez cos t z A2 ez cos t z
Z0
Z0
= ii
z,t
ir
z,t
第一部分表示由信号源向负载方向传播的行波,称之为入射波。
其中为电压入射波,为电流入射波。
第二部分表示由负载向信号源方向传播的行波,称之为反射波。
K
第二章 传输线理论
2-4 均匀无耗传输线工作状态的分析
对于均匀无耗传输线,其工作状态分为三种: (1)行波状态;(2)驻波状态;(3)行驻波状态
一、行波状态(无反射情况)
uz,t ui z,t A1 cos t z
iz,t
ii z,t
A1 Z0
cos
第二章 传输线理论
2-2 传输线方程及其解
一、传输线方程
duz,t uz,t dz
z
diz,t iz,t dz
z
瞬时值u, i与复数振幅U, I 的关系为
uz,t Re Uze j t
iz,t Re Ize j t
三、相速和相波长 相速是指波的等相位面移动速度。
入射波的相速为
t
z
c
vp
dz dt
对于微波传输线
L0C0 vp
1 L0C0
所谓相波长定义为波在一个周期T内等相位 面沿传输线移动的距离。即
p
vpT
vp f
f
2
0 0
第二章 传输线理论
(2-4)
通解为
U z A1e z A2e z
1
Iz Z0
A1e z A2 e z
式中, Z0
R0 jL0 G0 jC0
R0 jL0 G0 jC0 j
第二章 传输线理论
1. 已知传输线终端电压U2和电流I2,沿线电压电流表达式
Ur z Ui z
A2e j z A1e j z
A2 e j2 z A1
电流反射系数
i z
Ir z Ii z
A2 A1
e j2 z
u z
终端反射系数
L
A2 A1
A2 A1
e j2 1
e j L
L
传输线上任一点反射系数 与终端反射系数的关系
射波与反射波迭加形成驻波分布。驻波状态意味着入射波功率一点也没有被负载吸 阿收,即负载与传输线完全失配。
1. 终端短路
U 2 0 A1 A2 Ui2 U r2 0 Ui2 U r2
1
I2
0
Z0
A1 A2
1 Ii2 Ir2 Z0 Ui2 Ur2
在许多情况下,例如并联电路的阻抗计算,采用导纳比较方便
Yin z
1
Zin z
Y0
YL Y0
jY0 jYL
tg tg
z z
第二章 传输线理论
五、反射系数
距终端z处的反射波电压Ur(z)与入射波电压Ui(z)之比
定义为该处的电压反射系数u(z),即
u z
入射波和反射波沿线 的瞬时分布图如图
第二章 传输线理论
2-3 传输线的特性参量
传输线的特性参量主要包括:传播常数、特性阻抗、 相速和相波长、输入阻抗、反射系数、驻波比(行波系数) 和传输功率等。 一、传播常数
传播常数一般为复数,可表示为
R0 jL0 G0 jC0 j
对于低耗传输线有(无耗传输线 R0 0, G0 0 )
R0 C0 G0
2 L0 2
L0C0
L0 C0
c d
0
无耗 L0C0
第二章 传输线理论
二、特性阻抗
传输线的特性阻抗定义为传输线上入射波电压Ui (z) 与入射波电流Ii (z)之比,或反射波电压Ur (z)与反射波 电流Ir (z)之比的负值,即
dz段的等效电路
dU z ZI z
dz
dIz YU z
dz
(2-3)
第二章 传输线理论
二、传输线方程的解
将式(2-3)两边对z再求一次微分,并令,可得
d
2U z
dz 2
2U
z
0
d 2Iz
dz 2
2 Iz 0
Z0
Ui z Ii z
Ur z Ir z
R0 jL0 G0 jC0
对于无耗传输线(R0 0, G0 0 ),则 对于微波传输线 ,也符合。
Z0
L0 C0
在无耗或低耗情况下,传输线的特性阻抗为一实数, 它仅决定于分布参数L0和C0,与频率无关。
第二章 传输线理论
Z0
2
1
z
2
z
z
为了简便起见,一般在电压波腹点(最大值点)
或电压波节点(最小值点)处计算传输功率,即
Pz 1 U
I
1
U
2 max
K
2 max min 2 Z0
在不发生击穿情况下,传输线允许传输的最 大功率称为传输线的功率容量
Pbr
1 2
U br 2 Z0
即:
uz,t 2Ui2 sin z cos t 2 2 iz,t 2 Ii2 cos z cos t 2
