北航离散数学第11章习题答案
离散数学课后习题答案

1.3.1习题1.1解答1设S = {2,a,{3},4},R ={{a},3,4,1},指出下面的写法哪些是对的,哪些是错的?{a}∈S,{a}∈R,{a,4,{3}}⊆S,{{a},1,3,4}⊂R,R=S,{a}⊆S,{a}⊆R,φ⊆R,φ⊆{{a}}⊆R⊆E,{φ}⊆S,φ∈R,φ⊆{{3},4}。
解:{a}∈S ,{a}∈R ,{a,4,{3}} ⊆ S ,{{a},1,3,4 } ⊂ R ,R = S ,{a}⊆S ,{a}⊆ R ,φ⊆ R ,φ⊆ {{a}} ⊆ R ⊆ E ,{φ} ⊆ S ,φ∈R ,φ⊆ {{3},4 } 2写出下面集合的幂集合{a,{b}},{1,φ},{X,Y,Z}解:设A={a,{b}},则ρ(A)={ φ,{a},{{b}},{a,{b}}};设B={1,φ},则ρ(B)= { φ,{1},{φ},{1,φ}};设C={X,Y,Z},则ρ(C)= { φ,{X},{Y},{Z},{X,Y },{X,Z },{ Y,Z },{X,Y,Z}};3对任意集合A,B,证明:(1)A⊆B当且仅当ρ(A)⊆ρ(B);(2)ρ(A)⋃ρ(B)⊆ρ(A⋃B);(3)ρ(A)⋂ρ(B)=ρ(A⋂B);(4)ρ(A-B) ⊆(ρ(A)-ρ(B)) ⋃{φ}。
举例说明:ρ(A)∪ρ(B)≠ρ( A∪B)证明:(1)证明:必要性,任取x∈ρ(A),则x⊆A。
由于A⊆B,故x⊆B,从而x∈ρ(B),于是ρ(A)⊆ρ(B)。
充分性,任取x∈A,知{x}⊆A,于是有{x}∈ρ(A)。
由于ρ(A)⊆ρ(B),故{x}∈ρ(B),由此知x∈B,也就是A⊆B。
(2)证明:任取X∈ρ(A)∪ρ(B),则X∈ρ(A)或X∈ρ(B)∴X⊆A或X⊆B∴X⊆(A∪B)∴X∈ρ(A∪B)所以ρ(A)∪ρ(B) ⊆ρ( A∪B)(3)证明:先证ρ(A)∩ρ(B) ⊆ρ( A∩B)任取X∈ρ(A)∩ρ(B),则X∈ρ(A)且X∈ρ(B)∴X⊆A且X⊆B∴X⊆ A∩B∴X∈ρ( A∩B)所以ρ(A)∩ρ(B) ⊆ρ( A∩B)再证ρ( A∩B) ⊆ρ(A)∩ρ(B)任取Y∈ρ(A∩B),则Y⊆ A∩B∴Y⊆A且Y⊆B∴Y∈ρ(A)且Y∈ρ(B)∴Y∈ρ(A)∩ρ(B)所以ρ( A∩B) ⊆ρ(A)∩ρ(B)故ρ(A)∩ρ(B) = ρ( A∩B)得证。
离散数学(第二版)最全课后习题答案详解

-
(10)
p:天下大雨
q:他乘车上班
-
(11)
p:下雪
q:路滑
r:他迟到了
(12)
p:2 是素数
q:4 是素数
-
(13)
p:2 是素数
q:4 是素数
-
15.设 p:2+3=5. q:大熊猫产在中国. r:太阳从西方升起. 求下列符合命题的真值:
(1)
(2)
(3) (4) 解:p 真值为 1,q 真值为 1,r 真值为 0. (1)0,(2)0,(3)0,(4)1 16.当 p,q 的真值为 0,r,s 的真值为 1 时,求下列各命题公式的真值: (1) (2) (3) (4)
24.已知 的类型.
解:∵
是重言式,试判断公式
及
是重言式,而要使该式为重言式,其成真赋值只有
11,∴ 25.已知
解:∵
的类型.
都是重言式。
Hale Waihona Puke 是矛盾式,试判断公式及
是矛盾式,而要使该式为矛盾式,其成假赋值
只有 00,∴
都是重言式。
26. 已 知 解:
是重言式, 及
是矛盾式,试判断 的类型.
是矛盾式。
是重言式。
q:老王是河北人
-
(3)
p:天气冷
p:王欢与李乐组成
(4)
一个小组
p:李辛与李末是兄
(5)
弟
q:我穿羽绒服 -
-
p:王欢与李乐组成一个
-
小组
-
p:李辛与李末是兄弟
(6) p:王强学过法语
q:刘威学过法语
-
(7)
p:他吃饭
q:他听音乐
-
离散数学习题答案.docx

精品文档离散数学习题答案习题一及答案:( P14-15 )14、将下列命题符号化:( 5)李辛与李末是兄弟解:设 p:李辛与李末是兄弟,则命题符号化的结果是p( 6)王强与刘威都学过法语解:设 p:王强学过法语; q:刘威学过法语;则命题符号化的结果是p q ( 9)只有天下大雨,他才乘班车上班解:设 p:天下大雨; q:他乘班车上班;则命题符号化的结果是q p( 11)下雪路滑,他迟到了解:设 p:下雪; q:路滑; r :他迟到了;则命题符号化的结果是( p q)r15、设 p: 2+3=5.q:大熊猫产在中国 .r:太阳从西方升起 .求下列复合命题的真值:( 4)(p q r )(( p q)r )解: p=1, q=1,r=0 ,(p q r )(110)1,((p q)r )((11)0)(00)1(p q r )(( p q)r ) 1 1119、用真值表判断下列公式的类型:( 2)( p p)q解:列出公式的真值表,如下所示:p q p qp) ( p p)q( p001111011010100101110001由真值表可以看出公式有 3 个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:精品文档( 4)( p q)q解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:( p q)1p0q0q0所以公式的成真赋值有: 01,10, 11。
习题二及答案:( P38)5、求下列公式的主析取范式,并求成真赋值:( 2)(p q) (q r )解:原式( p q) q r q r( p p) q r( p q r ) ( p q r )m3m7,此即公式的主析取范式,所以成真赋值为011, 111。
6、求下列公式的主合取范式,并求成假赋值:( 2)( p q) ( p r )解:原式( pp r ) ( p q r )( p q r )M 4,此即公式的主合取范式,所以成假赋值为 100。
离散数学(第二版)最全课后习题答案详解

4.将下列命题符号化,并指出真值. (1)2 与 5 都是素数
答:p:2 是素数,q:5 是素数,符号化为 p q∧ ,其真值为 1.
(2)不但 π 是无理数,而且自然对数的底 e 也是无理数. 答:p:π 是无理数,q:自然对数的底 e 是无理数,符号化为 p q∧ ,其真值为 1.
若 p 为真,则真值为 0;若 p 为假,则真值为 1
14.将下列命题符号化:
(1) 刘晓月跑得快,跳得高;
(2) 老王是山东人或者河北人;
(3) 因为天气冷,所以我穿了羽绒服;
(4) 王欢与李乐组成一个小组;
(5) 李欣与李末是兄弟;
(6) 王强与刘威都学过法语;
(7) 他一面吃饭,一面听音乐;
(8) 如果天下大雨,他就乘班车上班;
1
0
1
0
1
0
0
1
1
1
0
0
0
0
1
0
1
0
1
1
1
1
0
0
1
0
1
0
1
0
0
1
1
1
此式为可满足式
20.求下列公式的成真赋值: (1)
(2)
(3)
(4)
p
q
解:
0
0
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
0
1
由真值表得:(1)的成真赋值是 01,10,11(2)的成真赋值是 00,10,11
离散数学第11章答案(刘玉珍 刘永梅)

习题11.11. 若n 个顶点的简单无向图G 中至少有2个孤立点,则结论自然成立;若G 中只有一个孤立点,而2n ≥,则G 中至少有3个顶点,其中至少有2个非孤立点,可不考虑孤立点;若G 中无孤立点,则G 中n 个顶点度数均不小于1.现设G 中n 个顶点的度数均不小于1,又G 为简单图,故所有顶点的度数均不大于n-1,即n 个顶点的度数的取值只能是1,2,…,n-1,由鸽舍原理知,结论成立。
2. 设G 有x 个顶点,则92)6(36)deg(122>⇒⨯-+⨯≤=⨯∑∈x x v Vv3. m n k n k n n k n v m k k k Vv 2)1()1()()deg(2-+=⇒+⨯-+⨯==∑∈4. ∑∈∈⨯≤=≤∈⨯Vv V v v n v m V v v n })max{deg()deg(2})deg(min{故所证不等式成立。
5.(1)非同构的4个顶点的自补图只有一个;非同构的5个顶点的自补图有2个(2)G 为自补图⇒G 与G 的边数相同,设均为m ,又G 与G 的边数之和为n K 的边数2)1(-n n ,即2)1(-n n =2m ,亦即)1(-n n =4m ,故n 为4的倍数,即n=4k ,或n-1为4的倍数,即n=4k+1,+∈I k6.(1)<0,1,1,2,3,3>,<3,3,3,3>均为可图解的,其对应图为<1,3,3,3>非可图解,否则,设3)deg()deg()deg(,1)deg(4321====v v v v ,由于要构成无向简单图,故,1v ,2v ,3v ,4v 之间必定有边关联,这与1)deg(1=v 矛盾,< 2,3,4,4,5>,<2,2,4>非可图解,以为简单图中所有顶点的度数多为n-1。
<1,2,2,3,4,5>z 中有奇数个,故非可图解。
(2)充分性:<1d 2-,1d 3-,…, 1d 1d -,1d 1d 1-+,2d 1d +,…,n d >可图解⇒添加度数为1d 的顶度,与度数为1d 2-,1d 3-,…, 1d 1d -,1d 1d 1-+的顶点相邻⇒<1d ,2d ,…, n d >可图解。
离散数学习题答案解析

离散数学习题答案解析(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p:李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语∧解:设p:王强学过法语;q:刘威学过法语;则命题符号化的结果是p q(9)只有天下大雨,他才乘班车上班→解:设p:天下大雨;q:他乘班车上班;则命题符号化的结果是q p (11)下雪路滑,他迟到了解:设p:下雪;q:路滑;r:他迟到了;则命题符号化的结果是()∧→p q r 15、设p:2+3=5.q:大熊猫产在中国.r:太阳从西方升起.求下列复合命题的真值:(4)()(())∧∧⌝↔⌝∨⌝→p q r p q r解:p=1,q=1,r=0,∧∧⌝⇔∧∧⌝⇔,p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型:(2)()→⌝→⌝p p q解:列出公式的真值表,如下所示:由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值: (4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值: (2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式, 所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式, 所以成假赋值为100。
离散数学答案版(全)

Q
P Q
( P Q)
( P Q) Q
0 0 1 1
0 1 0 1
1 1 0 1
0 0 1 0
0 0 0 0
1.4.2 命题公式的分类 定义 设 G 为公式: (1)如果 G 在所有解释下取值均为真,则称 G 是永真式 或重言式; (2)如果 G 在所有解释下取值均为假,则称 G 是永假式或矛盾式; (3) 如果至少存在一种解释使公式 G 取值为真,则称 G 是可满足式。 1.4.3 等价公式 定义 设 A 和 B 是两个命题公式,如果 A 和 B 在任意赋值情况下都具有相同 的真值,则称 A 和 B 是等价公式。记为 A B。 性质定理 设 A、B、C 是公式,则 (1)A A (2)若 A B 则 B A (3)若 A B 且 B C 则 A C 定理 设 A、B、C 是公式,则下述等价公式成立: A A (1)双重否定律 (2)等幂律 A∧A A ; A∨A A (3)交换律 A∧B B∧A ; A∨B B∨A (4)结合律 (A∧B)∧C A∧(B∧C) (A∨B)∨C A∨(B∨C) (5)分配律 (A∧B)∨C (A∨C)∧(B∨C) (A∨B)∧C (A∧C)∨(B∧C) (A∨B) A∧ B (6)德·摩根律 (A∧B) A∨ B (7)吸收律 A∨(A∧B) A;A∧(A∨B) A (8)零一律 A∨1 1 ; A∧0 0 (9)同一律 A∨0 A ; A∧1 A (10)排中律 A∨ A 1 (11)矛盾律 A∧ A 0 (12)蕴涵等值式 A→B A∨B (13)假言易位 A→B B→ A (14)等价等值式 A B (A→B)∧(B→A)
式中每一个析取项都是 P1,P2,…,Pn 的一个极大项,则称该合取范式为 G 的主 合取范式。通常,主合取范式用↕表示。重言式的主合取范式中不含任何极大项, 用 1 表示。 定理 任意的命题公式都存在一个唯一的与之等价的主合取范式。
离散数学第十一章群和环习题答案
习题十五
16
证明:每个阶数大于1的群必含有阶数大于1的交换子群. 证明: 因为G的阶数大于1,必有周期大于1的元aG,构造H=(a),即 为所求。
习题十五
17
证明:循环群的子群必是循环群. 证明: 设G的生成元为a, H为G的子群,并且H中具有最小正幂的元是 ak, G=(a), HG, H={e, ak, ak2, ak3,…},设ak是H中具有最小正指数 的元, amH,证明am=(ak)* ,H=(ak), 则 amH,令m=tk+r (0r<k), 则am=(ak)t ar, 由k的选择知,r=0, 即am=(合,试确定<A, +, >是否成环、整环或域。 (1)A={x|xZ且x 0},无加法逆元,不是环 (2)A={a+b√3|a,bQ},是域 (3)A={x|(y)[yZ且x=2y]}, 由偶数构成,是环,但无法幺元, 不是整环,不是域。 (4)A={a/b|a,b为正整数,且(a,b)=1},既约分数,但无0,不构 成环。
习题十五 30
设<G, · >是群,a是G中一个固定元素,定义映射f:G → G使得对任何x G,f(x)=a· a-1. 求证:f是G的 x· 自同构映射。
证明: 容易证明f是G的同态映射, f(x· =a· y· -1 =a· a-1· y· -1 y) x· a x· a· a =f(x) ·f(y) 再证明f是双射, 证单射:f(x)=f(y), a· a-1 = a· a-1 x=y x· y· 证满射:令a· a-1 = y, x=a-1· a x· y·
c
c
c c
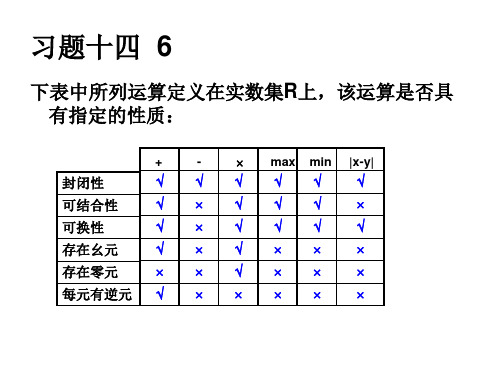
附加题:确定 2S,、 2S,、2S,各属于 哪一个层次?
• 2S,:闭,结,幺= S,无逆元,故含幺半群。 • 2S,:闭,结,幺= ,无逆元,故含幺半群。 • 2S,:闭,结,幺= ( A=A, AA= )A-1=A, 群。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章习题答案
3. 对图11.3的有向图,找出从u 1到u 4的长度为2,3,4的所有通路,并找出顶点u 4上的长
度为2,3,4的所有回路。
用M 2,M 3,,M 4
,来验证这些结果。
解:从u 1到u 4长度为2的通路有1条:(u 1,u 2,u 4)
从u 1到u 4长度为3的通路有2条:(u 1,u 2,u 3,u 4),(u 1,u 4,u 2,u 4) 从u 1到u 4长度为4的通路有3条:(u 1,u 2,u 3,u 2,u 4),(u 1,u 2,u 4,u 2,u 4),(u 1,u 4,u 2,
u 3,u 4)
顶点u 4上的长度为2的回路有1条:(u 4,u 2,u 4) 顶点u 4上的长度为3的回路有1条:(u 4,u 2,u 3,u 4) 顶点u 4上的长度为4的回路有2条:(u 4,u 2,u 3,u 2,u 4),(u 4,u 2,u 4,u 2,u 4)
M =⎥⎥
⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0010
101011001010 M 2=⎥⎥
⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11
00111010201110
M 3
=⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎣⎡10
20
212022102120
M 4
=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡221
323031403230
由M 2
,M 3
,,M 4
中的第1行第4列的元素可见,从u 1到u 4长度为2,3,4的通路分别有1
条,2条,3条。
由M 2,M 3,,M 4
中的第4行第4列的元素可见,u 4上的长度为2,3,4的回路分别有1条,1条,2条,说明所找的上述通路和回路正确。
5. 设有向图D 具有顶点集合{u 1,u 2,…,u n },M 是D 的邻接矩阵。
证明对于i ≠j 和k=1,2,…,
n-1,如果M k
(k=1,2,…,n-1)中第i 行第j 列上的元素均为0,则u i 和u j 必定属于D 的不同的强分图。
证明:假设u i 和u j 属于D 的同一个强分图,则u i 和u j 互相可达。
由定理9.2可知,从一顶点到另一顶点可达,则有基本通路,因此存在u i 到u j 的基本通路。
已知有向图D 中有n 个顶点,根据定理9.4:n 个顶点的有向图中,任何基本通路的长度都不超过n-1。
因此存在
u i 到u j 的长度不超过n-1的基本通路。
然而,根据定理11.1和已知条件:M k
(k=1,2,…,n-1)中第i 行第j 列上的元素均为0,说明从u i 到u j 不存在长度小于或等于n-1的通路。
这与前面所述存在u i 到u j 的长度不超过n-1的基本通路矛盾,因此u i 和u j 必定属于D 的不同的强分图。
6. 试用图11.4的有向图的邻接矩阵求出可达性矩阵,并利用可达性矩阵求其强分图。
解:
M=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0001010000000010100000010 M 2
=⎥⎥⎥
⎥
⎥⎥⎦⎤
⎢⎢⎢
⎢⎢⎢⎣⎡010*******
00010
1000001000
M 3
=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10000
010*******
0001010000 M 4
=⎥⎥⎥
⎥
⎥⎥⎦⎤
⎢⎢⎢
⎢⎢⎢⎣⎡0001001000
10000
010*******
I+M+M 2+M 3+M 4
=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢
⎢⎣⎡10000
010*******
0001000001
+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎢
⎢⎣⎡0001
01000
00000
1010000001
0+⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢
⎢⎢
⎢⎣⎡0100
00001
00001
010*******
0+
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡10000
01000010000001010000 +⎥⎥⎥
⎥⎥⎥⎦⎤
⎢⎢⎢
⎢⎢
⎢⎣⎡000100100010000
010******* =
⎥⎥⎥
⎥
⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎣⎡21020
13010111110202011021
R=B (I+M+M 2+M 3+M 4
)=⎥⎥⎥
⎥
⎥⎥⎦⎤
⎢⎢⎢⎢⎢
⎢⎣⎡11010
1101011111
1101011011
R T =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣
⎡1111111111001001111100101 R ×R T =⎥⎥⎥⎥
⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎣⎡1101011010001001101000001 由矩阵R ×R T 可知,该有向图的强分图有:{v 1},{ v 2,v 4,v 5},{ v 3}。
