清华大学-理论力学-习题解答-9-01
理论力学习题解答第九章

9-1在图示系统中,均质杆OA 、AB 与均质轮的质量均为m ,OA 杆的长度为1l ,AB 杆的长度为2l ,轮的半径为R ,轮沿水平面作纯滚动。
在图示瞬时,OA 杆的角速度为ω,求整个系统的动量。
ω125ml ,方向水平向左题9-1图 题9-2图9-2 如图所示,均质圆盘半径为R ,质量为m ,不计质量的细杆长l ,绕轴O 转动,角速度为ω,求下列三种情况下圆盘对固定轴的动量矩: (a )圆盘固结于杆;(b )圆盘绕A 轴转动,相对于杆OA 的角速度为ω-; (c )圆盘绕A 轴转动,相对于杆OA 的角速度为ω。
(a )ω)l R (m L O 222+=;(b )ω2ml L O =;(c )ω)l R (m L O 22+= 9-3水平圆盘可绕铅直轴z 转动,如图所示,其对z 轴的转动惯量为z J 。
一质量为m 的质点,在圆盘上作匀速圆周运动,质点的速度为0v ,圆的半径为r ,圆心到盘中心的距离为l 。
开始运动时,质点在位置0M ,圆盘角速度为零。
求圆盘角速度ω与角ϕ间的关系,轴承摩擦不计。
9-4如图所示,质量为m 的滑块A ,可以在水平光滑槽中运动,具有刚性系数为k 的弹簧一端与滑块相连接,另一端固定。
杆AB 长度为l ,质量忽略不计,A 端与滑块A 铰接,B 端装有质量1m ,在铅直平面内可绕点A 旋转。
设在力偶M 作用下转动角速度ω为常数。
求滑块A 的运动微分方程。
t l m m m x m m kxωωsin 2111+=++9-5质量为m,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A 和薄铁环B 的质量均为m ,半径都等于r ,两者用杆AB 铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为θ,如图所示。
如杆的质量忽略不计,求杆AB 的加速度和杆的内力。
θsin 74g a =; 9-7均质圆柱体A 和B 的质量均为m ,半径为r ,一绳缠在绕固定轴O 转动的圆柱A 上,绳的另一端绕在圆柱B 上,如图所示。
理论力学习题解答第九章

理论力学习题解答第九章题9-2图9-2 如图所示,均质圆盘半径为R,质量为m ,不计质量的细杆长,绕轴O转动,角速度为,求下列三种情况下圆盘对固定轴的动量矩:(a)圆盘固结于杆;(b)圆盘绕A轴转动,相对于杆OA的角速度为;(c)圆盘绕A轴转动,相对于杆OA的角速度为。
(a);(b);(c)9-3水平圆盘可绕铅直轴转动,如图所示,其对轴的转动惯量为。
一质量为m的质点,在圆盘上作匀速圆周运动,质点的速度为,圆的半径为r,圆心到盘中心的距离为。
开始运动时,质点在位置,圆盘角速度为零。
求圆盘角速度与角间的关系,轴承摩擦不计。
9-4如图所示,质量为m的滑块A,可以在水平光滑槽中运动,具有刚性系数为k的弹簧一端与滑块相连接,另一端固定。
杆AB长度为l,质量忽略不计,A端与滑块A铰接,B端装有质量,在铅直平面内可绕点A旋转。
设在力偶M作用下转动角速度为常数。
求滑块A的运动微分方程。
9-5质量为m ,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A和薄铁环B的质量均为m,半径都等于r,两者用杆AB铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为,如图所示。
如杆的质量忽略不计,求杆AB的加速度和杆的内力。
;9-7均质圆柱体A和B的质量均为m,半径为r,一绳缠在绕固定轴O转动的圆柱A上,绳的另一端绕在圆柱B上,如图所示。
摩擦不计。
求:(1)圆柱体B下落时质心的加速度;(2)若在圆柱体A上作用一逆时针转向,矩为M 的力偶,试问在什么条件下圆柱体B的质心加速度将向上。
9-8平面机构由两匀质杆AB,BO组成,两杆的质量均为m,长度均为l,在铅垂平面内运动。
在杆AB上作用一不变的力偶矩M,从图示位置由静止开始运动。
不计摩擦,试求当A即将碰到铰支座O时A 端的速度。
9-9长为l、质量为m的均质杆OA以球铰链O固定,并以等角速度绕铅直线转动,如图所示。
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
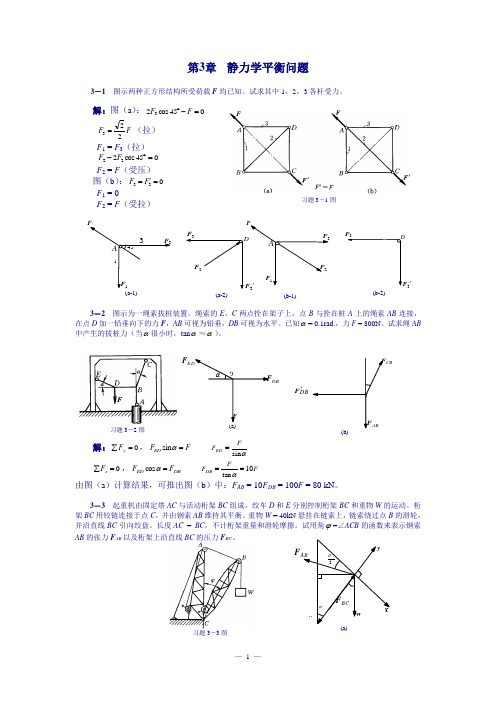
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
清华大学版理论力学课后习题答案大全

第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕc o s )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
《理论力学》第5-9章习题参考解答
《理论力学》第7章-习题解答
D
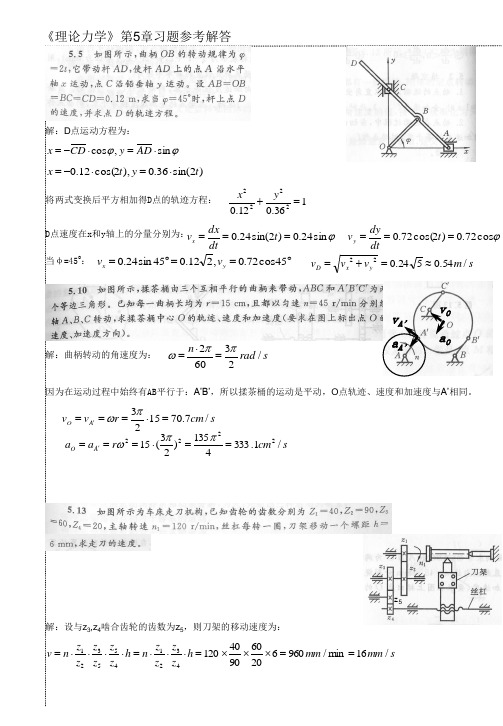
dϕ π 解:OA转动的角速度为 ω = = (rad / s ), v A = OA ⋅ ω = 0.05π (m / s ) dt 3 7π π 当s=7s时: ϕ = = 2π + , OB = OA = 0.15(m) 3 3 2 2 BD = OB tan ϕ = 0.15 3 (m), O1 B = O1O + OB = 0.25(m) BD v A = 0.05 3π (m / s ) 根据vA和vB可以确定AB的速度瞬心在D点: vB = OA
r F
a
r F
a
FN
图a
r G
FN
图b
r G
解:①当加速度较小时,物块A会有向下滑的趋势,受力图如图a,动力学方程为:
G 2 2 a = FN −F (1) g 2 2 2 2 0=F + FN − G (2) 2 2 1− f 联立(1)(2)(3)求得: a≥ g 1+ f
其中:
F ≤ FN f
ωOC
解:设杆AB上的A点为动点,摇杆OC为动系,则由速度合成定理得:
r r r v A = vr + ve
其中:
vA = v
r ac
r aA r ar rτ ae
r ve
α OC
r vA
r vr
将矢量方程分别在ve 和vr方向投影得:
Hale Waihona Puke r aenvr = v A sin ϕ = v sin 45°, ve = v A cos ϕ = v cos 45° v v cos 45° v 所以摇杆OC的角速度为: ωOC = e = = (方向如图所示) L OA 2L cos 45° r rτ r n r r 由加速度合成定理得:a A = ae + ae + ar + ac L v 2 v2 v 2v 2 2 n 其中: a A = 0, ae = OA ⋅ ωOC = ( ) = , ac = 2ωOC vr = 2 v sin 45° = cos 45° 2 L 2L 2L 2 2L rτ 2v 2 将矢量方程在 ae 方向投影得: τ 2 a 2L = v 2 α 所以OA的角加速度为: OC = e = 2v τ L OA 2 L2 0 = aτ − ac , ae = ac = e 2L cos 45°
清华理论力学课后答案9

及其变分
答 1
yC1 = 2 l sinϑ1 ,
1 δyC1 = 2 l cosϑ1 ⋅ δϑ1 ;
1
1
后 yC2 = l sinϑ1 + 2 l sinϑ2 , δyC2 = l cosϑ1 ⋅δϑ1 + 2 l cosϑ2 ⋅δϑ2 。
G1 tan β − (G1 + G2 ) f ≤ F ≤ G1 tan β + (G1 + G2 ) f 。
(b) 解:本体与上题在于ϑ 是变量,只要将上题中的 β 表示成 h 的
函数即可。易见ϑ = 90� − β , tan β = cotϑ =
上式结果,分别得到(1) F =
R2 − h
h2
.khdaw.co 题 9-13 图
题 9-13 图(a)
www 任一虚位移:AB 杆绕 A 的虚转动 δϑ ,BC 杆的瞬时虚平移 δrB = hδϑ = δrC ,CD 杆绕 D
的虚转动 δϕ = δrC 2h 。列出虚功方程:
网 Mδϑ − F1δrB − F2hδϕ = 0 ,解得: M A = (F1 + F2 / 2)h 。
题 9-11 图(a) 其中, δrD = hδr l 。
解得: FAy = F1 − F2h / l 。
9-12 水平力 F1 和 F2 分别作用于杆 BC 和杆 CD 的中点,如图示。不计`杆重,试计算固
定端 A 的约束力偶 MA。
m 解:解除固定端的转动约束而成为固定铰链,并代之以约束力偶,如图( a)所示。给机构
G1
理论力学习题解答

1、力使物体运动状态发生改变的效应称为___。
(1)A.外效应B.内效应C.A和BD.都不是8、作用在物体上的力是____。
(196489:第01-1章理论力学:8) A.定位矢量B.滑动矢量C.旋转矢量D.双向矢量11、变形体在已知力系的作用下处于平衡状态,那么如将它看成刚体,其平衡______ (196492:第01-1章理论力学:11)A.不受影响B.不再平衡C.变形增加D.无法确定刚化原理:变形体在已知力系的作用下处于平衡状态,那么如将它看成刚体,其平衡不受影响。
但刚体的平衡条件对于变形体来说只是必要条件,而非充分条件。
14、在保持力偶矩的大小和力偶转向不变的条件下,力偶______在作用面内任意转移。
(196495:第01-1章理论力学:15)A.可以B.不可以C.点D.无法确定18、___不是力偶的三要素。
(196499:第01-1章理论力学:19) A.力偶矩的大小B.力偶的转向C.力偶的作用平面D.力偶的作用点19、两个力偶等效,力偶臂_相等,组成力偶的力的大小_相等。
A.一定/一定B.一定/不一定C、不一定/一定D.不一定/不一定23、“当力偶中任一力沿作用线移动时,力偶矩的大小_。
(24) A.增加B.减小C.不变D.无法确定25、下列关于力偶的说法_是正确的。
①两个力偶的三要素中有一个不相同,它们的作用效果也有可能相同;②力偶不能和一个力等效;③力偶对物体只有单纯改变旋转运动的作用,而无平移的作用;④力偶对物体的作用效应与力偶的作用位置无关,即为偶可以在作用平面内任意移动。
(196506:第01-1章理论力学:26)A.①②③B.②③④C.①②④D.①②③④28、二力平衡原理适用于_。
(196509:第01-1章理论力学:29) A.刚体B.变形体C.刚体和变形体D.任意物体37、力在正交坐标轴上的投影大小_力沿这两个轴的分力的大小。
(196518:第01-1章理论力学:38)A.大于B.小于C.等于D.不等于43、约束反力的方向与该约束所能限制的运动方向____。
清华大学版理论力学课后习题答案大全第9章动量矩定理及其应用

习题9-2图习题20-3图OxF Oy F gm gDdα习题20-3解图第9章动量矩定理及其应用9-1计算下列情形下系统的动量矩。
1.圆盘以ω的角速度绕O 轴转动,质量为m 的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度v r 运动到OM =s 处(图a );求小球对O 点的动量矩。
2.图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ,质心为C ,且AC =e ;轮子半径为R ,对轮心A 的转动惯量为J A ;C 、A 、B 三点在同一铅垂线上(图b )。
(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对B 点的动量矩;(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对B 点的动量矩。
解:1、2s m L O ω=(逆)2、(1)1()(Remv e v m mv p A A C +=+==ω(逆)Rv me J R e R mv J e R mv L AA A C CB )()()(22-++=++=ω(2))(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9-2图示系统中,已知鼓轮以ω的角速度绕O 轴转动,其大、小半径分别为R 、r ,对O 轴的转动惯量为J O ;物块A 、B 的质量分别为m A 和m B ;试求系统对O 轴的动量矩。
解:ω)(22r m R m J L B A O O ++=9-3图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ,并在点A 焊成一体。
若此结构在图示位置由静止状态释放,计算刚释放时,杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解:令m =m OA =50kg ,则m EC =2m 质心D 位置:(设l =1m)m6565===l OD d 刚体作定轴转动,初瞬时ω=0lmg lmg J O ⋅+⋅=22α222232)2(212131ml ml l m ml J O =+⋅⋅+=即mglml 2532=α2rad/s 17.865==g lαgl a D 362565t =⋅=α由质心运动定理:OyD F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N (↑)0=ω,0n=Da ,0=Ox F 习题9-1图(a )(b )习题9-5解图习题9-5图9-4卷扬机机构如图所示。
