自相关性的检验和处理实验报告

合集下载

实验四--自相关性的检验及修正

实验四 -- 自相关性的检验及修正实验四自相关性的检验及修正一、实验目的掌握自相关性的检验与处理方法。

二、实验学时： 2三、实验内容及操作步骤建立我国城乡居民储蓄存款模型，并检验模型的自相关性。

1.回归模型的筛选2.自相关的检验3.自相关的调整四、实验要求利用表 5-1 资料，试建立我国城乡居民储蓄存款模型，并检验模型的自相关性。

我国城乡居民储蓄存款与GDP统计资料（ 1978 年＝ 100）存款GDP 年份存款余额Y GDP指数X年份余额指数Y X19919241.6 199211759.4 199315203.5 199421518.8 199529662.3 199638520.8 199746279.8 199853407.5 199959621.8 200064332.4308.2200286910.6888.5 351.52003103617.7981.6 399.62004119555.41084.5 452.020051410511201.7 494.22006161587.31361.2 544.520071725341560.5 596.920082178851717.8 640.620092607721861.1 691.520103033022050.0 750.62011343635.92228.9 811.12410.3200173762.43995512012【实验步骤】（一）回归模型的筛选⒈相关图分析SCAT X Y相关图表明， GDP指数与居民储蓄存款二者的曲线相关关系较为明显。

现将函数初步设定为线性、双对数、对数、指数、二次多项式等不同形式，进而加以比较分析。

⒉估计模型，利用LS命令分别建立以下模型⑴线性模型： LS Y C Xy?62251.79175.4516 xt (-9.5629) (33.3308)R2＝ 0.9823 F＝1110.940S.E＝15601.32⑵双对数模型： GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNX?0.59996 1.7452 ln xln yt(-1.6069) (31.8572)R2＝ 0.9807 F＝ 1014.878 S.E＝0.1567⑶对数模型： LS YCLNX?y1035947170915.4 ln xt(-10.2355)(11.5094)R2＝0.8688 F ＝132.4672 S.E ＝42490.60⑷指数模型： LS LNY C Xln y? 9.5657 0.001581xt (55.0657) (11.2557)2R ＝ 0.8637 F＝126.6908 S.E＝0.4163LS Y CXX2?16271.5477.8476x0.0378x2yt(-2.4325)(6.1317) (7.8569)R2＝ 0.9958F＝2274.040 S.E＝ 7765.275⒊选择模型比较以上模型，可见各模型回归系数的符号及数值较为合理。

自相关的检验与修正

实验2自相关的检验与修正一、实验目的：
掌握自相关模型的检验方法与处理方法.。

二、实验内容及要求：
表1列出了1985－2007年中国农村居民人均纯收入与人均消费性支出的统计数据。

（1）利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。

（2）检验模型是否存在自相关。

（3）如果存在自相关，试采用适当的方法加以消除。

实验如下：
首先对数据进行调整，将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。

图1
1、用OLS估计法估计参数
图2
图3
图形分析：
图4
从图4中可以看出，中国农村居民人均消费性支出与人均纯收入存在着显着的正相关关系。

估计回归方程：。

从图8中可以得出此时的D.W.=1.324681，在取显着水平为5%，n=23，k=2，d L=1.26, d U=1.44，模型中d L<DW<d U，此时不能确定是否存在自相关。

在广义差分法无法完成修正的情况下，现建立对对数模型：
图9
对双对数模型进行调整：
图10
图11
从图11中可以得出此时的D.W.=1.985950，在取显着水平为5%，n=23，k=2，d L=1.26,
d U=1.44，模型中d U<DW<4-d U，此时不存在自相关。

由此完成对自相关的修正。

实验四--自相关性的检验及修正

实验四--自相关性的检验及修正
自相关性的检验是研究经济数据中自身序列的行为特征，它可用于识别趋势、判断虚
假反应、探究影响力以及衡量规律的发展变化，以及有助于指导未来政策的制定。

因此，自相关性检验是一项重要的经济学技术，它可以为序列分析获取相关信息，让研究者对特
定事件影响有更深刻的认识。

自相关性检验大概分为两个步骤：也就是统计学检验和模型修正。

统计学检验流程大
致包括参数估计、假设检验和结论。

其中，假设检验可以让研究者判断序列是否有自相关性，而参数估计则可以得到自相关性的大小和方向。

从模型修正的角度来说，研究的目的
是建立一个能够自相关数据的特性并形式化处理的模型，这个模型必须注意记录自相关数
据的自身行为特征。

研究者也可以尝试采用其他方法进行模型修正，比如添加外生变量、增加时间序列滞后期、建立自回归模型和分析突变点等。

自相关性检验和模型修正在实践中都带有一定的挑战，例如原始数据的质量，可能存
在噪声；外生变量的准确性和凝聚力；记录的常数和参数的可靠性；动态变化趋势的准确
性等。

因此，研究者在进行自相关性检验和模型修正时要注意仔细进行检测和修正，以确
保研究结果的可靠性和有效性。

实验报告(自相关性)

实验6.美国股票价格指数与经济增长的关系——自相关性的判定和修正一、实验内容：研究美国股票价格指数与经济增长的关系。

1、实验目的:练习并熟练线性回归方程的建立和基本的经济检验和统计检验；学会判别自相关的存在，并能够熟练使用学过的方法对模型进行修正。

2、实验要求：（1）分析数据，建立适当的计量经济学模型（2）对所建立的模型进行自相关分析（3）对存在自相关性的模型进行调整与修正二、实验报告1、问题提出通过对全球经济形势的观察，我们发现在经济发达的国家，其证券市场通常也发展的较好，因此我们会自然地产生以下问题，即股票价格指数与经济增长是否具有相关关系？GDP是一国经济成就的根本反映。

从长期看，在上市公司的行业结构与国家产业结构基本一致的情况下，股票平均价格的变动跟GDP的变化趋势是吻合的，但不能简单地认为GDP增长，股票价格就随之上涨，实际走势有时恰恰相反。

必须将GDP与经济形势结合起来考虑。

在持续、稳定、高速的GDP增长下，社会总需求与总供给协调增长，上市公司利润持续上升，股息不断增加，老百姓收入增加，投资需求膨胀，闲散资金得到充分利用，股票的内在含金量增加，促使股票价格上涨，股市走牛。

本次试验研究的1970-1987年的美国正处在经济持续高速发展的状态下，据此笔者利用这一时期美国SPI与GDP的数据建立计量经济学模型，并对其进行分析。

2、指标选择：指标数据为美国1970—1987年美国股票价格指数与美国GDP数据。

3、数据来源：实验数据来自《总统经济报告》（1989年），如表1所示：表14、数据处理将两组数据利用Eviews绘图，如图1、2所示：图1 GDP数据简图图2 SPI数据简图经过直观的图形检验，在1970-1987年间，美国的GDP 保持持续平稳上升，SPI 虽然有些波动，但波动程度不大，和现实经济相符，从图形上我们并没有发现有异常数据的存在。

所以可以保证数据的质量是可以满足此次实验的要求。

计量经济学自相关性检验实验报告

计量经济学自相关性检验实验报告计量经济学自相关性检验实验报告实验内容：自相关性检验商品进口主要由GDP决定。

为了考察GDP对商品进口的影响，可使用如下模型：；其中，X表示GDP，Y表示商品进口。

下表列出了中国1981--2000商品进口和国内生产总值的统计数据。

资料来源：《中国统计年鉴》一、估计回归方程OLS法的估计结果如下：Y=-8352.304+50.28935X （-2.838588）（17.36553）R2=0.943673，R2=0.940544，SE=7263.295，D.W.=0.870122。

二、进行序列相关性检验（1）图示检验法通过残差与残差滞后一期的散点图可以判断，随机干扰项存在不存在序列相关性。

（2）回归检验法一阶回归检验et=0.583346et-1+εt二阶回归检验et=1.444793et-1－1.172908et-2+εt可见：该模型存在二阶序列相关。

（3）杜宾-瓦森（D.W）检验法由OLS法的估计结果知：D.W.=0.870122。

本例中，在5%的显著性水平下，解释变量个数为2，样本容量为20，查表得dl=1.284，du=1.567,而D.W.=0.870122，小于下限dl=1.284，所以存在自相关性。

（4）拉格朗日乘数（LM）检验法由上表可知：含二阶滞后残差项的辅助回归为：et=668.0079-1.592283X+1.502666et-1－1.145731et-2(0.357417)(-0.822879) (5.825633) (-4.289558)R2=0.679813于是，LM=18×0.679813=12.236634，该值大于显著性水平为5%，自由度为2的χ序列相关性。

2的临界值Χ20.05，由此判断原模型存在2阶三、序列相关的补救（1）广义差分法估计模型由D.W.=0.870122，得到一阶自相关系数的估计值ρ=1-DW/2=0.564939则DY=Y-0.564939*Y(-1)， DX=X-0.564939*X(-1)；以DY为因变量，DX为解释变量，用OLS法做回归模型，这样就生成了经过广义差分后的模型。

异方差与自相关实验报告

实验报告三实验名称：异方差性与自相关性的检验与处理一、实验预习报告内容（一）实验目的与任务实验目的：掌握异方差性与自相关性的检验方法与处理方法；实验任务：建立并估计我国北方地区农业产出线性模型；建立合适的北京市城镇居民家庭简单消费函数。

（二）实验内容及要求1、异方差性的检验与处理方法（1）异方差性的图形法检验、Goldfeld-Quandt检验法；White检验法；（2）使用加权最小二乘法（WLS）对异方差性进行修正；2、自相关性的检验与处理方法（1）自相关性的图形法检验；杜宾-沃特森（D-W）检验（2）利用广义差分法、科克伦-奥克特（Cochrane-Orcutt）迭代法对自相关性进行修正；（三）实验设备与数据（1）计算机与Eviews3.1软件包（2）使用数据：异方差性实验数据：（见表3.1）自相关性实验数据：（见表3.2）二、实验操作原始数据任务一：表3.1给出的是1998年我国中药制造业销售收入与销售利润数据，试完成：（1）求销售收入与销售利润的样本回归函数，并对模型进行经济意义检验和统计检验；（2）分别用图形法、White检验法检验模型是否存在异方差；（3）如果模型存在异方差，选用一定方法对异方差进行修正。

任务二：表3.2是北京市城镇居民家庭人均收入与消费支出数据。

试完成：（1）运用OLS方法建立该市城镇居民家庭的消费函数。

（2）选用适当的方法检验是否存在序列相关（自相关）问题。

（3）如果存在自相关，选用适当估计方法加以修正。

表3.2 北京市城镇居民家庭人均收入和消费支出数据来源：各年《中国统计年鉴》三、实验报告内容（参见课程上机指导文件（PDF格式））（一）实验的主要步骤，内容及其结果分析异方差性检验和处理设原假设H0：模型中不存在异方差；备择假设H1：模型中存在异方差1.样本回归在Eviews软件中对序列X和序列Y进行操作，得到X和Y的简单散点图如下，可以看出X与Y是带有截距的近似线性关系。

《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤：（只需关键步骤）
1、分析→回归→线性→保存→残差
2、转换→计算变量；分析→回归→线性。

3、转换→计算变量；分析→回归→线性
三、实验结果分析：（提供关键结果截图和分析）
1.用普通最小二乘法建立y与x1和x2的回归方程，用残差图和DW检验诊断序列的自相关性；
由图可知y与x1和x2的回归方程为：
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283，查DW表，n=23，k=2，显著性水平由DW<1.26，也说明残差序列存在正的自相关。

自相关系数，也说明误差存在高度的自相关。

分析：从输出结果中可以看到DW=0.745，查DW表，n=52，k=3，显著性水平 =0.05，dL=1.47，dU=1.64.由DW<1.47，也说明残差序列存在正的自相关。

α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。

2.用迭代法处理序列相关，并建立回归方程；
回归方程为：y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716，
查DW 表，n=52，k=3，显著性水平0.5 由此可知DW 落入无自相关性区
域，说明残差序列无自相关
3.用一阶差分法处理序列相关，并建立回归方程；
从结果中看到回归残差的DW=2.042，根据P 104表4-4的DW 的取值范围来诊断，误差项。

计量经济学实验报告自相关

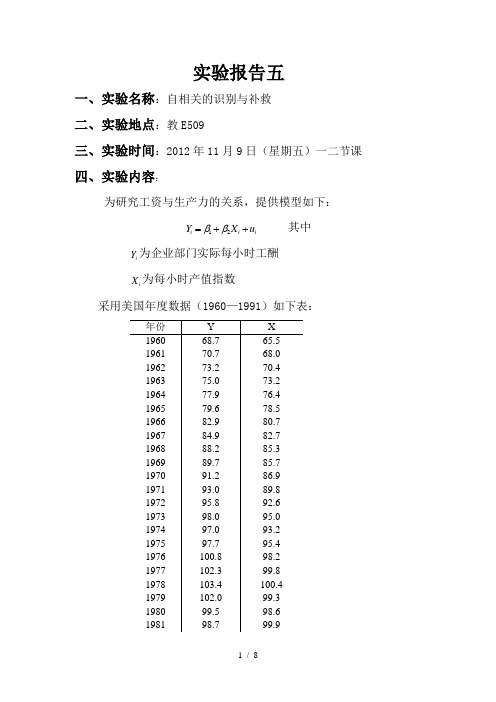
实验报告五一、实验名称：自相关的识别与补救二、实验地点：教E509三、实验时间：2012年11月9日（星期五）一二节课四、实验内容：为研究工资与生产力的关系，提供模型如下：12i i i Y X u ββ=++ 其中i Y 为企业部门实际每小时工酬 i X 为每小时产值指数采用美国年度数据（1960—1991）如下表：根据所给的模型与数据，利用计量经济学软件对模型参数进行估计，分析回归结果并完成以下问题：（1）根据DW 值判断是否存在自相关，并根据上述回归残差，画出残差与时间的关系图进行验证；（2）画出t e 与1t e -的散点图，判断自相关类型（3）分别用d 统计量、Cochrane-Orcutt 法与Durbin 两步法估计ρ，并对回归进行修正，比较修正结果，说明哪一种估计ρ的方法好。

五、实验目的：1. 掌握自相关的识别方法2. 能针对具体问题提出解决自相关问题的措施3. 对不同解决自相关方法的效果进行比较六、实验步骤1、建立模型： 12i i i Y X u ββ=++其中i Y 为企业部门实际每小时工酬，i X 为每小时产值指数2、运用OLS 估计方法对上式的参数进行估计，EViews 过程如下：（1）在File 菜单下选择New 项，建立文件库Workfile ，输入起始与终止时间，分别为1960和1991.（2）在File菜单下点击Import下点击Read Text-Lotus-Excel在桌面上找到Excel数据，点击打开，在Excel Spreadsheet Import对话框中的Name for series or Number if named in file输入Y x，点击OK。

（3）点击Quick菜单下的Estimate Equation,在新对话框中输入Y C x，点击确定。

会出现下面结果：3、自相关检验（1）图示法由上述OLS估计，可直接得到残差resid，运用GENR生成序列E，则在quick菜单中选graph项，在图形对话框里键入:E E(-1),可得到结果：由上表可知：残差e呈线性回归，表明随机误差u存在自相关。

自相关性的检验和处理实验报告

ˆ 1
3.7831 13.9366 1 0.72855
由此，我们得到最终的收入-消费模型为
Yt 13.9366 0.9484 X t
二、根据北京市连续 19 年城镇居民家庭人均收入与人均支出的数据进行相关分析 1、建立居民收入-消费函数以人均实际收入为 X，人均实际支出为 Y，创建工作文件，输入数据，命令如下： Create a 1 19 Data x y 建立居民收入-消费模型，输入命令 ls y c x，回归结果如下：
ˆ 0.72855 ，对原模型进行广义差分，得到差 ˆ 0.72855et 1 ，由回归方程可知回归方程为 e
分方程： Yt 0.72855Yt 1 1 (1 0.72855) 2 ( X t 0.72855 X t 1 ) t 对上式广义差分方程进行回归，在 Eviews 命令栏中输入命令： ls Y -0.72855*Y(-1) c X-0.72855*X(-1)，回归结果如下：由回归结果可得回归方程为：
关进行相关检验。（二）检验收入—消费模型的自相关情况 1、德宾-沃森检验（DW 检验）法因为 n=36， k=1，在 5%的显著水平下查表得 DL 1.411 ， DU 1.525 ，而 0<0.5234=DW< D L ，因此此模型存在一阶正自相关。 2、偏相关系数检验法由于 DW 法只能检验一阶自相关性，我们用偏相关系数检验法来检验是否存在高阶自相关性。在模型回归结果中选择操作：View/Residual Test/Correlogram-Q-statistics ，默认滞后期为 16，得到偏相关系数结果如下：
由偏相关系数分布图可知，该模型存在明显一阶自相关性，不存在显著高阶自相关性。 3、BG 检验法在偏相关系数检验之后，我们运用 BG 检验对前面的检验结果进行进一步验证，选择操作 View/Residual Test/Serial Correlation LM Test ，选择滞后期为 5，得到结果如下：

实验六自相关模型的检验和处理-学生实验报告

【模型3】消费品零售额SLC对收入法GDPS的回归模型
【模型4】财政收入的对数log（cs）对时间T的回归模型
【模型5】收入法GDPS的对数log（GDPS）对时间T的回归模型
数据见“附表：省宏观经济数据（部分）-第六章”
（一）自相关的检验
1.图形法检验
使用图形检验法分别检验上述【模型1-4】是否存在自相关问题。分别作这四个模型的残差散点图（即残差后一项对前一项的散点图：对）和残差趋势图（即残差对时间的线图），并判断模型是否存在自相关以及是正的自相关还是负的自相关。
S.E. of regression
0.058174
Akaike info criterion
-2.710105
Sum squared resid
0.074454
Schwarz criterion
实验室：普通配置的计算机，Eviews软件及常用办公软件。
实验训练容（包括实验原理和操作步骤）：
【实验原理】
自相关的检验：图形法检验、D-W检验
自相关的处理：广义差分变换、迭代法
【实验步骤】
本实验中考虑以下模型：
【模型1】财政收入CS对收入法GDPS的回归模型
【模型2】财政支出CZ对财政收入CS的回归模型
（请对得到的图表进行处理，以上在一页）
2.D-W检验
分别计算上述【模型1-3】和【模型5】的D-W统计量的值，判断模型是否存在自相关问题。
【模型1】
CS=12.50360 +0.080296GDPS
(15.58605) (0.001891)
(0.802615) (42.45297)
R^2=0.985232 SE=61.92234 DW=0.942712 F=1802.255

自相关实验报告

《计量经济学》上机实验报告一题目：自相关实验日期和时间：2013-12-5班级：学号：姓名：实验室：实验环境：Windows XP ; EViews 3.1实验目的：掌握自相关性的检验与处理方法实验内容：下表给出了美国1960到1995年36年个人可支配收入X和个人实际消费支出Y的数据。

年份个人实际可支配收入个人实际年份个人实际可支配收入个人实际X 消费支出X 消费支出Y Y1960 157 143 1978 326 295 1961 162 146 1979 335 302 1962 169 153 1980 337 301 1963 176 160 1981 345 305 1964 188 169 1982 348 308 1965 200 180 1983 358 324 1966 211 190 1984 384 341 1967 220 196 1985 396 357 1968 230 207 1986 409 371 1969 237 215 1987 415 382 1970 247 220 1988 432 397 1971 256 228 1989 440 406 1972 268 242 1990 448 413 1973 287 253 1991 449 411 1974 285 251 1992 461 422 1975 290 257 1993 467 434 1976 301 271 1994 478 447 1977 311 283 1995 493 458 1）用普通最小二乘法估计收入消费模型：y=b1+b2x2+u2）检验自相关。

（显著水平5%）3）用适当方法消除问题。

实验步骤：0- 利用普通最小二乘法估计收入消费模型，建立模型：LS Y C X 。

得到如下估计结果，如图1所示。

Dependent Variable: Y Method: Least Squares Date: 12/05/13 Time: 16:58 Sample: 1960 1995 Included observations: 36Variable Coefficient Std. Error t-Statistic Prob. C -9.428745 2.504347 -3.764951 0.0006 X0.935866 0.007467125.34110.0000 R-squared0.997841 Mean dependent var 289.9444 Adjusted R-squared 0.997777 S.D. dependent var 95.82125 S.E. of regression 4.517862 Akaike info criterion 5.907908 Sum squared resid 693.9767 Schwarz criterion 5.995881 Log likelihood -104.3423 F-statistic 15710.39 Durbin-Watson stat0.523428Prob(F-statistic)0.000000图1其检验报告如下：x y93587.043.9ˆ+-= =t (-3.764951) (125.3411) 2R ＝0.997841 F ＝15710.39二．对模型进行自相关检验。

检验和消除异方差和自相关的报告

消除异方差和自相关的实验报告【实验内容】通过查询中国统计局的2012年中国统计年鉴及新浪财经数据网，获得1980年--2012年各项指标的数据，如下表所示:年份Y-出口贸易总额（亿美元）X-外商直接投资（亿美元）1980181.19 3.54 1981220.10 3.54 1982223.20 3.54 1983222.309.20 1984261.4014.20 1985273.5019.56 1986309.4022.44 1987394.4023.14 1988475.2031.94 1989525.4033.92 1990620.9134.87 1991719.1043.66 1992849.40110.08 1993917.44275.15 19941210.06337.67 19951487.80375.21 19961510.48417.26 19971827.92452.57 19981837.09454.63 19991949.31403.1920002492.03407.1520012660.98468.7820023255.96527.4320034382.28535.0520045933.26606.3020057619.53603.2520069689.36630.21200712177.76747.68200814306.93923.95200912016.12900.33201015779.301057.40201118986.001160.23201220489.301116.16【实验步骤——检验并消除异方差】一检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出外商直接投资X与出口贸易总额Y的散点图（SCAT X Y）。

观察相关图可以看出，随着外商直接投资的增加，出口贸易总额的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

自相关的检验与修正

实验五自相关的检验与修正【实验目的】1、理解自相关的含义后果、2、学会自相关的检验与消除方法【实验内容】利用下表资料，试建立我国城乡居民储蓄存款模型，并检验模型的自相关性。

表3 我国城乡居民储蓄存款与GDP统计资料（1978年＝100）要求：1）建立对数模型2）分别用图示法和DW检验法，判断双对数模型是否存在自相关3）用科-奥迭代法对双对数模型进行补救（1）Dependent Variable: LNYMethod: Least SquaresDate: 06/05/13 Time: 10:06Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -8.075343 0.255516 -31.60412 0.0000LNX 2.958841 0.046096 64.18896 0.0000Adjusted R-squared 0.995168 S.D. dependent var 1.756767 S.E. of regression 0.122115 Akaike info criterion -1.277311 Sum squared resid 0.283330 Schwarz criterion -1.177832 Log likelihood 15.41176 F-statistic 4120.223 Durbin-Watson stat0.706200 Prob(F-statistic)0.000000ˆln-8.075343+2.958841lnX t Y （0.255516）（0.046096）t= (-31.60412) (64.18896)2R =0.995410 F=4120.223 DW=0.706200(2)对样本量为21，一个解释变量的模型，1%显著水平，差DW 统计表可知，l d =0.975，u d =1.161。

实验五-自相关性的检验与处理

实验五自相关性的检验及处理（2学时）一、实验目的（1）、掌握自相关检验的基本方法；（2）、掌握自相关的处理方法。

二、实验学时：2学时三、实验要求（1）掌握用MATLAB软件实现自相关的检验和处理；（2）掌握自相关的检验和处理的基本步骤。

四、实验原理1、自相关检验的常用方法(1)、图示法(2). 杜宾-瓦森（Durbin-Watson ）检验法 1）假定条件是： ①解释变量X 非随机；②随机误差项ui 为一阶自回归形式： ③回归模型中不应含有滞后应变量作为解释变量; ④回归含有截距项；⑤没有缺落数据，样本比较大。

2)检验步骤 ① 提出假设H0：ρ=0，即不存在一阶自相关； H1：ρ≠0，即存在一阶自相关。

② 构造统计量21221().ntt t ntt e eDW d e-==-=∑∑统计量： 1221ˆˆ2(1)ˆnt t t ntt uu d u-==≈-∑∑1222ˆˆˆˆnt t t ntt uu uρ-===∑∑定义：为样本的一阶自相关系数，作为ρ的估计量。

则有ˆ)ρ≈d 2(1- ，因为-1 ≤ ρ ≤ 1，所以，0 ≤ d ≤ 4③ 检验判断对给定样本大小和给定解释变量个数找出临界值dL 和dU ，按照下图的决策得出结论。

2、自相关的处理 (以一元线性回归模型为例)(1) 广义最小二乘法：01y t t t x u ββ=++设模型： …………(1) 1u t t t u v ρ-=+存在一阶线性自相关：10111y t t t x u ββ---⇒=++从而，(1) (2)100111y -y ()()t t t t t t x x u u ρβρββρρ---∴⇒=-+-+-(1)-(2) (3)*1*10=y -y =,(3)(1)t t t t t t y x x x ρραρβ--⎧⎪-⎨⎪=-⎩令则模型可变为：**1t t y x αβ+t =+v …….(4) 10ˆˆˆ(4)OLS αββ对使用即可求出：，，进而求出注：此方法在实际应用时要事先估计,当n 较大时， 12dρ≈-当n 较小时，221(1)()2ˆ11()d k n k nρ+-+≈++, k 为模型中的自变量（不包括常变量）。

计量经济学自相关的检验与修正实验报告

《计量经济学》实训报告实训项目名称自相关模型的检验与处理实训时间 2012-01-02实训地点实验楼308班级学号姓名实训 (实践 ) 报告实训名称自相关模型的检验与处理一、实训目的掌握自相关模型的检验及处理方法。

二、实训要求掌握自相关模型的图形法检验、DW 检验，与科克伦—奥克特迭代法对自相关修正。

三、实训内容1.检测进口额模型12i i i Y X u ββ=++的自相关性；2.检验模型中存在的问题，并采取适当的补救措施予以处理；四、实训步骤1.建立Workfile 和对象，录入数据；2.参数估计、检验模型的自相关；3.利用科克伦-奥科特迭代法处理模型中的自相关问题。

五、实训分析、总结表1列出了1985-2003年中国实际GDP 和进口额的统计数据。

假设实际GDP （X ）与实际进口额(Y ）之间满足线性约束，则理论模型设定为：12i i i Y X u ββ=++其中i Y 表示实际进口额，i X 表示实际GDP 。

表1 1985-2003年中国实际GDP和进口额年份实际GDP(X,亿元）实际进口额(Y,亿元）1985 8964.4 2543.21986 9753.27 2983.41987 10884.65 3450.11988 12114.62 3571.61989 12611.32 3045.91990 13090.55 2950.41991 14294.88 33381992 16324.75 4182.21993 18528.59 5244.41994 20863.19 6311.91995 23053.83 7002.21996 25267 7707.21997 27490.49 8305.41998 29634.75 9301.31999 31738.82 9794.82000 34277.92 10842.52001 36848.76 12125.62002 39907.21 14118.82003 43618.58 17612.21.建立Workfile和对象，录入1985-2003年中国实际GDP（X）和进口额(Y)图1 1985-2003年中国实际GDP（X）和进口额(Y)2.参数估计、检验模型的自相关使用普通最小二乘法估计消费模型得：图2 样本的回归估计结果-1690.3090.387979i Y X ∧=+20.965870 481.1009 0.523859R F DW ===通过分析可知：该回归方程可决系数较高，回归系数均显著。

自相关检验以及消除自相关

实验二自相关检验以及消除自相关【实验目的】掌握图示法和DW检验、LM检验自相关的方法，利用合适的方法消除自回归，并估计自回归参数。

【实验原理】1、图示法图示法就是依据残差对时间t的序列图作出判断。

由于残差是对误差项ut 的估计，所以尽管误差项ut 观测不到，但可以通过e的变化判断ut 是否存在自相关。

2、DW（Durbin-Watson）检验法(1) H0: ρ = 0 (ut 不存在自相关)H1: ρ≠ 0 (ut 存在一阶自相关)(2) 若DW取值在（0, dL）之间，拒绝原假设H0 ,认为ut 存在一阶正自相关。

若DW取值在（4 - dL , 4）之间，拒绝原假设H0 ,认为ut 存在一阶负自相关。

若DW取值在（dU, 4- dU）之间，接受原假设H0 ,认为ut 非自相关。

若DW取值在（dL, dU）或（４- dU, 4 - dL）之间，这种检验没有结论，即不能判别ut 是否存在一阶自相关。

3、变换原回归模型，使变换后的随机误差项消除自相关，进而利用普通最小二乘法估计回归参数。

【实验软件】Eview6【实验内容】建立并检验我国1982年至2002年进出口之间自相关模型，消除自回归，并估算回归参数。

【实验数据资料】下表列出了我国1982年至2002年进出口的统计资料年份EX IM1982223.2192.91983222.3213.91984261.4274.11985273.5422.51986309.44291987394.4432.21988475.2552.71989525.4591.41990620.9533.51991719.9637.91992849.4825.91993917.41039.619941210.11156.219951487.81320.819961510.51388.319971827.91423.719981837.11402.419991949.31657200024922250.9200126612435.520023255.72952【实验过程】1、启动Eviews6软件，建立新的workfile.在主菜单中选择【File】--【New】--【Workfile】,弹出Workfile Create对话框，在Workfile structure type中选择Dated-regular frequency，然后在Frequency 中选择annual，Start date中输入1982，End date中输入2002，然后在WF中输入Work1，点击OK按钮。

自相关实验报告

⾃相关实验报告《计量经济学》实训报告实训项⽬名称⾃相关的检验与消除实训时间实训地点班级学号姓名实训(实践) 报告实训名称⾃相关的检验与消除⼀、实训⽬的1、中国进⼝需求与国内⽣产总值是⼀个值得研究的问题。

通过实际出⼝额模型的分析可以判断中国进⼝需求，这是宏观经济分析的重要参数。

2、使学⽣掌握针对实际问题简历、估计、检验和应⽤计量经济学单⽅程模型的⽅法以及⾄少掌握⼀种计量经济学软件的使⽤，提⾼学⽣的动⼿能⼒。

⼆、实训要求1、要求学⽣能对⼀般的实际经济问题运⽤计量经济学⽅法进⾏分析研究2、掌握计量经济学软件包Eviews估计和检验单⽅程模型的同法和操作步骤3、对模型的结果进⾏经济解释三、实训内容1、⽤DW验证法，验证该模型是否存在⾃相关。

2、⽤⼴义差分法消除⾃相关，进⾏多次迭代法。

四、实训步骤课后练习题6.5的数据1985—2003年中国实际GDP和进⼝额1. ⽤OLS⽅法估计参数，建⽴回归模型：ls y c x回归结果：Y=-1690.309+0.387979XT= (-3.824856) (21.93401) R^2=0.96587 S.E.=822.3285 2. 检验是否存在⾃相关（1）图⽰法（scat e1 e2）：结果表明：由上图e1与e2的散点图可知，⼤部分的点落在I、III象限，表明随即误差项存在着正相关。

（2）DW检验法回归结果：Y = -1690.309+0.3880X , R^2=0.9659,df=17, DW=0.5239该⽅程的可绝系数较⾼，回归系数均显著。

对样本量为19、⼀个解释变量的模型，查DW统计表可知，dL=1.18,dU=1.4；模型中DW结论：显然该模型中存在⾃相关。

(3) BG检验（LM检验）结果表明：观察偏相关发现出现⾃相关（⼀维）结果表明：观察Prob=0.000942<0.5，显著，存在⾃相关3. 消除⾃相关的⽅法：使⽤⼴义差分法进⾏修正（1）genr e1=resid，genr e2=resid(-1)，Ls e1 e2，得到e1与e2的回归⽅程为：E1=0.9202E2;（2）对原模型进⾏⼴义差分，得到⼴义差分⽅程为：Y-0.9202*Y(-1) = β1*(1-0.9202)+β2*(X-0.9202X)+ µ回归结果：Y*= -921.9049+0.6264 X*（其中Y*= Y-0.9202*Y(-1)；X*= X-0.9202*X(-1)）；R^2=0.8381; df=16; DW=0.7151；由于使⽤了⼴义差分法，样本容量减少了1个，为18个。

计量经济学实验《自相关性的检验与补救》

实验三：自相关性的检验与补救【实验目的】1、熟悉计量经济学软件包EViews；2、理解自相关性的不良后果；3、掌握检验自相关性的若干方法及基本操作；4、掌握自相关性的补救方法及基本操作。

【实验类型】验证型【实验软硬件要求】计量经济学软件包EViews、微型计算机【实验内容】为了考察股票市场的繁荣程度与宏观经济运行情况之间的关系，取股票价格指数（Y）与国内生产总值（X），建立简单线性回归模型Y i=β1+β2X i+u i。

现请按照下列步骤完成实验三，每个步骤要写出操作过程：（1）打开EViews，新建适当的工作文件夹；打开Eviews后，依次点击File－New－Workfile，新建一个时间序列数据（Dated-regular frequencied）类型的文件，频率选择年度（Annual），键入起止日期1981-2006，点击ok，新建工作文件夹完成（2）在工作文件夹中新建变量X和Y，并输入数据；依次点击Objects－New Object，对象类型选择序列（Series），并输入序列名Y，点击OK，重复以上操作，新建系列对象X。

新建系列对象完成后如图按住ctrl并同时选定X和Y，用鼠标右击选择open—as group，点击Edit ＋/－开始编辑，输入数据，数据输入完毕再点击Edit＋/－一次。

数据输入后如图（3）用OLS法对模型Y i=β1+β2X i+u i做参数估计，将估计结果保存在工作文件夹中，命名为eq01，写出操作过程和回归分析报告；在窗口空白处输入：ls y c x ，回车，得到结果如图回归分析报告：Ŷi = -2123.864 + 0.784106Xi(324.8012) (0.041276)t = (-6.538966) (18.99680)P = 0.000000R2 = 0.937643 F=360.8784D.W.= 0.440822 n=26（4）采用图示法检验该模型的自相关性，将图片保存在工作夹中，命名为graph01，按检验步骤写出操作过程，并画出图像；该模型的自相关性明显吗，是正的还是负的自相关？依次点击Quick—Graph……，输入序列名resid(-1)和resid，点击OK，在弹出的对话框中选择Scatter，得到残差与滞后残差的散点图如下图由散点图可知模型的自相关性明显，是正的自相关（5）采用回归法检验该模型的自相关性，写出操作过程和回归检验法的回归分析报告，并在0.05的显著性水平下判断模型的自相关性；点击Objects－Generate Sereies，出现Generate Series by Equation窗口，在Enter equation 窗口中输入公式：e=resid，点击OK，如图在EViews工作文件窗口点击Quick——Estimate Eqution……，在模型设定对话框中输入e e(-1)，得到以当期残差为被解释变量，以滞后一期残差为解释变量的辅助回归模型回归分析报告：e = 0.768816e(-1)(0.127193)t = 6.044486P = 0.0000R2 = 0.603173P = 0.0000 < α= 0.05 ，所以该模型存在自相关性（6）在0.05的显著性水平下，采用DW法检验该模型的自相关性，写出检验步骤，并根据DW值估计一阶自相关系数；由（1）中可知 D.W.= 0.440822 K’= K-1=1 n=26查DW表可得d L=1.30 ，d U =1.46DW = 0.440822 < d L=1.30所以模型存在正的自相关性一阶自相关系数ρ≈ 1 - DW/2 = 1-0.440822/2 = 0.779589（7）在0.05的显著性水平下，采用BG法检验该模型的自相关性，先写出EViews操作过程，再根据结果写出BG检验的辅助回归估计式和nR2，最后写出BG检验的过程；双击eq01，在其工具条上选择View——Residual Diagnostics——Serial Correlation LM Test……，在Lags to include栏输入2，点击确定得到BG检验法的输出结果，如图由BG检验的输出结果可知:e t-1-0.681559e t-2辅助回归分析式：e t = -38.62611+0.006719x+1.296707nR2 = 20.09265提出原假设H0：ρ1 = ρ2 = 0α= 0.05，卡方分布的自由度p=2查卡方分布表得χ20.05(2) = 5.99则nR2 = 20.09265 > χ20.05(2) = 5.99故拒绝原假设，即原模型存在自相关（8）用广义差分法对原模型的自相关性进行补救，将估计结果保存在工作文件夹中，命名为eq02，写出操作过程和回归分析报告；在EViews工作文件窗口点击Quick——Estimate Eqution……，在模型设定对话框中依次输入Y C X ar(1)，点击OK，估计结果如下图β1 = -2914.286/（1-0.779589）= -13222.053回归分析报告:Ŷi =-13222.053 + 0.865050Xi(1192.273) (0.119983)t = (-2.444311) (7.209763)R2 = 0.975002F = 429.0384D.W.= 0.912240 n=26（9）对eq02再做BG检验，此时还有没有自相关性？双击eq02，在其工具条上选择View——Residual Diagnostics——Serial Correlation LM Test……，在Lags to include栏输入2，点击确定得到BG检验法的输出结果，如下图由输出结果可知nR2=11.85149提出原假设H0：ρ1 = ρ2 = 0α= 0.05，卡方分布的自由度p=2查卡方分布表得 20.05(2) = 5.99则nR2 = 11.85149> 20.05(2) = 5.99故拒绝原假设，即原模型依旧存在自相关（10）将工作文件夹保存在桌面，文件名为test3.wfl。

计量经济学自相关性检验报告分析(doc 7页)

计量经济学自相关性检验报告分析(doc 7页)计量经济学自相关性检验实验报告实验内容：自相关性检验工业增加值主要由全社会固定资产投资决定。

为了考察全社会固定资产投资对工业增加值的影响，可使用如下模型：Y=；其中，X 表示全社会固定资产投资，Y表示工业增加值。

下表列出了中国1998-2000的全社会固定资产投资X与工业增加值Y的统计数据。

单位：亿元年份固定资产投资X工业增加值Y年份固定资产投资X工业增加值Y1980910.91996.519915594.58087.1 198********.419928080.110284.519821230.42162.3199313072.314143.8 19831430.12375.6199417042.119359.6 19841832.92789199520019.324718.3 19852543.23448.7199622913.529082.6 19863120.63967199724941.132412.1 19873791.74585.8199828406.233387.9 19884753.85777.2199929854.735087.2 19894410.46484200032917.739570.3 199045176858一、估计回归方程OLS法的估计结果如下：Y=668.0114+1.181861X（2.24039）（61.0963）R2=0.994936，R2=0.994669，SE=951.3388，D.W.=1.282353。

二、进行序列相关性检验（1）图示检验法通过残差与残差滞后一期的散点图可以判断，随机干扰项存在正序列相关性。

（2）回归检验法一阶回归检验e=0.356978e1-t+εtt二阶回归检验e=0.572433e1-t－0.607831e2-t+εtt可见：该模型存在二阶序列相关。

（3）杜宾-瓦森（D.W）检验法由OLS法的估计结果知：D.W.=1.282353。