2019-2020年三年级数学模拟试卷
北师大版三年级上册数学试卷 - 期末水平测试卷(一) (含答案)

2019-2020学年北师大版小学三年级上册期末考试数学试卷一.填空题(共14小题,满分27分)1.(3分)今年2019年有个月,2月份有天,第三季度的天数有天.2.(3分)计算96﹣46÷2时,先算法,再算法,结果是.3.(3分)有一张挂历纸,不小心被墨水弄脏了,只能看见这个月6日是星期一,这个月26日是星期.4.(2分)在计算7□0×5时,要使积有两个0,□最大应填5.(1分)口算400×6时,可以看作4个乘6;口算400÷5时,可以看作个十除以5.6.(2分)2元6角=元6米4分米=米7.(4分)在横线上填上“>”、“<”、66×15×310+5“=”.3+33×36+66×2 15﹣63×3 65+351008.(2分)横线中填几:(﹣30)÷3=430=5×+109.(1分)小明在一个长80米,宽60米的长方形跑道上跑了4圈,他一共跑了米.10.(2分)找规律填数:(1)0、3、6、9、12、(2)1、4、9、16、25、11.(1分)一条游泳道长50米,小明游了2个来回,共游了米.12.(1分)加工一批零件,甲单独做3小时完成,乙单独做2小时完成.甲、乙合作的工作效率为.13.(1分)图中一共有块小正方体.14.(1分)食堂中一份盒饭含一种主食和一种炒菜.已知:今日午餐主食:米饭、面条炒菜:土豆片、麻婆豆腐、番茄炒蛋、烧土豆一共有种配餐方法.二.选择题(共6小题,满分6分,每小题1分)15.(1分)如图(单位:厘米)阴影部分的周长是()A.38.84B.57.68C.42.84D.18.84 16.(1分)下面得数最大的算式是()A.0÷100B.0×100C.100﹣0 17.(1分)1.88元中的两个“8”的大小()A.一样大B.相差7.2元C.相差0.72元18.(1分)下面的节日中在大月的是()A.元旦节B.教师节C.儿童节19.(1分)下面图形中()的周长最长.A.B.C.20.(1分)下面最接近十亿的数是()A.九亿九千万B.九亿零九千九百C.九亿零九万三.判断题(共6小题,满分6分,每小题1分)21.(1分)一年中有7个大月,那么还有5个月就是小月.(判断对错)22.(1分)在有余数的除法里,除数一定比余数大..(判断对错)23.(1分)四个正方形一定能拼成一个大正方形..24.(1分)三位数乘一位数,积一定是四位数..(判断对错)25.(1分)一张周长为40厘米的正方形纸剪成完全一样的两张长方形纸,每个长方形纸的周长都是20厘米.(判断对错)26.(1分)一根木料锯成4段用12分钟,另一根锯成8段要24分钟.(判断对错)四.计算题(共3小题,满分20分)27.直接写出得数.120×7=4500÷15=560×0=900÷6=140×60=7200÷90=640÷80=27×60=260÷13=620﹣180=17+3×6=25×4÷25×4=28.(8分)竖式计算.727+114+68=502×4=650×8=70元﹣7.9元=元角29.(12分)我会用我喜欢的方法计算.(35+28)÷7106﹣6×8500﹣94﹣06327+45﹣192五.操作题(共3小题,满分6分)30.(3分)连一连.31.(3分)按要求在横线上画一画.(1)△的个数比〇多3个.(2)□的个数是〇的3倍.32.请把下面这三个人看到的图连线:六.解答题(共5小题,满分21分)33.(4分)下面是“北京﹣﹣乌鲁木齐”沿线各大站的火车里程表.(1)北京到洛阳有多远?(2)从敦煌到郑州有多远?(3)你还能提出什么问题?试解答.34.(4分)红光小学3名老师带40名学生去海洋馆参观,用400元买门票够吗?35.(4分)李阿姨不小心将购物发票弄脏了,你能帮她算出排球的单价吗?36.(4分)一块长方形菜地,宽7米,长比宽的2倍多1米,(1)这块长方形菜地的长是多少米?(2)如果四周围上篱笆,篱笆长多少米?(3)如果这块长方形菜地一面靠墙,篱笆至少多少米?37.(5分)光明小学有298人去参观科技馆,每辆客车可乘坐52人,学校准备6辆客车够吗?七.填空题(共4小题,满分8分,每小题2分)38.(2分)一道除法算式中,商和余数都是4,除数比余数多5.被除数是.39.(2分)一个长方形鸡圈的宽是5米,长是宽的2倍.这个长方形鸡圈的长是米,周长是米.40.(2分)笑笑看一本80页的故事书,计划每天看10页,那么她第三天应该从第页看起.41.(2分)小明买了8根跳绳,共花了40元,还买了一个足球,花了30元,一根跳绳比一个足球便宜元.八.解答题(共3小题,满分12分,每小题4分)42.(4分)用22根同样长的小棒可以摆出几种不同的长方形?请用你喜欢的方法记录下来,一定不要遗漏哟.43.(4分)淘气在计算一个数乘27时,错误的看成了乘21,这样得到的结果就比少了48,那么正确的结果应该是多少呢?44.(4分)笑笑到爷爷家,如果去时坐车、回来步行一共需要20分钟,如果去时和回来都步行需要32分钟,那么去时和回来都坐车需要多少分钟?参考答案与试题解析一.填空题(共14小题,满分27分)1.解:2019÷4=504…3,所以2019年是平年,2月28天;31+31+30=92(天)答:今年2019年有12个月,2月份有28天,第三季度的天数有92天;故答案为:12,28,92.2.解:96﹣46÷2=96﹣23=73先算除法,再算减法,结果是73.故答案为:除;减;733.解:26﹣6=20(天)20÷7=2(个)……6(天)从星期一向后数6天为星期日.答:这个月26日是星期日.故答案为:日.4.解:根据末尾有零的整数乘法的运算法则可知,7□0×5的积末尾一定有一个零,要使7□0×5的积有两个0,则应使7□0的十位与5相乘的积的末尾是0,则那么□里可以填0或8.故答案为:8.5.解:口算400×6时,可以看作4个百乘6;口算400÷5时,可以看作40个十除以5.故答案为:百,40.6.解:2元6角=2.6元6米4分米=6.4米故答案为:2.6,6.4.7.解:(1)3+3=6,3×3=9,6<9,所以3+3<3×3;(2)6×1=6,6=6,所以6=6×1;(3)5×3=15,10+5=15,15=15,所以5×3=10+5;(4)6+6=12,6×2=12,12=12,所以6+6=6×2;(5)15﹣6=9,3×3=9,9=9,所以15﹣6=3×3;(6)65+35=100,100=100,所以65+35=100;故答案为:<,=,=,=,=,=.8.解:(1)3×4+30=12+30=42即:(42﹣30)÷3=4;(2)(30﹣10)÷5=20÷5=4即:30=5×4+10.故答案为:42,4.9.解:(80+60)×2×4=140×2×4=280×4=1120(米)答:一共跑了1120米.故答案为:1120.10.解:(1)12+3=15(2)6×6=36故答案为:15;36.11.解:50×(2×2)=50×4=200(米)答:共游了200米.故答案为:200.12.解:1÷3+1÷2==答:甲、乙合作的工作效率为.故答案为:.13.解:6×4×3=24×3=72(块)答:图中一共有72块小正方体.故答案为:72.14.解:4×2=8(种)答:一共有8种不同的配餐方法.故答案为:8.二.选择题(共6小题,满分6分,每小题1分)15.解:3.14×(4+4+4)÷2+4×5=3.14×12÷2+4×5=18.84+20=38.84(厘米);答:阴影部分的周长是38.84厘米.故选:A.16.解:因为0÷100=0,0×5=100,100﹣0=100;所以,得数最大的算式是100﹣0.故选:C.17.解:1.88元中的两个“8”一个在十分位上,表示0.8元,一个在百分位上,表示0.08元,相差:0.8﹣0.88=0.72(元);故选:C.18.解:元旦是1月1日,儿童节是6月1日,教师节是9月10日,在大月的是元旦节;故选:A.19.解:令图中小正方形的边长是1,A,它的周长是10;B,它的周长是12;C,它的周长是14;14>12>10;C的周长最大.故选:C.20.解:九亿九千万,写作:990000000;九亿零九千九百,写作:900009900;九亿零九万,写作:900090000;1000000000﹣990000000=10000000;1000000000﹣900009900=99990100;1000000000﹣900090000=99910000;10000000<99910000<99990100.所以最接近十亿的数是990000000.故选:A.三.判断题(共6小题,满分6分,每小题1分)21.解:一年有12个月,分为7个大月4个小月,二月份是特殊月,所以,一年中有7个大月,那么还有5个月就是小月的说法是错误的.故答案为:×.22.解:在有余数的除法里,除数一定比余数大,说法正确;故答案为:√.23.解:如图,2个边长1厘米的正方形和2个边长3厘米的正方形,则拼不成一个大正方形;故答案为:×.24.解:三位数乘一位数,积可能是三位数,也可能是四位数,如:210×3=630,900×9=8100.故答案为:×.25.解:40÷4=10(厘米)10÷2=5(厘米)(10+5)×2=15×2=30(厘米)答:每个长方形纸的周长都是30厘米.故答案为:×.26.解:12÷(4﹣1)×(8﹣1)=4×7=28(分钟).答:另一根锯成8段要28分钟.故答案为:×.四.计算题(共3小题,满分20分)27.解:120×7=8404500÷15=300560×0=0900÷6=150140×60=84007200÷90=80640÷80=827×60=1620 260÷13=20620﹣180=44017+3×6=3525×4÷25×4=16 28.解:727+114+68=909502×4=2008650×8=520070元﹣7.9元=62元1角故答案为:909,2008,5200,62,1.29.解:(1)(35+28)÷7=63÷7=9(2)106﹣6×8=106﹣48=58(3)500﹣94﹣6=500﹣(94+6)=500﹣100=400(4)327+45﹣192=372﹣192=180五.操作题(共3小题,满分6分)30.解:连一连:31.解:(1)(2)32.解:六.解答题(共5小题,满分21分)33.解:(1)答:北京到洛阳有813千米;(2)2493﹣689=1804(千米),答:从敦煌到郑州有1804千米;(3)郑州到乌鲁木齐有多远?3768﹣689=3079(千米),答:郑州到乌鲁木齐有3079千米.34.解:根据题意可得:3×12=36(元);40×9=360(元);36+360=396(元);396<400.答:用400元买门票够.35.解:(145﹣57)÷4=88÷4=22(元)答:排球的单价是22元.故答案为:22.36.解:(1)7×2+1=14+1=15(米)答:这块长方形菜地的长是15米.(2)(15+7)×2=22×2=44(米)答:篱笆长44米.(3)44﹣15=29(米)答:篱笆至少29米.37.解:52×6=312(人)312>298所以够;答:学校准备6辆客车够.七.填空题(共4小题,满分8分,每小题2分)38.解:4+5=99×4+4=40答:被除数是40.故答案为:40.39.解:5×2=10(米)(10+5)×2=15×2=30(米)答:.这个长方形鸡圈的长是10米,周长是30米.故答案为:10,30.40.解:10×2+1=20+1=21(页)答:第三天应该从第21页看起.故答案为:21.41.解:30﹣40÷8=30﹣5=25(元)答:一根跳绳比一个足球便宜25元.故答案为:25.八.解答题(共3小题,满分12分,每小题4分)42.解:摆成的长方形的长与宽的和是22÷2=11,则摆成的长方形的长和宽分别是:10、1;9、2;3、8;4、7;5、6;所以能摆5种.43.解:48÷(27﹣21)×27=48÷6×27=8×27=216答:正确的结果应该是216.44.解:(20﹣32÷2)×2=(20﹣16)×2=4×2=8(分钟)答:去时和回来都坐车需要8分钟.。
小学三年级质量监测数学试卷及答案
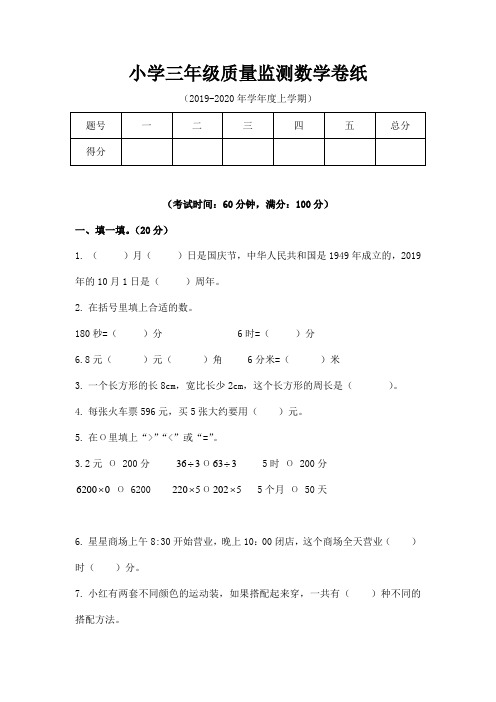
小学三年级质量监测数学卷纸(2019-2020年学年度上学期)(考试时间:60分钟,满分:100分)一、填一填。
(20分)1.()月()日是国庆节,中华人民共和国是1949年成立的,2019年的10月1日是()周年。
2.在括号里填上合适的数。
180秒=()分 6时=()分6.8元()元()角 6分米=()米3.一个长方形的长8cm,宽比长少2cm,这个长方形的周长是()。
4.每张火车票596元,买5张大约要用()元。
5.在Ο里填上“>”“<”或“=”。
3.2元Ο 200分363÷ 5时Ο 200分36÷Ο3220⨯Ο5202⨯ 5个月Ο 50天6200⨯Ο 6200 56.星星商场上午8:30开始营业,晚上10:00闭店,这个商场全天营业()时()分。
7.小红有两套不同颜色的运动装,如果搭配起来穿,一共有()种不同的搭配方法。
8. 亮亮的教室在5楼,每层楼梯有22级台阶,亮亮早晨从一楼到教室上课要上( )级台阶。
二、选一选。
(把正确答案的序号填在括号里)(6分) 1.量一片树叶的周长,下面哪种方法比较合适?( ) A.用线段测量 B.直接用直尺一段一段地量。
C.用细线沿树叶边绕一圈,再量出线的长度就是树叶的周长。
2.乘法2( )45⨯的积是三位数,( )里面最大能填( )。
A.3 B.4 C.5D.6 3. 关于6620⨯不正确的说法是( )。
A.620的6倍B.6个620相加C.6个620相乘D.6与620相乘 三、算一算。
(26分) 1.直接写得数。
(共8分)=⨯5500 =⨯320 560÷= 360⨯= =⨯+29016 =÷2260 =÷8400 =÷400 2. 竖式计算。
(最后一道要验算)(12分)3206⨯ 80.65-16.53. 脱式计算。
(共6分)6560÷⨯ 4136153⨯-)(四、做一做。
【数学】人教版三年级上册数学试题-期中测试卷-(含答案)

人教版三年级上册数学试题-期中测试卷-(含答案)满分:100分考试时间:90分钟一、填一填。
(14分)1.分针走1小格是()分,这时秒针走()小格。
时针走1大格,分针走()小格。
2.小强7:10上学,他在路上用了20分钟,他到学校的时间是()。
3.估算199+45时,可以把199看作(),加上45后估算结果是()。
4.笼子里有白兔3只,黑兔的只数是白兔的4倍,黑兔有()只。
5.有2个,的个数是()个2,的个数是的()倍。
6.填上合适的单位或数。
(1)高约1 。
(2)长约2 。
(3)厚约毫米。
(4)鲸鱼重32()。
(5)骑自行车每小时行15()。
二、单位换算。
(6分)3吨=()千克 8千米=()米5厘米=()毫米3米=()分米2000千克=()吨4分米=()厘米三、在○里填上“>”“<”或“=”。
(6分)340+26○360 270-18○250435+25○460384+270○600372-146○240400-315○85四、算一算。
(26分)1.直接写出得数。
(8分)73-37= 38+45=81-5=56÷7=270-90=720-400=340+470= 54÷9=2.用竖式计算。
(带☆的要验算)。
(12分)755+165= 404-186=978+36=301-56=☆467+533=☆634-182=3.脱式计算。
(6分)298+345+155208+155+342五、操作题。
(10分)1.量出下面线段的长度。
(4分)长()厘米长()毫米2.画一条线段,使它的长度是下面线段的2倍。
(3分)3.画○,使○的个数是△的3倍。
(3分)六、看图填空。
(10分)1.有()片,有()片,的片数是的()倍。
□÷□=□2.有()个,有()个,的个数是的()倍。
□÷□=□七、解决问题。
(28分)1.小刚看的页数是小明的多少倍?(5分)2.有一堆重50吨的沙石,已经运走了18吨,剩下的用载质量为4吨的卡车来运,需要几辆这样的卡车才能一次运完?(5分)3.小明有5本故事书,连环画的本数是故事书的7倍。
2020年海口市小学三年级数学下期末第一次模拟试题(附答案)
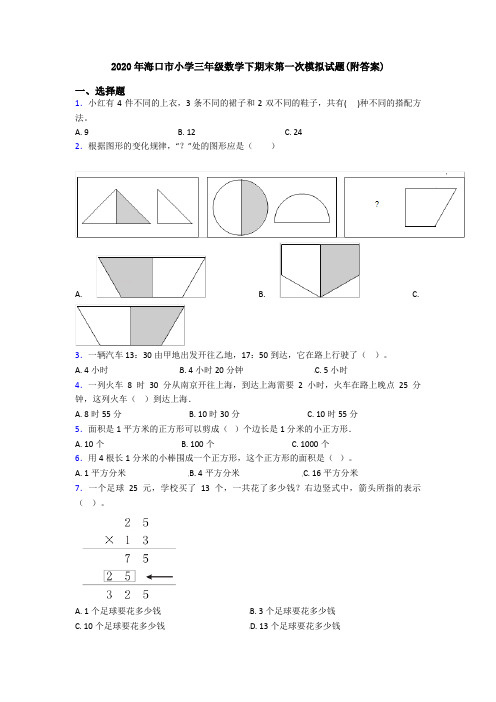
2020年海口市小学三年级数学下期末第一次模拟试题(附答案)一、选择题1.小红有4件不同的上衣,3条不同的裙子和2双不同的鞋子,共有( )种不同的搭配方法。
A. 9B. 12C. 242.根据图形的变化规律,“?”处的图形应是()A. B. C.3.一辆汽车13:30由甲地出发开往乙地,17:50到达,它在路上行驶了()。
A. 4小时B. 4小时20分钟C. 5小时4.一列火车8时30分从南京开往上海,到达上海需要2小时,火车在路上晚点25分钟,这列火车()到达上海.A. 8时55分B. 10时30分C. 10时55分5.面积是1平方米的正方形可以剪成()个边长是1分米的小正方形.A. 10个B. 100个C. 1000个6.用4根长1分米的小棒围成一个正方形,这个正方形的面积是()。
A. 1平方分米B. 4平方分米C. 16平方分米7.一个足球25元,学校买了13个,一共花了多少钱?右边竖式中,箭头所指的表示()。
A. 1个足球要花多少钱B. 3个足球要花多少钱C. 10个足球要花多少钱D. 13个足球要花多少钱8.636÷6的商()A. 中间有0B. 末尾有0C. 没有09.12.32在()相邻的两个整数之间.A. 11~12B. 12~13C. 13~1410.整数部分是0的最大的一位小数是()。
A. 0.1B. 0.9C. 111.如果我的家在小红家的西南面,小红家就在我家的()面.A. 东南B. 东北C. 西南D. 西北二、填空题12.用4,5,7可以组成________个不同的三位数,其中最大的数是________,最小的数是________。
13.妈妈坐了1小时的地铁回家,到家时刚好是18时。
妈妈是下午________时上地铁。
14.一个长方形的宽是50厘米,长是宽的2倍,它的面积是________平方分米。
15.□6×□3的积的个位上的数字是________,40个31的和是________。
2020年高中三年级数学下期中第一次模拟试卷及答案(2)

2020年高中三年级数学下期中第一次模拟试卷及答案(2)一、选择题1.若直线()100,0ax by a b ++=>>把圆()()224116x y +++=分成面积相等的两部分,则122a b+的最小值为( ) A .10B .8C .5D .42.等比数列{}n a 的前n 项和为n S ,若36=2S =18S ,,则105S S 等于( ) A .-3B .5C .33D .-313.若a 、b 、c >0且a (a +b +c )+bc =4-,则2a +b +c 的最小值为( ) A.1 B.1 C .+2D .24.设数列{}n a 是等差数列,且26a =-,86a =,n S 是数列{}n a 的前n 项和,则( ). A .45S S <B .45S S =C .65S S <D .65S S =5.设n S 为等差数列{}n a 的前n 项和,1(1)()n n n S nS n N *++∈<.若871a a <-,则( ) A .n S 的最大值为8S B .n S 的最小值为8S C .n S 的最大值为7S D .n S 的最小值为7S6.设2z x y =+,其中,x y 满足2000x y x y y k +≥⎧⎪-≤⎨⎪≤≤⎩,若z 的最小值是12-,则z 的最大值为( ) A .9-B .12C .12-D .97.数列{}n a 的前n 项和为21n S n n =++,()()1N*nn n b a n =-∈,则数列{}n b 的前50项和为( ) A .49B .50C .99D .1008.定义在()(),00,-∞⋃+∞上的函数()f x ,如果对于任意给定的等比数列{}n a ,若(){}nf a 仍是比数列,则称()f x 为“保等比数列函数”.现有定义在()(),00,-∞⋃+∞上的如下函数: ①()3f x x =;②()xf x e =;③()f x =④()ln f x x =则其中是“保等比数列函数”的()f x 的序号为( ) A .①②B .③④C .①③D .②④9.河南洛阳的龙门石窟是中国石刻艺术宝库之一,现为世界文化遗产,龙门石窟与莫高窟、云冈石窟、麦积山石窟并称中国四大石窟.现有一石窟的某处“浮雕像”共7层,每上层的数量是下层的2倍,总共有1016个“浮雕像”,这些“浮雕像”构成一幅优美的图案,若从最下层往上“浮雕像”的数量构成一个数列{}n a ,则()235log a a ⋅的值为( ) A .8B .10C .12D .1610.已知0,0x y >>,且91x y +=,则11x y+的最小值是 A .10B .12?C .14D .1611.已知数列{}n a 的通项公式为()*21log N 2n n a n n +=∈+,设其前n 项和为n S ,则使5n S <-成立的自然数n ( )A .有最小值63B .有最大值63C .有最小值31D .有最大值3112.若ln 2ln 3ln 5,,235a b c ===,则 A .a b c << B .c a b << C .c b a <<D .b a c <<二、填空题13.已知x y ,满足20030x y y x y -≥⎧⎪≥⎨⎪+-≤⎩,,,,则222x y y ++的取值范围是__________.14.已知等差数列{}n a 的公差为()d d 0≠,前n 项和为n S,且数列也为公差为d 的等差数列,则d =______.15.(广东深圳市2017届高三第二次(4月)调研考试数学理试题)我国南宋时期著名的数学家秦九韶在其著作《数书九章》中独立提出了一种求三角形面积的方法---“三斜求积术”,即ABC △的面积S =,其中a b c 、、分别为ABC △内角、、A B C 的对边.若2b =,且tan C =,则ABC △的面积S 的最大值为__________.16.在钝角ABC V中,已知1AB AC ==,若ABC VBC 的长为______.17.已知对满足4454x y xy ++=的任意正实数x ,y ,都有22210x xy y ax ay ++--+≥,则实数a 的取值范围为______.18.已知120,0,2a b a b>>+=,2+a b 的最小值为_______________. 19.已知数列{}n a 满足11a =,111n na a +=-+,*n N ∈,则2019a =__________. 20.已知三角形中,边上的高与边长相等,则的最大值是__________.三、解答题21.已知等差数列{}n a 的前n 项和为n S ,且满足37a =,999S =. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若()2nn n a b n N *=∈,求数列{}n b 的前n 项和n T . 22.已知等差数列{}n a 满足1210a a +=,432a a -=. (1)求{}n a 的通项公式;(2)设等比数列{}n b 满足2337,b a b a ==.若6k b a =,求k 的值. 23.已知数列{}n a 的前n 项和为n S ,且221n n n S na a =+-. (1)求数列{}n a 的通项公式; (2)若数列21n a ⎧⎫⎨⎬⎩⎭的前n 项和为n T ,证明:4nT <. 24.已知函数()3sin cos f x x x =-. (1)求函数()f x 在,2x ππ⎡⎤∈⎢⎥⎣⎦的值域; (2)在ABC ∆中,内角A 、B 、C 的对边分别是a 、b 、c ,若78663f A f B ππ⎛⎫⎛⎫+=+- ⎪ ⎪⎝⎭⎝⎭,求a b 的取值范围.25.已知等差数列{}n a 满足1359a a a ++=,24612a a a ++=,等比数列{}n b 公比1q >,且2420b b a +=,38b a =.(1)求数列{}n a 、{}n b 的通项公式;(2)若数列{}n c ,满足4nn n c b =-,且数列{}n c 的前n 项和为n B ,求证:数列n n b B ⎧⎫⎨⎬⎩⎭的前n 项和32n T <. 26.D 为ABC V 的边BC 的中点.222AB AC AD ===.(1)求BC 的长;(2)若ACB ∠的平分线交AB 于E ,求ACE S V .【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】由于直线将圆平分,故直线过圆的圆心,将圆心坐标代入直线方程,利用“1”的代换的方法以及基本不等式,求得所求和的最小值. 【详解】圆的圆心为()4,1--,由于直线将圆平分,故直线过圆心,即410a b --+=,即41a b +=,故()121284448222b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭,当且仅当82b aa b =,即11,82a b ==时,取得最小值为8.故选B. 【点睛】本小题主要考查直线和圆的位置关系,考查利用“1”的代换和基本不等式求解和式的最小值问题.直线能将圆平分成面积相等的两个部分,则这条直线是经过圆心的.要注意的是,圆的标准方程是()()222x a y b r -+-=,圆心是(),a b ,所以本题的圆心是()4,1--,而不是()4,1.2.C解析:C 【解析】 【分析】由等比数列的求和公式结合条件求出公比,再利用等比数列求和公式可求出105S S . 【详解】设等比数列{}n a 的公比为q (公比显然不为1),则()()61636333111119111a q S q q q S qa q q---===+=---,得2q =, 因此,()()101105510555111111233111a q S q q q S q a qq---===+=+=---,故选C. 【点睛】本题考查等比数列基本量计算,利用等比数列求和公式求出其公比,是解本题的关键,一般在求解等比数列问题时,有如下两种方法:(1)基本量法:利用首项和公比列方程组解出这两个基本量,然后利用等比数列的通项公式或求和公式来进行计算;(2)性质法:利用等比数列下标有关的性质进行转化,能起到简化计算的作用.3.D解析:D 【解析】由a (a +b +c )+bc =4-, 得(a +c )·(a +b )=4-∵a 、b 、c >0.∴(a +c )·(a +b )≤22b c 2a ++⎛⎫ ⎪⎝⎭(当且仅当a +c =b +a ,即b =c 时取“=”),∴2a +b +c=1)=-2. 故选:D点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误4.B解析:B 【解析】分析:由等差数列的性质,即2852a a a +=,得5=0a ,又由545S S a =+,得54S S =. 详解:Q 数列{}n a 为等差数列, 2852a a a ∴+= 又286,6a a =-=Q ,5=0a ∴由数列前n 项和的定义545S S a =+,54S S ∴= 故选B.点睛:本题考查等差数列的性质与前n 项和计算的应用,解题时要认真审题,注意灵活运用数列的基本概念与性质.5.C解析:C 【解析】 【分析】由已知条件推导出(n 2﹣n )d <2n 2d ,从而得到d >0,所以a 7<0,a 8>0,由此求出数列{S n }中最小值是S 7. 【详解】∵(n +1)S n <nS n +1, ∴S n <nS n +1﹣nS n =na n +1 即na 1()12n n d-+<na 1+n 2d ,整理得(n 2﹣n )d <2n 2d ∵n 2﹣n ﹣2n 2=﹣n 2﹣n <0 ∴d >0∵87a a -<1<0 ∴a 7<0,a 8>0 数列的前7项为负, 故数列{S n }中最小值是S 7 故选C . 【点睛】本题考查等差数列中前n 项和最小值的求法,是中档题,解题时要认真审题,注意等差数列的性质的灵活运用.6.B解析:B 【解析】 【分析】作出不等式对应的可行域,当目标函数过点A 时,z 取最小值,即min 12z =-,可求得k 的值,当目标函数过点B 时,z 取最大值,即可求出答案. 【详解】作出不等式对应的可行域,如下图阴影部分,目标函数可化为2y x z =-+, 联立20x y y k+=⎧⎨=⎩,可得()2,A k k -,当目标函数过点A 时,z 取最小值,则()2212k k ⨯-+=-,解得4k =,联立0x y y k-=⎧⎨=⎩,可得(),B k k ,即()4,4B ,当目标函数过点B 时,z 取最大值,max 24412z =⨯+=.故选:B.【点睛】本题考查线性规划,考查学生的计算求解能力,利用数形结合方法是解决本题的关键,属于基础题.7.A解析:A 【解析】试题分析:当1n =时,113a S ==;当2n ≥时,()()()22111112n n n a S S n n n n n -⎡⎤=-=++--+-+=⎣⎦,把1n =代入上式可得123a =≠.综上可得3,1{2,2n n a n n ==≥.所以3,1{2,12,n n b n n n n n -==-≠为奇数且为偶数.数列{}n b 的前50项和为()()503235749224650S =--+++++++++L L ()()24349252503224922++=--⋅+⋅=.故A 正确.考点:1求数列的通项公式;2数列求和问题.8.C解析:C 【解析】 【分析】设等比数列{}n a 的公比为q ,验证()()1n n f a f a +是否为非零常数,由此可得出正确选项. 【详解】设等比数列{}n a 的公比为q ,则1n na q a +=. 对于①中的函数()3f x x =,()()3313112n n n n n n f a a a q f a a a +++⎛⎫=== ⎪⎝⎭,该函数为“保等比数列函数”;对于②中的函数()xf x e =,()()111n n n n a a a n a n f a e e f a e++-+==不是非零常数,该函数不是“保等比数列函数”; 对于③中的函数()f x =()()1n n f a f a +===,该函数为“保等比数列函数”;对于④中的函数()ln f x x =,()()11ln ln n n n na f a f a a ++=不是常数,该函数不是“保等比数列函数”.故选:C. 【点睛】本题考查等比数列的定义,着重考查对题中定义的理解,考查分析问题和解决问题的能力,属于中等题.9.C解析:C 【解析】 【分析】数列{}n a ,是等比数列,公比为2,前7项和为1016,由此可求得首项1a ,得通项公式,从而得结论. 【详解】Q 最下层的“浮雕像”的数量为1a ,依题有:公比()717122,7,101612a q n S -====-,解得18a =,则()12*82217,n n n a n n N -+=⨯=≤≤∈,57352,2a a ∴==,从而()()571212352352222,log log 212a a a a ⋅=⨯=∴⋅==,故选C .【点睛】本题考查等比数列的应用.数列应用题求解时,关键是根据题设抽象出数列的条件,然后利用数列的知识求解.10.D解析:D 【解析】 【分析】通过常数代换后,应用基本不等式求最值. 【详解】∵x >0,y >0,且9x+y=1,∴()111199911016y x x y x y x y x y ⎛⎫+=+⋅+=+++≥+= ⎪⎝⎭当且仅当9y x x y =时成立,即11,124x y ==时取等号. 故选D. 【点睛】本题考查了应用基本不等式求最值;关键是注意“1”的整体代换和几个“=”必须保证同时成立.11.A解析:A 【解析】 【分析】利用对数运算,求得n S ,由此解不等式5n S <-,求得n 的最小值. 【详解】 ∵()*21log N 2n n a n n +=∈+, ∴12322223log log log 3142n n S a a a a n n =++++⋯+=++⋯++222312log log 3422n n n +⎛⎫=⨯⨯⋯⨯= ⎪++⎝⎭, 又因为21215log 6232232n S n n <-=⇒<⇒>+, 故使5n S <-成立的正整数n 有最小值:63. 故选:A. 【点睛】本小题主要考查对数运算和数列求和,属于基础题.12.B解析:B 【解析】 试题分析:因为ln 2ln 3ln8ln 9ln 2ln 30,23623--=<<,ln 2ln 5ln 32ln 25ln 2ln 50,251025--=>>,故选B. 考点:比较大小.二、填空题13.;【解析】【分析】利用表示的几何意义画出不等式组表示的平面区域求出点到点的距离的最值即可求解的取值范围【详解】表示点到点的距离则三角形为等腰三角形则点到点的距离的最小值为:1最大值为所以的最小值为:解析:[]0,9; 【解析】 【分析】 利用()()2201x y -++表示的几何意义,画出不等式组表示的平面区域,求出点(0,1)A -到点(,)x y 的距离的最值,即可求解222x y y ++的取值范围.【详解】()()22222011x y y x y ++=-++-()()2201x y -++表示点(0,1)A -到点(,)x y 的距离1AO =,1910,9110AD AC =+==+=ACD 为等腰三角形则点(0,1)A -到点(,)x y 的距离的最小值为:110 所以222x y y ++的最小值为:2110-=,最大值为:101=9-故222x y y ++的取值范围为[]09,故答案为:[]09,【点睛】本题主要考查了求平方和型目标函数的最值,属于中档题.14.【解析】【分析】表示出再表示出整理并观察等式列方程组即可求解【详解】等差数列的公差为前项和为设其首项为则=又数列也为公差为的等差数列首项为所以=即:整理得:上式对任意正整数n 成立则解得:【点睛】本题 解析:12【解析】表示出n S【详解】等差数列{}n a 的公差为()0d d ≠,前n 项和为n S ,设其首项为1a , 则n S =()112n n na d -+,又数列也为公差为d=()1n d -()1n d =-=上式对任意正整数n成立,则)2120122d d d da d d⎧=⎪=⎪-+=⎪⎩,解得:12d =,134a =-【点睛】本题主要考查了等差数列的前n 项和及通项公式,考查了方程思想及转化思想、观察能力,属于中档题.15.【解析】由题设可知即由正弦定理可得所以当时故填【解析】由题设可知)sin sin sin cos cos sin cos C C B C BC C =⇒=+,即sin C A =,由正弦定理可得c=,所以S ==242a a =⇒=时, maxS ==16.【解析】【分析】利用面积公式可求得再用余弦定理求解即可【详解】由题意得又钝角当为锐角时则即不满足钝角三角形故为钝角此时故即故答案为:【点睛】本题主要考查了解三角形中面积公式与余弦定理的运用属于中等题【解析】利用面积公式可求得A ,再用余弦定理求解BC 即可. 【详解】由题意得,11sin sin 22A A =⨯⇒=又钝角ABC V ,当A 为锐角时,cos A ==则2717BC =+-=,即BC =.故A 为钝角.此时cos A ==故27110BC =++=.即BC =【点睛】本题主要考查了解三角形中面积公式与余弦定理的运用,属于中等题型.17.(﹣∞【解析】【分析】由正实数xy 满足可求得x+y≥5由x2+2xy+y2﹣ax ﹣ay+1≥0恒成立可求得a≤x+y+恒成立利用对勾函数的性质即可求得实数a 的取值范围【详解】因为正实数xy 满足而4x解析:(﹣∞,265] 【解析】 【分析】由正实数x ,y 满足4454x y xy ++=,可求得x +y≥5,由x 2+2xy+y 2﹣ax ﹣ay+1≥0恒成立可求得a ≤x+y+1x y+恒成立,利用对勾函数的性质即可求得实数a 的取值范围.【详解】因为正实数x ,y 满足4454x y xy ++=,而4xy ≤(x+y )2,代入原式得(x +y )2﹣4(x+y )﹣5≥0,解得x +y≥5或x +y≤﹣1(舍去), 由x 2+2xy+y 2﹣ax ﹣ay+1≥0可得a (x +y )≤(x+y )2+1, 即a ≤x+y+1x y+,令t=x +y ∈[5,+∞), 则问题转化为a ≤t+1t,因为函数y=t +1t在[5,+∞)递增, 所以y min =5+15=265,所以a ≤265, 故答案为(﹣∞,265] 【点睛】本题考查基本不等式,考查对勾函数的单调性质,求得x +y≥5是关键,考查综合分析与运算的能力,属于中档题.18.【解析】【分析】先化简再利用基本不等式求最小值【详解】由题得当且仅当时取等故答案为:【点睛】本题主要考查基本不等式求最值意在考查学生对这些知识的掌握水平和分析推理能力解题的关键是常量代换解析:92【解析】 【分析】 先化简11122(2)2(2)()22a b a b a b a b+=⋅+⋅=⋅+⋅+,再利用基本不等式求最小值. 【详解】 由题得11121222(2)2(2)()(5)222a b a b a b a b a b b a+=⋅+⋅=⋅+⋅+=++19(522≥+=. 当且仅当221223222a b a ba b ⎧+=⎪==⎨⎪=⎩即时取等. 故答案为:92【点睛】本题主要考查基本不等式求最值,意在考查学生对这些知识的掌握水平和分析推理能力.解题的关键是常量代换.19.-2【解析】【分析】根据题干中所给的表达式得到数列的周期性进而得到结果【详解】根据题干表达式得到可以得数列具有周期性周期为3故得到故得到故答案为:-2【点睛】这个题目考查了求数列中的某些项一般方法是解析:-2 【解析】 【分析】根据题干中所给的表达式得到数列的周期性,进而得到结果. 【详解】根据题干表达式得到2341231111,2, 1.1211a a a a a a =-=-=-=-=-=+++ 5674551111,2, 1.1211a a a a a a =-=-=-=-=-=+++ 可以得数列具有周期性,周期为3,故得到20193673.÷= 故得到2019 2.a =- 故答案为:-2. 【点睛】这个题目考查了求数列中的某些项,一般方法是求出数列通项,对于数列通项不容易求的题目,可以列出数列的一些项,得到数列的周期或者一些其它规律,进而得到数列中的项.20.22【解析】试题分析:由题意得12bcsinA=12a2⇒bcsinA=a2因此ACAB+ABAC+BC2AB ⋅AC=bc+cb+a2bc=b2+c2+a2bc=a2+2bccosA+a2bc=2c 解析:【解析】试题分析:由题意得,因此,从而所求最大值是考点:正余弦定理、面积公式【方法点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是: 第一步:定条件即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向. 第二步:定工具即根据条件和所求合理选择转化的工具,实施边角之间的互化. 第三步:求结果.三、解答题21. (Ⅰ)21n a n =+,n *∈N (Ⅱ)2552n nn T +=- 【解析】试题分析:(1)先根据条件列出关于首项与公差的方程组,解得首项与公差,代入等差数列通项公式即可(2)利用错位相减法求和, 利用错位相减法求和时,注意相减时项的符号变化,中间部分利用等比数列求和时注意项数,最后要除以1q -试题解析:(Ⅰ)由题意得:1127989992a d a d +=⎧⎪⎨⨯+=⎪⎩,解得132a d =⎧⎨=⎩ , 故{}n a 的通项公式为21n a n =+,*n N ∈ (Ⅱ)由(Ⅰ)得:212n nn b +=23435792122222n n n T +=++++⋯+ ① 234113572121222222n n n n n T +-+=+++⋯++ ② ①-②得:23411311112122222222n n n n T ++⎛⎫=++++⋯+- ⎪⎝⎭ 152522n n ++=-故2552n nn T +=-点睛:用错位相减法求和应注意的问题(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解. 22.(1)22n a n =+;(2)63 【解析】 【分析】(1)求出公差d 和首项1a ,可得通项公式;(2)由23,b b 得公比,再得6b ,结合{}n a 通项公式求得k . 【详解】(1)由题意等差数列{n a 的公差432d a a =-=,121210a a a d +=+=,14a =, ∴1(1)4(1)222n a a n d n n =+-=+-⨯=+; (2)由(1)23378,16b a b a ====,∴321628b q b ===,446282128b b q ==⨯=, ∴22128k a k =+=,63k =. 【点睛】本题考查等差数列与等比数列的通项公式,掌握基本量法是解题基础. 23.(1)1()2n n a n N *+=∀∈;(2)见解析 【解析】 【分析】(1)根据前n 项和与通项间的关系得到,221n n n S na a =+-,()1112121n n n S n a a ---=-+-,两式做差即可得到数列11n n a a n n -=+,数列1n a n ⎧⎫⎨⎬+⎩⎭为常数列,112n a n =+,即12n n a +=;(2)根据第一问得到()()22144114111n a n n n n n ⎛⎫=<=- ⎪++⎝⎭+,裂项求和即可. 【详解】(1)当1n =时,111221S a a =+-,即11a =,当2n ≥时,221n n n S na a =+- ①, ()1112121n n n S n a a ---=-+- ②-①②,得()112122n n n n n a na n a a a --=--+-,即()11n n na n a -=+,所以11n n a a n n -=+,且1122a =, 所以数列1n a n ⎧⎫⎨⎬+⎩⎭为常数列,112n a n =+,即()*12n n a n N +=∀∈. (2)由(1)得12n n a +=,所以()()22144114111n a n n n n n ⎛⎫=<=- ⎪++⎝⎭+, 所以()()22224444444423412233411n T n n n =++++<++++⨯⨯⨯++L L ,11111111414142233411n n n L ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-=-< ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.【点睛】这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知n S 和n a 的关系,求n a 表达式,一般是写出1n S -做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等. 24.(1)[]1,2;(2)1,33⎡⎤⎢⎥⎣⎦.【解析】 【分析】(1)利用两角差的正弦公式得出()2sin 6f x x π⎛⎫=-⎪⎝⎭,由,2x ππ⎡⎤∈⎢⎥⎣⎦计算出6x π-的取值范围,再由正弦函数的基本性质可求出函数()y f x =在区间,2ππ⎡⎤⎢⎥⎣⎦上的值域; (2)根据题中条件得出4sin sin 3A B +=,可得出4sin sin 3A B =-,由0sin 1A <≤,0sin 1B <≤,可求出1sin 13B ≤≤,利用正弦定理以及不等式的性质可得出sin 41sin 3sin a A b B B ==-的取值范围. 【详解】(1)()1cos 2cos 2sin cos cos sin 2266f x x x x x x x ππ⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭Q 2sin 6x π⎛⎫=- ⎪⎝⎭,,2x ππ⎡⎤∈⎢⎥⎣⎦Q ,5366x πππ∴≤-≤,则1sin 123x π⎛⎫≤-≤ ⎪⎝⎭,()12f x ∴≤≤,因此,函数()y f x =在,2x ππ⎡⎤∈⎢⎥⎣⎦的值域为[]1,2; (2)78663f A f B ππ⎛⎫⎛⎫+=+- ⎪ ⎪⎝⎭⎝⎭Q ,即()82sin 2sin 3A B π+=-,化简得4sin sin 3A B +=,4sin sin 3A B ∴=-, 由0sin 1A <≤,0sin 1B <≤,即40sin 130sin 1B B ⎧<-≤⎪⎨⎪<≤⎩,得1sin 13B ≤≤. 由正弦定理得4sin sin 4131,3sin sin 3sin 3Ba Ab B B B -⎡⎤===-∈⎢⎥⎣⎦.因此,a b 的取值范围是1,33⎡⎤⎢⎥⎣⎦.【点睛】本题考查正弦型函数值域的求解,同时也考查了三角形中边长比值取值范围的计算,考查运算求解能力,属于中等题.25.(1)n a n =,2nn b =;(2)证明见解析.【解析】 【分析】(1)设等差数列{}n a 的公差为d ,由等差中项的性质可得出3434a a =⎧⎨=⎩,可计算出1a 和d的值,利用等差数列的通项公式可求出n a ,根据题意得出1b 与q 的方程组,结合条件1q >,求出1b 和q 的值,利用等比数列的通项公式可求出n b ;(2)利用分组求和法结合等比数列的求和公式得出()()1122213n n nB++--=,可得出131122121n n n n b B +⎛⎫=- ⎪--⎝⎭,然后利用裂项法可求出n T ,即可证明出32n T <. 【详解】(1)1359a a a ++=Q ,由等差中项的性质得339a =,33a ∴=,同理可得44a =, 设等差数列{}n a 的公差为d ,43431d a a ∴=-=-=,1323211a a d =-=-⨯=,()1111n a a n d n n ∴=+-=+-=.由题意得()22412311208b b b q q b b q ⎧+=+=⎪⎨==⎪⎩,两个等式相除得2152q q +=,整理得22520q q -+=.1q >Q ,解得2q =,12b ∴=,因此,111222n n n n b b q --==⨯=;(2)442n n nn n c b =-=-Q ,()()()1122424242n n n B =-+-++-Q L ()()()()()112121414212444442222214123n n n nnn ++---=+++-+++=-=----L L ()()11112221432233n n n n ++++---⋅+==,()()()()()()111112323222221222121213n n nn n n n n nn n b B +++++⋅∴===⋅------()()()()111212133112221212121n nn n n n +++---⎛⎫=⋅=- ⎪----⎝⎭,22311313113113131122122121221212212n n n n T ++⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-++-=-< ⎪ ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭⎝⎭L .【点睛】本题考查等差数列与等比数列通项公式的求解,数列不等式的证明,涉及了裂项求和法与分组求和法,考查计算能力,属于中等题. 26.(1)=BC 2)20【解析】 【分析】(1)由题意知21AB AC AD ===,.设BD DC m ==,在ADB △与ADC V 中,由余弦定理即可解得m 的值.(2)在ACE △与BCE V 中,由正弦定理,角平分线的性质可得AE AC BE BC ==.可求BE =,215AE =().利用余弦定理可求cos BAC ∠的值,根据同角三角函数基本关系式可求sin BAC ∠的值,利用三角形的面积公式即可计算得解. 【详解】解:(1)由题意知21AB AC AD ===,.设BD DC m ==.在ADB V 与ADC V 中,由余弦定理得:2222cos AB AD BD AD BD ADB =+-⋅∠,2222cos AC AD DC AD DC ADC =+-⋅∠.即:212cos 4m m ADB +-∠=,①212cos 1m m ADB ++∠=.②由①+②,得:232m =,所以m =BC = (2)在ACE V 与BCE V 中,由正弦定理得:,sin sin sin sin AE EC BE ECACE EAC BCE CBE==∠∠∠∠,由于ACE BCE ∠=∠,且sin sin BC ACBAC CBA=∠∠,所以6AE AC BE BC ==.所以BE =,所以215AE =().又222222121cos 22214AB AC BC BAC AB AC +-+-∠===-⋅⨯⨯,所以sin BAC ∠=,所以11211225420ACE S AC AE sin BAC =⋅⋅∠=⨯⨯⨯=V (). 【点睛】本题主要考查了余弦定理,正弦定理,角平分线的性质,同角三角函数基本关系式,三角形的面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.。
人教版2019-2020学年三年级数学上学期期末模拟试卷 ( 带答案)

2019〜2020学年上学期期期末模拟试卷三年级数学(时间:90分钟 满分:100分)一、细心计算,我能做到!(共26分)1.直接写得数。
(8分)65+35= 86-26= 45×2= 201×3=34+43= 60-32= 800×9= 0×999=85+70= 52-6= 36+54÷6= 250×4-80=3155+= 118-= 1211212-= 131111+=2.用竖式计算下面各题。
(带※的要验算)(14分)※(1)887+265= ※(2)643-57=(3)426 × 5 (4)780-403(5)450 × 6 (6)608 × 53.某商场要购进3个高压锅,900元够吗?(4分)佳佳这样想:因为308=300,308×3≈900(元),所以900元够了。
琳琳这样想:因为308超过300元,308×3一定超过900元,所以900元不够。
(1)我认为( )估的方法比较合理。
A.佳佳B.琳琳(2)( )不合理的原因是:(3)我的建议:在估算钱数够不够时,应当把数估( )(填“大”或“小”)二、我会填!(共23分)1.小浩在看上午10:30〜上午11:20场次的《熊出没之熊心归来》电影,距离电影结束还有15分钟,现在是( )时( )分。
2.在〇里填上或“>”“<”或“=”。
2时○200分 70米〇7千米 454〇999-54658〇38 19○12 1分3〇秒〇90秒3.在( )里填上合适的单位名称。
小明朗诵一首诗大约需要30( );踢一场足球赛约用2( );地铁平均每小时行驶90( );—辆卡车的载质量是2000( )。
4.行2千米需要多长时间?把出行方式和相应的时间连起来。
5.有15根小棒,取出了10根,取出了它的( )( )。
6.小明围着一个正方形花坛走一圈,走了160米,花坛的边长为( )米。
苏教版三年级数学下册期末试卷及答案(江苏南京2020年真卷)

2019-2020(下)三年级数学期末学业质量调研 2020.07一、填空(每空1分,共25分。
)1. 要买39本《三国演义》,每本售价51元。
求大约需要元,可以这样列式估算()。
如右图,方框里的这一步表示的是()。
2. 填上合适的单位名称:①南京绕城公路长度大约是147.2()。
②一袋大米重50(),20袋这样的大米重1()。
③小明在作业本上画了一个边长为10()的正方形,它的面积是1()。
3.小丽跑完1千米用了4.2分钟,明明跑完1千米用了4.3分钟,()跑得快。
4.在下面的括号里填上适当的数。
40平方米=()平方分米 7厘米= ()()分米6000 米 =( ) 千米 3元2角=()元(填小数)5.不计算,在○里填“>”“<”或“=”。
143-85-15 143-(85-15) 180-120÷5 (180-120)÷5 240÷(3×4 240÷3÷4 5吨40千克 5400千克6. 右图所示,每一个小方格都是边长2厘米的小正方形。
涂色部分的面积是()平方厘米,涂色部分占整个长方形的()()。
7.从你出生的那一年算起,到今年一共有()个闰年。
8.在一个长20厘米,宽15厘米的长方形纸中,剪下一个最大的正方形,这个正方形的面积是()平方厘米。
9.G1113次高铁列车7:24从南京南站出发,经过7小时16分到达广州南站。
G1113次高铁到达广州南站的时间是()。
10. “王老师买30本《新华字典》,付了700元,找回多少元?”还需要知道什么信息?请将你认为所需要的信息写在括号里()。
根据所填信息,要求找回多少元可以列出综合算式()。
11. 猴妈妈有18个桃,小猴第一天吃了这些桃的16,第二天吃了剩下的13。
小猴第一天吃了()个桃,第二天吃了()个桃。
二、判断(正确的打“√”,错误的打“×”。
每题1分,共5分)12. 五十几乘以二十几的积可能是三位数,也可能是四位数。
2019-2020学年三年级下学期数学期中考试试卷A卷(模拟)

2019-2020学年三年级下学期数学期中考试试卷A卷姓名:________ 班级:________ 成绩:________同学们,经过一段时间的学习,你一定长进不少,让我们好好检验一下自己吧!一、填空。
(共22分) (共10题;共22分)1. (2分)在横线上填上适当的数.(1)________×30=________(2)________×30=________2. (2分)在()里填上适当的运算符号,使等式成立。
560()8=70 48()52=100 35()9=315 5()600=3000 260()4=1040 999()1=999 803()2=1606 888()0=03. (1分) (2018四上·青岛期末) 一个数除以16,商是25,余数最大是________,当余数最大时,被除数是________。
4. (2分)猜电话号码:0713—提示:A—8的最小倍数;B—最小的自然数;C—5的最大因数;D—既是4的倍数,又是4的因数;E—它的所有因数是1、2、3、6;F—它的所有因数是1、3;G—它只有一个因数。
这个号码是:0731—________5. (1分)根据87×13=1131,直接写出下列各题的答案:(1)870×130=________(2)870×130=________(3)8700×130=________(4)8700×130=________(5)8700×1300=________(6)8700×1300=________(7)870×1300=________(8)870×1300=________6. (6分) (2016四下·泗阳期中) 根据25×4=100,直接写出下面算式的得数.25×8=________25×12=________250×40=________ 25×24=________.7. (2分)口算.12×3=________48×2=________24×5=________ 120×3=________48×20=________24×25=________ 1200×3=________48×200=________24×75=________8. (2分)数一数,填一填.七星瓢虫E和七星瓢虫F到对称轴的距离都是________小格.七星瓢虫C和七星瓢虫________到对称轴的距离是相等的.七星瓢虫________和七星瓢虫________到对称轴的距离都是1小格9. (2分)□÷□=27……15,被除数最小是________.10. (2分)将一张圆形的纸对折三次,得到的角是________度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年三年级数学模拟试卷
班级姓名成绩
一、轻松填空动动脑。
1>”“<”。
18××8 180÷3÷7 70×50×7 69÷÷3
2、8吨 =()千克()克 = 3千克
( )分=1时50分 3年 =()个月
3、一个长方形的长8cm,宽比长少3cm,这个长方形的周长是()。
用一根40厘米长的铁丝首尾相连围城一个长方形,它的周长是()厘米。
4、在除式☆÷8=15……□中,□里的数最大是()。
5、“6+6+6+……+6=804”,算一算一共有()个6相加。
6、()里最大填几?
7×()< 54 ( )×8<46 ( )×9<22
二、心细计算快又好。
1、口算。
4×12= 600÷3= 32×3= 4×16= 2×40=
60+8= 150÷5= 240÷8= 25×4= 630÷7=
302×3= 300÷6= 48÷4= 17×5= 16×5=
9+6×3= 5+4×7= 8÷2+9= 8+5×6= 2400÷8=
700×4 = 103×3 = 500÷5 = 17 + 18 = 300×5 = 840÷4 = 420×1 = 96÷3 = 88÷2 = 5600÷7 =
2、用竖式计算,除法要验算。
708×4= 654÷6= 581÷7=
验算验算
246×7= 504×9= 824÷4=
验算1890+3879= 3679—182= 1040×2=
3、脱式计算。
905—150×4 168×5÷6 (71+37)÷9 (540-370)×6 33×8÷6 745+625÷5
三、动手操作难不倒。
1、小熊从下面盒子里分别摸出一颗弹珠,结果是哪个?
一定是红
红的可能性大
有可能是红,
也有可能是黄.
很可能是黄
2、求下面图形的周长:(单位:厘米)
图1 图2 图3 图4
图1 图2 图3 图4
3、填一填,算一算
经过()分经过()分
: : :
四、数学运用身手巧。
1、汽车厂的生产线9分钟能生产36辆汽车,照这样计算,1小时能生产多少辆汽车?
2、小明的爷爷、爸爸的体重各是多少?
3、学校操场长400米, 宽120米, 小方绕操场四周跑3圈, 他跑了多少米?
五、思考与操作
1、下面的物体分别从正面、侧面、上面看到的形状分别是什么?请你在方格纸上画出来。
2、画一画,填一填。
(1)主持班有5位(3男2女)非常优秀的同学,要选一男一女两位同学作为期末表彰会的主持人,请帮助老师想一想,一共有()种不同的选法。
(2)用你喜欢的方式表示你组合的方法。
3、画一画,拼一拼。
用三张长3厘米,宽2厘米的长方形拼成一个大长方形。
有几种不同
的拼法?(1)请画出来。
(2)它们的周长分别是多少?
六、解决问题
1、有一根铁丝刚好能围城一个长10cm,宽6cm的长方形。
如果用这根铁丝围一个正方形,这个正方形的边长是多少?
2、食堂11月运来3吨煤,平均每天要烧90千克,这些煤够烧一个月吗?
3、希望小学一共有6个年级,每个年级有4个班,平均每个班有45个学生。
全校一共有多少个学生?
4、小黄、小蓝、小白、小王和小丽5人参加体育比赛,见面时每两人都握手一次,小黄已握手了4次,小蓝已握手了三次,小白已握手了两次,小王握手了一次,问小丽已握了几次手?
附送:
2019-2020年三年级数学测量测试卷
一、想一想,填一填。
1、在()里填上适当的单位。
树高约10()马拉松长跑比赛一块橡皮长
全长约42()约4()
一壶花生油一只曲别针重一辆货车能载重
重5()约2()约10 ()
2、在○里填上>、<或=
6厘米○60毫米50千米○400厘米800克○1千克
2米○19分米3吨○3000千克6吨○7千克
3、我估计我家到学校的距离
..大约是(),
我估计数学老师的体重
..大约是()。
二、判断对错,我能行。
1、如果每个学生的体重是25千克, 那么40个学生的体重就是1吨。
( )
2、丽丽的身高是136分米。
()
3、1200千克-200千克=1000吨()
4、3000米+8000米=11千米()
5、1千克棉花比1千克盐重。
()
三、找朋友,连一连。
1、
200千克40吨2千克400克
20米35毫米2313千米20分米四、选一选,把你认为正确答案的序号填在()里。
1、一辆汽车每小时大约行驶()。
A、90千米B、90米C、90分米
2、一课桌高约()。
A、70毫米B、70厘米C、70分米
3、一个西瓜重5()。
A、克B、千克C、吨
4、水杯的高约1()。
A、毫米B、厘米C、分米
5、走1千米大约需要()。
A、50秒B、12分C、1时
6、数学课本的宽约是145( )。
A 、毫米B、厘米C、分米
7、一枝钢笔长大约14( )。
A 、分米B、厘米C、毫米
8、厚度最接近1厘米的物体是( )。
A 、文具盒 B 、电视机C、数学书
9、自行车每分钟行300( )。
A 、分米 B 、米C、千米
10、4千克( )4千米。
A、大B、等于C、不能比较
五、解决问题。
1、聪聪早晨从家到学校,中午放学回到家.这两次一共要走多少千米?
2、农场有45吨粮食,请你算一算,用一辆载重5000千克的卡车运几次可将
这些粮食运完?
3、在一辆载重2吨的货车上装9只重200千克的箱子,超载了吗?
小学教育资料
好好学习,天天向上!
第7 页共7 页。
