第十届华罗庚金杯数学竞赛试卷
第十届全国华罗庚金杯少年数学邀请赛初赛答
中考电功率计算题走向电功率计算是历年中考命题的热点内容之一,纵观近几年中考电功率计算题的走向,笔者发现除了一直保持着的紧密联系工农业生产和日常生活实际这一大特色外,从05年开始又有了新动向,就是将计算与其它题型结合起来,改单纯的计算为计算与说理、计算与设计、计算与评估等,向以计算为主体的综合型计算方向发展。
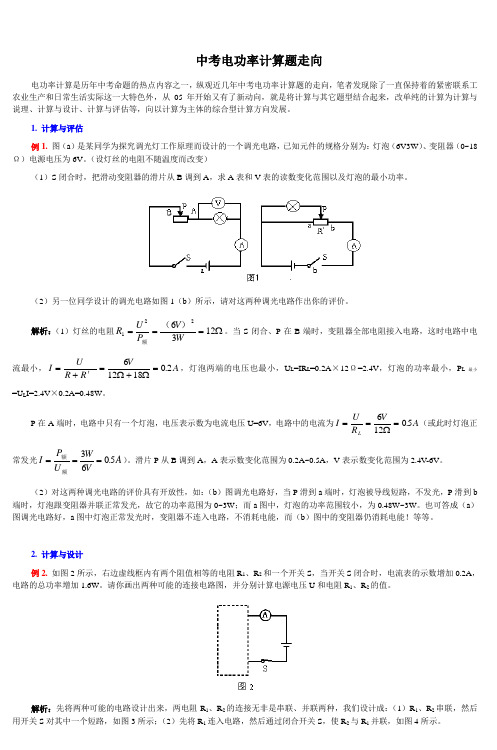
1. 计算与评估例1. 图(a)是某同学为探究调光灯工作原理而设计的一个调光电路,已知元件的规格分别为:灯泡(6V3W)、变阻器(0~18Ω)电源电压为6V。
(设灯丝的电阻不随温度而改变)(1)S闭合时,把滑动变阻器的滑片从B调到A,求A表和V表的读数变化范围以及灯泡的最小功率。
(2)另一位同学设计的调光电路如图1(b)所示,请对这两种调光电路作出你的评价。
解析:(1)灯丝的电阻R UPVW1226312===额()Ω。
当S闭合、P在B端时,变阻器全部电阻接入电路,这时电路中电流最小,IUR RVA=+=+=′6121802ΩΩ.,灯泡两端的电压也最小,U L=IR L=0.2A×12Ω=2.4V,灯泡的功率最小,P L最小=U L I=2.4V×0.2A=0.48W。
P在A端时,电路中只有一个灯泡,电压表示数为电流电压U=6V,电路中的电流为IURVAL===61205Ω.(或此时灯泡正常发光IPUWVA===额额3605.)。
滑片P从B调到A,A表示数变化范围为0.2A~0.5A,V表示数变化范围为2.4V-6V。
(2)对这两种调光电路的评价具有开放性,如:(b)图调光电路好,当P滑到a端时,灯泡被导线短路,不发光,P滑到b 端时,灯泡跟变阻器并联正常发光,故它的功率范围为0~3W;而a图中,灯泡的功率范围较小,为0.48W~3W。
也可答成(a)图调光电路好,a图中灯泡正常发光时,变阻器不连入电路,不消耗电能,而(b)图中的变阻器仍消耗电能!等等。
2. 计算与设计例2. 如图2所示,右边虚线框内有两个阻值相等的电阻R1、R2和一个开关S,当开关S闭合时,电流表的示数增加0.2A,电路的总功率增加1.6W。
第十届全国“华罗庚金杯”少年数学邀请赛

第十届全国“华罗庚金杯”少年数学邀请赛 决赛试题 初一组 (完卷时间:一小时三十分钟) 一、填空(每题10分,共80分)1.①计算:[]=--⨯-⨯÷-÷⎪⎭⎫ ⎝⎛-⨯-222)2(343443)5.0(121124112113( ) ②已知:abc ≠0且a +b +c =0,则=++a c ac c b cb b a ba ( )2.设m 和n 均不为零,3x ²y ³和-5x 2+2m+n y ³是同类项,则=+-+++-322332239635933n mn n m m n mn n m m ( ) 3.由于浮力的作用,金放在水里秤量和它的重量比较,在水中的“重量”会减少191;银放在水里秤量和它的重量相比较,在水中的“重量”会减少101。
某个只含有金银成分的古文物,重量是150克,在水中称量,“重量”是141克,则古文物中金占( )%。
(精确到1%)4.图1是几何学中非常著名的美丽的轴对称的图形,他有( )条对称轴。
5.甲加工一种零件,乙加工另一种零件。
甲用A 型机器需要6小时才能完成任务,用B 型机器效率降低60%;乙用B 型机器需要10小时才能完成任务,用A 型机器效率提高20%。
如果甲用A 型机器、乙用B 型机器同时开始工作,中途某一时刻交换使用机器,甲和乙恰好同时完成任务。
则甲完成任务所用的时间是( )小时。
6.一个直角三角形三条边的长度是3、4、5,如果分别以各边为轴旋转一周,得到三个立体,那么三个立体中最大的体积和最小的体积的比是( )。
7.一列自然数0,1,2,3,…,2005,…,2024,第一个数是0,从第二个数开始,每一个都比它前一个大0 3 8 15 …1 2 7 14 …4 5 6 13 …9 10 11 12 …… … … … …( )列。
8.(3m -1)x =6x -35是关于x 的方程,为确保该方程的解是负整数,m 能取的最大值是( )。
2019年四年级数学第十届华罗庚金杯初赛试题

2019年四年级数学第十届华罗庚金杯初赛试题1. 2005年是中国伟大航海家郑和首次下西洋600周年, 西班牙伟大航海家哥伦布首次远洋航行是在1492 年. 问这两次远洋航行相差多少年?2. 从冬至之日起每九天分为一段, 依次称之为一九, 二九, …, 九九. 2004年的冬至为12月21日, 2005年的立春是2月4日. 问立春之日是几九的第几天?3. 左下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于 1 的正方形. 问这个直三棱柱的体积是多少?4. 爸爸、妈妈、客人和我四人围着圆桌喝茶. 若只考虑每人左邻的情况,问共有多少种不同的入座方法?5. 在奥运会的铁人三项比赛中,自行车比赛距离是长跑的 4 倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米. 求三项的总距离.6. 如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形. 其中最小的三角形顶点的个数(重合的顶点只计一次)依次为: 3, 6, 10, 15, 21, …问这列数中的第 9 个是多少?7. 一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示. 若用甲容器取水来注满乙容器, 问: 至少要注水多少次?8. 100 名学生参加社会实践, 高年级学生两人一组, 低年级学生三人一组,共有 41组. 问: 高、低年级学生各多少人?9. 小鸣用48元钱按零售价买了若干练习本. 如果按批发价购买, 每本便宜 2元, 恰好多买4本. 问: 零售价每本多少元?10. 不足100 名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈. 问最多有多少名同学?11. 输液100毫升, 每分钟输2.5毫升. 请你观察第12分钟时吊瓶图像中的数据, 回答整个吊瓶的容积是多少毫升?12. 两条直线相交所成的锐角或直角称为两条直线的“夹角”. 现平面上有若干条直线,它们两两相交,并且“夹角”只能是 300, 600 或 900. 问: 至多有多少条直线?初赛试题答案1 87年.2 六九的第一天.3 1/24 共有6种不同的入座方法。
初中竞赛数学第十届“华罗庚金杯”少年数学邀请赛初一第一试(含答案)

第十九届“华罗庚金杯”少年数学邀请赛试题初一年级 第一试(时间:2018年4月9日上午10:00—11:30)一、选择题:(每小题6分,共60分)1、已知a 、b 都是有理数,且|a|=a ,|b|≠b ,则ab=( )(A )负数; (B )正数; (C )负数或零; (D )非负数2、如图,数轴上每个刻度为1个单位长,点A 对应的数为a ,B 对应的数为b ,且b-2a=7,那么数轴上原点的位置在( )(A )A 点; (B )B 点; (C )C 点; (D )D 点。
3、下列说法正确的是( )(A )-a 的相反数是a; (B )-a 的倒数是-1a; (C )-a 的绝对值是a; (D )-a 2一定是负数; 4、大于353-⎛⎫ ⎪⎝⎭而不大于(-3)2的整数总共有( ) (A )12个; (B )13个; (C )14个; (D )15个。
5、有8个编号分别是①至⑧的球,其中有6个球一样重,另外两个球都轻1克,为了找出这两面三刀个球,用天平称了3次:第一次:①+②比③+④重;第二次:⑤+⑥比⑦+⑧轻;第三次:①+③+⑤与②+④+⑧一样重,则两个轻球的编号分别为( )(A )①③; (B )②④; (C )⑥⑧; (D )④⑤。
6、如图,AB ∥CD 则下列等式成立的是( ) (A )B F D E G ∠+∠+∠=∠+∠ (B )E F G B D ∠+∠+∠=∠+∠(C )F G D E B ∠+∠+∠=∠+∠ (D )B E F D G ∠+∠+∠=∠+∠7、点P 为线段MN 上任意一点,点Q 为NP 的中点,若MQ=6,则MP+MN 为( )(A )8. (B )10。
(C )12 (D )不确定8、已知p+2q=0,(q ≠0),则123p p p q q q-+-+-=( )(A )4; (B )6; (C )3; (D )4或6。
9.若abcd 表示一个四位数,且ab dc =,如1331,2552,则abcd 称为四位对称数,将这样的四作画数由小到大排列起来,第12个四位对称数是( )(A )2442 (B )2112 (C )2332 (D )222210、若A 、B 、C 、D 、E 五名运动员进行乒乓球单循环赛(即每两人赛一场),比赛进行一段时间后,进行过的场次数与队员的对照统计表如下:A C B那么与E (A )A 和B (B )B 和C (C )A 和C (D )A 和D二、填空题:(每小题6分,共90分)11、请将2、2、11、11这四个数用加减乘除四则运算以及括号组成结果为24的算式(每个数有且只能用一次): 。
第十届全国“华罗庚金杯”少年数学邀请赛决赛小学组试题
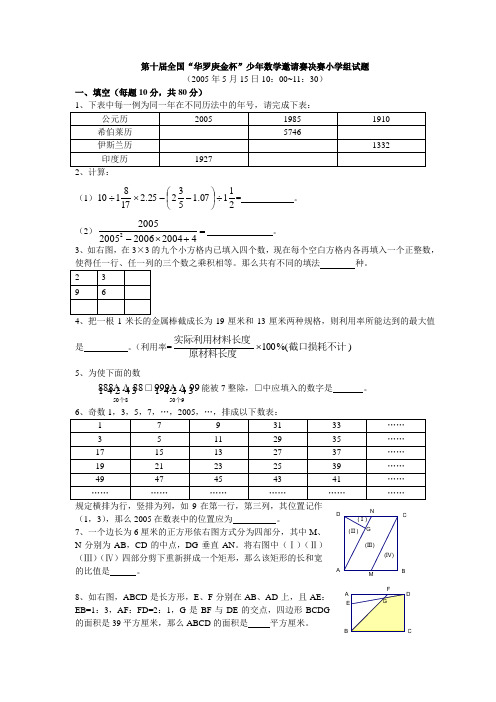
第十届全国“华罗庚金杯”少年数学邀请赛决赛小学组试题(2005年5月15日10:00~11:30)一、填空(每题10分,共80分)(1)21107.153225.2178110÷⎪⎭⎫ ⎝⎛--⨯÷= 。
(2)=+⨯-420042006200520052 。
3、如右图,在3×3的九个小方格内已填入四个数,现在每个空白方格内各再填入一个正整数,使得任一行、任一列的三个数之乘积相等。
那么共有不同的填法 种。
4、把一根1米长的金属棒截成长为19厘米和13厘米两种规格,则利用率所能达到的最大值是 。
(利用率=)%(100截口损耗不计原材料长度实际利用材料长度⨯5、为使下面的数85088888个□95099999个能被7整除,□中应填入的数字是 。
规定横排为行,竖排为列,如9在第一行,第三列,其位置记作(1,3),那么2005在数表中的位置应为 。
7、一个边长为6厘米的正方形依右图方式分为四部分,其中M 、N 分别为AB ,CD 的中点,DG 垂直AN 。
将右图中(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ)四部分剪下重新拼成一个矩形,那么该矩形的长和宽的比值是 。
8、如右图,ABCD 是长方形,E 、F 分别在AB 、AD 上,且AE :EB=1:3,AF :FD=2:1,G 是BF 与DE 的交点,四边形BCDG 的面积是39平方厘米,那么ABCD 的面积是 平方厘米。
CB A G Ⅳ()Ⅲ()Ⅱ()Ⅰ()N MDCBA二、解答下列各题,要求写出简要过程(每题10分,共40分)9、r 可以表示为形如abcd .0的十进制小数,其中a ,b ,c ,d 代表0~9中的任意一个数字,现有若干既约分数,这些分数的分子为1或2,这样的一些分数中与r 最接近的是72,那么r 可能有多少种不同的值?10、某车间把一批零件平均分给三个工人同时开始加工,赵师傅比张师傅早18分钟完成,张师傅比孙师傅早16分钟完成,已知赵师傅每小时比张师傅多加工6个,张师傅每小时比孙师傅多加工4个。
最新第10~16届全国华罗庚金杯少年数学邀请赛决赛试题详细解释答案

第十届全国"华罗庚金杯"少年数学邀请赛决赛试题一、填空(每题10分,共80分)1.下表中每一列为同一年在不同历法中的年号,请完成下表:第1小题:2.计算:① 18.3×0.25+5.3÷0.4-7.13 = ( ); ②= ( )。
答案:10.695;13.计算机中最小的存储单位称为“位”,每个“位”有两种状态:0和1。
一个字节由8个“位”组成,记为B。
常用KB,MB等记存储空间的大小,其中1KB=1024B, 1MB=1024KB。
现将240MB的教育软件从网上下载,已经下载了70%。
如果当前的下载速度为每秒72KB,则下载完毕还需要()分钟。
(精确到分钟)答案:174.a,b和c都是二位的自然数,a,b的个位分别是7与5,c的十位是1。
如果它们满足等式ab+c=2005,则a+b+c=( )。
答案:1025.一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(图1中的阴影部分)和正方体体积的比是()。
答案:6.某种长方体形的集装箱,它的长宽高的比是4∶3∶2,如果用甲等油漆喷涂它的表面,每平方米的费用是0.9元,如果改用乙等油漆,每平方米的费用降低为0.4元,一个集装箱可以节省6.5元,则集装箱总的表面积是()平方米,体积是()立方米。
答案:13:37.一列自然数0,1,2,3,…,2005,…,2004,第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2024。
现在将这列自然数排成以下数表:规定横排为行,竖排为列,则2005在数表中位于第()行和第()列。
答案:20;458.图2中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG 的面积是40平方厘米,那么ABCD的面积是()平方厘米。
图2答案:60二、解答下列各题,要求写出简要过程(每题10分,共40分)9.图3是由风筝形和镖形两种不同的砖铺设而成。
第十届全国“华罗庚金杯”少年数学邀请赛决赛试题初一组

第十届全国“华罗庚金杯”少年数学邀请赛决赛试题初一组徐淮源
【期刊名称】《时代数学学习:7年级》
【年(卷),期】2005(000)007
【总页数】7页(P52-58)
【作者】徐淮源
【作者单位】江苏省常州市
【正文语种】中文
【中图分类】G4
【相关文献】
1.第九届“华罗庚金杯”少年数学邀请赛决赛试题(初一组) [J], 无
2.第九届全国“华罗庚金杯”少年数学邀请赛决赛试题(初二组) [J], 徐淮源
3.第十一届全国“华罗庚金杯”少年数学邀请赛初赛试卷(初一组) [J], 无
4.第十一届全国“华罗庚金杯”少年数学邀请赛决赛试卷(初一组) [J], 满涛
5.第六届华罗庚金杯少年数学邀请赛初一决赛试题及答案(1997·5) [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
第十届全国华罗庚金杯少年数学邀请赛初一组决赛试卷与解答

第十届全国”华罗庚金杯”少年数学邀请赛决赛试题:初一组一. 填空(每题10分,共80分)1.①计算: 22111134413(12)(0.5)(2)22412433⎡⎤-⨯-÷-÷⨯-⨯--=⎣⎦ . ②已知: 0abc ≠且0a b c ++=,则a b b c c a a b b c c a++= . 2.m 和n 均不为零, 233x y 和2235m nx y ++-是同类项,则322332233395369m m n mn n m m n mn n -++=+-+ . 3.由于浮力的作用,金放在水里秤量和它的重量比较,在水中的”重量”会减少119;银放在水里秤量和它的重量相比较,在水中的”重量”会减少110.某个只含有金银成分的古文物,重量是150克,在水中秤量,”重量”是141克,则古文物中金占 %.(精确到1%)4.图1是几何学中非常著名的美丽的轴对称的图形,它有 条对称轴.5.甲加工一种零件,乙加工另一种零件.甲用A 型机器需要6小时才能完成任务,用B 型机器效率降低60%;乙用B 型机器需要10小时才能完成任务,用A 型机器效率提高20%.如果甲用A 型机器,乙用B 型机器同时开始工作,中途某一时刻交换使用机器,甲和乙同时完成任务.则甲完成任务所用的时间是 小时.6.一个直角三角形三条边的长度是3,4,5.如果分别以各边为轴旋转一周,得到三个立体,那么三个立体中最大的体积和最小的体积的比是 .7.一列自然数0,1,2,3……,2005,……,2024.第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2004.现在将这列自然数排成以下数表:3 8 15 (1)2 7 14 (4)5 6 13 …… 9 10 11 12 ………… …… …… …… ……规定横排为行,竖排为列,则2005在数表中位于第 行和第 列。
8。
(31)635m x x -=-是关于x 的方程,为确保该方程的解是负整数,m 能取的最大 值 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十届华罗庚金杯初赛试题
1. 2005年是中国伟大航海家郑和首次下西洋600周年, 西班牙伟大航海家哥伦布首次远洋航行是在1492 年. 问这两次远洋航行相差多少年?
2. 从冬至之日起每九天分为一段, 依次称之为一九, 二九, …, 九九. 2004年的冬至为12月21日, 2005年的立春是2月4日. 问立春之日是几九的第几天?
3. 左下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于 1 的正方形. 问这个直三棱柱的体积是多少?
4. 爸爸、妈妈、客人和我四人围着圆桌喝茶. 若只考虑每人左邻的情况,问共有多少种不同的入座方法?
5. 在奥运会的铁人三项比赛中,自行车比赛距离是长跑的 4 倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米. 求三项的总距离.
6. 如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形. 其中最小的三角形顶点的个数(重合的顶点只计一次)依次为: 3, 6, 10, 15, 21, …
问这列数中的第 9 个是多少?
7. 一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示. 若用甲容器取水来注满乙容器, 问: 至少要注水多少次?
8. 100 名学生参加社会实践, 高年级学生两人一组, 低年级学生三人一组,共有 41组. 问: 高、低年级学生各多少人?
9. 小鸣用48元钱按零售价买了若干练习本. 如果按批发价购买, 每本便宜 2元, 恰好多买4本. 问: 零售价每本多少元?
10. 不足100 名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈. 问最多有多少名同学?
11. 输液100毫升, 每分钟输2.5毫升. 请你观察第12分钟时吊瓶图像中的数据, 回答整个吊瓶的容积是多少毫升?
12. 两条直线相交所成的锐角或直角称为两条直线的“夹角”. 现平面上有若干条直线,它们两两相交,并且“夹角”只能是 300, 600 或 900. 问: 至多有多少条直线?
初赛试题答案
1 87年.
2 六九的第一天.
3 1/2
4 共有6种不同的入座方法。
5 三项的总距离为51.5千米.
6 第9个是55.
7 至少要注水8次.
8 高年级学生 46人、低年级学生 54人.
9 零售价每本6元.
10 93名.
11 150毫升.
12 至多有6条直线.。
