自控原理I复习
自动控制原理复习提纲

第一章绪论1、基本概念(1)自动控制:在没有人直接参与的情况下,利用控制器使被控对象(或过程)的某些物理量(被控量)自动地按预先给定的规律去运行。
(2)自动控制系统:能够实现自动控制任务的系统,由控制装置与被控对象组成。
(3)被控对象:指被控设备或过程。
(4)输出量,也称被控量:指被控制的量。
它表征被控对象或过程的状态和性能,它又常常被称为系统对输入的响应。
(5)输入量:是人为给定的系统预期输出的希望值。
(6)偏差信号:参考输入与实际输出的差称为偏差信号,偏差信号一般作为控制器的输入信号。
(7)负反馈控制:把被控量反送到系统的输入端与给定量进行比较,利用偏差引起控制器产生控制量,以减小或消除偏差。
2、自动控制方式(1)开环控制开环控制系统指系统的输出量对系统的控制作用没有影响的系统。
它分为按给定控制和按扰动控制两种形式。
按给定控制:信号由给定输入到输出单向传递。
按扰动控制(顺馈控制):根据测得的扰动信号来补偿扰动对输出的影响。
(2)闭环控制(反馈控制)闭环控制系统指系统的输出量与输入端存在反馈回路,即输出量对控制作用有直接影响的系统。
系统根据实际输出来修正控制作用,实现对被控对象进行控制的任务,这种控制原理称为反馈控制原理。
3、自动控制系统的分类(1)按给定信号的特征分类①恒值控制系统:希望系统的输出维持在给定值上不变或变化很小。
②随动控制系统:给定信号的变化规律是事先不确定的随机信号。
③程序控制系统:系统的给定输入不是随机的,而是确定的、按预先的规律变化。
(2)按系统的数学模型分类⎧⎧⎧⎪⎪⎪⎪⎪⎪−−−→⎨⎪⎪⎪⎪⎪⎨⎪⎪⎩⎪⎪⎪⎧⎪⎪−−−→⎨⎨⎪⎩⎩⎪⎪⎧−−−→⎪⎪⎪⎧⎪⎨⎪⎪−−−→⎨⎪⎪⎪⎪⎪⎩⎩⎩分析法分析法分析法分析法时域法根轨迹法线性定常系统频域法线性系统状态空间法时域法线性时变系统状态空间法非本质非线性线性化法描述函数法非线性系统本质非线性相平面法状态空间法 (3)按信号传递的连续性划分①连续系统:系统中的所有元件的输入输出信号均为时间的连续函数,所以又常称为模拟系统。
自动控制原理知识点复习资料整理

自动控制原理知识点总结第一章1、自动控制:是指在无人直接参与的情况下,利用控制装置操纵受控对象,是被控量等于给定值或按给定信号的变化规律去变化的过程。
2、被控制量:在控制系统中.按规定的任务需要加以控制的物理量。
3、控制量:作为被控制量的控制指令而加给系统的输入星.也称控制输入。
4、扰动量:干扰或破坏系统按预定规律运行的输入量,也称扰动输入或干扰掐入。
5、反馈:通过测量变换装置将系统或元件的输出量反送到输入端,与输入信号相比较。
反送到输入端的信号称为反馈信号。
6、负反馈:反馈信号与输人信号相减,其差为偏差信号。
7、负反馈控制原理:检测偏差用以消除偏差。
将系统的输出信号引回插入端,与输入信号相减,形成偏差信号。
然后根据偏差信号产生相应的控制作用,力图消除或减少偏差的过程。
8、自动控制系统的两种常用控制方式是开环控制和闭环控制。
9、开环控制:控制装置与受控对象之间只有顺向作用而无反向联系特点:开环控制实施起来简单,但抗扰动能力较差,控制精度也不高。
10、闭环控制:控制装置与受控对象之间,不但有顺向作用,而且还有反向联系,既有被控量对被控过程的影响。
主要特点:抗扰动能力强,控制精度高,但存在能否正常工作,即稳定与否的问题。
11、控制系统的性能指标主要表现在:(1)、稳定性:系统的工作基础。
(2)、快速性:动态过程时间要短,振荡要轻。
(3)、准确性:稳态精度要高,误差要小。
12、实现自动控制的主要原则有:主反馈原则、补偿原则、复合控制原则。
第二章1、控制系统的数学模型有:微分方程、传递函数、动态结构图、频率特性。
2、传递函数:在零初始条件下,线性定常系统输出量的拉普拉斯变换域系统输入量的拉普拉斯变换之比3、求传递函数通常有两种方法:对系统的微分方程取拉氏变换,或化简系统的动态方框图。
对于由电阻、电感、电容元件组成的电气网络,一般采用运算阻抗的方法求传递函数。
4、结构图的变换与化简化简方框图是求传递函数的常用方法。
《自动控制原理》课程考试复习要点

《自动控制原理》课程考试复习要点第1章控制原理绪论一、主要内容1、自动控制的概念,控制系统中各部分名称及概念2、开环控制于闭环控制的区别,负反馈原理3、系统的分类4、方框图绘制(原理图)5、对自动控制系统的一般要求(稳、准、快)二、自动控制概念中的基本知识点1、闭环系统(或反馈系统)的特征:采用负反馈,系统的被控变量对控制作用有直接影响,即被控变量对自己有控制作用。
2、典型闭环系统的功能框图。
自动控制在没有人直接参与的情况下,通过控制器使被控对象或过程按照预定的规律运行。
自动控制系统由控制器和被控对象组成,能够实现自动控制任务的系统。
被控制量在控制系统中.按规定的任务需要加以控制的物理量。
控制量作为被控制量的控制指令而加给系统的输入星.也称控制输入。
扰动量干扰或破坏系统按预定规律运行的输入量,也称扰动输入或干扰掐入。
反馈通过测量变换装置将系统或元件的输出量反送到输入端,与输入信号相比较。
反送到输入端的信号称为反馈信号。
负反馈反馈信号与输人信号相减,其差为偏差信号。
负反馈控制原理检测偏差用以消除偏差。
将系统的输出信号引回插入端,与输入信号相减,形成偏差信号。
然后根据偏差信号产生相应的控制作用,力图消除或减少偏差的过程。
开环控制系统系统的输入和输出之间不存在反馈回路,输出量对系统的控制作用没有影响,这样的系统称为开环控制系统。
开环控制又分为无扰动补偿和有扰动补偿两种。
闭环控制系统凡是系统输出端与输入端存在反馈回路,即输出量对控制作用有直接影响的系统,叫作闭环控制系统。
自动控制原理课程中所讨论的主要是闭环负反馈控制系统。
复合控制系统复合控制系统是一种将开环控制和闭环控制结合在一起的控制系统。
它在闭环控制的基础上,用开环方式提供一个控制输入信号或扰动输入信号的顺馈通道,用以提高系统的精度。
自动控制系统组成组成一个自动控制系统通常包括以下基本元件1.给定元件给出与被控制量希望位相对应的控制输入信号(给定信号),这个控制输入信号的量纲要与主反馈信号的量纲相同。
完整版)自动控制原理知识点汇总

完整版)自动控制原理知识点汇总自动控制原理总结第一章绪论在自动控制中,被控对象是要求实现自动控制的机器、设备或生产过程,而被控量则是表征被控对象工作状态的物理参量或状态参量,如转速、压力、温度、电压、位移等。
控制器是由控制元件组成的调节器或控制装置,它接受指令信号,并输出控制作用信号于被控对象。
给定值或指令信号r(t)是要求控制系统按一定规律变化的信号,是系统的输入信号。
干扰信号n(t)又称扰动值,是一种对系统的被控量起破坏作用的信号。
反馈信号b(t)是指被控量经测量元件检测后回馈送到系统输入端的信号。
偏差信号e(t)是指给定值与被控量的差值,或指令信号与反馈信号的差值。
闭环控制的主要优点是控制精度高,抗干扰能力强。
但是使用的元件多,线路复杂,系统的分析和设计都比较麻烦。
对控制系统的性能要求包括稳定性、快速性和准确性。
稳定性和快速性反映了系统的过渡过程的性能,而准确性则是衡量系统稳态精度的指标,反映了动态过程后期的性能。
第二章控制系统的数学模型拉氏变换是一种将时间域函数转换为复频域函数的数学工具。
单位阶跃函数1(t)、单位斜坡函数、等加速函数、指数函数e-at、正弦函数sinωt、余弦函数cosωt和单位脉冲函数(δ函数)都有其典型的拉氏变换。
拉氏变换的基本法则包括线性法则、微分法则、积分法则、终值定理和位移定理。
传递函数是线性定常系统在零初始条件下,输出信号的拉氏变换与输入信号的拉氏变换之比,称为系统或元部件的传递函数。
动态结构图及其等效变换包括串联变换法则、并联变换法则、反馈变换法则、比较点前移“加倒数”和比较点后移“加本身”,以及引出点前移“加本身”和引出点后移“加倒数”。
梅森公式是一种求解传递函数的方法,典型环节的传递函数包括比例(放大)环节、积分环节、惯性环节、一阶微分环节、振荡环节和二阶微分环节。
第三章时域分析法时域分析法是一种分析控制系统时域特性的方法。
其中,时域响应包括零状态响应和零输入响应。
《自动控制原理》复习提纲

《自动控制原理》复习提纲自动控制原理复习提纲第一章:自动控制系统基础1.1自动控制的基本概念1.2自动控制系统的组成1.3自动控制系统的性能指标1.4自动控制系统的数学建模第二章:系统传递函数与频率响应2.1一阶惯性系统传递函数及特性2.2二阶惯性系统传递函数及特性2.3高阶惯性系统传递函数及特性2.4惯性环节与纯时延环节的传递函数2.5开环传递函数与闭环传递函数2.6频率响应曲线及其特性第三章:传递函数的绘制和分析3.1 Bode图的绘制3.2 Bode图的分析方法3.3 Nyquist图的绘制和分析3.4极坐标图的应用3.5稳定性分析方法第四章:闭环控制系统及稳定性分析4.1闭环控制系统4.2稳定性的概念和判据4.3 Nyquist稳定性判据4.4 Bode稳定性判据4.5系统的稳态误差分析第五章:比例、积分和微分控制器5.1比例控制器的原理和特性5.2积分控制器的原理和特性5.3微分控制器的原理和特性5.4比例积分(P)控制系统5.5比例积分微分(PID)控制系统第六章:根轨迹法6.1根轨迹的概念和基本性质6.2根轨迹的绘制方法6.3根轨迹法的稳定性判据6.4根轨迹设计法则6.5根轨迹法的应用案例第七章:频域设计方法7.1频域设计基本思想7.2平衡点反馈控制法7.3频域设计法的应用案例7.4系统频率响应的优化设计7.5频域方法的灵敏度设计第八章:状态空间分析和设计8.1状态空间模型的建立8.2状态空间的矩阵表示8.3状态空间系统的特性8.4状态空间系统的稳定性分析8.5状态空间设计方法和案例第九章:模糊控制系统9.1模糊控制的基本概念9.2模糊控制系统的结构9.3模糊控制器设计方法9.4模糊控制系统的应用案例第十章:遗传算法与控制系统优化10.1遗传算法的基本原理10.2遗传算法在控制系统优化中的应用10.3遗传算法设计方法和案例第十一章:神经网络及其应用11.1神经网络的基本概念和结构11.2神经网络训练算法11.3神经网络在控制系统中的应用11.4神经网络控制系统设计和优化方法第十二章:自适应控制系统12.1自适应控制的基本概念12.2自适应控制系统的结构12.3自适应控制器设计方法12.4自适应控制系统的应用案例第十三章:系统辨识与模型预测控制13.1系统辨识的基本概念13.2建模方法及其应用13.3模型预测控制的原理13.4模型预测控制系统设计和优化方法第十四章:多变量控制系统14.1多变量控制系统的基本概念14.2多变量系统建模方法14.3多变量系统稳定性分析14.4多变量系统控制器设计14.5多变量系统优化控制方法以上是《自动控制原理》的复习提纲,内容覆盖了自动控制系统的基本概念、传递函数与频率响应、传递函数的绘制和分析、闭环控制系统及稳定性分析、比例、积分和微分控制器、根轨迹法、频域设计方法、状态空间分析和设计、模糊控制系统、遗传算法与控制系统优化、神经网络及其应用、自适应控制系统、系统辨识与模型预测控制、多变量控制系统等知识点。
自动控制原理总复习资料(完美)
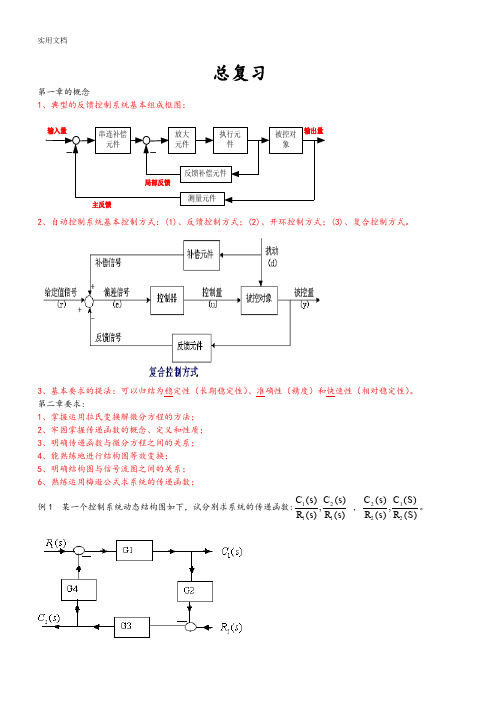
总复习第一章的概念1、典型的反馈控制系统基本组成框图:2、自动控制系统基本控制方式:(1)、反馈控制方式;(2)、开环控制方式;(3)、复合控制方式。
3、基本要求的提法:可以归结为稳定性(长期稳定性)、准确性(精度)和快速性(相对稳定性)。
第二章要求:1、掌握运用拉氏变换解微分方程的方法;2、牢固掌握传递函数的概念、定义和性质;3、明确传递函数与微分方程之间的关系;4、能熟练地进行结构图等效变换;5、明确结构图与信号流图之间的关系;6、熟练运用梅逊公式求系统的传递函数;例1 某一个控制系统动态结构图如下,试分别求系统的传递函数:)()(,)()(1211s R s C s R s C ,)()(,)()(2122S R S C s R s C 。
43213211243211111)()(,1)()()(G G G G G G G s R s C G G G G s G s R s C --=-=例2 某一个控制系统动态结构图如下,试分别求系统的传递函数:)()(,)()(,)()(,)()(s N S E s R s E s N s C s R s C 。
例例4、一个控制系统动态结构图如下,试求系统的传递函数。
X r5214323211)()(W W W W W W S X S X r c ++=例5 如图RLC 电路,试列写网络传递函数 U c (s)/U r (s).解: 零初始条件下取拉氏变换:例6某一个控制系统的单位阶跃响应为:t te et C --+-=221)(,试求系统的传递函数、微分方程和脉冲响应。
解:传递函数: )1)(2(23)(+++=s s s s G ,微分方程:)(2)(3)(2)(3)(22t r dt t dr t c dt t dc dtt c d +=++ 脉冲响应:t te et c 24)(--+-=例7一个控制系统的单位脉冲响应为t te et C ---=24)(,试求系统的传递函数、微分方程、单位阶跃响应。
自动控制原理复习资料
第二章 控制系统的数学模型1、传递函数(线性系统在零初始状态,脉冲输入下的响应)2、计算系统的传递函数1)列写常微分方程,得到输入r(t)与c(t)的常微分方程,再使用拉普拉斯变换为频域形式(记得系统初始状态为零),求取)()(s R s C 。
2)一些最基本的拉普拉斯变换公式as A Ae s A At s A At sA A s R s dtt r d s Y s dtt y d atnnnn+⇔⇔⇔⇔⇔⇔-,21,,),()(),()(322 3)进行反拉普拉斯变换时,即将系统的频域表达式转换成为时域表达式,一般采用部分分式分解的方法,求其中的系数时用到了留数法,见p63例2-35。
4)系统的开环传递函数与闭环传递函数的异同,注意开环传递函数和单位负反馈系统闭环传递函数之间的数学关系。
对单位负反馈系统,即H(s)=1,开环和闭环传递函数关系)()(1)(,)(11)(s s s G s G s ΦΦ-=+=Φ。
3、结构图化简和梅逊增益公式 1)理解一些基本概念比较点,引出点,前向通路,回路2)结构图化简的基本原则:保持前向通路传递函数不变,保持回路传递函数不变3)化简规则包括:引出点的前(后)移动,比较点的前(后)移动,并联相加,串联相减,回路等效(见下图)。
4)根据信号流图使用梅逊增益公式计算传递函数步骤:(a )找出所有回路,并列写回路传递函数i L ;(b)找出所有前向通路,并列写前向通路的传递函数k P ;(c )判断是否存在互不接触的独立回路,并根据公式 (11)-⎪⎪⎭⎫⎝⎛+-=∆∑∑=≠ni n j i j i i L L L 计算分母∆,其中第i 个和第j 个回路互不接触;(d )利用相同的原理计算(a )中与第k 条前向通路不接触的回路的k ∆;(e )根据梅逊增益公式∆∆∑=mk kkP 1计算系统输入到输出的传递函数)()(s R s C 。
第二章 典型习题答案课本的以下典型例题,要认真看一下,最好能试做一下。
自控原理复习资料
自控原理复习资料各章考试题型第一章自动控制的一般概念基本概念第二章控制系统的数学模型第三章线性系统的时域分析法第二、三章考试题型:一个大题考察全部内容:1.建模与模型化简。
给出一个结构图,要求化简(可能需要用到梅森公式)得到系统的传递函数。
或者给出一个物理系统求系统的微分方程或传递函数。
2.稳定性问题。
根据求得的传递函数利用劳斯判据判断系统的稳定性及特征根分布,说出系统动态过程的特点。
或者说出能使系统稳定的参数选择范围。
或者相对稳定性。
3.求解时间响应。
如果系统稳定,求系统的的响应(包括输入作用和扰动作用同时存在时)4.计算稳态误差。
求系统在输入作用下的稳态误差(注意正弦信号输入怎么求稳态误差)和扰动作用下的稳态误差。
5.定性讨论。
说出减小系统稳态误差的措施(针对输入和扰动两种情况)。
注:第3点,(求系统的单位阶跃响应或者脉冲响应较多。
)(如果是高阶系统可能不需要求,但有可能讨论主导极点)第四章线性系统的根轨迹法第四章考试题型题型一1.给定系统的开环传递函数,绘制系统的根轨迹2.根据稳定性或者稳态误差的要求,确定更轨迹增益的取值或取值范围。
进而确定响应的闭环极点。
3.讨论改善系统性能的举措(添加零极点等)题型二1.给定系统的开环传递函数,绘制根轨迹图。
2.进一步给定系统的动态性能要求(比如阻尼比),利用主导极点的概念确定系统的闭环极点,和所对应的根轨迹增益。
题型三参数根轨迹绘制注:以上题型不会单独出,往往会结合第二章和第三章的题一起出。
第五章线性系统的频域分析法第五章考试题型题型一1.建模。
2.求出系统的传递函数。
3.写出系统的频率特性,画出系统开环奈奎斯特图、bode图(画图注意事项,并注意区分最小相位系统和非最小相位系统)。
4.用奈奎斯特稳定性判据或者对数稳定判据判断系统的稳定性。
5.系统稳定时,求系统的稳定裕度(相角裕度、幅值裕度)。
6.求闭环系统的频率特性(怎么从等M圆上看出谐振峰值)。
自动控制原理复习1资料
(1)一、填空(每空1分,共18分)1.自动控制系统的数学模型有 微分方程 、 传递函数 、 频率特性 、 结构图 共4种。
2.连续控制系统稳定的充分必要条件是 闭环极点位于S 平面左侧 。
离散控制系统稳定的充分必要条件是 系统的特性方程的根都在Z 平面上以原点为圆心的单位圆内。
。
3.某统控制系统的微分方程为:dtt dc )(+0.5C(t)=2r(t)。
则该系统的闭环传递函数 Φ(s)= ;该系统超调σ%= ;调节时间t s (Δ=2%)= 。
4.某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ,则该系统是 4 阶二 型系统;其开环放大系数K= 62.5 。
5.已知自动控制系统L(ω)曲线为:则该系统开环传递函数G(s)= ;ωC = 。
6.相位滞后校正装置又称为 调节器,其校正作用是 。
7.采样器的作用是 ,某离散控制系统)()1()1()(10210TT e Z Z e Z G -----=(单位反馈T=0.1)当输入r(t)=t 时.该系统稳态误差为 。
二. 1.求图示控制系统的传递函数.求:)()(S R S C (10分)R(s)2.求图示系统输出C (Z )的表达式。
(4分)三、 计算1、 已知t Te tf 11)(--=求F (s )(4分)2、 已知)5(1)(2+=s s s F 。
求原函数f (t )(6分)3.已知系统如图示,求使系统稳定时a 的取值范围。
(10分)R (s )四.反馈校正系统如图所示(12分)求:(1)K f=0时,系统的ξ,ωn和在单位斜坡输入下的稳态误差e ss.(2)若使系统ξ=0.707,k f应取何值?单位斜坡输入下e ss.=?五.已知某系统L(ω)曲线,(12分)(1)写出系统开环传递函数G(s)(2)求其相位裕度γ(3)欲使该系统成为三阶最佳系统.求其K=?,γmax=?(1) (2) (3)六、已知控制系统开环频率特性曲线如图示。
(完整word版)自动控制原理复习提纲(整理版)
(完整word版)自动控制原理复习提纲(整理版)《自动控制原理》课程概念性知识复习提纲详细版第一章:1.自动控制的任务(背):是在没有人直接参与下,利用控制装置操纵被控对象,使被控量等于给定值。
2.自动控制基本方式一.按给定值操纵的开环控制二.按干扰补偿的开环控制三.按偏差调节的闭环控制3.性能要求:稳快准第二章:4.微分方程的建立:课后2.55.传递函数定义(背)线性定常系统(或元件)的传递函数为在零初始条件下,系统(或元件)的输出变量拉氏变换与输入变量拉氏变换之比。
这里的零初始条件包含两方面的意思,一是指输入作用是在t=0以后才加于系统,因此输入量及其各阶导数,在t=0-时的值为零。
二是指输入信号作用于系统之间系统是静止的,即t=0-时,系统的输出量及其各阶导数为零。
这是反映控制系统的实际工作情况的,因为式(2-38)表示的是平衡工作点附近的增量方程,许多情况下传递函数是能完全反映系统的动态性能的。
6.结构图化简:课后2.14(结构图化简一道大题,梅森公式化简一道大题)复习要点7.几种传递函数(要求:懂得原理)一.输入信号r(t)作用下的系统闭环传递函数二.干扰信号n(t)作用下的系统闭环传递函数三.闭环系统的误差传递函数8.阶跃响应,脉冲响应,传递函数之间的关系阶跃响应:H(s)=1s 单位斜坡响应:t C (s )=21s 单位脉冲响应:K(s)=Φ(s) 11()()()H s s K s s s =Φ?=? 211()()()t C s s H s s s=Φ?=? 综合可得 K(s)=sH(s) H(s)=s t C第三章:9.阶跃响应的性能指标有哪些,各个性能指标的意义是什么。
10.从平稳性,快速性和稳态精度三个方面,简述典型二阶欠阻尼系统结构参数,n对阶跃相应的影响。
由于欠阻尼二阶系统具有一对实部为负的共轭复特征根,时间响应呈衰减振荡特性,故又称为振荡环节。
系统闭环传递函数的一般形式为222()()2n n nC s R s s s ωζωω=++ 由于0<ζ<1,所以一对共轭复根为1,2n s j ζωω=-±d j σω-±式中,n σζω=,为特征根实部之模值,具有角频率量纲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 3:s来自, 2 = −σ ± jω d
Solution of Differential Equations
h(t ) = 1 − e −ξω n t 1−ξ
2
欠阻尼系统单位阶跃响应:
σ = ξω n
sin (ω d t + β )
ωd = ωn 1− ξ 2
2 β = arctg 1 − ξ / ξ = arccos ξ
2. 动态性能与稳态性能(通常在阶跃响应作用下测定)
误差带
稳态误差 (tÆ ∞)
t 峰值时间
调节时间
σ% =
h(t p ) − h(∞) h (∞ )
× 100%
Chapter 3:
3. 一阶系统的时域分析
输入 信号 1(t) 输出响应 ( t≥ 0 ) 性能指标 td=0.69T tr=2.20T ts=3T ts=3T
+ cn u
步骤: 基尔霍夫定律(电路系统) 能量守恒定律(加热炉) 牛顿运动定理(弹簧-位移) 物料平衡(液位系统) 1、确定输入输出变量 2、分析系统所遵循的物理规 律或化学规律, 3、消去中间变量,得输入输 出之间的微分方程
Chapter 2:
2. 传递函数模型
Writing System Equations
一、自动控制的一般概念
1. 自动控制的基本原理——反馈控制原理 2. 自动控制的组成(原理框图的绘制)
控制对象、控制阀、测量元件和控制器
控制器Gc(s)
控制阀Gv(s)
控制对象Gp(s)
测量Gm(s)
一、自动控制的一般概念
3. 自动控制系统的分类:
线性连续控制系统(微分方程):定常系统、时变系统 恒值控制系统——设定值是一个常数 随动系统——设定值是事先未知的,随时间任意变化的 函数; 程序控制系统——设定值是按照预定规律随时间变化的 函数; 线性定常离散控制系统(差分方程) 非线性控制系统:特点是系数与变量有关,或者方程中含 有变量及其导数的高次幂或乘积项
Chapter 3:
高阶系统的动态性能
Solution of Differential Equations
闭环零点
峰值时间 减小峰值时间,使响应加快,闭 环零点越接近虚轴,这种作用越 明显 减小系统阻尼,增大系统的超调 量 增大调节时间,这种作用将随闭 环零点接近虚轴而加剧
闭环非主导极点
增大峰值时间,使响 应变慢
闭环极点负实部的绝对值越大,其对应的响应分量衰减得越迅速;反之 则衰减缓慢;
主导极点法:
主导极点——距虚轴最近的极点周围没有闭环零点,而其他闭环极点又 远离虚轴 主导极点所对应的响应分量随时间的推移衰减缓慢,在系统的时间响应 过程中起主导地位。 采用主导极点法将高阶系统用二阶或者一阶系统进行近似,然后估算其 动态性能
j
ωn ξ 2 −1
ωn2 s(s+2ξωn)
无阻尼
s1, 2 = −ξω n ± ω n ξ 2 − 1 欠阻尼 1>ξ > 0
j
ωn ξ 2 −1
ξ <0
s1,1
ξ =0
临界阻尼
s5,1
j
ωn
过阻尼 s3,1
ξωn
s2,1
− ωn ξ 2 −1
ξ >1
s2,2
s4,1 s3,2
ξωn
ξ =1
s7,1,2
拉氏变换 求导
传递函数
求导
Chapter 3:
4. 二阶系统的时域分析
Solution of Differential Equations
2 ωn C ( s) Φ( s) = = 2 R( s ) s 2 + 2ξω n s + ω n
ωn——自然频率(或无阻尼振荡频率) ξ——阻尼比(或相对阻尼系数) 特征根(闭环极点)
ωd——阻尼振荡频率 σ = ξωn——衰减系数
s1
延迟时间: t d = 上升时间: t r =
1 + 0.6ξ + 0.2ξ 2
ωn
td =
1 + 0.7ξ
ωn
π −β ωd
ωn β
σ = ξω n
ωd = ωn 1− ξ
2
峰值时间: t p =
π ωd
1−ξ 2
超调量: σ % = e −πξ /
Steady-State Response Transient Response Definition of time constant Examples: second-order system Transients(Dynamic) of system Time-response specifications Complete solution of the state-variable equations
Chapter 2:
Writing System Equations
微分方程模型、传递函数模型、状态方程模型 1. 微分方程模型
dny dt
n
+ a1
d n−1 y dt
n −1
+
dy d n −1u d n − 2u + an −1 + an y = c1 n −1 + c2 n −2 + dt dt dt
超调量
增大系统阻尼,减小 系统超调量 调节时间缩短
调节时间
State-variable equations
State space model
x (t ) = Ax (t ) + Bu(t ) State equation y(t ) = Cx (t ) + Du
Output equation
u1 u2 um
阻尼比 ξ<0 ξ=0 0<ξ<1 ξ=1 ξ>1
特征根 在右半平面 一对纯虚根 具有负实部的 共轭复根 相等的负实根 不等的负实根
动态响应 发散正弦振荡或单调发散,不稳定 无阻尼情况,等幅振荡 欠阻尼情况,衰减振荡过程 临界阻尼情况,非周期地趋于稳态输出 过阻尼情况,非周期地趋于稳态输出,当响 应速度比临界阻尼缓慢
系统初始条件为零,对微分方程取拉氏变换
dny dt
n
+ a1
d n−1 y dt
n −1
+
dy d n−1u d n − 2u + an−1 + an y = c1 n −1 + c2 n −2 + dt dt dt
+ cn u
拉氏变换
Y (s ) = U (s )
拉氏反变换
G (s ) =
∑
n
cn − j +1s j −1
复习大纲(2)
5)掌握线性系统的稳定性分析方法:线性系统的稳定性分 析、稳态误差计算; 6)掌握线性系统的根轨迹法: 根轨迹法的基本概念、根轨 迹绘制的基本法则及推广、利用根轨迹进行系统性能的 分析; 7)掌握线性系统的频率分析法:线性系统的频率特性概念、 开环系统的典型环节分解与开环频率特性曲线、频率域 稳定判据以及稳定裕度; 8)一般性了解线性系统的校正方法。
n− j s j
j =1 n
∑a
j =0
初始条件为零的条件下, 输出拉氏变换与输入拉 氏变换之比
Chapter 2:
3. 状态空间模型
Writing System Equations
X (t ) = AX (t ) + BU (t )
Y (t ) = CX (t ) + DU (t )
状态方程与传递函数之间的转换:
3.5
× 100%
s2
调节时间:t s = ξω = σ n
3.5
Chapter 3:
系统的单位 阶跃响应
Solution of Differential Equations
系统的单位 脉冲响应
传递函数
ξ, ωn
特征根
动态性能指标
Chapter 3:
5. 高阶系统的时域分析
Solution of Differential Equations
Chapter 2:
9 9 9
Writing System Equations
9 9 9 9 9
Introduction Electric Circuits and Components Basic Linear Matrix Algebra & State Concepts Transfer Function and Block Diagram Mechanical Translation Systems Analogous Circuits Other Mathematic Modeling Examples Linearization
1 − e −t / T
1 −t / T e T
t − T + Te
δ(t) t 1/2t2
稳态误差T
1 2 t − Tt + T 2 (1 − e −t / T ) 2
Chapter 3:
对于线性定常系统: 脉冲响应 积分 阶跃响应 积分 斜坡响应
Solution of Differential Equations
X (t ) = AX (t ) + BU (t ) Y (t ) = CX (t ) + DU (t )
Y (s) −1 G (s ) = = C (sI − A) B + D U (s)
可控标准型、可观标准型、对角标准型
Linearization
非线性环节线性化小结
¾ 要建立整个系统的线性化微分方程式, 1. 首先确定系统处于平衡状态时,各元件的工作 点; 2. 然后列出各元件在工作点附近的偏量方程式, 消去中间变量; 3. 最后得到整个系统以偏量表示的线性化方程式。
