晋江市2017年秋季八年级期末跟踪检测数学试题
晋江初二期末考试卷子数学

考试时间:120分钟满分:100分一、选择题(本大题共10小题,每小题3分,共30分。
每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列各数中,有理数是()A. √-1B. √4C. πD. 无理数2. 已知x是实数,下列不等式中,正确的是()A. x > 0B. x ≥ 0C. x < 0D. x ≤ 03. 下列各数中,属于负数的是()A. -3B. 3C. 0D. -3/24. 如果a > b,那么下列不等式中一定成立的是()A. a + 1 > b + 1B. a - 1 > b - 1C. a × 1 > b × 1D. a ÷ 1 > b ÷ 15. 已知函数f(x) = 2x - 3,那么f(-1)的值是()A. -1B. 1C. 5D. -56. 在直角坐标系中,点A(2, 3)关于y轴的对称点是()A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)7. 下列各图中,与x轴平行的直线是()A.B.C.D.8. 在等腰三角形ABC中,AB = AC,如果∠B = 40°,那么∠A的度数是()A. 40°B. 50°C. 60°D. 70°9. 下列各数中,不是正比例函数图象的是()A. y = 2xB. y = 3x + 1C. y = -4xD. y = 5x - 210. 下列关于一元二次方程的解的说法中,正确的是()A. 一元二次方程的解一定是实数B. 一元二次方程的解一定是整数C. 一元二次方程的解可能是复数D. 一元二次方程的解可能是无理数二、填空题(本大题共10小题,每小题3分,共30分。
把答案填写在题后的横线上。
)11. 已知x² - 5x + 6 = 0,那么x的值是__________。
2017-2018学年福建省泉州市八年级(上)期末数学试卷

2017-2018学年福建省泉州市八年级(上)期末数学试卷一、选择题(本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有项是符合题目 要求的,请在答题卡上相应题目的答题区域内作答)1、 64的立方根是() A. 4 B ・ 8 2、 下列实数是无理数的是() 22 A. —B. y/S 73、 下列计算正确的是() A ・&C ・ a 2+a 2+a 2=3a 1 C ・±4D ・±8C. 0 D ・-1010101B. 2d+3a=6c D. a 2+a 2+a 1=a 64、如图,AC 丄BE, ZA = ZE,不能判断AABC^/\EDC 的条件是() 5、下列四组线段中,能组成直角三角形的是()6、如图,等腰三角形JPC 中,肋平分Z43C, Z2 = 36° ,则Z1的度数为() 7、空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是()C. AB=DED ・ AC =CEA ・ a=l, b=2, c=3B ・ a=4, b=2、c=3 C. a=4, 6=2, c=5 D ・ a = 12, b=5, c=13C. 72° D ・ 108°A.条形图B. 折线图C. 扇形图D. 直方图B.8、如图,边长为e b的矩形的周长为14,而积为10,则a2b^ab2的值为(A. 140 B・ 70 C・ 35 D・ 249、如图,在已知的厶松©中,按以下步骤作图:①分别以D C为圆心,以大于的长为半径作弧,两弧相交于两点M N;②作直线交肿于点D连接CD 若CD=AC.乙3 = 25° ,则Zd的度数为10、如图,P是等边三角形,毎C内的一点,且刃=3, PB=4, PC=5,将厶砂绕点2顺时针旋转60° 到△CB0位置.连接P0,则以下结论错误的是()OA・ZOPB=6L B・ZPOC=90° C・ Z-£PB=150° D・ZJPC=135°二填空题(本大题共6小题,每小题4分,共24分•把答案填在答题卡的相应位置)11、比较大小:3 ______ x/7 (填写“V”或“〉”)12)分解因式:A T2 - 9x= _______ •13、 _____________________________________________________ 在等腰'ABC中,ZJ = 80° ,那么ZB=度.14、学校为了解七年级学生参加课外兴趣小组的情况,随机调查了40名学生,将结果绘制成了如图所示的统计图,则七年级学生参加书法兴趣小组的频率是________ ・15.如图,OC平分ZAOB,点P是射线OC上的一点,PD丄0B于点D,且PD=3,动点。
福建省泉州市2017-2018学年八年上学期期末教学质量检测数学试题(附答案精品)

…20.(8 分)如图,四边形 ABCD 中,AB =CD ,AC ⊥AB 于点 A ,BD ⊥CD 于点 D .A(1)求证:AC =BD ;D(2)若 AB =AD ,试求出∠ABD 的度数.A DBC 的延长 BCEO第 14 题图 BC.则它的第三条边长为cm .a b,叫做 2 阶行列式,定义其运算c d2 x + 32 x -3 2 x - 3= .2 x + 321.(8 分)已知 a,b,c,为△ABC 的三边长,且满足 a 2c 2-b 2c 2=a 4-b 4,试判断△ABC 的形状.-1) . D 3小明∵a 2c 2-b 2c 2=a 4-b 4 ∴c 2(a 2-b 2)=(a 2-b 2)(a 2+b 2) ∴c 2= a 2+b 2∴△ABC 是直角三角形- 3x ) ,其中 x = - 5 .试判断小明的解题过程是否正确?若正确,请写出各步骤的理由;若不正确,请写出正确CF .求证:∠B =∠D .的解题过程.2017 年秋季八年级期末教学质量检测 数学试题 第 1 页(共 6 页) 2017 年秋季八年级期末教学质量检测 数学试题 第 2 页(共 6 页) 2017 年秋季八年级期末教学质量检测 数学试题 第 3 页(共 6 页)25.(14分)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB分别交CD、CB于E、F.(1)尺规作图:作线段AF,使得AF平分∠CAB分别交CD、CB于E、F(保留痕迹,不写作法);(2)求证:CE=CF;(3)将线段DE 向右平移至点E 恰好在CB 上,得到新的线段记为D'E',D'、E'分别在AB、CB 上.已知CF=3,请求出BE'的长度.CA D Bb 的长方形卡片拼出一个边页(共 6 页)2017 年秋季八年级期末教学质量检测数学试题第 6 页(共 6 页)…………………………………………………………………………………………………………………………………………………密封线内不要答题。
福建省晋江市2017年初中学业质量检查数学试题(含答案)

y42017年晋江市初中学业质量检查数 学 试 题(试卷满分:150分;考试时间:120分钟)一、选择题(每小题3分,共21分.每小题有四个答案,其中有且只有一个答案是正确的,请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答的一律得0分.) 1.52011-的相反数是( ). A .5201 B .5201- C .52011D .52011-2.下列运算正确的是( ).A .523a a a =+B .22223=-a aC .523a a a =⋅D .236a a a =÷ 3.下列左图所示的立体图形的主视图...是( ).4.对于解不等式2332>-x ,正确的结果是( ). A .49-<x B .49->x C .1->x D .1-<x5.下列四边形不是..轴对称图形的是( ). A .正方形B .矩形C .菱形D .平行四边形6.若一个多边形的内角和︒900,则这个多边形的边数为( ). A .5B .7C .9D .127.若二次函数()02<++=a c bx ax y 的图象如图所示, 且关于x 的方程k c bx ax =++2有两个不相等的实根, 则常数k 的取值范围是( ).A.B. C. D.B(第9题图)AT(第15题图)A .40<<kB .13<<-kC .3-<k 或1>kD .4<k二、填空题(每小题4分,共40分):在答题卡上相应题目的答题区域内作答.8.据报道,春节期间微信红包收发高达3270000000次,则3270000000用科学记数法表示为 .9.如图,直线OB AO ⊥于点O ,OT 平分AOB ∠, 则=∠AOT °. 10.计算:___________111=---m m m . 11.已知点()3,2-A 在双曲线xky =上,则______=k . 12.在学生演讲比赛中,六名选手的成绩(单位:分)分别为:80、85、86、88、90、93,则这组数据的中位数为 分.13.如图,直线a ∥b ,直线c 与直线a 、b 都相交,︒=∠1151,则=∠2 °.14.如图,在等腰ABC ∆中,AC AB =,若︒=∠100A ,则︒=∠______B . 15.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,点M 是CD 边的中点,连结ABCD 的周长为cm________.16.如图,在矩形ABCD 中,AC DE ⊥于点E ,12=AB ,20=AC ,则________cos =∠ADE .17.如图,CD 是半圆O 的直径, AB 是弦,且6=CD ,︒=∠30ADB , 则︒=∠_____AOB ;若用扇形AOB 围成一个圆锥,则该圆锥的底面圆的半径为________.(第13题图)(第14题图)(第17题图)三、解答题(共89分):在答题卡上相应题目的答题区域内作答. 18.(9分)计算:5312)15(6410--⨯+---.19.(9分)先化简,再求值:())3(3)4(2-+++a a a ,其中5=a .20.(9分)如图,AB ∥CD , AB =CD ,点E 、F 在AD 上,且AE DF =.求证:ABE ∆≌DCF ∆.(第16题图)ABDE F(第20题图)21.(9分)如图(一)(二),现有两组扑克牌,每组3张扑克,第一组分别是红桃5、红桃6、红桃7,第二组分别是梅花3、梅花4、梅花5.(1)现把第一组扑克牌背面朝上并搅匀,如图(一)所示,若从第一组中随机抽取一张牌, 求“抽到红桃6”的概率;(2)如图(一)(二),若把两组扑克牌背面朝上各自搅匀,并分别从两组中各抽取一张牌, 试求“抽出一对牌(即数字相同)”的概率(要求用树状图或列表法求解).22.(9分)如图,在等腰OAB ∆中,OB OA =,以点O 为圆心,作圆与底边AB 相切于点C . (1)求证:BC AC =;(2)若42=AB ,9=OC ,求等腰OAB ∆的周长.23.(9分)如图,某校合作学习小组随机抽样统计部分高年级男同学对必修球类“篮球、足球、(图一)(图二)第一组第二组(第21题图)(第22题图)B排球”三大球的喜爱程度的人数,绘制出不完整的统计图表如下: (1)试把表格中的数据填写完整:(2)试利用上述表格中的数据,补充完成条形统计图的制作(用阴影部分表示); (3)若再随机抽查该校高年级男学生一人,则该学生喜爱的三大球最大可能是什么?24.(9分)一队学生从学校出发去劳动基地军训,行进的路程与时间的图象如图所示,队伍走了0.9小时后,队伍中的通讯员按原路加快速度返回学校拿材料,通讯员经过0.5小时后回到学校,然后随即按原来加快的速度追赶队伍................,恰好在劳动基地追上学生队伍.设学(第23题图)球类篮球 足球 排球 三大球喜爱人数分布直方图三大球喜爱人数扇形统计图(第23题图)t (时)(第24题图)d 学生队伍 通讯员OAC0.9 4.5B(千米)3.15生队伍与学校的距离为1d ,通讯员与学校的距离为2d ,试根据图象解决下列问题: (1)填空:学生队伍的行进速度______=v 千米/小时; (2)当15.39.0≤≤t 时,求2d 与t 的函数关系式; (3)已知学生队伍与通讯员的距离不超过3千米时, 能用无线对讲机保持联系,试求在上述过程中 通讯员离开队伍后........他们能用无线对讲机保持联 系时t 的取值范围.25.(13分)已知抛物线c bx x y ++=231与直线BC 相交于B 、C 两点,且()0,6B 、()3,0C .(1)填空:_____=b ,_____=c ;(2)长度为5的线段DE 在线段CB 上移动,点G 与点F 在上述抛物线上,且线段EF 与DG 始 终平行于y 轴.①连结FG ,求四边形DGFE 的面积的最大值, 并求出此时点D 的坐标;②在线段DE 移动的过程中,是否存在GF DE =?若存在,请直接写出....此时点D 的 坐标,若不存在,试说明理由.26.(13分)已知直线b x y +=43与x 轴、y 轴分别相交于A 、B 两点,点D 在x 轴正半 轴上,且6=OD ,点C 、M 是线段OD 的三等分点(点C 在点M 的左侧).(第25题图)(备用图)(1)若直线AB 经过点()6,4, ①求直线AB 的解析式; ②求点M 到直线AB 的距离; (2)若点..Q 在.x 轴上方的直线......AB 上.,且 CQD ∠是 锐角,试探究:在直线 AB 上是否存在符合条件的点Q ,使得54sin =∠CQD ;若存在,求出b的取值范围,若不存在,请说明理由.(以下空白作为草稿纸)2017年初中学业质量检查数学试题参考答案及评分标准xyABOC DM (备用图)xABOC D My(第26题图)说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分.(二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题3分,共21分) 1.C2.C3.A 4.A5. D6.B7.D二、填空题(每小题4分,共40分)8.91027.3⨯ 9.45 10.1 11.6- 12.87 13.65 14.40 15.20 16.53 17.60; 21 三、解答题(共89分) 18.(本小题9分) 解:原式=5418-+- ………………………………………………………………………………8分 =6 ………………………………………………………………………………………… 9分19.(本小题9分) 解:原式=916822-+++a a a ……………………………………………………………………4分 =7822++a a ……………………………………………………………………………6分当5=a 时,原式758)5(22+⨯+⨯=75852++⨯=5817+=………………………………………9分20.(本小题9分) 证明:∵AB ∥CD ,∴A D ∠=∠, ……………………………………4分又∵AB =CD ,AE DF =………………………………………………6分 ∴ABE ∆≌DCF ∆.………………………………………………9分21.(本小题9分) 解:(1)P (抽到红桃6)31=;……………………………………4分 (2)方法一:画树状图如下:……………………………………………………………………………………………8分 由树状图可知,共有9种机会均等的情况,其中抽出一对牌(即数字相同)只有一种情况,∴P (抽出一对牌)=91. ……………………………………………………………9分 方法二:列表如下:第一组567 第二组345345345ABDF………………………………………………………………………………………8分 由树状图可知,共有9种机会均等的情况,其中抽出一对牌(即数字相同)只有一种情况,∴P (抽出一对牌)=91. ………………………………………………9分 22.(本小题9分) (1) 证明:∵AB 与⊙O 相切于点C ,∴AB OC ⊥.…………………………………………………………………………………2分 又∵OAB ∆是等腰三角形,∴BC AC =. …………………………………………………………………………………4分 (2)解:由(1)得:BC AC =,又42=AB , ∴12242121=⨯===AB BC AC .………………………………………………………6分 在OCB Rt ∆中,9=OC ,12=BC ,由勾股定理得:151292222=+=+=BC OC OB …………………………………………………8分∴等腰OAB ∆的周长54152415=++=++=OB AB OA .……………………………9分23.(本小题9分) 解:(1)…………………………………………6分(2)补全条形统计图如图所示:……………………………………………8分 (3)篮球…………………………………9分24.(本小题9分)解:(1)5;………………………………2分 (2)设线段AB 的解析式为:()02≠+=k b kt d ()4.19.0≤≤t ,又过点()5.4,9.0A 、()0,4.1B ,(第23题图)球类篮球 足球 排球 三大球喜爱人数分布直方图∴⎩⎨⎧=+=+04.1,5.49.0b k b k ,解得⎩⎨⎧=-=6.129b k ,∴线段AB 的解析式为:6.1292+-=t d ()4.19.0≤≤t .………………………………………………………………………………………4分 ∵通讯员按原来的速度随即追赶队伍,∴速度为9千米/小时.设线段BC 的解析式为:m t d +=92()1.4 3.15t <≤,又过点()0,4.1B , m +⨯=4.190,6.12-=m ,∴线段BC 的解析式为:6.1292-=t d ()1.4 3.15t <≤.∴2912.6(0.9 1.4)912.6(1.4 3.15)t t d t t -+≤≤⎧=⎨-<≤⎩……………………………………6分(3)设线段OC 的解析式为:()01≠=n nt d ,又过点()5.4,9.0A ,∴n 9.05.4=,5=n .∴线段OC 的解析式为:t d 51=.………………………………………………………………7分设时间为t 小时,学生队伍与通讯员相距不超过3千米,下面分两种情况讨论: ①当4.19.0≤<t 时,321≤-d d ,即()36.1295≤+--t t ,解得:3539≤t ,∴35399.0≤<t . ②当1.4 3.15t <≤时,321≤-d d ,即()36.1295≤--t t ,解得:512≥t ,∴2.4 3.15t ≤≤. 故通讯员离开队伍后他们能用无线对讲机保持联系时t 的取值范围为35399.0≤<t 或2.4 3.15t ≤≤.……………………………………………………………………………………9分(注:若第②种情况答案如下,则不扣分:当1.4 3.15t <<时,321≤-d d ,即()36.1295≤--t t ,解得:512≥t ,∴2.4 3.15t ≤<). 25.(本小题13分)(1) 25-=b ,3=c ;……………………………………………………………4分 (2) ①设直线BC 的解析式为:()110y k x b k =+≠ ,又过点()0,6B 、()3,0C ,∴11160,3k b b +=⎧⎨=⎩,解得:111,23k b ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为:321+-=x y .……………………………………………………………7分∵点D 、E 在直线321+-=x y 上,∴设⎪⎭⎫ ⎝⎛+-321,p p D 、⎪⎭⎫⎝⎛+-321,q q E ,其中p q >,如图,过点E 作DG EH ⊥于点H ,则p q EH -=,EH ∥x 轴,则CBO DEH ∠=∠ ∴CBO DEH ∠=∠tan tan ,OB CO HE DH =,2163==HE DH , 在DHE Rt ∆中,令DH t =,则2EH t =,由勾股定理得:222DE EH DH =+,即()2222t t +=,解得:1t =(舍去负值),则1=DH ,2=EH .2=-p q ……………9分∵DG ∥y 轴∥EF ,∴⎪⎭⎫ ⎝⎛+-32531,2p p p G ,⎪⎭⎫ ⎝⎛+-32531,2q q q F ∴p p p p p DG 2313253132122+-=⎪⎭⎫⎝⎛+--⎪⎭⎫ ⎝⎛+-=,q q q q q EF 2313253132122+-=⎪⎭⎫⎝⎛+--⎪⎭⎫ ⎝⎛+-=.∴(第25题图)()()()q p q p q q p p EH EF DG S DGFE+++-=⋅⎪⎭⎫⎝⎛+-+-=⋅+=2312223123122222梯形 把2+=p q 代入上式,得:()()()222212882162222333333DGFE S p p p p p p p ⎡⎤=-+++++=-++=--+⎣⎦四边形.当2=p 时,DGFE S 四边形有最大值,最大值为316.∴此时点D 的坐标为()2,2………………………………………………………………………………………11分 ②符合条件的点D 的坐标为()2,2或⎪⎭⎫⎝⎛45,27. ……………………………………………………………………………………………13分 26.(本小题13分) 解:(1) ①把()6,4代入b x y +=43中,得:b +⨯=4436,解得:3=b . ∴直线AB 的解析式为:343+=x y .……………………………………………………3分②∵6=OD ,点C 、M 是线段OD 的三等分点. ∴463232=⨯==OD OM , ∴点M 的坐标为()0,4.过点M 作AB ME ⊥于点E ,则ME 的长是点M 到直线AB 的距离. 在343+=x y 中,令0=x ,则3=y , ∴3=OB .…………………………………4分 令0=y ,则4-=x ,∴4=OA .(第26题图)在AOB Rt ∆中,由勾股定理,得:53sin ==∠AB OB BAO , 在EAM Rt ∆中,sin AM EM MAE ==∠∴点M 到直线AB 的距离524.……………………………7分 (2)在CD 的垂直平分线上取点I (41.5)以I 为圆心,ID 为半径作圆,则⊙I 过点C , 在MID Rt ∆中, 由勾股定理,得5.25.1222=+=ID .54sin ==∠ID MD MID …………8分当直线AB 与⊙I 相切点),使得54sin =∠CQD ,此时设在直线b x y +=43中,令0=y ,则x =由勾股定理,得:b AB 35=.∵QNI ABO ∠=∠,90IQN AOB ∠=∠=︒,∴IQN ∆∽AOB ∆,∴ABNIAO IQ =,b NI b 35345.2=,825=NI .∴252512371.58888NM =+=+=,⎪⎭⎫ ⎝⎛837,4N .…………………………………10分 则把⎪⎭⎫⎝⎛837,4N 代入b x y +=43中,得:813=b , 此时直线AB 的解析式为:81343+=x y . 若直线AB 过点C ,则把()0,2C 代入b x y +=43中,得:23-=b ,若直线AB 过点D ,则把()0,6D 代入b x y +=43中,得:29-=b ,∴当813>b 或29-≤b 时,点Q 不存在;当813=b 或2329-≤-b <时,存在符合条件的一个点Q ;当81323<-b <时,存在符合条件的两个点Q .…………………………………………………………………………13分。
晋江市八年级下期末学业跟踪检测数学试卷包括
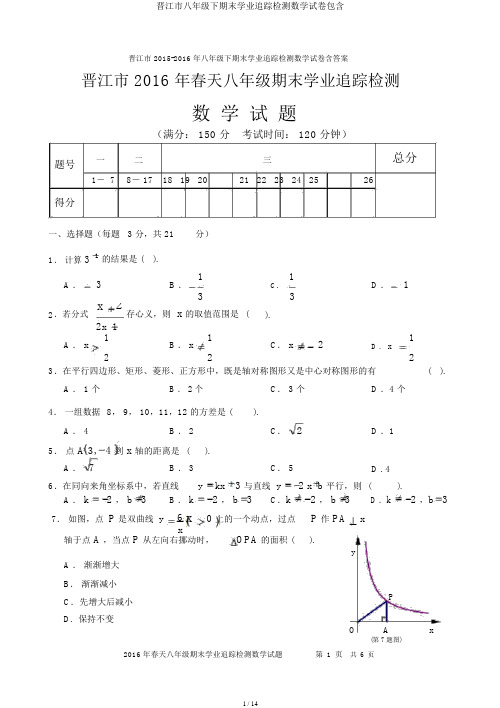
晋江市 2015-2016 年八年级下期末学业追踪检测数学试卷含答案晋江市 2016 年春天八年级期末学业追踪检测题号得分数学试题(满分: 150 分考试时间: 120 分钟)一二三总分1-78- 17 18 19 2021 22 23 24 2526一、选择题(每题 3 分,共 21分)1.计算 31的结果是 ( ).A .3B .11D .1 3C.32.若分式x2存心义,则 x 的取值范围是(). 2x 1A .x 1B .x1C.x21 22D .x23.在平行四边形、矩形、菱形、正方形中,既是轴对称图形又是中心对称图形的有( ).A . 1 个B . 2 个C. 3 个 D .4 个4.一组数据8, 9, 10,11,12 的方差是 ().A . 4B . 2C.2 D .15.点 A 3, 4 到 x 轴的距离是().A .7B . 3C. 5 D . 46.在同向来角坐标系中,若直线y kx 3 与直线 y 2 x b 平行,则().A .k 2 , b 3B .k 2 , b 3C.k 2 , b 3 D .k 2 ,b 3 7.如图,点P是双曲线y 6 x0 上的一个动点,过点P 作 PA xx轴于点 A ,当点 P 从左向右挪动时,OPA 的面积().yA .渐渐增大B.渐渐减小C.先增大后减小PD.保持不变O A x(第 7 题图)二、填空题(每题4 分,共 40 分)8.计算: 2 2 0_____ ;9.某种细菌病毒的直径为 0.000 000 5 米,0.000 000 5米用科学记数法表示为米 .10. 计算: a2=.ya 2 a 211. 在正比率函数yk2 x 中, y 随 x 的增大而增大,则 k 的取值Ox范围是 ____________.12. 已知:一次函数ykx b 的图象在直角坐标系中如下图,则 kb ____ 0 ( 填“”、“”或“ =”).13. 如图,把矩形 ABCD 纸片沿着过点A 的直线 AE 折叠,使得点 D(第 12 题图 )落在 BC 边上的点 F 处,若 BAF40 ,则DAE_____ .ADDB QPADEAOCBF CBCCMA N(第 15 题图 )B( 第 13 题图 )( 第 17 题图 )m 1(第 16 题图 )14. 若反比率函数 yx图象的两个分支散布在第二、四象限,则整数 ..m 能够是(写出一个即可 ).15. 如图,在 □ ABCD 中, AB 40 ,则 A _____ .16.如图,菱形 ABCD 的周长为20,对角线 AC 与 BD 订交于点 O , AC8 ,则BD ______ .17. 已知等腰直角ABC 的直角边长与正方形 MNPQ 的边长均为 10cm , CA 与 MN 在同一条直线上,点 A 从点 M 开始向右挪动,设点A 的挪动距离为 xcm 0 ≤ x ≤20 ,重叠部分的面积为S cm 2 .(1) 当点 A 向右挪动 4cm 时,重叠部分的面积 S_____ cm 2 ;(2) 当 10cm < x ≤ 20cm 时,则 S 与 x 的函数关系式为 ________________.三、解答题(共 89 分)18.( 9 分)计算:2a1.a 2 16 a419.( 9 分)先化简,再求值:1a a 23a,此中 a2 .a3 a 2920. (9 分)如图 ,在□ ABCD 中,点 E 、 F 分别为 AD 、 BC 边上的一点,且 AE CF .求证:四边形 BFDE 是平行四边形.A EDBF C(第 20 题图 )21. (9 分)如图,直线y 1 x 2分别与 x 轴、y轴订交于点A、点B.2⑴求点 A 和点 B 的坐标;y⑵若点 P 是 y 轴上的一点,设AOB 、 ABP 的面积分别为 S AOB与 S ABP,且 S ABP2S AOB,求点P的坐标.BA O x(第 21 题图)22. ( 9 分)某校举办“书香校园”念书活动,经过对八年级(1)班的 42 个学生的每人念书数目进行统计剖析,获得条形统计图如下图:人数16⑴填空:该班每个学生念书数目的1412众数是本,中位数是本;108⑵若把上述条形统计图变换为扇形统计图,求该班学生“念书数目为 4 本的人数”所对应扇形的64212345念书数目 ( 本)圆心角的度数.( 第 22 题图 )23.( 9 分)在校园手工制作活动中,现有甲、乙两人接得手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20 朵,甲制作120 朵纸花的时间与乙制作160 朵纸花的时间同样,求乙每小时制作多少朵纸花?24. (9 分)已知:在ABC 中, AB AC ,点 D 、 E 、 F 分别在边 BC 、 AB 、 AC 上,⑴若 DE ∥ AC , DF ∥ AB ,且 AE AF ,则四边形AEDF 是______形;⑵如图,若DE AB 于点 E , DF AC 于点 F ,作 CH AB 于点 H ,求证: CH DE DF .AHEFB D C(第 24 题图 )25. ( 13 分)已知:如图,正比率函数y1kx k0 的图象与反比率函数y26的图象相交于点 A 和点 C ,设点 C 的坐标为2, n .x(1) ①求k与n的值;6②试利用函数图象,直接写出不等式kx0 的解集;..x(2) 点B是x轴上的一个动点,连结AB 、 BC ,作点 A 对于直线 BC 的对称点 Q ,在点B 的挪动过程中,能否存在点 B ,使得四边形 ABQC 为菱形?若存在,求出点 B 的坐标;若不存在,请说明原因 .yCO B xA(第 25 题图 )yCO xA(备用图 )26.( 13 分)如图,正方形 ABCO 的边 OA 、 OC 在座标轴上,点 B 坐标为 6, 6 ,将正方形 ABCO 绕点 C 逆时针旋转角度 0 90 ,获得正方形 CDEF , ED 交线段AB 于点 G , ED 的延伸线交线段 OA 于点 H ,连结 CH 、 CG . (1)求证: CG 均分 DCB ; (2)在正方形 ABCO 绕点 C 逆时针旋转的过程中,求线段 HG 、 OH 、 BG 之间的数量关系;(3)连结 BD 、 DA 、 AE 、 EB ,在旋转过程中,四边形AEBD 可否成为矩形?若能,试求出直线 DE 的分析式;若不可以,请说明原因.FyCBEGO DA xH( 第 26 题图 )晋江市 2016 年春天八年级期末学业追踪检测数学试题参照答案及评分标准一、选择题: ( 每题 3 分,共 21 分 );2 .B ;3 .C ;4 .B ; 5.D ; 6.A ; 7 .D ;二、填空题:(每题 4 分,共 40 分)8.1 ;9.5 10 7 ; 10. 1;11.k2 ; 12.; 13.25; 14.0(答案不独一 ) ;15.110 ;; 17. (1)8;(2)S1 x2 10x .三、解答题:(共89 分)18.(9分)解:原式2a a4⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分a 4 a4 a 4 a 42a a4⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a4a4⋯⋯⋯ 6 分2a a4a4a4a4⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a 4 a 4⋯⋯⋯8 分1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a 4⋯⋯⋯9 分19.(9分)解:原式a3a a a23a⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分a33a29a3a a23a⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a3a29⋯⋯ 3 分3 a a3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a 3 a 3 a 3⋯⋯ 5 分3 a 3 a 3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a 3 a a3⋯⋯ 6 分3a⋯⋯⋯7 分⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯当a2时,原式3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分2=3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2⋯⋯ 9 分20. (9 分 )证明:∵四边形 ABCD 是平行四边形, ∴AD∥BC,AD BC ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∵ AE CF∴ AD AE BC CF即DE BF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分又 AD ∥ BC ,即 DE ∥ BF ∴四边形 BFDE 是平行四边形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分 21.(9 分 )解:(1) 在 y1 x2 中,令 y 0 ,则 1x 2 0 ,解得: x4 ,y22∴点 A 的坐标为 4, 0 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分 P 1令 x 0 ,则 y 2 ,∴点 B 的坐标为0, 2 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分B(2)∵点 P 是 y 轴上的一点,∴设点P 的坐标为 0, yAOP 2又点 B 的坐标为 0, 2 ,∴ BPy 2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分 (第 21 题图 )∵ S又 SAOB1OA OB1 42 4 , S ABP 1BP OA1 y2 4 2 y 22222ABP2S AOB ,∴ 2 y 2 2 4,解得: y6 或 y2 .∴ 点P的 坐 标 为0, 6或0, 2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分22.(9 分 )(1)44⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分(2)14360 120 42∴ 该 班 学 生 “ 读 书 数 量 为 4 本 的 人 数 ” 所 对 应 的 扇 形 的 圆 心 角 的 度 数 为120 . ⋯⋯⋯⋯⋯ 9 分23.(9 分 )解: 设 乙 每 小 时 制 作x朵 纸 花 , 依 题 意得: ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分120 160 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯x 20x⋯⋯ 5 分解得:x80 , ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分经 检验 ,x 80 是 原 方程的 解 ,且 符 合题 意 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分答 :乙每小时制作80朵纸花 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分 24.(9分 )解: (1) 菱 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(2) 解法一 : 如图 1, 连结 AD ,A∵ S ABC 1AB CH , SABD 1 AB DE , S ACD 1AC DF222又SABCSABDS ACD,∴ 1AB CH1AB DE 1AC DF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分2 2 2又 AB AC ,∴ CHDE DF . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分HEFBDC(第 24 题图 1)解法二 : 如 2,C 作 CGDE 交 ED 的延 于点 G ,CGE 90 ,∵GEHEHC 90 ,∴四形 EGCH 是矩形,A∴ CH EG ED DG ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分∵ B BDE90,ACB CDF 90 ,而由 AB AC 可知:B ACB∴BDECDF ,又∵BDE CDG ,∴CDF CDG ,H DFC DGC90 , CD CD ,∵E F∴CDF ≌ CDG ,B C∴ DF DG ,D ∴ CH DE DF .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分G( 第24题图 2) 25. (13分 )解:( 1)①把点C的坐2, n 代入y26n3得:∴点 C 的坐x2, 3 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分把点 C2, 3 代入 y1kx得:32k ,解得:k3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯42分②由两函数象可知,kx 60 的解集是 x 2 或 0x 2 .⋯⋯⋯⋯⋯⋯⋯⋯⋯8分y x(2) (2) 当点B在x的正半且AB AC ,四形 ABQC 菱形.C ∵点 A 与点 Q 对于直 BC 称O B ∴ AC QC , AB QB ,Q∴ AC QC AB QB .AQ y∴四形 ABQC 菱形.( 第 25 题图 1)C由 (1) 中点C的坐2, 3,可求得: OC13 ,∵点 A与点 C对于原点称,HBxO( 第 25 题图 1)∴点 A 的坐标为2, 3 ,∴ OA OC13 , AC 2 13 ,∴AC AB 2 13 .作 AH x 轴于点 H ,则 AH 3 .在 Rt AHB 中,由勾股定理得:2243,又 OH 2 BH2 133∴OB BH OH43 2,∴点 B 的坐标为432, 0 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 11 分,当点 B 在x轴的负半轴且AB AC 时,四边形ABQC 为菱形.作 BT x 轴于点 T ,Q232y同理可求得:BT21343 ,又OT 2,C∴ OB BT OT43 2 ,Tx ∴点 B 的坐标为432, 0 ,B O综上,当点 B 的坐标为43 2, 0 或A432, 0时,四边形ABQC为菱形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯13分(第 25 题图 2)26. (13分)( 1)证明:∵正方形 ABCO 绕点 C 旋转获得正方形CDEF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴ CD CB ,CDG CBG 90在 Rt CDG 和 Rt CBG 中,CG CG, CD CB∴ Rt CDG ≌ Rt CBG HL .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∴DCG BCG即 CG 均分DCB ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分F( 2)y由 (1) 证得: Rt CDG ≌ Rt CBGB G D G ∴BCECHCH ,在 Rt CHO 和 Rt CHD 中,CDGCO ∴ CHO ≌ CHD .DO HAx( 第 26 题图)∴ OH HD , ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分∴ HG HD DG OH BG ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分( 3)四边形 AEBD 可为矩形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分 当 G 点为 AB 中点时,四边形AEBD 为矩形.如图, BG GA1AB ,由 (2)证得:1AB1DE GE ,又 AB 2BG DG ,则 BG GADGDE22∴ 四边形 AEBD 为矩形 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分∴ AG EGBG DG . ∵ AG1AB3 ,2∴ G 点的坐标为(6,3) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分设 H 点的坐标为 x, 0 ,则 HO x .∴ HD x , DG 3 ,∵ OHDH , BG DG ,在 Rt HGA 中,HG x 3 ,GA3 ,HA 6 x ,由勾股定理得: x 3 2 326 x 2 ,解得: x2∴ H点的坐标为2, 0.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分设直线 DE 的分析式为: y kx b k0 ,2k b0,k 3 ,4又过点 H 2, 0、G 6, 3,∴b ,解得:36k3b2∴直线 DE 的分析式为: y 3 x3.4 2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯13 分。
2017-2018学年八年级(下)期末数学试卷(含答案)

2017-2018学年八年级(下)期末数学试卷一、选择题(本大题共10小题,每小题2分,共20分;在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填涂在答题卡上)1.若分式的值为零,则x等于()A.﹣l B.1 C.D.02.下列根式中,与是同类二次根式的是()A.B.C.D.3.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.4.已知1<x≤2,则|x﹣3|+的值为()A.2x﹣5 B.﹣2 C.5﹣2x D.25.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页、数学2页、英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为()A.B.C.D.6.在函数(k为常数)的图象上有三个点(﹣2,y1),(﹣1,y2),(,y3),函数值y1,y2,y3的大小为()A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y1>y27.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是()A. B. C. D.8.反比例函数的图象如图所示,则这个反比例函数的解析式可能是()A.B.C.D.9.如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是()A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG 10.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为()A.6B.2C.4D.4二、填空题(本大题共8小题,每小题3分,共24分,请把答案直接填写在答卷纸相应位置上)11.在函数y=中,自变量x的取值范围是.12.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD 的长为.13.某校九年级一班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),则成绩在90.5~95.5这一分数段的频率是.14.如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD=.15.代数式a+2﹣+3的值等于.16.已知a2+3ab+b2=0(a≠0,b≠0),则代数式+的值等于.17.如图,直线与双曲线(k>0)在第一象限内的交点为R,与x 轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积是4:1,则k等于.18.如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=CE时,EP+BP=.三、解答题(本大题共9小题,共56分,请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.计算:(1)﹣()2﹣+|﹣2|(2)(﹣)÷.20.解分式方程:(1)=(2)=﹣1.21.先化简,再求值:(1﹣)÷,其中a=﹣1.22.如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.23.“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:(1)补全条形统计图;(2)估计该市这一年空气质量达到“优”和“良”的总天数;(3)计算随机选取这一年内某一天,空气质量是“优”的概率.24.如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;(2)写出点A′,B′,C′的坐标:A′(),B′(),C′();(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为().25.如图在平面直角坐标系xOy中,反比例函数y1=(x>0)的图象与一次函数y2=kx﹣k的图象的交点为A(m,2).(1)求一次函数的解析式;(2)观察图象,直接写出使y1≥y2的x的取值范围;(3)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.26.小明用12元买软面笔记本,小丽用21元买硬面笔记本.(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.27.如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C 的坐标分别为A(﹣3,0),C(1,0),BC=AC.(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,若P、Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,若△APQ与△ADB相似,求出m的值.参考答案与试题解析一、选择题(本大题共10小题,每小题2分,共20分;在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填涂在答题卡上)1.若分式的值为零,则x等于()A.﹣l B.1 C.D.0【考点】分式的值为零的条件.【分析】根据分式值为零的条件可得x+1=0,且3x﹣2≠0,再解即可.【解答】解:由题意得:x+1=0,且3x﹣2≠0,解得:x=﹣1,故选:A.2.下列根式中,与是同类二次根式的是()A.B.C.D.【考点】同类二次根式.【分析】运用化简根式的方法化简每个选项.【解答】解:A、=2,故A选项不是;B、=2,故B选项是;C、=,故C选项不是;D、=3,故D选项不是.故选:B.3.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.【考点】中心对称图形.【分析】根据中心对称图形的定义和图形的特点即可求解.【解答】解:由中心对称图形的定义知,绕一个点旋转180°后能与原图重合,只有选项B是中心对称图形.故选:B.4.已知1<x≤2,则|x﹣3|+的值为()A.2x﹣5 B.﹣2 C.5﹣2x D.2【考点】二次根式的性质与化简.【分析】首先根据x的范围确定x﹣3与x﹣2的符号,然后即可化简二次根式,然后合并同类项即可.【解答】解:∵1<x≤2,∴x﹣3<0,x﹣2≤0,∴原式=3﹣x+(2﹣x)=5﹣2x.故选C.5.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页、数学2页、英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为()A.B.C.D.【考点】概率公式.【分析】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.【解答】解:∵小明的讲义夹里放了大小相同的试卷共12页,数学2页,∴他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为=.故选C.6.在函数(k为常数)的图象上有三个点(﹣2,y1),(﹣1,y2),(,y3),函数值y1,y2,y3的大小为()A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y1>y2【考点】反比例函数图象上点的坐标特征.【分析】先判断出﹣k2﹣2<0的符号,再根据反比例函数的性质进行比较.【解答】解:∵﹣k2﹣2<0,∴函数图象位于二、四象限,∵(﹣2,y1),(﹣1,y2)位于第二象限,﹣2<﹣1,∴y2>y1>0;又∵(,y3)位于第四象限,∴y3<0,∴y2>y1>y3.故选B.7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是()A. B. C. D.【考点】相似三角形的判定.【分析】根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.【解答】解:根据题意得:AB==,AC=,BC=2,∴AC:BC:AB=:2:=1::,A、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;B、三边之比为::3,图中的三角形(阴影部分)与△ABC不相似;C、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.故选C.8.反比例函数的图象如图所示,则这个反比例函数的解析式可能是()A.B.C.D.【考点】反比例函数的图象.【分析】首先设出函数关系式,根据图象可以计算出k的取值范围,再根据k的取值范围选出答案即可.【解答】解:设函数关系式为y=(k≠0),当函数图象经过A(1,2)时,k=1×2=2,当函数图象经过B(﹣2,﹣2)时,k=(﹣2)×(﹣2)=4,由图象可知要求的函数解析式的k的取值范围必是:2<k<4,故选:C.9.如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是()A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG【考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质.【分析】由四边形ABCD是正方形,可得AB=AD,由DE⊥AG,BF∥DE,易证得BF⊥AG,又由同角的余角相等,可证得∠BAF=∠ADE,则可利用AAS判定△AED ≌△BFA;由全等三角形的对应边相等,易证得DE﹣BF=EF;有两角对应相等的三角形相似,可证得△BGF∽△DAE;利用排除法即可求得答案.【解答】解:∵四边形ABCD是正方形,∴AB=AD,AD∥BC,∵DE⊥AG,BF∥DE,∴BF⊥AG,∴∠AED=∠DEF=∠BFE=90°,∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,∴∠BAF=∠ADE,∴△AED≌△BFA(AAS);故A正确;∴DE=AF,AE=BF,∴DE﹣BF=AF﹣AE=EF,故B正确;∵AD∥BC,∴∠DAE=∠BGF,∵DE⊥AG,BF⊥AG,∴∠AED=∠GFB=90°,∴△BGF∽△DAE,故C正确;∵DE,BG,FG没有等量关系,故不能判定DE﹣BG=FG正确.故选D.10.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为()A.6B.2C.4D.4【考点】翻折变换(折叠问题);矩形的性质.【分析】首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=6,继而求得BF的值,又由勾股定理,即可求得BC的长.【解答】解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,在△ENG与△BNM中,,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=1,∴NG=1,∵BG=AB=CD=CF+DF=6,∴BN=BG﹣NG=6﹣1=5,∴BF=2BN=10,∴BC===4.故选D.二、填空题(本大题共8小题,每小题3分,共24分,请把答案直接填写在答卷纸相应位置上)11.在函数y=中,自变量x的取值范围是x≥1.【考点】函数自变量的取值范围.【分析】因为当函数表达式是二次根式时,被开方数为非负数,所以x﹣1≥0,解不等式可求x的范围.【解答】解:根据题意得:x﹣1≥0,解得:x≥1.故答案为:x≥1.12.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD 的长为4.【考点】射影定理.【分析】根据射影定理得到:CD2=AD•BD,把相关线段的长度代入计算即可.【解答】解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,∴CD2=AD•BD=8×2,则CD=4.故答案是:4.13.某校九年级一班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),则成绩在90.5~95.5这一分数段的频率是【考点】频数(率)分布直方图.【分析】由每一组内的频数总和等于总数据个数得到学生总数,再由频率=频数÷数据总和计算出成绩在90.5~95.5这一分数段的频率.【解答】解:读图可知:共有(1+4+10+15+20)=50人,其中在90.5~95.5这一分数段有20人,则成绩在90.5~95.5这一分数段的频率是=0.4.故本题答案为:0.4.14.如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD= 2.【考点】三角形中位线定理.【分析】由题意可知EF是△ADC的中位线,由此可求出AD的长,再根据中线的定义即可求出BD的长.【解答】解:∵点E、F分别是AC、DC的中点,∴EF是△ADC的中位线,∴EF=AD,∵EF=1,∵CD是△ABC的中线,∴BD=AD=2,故答案为:2.15.代数式a+2﹣+3的值等于4.【考点】二次根式有意义的条件.【分析】根据二次根式的意义先求出a的值,再对式子化简.【解答】解:根据二次根式的意义,可知,解得a=1,∴a+2﹣+3=1+3=4.16.已知a2+3ab+b2=0(a≠0,b≠0),则代数式+的值等于﹣3.【考点】分式的化简求值.【分析】将a2+3ab+b2=0转化为a2+b2=﹣3ab,原式化为=,约分即可.【解答】解:∵a2+3ab+b2=0,∴a2+b2=﹣3ab,∴原式===﹣3.故答案为:﹣3.17.如图,直线与双曲线(k>0)在第一象限内的交点为R,与x 轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积是4:1,则k等于.【考点】反比例函数综合题.【分析】先求出Q的坐标为(0,﹣2),P点坐标为(,0),易证Rt△OQP ∽Rt△MRP,根据三角形相似的性质得到==,分别求出PM、RM,得到OM的长,从而确定R点坐标,然后代入(k>0)求出k的值.【解答】解:对于y=x﹣2,令x=0,则y=﹣2,∴Q的坐标为(0,﹣2),即OQ=2;令y=0,则x=,∴P点坐标为(,0),即OP=;∵Rt△OQP∽Rt△MRP,而△OPQ与△PRM的面积是4:1,∴==,∴PM=OP=,RM=OQ=1,∴OM=OP+PM=,∴R点的坐标为(,1),∴k=×1=.故答案为.18.如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=CE 时,EP+BP=8.【考点】相似三角形的判定与性质.【分析】如图,延长EF交BQ的延长线于G.首先证明PB=PG,EP+PB=EG,由EG∥BC,推出==2,即可求出EG解决问题.【解答】解:如图,延长EF交BQ的延长线于G.∵EG∥BC,∴∠G=∠GBC,∵∠GBC=∠GBP,∴∠G=∠PBG,∴PB=PG,∴PE+PB=PE+PG=EG,∵CQ=EC,∴EQ=2CQ,∵EG∥BC,∴==2,∵BC=4,∴EG=8,∴EP+PB=EG=8,故答案为8三、解答题(本大题共9小题,共56分,请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.计算:(1)﹣()2﹣+|﹣2|(2)(﹣)÷.【考点】二次根式的混合运算;分式的混合运算.【分析】(1))原式各项化为﹣3﹣3+2﹣,合并同类二次根式即可得到结果.(2)先计算括号里面的分式的减法,再分式的除法的方法计算.【解答】(1)解:(1)原式=﹣3﹣3+2﹣=﹣1﹣3;(2)原式=﹣=.20.解分式方程:(1)=(2)=﹣1.【考点】解分式方程.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母,得x+2=3,解得:x=1经检验,x=1是增根,原方程无解;(2)去分母,得3(5x﹣4)=﹣(4x+10)﹣3(x﹣2),解得:x=,经检验,x=是原方程的解.21.先化简,再求值:(1﹣)÷,其中a=﹣1.【考点】分式的化简求值.【分析】先根据整式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.【解答】解:原式=÷=×=a+1.当a=﹣1时,原式=﹣1+1=.22.如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.【考点】平行四边形的判定;全等三角形的判定与性质.【分析】(1)根据全等三角形的判定定理ASA证得△AFD≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到AD=CB,则由“有一组对边相等且平行的四边形是平行四边形”证得结论.【解答】证明:(1)如图,∵AD∥BC,DF∥BE,∴∠1=∠2,∠3=∠4.又AE=CF,∴AE+EF=CF+EF,即AF=CE.在△AFD与△CEB中,,∴△AFD≌△CEB(ASA);(2)由(1)知,△AFD≌△CEB,则AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.23.“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:(1)补全条形统计图;(2)估计该市这一年空气质量达到“优”和“良”的总天数;(3)计算随机选取这一年内某一天,空气质量是“优”的概率.【考点】条形统计图;用样本估计总体;扇形统计图;概率公式.【分析】(1)根据良的天数除以良的天数所占的百分比,可得样本容量,根据样本容量乘以轻微污染所占的百分比求出轻微污染的天数,可得答案;(2)根据一年的时间乘以优良所占的百分比,可得答案;(3)根据根据一年中优的天数比上一年的天数,可得答案.【解答】解:(1)样本容量3÷5%=60,60﹣12﹣36﹣3﹣2﹣1=6,条形统计图如图:(2)这一年空气质量达到“优”和“良”的总天数为:365×=292;(3)随机选取这一年内某一天,空气质量是“优”的概率为:=.24.如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;(2)写出点A′,B′,C′的坐标:A′(3,5),B′(5,5),C′(7,3);(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为(2a﹣1,2b﹣1).【考点】作图﹣位似变换.【分析】(1)利用位似图形的性质得出变化后图形即可;(2)利用已知图形得出对应点坐标;(3)利用各点变化规律,进而得出答案.【解答】解:(1)如图所示:四边形TA′B′C′即为所求;(2)A′(3,5),B′(5,5),C′(7,3);故答案为:(3,5),(5,5),(7,3);(3)在(1)中,∵A(2,3),B(3,3),C(4,2),A′(2×2﹣1=3,2×3﹣1=5),B′(2×3﹣1=5,2×3﹣1=5),C′(2×4﹣1=7,2×2﹣1=3);∴D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为(2a﹣1,2b﹣1).故答案为:(2a﹣1,2b﹣1).25.如图在平面直角坐标系xOy中,反比例函数y1=(x>0)的图象与一次函数y2=kx﹣k的图象的交点为A(m,2).(1)求一次函数的解析式;(2)观察图象,直接写出使y1≥y2的x的取值范围;(3)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.【考点】反比例函数与一次函数的交点问题.【分析】(1)将A点坐标代入代入y=(x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式;(2)根据图象即可求得;(3)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加.【解答】解:(1)将A(m,2)代入y=(x>0)得,m=2,则A点坐标为A(2,2),将A(2,2)代入y=kx﹣k得,2k﹣k=2,解得k=2,则一次函数解析式为y=2x﹣2;(2)∵A(2,2),∴当0<x≤2时,y1≥y2;(3)∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为B(0,﹣2),S△ABP=S△ACP+S△BPC,∴×2CP+×2CP=4,解得CP=2,则P点坐标为(3,0),(﹣1,0).26.小明用12元买软面笔记本,小丽用21元买硬面笔记本.(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.【考点】分式方程的应用.【分析】(1)设每本软面笔记本x元,则每本硬面笔记本(x+1.2)元,根据小明和小丽能买到相同数量的笔记本建立方程求出其解就可以得出结论;(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,根据小明和小丽能买到相同数量的笔记本建立方程就可以得出m与a的关系,就可以求出结论.【解答】解:(1))设每本软面笔记本x元,则每本硬面笔记本(x+1.2)元,由题意,得,解得:x=1.6.此时=7.5(不符合题意),所以,小明和小丽不能买到相同数量的笔记本;(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,由题意,得,解得:a=m,∵a为正整数,∴m=4,8,12.∴a=3,6,9.当时,(不符合题意)∴a的值为3或9.27.如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C 的坐标分别为A(﹣3,0),C(1,0),BC=AC.(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,若P、Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,若△APQ与△ADB相似,求出m的值.【考点】相似形综合题.【分析】(1)根据点A、C的坐标求出AC的长,根据题意求出点B的坐标,利用待定系数法求出过点A,B的直线的函数表达式;(2)过点B作BD⊥AB,交x轴于点D,根据相似三角形的性质列出比例式,计算即可;(3)分PQ∥BD时和PQ⊥AD时两种情况,根据相似三角形的性质列出比例式,计算即可.【解答】解:(1)∵点A(﹣3,0),C(1,0),∴AC=4,又BC=AC,∴BC=3,∴B点坐标为(1,3),设过点A,B的直线的函数表达式为:y=kx+b,则,解得,,∴直线AB的函数表达式为:y=x+;(2)如图1,过点B作BD⊥AB,交x轴于点D,∵∠A=∠A,∠ABD=∠ACB,∴△ADB∽△ABC,∴D点为所求,∵△ADB∽△ABC,∴,即=,解得,CD=,∴,∴点D的坐标为(,0);(3)在Rt△ABC中,由勾股定理得AB==5,如图2,当PQ∥BD时,△APQ∽△ABD,则=,解得,m=,如图3,当PQ⊥AD时,△APQ∽△ADB,则=,解得,m=,所以若△APQ与△ADB相似时,m=或.。
秋季晋江市八年级期末跟踪测试数学试题

秋季晋江市八年级期末跟踪测试数学试题LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】2016年秋季晋江市八年级期末跟踪测试数学试题(满分:150分,考试时间:120分钟)一.选择题(每小题4分,共40分)1.实数15是( )A. 整数B. 分数C.有理数D. 无理数 2. 64的平方根是( ) A .8 B .-8 C .8±D .323.抛一枚硬币若干次,有11次出现正面,9次出现反面,则出现正面的频率是( ) A .11B .9C .55%D .45%4.下列算式中,计算结果等于6a 的是( )A.33a a +B. a a ⋅5C. (a 4)2D.212a a ÷ 5.如图,在四边形ABCD 中AB=AD ,添加下列一个条件后,仍然不能证明ABC ∆≌ADC ∆,那么这个条件是( )=CB B. AC 平分∠BAD C. ∠B=∠D=90° D. ∠ACB=∠ACD 6.在Rt △ABC 中,∠A=90°,AB=5,BC=12,则AC 的长是( ) A .13B 119C .13119或D .177.下列选项中,可以用来说明命题“若a 2>4,则a>2”是假命题的反例是( )=-3 B. a=3 =2 =-28.如图,用4张全等的长方形拼成一个正方形,用两种方法表示图中阴影部分的面积题号 一二三总分 得分 1~10 11~1617 18 19 20 21 22 23 24 2526可得出一个代数恒等式。
若长方形的长和宽分别为a、b,则这个代数恒等式是()A.(a+b)2=a2+2ab+b2B. (a-b)2=(a+b)2-4abC.(a+b)(a-b)=a2-b2D. (a-b)2=a2-ab+b29.259120175912016201720182016x y z=⨯-⨯=-⨯设,,则x、y、z的大小关系是()<z<x <z<y <x<z <y<x10.如图,是一个长、宽、高分别为4cm、2cm、8cm一只蚂蚁从点A处沿盒子的内壁爬到点B,则爬行的最短距离为()B.(2cm+ C.二、填空题(每小题4分,共24分)11.___________12.那么表示购物的扇形圆心角的度数为__________.13.命题“直角三角形的两个锐角互余”的逆命题是__________________________________.14.如图,在△ABC中,AC<BC,AB的垂直平分线交AB于点D,交BC于点E,连结AE,若△ACE的周长为14cm,BD=5cm,则△ABC的周长是15.如图在4×4的方格中,每个小方格的边长都为1,点A、B则线段AB的长度是__________.16.已知4=-ba,abba<+-)4)(3(.(1)a的取值范围是.(2)若53222=+-++bbabaa,则ba+的值是.三、解答题(共86分)第14题图A B第12题图第15题图A第10题图8cm第8题图17.(10分)(1)3528)1(5a a a a ÷-- (2)26(6)(6)x x x +-+-()18.(6分)因式分解:222753b b a -19.(9分)先化简,再求值:[])()4(3)6(222xy y x xy xy -÷---+)(,其中65=x ,53-=y .20. (9分) 如图,点E C F B 、、、在同一直线上,已知AB=DE ,AC=DF ,BF=EC.求证:DFE ACB ∠=∠.E21.(8分)某中学组织“纪念红军长征胜利80周年”知识竞赛活动,其中八年级6个班每班参赛人数相同,学校对该年级的获奖人数进行统计,得到平均每班获奖15人,并制作如下图所示不完整的条形统计图。
福建省晋江市八年级数学上学期期末跟踪测试试题

(满分:150分考试时间:120分钟)题号一二三总分1-7 8-17 18 19 20 21 22 23 24 25 26 得分一、选择题(每小题3分,共21分)1. 实数6的相反数是().A. 3- B. 6- C. 6 D. 6-2. 计算23)3(a中,结果正确的是()A. 69a B. 66a C. 63a D. 59a3. 下列各图案中,不是中心对称图形的是().4. △ABC中,已知90B∠=︒,5AB=,12AC=,则BC的长是().A. 7B. 13或119C. 13D. 1195. 下列四边形中,对角线不.互相平分的是().A. 平行四边形B. 菱形C. 正方形D. 等腰梯形6. 如图,在Rt ABC中,︒=∠90ACB,3AC=,4BC=,O是AB的中点,则OC的长是().A.3B.4C.2.5D.57. 给出一列式子:yx2,2421yx-,3641yx,4881yx-,……,根据其蕴含的规律可知这一列式子中的第8个式子是().A.816641yx B.814641yx- C.8161281yx- D.9182561yx-二、填空题(每小题4分,共40分)8. 4的平方根是 .9. 计算:364-= .10. 地球赤道长约为4×104千米,我国最长的河流--长江全长约为6.3×103千米,赤道长约等于长江长的倍.(结果精确到0.1)11. 如图,将△ABC沿着射线BC的方向平移到△DCE的位置,若14BE=cm,则平移的距离是 cm.D.A.B.C.ABCO第6题图CABDE第11题图A12. 因式分解:=-x y x 622. 13. 请写出一个介于1与2之间的无理数: .14. 如图,矩形ABCD 中,AC 、BD 相交于点O ,已知62AOB ∠=︒,则CAD ∠= (度).15. 如图,将一根21cm 的筷子,置于底面直径为8cm ,高15cm 的圆柱形水杯中,则筷子露在杯子外面的最短长度是 cm. 16. 已知5=-b a ,则=+-222b ab a .17. 如图,已知□ABCD ,DAB ∠与ABC ∠的平分线交于点E . (1)AEB ∠= (度);(2)当□ABCD 满足条件 时,点E 刚好落在CD 上. 三、解答题(共89分)18.(9分)计算:)3(625432352y x y x x x -÷+⋅.19.(9分)计算:)1()1)(3(--++x x x x .20.(9分)先化简,再求值:)2()2128()2(2232a ab b a a b a -÷+-+-,其中 52-=a ,10=b .第15题图 ABCDE第17题图21.(9分)如图,在正方形网格中每个小正方形的边长都是单位长度1,△ABC 的顶点都在格点上,且△ABC 与△DEF 关于点O 成中心对称. (1)在网格图中标出对称中心点O 的位置;(2)画出将△ABC 沿水平方向向右平移5个单位后的△111D E F .22.(9分)如图,已知菱形ABCD 的周长为52cm ,对角线AC 、BD 交于点O ,且AC =10, 试求菱形的边长与面积.23.(9分) 某校生物兴趣小组有一块正方形种植基地,现要对它进行扩建,若把边长增加2米,则所得的新正方形种植基地面积比原来增加了32平方米,求:原来正方形种植基地的边长是多少?ABCD E F A BCDO24.(9分)如图,在等腰梯形ABCD 中,AD ∥BC ,已知120ADC ∠=︒, (1)求B ∠的度数;(2)若6AD =,4CD =,试求等腰梯形ABCD 的周长.25.(12分) 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A 可以用来解释2222()a ab b a b ++=+,实际上利用一些卡片拼成的图形面积也可以 对某些二次三项式进行因式分解.(1)图B 可以解释的代数恒等式是_____________ ; (2)现有足够多的正方形和矩形卡片,如图C :①.若要拼出一个面积为))(2(b a b a ++的矩形,则需要1号卡片 张,2号卡片A B C D aa1b2ab3图Caba b图An n 图Bnn张,3号卡片 张;②.试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为22252a ab b ++,并利用你画的图形面积对22252a ab b ++进行因式分解.26.(14分)如图,在直角梯形ABCD 中,AD ∥BC ,90B ∠=︒,4AD =,6BC =,CD =104,点E 在AB 上,BE =4. (1)线段AB = ;(2)试判断△CDE 的形状,并说明理由;(3)现有一动点P 在线段EA 上从点E 开始以每秒1个单位长度的速度向终点A 移动,设移动时间为t 秒(t >0).问是否存在t 的值使得△CDP 为直角三角形?若存在直接写出t 的值;若不存在,请说明理由.2012年秋季八年级期末跟踪测试数学试题 参考答案及评分标准一、选择题 (每小题3分,共21分)BCBC备用图1.B 2.A 3.B 4.D 5.D 6.C 7.C 二、填空题(每小题4分,共40分)8.±2 9.-4 10.6.3 11.7 12.)3(2-xy x 13.如:2(答案不惟一) 14.31 15.4 16.5 17.⑴ 90 ⑵ CD=2AD 三、解答题(共89分)18.(9分)解:原式=33210x x ---------------6分 =38x ------------------------9分 19.(9分)解:原式=x x x x x +-+++2233---------6分 =35+x --------------------------------9分 20.(9分)解:原式=22226444b ab a b ab a -+-+--------5分=ab 2---------------------------------------------7分当52-=a ,10=b 时,原式=10)52(2⨯-⨯--------8分=8----------------------9分21.(9分)解:⑴如图,点O 所求画的点----------4分⑵如图,△D 1E 1F 1就是所求画的三角形------9分22.(9分)解:⑴∵ 四边形ABCD 是菱形∴AB=BC=CD=DA ∵AB+BC+CD+DA=52 ∴AB=13-------------------3分⑵ ∵四边形ABCD 是菱形∴AO=OC BO=OD AC ⊥BD----------5分在Rt △AOB 中,∠AOB=90°∴BO=2222135AB AO --分∴BD=2BO=24∴S 菱形ABCD =21AC ·BD=120-----------------9分_ 第 21 题图BA C OD EFD 1E 1F 123.(9分)解:设原来正方形种植基地的边长是x 米,依题意得-----------------------------1分32)2(22=-+x x -------------------------------------5分324422=-++x x x ---------------------------------------7分 7=x -------------------------------------------8分答:原来正方形种植基地的边长是7米---------------------9分24.(9分)解:⑴∵等腰梯形ABCD 中, AD ∥BC -----------1分∴∠B=∠C ---------------------------------2分 ∵∠ADC+∠C=180°----------------------3分 ∴∠C=60°∴∠B=60°----------------------------------4分 ⑵过点D 作DE ∥AB 交BC 于点E ----------------5分 ∴四边形ABED 是平行四边形∴BE=AD=6 AB=DE ---------------------------------6分 ∵AB=CD ∴CD =DE ------------------------------------------------7分 ∵∠C=60°∴△CDE 是等边三角形∴CE=CD=DE=4 -------------------------------------------8分 ∴等腰梯形ABCD 的周长为AB+BC+CD+DA=24 -----9分 25.(12分)解:⑴.224)2(n n = --------------------3分⑵ ①. 1 , 2 , 3-------------------------6分 ②.如图;-----------------------------9分22252a ab b ++=)2)(2(b a b a ++-----12分26.(14分)解:⑴. 10-------------------------3分⑵. △CDE 的形状是等腰直角三角形,理由如下:--------------------4分∵在△BEC 中∠B=90°∴22BC BE CE +==526422=+-----------------5分 ∵在△AED 中,∠A=90°,AD=4 AE=AB-BE=6∴52462222=+=+=AE AD DE -----------------6分 ∴CE=DE----------------------------------------------------------7分∵104)52()52(2222=+=+DE CE104)104(22==CD∴222CD DE CE =+-------------------------------8分 ∴∠DEC=90°∴△CDE 的形状是等腰直角三角形-----------------10分 ⑶.t=2或t=5.2-----------------14分A B CDE。
