习题6-2 定积分在几何学上的应用(二)
微积分(二)课后题答案,复旦大学出版社__第六章

(x)
=
max{1,
x2}
=
⎪ ⎨
1
⎪ ⎩
x2
−2 ≤ x < −1 −1 ≤ x < 1 ,于是 1≤ x≤ 2
∫ ∫ ∫ ∫ 2 max{1, x2}dx = −2
−1 x2dx +
−2
1 1dx +
−1
2 1
x2dx
=
1 3
x3
−1 −2
+
x
1 −1
+
1 3
x3
2 1
=
20 3
∫ ∫ 6.
已知 f(x)连续,且 f(2)=3,求 lim x→2
a i)2
+1,
于是
∑ ∑ n
i=1
f (ξi )Δxi
=
n [(a + b − a i)2 +1] b − a
i=1
n
n
∑ =
(b
−
a)
n i=1
[a2
+
(b
−
a)2
i2 n2
+
2 a(b
−
a)
i n
+1]
1 n
= (b − a)[na2 + (b − a)2 ⋅ 1 ⋅ 1 n(n +1)(2n +1) + 2(b − a)a⋅ 1 ⋅ n(n + 1) + n]⋅ 1
x⎡ 2 ⎢⎣
2 t
f
(u)du
⎤ ⎥⎦
dt
(x − 2)2
.
解
∫ ∫ ∫ ∫ ∫ ∫ lim
x→2
x⎡ 2⎣
定积分在几何学上的应用笔记

定积分在几何学上的应用笔记一、引言定积分是微积分中的重要内容之一,它在几何学中有广泛的应用。
本文将介绍定积分在几何学中的几个典型应用,并讨论其应用意义。
二、计算曲线长度在平面几何中,计算曲线的长度是一个经常出现的问题。
假设有一条平面曲线f(x)在区间[a, b]上,想要求出曲线的长度L。
利用定积分的概念,可以通过以下步骤进行计算:1. 将曲线分为无穷小的线段;2. 计算每个无穷小线段的长度;3. 对所有无穷小线段的长度求和,得到曲线的长度。
要计算曲线y = x^2在区间[0, 1]上的长度,可以将曲线分为无穷小线段y = x^2 + dx,其中dx为无穷小的自变量增量。
根据勾股定理,每个无穷小线段的长度为√(dx^2 + dy^2) = √(1 + (dy/dx)²)dx。
通过对所有无穷小线段的长度进行积分,即可求出曲线的长度L。
三、计算曲率曲率描述了曲线弯曲的程度,在计算曲线的曲率时,定积分也有应用。
假设有一条平面曲线f(x)在区间[a, b]上,想要求出曲线在某点x处的曲率K。
可以通过以下步骤进行计算:1. 根据曲线方程,求出曲线的切线斜率dy/dx;2. 计算切线斜率的导数d²y/dx²;3. 利用曲率公式K = |d²y/dx²| / (1 + (dy/dx)²)^(3/2),求出曲线的曲率。
通过将切线斜率的导数进行积分,可以得到曲线在区间[a, b]上的曲率函数,进而帮助我们分析曲线的特征。
四、计算曲面面积在空间几何中,计算曲面的面积也是一个常见的问题。
假设有一个曲面z = f(x, y),想要求出曲面的面积S。
可以使用定积分的方法进行计算:1. 将曲面分为无穷小的面元;2. 计算每个无穷小面元的面积;3. 对所有无穷小面元的面积求和,得到曲面的面积。
要计算平面上的一条曲线y = g(x)在[a, b]上旋转后生成的曲面的面积,可以先计算曲线上每个点x的切线斜率dy/dx,然后利用曲线的长度L求出无穷小面元的面积dS = 2πg(x)√(1 + (dy/dx)²)dx,最后通过求积分得到曲面的面积S。
高等数学第六章第二节定积分在几何学上的应用课件.ppt
解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
定积分在几何上的应用

定积分在几何上的应用
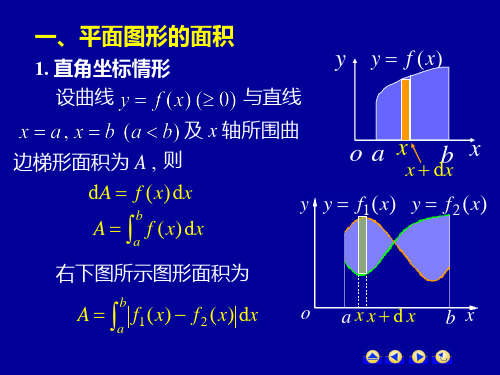
定积分就是求函数f(X)在区间[a,b]中图线下包围的面积。
即由y=0,x=a,x=b,y=f(X)所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
绕x轴旋转体体积公式是V=π∫[a,b]f(x)^2dx。
绕y轴旋转体积公式同理,将x,y互换即可,
V=π∫[a,b]φ(y)^2dy。
或者是V=2π∫[a,b]y*f(y)dy,也是绕x轴旋转体积。
绕x轴旋转体的侧面积为A=2π∫[a,b]y*(1+y'^2)^0.5dx,其中y'^2是y对x的导数的平方。
若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
几何,就是研究空间结构及性质的一门学科。
它是数学中最基本的研究内容之一,与分析、代数等等具有同样重要的地位,并且关系极为密切。
几何学发展历史悠长,内容丰富。
它和代数、分析、数论等等关系极其密切。
6.2 定积分在几何学上的应用

圆柱
圆锥
圆台
问题:一般地,考虑如图所示的曲边梯形绕 x 轴旋 转一周而形成的空间立体,其体积为多少?
y
y = f (x)
0a
bx
取积分变量为 x, x ∈[a,b] y
y = f (x)
在[a, b]上任取小区间 [ x, x + dx]
o
x x + dx
x
考虑以 d x 为底的窄曲边梯形 绕 x 轴旋转而成的薄片 ∆V 体积的近似值
设曲线弧为 y = f ( x) (a ≤ x ≤ b),
其中 f ( x)在[a, b]上有一阶连续导数 y = f ( x)
y
取积分变量为 x,x∈ [a, b]
在 [a, b] 上任取小区间[ x, x + dx],
以对应小切线段的长代替小弧段的长
} dy
dx
∆s ≈ (dx)2 + (dy)2 = 1 + y′2dx o ax x + dx b x
∫1
A= ( 0
y
−
y2 ) d
y
=
2
3
3
y2
−
y3 1
3
=
0
1. 3
例2 计算抛物线 y2 = 2x 与直线 y = x − 4 所围图形 的面积 .
例2 计算抛物线 y2 = 2x 与直线 y = x − 4 所围图形 的面积 .
解:( 一)取 y 为积分变量。
y
∫ s = 4 [ ( y + 4) − y2 ] d y
其体积可以近似看作以 f (x) 为底半径,高为 d x 的 薄圆柱体的体积,即 两个量的乘
∆V ≈ π [ f ( x)]2 dx = dV
定积分在几何计算中的应用

定积分在几何计算中的应用定积分是高等数学中的一个重要概念,它在几何计算中有着广泛的应用。
在几何学中,定积分可以用来计算曲线的长度、曲面的面积、体积等等。
下面我们就来看看定积分在几何计算中的应用。
定积分可以用来计算曲线的长度。
对于一条曲线,我们可以将其分成无数个小段,然后对每个小段的长度进行求和,最终得到整条曲线的长度。
这个过程可以用定积分来表示,即:L = ∫a^b √(1+(dy/dx)^2) dx其中,a和b分别表示曲线的起点和终点,dy/dx表示曲线在每个点的斜率。
这个式子的意义是,将曲线分成无数个小段,每个小段的长度为√(1+(dy/dx)^2) dx,然后对所有小段的长度进行求和,最终得到整条曲线的长度。
定积分可以用来计算曲面的面积。
对于一个曲面,我们可以将其分成无数个小面元,然后对每个小面元的面积进行求和,最终得到整个曲面的面积。
这个过程可以用定积分来表示,即:S = ∫∫D √(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy其中,D表示曲面的投影区域,z表示曲面在每个点的高度,∂z/∂x和∂z/∂y分别表示曲面在每个点在x和y方向上的斜率。
这个式子的意义是,将曲面分成无数个小面元,每个小面元的面积为√(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy,然后对所有小面元的面积进行求和,最终得到整个曲面的面积。
定积分可以用来计算体积。
对于一个立体图形,我们可以将其分成无数个小体元,然后对每个小体元的体积进行求和,最终得到整个立体图形的体积。
这个过程可以用定积分来表示,即:V = ∫∫∫E dxdydz其中,E表示立体图形的空间区域。
这个式子的意义是,将立体图形分成无数个小体元,每个小体元的体积为dxdydz,然后对所有小体元的体积进行求和,最终得到整个立体图形的体积。
定积分在几何计算中有着广泛的应用,可以用来计算曲线的长度、曲面的面积、体积等等。
这些应用不仅在数学中有着重要的意义,也在实际生活中有着广泛的应用,例如在建筑设计、工程计算等领域中都有着重要的作用。
定积分在几何,物理学中的简单应用

定积分在几何,物理学中的简单应用
定积分是一种常见的数学工具,用来解决许多几何和物理问题。
它可以在几何学、物理学中解决积分、面积和容积计算题中应用。
首先,定积分在几何学中的简单应用。
比如,如果我们要计算一个几何图形的面积,则可以通过定积分来计算。
它可以计算任意形状的几何图形的面积,比如三角形、椭圆、圆形等。
它的应用范围非常广泛,比如可以用它来计算面积、周长、体积等。
其次,定积分也可以用在物理学中。
比如,如果我们要计算一个物体在多次不同力作用之下移动的路程,可以用定积分来计算。
它可以帮助我们精确地计算物体受力作用前后的距离,也可以帮助我们精确计算弹性作用力等。
最后,定积分也可以应用于物理学的温度问题中。
比如,我们可以通过定积分求出一个物体在单位温差下的热量传递,也可以求出一个物体的总热量。
还可以用它求解温度场、热传导率、热导率等问题。
以上是定积分在几何、物理学中的简单应用。
定积分是一种通用而有效的数学工具,在几何、物理学中都有着广泛的应用,不仅可以用来解决相关的面积、容积计算题,而且还可以用来解决物理热力学、温度等问题。
只要我们掌握它的基本使用方法以及它的一些特性和用途,就可以在几何、物理学中更好地应用它来解决其它问题。
- 1 -。
《微积分》课后答案(复旦大学出版社(曹定华 李建平 毛志强 著))第六章 定积分

x
ar
1
1 (b3 a 3 ) (b a) 3
1+x.所以
4. 估计下列各积分值的范围:
1
天天learn()为您提供大学各个学科的课后答案、视频教程在线浏览及下载。
n.
2 3 1
x
n b 1 S ( x 2 1)dx lim f (i )Δxi (b a)[a 2 (b a) 2 a(b a) 1] a n 3 i 1
t
此文档由天天learn()为您收集整理。
(1)
4
1
( x 2 1)dx ; e x dx (a>0);
2
2
(2)
3 1 3 0
x arctan xdx ;
2
(3) 解
a
a
(4)
2
ex
x
dx .
(1)在区间[1,4]上,函数 f ( x) x 1 是增函数,故在[1,4]上的最大值 M f (4) 17 ,最
2
w.
f (a ) f ( a ) e a ,a>0 时, e a 1 ,故 f ( x) 在[-a,a]上的最大值 M=1,最小值
m e a ,所以
ww
2
tt
2
le
2
2ae a e x dx 2a .
2
ar
a
,令 f ( x) 0 得驻点 x=0,又 f (0) 1 ,
2
0
(1)
4
le
1
所以当 x=0 时,I(x)有极小值,且极小值为 I(0)=0. 5. 计算下列定积分:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
0
1
1 x 2 1 ( x ln ) ln 3 1 x 0 2
6. 求曲线 ρ 2(1 cos ) 的全长。
s a
2
0 2
2 ( ) 2 d
2
0
a 2 (1 cos ) 2 ( a sin ) 2 d
4.有一立体以抛物线 y 2 x 与直线 x 2 所围成图形为底,而垂直于抛物线轴的截面
2
都是等边三角形,求其体积.
A( x)
3 (2 y ) 2 3 y 2 2 3 x 4
2 2 1 0 0 0
V A( x)dx 2 3 xdx 3 x 2 3
·高等数学练习册·习题答案
5. 求曲线 y ln(1 x ),
2
0 x
1 的弧长。 2
1 1 1 2 x 2 4x2 2 s 2 1 ( y) 2 dx 2 1 ( ) dx 1 dx 0 0 0 1 x2 (1 x 2 ) 2
2
0
1
1 (1 x 2 ) 2 4 x 2 (1 x 2 ) 2 2 dx 0 (1 x 2 )2 dx (1 x 2 ) 2 1 1 1 x2 2 1 1 2 2 dx ( 1 ) dx (1 )dx 2 2 0 0 1 x 1 x 1 x 1 x 1
a 2 (3 cos t ) 2 a (1 cos t )dt 8 2 a 3 a 3 (3 cos t ) 2 (1 cos t )dt 8 2 a 3
0 29 15cos t 7 cos 2 t cos3 t )dt 8 2 a 3
·高等数学练习册·习题答案
习题 6-2
2
定积分在几何学上的应用(二)
1. 求曲线 y x , x 0 及其在(1,1)点的法线与 x 轴围成的图形绕 x 轴旋转一周所得 的旋转体的体积。
y 2 x y
x 1
2 k法
1 2
所以,法线方程为: y 1
1 1 3 ( x 1) 即 y x 2 2 2
2
4 ,且使该图形 9
绕 x 轴旋转而成的旋转体的体积最小. (1)通过点(0, 0) ,所以, c 0
a 3 b 2 a b 4 (2) ( ax bx) dx ( x x ) 0 3 2 3 2 9 0
1 2
1
a
4 3 b ……………………………………………………① 3 2
3a | sin t cos t | dt 12a 2 sin t cos tdt
0 0
(6a sin 2 t ) 2 6a
0
·高等数学练习册·习题答案
1 1 2 2
a 2 5 ab 4 b 2 3 a 2 ab b 2 (3) V ( ax bx) dx ( x x x ) 0 5 2 3 5 2 3 0
将①代入得到, V
16 2 1 b b2 45 15 30
2 1 b0b2 15 15 1 V (b) 0 15 V (b) b 2 时, V 最小,此时, a 5 3
3 2
3
2 . 求 摆 线 x a (t sin t ), y a (1 cos t )(a 0) 的 一 拱 与 y 0 所 围 成 的 图 形 绕
y 2a 旋转所得旋转体的体积. V
2 0 2 a
0
[ y ( x) 2a ]2 dx 2 a (2a ) 2
25 2 a 3 8 2 a 3 17 2 a 3
·高等数学练习册·习题答案
3.设抛物线 y ax bx c 通过点(0, 0) ,且 0 x 1 时, y 0 ,试确定 a, b, c 的
2
值,使得抛物线 y ax bx c 与直线 x 1, y 0 所围成的图形的面积为
2
0
2 2 cos d 2a sin
0
2
d
(4a cos ) 8a 2 0
2
·高等数学练习册·习题答案
7.计算星形线 x a cos t , y a sin t 的全长。
3 3
s
2
0 2
(
2 dx 2 dy 2 ) ( ) dt (3a cos 2 t sin t ) 2 (3a sin 2 t cos t ) 2 dt 0 dt dt
法线与 x 轴的交点为 (3, 0) ,所以,旋转体体积为:
1 3 1 1 3 3 V ( x 2 ) 2 dx ( x ) 2 dx x 4 dx ( x 2 6 x 9)dx 0 1 0 2 2 4 1
5
1
x
5 0
1
2 13 ( x 3x 9 x) 4 3 5 3 15 1
