钢结构的-稳定性验算
钢结构连接、钢结构强度稳定性、钢筋支架、格构柱计算

钢结构连接、钢结构强度稳定性、钢筋支架、格构柱计算◆钢结构连接计算一、连接件类别不焊透的对接焊缝二、计算公式1.在通过焊缝形心的拉力,压力或剪力作用下的焊缝强度按下式计算:2.在其它力或各种综合力作用下,σf,τf共同作用处。
式中N──-构件轴心拉力或轴心压力,取 N=100N;lw──对接焊缝或角焊缝的计算长度,取lw=50mm;γ─-作用力与焊缝方向的角度γ=45度;σf──按焊缝有效截面(helw)计算,垂直于焊缝长度方向的应力;hf──较小焊脚尺寸,取 hf=30mm;βt──正面角焊缝的强度设计值增大系数;取1;τf──按焊缝有效截面计算,沿焊缝长度方向的剪应力;Ffw──角焊缝的强度设计值。
α──斜角角焊缝两焊脚边的夹角或V形坡口角度;取α=100度。
s ──坡口根部至焊缝表面的最短距离,取 s=12mm;he──角焊缝的有效厚度,由于坡口类型为V形坡口,所以取he=s=12.000mm.三、计算结果1. 正应力:σf=N×sin(γ)/(lw×he)=100×sin(45)/(50×12.000)=0.118N/mm2;2. 剪应力:τf=N×cos(γ)/(lw×he)=100×cos(45)/(50×12.000)=0.118N/mm2;3. 综合应力:[(σf/βt)2+τf2]1/2=0.167N/mm2;结论:计算得出的综合应力0.167N/mm2≤对接焊缝的强度设计值ftw=10.000N/mm2,满足要求!◆钢结构强度稳定性计算一、构件受力类别:轴心受弯构件。
二、强度验算:1、受弯的实腹构件,其抗弯强度可按下式计算:Mx/γxWnx + My/γyWny ≤ f式中 Mx,My──绕x轴和y轴的弯矩,分别取100.800×106 N·mm,10.000×106 N·mm;γx, γy──对x轴和y轴的截面塑性发展系数,分别取 1.2,1.3;Wnx,Wny──对x轴和y轴的净截面抵抗矩,分别取 947000 mm3,85900 mm3;计算得:Mx/(γxWnx)+My/(γyWny)=100.800×106/(1.2×947000)+10.000×106/(1.3×85900)=178.251 N/mm2受弯的实腹构件抗弯强度=178.251 N/mm2 ≤抗弯强度设计值f=215N/mm2,满足要求!2、受弯的实腹构件,其抗剪强度可按下式计算:τmax = VS/Itw ≤ fv式中V──计算截面沿腹板平面作用的剪力,取V=10.300×103 N;S──计算剪力处以上毛截面对中和轴的面积矩,取 S= 947000mm3;I──毛截面惯性矩,取 I=189300000 mm4;tw──腹板厚度,取 tw=8 mm;计算得:τmax = VS/Itw=10.300×103×947000/(189300000×8)=6.441N/mm2受弯的实腹构件抗剪强度τmax =6.441N/mm2≤抗剪强度设计值fv = 175 N/mm2,满足要求!3、局部承压强度计算τc = φF/twlz ≤ f式中φ──集中荷载增大系数,取φ=3;F──集中荷载,对动力荷载应考虑的动力系数,取 F=0kN;tw──腹板厚度,取 tw=8 mm;lz──集中荷载在腹板计算高度上边缘的假定分布长度,取lz=100(mm);计算得:τc = φF/twlz =3×0×103/(8×100)=0.000N/mm2局部承压强度τc =0.000N/mm2≤承载力设计值f = 215 N/mm2,满足要求!4、在最大刚度主平面内受弯的构件,其整体稳定性按下式计算:Mx/φbWx ≤ f式中Mx──绕x轴的弯矩,取100.8×106 N·mm;φb──受弯构件的整体稳定性系数,取φb= 0.9;Wx──对x轴的毛截面抵抗矩Wx,取 947000 mm3;计算得:Mx/φbwx = 100.8×106/(0.9×947000)=118.268 N/mm2≤抗弯强度设计值f= 215 N/mm2,满足要求!5、在两个主平面受弯的工字形截面构件,其整体稳定性按下式计算:Mx/φbWx + My/γyWny ≤ f式中 Mx,My──绕x轴和y轴的弯矩,分别取100.8×106 N·mm,10×106 N·mm;φb──受弯构件的整体稳定性系数,取φb= 0.9;γy──对y轴的截面塑性发展系数,取 1.3;Wx,Wy──对x轴和y轴的毛截面抵抗矩,分别取 947000 mm3, 85900 mm3;Wny──对y轴的净截面抵抗矩,取 85900 mm3计算得:Mx/φbwx +My/ γyWny =100.8×106/(0.9×947000)+10×106/(1.3×85900)=207.818 N/mm2≤抗弯强度设计值f=215 N/mm2,满足要求!◆钢筋支架计算公式一、参数信息钢筋支架(马凳)应用于高层建筑中的大体积混凝土基础底板或者一些大型设备基础和高厚混凝土板等的上下层钢筋之间。
钢结构吊装及结构验算

第一部分钢结构吊装方案及验收数据第一章工程概况1.1、钢结构工程概况1.工程名称:厂房屋面钢结构工程2、建设单位:3、设计单位:4、供料单位:5、施工单位:6、施工地点:\7、安装工期:80天8、建筑面积:约26000平方米(仅指钢结构屋顶覆盖面积)2、建筑物简介: 本工程分厂房混凝土柱,屋面梁、屋面围护结构等。
本工程屋面为双坡,主体结构为混凝土框架结构,屋面为轻钢结构,柱间距为6米、8米、9米12米,东西向为A-M轴,112米。
南北向为1-30轴线,232米。
根据业主施工要求在变形处进行进行分区,其中1-10轴线为A区,11-30轴线为B区。
立面檐口标高为A轴为10.6M、M 轴为10.8M。
主要工程范围包括:屋面结构系统屋面梁、屋面檩条及次檩等构件的吊装、屋面围护系统屋面板及内顶板的安装、墙面结构系统及外墙面板的安装、雨棚结构系统及围护系统的安装。
主要结构形式为轻型门式刚架结构。
主体结构由焊接H型钢(梁)、水平支撑、圆管撑组成;次结构由隅撑、Z型檩条、支撑、拉条组成。
主体钢梁与钢梁之间采用10.9级扭剪型高强度螺栓连接。
檩条用C级普通螺栓连接。
其中梁、檩条等主材采用Q345级钢,钢支撑、拉条采用Q235级钢。
第二章屋面钢梁吊装方案的选择及结构验算2.1施工工作段的划分屋面钢梁的安装是本工程的吊装难点,以伸缩缝为分界分为AB个工作区段,每个工作段的作业相同。
1)区域划分B区:11-30轴/A-M轴A区:1-10/A-M轴2)吊装顺序B区 A区推进吊装2.2钢构安装方案选择吊装施工工艺及技术措施1.主结构的吊装步骤1.1 根据吊装类型划分:吊装区域划分为个五区域(附图),采用50汽吊与抱杆组合吊装。
1.2 据工期要求,配备多组安装人员按照现场材料到货情况分轴线进行多班组吊装工作,吊装先从B区开始,同时安排一组人员进行结构的固定工作;然后是否增加吊装班组及抱杆数量根据现场的实际情况进行。
2. 钢梁安装1.1 根据每榀钢梁的节点进行分段:分为1-10节1.2钢梁吊装顺序1→2→3→4→5→---10节(附图)3.吊装步骤用抱杆、人力安装屋面梁;由于整体屋面梁最大长112米,根据钢梁吊装顺序将其钢梁第一节安装好之后,然后逐节安装。
钢梁稳定性计算步骤

钢梁整体稳定性验算步伐之巴公井开创作1. 根据《钢结构设计规范》(GB 50017-2003)4.2.1条,判断是否可不计算梁的整体稳定性.2. 如需要计算2.1 等截面焊接工字形和轧制H型钢简支梁1)根据表B.1注1,求ξ.l1——H型钢或等截面工字形简支梁受压翼缘的自由长度,对跨中无侧向支承点的梁,l1为其跨度;对跨中有侧向支撑点的梁,l1为受压翼缘侧向支承点间的距离(梁的支座处视为有侧身支承).b1——截面宽度.2)根据表B.1,求βb.3)根据公式B.1-1注,求I1和I2,求αb.如果αb>0.8,根据表B.1注6,调整βb.4)根据公式B.1-1注,计算ηb.5)根据公式B.1-1,计算φb.6)如果φb>0.6,根据公式B.1-2,采纳φ’b取代φb.7)根据公式4.2.2,验算稳定性.2.2 轧制普通工字钢简支梁1)根据表B.2选取φb.2)如果φb>0.6,根据公式B.1-2,采纳φ’b取代φb.2.3 轧制槽钢简支梁1)根据公式B.3,计算φb.2)如果φb>0.6,根据公式B.1-2,采纳φ’b取代φb.3)根据公式4.2.2,验算稳定性.2.4 双轴对称工字形等截面(含H型钢)悬臂梁1)根据表B.1注1,求ξ.l1——悬臂梁的悬伸长度.b1——截面宽度.2)根据表B.4,求βb.3)根据公式B.1-1,计算φb.4)如果φb>0.6,根据公式B.1-2,采纳φ’b取代φb.5)根据公式4.2.2,验算稳定性.2.5 受弯构件整体稳定系数的近似计算(均匀弯曲,)2.5.1 工字形截面(含H型钢)双轴对称1)根据公式 B.5-1,计算φb,当φb>0.6时,不用根据公式B.1-2,采纳φ’b取代φb,当φb>1.0,取φb=1.0.2)根据公式4.2.2,验算稳定性.2.5.2 工字形截面(含H型钢)单轴对称1)根据公式 B.5-2,计算φb,当φb>0.6时,不用根据公式B.1-2,采纳φ’b取代φb,当φb>1.0,取φb=1.0.2.5.3T型截面(弯矩作用在对称轴平面,绕x轴),翼缘受压,双角钢T形截面1)根据公式 B.5-3,计算φb,当φb>0.6时,不用根据公式B.1-2,采纳φ’b取代φb.2)根据公式4.2.2,验算稳定性.2.5.4T型截面(弯矩作用在对称轴平面,绕x轴),翼缘受压,部份T型钢和两板组合T形截面1)根据公式 B.5-4,计算φb,当φb>0.6时,不用根据公式B.1-2,采纳φ’b取代φb.2)根据公式4.2.2,验算稳定性.2.5.5T型截面(弯矩作用在对称轴平面,绕x轴),弯矩使翼缘受拉且腹板宽厚比不年夜于1)根据公式 B.5-5,计算φb,当φb>0.6时,不用根据公式B.1-2,采纳φ’b取代φb.2)根据公式4.2.2,验算稳定性.钢梁局部稳定性验算步伐1. 根据《钢结构设计规范》(GB 50017-2003)4.3.1条,判断钢梁是否需要配置加劲肋,以及是否需要计算配置加劲肋后腹板的稳定性.2. 如需要配置加劲肋,根据 4.3.2条,判断加劲肋的安插形式.3. 如需要计算腹板稳定性3.1 仅配置横向加劲肋的腹板1)根据式4.3.3-2d或式4.3.3-2e,计算“用于腹板受弯计算时的通用高厚比λb”;2)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c,计算σcr;3)根据式4.3.3-3d或式4.3.3-3e,计算λs;4)根据式4.3.3-3a、式4.3.3-3b或式4.3.3-3c,计算τcr;5)根据式4.3.3-4d或式4.3.3-4e,计算λc;6)根据式4.3.3-4a、式4.3.3-4b或式4.3.3-4c,计算σc,cr;7)根据式4.3.3-1,计算各区格的局部稳定性.3.2 同时用横向加劲肋和纵向加劲肋加强的腹板3.2.1 受压翼缘与纵向加劲肋之间的区格1)根据式4.3.4-2d或式4.3.4-2e,计算λb1;2)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c,计算σcr1;3)根据式4.3.3-3d或式4.3.3-3e,计算λs1,其中h0要换成h1,h1是纵向加劲肋至腹板计算高度受压边缘的距离;4)根据式4.3.3-3a、式4.3.3-3b或式4.3.3-3c,计算τcr1;5)根据式4.3.4-3a或式4.3.4-3b,计算λc1;6)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c,计算σc,cr1;7)根据式4.3.4-1,计算受压翼缘与纵向加劲肋之间区格的局部稳定性.3.2.2 受拉翼缘与纵向加劲肋之间的区格1)根据式4.3.4-5,计算λb2;2)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c,计算σcr2.3)根据式4.3.3-3d或式4.3.3-3e,计算λs2,其中h0要换成h2,h2=h0-h1;4)根据式4.3.3-3a、4.3.3-3b或4.3.3-3c,计算τcr2;5)根据式4.3.3-4d或式4.3.3-4e,计算λc2,其中h0要换成h2,当a/h2>2时,取a/h2=2;6)根据式4.3.3-4a、式4.3.3-4b或式4.3.3-4c,计算σc,cr2.7)根据式4.3.4-4计算受拉翼缘与纵向加劲肋区格的稳定性.3.2.3 在受压翼缘与纵向加劲肋之间设有短加劲肋的区格1)根据式4.3.4-2a或4.3.4-2b,计算λb1;2)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c,计算σcr1;3)根据式4.3.3-3d或式4.3.3-3e,计算λs1;4)根据式4.3.3-3a、4.3.3-3b或4.3.3-3c,计算τcr1,其中将a要换成a1,a1为短加劲肋间距;5)根据式4.3.5a或式4.3.5b计算λc1;6)根据式4.3.3-2a、式4.3.3-2b或式4.3.3-2c计算σc,cr1;7)根据式4.3.4-1计算在受压翼缘与纵向加劲肋之间设有短加劲肋区格的稳定性.。
钢结构设计中的强度与稳定性分析

钢结构设计中的强度与稳定性分析钢结构作为一种重要的建筑构造形式,在现代建筑中得到了广泛的应用。
其独特的特点使其成为了建筑设计师们的首选,然而,正确理解和分析钢结构的强度与稳定性是确保其安全性和可靠性的关键。
本文将深入探讨钢结构设计中的强度与稳定性分析,以期对读者有所启发。
一、强度分析钢结构的强度分析是确保建筑结构能够承受正常和异常荷载的重要步骤。
在设计过程中,工程师需要考虑到以下几个关键因素。
1.1 材料强度钢材作为钢结构的主要构造材料,其强度参数决定了整个结构的抗力能力。
工程师需要详细了解所选用的钢材的性能指标,包括屈服强度、抗拉强度、弹性模量等,以确保设计结构的强度能够满足要求。
1.2 荷载计算在设计过程中,荷载计算是非常重要的一环。
工程师需要根据建筑的用途和具体情况,准确计算出可变荷载、恒载和地震荷载等,以保证设计的结构能够承受这些荷载。
当荷载不均匀分配时,还需要进行统一系数的计算。
1.3 结构稳定钢结构的稳定性是强度分析中不可忽视的一部分。
当结构受到垂直或水平方向的外力作用时,其稳定性要求结构能够保持稳定。
工程师需要根据实际情况,采用适当的稳定性分析方法,确保设计的结构能够满足要求。
二、稳定性分析稳定性分析是钢结构设计中非常重要的一环,它主要考虑结构在受荷时的稳定性能。
以下是一些常见的稳定性分析方法。
2.1 弯曲稳定性分析在弯曲稳定性分析中,工程师需要计算并分析结构受弯矩作用下的稳定性。
通过计算结构的屈曲系数和容许屈曲荷载,可以确定结构的弯曲稳定性是否得到满足。
2.2 屈曲稳定性分析屈曲稳定性分析主要考虑结构在压力作用下的稳定性。
工程师需要计算结构的临界荷载和理论强度,以保证结构在受压力作用时不发生屈曲。
2.3 应力稳定性分析应力稳定性分析是为了保证结构在受荷时不发生破坏。
工程师需要计算结构的应力集中系数和容许应力,以确保结构在实际使用条件下能够稳定且不发生破坏。
三、结构设计的实践在实际结构设计中,强度与稳定性分析是紧密相连的。
钢管支撑强度及稳定性验算

钢管支撑强度及稳定性验算注意《建筑基坑支护技术规程》JGJ120-2012(《全国规程》)与地方规程输入区别输入围护结构计算软件单根支撑计算轴力标准值《全国规程》4.9.8 L:支撑构件的受压计算长度《全国规程》第3.1.6 作用基本组合的综合分项系数不应小于1.25;对安全等级为一级、二级、三级的支护结构γ0分别不应小于1.1、《全国规程》第4.9.7取(1/1000)L与40mm的较大值,《上海规范》10.2.9.3取(2/1000~3/1000)L与40mm的较大值等于均布面荷载乘以钢管外径,钢支撑施工荷载取值不超过1KN/m《钢结构》4.4.8跨中弯矩:M自重=1/8(g钢*A*L*L)*γ0*γf;M施=1/8*(q0*L*L)*γ0*γf《钢结构》8.2.4-2 跨中最大弯矩M=Me+M0《钢结构》表8.1.1 表3.5.1 当截面板件宽厚比等级满足S3级要求时,按表8.1.1采用根据钢支撑型号填写壁厚16填0.577、壁厚14填0.581、壁厚12填0.585《钢结构》13.1.2 圆管截面的受压构件,其外径与壁厚之比不应超过100(εк)^2《钢结构》8.2.4《钢结构》4.4.8《钢结构》4.4.8《全国规程》4.9.8《全国规程》4.9.14《钢结构》8.2.4-3《钢结构》8.2.1-2《钢结构》3.5.1 其值为235与钢材牌号中屈服点数值的比值的平方根《钢结构》附录D D.0.5-2《钢结构》附录D D.0.5《钢结构》附录D 表D.0.5《钢结构》8.1.1-2 f≤[f]=215MPa,满足要求《钢结构》8.2.4-1 f/[f]≤1.0,满足要求支撑轴力标准值:1,如果是理正计算,则直接输入计算轴力即可,因为理正计算的轴力是支撑间距跨度上的总轴力。
2,如果是启明星计算,则支撑轴力为计算结果乘以支撑间距。
因为启明星计算的轴力是每延米上的轴力。
注:1、蓝色部分-填入2、粉色部分-需与规范确认3、红色部分-计算结果γ0分别不应小于1.1、1.0、0.9:。
钢结构设计原理第4章(2) 稳定性(整体)

﹡缀材计算 按实际剪力和弯曲失稳剪力的较大值计算
V Af 85
fy 235
4.6 板件的稳定和屈曲后强度的利用
4.6.1 轴心受压构件的板件稳定
﹡均匀受压板件的屈曲现象
①板件宽厚比 原则: ● 允许板件先屈曲 ● 不允许板件先于构件整体屈曲,临界应力相等 (等稳原则)
是构件在弯矩作用平面内的长细比,
当<30 =30; 当>100时,取=100
横隔(每个单元不少于2个,间距不大于8m)
﹡翼缘的稳定与梁相同
不考虑塑性,
b1 / t 15 235 fy
部分考虑塑性,
b1 / t 13 235 fy
f
x A W1x 1 x N NEx
W1x=Ix /y0
x 是由0x确定的b类截面轴心压杆稳定系数。
﹡单肢计算(弯矩绕虚轴作用)
单肢1 N1 =Mx /a+N z2 /a
单肢2 N2 =N N1
按轴心受压构件计算。 注意计算长度取值。
﹡弯矩作用平面外稳定计算
●弯矩绕虚轴作用:单肢已经验算 ●弯矩绕实轴作用:按箱形截面的平面外计算,
c=0时,可不配置;否则按构造配置0.5h0≤a≤2h0
2、对于 h0 tw > 80 235 fy 的梁,一般应配置横
向加劲肋并按要求计算局部稳定。
3、h0 tw > 150 235 fy 时(受压翼缘扭转未约束),
h0 tw > 170 235 fy 或(受压翼缘扭转受约束),
应配置纵横加劲肋,必要时配置短加劲肋(下图)。
D / t 23500/ fy
4.6.2 受弯构件的板件稳定
钢梁稳定性计算步骤之欧阳术创编

钢梁整体稳定性验算步骤1. 根据《钢结构设计规范》(GB 50017-2003)4.2.1条,判断是否可不计算梁的整体稳定性。
2. 如需要计算2.1 等截面焊接工字形和轧制H型钢简支梁1)根据表B.1注1,求ξ。
l1——H型钢或等截面工字形简支梁受压翼缘的自由长度,对跨中无侧向支承点的梁,l1为其跨度;对跨中有侧向支撑点的梁,l1为受压翼缘侧向支承点间的距离(梁的支座处视为有侧身支承)。
b1——截面宽度。
2)根据表B.1,求βb。
3)根据公式B.1-1注,求I1和I2,求αb。
如果αb>0.8,根据表B.1注6,调整βb。
4)根据公式B.1-1注,计算ηb。
5)根据公式B.1-1,计算φb。
6)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
7)根据公式4.2.2,验算稳定性。
2.2 轧制普通工字钢简支梁欧阳术创编2021.02.02 欧阳美创编1)根据表B.2选取φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.3 轧制槽钢简支梁1)根据公式B.3,计算φb。
2)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
3)根据公式4.2.2,验算稳定性。
2.4 双轴对称工字形等截面(含H型钢)悬臂梁1)根据表B.1注1,求ξ。
l1——悬臂梁的悬伸长度。
b1——截面宽度。
2)根据表B.4,求βb。
3)根据公式B.1-1,计算φb。
4)如果φb>0.6,根据公式B.1-2,采用φ’b代替φb。
5)根据公式4.2.2,验算稳定性。
2.5 受弯构件整体稳定系数的近似计算(均匀弯曲,)2.5.1 工字形截面(含H型钢)双轴对称1)根据公式B.5-1,计算φb,当φb>0.6时,不必根据公式B.1-2,采用φ’b代替φb,当φb>1.0,取φb=1.0。
2)根据公式4.2.2,验算稳定性。
欧阳术创编2021.02.02 欧阳美创编2.5.2 工字形截面(含H型钢)单轴对称1)根据公式B.5-2,计算φb,当φb>0.6时,不必根据公式B.1-2,采用φ’b代替φb,当φb>1.0,取φb=1.0。
第四章 钢结构的稳定
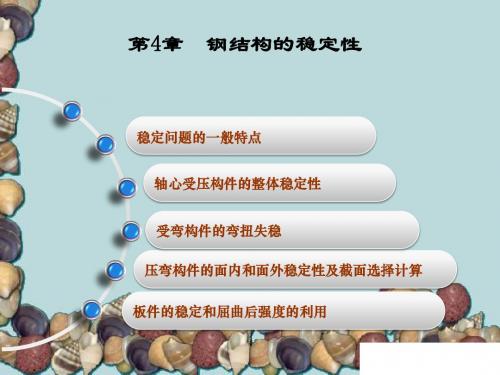
②型钢热轧后的不均匀冷却;
③板边缘经火焰切割后的热塑性收缩; ④构件经冷校正产生的塑性变形。其中,以热轧残余应力的影响 最大。
4.2 轴心受压构件的整体稳定性
残余应力对轴心受压构件稳定性的影响与它的分布有关。下面以 热轧制H型钢为例说明残余应力对轴心受压的影响(如下图所示)。
H型钢轧制时,翼缘端出现纵向残余压应力(图中阴影区称为I区),其余部分存在 纵向拉应力(称为Ⅱ区),并假定纵向残余应力最大值为0.3fy,由于轴心压应力 与残余应力相叠加,使得I区先进入塑料性状态而Ⅱ区仍工作于弹性状态,图(b), (c),(d),(e)反应了弹性区域的变化过程。 I区进入塑性状态后其截面应力不可 能再增加,能够抵抗外力矩(屈曲弯矩)的只有截面的弹性区,此时构件的欧拉临 界力和临界应力为:
根据上式可绘出N—V变化曲线, 如图所示。由此图可以看出:
(1)当轴心压力较小时,总挠
度增加较慢,到达 A或A’后,总
挠度增加加快。 (2)杆件开始时就处于弯曲平
衡状态,这与理想轴心压杆的直线平衡状态不同。
(3)对无限弹性材料,当轴压力达到欧拉临界力时,总挠度无限增大。 而实际材料是,当轴压力达到图中B或B'时,杆件中点截面边缘纤维屈 服而进入塑性状态,杆件挠度增加,而轴力减小,构件开始弹性卸载。
临界状态 (微弯平衡)
【又称】分岔失稳或第一类稳定问题 (bifurcation instability) 【定义】由原来的平衡状态变为一种新的微弯(或微 扭)平衡状态。 相应的荷载NE——屈曲荷载、临界荷载、 平衡分岔荷载
此类稳定又可分为两类:
稳定分岔失稳
不稳定分岔失稳
稳定分岔失稳
不稳定分岔失稳
例:求解图示刚性杆体系的临界力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴心受压构件往往发生整体失稳现象,而且是突然地发生,危害较大。构件由直杆的稳定状态到不能 保持整体的不稳定状态;有一个很小的干扰力,结构的弯曲变形即迅速增大,结构中出现很大的偏心力, 产生很大的弯矩,截面应力增加很多,最终使结构丧失承载能力。这种现象就叫做构件的弯曲失稳或弯曲 屈曲。不同的截面形式,会发生不同的屈曲形式:工字形、箱形可能发生弯曲屈曲,十字形可能发生扭转 屈曲;单轴对称的截面如 T 形、Π形、角钢可能发生弯曲扭转屈曲;工程上认为构件的截面尺寸较厚,主 要发生弯曲屈曲。
(7-4)
N cr
2 EI / l 2
2 EA / 2
cr
2E / 2
精彩文档
实用标准文案
实际上轴心受压杆件存在着各种缺陷:残余应力、初始弯曲、初始偏心等。此时的极限承载力
Nu,
N u / Af y 叫整体稳定系数。
残余应力的分布:见 P104、P157,残余应力的存在使构件受力时过早地进入了弹塑性受力状态,使屈 曲时截面抗弯刚度减小,导致稳定承载能力降低,降低了构件的临界应力。
令 k=be/b;
则
cr
2 Ek /
2 x
;
cr
2 Ek 3 /
2 y
(7-8) 所以残余应力对绕弱轴的临界应力的降低影响要比对绕强轴的要大。
初始弯曲、初始偏心使理想轴心受压构件变成偏心受压构件,使稳定从平衡分枝(第一类稳定)问题 变成极值点(第二类稳定)问题,均降低了构件的临界应力。
我国规范考虑残余应力、 l / 1000的初弯曲、未计入初偏心,采用极限承载力理论进行计算,用计算
)
(
t b
)
2
(7-15)
其它支承条件可引入弹性嵌固系数 临界应力完整的格式为:
;弹塑性屈曲引入系数 ,
Et / E ;
cr
2E 12(1
2)
( t )2 b
18.6
100t (
)
2
b
(7-16)
确定板件宽厚比或高厚比的原则是: 局部屈曲临界力大于或等于整体临界应力得等稳定原则, 范规定:
工字形轴心受压构件的板件宽厚比限值:
我国规
翼缘:
b / t (10 0.1 ) 235 / f y
(7-17)
腹板:
h0 / t w (25 0.5 ) 235 / f y
(7-18)
其中: - 构件的长细比;当
30 时取
30;当 100时取
T 形轴心受压构件的板件宽厚比限值:
翼缘:
b / t (10 0.1 ) 235 / f y
100;
y Asin kz B cos kz
边界条件为: z=0 和 l 处 y=0;
则 B=0, Asinkl=0 ,微弯时 A 0 sin kl 0, kl n
最小临界力时取 n=1, k / l ,
故
(7-5) 其它支承情况时欧拉临界力为:
N cr
(7-6)
2 EI /( l ) 2
2 EA / 2
欧拉临界 应力为: (7-7)
(7-19)
腹板:
h0 / t w
箱形轴心受压构件的板件宽厚比限值:
(10 0.1 ) 235 / f y
(7-20)
b0 / t 40 235 / f y ; h0 / tw 40 235 / f y
(7-21)
圆管截面轴心受压构件的板件宽厚比限值:
D / t 100(235 / f y ) ;
(7-22)
弹性理想轴心受压构件两端铰接的临界力叫做欧拉临界力:
N cr
2 EI / l 2
2 EA / 2
(7-1)
推导如下:临界状态下:微弯时截面 C 处的内外力矩平衡方程为:
EId 2 y / dz2 Ny 0
(7-2)
令 k 2 N / EI ,则:
d 2 y / dz 2 k 2 y 0
(7-3)
解得:
实用标准文案
第七章 稳定性验算
整体稳定问题的实质:由稳定状态到不能保持整体的不稳定状态;有一个很小的干扰力,结构的变形
即迅速增大, 结构中出现很大的偏心力, 产生很大的弯矩, 截面应力增加很多, 最终使结构丧失承载能力。
注意:截面中存在压应力,就有稳定问题存在!如:轴心受压构件(全截面压应力)
、梁(部分压应力) 、
0.215 时,
P496 开始的附表。注意不同的钢材、不同的截面形式(分
(7-10) (7-11)
1
2 1
当 0.215 时
[( 2 3
2) ( 2
3
2) 4 2 ]/ 2 2
其中
fy
叫构件的相对长细比。
E
1 , 2 , 3 见 P164 表 5-6 。
二、轴心受压构件的局部稳定
轴心受压构件的板件屈曲,实际上是薄板在轴心压力作用下的屈曲问题,相连板件互为支承。
得到的 96 条柱子曲线 (最后分成 3 组)表达, 同时用表和公式的形式给出
的关系。 见 P162 图 5-17 。
规范规定: 轴心受压构件的整体稳定要验算:
N /( A) f
(7-9)
其中: - 轴心受压构件的整体稳定系数,参见
a、 b、 c、d 四类,见 P163 表 5-4 )。
拟合公式为:
u
Amn sin
m1n1
sin a
b
时 u=0,弯矩 =0
(7-13)
精彩文档
实用标准文案
最小临界力:
N cr
2D a 2 (m
a b2
2
m
)
2
或
N cr
2 D mb 2(
a )2
b a mb
(a )2 mb
,
N cr
2D , b2
临界应力:
cr
N cr / t
12(1
2
E
2
偏心受压构件(部分压应力) 。
局部稳定问题的实质:组成截面的板件尺寸很大,厚度又相对很薄,可能在构件发生整体失稳前,各
自先发生屈曲,即板件偏离原来的平衡位置发生波状鼓曲,部分板件因局部屈曲退出受力,使其他板件受
力增加,截面可能变为不对称,导致构件较早地丧失承载力。
注意:热轧型钢不必验算局部稳定!
第一节 轴心受压构件的整体稳定和局部稳定
四面简支单向均匀受压的弹性矩形薄板(尺寸
4u 2 4 u
4u
D( z4
z2 y 2
y4 )
a× b),其弯曲平衡微分方程为: 2u
N z2 0
(7-12)
式中: u- 薄板的挠度;
N- 单位板宽的压力;
D
Et 3 ,板的柱面刚度; 12(1 2 )
解得: 边界条件: z=0,z=a,y=0,y=b
mz ny
注意:热轧型钢不必验算局部稳定! 对工字形截面和箱形截面,如果板件宽厚比不满足要求,可以采用设置纵向加劲肋的办法予以加强。
也可以让腹板中间部分屈曲, 在计算构件的强度和稳定时, 仅考虑腹板计算高度边缘范围内两侧宽度各为
