2014年高考天津理科卷的第20题几种解法尝试
2014英语高考天津卷答案及解析

2014英语高考天津卷答案及解析篇一:2014年全国高考英语试题及答案-天津卷2014 年普通高等学校招生全国统一考试(天津卷)第一部分: 英语知识运用(共两节,满分45分)第一节: 单项填空 (共15小题;每小题1分,满分15分)1. Give me a chance, ________ I’ll give you a wonderful surprise.A. ifB. orC. andD. while2. ---Ok, I’ll fix your computer right now. ---Oh, take your time. __________.A. I can’t stand itB. I’m in no hurryC. That’s agreat idea D. It’s not my cup of tea3. Wind is now the world’s fastest growing ________ of power.A. sourceB. senseC. resultD. root4. _______ you start eating in a healthier way, weightcontrol will become much easier.1A. unlessB. AlthoughC. BeforeD. Once5. Anxiously, she took the dress out of the package and tried it on, only _________ id didn’t fitA. to findB. foundC. findingD. having found6. _______ the school, the village has a clinic, which was alsobuilt with government support.A. In reply toB. In addition toC. In charge ofD. In place of7. Clearly and thoughtfully________, the book inspires confidence in students who wish to seek their own answers.A. writingB. to writeC. writtenD. being written8. Life the like ________ ocean; Only________strong-willed can reach the other shore.A. an; theB. the; aC. the ;/D. / ; a9. My parents always _______ great importance to my getting a good education.A. haveB. attachC. acceptD. pay10. ---How long have you been learning English? ----_________! Your English is so good.A. You can’t be seriousB. You got itC. I couldn’tagree more D. I’m stuck11. We won’t start the w ork until all the preparations2__________.A. are being madeB. will be madeC. have been madeD. had been made12. English is a language shared by several diverse cultures,_________ uses it differently.A. all of whichB. each of whichC. all of themD. each of them13. The two countries are going to meet to _______ some barriers to trade between them.A. make upB. use upC. turn downD. break down14. I think _______ impresses me about his painting is the colourshe uses.A. whatB. thatC. whichD. who15. ________ the morning train, he would not have been late for the meeting.A. Did he catchB. should be catchC. has he caughtD. Had he caught第二节: 完形填空(共20小题,每小题1.5分,满分30分)阅读下面短文,掌握其大意,然后从16-35各题所给A,B,C,D的四个选项中,选出最佳选项。
2014年天津市高考数学试卷分析及2015年备考建议

2014年天津高考数学试卷分析及2015年备考建议2014年天津高考数学试题与去年相比,在试卷结构上呈稳定连续的趋势。
试卷的题型与题目的数量较前几年无变化,所考察的知识点均在考纲规定的范围内;在考查基础知识的同时注重对思想方法与能力的考查,试卷从试题的综合性、应用性和创新性的角度设计了由易到难的整体布局,试题的难易分布梯度较为平缓,试题情景设置合理,紧扣教材选题的同时也有着相当的创新要素,对于考生能力的要求进一步提高。
与2013年相比,今年试卷总体难度稍有上升。
下面对2014年天津高考数学进行全面的分析:一.总体分析1.试卷结构稳定,更加重视教材今年高考试卷结构上很好地秉承了天津高考以稳为主的命题思路,题型分布和考点设置上没有太大变化,严格依照《考试说明》中规定的考查内容,准确把握考查要求,对基础知识的考查既注重全面又突出重点。
试卷每种题型均设置了数量较多的基础题,许多试题都是考查单一的知识点或是在最基础的知识交汇点上设置,例如试卷中的选择题第1、2、3、4题,填空题第9、10、11、12题,这部分试题就是通常意义上的送分题,考查考生的基本功,需要牢牢把握。
2. 中等题目减少,强调通性通法2014天津高考还有一个显著的特征是试卷中等题比重在下降,在保证良好区分度与选拔功能的前提下逐步回归基础。
在试题命题上注重解题思路起点低,入口宽,更加强调“通性通法”在解题中的运用,要求运用基本概念分析问题,运用基本公式运算求解,利用基本定理推理论证,这些要求在各题中都有所体现,但各有不同侧重。
同时,还要求考生利用基本数学思想方法寻找解题思路,如试卷第7题需就题目中的绝对值来进行分类讨论分析,而第14题则需用到转化化归思想将函数零点问题转化为函数图象交点问题来考虑。
试卷强调通性通法,有利于引导中学数学教学回归基础。
3. 注重能力立意,更加注重创新2014年天津数学试题体现了《考试说明》规定的各项能力要求,运算求解能力贯穿试卷始终,空间想象能力考查也达到一定深度,推理论证能力和抽象概括能力依然是考查的重点,在区分考生时起到重要作用。
2014年全国高考语文试题及答案-天津卷

2014年普通高等学校招生全国统一考试(天津卷)语文本试卷分为第I卷(选择题)和第Ⅱ卷两部分,共150分,考试用时150分钟,第I卷1至6页,第II卷7至11页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效,考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
一、(15分)1.下列词语中加点字的读音,完全正确的一组是A.缜.(zhěn)密商榷.(què)和.(huò)稀泥揆情度.(duó)理B.取缔.(tì)木讷.(nè)档.(dàng)案袋疾风劲.(jìn)草C.栖.(qī)息挟.(xiá)持白炽.(chì)灯戎马倥偬.(zǒng)D.葳蕤.(ruí) 豢.(huàn)养软着.(zhuó)陆扣人心弦.(xuán)2.下列词语中没有..错别字的一组是A.焕发剽悍鼎力相助失之毫厘,谬以千里B.璘选更迭流光异彩鹬蚌相争,渔人得利C.砥砺斡旋别出心裁黄钟毁弃,瓦釜雷鸣D.甄别笼络休养生息天网灰灰,疏而不漏3.下面语段横线处应填入的词句,最恰当的一组是中国文人对审美具有的感知力,他们可以在安然怡悦中鸟翼几乎无声的扑动,还有花瓣簇簇飘落的声音,他们喜爱“”那种让静寂更显清幽的氛围。
A.精细用心倾听星垂平野阔,月涌大江流B.精细凝神谛听明月松间照,清泉石上流C.精确凝神谛听星垂平野阔,月涌大江流D.精确用心倾听明月松间照,清泉石上流4.下列各句中没有语病的一句是A. 每一个学生都具有创新的潜能,要激发这种潜能,就要看能否培养学生自主学习的能力。
2014年天津高考理科数学试题含答案(Word版)

则该几何体的体积 _______ m . 其前 n 和.若 S1 , S 2 , S 4 成等比数列 则 a1 的
3
11 设 { an }是首 值 __________.
a1 公差 -1 的等差数列 Sn
12 在 D ABC 中 内角 A, B, C 所对的边 别是 a, b, c . 知 b - c = 的值 _______. 13 在
数 a 的取值范围 __________. 解答题 15 本题共 6 道大题 13 满 80 .解答 写出文 说明 证明过程或演算 骤.
本小题满
知函数 f ( x ) = cos x ⋅ sin x + 求 f ( x ) 的最小 周期 求 f ( x) 在 16 本小题满 区间 − 13 男
0,1,2,L, q - 1} 集合 知 q 和 n 均 给定的大于 1 的自然数.设集合 M = {
D
-
17 25 + i 7 7
2 设变
x y 满足 束条
x + y − 2 ≥ 0, x − y − 2 ≤ 0, 则目标函数 z = x + 2 y 的最小值 y ≥ 1,
C 4 D 5
A 2
B
3
3 阅读右边的程序框
行相 的程序 输出的 S 的值
A 15
B 105
1
C 245
π
3 2 − 3 cos x + 3 4
x∈R .
π π , 4 4
学 4
的最大值和最小值.
某大学志愿者协会有 6
女 学. 在这 10
学中 3
学来自数学学院 其余 7 学 到希望小学
学来自物理 化学等其他互 相 的七个学院. 现从这 10 进行支教活动 求选出的 3 设X 17 如 位 学被选到的可能性相 .
2023年全国高考乙卷理科第20题的解法探究与拓展

圆锥曲线中的定点、定值问题一直是高考热点问题.本文以2023年全国高考乙卷理科第20题的第二问为例,多角度探究求解,有利于学生系统掌握解题方法、拓宽视野和全面提升解题能力.1真题呈现题目:(2023年全国乙卷理科第20题)已知椭圆C :y 2a 2+x 2b2=1()a >b >0的离心率为,点A ()-2,0在C 上.(1)求C 的方程;(2)过点()-2,3的直线交C 于P ,Q 两点,直线AP ,AQ 与y 轴的交点分别为M ,N ,证明:线段MN 的中点为定点.此题以椭圆为载体,背景是高等几何中的极点、极线模型,以极点、极线为背景的问题一直是高考中的常青树.试题新颖别致,立意高远而厚重,构思独具匠心,突出关键能力考查,体现了高考试题从能力立意到素养导向的功能.试题解法十分灵活,解题入口宽,深入难,区分度较高,凸显了高考试题的选拔性,是一道有丰厚内涵的经典试题.[1]2多维视角,解法探究(1)解析:由椭圆中a ,b ,c 的关系易得椭圆方程为y 29+x 24=1(略).(2)多维视角的解法探究思维视角一:联立方程,设而不求解法1:普通方程法由题意可知直线PQ 的斜率存在,设P ()x 1,y 1,Q ()x 2,y 2,PQ :y =k ()x +2+3,联立方程ìíîïïy =k ()x +2+3y 29+x 24=1,消去y 得()4k 2+9x 2+8k (2k +3)x +16()k 2+3k =0,由Δ>0,解得k <0,可得x 1+x 2=-8k ()2k +34k 2+9,x 1x 2=16()k 2+3k 4k 2+9.因为A ()-2,0,则直线AP :y =y 1x 1+2(x +2),令x =0,解得y =2y 1x 1+2,即M æèçöø÷0,2y 1x 1+2,同理可得N æèçöø÷0,2y 2x 2+2,则2y 1x 1+2+2y 2x 2+22=2023年全国高考乙卷理科第20题的解法探究与拓展宁夏六盘山高级中学陈熙春李小刚750002摘要:借“题”发挥,从六种思维视角切入,多角度地对2023年高考乙卷理科第20题进行探究,旨在通过一题多解、寻根溯源、拓展延伸,深入挖掘试题背后隐藏的“秘密”,剖析此类问题的本质,归纳解题策略,提炼数学思想,实现从“一道题”到“一类题”质的飞跃.关键词:定点;解法探究;拓展··5[]k ()x 1+2+3x 1+2+[]k ()x2+2+3x 2+2=[]kx 1+()2k +3()x2+2+[]kx 2+()2k +3()x 1+2()x 1+2()x 2+2=2kx 1x 2+()4k +3()x 1+x 2+4()2k +3x 1x 2+2()x 1+x 2+4=32k ()k 2+3k 4k 2+9-8k ()4k +3()2k +34k 2+9+4()2k +316()k 2+3k 4k 2+9-16k ()2k +34k 2+9+4=10836=3,所以线段MN 的中点为定点()0,3.评析:解析几何中的定点问题,实质是定值问题,即求线段PQ 的中点纵坐标为定值.通过设点、设线,借助点的坐标,再结合根与系数的关系验证y M +yN 2为定值即可.求定点、定值问题常见的方法有两种,一种是从特殊入手,求出定值,再证明这个值与变量无关,直线过定点,由对称性知定点一般在坐标轴上;另一种是直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.解法2:整体代换法设P ()x 1,y 1,Q ()x 2,y 2,B ()-2,3,M ()0,y M ,N ()0,y N ,直线PQ 的方程为y =k ()x +2+3,联立ìíîïïy =k ()x +2+3y 29+x 24=1,整理得()4k 2+9(x +2)2+()24k -36(x +2)+36=0,由根与系数的关系得(x 1+2)+(x 2+2)=36-24k 4k 2+9,(x 1+2)(x 2+2)=364k 2+9,因为A ()-2,0,则直线AP :y =y 1x 1+2·()x +2,令x =0,解得y M =2y 1x 1+2,同理可得y N =2y 2x 2+2,所以y M +y N 2=y 1x 1+2+y 2x 2+2=2k +3(x 1+2+x 2+2)(x 1+2)(x 2+2)=2k +3(36-24k 4k 2+9)364k 2+9=3,所以线段MN 的中点为定点()0,3.评析:利用整体的思想,通过构造出关于x +2的一元二次方程,得到斜率间的等量关系,把x +2看成整体以后,比解法1要简洁,运算量大大简化,这种整体代换的思想是处理解析几何繁琐运算的有效策略.思维视角二:构造齐次式解法3:构造+齐次化法设直线PQ 的方程为m ()x +2+ny =1,因为直线PQ 过点()-2,3,代入得n =13.因为点P ,Q 在椭圆C :9x 2+4y 2=36上,变形为9[](x +2)-22+4y 2=36,即9(x +2)2-36(x +2)+4y 2=0,齐次化得9(x +2)2-36(x +2)[m (x +2)]+ny +4y 2=0,化简得4y 2-36ny (x +2)+(9-36m )(x +2)2=0,等式两边同除以()x +22构造斜率式得4(y x +2)y 2-36n yx +2+9-36m =0,把n =13代入得4(y x +2)y 2-12yx +2+9-36m =0,由根与系数的关系得k AQ +k AP =3.因为A ()-2,0,设直线AP 的方程为y =k AP (x+2),令x =0得y M =2k AP ,同理可得y N =2k AQ .故线段MN 的中点的纵坐标为y M +y N 2=2k AP +2k AQ2=k AP +k AQ =3,所以线段MN 的中点为定点()0,3.思维视角三:点差法解法4:点差法+三点共线设点B (-2,3),P (x 1,y 1),Q (x 2,y 2),直线AP ,AQ 的斜率分别为k 1,k 2,则有MN 的中点坐标为(0,k 1+k 2).因为点P ,Q 在椭圆C :y 29+x 24=1上,变形为(x 1+2-2)24+y 219=1⇒··614+19æèçöø÷y 1x 1+22=1x 1+2①,同理可得14+19⋅æèçöø÷y 2x 2+22=1x 2+2②,①-②可得19æèçy 1x 1+2-öø÷y 2x 2+2æèçöø÷y 1x 1+2+y 2x 2+2=1x 1+2-1x 2+2③,又知B ,P ,Q 三点共线可得y 1-3x 1+2=y 2-3x 2+2,变形可得y 1x 1+2-y 2x 2+2=3x 1+2-3x 2+2④,将④代入③可得y 1x 1+2+y 2x 2+2=3,即k 1+k 2=3,从而可得线段MN 的中点是定点()0,3.评析:利用“点差法”的思想方法,通过设点、代点、作差构造出k AP ,k AQ 的表达式,便可轻松解决.解法5:点差法+斜率双用设点B (-2,3),P (x 1,y 1),Q (x 2,y 2),直线AP ,AQ 的斜率分别为k 1,k 2,易得MN 的中点坐标为(0,k 1+k 2).由于ìíî9x 21+4y 12=36①9×(-2)2=36②,①-②可得k 1=y 1x 1+2=-94x 1-2y 1.同理可得k 2=y 2x 2+2=-94x 2-2y 2,不妨设k 1+k 2=m .则m =y 1x 1+2-94x 2-2y 2,化简可得4y 1y 2-9x 1x 2+18x 1-18x 2+36=4my 2x 1+8my 2③,同理可得4y 1y 2-9x 1x 2+18x 2-18x 1+36=4my 1x 2+8my 1④,③-④可得9(x 1-x 2)=m (y 1x 2-y 2x 1)+2m (y 2-y 1)⑤,又知直线B ,P ,Q 三点共线可得y 1-3x 1+2=y 2-3x 2+2,化简可得9(x 1-x 2)=3(y 1x 2-y 2x 1)+6(y 2-y 1)⑥,⑤与⑥对比可得m =3,所以线段MN 的中点是定点()0,3.评析:本题为“斜率和”问题,在解题中涉及到斜率和问题时的解题规律为,第一步,写出原式;第二步,交叉使用;第三步,化整做差;第四步,对照两点式.这种方法同样可以解决“斜率积”问题.解法6:定比点差法设点B (-2,3),P (x 1,y 1),Q (x 2,y 2),又设PB =λBQ ,所以有-2-x 1=λ(x 2+2),3-y 1=λ(y 2-3).变形得-2-2λ=λx 2+x 1,3+3λ=λy 2+y 1①.因为点P ,Q 在椭圆C :y 29+x 24=1上,所以有ìíîïïïïy 129+x 124=1(λy 2)29+(λx 2)24=λ2,两式作差得(y 1-λy 2)(y 1+λy 2)9+(x 1+λx 2)(x 1-λx 2)4=(1-λ)·(1+λ).把①式代入得y 1-λy 23-x 1-λx 22=1-λ.再由①式把λx 2,λy 2消去得2y13-x 1=3+λ②,又因为k AP =y 1x 1+2,把②式代入消去x 1得k AP =3y 12y 1-3-3λ.又因为k AQ =y 2x 2+2把①、②式代入得k AQ =-3+3λ-y 1x 1+2=-3(3+3λ-y 1)2y 1-3-3λ.所以k AP +k AQ =3y 12y 1-3-3λ-3(3+3λ-y 1)2y 1-3-3λ=3.即线段MN 的中点的纵坐标为y M +y N 2=2k AP +2k AQ2=k AP +k AQ =3,所以线段MN 的中点是定点()0,3.评析:定比点差法的一般变形公式,椭圆x 2a 2+y 2b2=1(a >b >0),点A (x 1 , y 1),B (x 2, y 2)是椭圆上的点,且 AP =λ PB ,P (x 0 , y 0),··7则ìíîïïïïλx 2=x 0(1+λ)-x 1λy 2=y 0(1+λ)-y 12(x 0x 1a2+y 0y 1b 2-1)=(x 20a 2+y 20b 2-1)⋅(1+λ)点A (x 1,y 1)、B (x 2 ,y 2)的坐标都可以用只含有x 1(或y 1)的式子表示出来.思维视角四:借梯登高思维解法7:参数方程法设直线PQ 的参数方程为{x =-2+t cos αy =3+t sin α(t 为参数),(其中α为直线PQ 的倾斜角).代入椭圆方程y 29+x 24=1,化简可得(4+5cos 2α)t 2+12(2sin α-3cos α)t +36=0,设P 、Q 对应的参数分别为t 1,t 2,则t 1+t 2=12(3cos α-2sin α)4+5cos 2α,t 1⋅t 2=364+5cos 2α.又因为P (-2+t 1cos α,3+t 1sin α),Q (-2+t 2cos α,3+t 2sin α).又因为直线AP 的方程为y =3+t 1sin αt 1cos α()x +2,令x =0得y M =2(3+t 1sin α)t 1cos α,同理可得y N =2(3+t 2sin α)t 2cos α.故线段MN 的中点的纵坐标为y M +yN 2=3+t 1sin αt 1cos α+3+t 2sin αt 2cos α=3(t 1+t 2)t 1t 2cos α+2sin αcos α==3(3cos α-2sin α)3cos α+2sin αcos α=3.所以线段MN 的中点是定点()0,3.评析:充分利用直线分别与椭圆相交这一几何条件,利用参数方程实现了几何问题代数化,体现了解析几何的基本思想——“数形结合”,有效地减少了运算量,应用参数方程法是破解此类问题的一个有效策略.解法8:三角代换法因为cos θ=cos 2θ2-sin 2θ2cos 2θ2+sin 2θ2,sin θ=2sin θ2cos θ2cos 2θ2+sin 2θ2,令t =tan θ2,故cos θ=1-t 21+t 2,sin θ=2t 1+t 2,于是设椭圆的参数方程为ìíîïïïïx =2(1-t 2)1+t 2y =6t 1+t 2(t 为参数).设B (-2,3),P ,Q 对应的参数分别为t 1,t 2,由B ,P ,Q 三点共线可得6t 11+t 21-32(1-t 21)1+t 21+2=6t 21+t 22-32(1-t 22)1+t 22+2,化简得t 1+t 2=2.又知k AP =6t 11+t 212(1-t 21)1+t 21+2=3t 12,同理k AQ =3t 22,所以k AP +k AQ =32(t 1+t 2)=3.又因为A ()-2,0,设直线AP 的方程为y =k AP ()x +2,令x =0得y M =2k AP ,同理可得y N =2k AQ .故线段MN的中点的纵坐标为y M +y N 2=2k AP +2k AQ2=k AP +k AQ =3,所以线段MN 的中点是定点()0,3.评析:引入椭圆的参数方程,巧妙地实现了几何问题与三角函数的精彩联袂,解题方向清晰明了.当然也可以设P æèççöø÷÷2()1-t 121+t 12,6t 11+t 12,Q æèççöø÷÷2()1-t 221+t 22,6t 21+t 22,进而得到直线PQ 的方程为2(t 1+t 2)y -3(t 1t 2-1)x=6(1+t 1t 2),代入点B ()-2,3得到t 1+t 2=2.解法9:定比插参法设点B (-2,3),P (x 1,y 1),Q (x 2,y 2),直线AP ,AQ 的斜率分别为k 1,k 2,则有MN 的中点坐标为(0,k 1+k 2).因为B ,P ,Q 三点共线可··8得y 1-3x 1+2=y 2-3x 2+2,变形得y 1-3y 2-3=x 1+2x 2+2=λ,故可得{y 1=λy 2+3(1-λ)x 1=λx 2+2(λ-1),代入椭圆方程y29+x 24=1化简可得1λ=3+x 2-23y 2.又因为k 1+k 2=y 1x 1+2+y 2x 2+2=λy 2+3(1-λ)λx 2+2λ+y 2x 2+2=1x 2+2æèöø2y 2+3λ-3.把1λ=3+x 2-23y 2代入并化简可得k 1+k 2=1x 2+2æèöø2y 2+3λ-3=3,从而可得线段MN 的中点是定点()0,3.评析:解决此题的难点在于如何“设参”,焦点在于如何“用参”,重点在于如何“消参”,设参、用参、消参是解圆锥曲线问题的基本方法.因此定值问题的解题思路是:设参数→用参数来表示要求定值的式子→消参数.思维视角五:同构法解法10:同构法1设直线AP :x =m 1y -2,AQ :x =m 2y -2,PQ :x =m 0y +n .直线AP ,PQ 联立可得ìíîïïïïx =m 1n +2m 0m 1-m 0y =2+n m 1-m 0,代入椭圆方程得(9n 2-36)m 21+(72m 0+36m 0n )m 1+4(2+n )2=0,同理可得(9n 2-36)m 22+(72m 0+36m 0n )m 2+4(2+n )2=0.从而m 1,m 2为方程(9n 2-36)m 2+(72m 0+36m 0n )·m +4(2+n )2=0的两根,又由直线PQ 过点()-2,3,代入得n =-2-3m 0,代入上式得(81m 20+108m 0)m 2-108m 20m +36m 20=0.设直线AP ,AQ 的斜率分别为k 1,k 2,故MN 的中点坐标为(0,k 1+k 2).k 1+k 2=1m 1+1m 2=3.故MN 的中点是定点()0,3.评析:同构是一种常见的思想方法,是映衬着数学的对称和谐之美的数学方法,是“同理可得”的理论基础,是函数与方程思想的代名词与具体体现.在解题中灵活利用同构式,可以起到化繁为简的作用.解法11:同构法2设直线AP 的方程为y =k ()x +2,联立ìíîïïy =k ()x +2y 29+x 24=1,消去y 得()4k 2+9x 2+16k 2x +16k 2-36=0,当Δ>0时,由根与系数的关系得x A x P =16k 2-364k 2+9,又由x A =-2得到x P =-8k 2+184k 2+9,故P (-8k 2+184k 2+9,36k 4k 2+9).设直线PQ :y =m (x +2)+3,把点P 的坐标代入并化简可得12k 2-36k +36m +27=0.同理设直线AQ 的斜率为k 1,同理可得12k 12-36k 1+36m +27=0.所以k ,k 1是二次方程12x 2-36x +36m +27=0的两根,k +k 1=3,下同解法3.[2]评析:利用同构思想解题相当于寻找斜率满足的二次方程,可以收到事半功倍的效果.本题中方程有一个根是-2,利用根与系数的关系求出另一个根,减少了计算量.思维视角六:营造对称,方便计算解法12:构造对偶式法设点B (-2,3),P (x 1-2,y 1),Q (x 2-2,y 2),因为B ,P ,Q 三点共线可得y 1-3x 1=y 2-3x 2,变形可得y 1x 2-y 2x 1=3(x 2-x 1).构造对偶式y 1x 2+y 2x 1=(y 1x 2)2-(y 2x 1)2y 1x 2-y 2x 1=x 22(9x 1-94x 12)-x 12(9x 2-94x 22)3(x 2-x 1)=3x 1x 2.因为直线AP 的方程为y =y1x 1()x +2,令x =0得y M =2y 1x 1,同理可得y N =2y 2x 2.故线段MN 的··9中点的纵坐标为y M +y N2=y 1x 1+y 2x 2=y 1x 2+y 2x 1x 1x 2=3,所以线段MN 的中点是定点()0,3.评析:构造对偶式重在“构造”,在运用时要对已知等式进行整体观察,利用代数式的对称性,设法构造有利于计算的代数式,使问题简捷获解.对偶式主要是用于化简、转化定点、定直线的坐标表示,构造对偶式法在解题中具有广泛性、灵活性和简洁性的特点.3探究与拓展探究1:已知椭圆C :x 2a 2+y 2b 2=1()a >b >0,左顶点为A ()-a ,0,上顶点为B ()0,b ,过点R ()-a ,b 的直线交椭圆C 于P ,Q 两点,直线AP ,AQ 与y 轴的交点分别为M ,N ,证明:线段MN 的中点为上顶点B ()0,b .证明:设直线AP 的方程为y =k (x +a ),联立ìíîïïy =k ()x +a x 2a 2+y 2b2=1,消去y 得()a 2k 2+b 2x 2+2a 3k 2x +a 4k 2-a 2b 2=0,当Δ>0时,由根与系数的关系得x A x P =a 4k 2-a 2b 2a 2k 2+b 2,又由x A =-a 得到x P =ab 2-a 3k 2a 2k 2+b 2,故P (ab 2-a 3k 2a 2k 2+b 2,2ab 2k a 2k 2+b2).设直线PQ :y =m (x +a )+b ,把点P 的坐标代入并化简可得a 2bk 2-2ab 2k +2ab 2m +b 3=0.设直线AQ 的斜率为k 1,同理可得a 2bk 12-2ab 2k 1+2ab 2m +b 3=0.所以k ,k 1是二次方程a 2bx 2-2ab 2x +2ab 2m +b 3=0的两根,k +k 1=2b a.设直线AP 的方程为y =k ()x +a ,令x =0得y M =ka ,同理可得y N =k 1a .故线段MN 的中点的纵坐标为y M +y N 2=ka +k 1a2=2b a ⋅a 2=b ,所以线段MN 的中点是上顶点B ()0,b .由此可见,2023年全国高考乙卷理科第20题是本结论的特殊情况.探究2:已知椭圆C :x 2a 2+y 2b2=1()a >b >0,左顶点为A ()-a ,0,上顶点为B ()0,b ,过点R ()-a ,b 的直线交椭圆C 于P ,Q 两点,直线BP ,BQ 与x 轴的交点分别为M ,N ,证明:线段MN 的中点为左顶点A ()-a ,0.证明过程与探究1类似.探究3:已知椭圆C :x 2a 2+y 2b 2=1()a >b >0,左顶点为A ()-a ,0,上顶点为B ()0,b ,点R 是直线x =-a 上的任意一点,过点R 作椭圆C 的两条切线,分别交椭圆C 于A ,B 两点,过点R 的直线交椭圆C 于P ,Q 两点,直线AB ,AP ,AQ 的斜率分别为k ,k 1,k 2.证明:k 1+k 2=2k .简证:设R ()-a ,m ,则AB 是R 的切点弦所在的直线,故直线AB 的方程为-ax a 2+my b 2=1,所以k =b 2ma .后面证明过程与探究1的方法类似,得到k 1+k 2=2b 2am.故有k 1+k 2=2k .4往年高考试题链接变式1:如图1,过点P 作y 轴的平行线,分别与AE ,AQ ,交于点T ,H ,满足 PT =TH .证明:直线HQ 过定点.便得到2022年全国乙卷理科第20题的模型.变式2:过点P 作x 轴的垂线,分别EBPTHA N Q -22图1xy(下转第13页)O ··10cos (B +π4)=3sin A -cos(π-A )=3sin A+cos A =2sin (A +π6).于是0<A <3π4,故π6<A +π6<11π12,从而当A +π6=π2,即A =π3时,2sin (A +π6)取得最大值2.综上所述,3sin A -cos(B +π4)的最大值为2,此时A =π3,B =5π12.点评:本题主要考查三角函数的基本公式、解斜三角形的基础知识和基本运算能力.高考中有关三角函数求值问题,一方面考查纯三角函数求值;另一方面就是结合三角形考查求角以及求三角函数值;再就是在知识交汇点出题,三角函数的最值与三角形的结合.通过对以上几例的解析,希望对同学们学好、用活这部分知识有所帮助.与AE ,AQ 交于点T ,H .证明:T 为线段PH 的中点.试题链接:(2022年全国乙卷理科第20题)已知椭圆E 的中心为坐标原点,对称轴为x 轴、y 轴,且过A ()0,-2,B æèöø32,-1两点.(Ⅰ)求E 的方程;(Ⅱ)设过点P ()1,-2的直线交E 于M ,N 两点,过M 且平行于x 轴的直线与线段AB 交于点T ,点H 满足 MT =TH .证明:直线HN 过定点.不难发现,2023年全国高考乙卷理科第20题的第二问与2022年全国乙卷理科第20题极其相似,可以看作“姊妹题”.5解题感悟圆锥曲线中的定值、定点问题淋漓尽致地体现了“几何”与“代数”的深度融合,“动态”与“静态”的和谐统一.定点、定值问题都是探求“变中有不变的量”.因此要注意挖掘问题中各个量之间的相互关系,恰当地运用函数与方程、转化与化归、数形结合、分类讨论、特殊到一般、相关点法、设而不求、换元、消元等基本思想方法.该类问题综合性强,方法灵活,在解题过程中,既有探索性的历程,又有严密的逻辑推理及复杂的运算,成为考查学生数学核心素养的一道亮丽的风景线.文中的解法各有千秋,展示了各种解法的思维轨迹,凸显了思维的灵活性.从深度和广度上做文章,进行了系统性探究、整合、推广,实现了从“一道题”到“一类题”质的飞跃,进而提升学生的核心素养.参考文献[1]陈熙春.2022年全国高考乙卷第20题的解法探究与拓展[J ].理科考试研究,2022(11):16-20.[2]陈熙春.2021年全国新高考I 卷第21题的解法探究与拓展[J ].数理化学习,2022(3):8-13.基金项目:宁夏教育科学规划“基础教育质量提升行动”专项课题“公费师范生教师队伍建设实践研究—以宁夏六盘山高级中学为例”(编号:NXJKG22174)成果.(上接第10页)··13。
3用分离常数法解2014年高考题
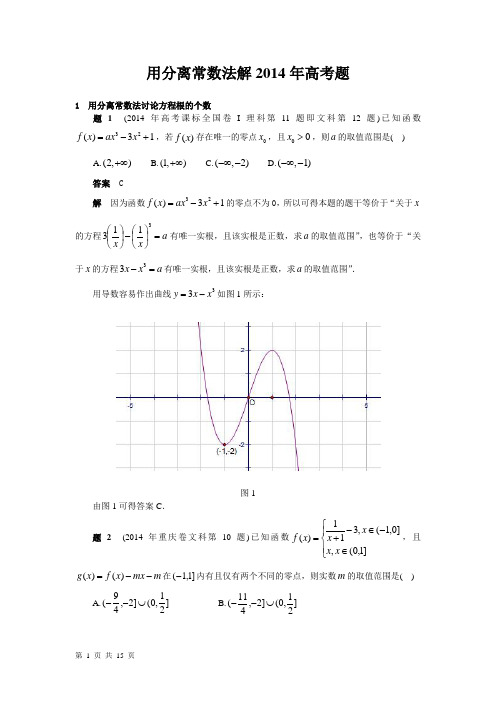
用分离常数法解2014年高考题1 用分离常数法讨论方程根的个数题1 (2014年高考课标全国卷I 理科第11题即文科第12题)已知函数32()31f x ax x =-+,若()f x 存在唯一的零点0x ,且00x >,则a 的取值范围是( )A.(2,)+∞B.(1,)+∞C.(,2)-∞-D.(,1)-∞- 答案 C解 因为函数32()31f x ax x =-+的零点不为0,所以可得本题的题干等价于“关于x的方程a x x =⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛3113有唯一实根,且该实根是正数,求a 的取值范围”,也等价于“关于x 的方程a x x =-33有唯一实根,且该实根是正数,求a 的取值范围”.用导数容易作出曲线33x x y -=如图1所示:图1由图1可得答案C .题2 (2014年重庆卷文科第10题)已知函数⎪⎩⎪⎨⎧∈-∈-+=]1,0(,]0,1(,311)(x x x x x f ,且m mx x f x g --=)()(在]1,1(-内有且仅有两个不同的零点,则实数m 的取值范围是( )A.]21,0(]2,49(⋃--B.]21,0(]2,411(⋃--C.]32,0(]2,49(⋃--D.]32,0(]2,411(⋃-- 答案 A 解 设)11(1)()(≤<-+=x x x f x h ,题意即曲线)(x h y =与直线m y =有两个公共点. 因为⎪⎪⎩⎪⎪⎨⎧≤<+-≤<-⎪⎭⎫⎝⎛-+=)10(111)01(2311)(2x x x x x h ,由复合函数单调性的判别法则“同增异减”可得函数)(x h 在⎥⎦⎤ ⎝⎛--31,1上是减函数,在]1,0(,0,31⎥⎦⎤⎢⎣⎡-上均是增函数,从而可作出曲线)(x h y =的草图如图2所示,由此可得答案.图2题3 (2014年高考江苏卷第13题)已知()f x 是定义在R 上且周期为3的函数,当[0,3)x ∈时,21()22f x x x =-+,若函数()y f x a =-在区间[]3,4-上有10个零点(互不相同),则实数a 的取值范围是 .答案 10,2⎛⎫ ⎪⎝⎭解 作出函数21()2(03)2f x x x x =-+≤<的图象如图3所示:图3有1(0)2f =;当且仅当1x =时,1()=2f x 极大;7(3)=2f .关于x 方程()0f x a -=即()=f x a 在[3,4]x ∈-上有10个零点,即曲线()y f x =与直线y a =在[3,4]-上有10个交点.因为函数()f x 的周期为3,所以直线y a =与曲线212(03)2y x x x =-+≤<有4个交点,得所求实数a 的取值范围是10,2⎛⎫⎪⎝⎭. 题4 (2014年高考天津卷理科第14题)已知函数f (x )=|x 2+3x |,x ∈R .若方程f (x )-a |x -1|=0恰有4个互异的实数根,则实数a 的取值范围为________.答案 (0,1)∪(9,+∞)解 因为1=x 不是原方程的根,所以设x x '=-1后可得本题等价于:若关于x 的方程a xx =++54恰有4个互异的实根,则实数a 的取值范围为________. (1)作出对勾函数xx x f 4)(+=的图象如图4所示:图4(2)再由平移可作出函数54)(++=xx x g 的图象如图5所示:图5(3)作出函数54)(++=xx x h 的图象如图6所示:图6因为关于x 的方程a x x =++54的互异实根个数即两条曲线a y xx y =++=,54公共点的个数,所以由图6可得结论:①当0<a 时,原方程互异实根的个数是0;②当0=a 或91<<a 时,原方程互异实根的个数是2; ③当1=a 或9时,原方程互异实根的个数是3;④当10<<a 或9>a 时,原方程互异实根的个数是4. 所以本题的答案是(0,1)∪(9,+∞).题5 (2014年高考天津卷文科第14题)已知函数f (x )=⎩⎪⎨⎪⎧|x 2+5x +4|,x ≤0,2|x -2|,x >0.若函数y=f (x )-a |x |恰有4个零点,则实数a 的取值范围为________.答案 (1,2)简解 因为0=x 不是函数y =f (x )-a |x |的零点,所以可得本题等价于:若两条曲线a y x xx x x y =⎪⎪⎩⎪⎪⎨⎧>-<++=,)0(122)0(54恰有4个公共点,则实数a 的取值范围为________.同题4的解法,可作出曲线⎪⎪⎩⎪⎪⎨⎧>-<++=)0(122)0(54x xx x x y 如图7所示:图7由图7可得结论:①当0<a 时,原方程互异实根的个数是0;②当0=a 或2≥a 时,原方程互异实根的个数是3; ③当10<<a 时,原方程互异实根的个数是6; ④当1=a 时,原方程互异实根的个数是5; ⑤当21<<a 时,原方程互异实根的个数是4. 所以本题的答案是(1,2).题6 (2014年高考天津卷理科第20(1)题)设f (x )=x -a e x (a ∈R ),x ∈R .已知函数y =f (x )有两个零点x 1,x 2,且x 1<x 2,求a 的取值范围.解 题设关于x 的方程a x x=-e有两个零点.用导数可得函数xx x g -=e )(在),1(),1,(+∞-∞上分别是增函数、减函数,且0)(lim ,e 1)1(,)(lim ==-∞=+∞→-∞→x g g x g x x .由此可作出函数)(x g 的图象如图8所示:图8所以所求答案为⎪⎭⎫⎝⎛e 1,0.题7 (2014年高考课标全国卷II 文科第21题)已知函数32()32f x x x ax =-++,曲线()y f x =在点(0,2)处的切线与x 轴交点的横坐标为2-.(1)求a ;(2)证明:当1k <时,曲线()y f x =与直线2y kx =-只有一个交点. 解 (1)1a =.(2)题意即证“当1k <时,关于x 的方程3232=2x x ax kx -++-即有唯一实根”.设24g()31x x x x=-++,得22115248()(2)x g x x x ⎛⎫++⎪⎝⎭'=-,所以函数()g x 在)2,0(),0,(-∞上均是减函数,在),2(+∞上是增函数.由此可作出函数24g()31x x x x=-++的图象如图9所示:图9由图9可得欲证成立.题8 (2014年高考北京卷文科第20题)已知函数3()23f x x x =-.(1)求()f x 在区间[2,1]-上的最大值;(2)若过点(1,)P t 存在3条直线与曲线()y f x =相切,求t 的取值范围;(3)问过点(1,2),(2,10),(0,2)A B C -分别存在几条直线与曲线()y f x =相切?只需写出结论.解 (1)(3)略.(2)2()63f x x '=-.当点P 在曲线()y f x =上即1-=t 时:又当点(1,1)P -是切点时,曲线()y f x =过点P 的切线是1条. 又当点(1,1)P -不是切点时,可设切点为3(,23)(1)P P P P x x x x -≠,得3223163(1)1P P P P P x x x x x -+=-≠-12P x =-所以此时过点P 的切线是1条.得过点P 存在2条直线与曲线()y f x =相切,不合题意.所以1-≠t ,即点P 不在曲线()y f x =上.可设切点为3(,23)PP P x x x '''-,得 3223631PP PPx x t x x ''--'=-'- 324630PP x x t ''-++= 题意即这个一元三次方程也即关于x 的一元三次方程)1(36423-≠=-+-t t x x 有三个实根.用导数知识可作出函数364)(23-+-=x x x g 的图象如图10所示:图10由图10可得所求t 的取值范围是)1,3(--. 题9 (2014年广东卷文科第21题)已知函数321()1(3f x x x ax a =+++∈R ). (1)求函数()f x 的单调区间;(2)当0a <时,试讨论是否存在0110,,122x ⎛⎫⎛⎫∈⋃ ⎪ ⎪⎝⎭⎝⎭,使得01()2f x f ⎛⎫= ⎪⎝⎭. 解 (1)略. (2)方程0011()22f x f x ⎛⎫⎛⎫=≠⎪⎪⎝⎭⎝⎭,即 323200001111111=1332222x x ax a x ⎛⎫⎛⎫⎛⎫⎛⎫++++++≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 3232000011111032222x x a x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+-+-=≠⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦2000011111032422x x x a x ⎛⎫⎛⎫⎛⎫+++++=≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2000141412702x x a x ⎛⎫+++=≠ ⎪⎝⎭ ①所以 “当0a <时,存在0110,,122x ⎛⎫⎛⎫∈⋃ ⎪⎪⎝⎭⎝⎭,使得01()2f x f ⎛⎫= ⎪⎝⎭”⇔“当0a <时,方程①在0110,,122x ⎛⎫⎛⎫∈⋃ ⎪⎪⎝⎭⎝⎭时有解”⇔ “当0a <时,关于0x 的方程2000114147120,,122x x a x ⎛⎫⎛⎫⎛⎫++=-∈⋃ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭有解”因为函数2000011()41470,,122g x x x x ⎛⎫⎛⎫⎛⎫=++∈⋃ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值域是)25,15()15,7(⋃,所以“当0a <时,存在0110,,122x ⎛⎫⎛⎫∈⋃ ⎪⎪⎝⎭⎝⎭,使得01()2f x f ⎛⎫= ⎪⎝⎭”⇔ ⇔⋃∈-)25,15()15,7(12a 25557,,124412a ⎛⎫⎛⎫∈--⋃-- ⎪ ⎪⎝⎭⎝⎭由此得本题的答案是:当0a <时,当且仅当25557,,124412a ⎛⎫⎛⎫∈--⋃-- ⎪ ⎪⎝⎭⎝⎭时,存在0110,,122x ⎛⎫⎛⎫∈⋃ ⎪ ⎪⎝⎭⎝⎭,使得01()2f x f ⎛⎫= ⎪⎝⎭.注 由以上解法还可得下面的结论: 若3211()1(32f x x x ax x a ⎛⎫=+++≠∈ ⎪⎝⎭R ),则 (1)当且仅当61>a 时,关于x 的方程1()2f x f ⎛⎫= ⎪⎝⎭无解; (2)当且仅当67,61-=a 时,关于x 的方程1()2f x f ⎛⎫= ⎪⎝⎭有唯一解; (3)当且仅当61<a 且67-≠a 时,关于x 的方程1()2f x f ⎛⎫= ⎪⎝⎭有且仅有两个解.题10 (2014年高考山东卷理科第20题)设函数()2e 2ln (x f x k x k x x ⎛⎫=-+ ⎪⎝⎭为常数,e 2.71828=是自然对数的底数).(1)当0k ≤时,求函数()f x 的单调区间;(2)若函数()f x 在()0,2内存在两个极值点,求k 的取值范围.解 (1)()3e (2)(>0)x kxf x x x x -'=-. 当0k ≤时,得3e 0,0x kx x ->>,所以()f x '与2x -同号,得函数()f x 的单调增区间、减区间分别是(0,2),(2,)+∞.(2)由(1)的结论知,()22e (0<2)x x f x k x x x ⎛⎫-'=-< ⎪⎝⎭,()f x '与e xk x-同号.设()e (0<2)x g x x x =<,得()21e (0<2)x x g x x x-'=<. 所以函数()g x 在(0,1),(1,2)上分别是减函数、增函数.又因为()20e lim ,(2)2x g x g +→=+∞=,所以函数()f x '在(0,2)有两个零点2e e 2k ⇔<<. 设这两个零点分别是1212,(02)x x x x <<<,还可证它们分别是函数()f x 的极小值点、极大值点.所以所求k 的取值范围是2e,e 2⎛⎫⎪⎝⎭.2 用分离常数法求解恒成立、存在性问题题11 (2014年高考辽宁卷文科第12题)当[2,1]x ∈-时,不等式32430ax x x -++≥恒成立,则实数a 的取值范围是( )A .[5,3]--B .96,8⎡⎤--⎢⎥⎣⎦C .[6,2]--D .[4,3]--答案 C解 分10,0,02≤<=<≤-x x x 三种情形讨论,并用分离常数法,可求得答案. 题12(2014年高考湖南卷理科第10题)已知函数221()(0)()ln()2x f x x e x g x x x a =+-<=++与的图象上存在关于y 轴对称的点,则a 的取值范围是( ) A.1(,)e -∞ B.(,)e -∞ C.1(,)e e - D.1(,)e e -答案 B解 题意即关于x 的方程221e ln()(0)2xx x a x x +-=+-<也即1e 2e (0)x x a x -+=<有解.易知函数1e 2()=e(0)x h x x x -+<是增函数(两个增函数之和是增函数),所以e )0(=<h a .题13 (2014年高考课标全国卷II 理科第12题)设函数()3sin x f x mπ=.若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦,则m 的取值范围是( )A.(,6)(6,)-∞-⋃+∞B.(,4)(4,)-∞-⋃+∞C.(,2)(2,)-∞-⋃+∞D.(,1)(4,)-∞-⋃+∞ 答案 C 解 ()3c o s x f x m m ππ'=.得()0003cos 0,(2x m f x x mk k m m ππ'===+∈Z )(还可得这样的0x 一定是函数()f x 的极值点).0x ∃满足()22200x f x m +<⎡⎤⎣⎦,即k ∃∈Z 满足221312k m ⎛⎫+<- ⎪⎝⎭,也即22min1312k m ⎡⎤⎛⎫+<-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,还即221312m ⎛⎫<- ⎪⎝⎭,进而可得答案.题14 (2014年高考浙江卷理科第13题)当实数x ,y 满足⎪⎩⎪⎨⎧≥≤--≤-+101042x y x y x 时,14ax y ≤+≤恒成立,则实数a 的取值范围是________.答案 31,2⎡⎤⎢⎥⎣⎦解 所给区域是以三点3(1,0),1,,(2,1)2⎛⎫ ⎪⎝⎭为顶点的三角形,所以12x ≤≤. “14ax y ≤+≤恒成立”即“41y y a x x--≤-≤恒成立”,由斜率的几何意义可得答案.题15 (2014年高考江苏卷第19(2)题)已知函数()e e x xf x -=+,其中e 是自然对数的底数.若关于x 的不等式()e1xmf x m -≤+-在(0,)+∞上恒成立,求实数m 的取值范围.解 设e (0)xt x =>,得题设即21(1)1t m t t t --≥>-+恒成立.可得0m <,所以题设即11112(1)1t t m t -≤-++>-恒成立,可得114m -≤,得实数m 的取值范围1,3⎛⎤-∞- ⎥⎝⎦.题16 (2014年高考陕西卷文科第21题)设函数()ln ,mf x x m x=+∈R . (1)当e(e m =为自然对数的底数)时,求()f x 的极小值;(2)讨论函数()'()3xg x f x =-零点的个数;(3)若对任意()()0,1f b f a b a b a->><-恒成立,求m 的取值范围.解 (1)略.(2)用分离常数法可求得答案: 当0m ≤或23m =时,函数()g x 零点的个数是1;当203m <<时,函数()g x 零点的个数是2;当23m >时,函数()g x 零点的个数是0. (3)题设即()()(0f a a f b b a b ->-<<恒成立,也即函数()()l n (0)mh x f x x x x x x=-=+->是减函数. 用分离常数法可求得m 的取值范围是1,4⎡⎫+∞⎪⎢⎣⎭. 练习1.(2013年高考陕西卷理科第21(2)题)设x >0,讨论曲线2e ,(0)x y y mx m ==>公共点的个数.2.(2013年高考新课标卷I 理科第21题)已知函数)(e )(,)(2d cx x g b ax x x f x +=++=.若曲线)(x f y =和曲线)(x g y =都过点)2,0(P ,且在点P 处有相同的切线24+=x y .(1)求d c b a ,,,的值;(2)若2-≥x 时,)()(x kg x f ≤,求k 的取值范围.3.(2013年高考福建卷文科第22题)已知函数∈+-=a ax x f x(e 1)(R ,e 为自然对数的底数).(1)若曲线)(x f y =在点))1(,1(f 处的切线平行于x 轴,求a 的值; (2)求函数)(x f 的极值;(3)当1=a 时,若直线1:-=kx y l 与曲线)(x f y =没有公共点,求k 的最大值. 答案:1.当4e 02<<m 时,有0个公共点;当 4e 2=m 时,有1个公共点;当4e 2>m 有2个公共点.2.(1)2,4====d c b a .(2)题设即)2)(1(e 2242-≥+≤++x x k x x x恒成立.设)1(e 24)(2+++=x x x x h x ,可得题设即⎩⎨⎧->≤-<≤-≥)1(2)()12(2)(x k x h x k x h 恒成立.得22)1(e )2()(++-='x x x x h x ,所以: 当12-<≤-x 时,0)(≥'x h 恒成立,)12)((-<≤-x x h 是增函数,所以)12(2)(-<≤-≥x k x h 恒成立即2e ,2)2(≤≥-k k h .当1->x 时,可得2)0()]([max ==h x h ,所以)1(2)(->≤x k x h 恒成立即1,22≥≤k k .所以所求k 的取值范围是]e 1,[2. 3.(1)e .(2)略.(3)题意即方程xx kx e111+-=-也即1e )1(=-xx k 无解,1=k 满足. 当1≠k 时,即方程11e -=k x x无解.用导数可求得函数x x y e =的值域是⎪⎭⎫⎢⎣⎡+∞-,e 1,所以e111-<-k ,即e 11,e 10->>->->k k . 总之,k 的取值范围是]1,e 1(-,所以k 的最大值是1.。
2014年高考试题分项版解析:专题08农业

2014年高考试题分项版解析:专题08农业2014年高考试题分项版解析专题8 农业(2014新课标II卷)图4示意某岛的地理位置,读图4,完成10-11题。
10.图示岛屿西南部降水丰沛,主要是因为()①盛行西风②地形抬升③暖流增湿④反气旋控制A.①②B.②③C.③④D.①④11.下列农业生产类型中,最适宜在图示岛屿发展的是()A.水田农业B.迁移农业C.种植园农业D.乳畜业【答案】10. A、11.D【解析】地图信息显示该岛纬度大部分位于南纬42°—46°,地处太平洋中,中部山脉海拔较高(超过3000米)、大致呈东北—西南走向分布,河流、湖泊众多。
10、南纬42°—46°,地处西风带,来自海洋的湿润气流受高达山脉阻挡抬升,形成地形雨,因此降水丰富。
岛屿西南部受西风漂流(寒流)影响较大,而非暖流。
反气旋(高压)控制、降水少,错误。
11、降水丰沛、气候温和(南纬42°—46°,岛屿、气候海洋性强),多山地,适合草类生长,因地制宜发展畜牧业最合适。
如果能判断出是新西兰,则直接选D。
【考察能力】读图能力(定位、定气压带风带、洋流、判断地形、根据河流和湖泊的数量判断降水的多少)【地理原理】降水的影响因素(纬度、海陆、地形、大气环流、洋流、)农业地域类型的分布(2014广东卷)9.图4为根据统计资料计算出的我国1980-2010年水稻产量重心移动方向图。
若下列地区的水稻产量均有增加,则对图示水稻产量重心移动趋势贡献最大的地区是A、西南地区 B东北地区 C、华南地区 D、西北地区(2014重庆卷)素有“欧洲粮仓”之称的乌克兰在1992-2007年期间耕地总量减少2.78%,但人均耕地增加8.32%。
据此完成3-4题。
3.1992-2007年乌克兰耕地的变化标明这一时期该国A.人口数量减少B.城市化率提高C.土壤质量下降D.粮食单产提高4.1992-2007年乌克兰人均耕地增加最可能引起该国A.人均粮食产量增加B.农业生产投入增加C.粮食进口总量增加D.亩均农业产值增加【答案】3.A 4.A【解析】试题分析:3.乌克兰在1992-2007年期间耕地总量减少2.78%,但人均耕地增加8.32%,则说明该国人口总数在下降,且超过耕地面积的下降速度,与城市化率没有必然联系,土壤质量是否下降也不能确定,粮食单产提高与耕地变化无关。
第14讲 函数的零点、隐零点、极值点偏移问题(学生版) 备战2025年高考数学一轮复习(天津专用)
第14讲函数的零点、隐零点、极值点偏移问题(6类核心考点精讲精练)1.5年真题考点分布【命题规律】本节内容是天津高考卷的必考内容,设题稳定,难度较低,分值为16分【备考策略】1.理解、掌握函数零点与方程的关系2.能掌握函数零点的求解方法3.具备数形结合的思想意识,会借助函数图像的交点解决函数的零点问题4.会解隐零点与极值点偏移问题【命题预测】本节内容是天津高考卷的必考内容,一般给出函数的解析式解决函数的零点相关问题。
知识讲解知识点一.函数零点个数问题用导数研究函数的零点,一方面用导数判断函数的单调性,借助零点存在性定理判断;另一方面,也可将零点问题转化为函数图象的交点问题,利用数形结合来解决,对于函数零点个数问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围,从图象的最高点、最低点、分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等。
但需注意探求与论证之间区别,论证是充要关系,要充分利用零点存在定理及函数单调性严格说明函数零点个数.知识点二.零点存在性赋值理论1.确定零点是否存在或函数有几个零点,作为客观题常转化为图象交点问题,作为解答题一般不提倡利用图象求解,而是利用函数单调性及零点赋值理论.函数赋值是近年高考的一个热点,赋值之所以“热”,是因为它涉及到函数领域的方方面面:讨论函数零点的个数(包括零点的存在性,唯一性);求含参函数的极值或最值;证明一类超越不等式;求解某些特殊的超越方程或超越不等式以及各种题型中的参数取值范围等,零点赋值基本模式是已知f(a)的符号,探求赋值点m(假定m<a)使得f(m)与f(a)异号,则在(m,a)上存在零点2.赋值点遴选要领:讲选赋值点须做到三个确保:确保参数能取到它的一切值;确保赋值点x0落在规定区间内;确保运算可行三个优先:(1)优先常数赋值点;(2)优先借助已有极值求赋值点;(3)优先简单运算.知识点三.隐零点问题1.函数零点按是否可求精确解可以分为两类:一类是数值上能精确求解的,称之为“显零点”;另一类是能够判断其存在但无法直接表示的,称之为“隐零点”2.利用导数求函数的最值或单调区间,常常会把品值问题转化为求导函数的零点问题、若导数零点存在,但无法求出,我们可以设其为0,再利用导函数单调性确定0所在区间,最后根据f’(0)=0,研究f(0),我们把这类问题称为隐零点问题.注意若f(x)中含有参数a,关系式f(0)=0是关于0,a的关系式,确定0的合适范围,往往和a的范围有关.考点一、函数零点个数问题1.(2024·四川凉山·二模)若=Lin+cos−1,∈−π2,π,则函数的零点个数为()A.0B.1C.2D.32.(2024高三·全国·专题练习)函数f(x)=x-sin x的零点个数为.1.(2024高三·全国·专题练习)已知函数f(x)=x3-x-1.(1)求证:函数f(x)在区间(1,2)内恰有一个零点;(2)将(1)中的零点记为a,且a4r14n的值.2.(2024·山西晋中·模拟预测)已知函数=ln+sin+sinπ10.(1)求函数在区间1,e上的最小值;(2)判断函数的零点个数,并证明.考点二、数形结合法研究零点问题1.(2023·四川甘孜·一模)设定义在上的函数是偶函数,且+π=−π,'是的导函数,当∈0,π时,0<<1;当∈0,π且≠π2时,π2'>0,则函数=−sin在−2π,2π上的零点个数为()A.2B.4C.5D.82.(2024高三下·全国·专题练习)已知是定义在R上的奇函数,当>0时,=e3−3ln,则函数的零点个数为()A.2B.3C.4D.51.(24-25高三上·广东·开学考试)若函数op=sin−cos+B+1(>0),∈[0,2π]的图象与直线=0,=π,=0所围成的封闭图形的面积为12π2+π+2.(1)求的值;(2)求函数op单调区间及最值;(3)求函数op=op−在区间∈[0,2π]上的零点个数.2.(2024·浙江·模拟预测)已知函数=e+sin−−1.(1)当=12时,求的单调区间;(2)当=1时,判断的零点个数.3.(22-23高三上·全国·阶段练习)已知函数op=133−2B2+2,其中≥0.(1)若的极小值为−286,求单调增区间;(2)讨论的零点个数.1.(2024·山东聊城·一模)已知函数=e−1,=ln−B,=e−ln−1.(1)求的单调递增区间;(2)求的最小值;(3)设ℎ=−,讨论函数ℎ的零点个数.2.(2024·湖南·二模)已函数op=3+B2+B+os s∈p,其图象的对称中心为(1,−2).(1)求−−的值;(2)判断函数的零点个数.1.(2024·河南郑州·三模)已知函数=e B−.(1)若=2,求在1,1处的切线方程;(2)讨论的零点个数.2.(2024·湖北·模拟预测)函数op=x−−1(∈p.(1)当=1时,证明:op≥0;(2)讨论函数op的零点个数.3.(23-24高三上·河北邢台·阶段练习)已知函数=23−32−12+5.(1)求的极值;(2)讨论函数=−的零点个数.4.(23-24高三上·陕西·阶段练习)已知函数=3ln+122−4+1.(1)求的图象在=2处的切线方程;(2)讨论函数=−的零点个数.1.(2024·山西·三模)已知函数op=2+1,>0e,≤0,若函数op=op−+o∈p恰有一个零点,则的取值范围是.2.(2018·全国·高考真题)已知函数=-B2.(1)若=1,证明:当≥0时,≥1;(2)若在(0,+∞)只有一个零点,求的值.1.(2017·全国·高考真题)已知函数=e2+−2e−(1)讨论的单调性;(2)若有两个零点,求的取值范围.2.(2024·内蒙古包头·三模)设函数=ln+−.(1)当=1时,求的最小值;(2)若恰有两个零点,求a的取值范围.考点五、隐零点问题1.22-23高三上·河南洛阳·开学考试)(1)证明不等式:e K2>ln(第一问必须用隐零点解决,否则不给分);(2)已知函数op=(−2)e+o−1)2有两个零点.求a的取值范围.(第二问必须用分段讨论解决,否则不给分)2.(23-24高三上·海南省直辖县级单位·阶段练习)已知函数=2−En∈R.(1)判断函数的单调性;(2)设=2−−2ln,证明:当=2时,函数有三个零点.1.(22-23高三上·河北·期中)已知函数=2e+o2−lnp+.(1)若=−2e−1,求的单调区间;(2)记函数=−2−En+1++4,若+1≥恒成立,试求实数的取值范围.2.(23-24高三下·广东广州·阶段练习)已知函数=e−2.(1)求函数的极值;(2)讨论函数=−sin在R上的零点个数.(参考数据:sin1≈0.84,cos1≈0.54)3.(2024·山东·模拟预测)已知函数=14e−.(1)求曲线=在点1,1处的切线在轴上的截距;(2)探究的零点个数.4.(23-24高三上·福建莆田·阶段练习)已知函数=e−sin.(1)求在0,0处的切线方程;(2)求证:当∈−π,+∞时,函数有且仅有2个零点.1.(2024高三·全国·专题练习)设函数op=e−12e2−13(−1)3+5e2,∈[0,+∞).(1)判断函数op的单调性;(2)若1≠2,且1+2=6e,求证:1+2<2.2.(22-23高三上·黑龙江哈尔滨·期末)已知函数=B2,=1−ln.(1)若对于任意∈0,+∞,都有<,求实数的取值范围;(2)若函数=−有两个零点1,2,求证:11+12>2.1.(23-24高三上·江苏连云港·阶段练习)已知函数=ln+12B2−+1∈.(1)当=1时,求函数=的零点个数.(2)若关于的方程=12B2有两个不同实根1,2,求实数的取值范围并证明1⋅2>2.2.(22-23高三上·河北唐山·阶段练习)已知函数=−1ln−2+B∈.(1)若函数='有两个零点,求的取值范围;(2)设1,2是函数的两个极值点,证明:1+2>2.3.(21-22高三上·广东清远·期末)已知函数op=K1−o−1).(1)讨论op的零点个数.(2)若op有两个不同的零点1,2,证明:1+2>4.4.(21-22高三上·北京昌平·期末)已知函数op=163−2B+8ln.(1)若函数op在定义域内单调递增,求实数的取值范围;(2)若函数op存在两个极值点1,2,求证:1+2>4.1.(22-23高三上·天津和平·期末)设函数op=e−e−,≥0−2−2−4,<0,若函数=−B恰有两个零点,则实数的取值范围为()A.0,2B.0,2C.2,+∞D.2 2.(2020·重庆·一模)已知为R上的可导函数,当≠0时,'+>0,若=+1,则函数的零点个数为()A.0B.1C.2D.0或23.(21-22高三上·天津河北·期中)已知函数=En−1,则的零点所在的区间是()A.0,1B.1,2C.2,3D.3,44.(2024高三·全国·专题练习)函数f(x)=2x+x-2的零点个数是()A.0B.1C.2D.36.(23-24高三下·重庆·阶段练习)已知函数=2+B+e,若函数有两个不同零点,则极值点的个数为.7.(23-24高三上·天津滨海新·阶段练习)已知函数=133−2+1.(1)求曲线=在点1,1处的切线方程;(2)求函数在−2,2上的单调区间、最值.(3)设=−在−2,2上有两个零点,求的范围.1.(23-24高三上·天津南开·阶段练习)若函数=+2−En−−2,(>0且≠1)有两个零点,则m的取值范围()A.−1,3B.−3,1C.3,+∞D.−∞,−12.(20-21高三上·天津南开·阶段练习)设函数f(x)=ln, >0,e(+1),≤0,若函数g(x)=f(x)–b有两个零点,则实数b的取值范围是()A.(–12,0)B.(–12,0]C.(–12,0]∪(1,+∞)D.(–12,1) 3.(2023·吉林·一模)已知函数=eK1,>0且≠1,−−,<0且≠−1,若函数op=2(p−B(p−e4有4个零点.则实数的取值范围是.4.(2023·天津河北·一模)设∈,函数=B2−+1,<0e−B,≥0,若恰有两个零点,则的取值范围是.5.(23-24高三上·天津河北·期中)已知函数=23−22+1.(1)求曲线=在点1,1处的切线方程;(2)求函数=的单调区间和极值;(3)若函数=−在区间−1,1上有一个零点,求实数的取值范围.6.(22-23高三上·天津·期中)已知函数=3+B2+B+在点1,2处的切线斜率为4,且在=−1处取得极值.(1)求函数的单调区间;(2)若函数=+−1恰有两个零点,求实数m的取值范围.7.(21-22高三上·天津东丽·阶段练习)已知函数op=B3−62+1,∈.(1)若=2,求函数op的单调区间;(2)若=−4,求函数在区间[−2,3]的最值;(3)若op恰有三个零点,求a的取值范围.1.(2023·全国·高考真题)函数=3+B+2存在3个零点,则的取值范围是()A.−∞,−2B.−∞,−3C.−4,−1D.−3,02.(2022·全国·高考真题)已知函数op=B−1−(+1)ln.(1)当=0时,求op的最大值;(2)若op恰有一个零点,求a的取值范围.3.(2020·全国·高考真题)已知函数op=3−B+2.(1)讨论op的单调性;(2)若op有三个零点,求的取值范围.4.(2020·全国·高考真题)已知函数op=−o+2).(1)当=1时,讨论op的单调性;(2)若op有两个零点,求的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
陕西蓝田城关中学 靳小平 题目:设 f ( x) x ae x (a R) , x R. 已知函数 y f ( x) 有两个零点 x1 , x2 ,且 x1 x2 . (I)求 a 的取值范围 (II)证明:
x2 随着 a 的减小而增大; x1
1 令 k (a, x) x ae x ,即对任意 a1 , a2 (0, ) , x R 且 a1 a2 ,有 k (a1 , x) k (a2 , x) e
又由(I)知,在区间 (, ln a) 内 y f ( x) 为增函数,在区间 ( ln a, ) 内 y f ( x) 为减函 数,设 k (a1 , x) 0 有两解 x1 , x2 ,且 0 x1 ln a1 , ln a2 x2 , k (a2 , x) 0 有两解 x3 , x4 ,且
(III) 证明: x1 x2 随着 a 的减小而增大. 解析:(I) f ( x) 1 ae x ,当 a 0 时, f ( x) 0 , y f ( x) 至多有一个零点,与题意不符; 当 a 0 时, f ( x) 0 有一解 x ln a ,在区间 (, ln a) 内 f ( x) ,在区间 ( ln a, ) 内 f ( x) 0 , y f ( x) 有最大值 f ( ln a) ln a 1 ,要使函数 y f ( x) 有两个不同的零点
ea
1
1
1
1
1 1 1 e a 1 a e a 令 (a) ln a e a ,则 (a) 2 2 , a a a a a2
1
ea 再令 (a ) 1 a e ,则 (a) 1 2 0 , a
1 1 所以 (a) ( ) 1 ee 0 ,即 (a) 0 ,所以 (a) 为增函数, e e
x2 增大. x1
ex ,当 x1 ln a 1 ae x
证法 3:对 x ae x 两边求关于 a 的导数,得 x e x ae x x ,所以 x 时, x1
e x1 e x2 0 ,当 x2 ln a 时, x2 0 ,设 p(a) x2 x1 , x1 1 ae x2 1 ae
1 x1 , x2 ,必须满足 f ( ln a) ln a 1 0 ,解得 0 a ,取 p 0 , f ( p) f (0) a 0 , e
1 1
1
ln ea 1 ea 1 取 q ln 1 此时 q e 1 1 ln a , f (q) ln ae a ln a e a , a a a a
0 x3 ln a1 , ln a2 x4 ,则 0 k (a1 , x1 ) k (a2 , x3 ) k (a1 , x3 ) ,所以 0 x3 x1 ; 0 k (a1 , x2 ) k (a2 , x4 ) k (a1 , x4 ) ,所以 x2 x4 ,
(,1) 内随着 x1 的增大, a 增大,也就是说,随着 a 的减小, x1 减小;而当
x2 ln a ln
1 1 时, a 0 , a 为 x 的减函数,即在 (1, ) 内随着 x2 的增大, a 减小, e
也就是说,随着 a 的减小, x2 增大. 总之,随着 a 的减小,
小,
1
1 a
1 ea f (ln ) (a) ( ) e 1 ee 0 . e a 1 综上所述知,函数 f ( x) x ae x (a R) 存在两个相异零点的条件是 0 a . e 1 (II)证明:设 g (a) x ae x (a (0, )) ,则 g (a) ex 0 ,即函数 y g (a) 为减函数. e
x4 x2 x ,所以 2 随着 a 的减小而增大. x3 x1 x1
引理:函数 y f ( x) 是定义域为 D ,值域为 E 的连续增(减)函数,则在区间 E 内,随着
y 的增大, x 增大(缩小)
证法 2: 由题意, a
x 1 x 1 , a x ,当 x1 1 ln ln a 时, a 0 , a 为 x 的增函数,即在 e ex e
e x2 e x1 0 x2 1 ae 1 ae x1
p (a) x2 x1
因为
x2 x x e x2 x1 ,所以 ( 2 ) (e x2 x1 ) e x2 x1 p (a) 0 ,故而 2 是 a 的减函数,即随着 a 的减 x1 x1 x1 x2 增大. x1
