初二几何专题训练整理

合集下载

初二上册几何专项训练

初二上册几何专项训练题目一：已知在三角形ABC 中，AB = AC，∠A = 40°，求∠B 的度数。

解析：因为AB = AC，所以三角形ABC 是等腰三角形。

根据等腰三角形两底角相等的性质，∠B = ∠C。

又因为三角形内角和为180°，所以∠B = (180° - ∠A)÷2 = (180° - 40°)÷2 = 70°。

题目二：在平行四边形ABCD 中，∠A = 60°，求∠C 的度数。

解析：平行四边形的对角相等，所以∠A = ∠C。

已知∠A = 60°，则∠C = 60°。

题目三：矩形ABCD 的对角线AC、BD 相交于点O，若AB = 3，BC = 4，求AC 的长。

解析：在矩形ABCD 中，∠ABC = 90°。

根据勾股定理，AC² = AB² + BC²。

已知AB = 3，BC = 4，则AC = √(3² + 4²)=5。

题目四：菱形ABCD 的边长为5，一条对角线长为6，求另一条对角线的长。

解析：菱形的对角线互相垂直且平分。

设另一条对角线长为x。

根据菱形的性质和勾股定理可得，(6÷2)² + (x÷2)² = 5²，9 + (x²÷4) = 25，x²÷4 = 16，x² = 64，解得x = 8。

题目五：等腰梯形ABCD 中，AD∠BC，AB = CD，∠B = 60°，AD = 3，BC = 7，求梯形的周长。

解析：过点A 作AE∠DC，因为AD∠BC，所以四边形AECD 是平行四边形，所以AE = CD = AB，EC = AD = 3。

又因为∠B = 60°，所以三角形ABE 是等边三角形，AB = BE = BC - EC = 7 - 3 = 4。

初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题：1. 若两角互为补角，则它们的差是（）。

A.0°B.45°C.60°D.90°2. 在图中，如点S、T分别在边AB的延长线上，且∠ASP=60°，∠BAT=20°，则∠AST为（）。

A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm，点E、F分别在边AD、AB上，且AE=BF，则三角形CEF的面积为（）。

A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°，则它所对的弧度数是（）。

A.π/6B.π/3C.π/4D.π/2填空题：1.如图，已知BC平分∠ABD，设∠BAC=a°，∠BCA=b°，则∠CBD=\_\_\_\_°。

2.如图，点A、B、C在同一条直线上，则对于ΔABC来说，以下说法正确的是：①AB＝AC；②\angleBAC是钝角；③\angleABC＋\angleACB ＝180^\circ，所以\angleABC＝\_\_\_\_°，\angleACB＝\_\_\_\_°。

3. 已知直角三角形ABC，其中\angleC=90°，BC＝3，AC＝4，则AB=\_\_\_\_。

4.如图，长方形ABCD中，点E、F分别为BC、CD上的点，若∠BAE=∠EFD，AB=10cm，则DF=\_\_\_\_cm。

解答题：1.如图，在\triangleABC中，垂足分别为D、E、F。

若AC＝6，BD＝8，DE＝5，EF＝9，则BC＝（）。

2.如图，已知\angleBAC=60°，AD平分\angleBAC，且BD=AD，点E为AD的延长线上的点，且\angleBEC=140°，则\angleACD=\_\_\_\_\_\_°。

初二几何必备练习题

初二几何必备练习题几何学是数学的一个分支，研究形状、大小、相对位置以及与它们相关的属性和变换。

在初二阶段，几何学作为数学课程的一部分，对学生的逻辑思维和空间想象力提出了很高的要求。

为了帮助初二学生提升几何学的学习效果，以下是一些初二几何的必备练习题。

1. 圆的面积计算题问题：给定一个半径为5cm的圆，请计算它的面积。

解答：圆的面积公式为S = πr^2，其中π取近似值3.14，r为半径。

根据题目，半径r = 5cm，将这些值代入公式中即可得到面积S的结果。

计算过程如下：S = 3.14 * 5^2= 3.14 * 25≈ 78.5所以，给定半径为5cm的圆的面积约为78.5平方厘米。

2. 直角三角形的斜边计算题问题：一个直角三角形的两条直角边长分别为3cm和4cm，请计算斜边的长度。

解答：根据勾股定理，直角三角形的斜边长度等于两个直角边长度的平方和的平方根。

即c = √(a^2 + b^2)，其中a和b分别为直角边的长度。

根据题目，直角边a = 3cm，b = 4cm。

代入勾股定理的公式中进行计算：c = √(3^2 + 4^2)= √(9 + 16)= √25= 5所以，直角三角形的斜边长度为5cm。

3. 平行四边形的面积计算题问题：一个平行四边形的底边长为6cm，高为8cm，请计算它的面积。

解答：平行四边形的面积等于底边长乘以高。

即S = 底边 * 高。

根据题目，底边长为6cm，高为8cm。

代入公式进行计算：S = 6 * 8= 48所以，给定底边长为6cm，高为8cm的平行四边形的面积为48平方厘米。

4. 平面镜成像问题问题：在平面镜前放一个物体，其距离镜面为20cm，物体的高度为2cm，请问成像的高度是多少？解答：根据平面镜成像规律，平面镜所成的像与物距和物高之间有特定的关系。

对于平面镜而言，像的高度等于物体高度。

所以，在这个问题中，成像的高度为2cm。

5. 三角形内角和问题问题：一个三角形的两个角分别为70°和45°，请计算第三个角的度数。

初二几何专项练习题及答案

初二几何专项练习题及答案1. 题目：三角形的内角和题目描述：求解一个任意三角形的内角和是多少。

解答：任意三角形的内角和都是180度。

这是由三角形的定义决定的。

根据定义，任意三角形是由三条线段组成，这三条线段的端点构成了三个角。

三角形的三个内角相加等于180度。

2. 题目：等腰三角形的性质题目描述：列举并解释等腰三角形的性质。

解答：等腰三角形是指有两边相等的三角形。

等腰三角形的性质包括：a) 等腰三角形的底角（底边两边的夹角）相等。

b) 等腰三角形的顶角（等腰边两边夹角的对应角）相等。

c) 等腰三角形的底边上的高等于等腰边的中线。

3. 题目：直角三角形的勾股定理题目描述：阐述直角三角形的勾股定理。

解答：直角三角形是指其中一个角是直角（即90度）的三角形。

勾股定理是直角三角形中的一个重要定理，它表明直角三角形的斜边的平方等于两个直角边的平方之和。

勾股定理可以用公式表示为：c^2 = a^2 + b^2其中，c表示直角三角形的斜边，a和b分别表示直角三角形的两个直角边。

4. 题目：平行线与转角定理题目描述：解释平行线与转角定理的相关概念。

解答：平行线与转角定理是几何中的一个重要定理，它与平行线之间的角度关系有关。

定理1：如果两条直线与一条截线相交，且两个转角是相等的，则这两条直线是平行线。

定理2：如果两条直线被一条截线相交，且两个转角互补，则这两条直线是平行线。

平行线与转角定理在解决直角三角形、平行四边形等几何问题中起到重要的作用。

综上所述，初二几何专项练习题及答案主要包括三角形的内角和、等腰三角形的性质、直角三角形的勾股定理以及平行线与转角定理等。

通过对这些题目的学习和理解，可以提高对几何知识的掌握和应用能力。

八年级几何证明专题训练(50题)

八年级几何证明专题训练1. 如图，已知△EAB≌△DCE，AB，EC分别是两个三角形的最长边，∠A＝∠C＝35°，∠CDE＝100°，∠DEB＝10°，求∠AEC的度数．2. 如图,点E、A、B、F在同一条直线上,AD与BC交于点O, 已知∠CAE=∠DBF,AC=BD.求证：∠C=∠D3.如图，OP平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论进行证明．4. 已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE＝EC。

5. 如图，在△ABC中，AB=AD=DC，∠BAD=28°，求∠B和∠C的度数。

7. 写出下列命题的逆命题，并判断逆命题的真假．如果是真命题，请给予证明；•如果是假命题，请举反例说明．命题：有两边上的高相等的三角形是等腰三角形．8. 如图，在△ABC中，∠ACB=90º，D是AC上的一点，且AD=BC，DE AC于D，∠EAB=90º．求证：AB=AE．9. 如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q三点在一条直线上，且∠ABP=∠ACQ，BP=CQ，问△APQ是什么形状的三角形？试证明你的结论．10. 如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=13，AC=5，则△ACD的周长为多少？6. 如图，B、D、C、E在同一直线上，AB=AC，AD=AE，求证：BD=CE。

11. 如图所示，AC ⊥BC ，AD ⊥BD ，AD ＝BC ，CE ⊥AB ，DF ⊥AB ，垂足分别是E ，F ，求证：CE ＝DF.12. 如图，已知△ABC 中，∠ACB ＝90°，AC ＝BC ，BE ⊥CE ，垂足为E ，AD ⊥CE ，垂足为D. (1)判断直线BE 与AD 的位置关系是____；BE 与AD 之间的距离是线段____的长； (2)若AD ＝6 cm ，BE ＝2 cm ，求BE 与AD 之间的距离及AB 的长．13. 如图，已知 △ABC 、△ADE 均为等边三角形，点D 是BC 延长线上一点，连结CE ，求证：BD=CE14. 如图，△ABC 中，AB =AC ，∠BAC =120°，AD ⊥AC 交BC •于点D ，求证：•BC =3AD .B AE DC15. 如图，四边形ABCD中，∠DAB=∠BCD=90°，M为BD中点，N为AC中点，求证：MN⊥AC．16、已知：如图所示，在△ABC中，∠ABC=45°，CD⊥AB于点D，BE平分∠ABC，且BE⊥AC于点E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G．（1）求证：BF=A C；（2）求证：DG=DF．17. 如图，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数.18. 如图所示，在△ABC中，AB=AC，BD⊥AC于点D，CE⊥AB于点E，BD，CE相交于F.求证：AF平分∠BAC.19. 如图所示，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．20. 已知：如图，在△ABC中，AB=AC，点D在边BC上，DE⊥AB，DF⊥AC，且DE=DF，求证：△ABD≌△ACD21. 如图，一张直角三角形的纸片ABC，两直角边AC=6cm，BC=8cm．现将直角边AC沿直线AD折叠，使它落在斜边AB上，且AC与AE重合，求CD的长．22. 已知：如图，在△ABC中，AB=AC，BD平分∠ABC，E是底边BC的延长线上的一点且CD=CE.（1）求证：△BDE是等腰三角形（2）若∠A=36°，求∠ADE的度数.23. 如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上且BE=BD，连结AE、DE、DC．（1）求证：AE=CD；（2）若∠CAE=30°，求∠BDC的度数．24. 如图，在ABC∆中，点D在AC边上，DB=BC，点E是CD的中点，点F是AB的中点，则可以得到结论：12EF AB=，请说明理由.EFDB CAAB CDE25. 已知：如图，在ABC ∆中，C ABC ∠=∠，点D 为边AC 上的一个动点，延长AB 至E ，使BE=CD ，连结DE ，交BC 于点P. （1）DP 与PE 相等吗？请说明理由.（2）若60C ∠=︒，AB=12，当DC=_________时，BEP ∆是等腰三角形.（不必说明理由）26. 如图，C 为线段BD 上一点（不与点B ，D 重合），在BD 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于一点F ，AD 与CE 交于点H ，BE 与AC 交于点G 。

八年级经典几何题

八年级经典几何题一、三角形全等类。

题1：如图，在△ABC中，AB = AC，AD是BC边上的中线，求证：△ABD≌△ACD。

解析：1. 在△ABD和△ACD中：- 已知AB = AC（题目所给条件）。

- 因为AD是BC边上的中线，所以BD = CD（中线的定义）。

- AD = AD（公共边）。

2. 根据SSS（边 - 边 - 边）全等判定定理，可得△ABD≌△ACD。

题2：已知：如图，点B、E、C、F在同一直线上，AB = DE，AC = DF，BE = CF。

求证：∠A = ∠D。

解析：1. 因为BE = CF，所以BE+EC = CF + EC，即BC = EF。

2. 在△ABC和△DEF中：- AB = DE（已知）。

- AC = DF（已知）。

- BC = EF（已证）。

3. 根据SSS全等判定定理，△ABC≌△DEF。

4. 所以∠A = ∠D（全等三角形的对应角相等）。

二、等腰三角形性质类。

题3：等腰三角形的一个角是70°，求它的另外两个角的度数。

解析：1. 当70°角为顶角时：- 因为等腰三角形两底角相等，设底角为x。

- 根据三角形内角和为180°，则2x+70° = 180°。

- 2x = 180° - 70° = 110°，解得x = 55°。

- 所以另外两个角都是55°。

2. 当70°角为底角时：- 则另一个底角也是70°，顶角为180°-70°×2 = 180° - 140° = 40°。

- 所以另外两个角是70°和40°。

题4：已知等腰三角形ABC中，AB = AC，AD⊥BC于D，若∠BAD = 30°，求∠C的度数。

解析：1. 因为AB = AC，AD⊥BC，根据等腰三角形三线合一的性质，AD是∠BAC的平分线。

(完整)八年级数学经典几何专题练习1

专题11.如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为______．如图，取AB的中点E，连接OE、DE、OD，∵OD≤OE+DE，∴当O、D、E三点共线时，点D到点O的距离最大，此时，∵AB=2，BC=1，∴OE=AE=12AB=1。

DE=，∴OD的最大值为：2.如图，已知菱形ABCD的对角线AC 、BD相交于点O，延长AB至点E，使BE=AB，连接CE．（1）求证：四边形BECD是平行四边形；（2）若∠E=60°，AC=43求菱形ABCD的面积．试题解析：（1）∵四边形ABCD是菱形，∴AB=CD，AB∥CD.；又∵BE=AB，∴BE=CD.∵BE∥CD, ∴四边形BECD是平行四边形.∵四边形BECD是平行四边形，∴BD∥CE.∴∠ABO=∠E=60°.又∵四边形ABCD是菱形，∴AC丄BD,OA=OC. ∴∠BOA=90°，∴∠BAO=30°.∵AC=43∴OA=OC=23∴OB=OD=2. ∴BD=4.∴菱形ABCD的面积=1143483 22AC BD⨯⨯=⨯=2.如图，在矩形ABCD 中，点E 在边CD 上，将该矩形沿AE 折叠，使点D 落在边BC 上的点F 处，过点F 作分、FG ∥CD ，交AE 于点G 连接DG ．（1）求证：四边形DEFG 为菱形；（2）若CD=8，CF=4，求DE CE的值．【答案】（1）证明见解析；（2）DE CE =53【解析】（1）证明：由折叠的性质可知：DG=FG ，ED=EF ，∠1=∠2，∵FG ∥CD ，∴∠2=∠3，∴FG=FE ，∴DG=GF=EF=DE ，∴四边形DEFG 为菱形；（2）解：设DE=x ，根据折叠的性质，EF=DE=x ，EC=8﹣x ，在Rt △EFC 中，FC2+EC2=EF2，即42+（8﹣x ）2=x2，解得：x=5，CE=8﹣x=3， ∴DE CE =53．3.如图所示，在菱形ABCD 中，AB=4，∠BAD=120°，△AEF 为正三角形，点E 、F 分别在菱形的边BC ．CD 上滑动，且E 、F 不与B ．C ．D 重合．（1）证明不论E 、F 在BC ．CD 上如何滑动，总有BE=CF ；（2）当点E 、F 在BC ．CD 上滑动时，分别探讨四边形AECF 和△CEF 的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．解：（1）证明：如图，连接AC ，∵四边形ABCD 为菱形，∠BAD=120°，∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，∴∠BAE=∠FAC 。

八年级上期末复习几何专题(全等三角形、轴对称、勾股定理)

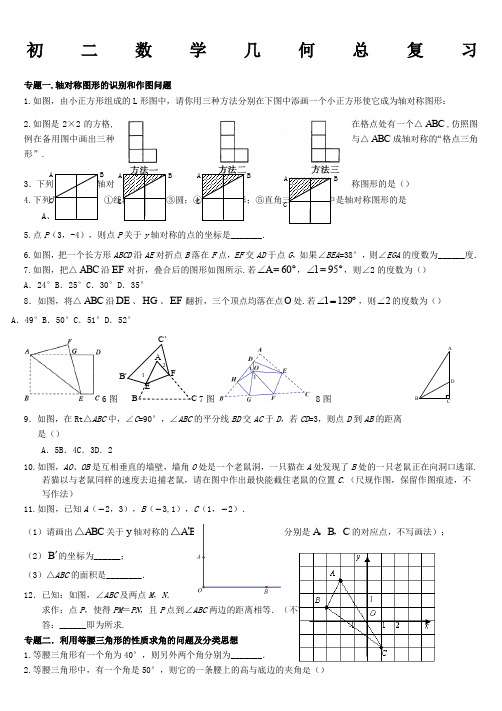
初二数学几何总复习专题一.轴对称图形的识别和作图问题1.如图，由小正方形组成的L 形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形：2.如图是2×2的方格,在格点处有一个△ABC ,仿照图例在备用图中画出三种与△ABC 成轴对称的“格点三角形”.3．称图形的是（）4. A5.点P （3，-4），则点P 关于y 轴对称的点的坐标是_______．6.如图，把一个长方形ABCD 沿AE 对折点B 落在F 点，EF 交AD 于点G ，如果∠BEA =38°，则∠EGA 的度数为______度．7.如图，把△ABC 沿EF 对折，叠合后的图形如图所示.若60A ∠=︒，195∠=︒，则∠2的度数为（） A ．24°B ．25°C ．30°D ．35°8．如图，将△ABC 沿DE 、HG 、EF 翻折，三个顶点均落在点O 处.若1129∠=︒，则2∠的度数为（） A ．49°B ．50°C ．51°D ．52°6图7图8图9．如图，在Rt △ABC 中，∠C =90°，∠ABC 的平分线BD 交AC 于D ，若CD =3，则点D 到AB 的距离是（）A ．5B ．4C ．3D ．210.如图，AO 、OB 是互相垂直的墙壁，墙角O 处是一个老鼠洞，一只猫在A 处发现了B 处的一只老鼠正在向洞口逃窜.若猫以与老鼠同样的速度去追捕老鼠，请在图中作出最快能截住老鼠的位置C .（尺规作图，保留作图痕迹，不写作法） 11.如图，已知A （-2，3），B （-3,1），C （1，-2）．（1）请画出ABC △关于y 轴对称的A B C '''△（其中A B C '''，，分别是A B C ，，的对应点，不写画法）；（2）B '的坐标为______；（3）△ABC 的面积是________． 12．已知：如图，∠ABC 及两点M ，N ．求作：点P ，使得PM ＝PN ，且P 点到∠ABC 两边的距离相等．（不写画法，保留作图痕迹）答：______即为所求.专题二．利用等腰三角形的性质求角的问题及分类思想 1.等腰三角形有一个角为40°，则另外两个角分别为_______．2.等腰三角形中，有一个角是50°，则它的一条腰上的高与底边的夹角是（）AB C B'C'EF12BBBBBDCA3.一个等腰三角形的一边长是6，一个外角是120°，则它的周长为（） A ．12B ．15C ．16D ．184.已知：如图1，P 、Q 是△ABC 边BC 上的两点，且BP=PQ=QC=AP=AQ ，求：∠BAC 的度数．图15.如图2，在△ABC 中，∠B ＝∠C ，FD ⊥BC 于D ，DE ⊥AB 于E ，∠AFD ＝158°，则∠EDF 等于＝__________．图2图3图46. 如图3，在Rt △ABC 中，∠B ＝90°，ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E ．已知∠BAE ＝10°，则∠C 的度数为（）7．如图4，AB=AC ，AD=AE ，∠BAD=40°，则∠CDE=_______． 8．如图5，△ABC 中，AB=AC ，BD=BC ，AD=DE=EB ，则∠A 为（）A ．30°B ．36°C ．45°D ．54° 图5图6图79．如图6，△ABC 中，AB=AC=BD ，那么∠1与∠2之间的关系满足（） A ．∠1=2∠2B ．2∠1+∠2=180°C ．∠1+3∠2=180°D ．3∠1-∠2=180°10．如图7，AC ⊥BC ，AC=BC ，CD ⊥AB ，DE ⊥BC ，则图中共有等腰三角形（） A ．1个B ．2个C ．5个D ．4个11．如图8，∠A=90°，E 是BC 上一点，A 点和E 点关于BD 对称，B 点、C 点关于DE 对称，求∠ABC 和∠C 的度数．图812.如图，在△ABC 中，AB ＝AC ，点D 在AC 上，且BD ＝BC=AD ，求△ABC 各角的度数. 专题三．利用等腰三角形的性质求线段的问题1.已知：在△ABC 中，AB ＜AC ，BC 边上的垂直平分DE 交BC 于点D ，交AC 于点E ，AC ＝8cm ，△ABE 的周长是14cm ，求：AB 的长。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初中几何综合测试题一.填空题1.一个三角形的两条边长分别为9和2，第三边长为奇数，则第三边长为_______.2.△ABC三边长分别为3、4、5，与其相似的△A′B′C′的最大边长是10，则△A′B′C′的面积是_________.4.点O是平行四边形ABCD对角线的交点，若平行四边行ABCD的面积为8cm，则△AOB的面积为________.5.直角三角形两直角边的长分别为5cm和12cm，则斜边上的中线长为.6.梯形上底长为2，中位线长为5，则梯形的下底长为________.7.如图，分别延长四边形ABCD两组对边交于E、F，若DF=2DA，8.在Rt△ABC中，AD是斜边BC上的高，如果BC=a，∠B=30°，那么AD等于_________.二．选择题1.一个角的余角和它的补角互为补角，则这个角是 [ ]A.30°B.45°C.60°D.75°2.依次连结等腰梯形的各边中点所得的四边形是 [ ]A.矩形B.正方形C.菱形D.梯形3.如图，DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的面积之比为 [ ]A.1∶2∶3B.1∶1∶1C.1∶4∶9D.1∶3∶54.已知：AB∥CD，EF∥CD,且∠ABC=20°，∠CFE=30°,则∠BCF的度数是 [ ]A.160°B.150°C.70°D.50°5.如图OA=OB，点C在OA上，点D在OB上，OC=OD，AD和BC相交于E，图中全等三角形共有 [ ]A.2对B.3对C.4对D.5对6.既是轴对称，又是中心对称的图形是 [ ]A.等腰三角形B.等腰梯形C.平行四边形D.线段三.解答题第一次在B处望见该船在B的南偏西30°，半小时后，又望见该船在B的南偏西60°，求该船的速度．2.如图，在△ABC中，BF⊥AC,CG⊥AD,F、G是垂足，D、E分别是BC、FG的中点，求证：DE⊥FG3.如图已知在平行四边形ABCD中，AF=CE，FG⊥AD于G，EH⊥BC于H，求证：GH与EF互相平分4.如图，AE∥BC,D是BC的中点，ED交AC于Q，ED的延长线交AB的延长线于P，求证：PD·QE=PE·QD5.如图矩形ABCD对角线AC、BD交于O，E F分别是OA、OB的中点（1）求证△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求CF的长。

6. 如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC，对角线AC⊥BD，垂足为F，过点F作EF∥AB，交AD于点E，CF=4cm．（1）求证：四边形ABFE是等腰梯形；（2）求AE的长．7. 如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，（1）若AB=6，求线段BP的长；（2）观察图形，是否有三角形与△ACQ全等？并证明你的结论8. 已知点E,F在三角形ABC的边AB所在的直线上,且AE=BF，FH//EG//AC，FH、EC分别交边BC所在的直线于点H，G（1）如果点E、F在边AB上，那么EG+FH=AC，请证明这个结论（2）如果点E在AB上，点F在AB的延长线上，那么线段EG，FH，AC的长度关系是什么？9. 如图是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA=15mm，DO=24mm，DC=10mm，我们知道铁夹的侧面是轴对称图形，请求出A、B两点间的距离．10. 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE，F为AE上一点，且∠BFE=∠C，（1）求证：△ABF∽△EAD ；（2）若AB=5，AD=3，∠BAE=30°，求BF 的长11. 如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G，若CF=15cm ，求GF 之长。

12. 如图，已知直角梯形ABCD 中，AD ∥BC ，∠B=90°，AB=12cm ，BC=8cm ，DC=13cm ，动点P 沿A →D →C 线路以2cm/s 的速度向C 运动，动点Q 沿B →C 线路以1cm/s 的速度向C 运动．P 、Q 两点分别从A 、B 同时出发，当其中一点到达C 点时，另一点也随之停止．设运动时间为t 秒，△PQB 的面积为y 2cm ．（1）求AD 的长及t 的取值范围；（2）当1.5≤t ≤0t （0t 为（1）中t 的最大值）时，求y 关于t 的函数关系式；（3）请具体描述：在动点P 、Q 的运动过程中，△PQB 的面积随着t 的变化而变化的规律．初中几何综合测试题二.填空题1.一个三角形的两条边长分别为9和2，第三边长为奇数，则第三边长为_______.2.△ABC三边长分别为3、4、5，与其相似的△A′B′C′的最大边长是10，则△A′B′C′的面积是_________.6.点O是平行四边形ABCD对角线的交点，若平行四边行ABCD的面积为8cm，则△AOB的面积为________.7.直角三角形两直角边的长分别为5cm和12cm，则斜边上的中线长为.6.梯形上底长为2，中位线长为5，则梯形的下底长为________.8.如图，分别延长四边形ABCD两组对边交于E、F，若DF=2DA，8.在Rt△ABC中，AD是斜边BC上的高，如果BC=a，∠B=30°，那么AD等于_________.二．选择题1.一个角的余角和它的补角互为补角，则这个角是 [ ]A.30°B.45°C.60°D.75°2.依次连结等腰梯形的各边中点所得的四边形是 [ ]A.矩形B.正方形C.菱形D.梯形3.如图，DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的面积之比为 [ ]A.1∶2∶3B.1∶1∶1C.1∶4∶9D.1∶3∶54.已知：AB∥CD，EF∥CD,且∠ABC=20°，∠CFE=30°,则∠BCF的度数是 [ ]A.160°B.150°C.70°D.50°5.如图OA=OB，点C在OA上，点D在OB上，OC=OD，AD和BC相交于E，图中全等三角形共有 [ ]A.2对B.3对C.4对D.5对6.既是轴对称，又是中心对称的图形是 [ ]A.等腰三角形B.等腰梯形C.平行四边形D.线段三.解答题第一次在B处望见该船在B的南偏西30°，半小时后，又望见该船在B的南偏西60°，求该船的速度．2.如图，在△ABC中，BF⊥AC,CG⊥AD,F、G是垂足，D、E分别是BC、FG的中点，求证：DE⊥FG3.如图已知在平行四边形ABCD中，AF=CE，FG⊥AD于G，EH⊥BC于H，求证：GH与EF互相平分4.如图，AE∥BC,D是BC的中点，ED交AC于Q，ED的延长线交AB的延长线于P，求证：PD·QE=PE·QD5.如图矩形ABCD对角线AC、BD交于O，E F分别是OA、OB的中点（1）求证△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求CF的长。