人教版九年级数学下册平面直角坐标系中的位似同步练习
2022年人教版九年级下《平面直角坐标系中的位似》同步练习(附答案)

第2课时 平面直角坐标系中的位似1.如下图,左图与右图是相似图形,如果右图上一个顶点坐标是〔a ,b 〕,那么左图上对应) D.(-2b ,-2a ),0),试将△ABO 放大,使放大后的△EFO 与△ABO 对应边的比为2:1,那么E 、F 的坐标分别是〔 〕 A.〔-6,6〕〔6,6〕 B.〔6,-6〕〔6,6〕O 是位似中心,假设△OABP 1的坐标是 。
4.如下图,AB ∥A`B`,BC ∥B`C`,且OA`:A`A=4:3,那么△ABC 与 是位似图形,位似比是 。
BO△ABC 的三边缩小为原来的二分之一,如下图,任取一点O ,连结OA 、OB 、OC 并取它们的中点D 、E 、F ,得△DEF ,那么以下说法正确的个数是〔 〕 ①△ABC 和△DEF 是位似图形;②△ABC 和△DEF 是相似图形;③△ABC 和△DEF 的周长比是4:1; ④△ABC 和△DEF 的面积比是4:16.在平面直角坐标系中有两点A 〔6,3〕,B 〔6,0〕,以原点O 为位似中心,相似比为1:3,O把线段AB 缩小方法一:4225101520B'OABA'方法二:4225510B''OABA''探究:〔1〕在方法一中,A ’的坐标是 ,B ’的坐标是 ,对应点坐标之比是31;〔2〕在方法二中,A ’’的坐标是 ,B ’’的坐标是 ,对应点坐标之比是-317.如图,O 为原点,B ,C 两点坐标分别为〔3,-1〕〔2,1〕(1)以O 为位似中心在y 轴左侧将△OBC 放大两倍,并画出图形; 〔2〕分别写出B ,〔3〕M 〔x ,y第2课时 12.如图4-3-26,以下图形都是几何体的平面展开图,你能说出这些几何体的名称吗?3.如图,从不同方向看下面左图中的物体,右图中三个平面图形分别是从哪个方向看到的?4.一天,小明的爸爸送给小明一个礼物,小明翻开包装后画出它的主视图和俯视图如下图.根据小明画的视图,你猜小明的爸爸送给小明的礼物是〔〕A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服5.一个几何体的主视图和左视图如下图,它是什么几何体?请你补画出这个几何体的俯视图.6.一个物体的三视图如下图,试举例说明物体的形状.7.几何体的主视图和俯视图如下图.〔1〕画出该几何体的左视图;〔2〕该几何体是几面体?它有多少条棱?多少个顶点?〔3〕该几何体的外表有哪些你熟悉的平面图形?8.小刚的桌上放着两个物品,它的三视图如下图,你知道这两个物品是什么吗?9.一个由几个相同的小立方体搭成的几何体的俯视图如下图,方格里的数字表示该位置的小立方体的个数,请你画出这个几何体的主视图和左视图.。
人教版九年级数学下册27.3位似同步练习含答案
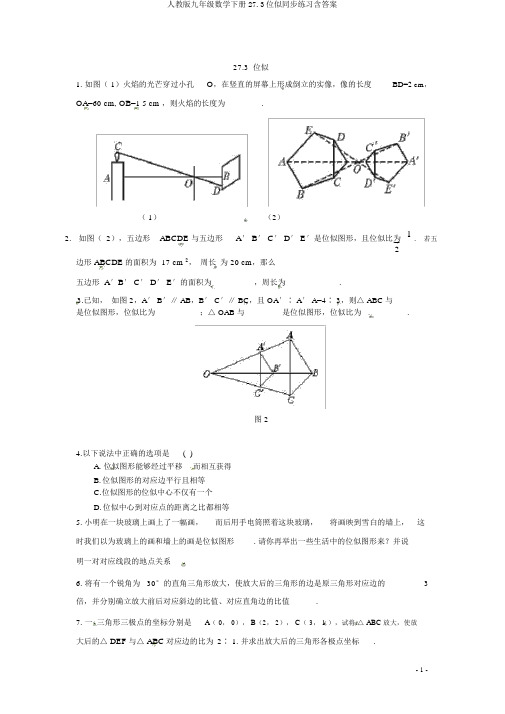
27.3 位似1. 如图( 1)火焰的光芒穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm, OB=1 5 cm,则火焰的长度为________.( 1)(2)2.如图(2),五边形ABCDE 与五边形A′ B′ C′ D′ E′是位似图形,且位似比为1.若五2边形 ABCDE的面积为17 cm2,周长为20 cm,那么五边形 A′B′ C′ D′ E′的面积为________,周长为________.3.已知,如图 2,A′ B′∥ AB,B′ C′∥ BC,且 OA′∶ A′ A=4∶ 3,则△ ABC 与 ________是位似图形,位似比为________;△ OAB 与 ________是位似图形,位似比为________.图 24.以下说法中正确的选项是()A. 位似图形能够经过平移而相互获得B.位似图形的对应边平行且相等C.位似图形的位似中心不仅有一个D.位似中心到对应点的距离之比都相等5.小明在一块玻璃上画上了一幅画,而后用手电筒照着这块玻璃,将画映到雪白的墙上,这时我们以为玻璃上的画和墙上的画是位似图形. 请你再举出一些生活中的位似图形来?并说明一对对应线段的地点关系.6. 将有一个锐角为 30°的直角三角形放大,使放大后的三角形的边是原三角形对应边的3倍,并分别确立放大前后对应斜边的比值、对应直角边的比值.7. 一三角形三极点的坐标分别是A(0,0), B(2,2), C(3,1),试将△ ABC放大,使放大后的△ DEF与△ ABC对应边的比为2∶ 1. 并求出放大后的三角形各极点坐标.8、经过不一样位似中心将同一图形进行放大和减小,试问放大后的图形和减小后的图形可否也是位似图形?说说你的见解.答案: 1、 8 cm 2、17cm 210 cm 3、△ A′B′ C′7∶4 △OA′B′47∶ 4 4 、D 5 、略 6 、(1)1 ∶ 31∶ 37、位似中心取点不一样, 所得D、E、F各点坐标不一样,即答案不唯一.8、由放大或减小猴图形中对应线段与原图形中对应线段相互平行,故而放大后的图形和缩小后的图形的对应线段也相互平行,因此它们也是位似图形.。
人教版九年级数学下册27.3 位似同步练习3 及答案【新】

3 位似专题一 开放探究题1.在如图所示的方格纸中(每个小方格的边长都是1个单位)有一点O 和△ABC.(1)请以点O 为位似中心,把△ABC 缩小为原来的一半(不改变方向),得到△C B A ''';(2)请用适当的方式描述△C B A '''的顶点C B A ''',,的位置.专题二 实际应用题2.如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm ,则投影三角形的对应边长为( )A.8 cmB.20 cmC.3.2 cmD.10 cm3.如图,印刷一张矩形的张贴广告,它的印刷面积是32 dm 2,两边空白各0.5 dm ,上下空白各1 dm ,设印刷部分从上到下长是x dm ,四周空白的面积为S dm 2.(1)求S 与x 的关系式;(2)当要求四周空白处的面积为18 dm 2时,求用来印刷这张广告的纸张的长和宽各是多少?(3)在(2)问的条件下,内外两个矩形是位似图形吗?为什么?专题三 一题多变题4.已知五边形ABCDE 与五边形A′B′C′D′E′是位似图形,O 是位似中心,OD ∶OD ′=2∶3,如图所示,求S 五边形ABCDE 与S 五边形A′B′C′D′E′之比是多少?(1)一变:若已知条件不变,五边形ABCDE 的周长为32 cm ,求五边形A′B′C′D′E′的周长;(2)二变:已知条件不变,试判断△ODE 与△OD′E′是位似图形吗?专题四 阅读理解题5.阅读下面材料:“如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位似中心.利用三角形的位似可以将一个三角形缩小或放大.”(1)选择:如图1,点O 是等边△PQR 的中心,P′、 Q′、R′分别是OP 、OQ 、OR 的中点,则△P′Q′R ′与△PQR 是位似三角形,此时,△P′Q′R′与△PQR 的位似比、位似中心分别为( )A .2,点PB .12 ,点PC .2,点OD .12,点O (2)如图2,用下面的方法可以画△AOB 的内接等边三角形,阅读后证明相应的问题的画法: ①在△AOB 内画等边△CDE ,使点C 在OA 上,点D 在OB 上,②连结OE 并延长交AB 于点E ′,过点E ′作E ′C′∥EC ,交OA 于点C′,过点E ′作E ′D′∥ED 交OB 于点D′;③连结C′D′,则△C′D′E′是△AOB 的内接三角形,求证:△C′D′E′是等边三角形.【知识要点】1.两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,这样的两个图形叫做位似图形.2.在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或者-k .【温馨提示】1.位似图形的位似中心可以在任何位置.2.解决位似图形中相关图形的周长、面积问题时,一般地首先要确定位似图形的相似比,然后再根据相似形的性质解决问题.【方法技巧】1.利用位似,可以将一个图形放大或缩小.2.判定两个图形是位似图形,必须同时满足两个条件:(1)两个图形相似;(2)两个图形所有对应顶点所在直线相交于同一点.3.在数学上,往往先在一个已知图形中通过探究找出一个正确的结论,再将图形进行适当变换,然后探究这个结论在变换后的图形中是否成立,最后利用发现的一般规律去指导并解决问题,这种研究问题的方法是训练发散思维与创新意识的有效途径.参考答案1. 解:(1)按位似作图在O 点与△ABC 同侧把△ABC 缩小一半,得到△C B A ''';第(2)问是一个开放性问题,对描述△C B A '''的顶点C B A ''',,的位置的方式不确定,如果建立直角坐标系来描述C B A ''',,的位置,假设以O 为坐标原点,建立平面直角坐标系.那么A′的坐标为(-4,1),B′的坐标为(-5,-1),C′的坐标为(-2,-1).2.B 【解析】8:投影三角形的对应边长=2:5.3.解:(1)根据题意,得S =32(2)(1)32x x ++-=x +x 64+2. (2)根据题意,得x +x64+2=18,整理,得x 2-16x +64=0,∴(x -8)2=0,∴x =8,∴x +2=10.所以这张广告纸的长为10 dm,宽为832+2×0.5=5(dm). (3)内外两个矩形是位似图形,理由如下:因为内外两矩形的长,宽的比都为2, ∴45=''=''=''=''A D DA D C CD C B BC B A AB . ∵矩形的各角都为90°,所以矩形ABCD∽矩形A′B′C′D′.∵AC 和BD ,A′C′和B′D′都相交于O 点,∴矩形ABCD 与矩形A′B′C′D′是位似图形.4.解:∵五边形ABCDE 与五边形A′B′C′D′E′是位似图形,OD :OD′=2:3,∴ABCDEA B C D E S S '''''五边形五边形=2OD OD ⎛⎫ ⎪⎝⎭'=223⎛⎫ ⎪⎝⎭=49. (1)由题意可知五边形ABCDE 与五边形A′B′C′D′E′的位似比为′OD OD =23, ∴ABCDE A B C D E C C '''''五边形五边形=OD OD '=23. ∵C 五边形ABCDE =32cm ,∴C 五边形A′B′C′D′E′=C 五边形ABCDE ×32=32×32=48(cm ). (2)∵五边形ABCDE 与五边形A 'B 'C 'D 'E '是位似图形,∴OD OD '=OE DE OE D E '=''=23,• ∴△ODE∽△OD′E′.由题图可知△ODE 与△OD′E′的对应点的连线都经过点O ,∴△ODE 与△OD′E′是位似图形.5.解:(1)由位似的定义,观察图l 知:点O 是位似中心,根据三角形中位线的性质可推出位似比为1/2,故选D .(2)证明:∵EC∥E′C′,∴CE OE C E O E ='''',∠CEO=∠C′E′O . ∵ED∥E′D′,∴ED OE E D O E ='''',∠DEO=∠D′E′O ′, 故′′′′DE ED E C CE =,∠CED=∠C′E′D′. ∵△CDE 是等边三角形,∴CE=DE ,∠CED =60°.∴C′E′=E′D′,∠C′E′D′=60°,∴△C′D′E′是等边三角形.。
精品 九年级数学下册 相似形-位似 同步讲义同步练习题

相似形第03课位似定义:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.注意:(1)位似图形是一种特殊的相似图形,而相似图形未必都能构成位似关系。
(2)在平面直角坐标系中,如果位似变换以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.位似图形性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.例1.如图,以O为位似中心,将△ABC放大为原来的两倍.例2.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.例3.如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.(1)求证:△ADE∽△BEF;(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.例4.如图,在△ABC 中,BC>AC,点D 在BC 上,且DC=AC,∠ACB 的平分线CF 交AD 于F,点E 是AB 的中点,连结EF.(1)求证:EF ∥BC;(2)若四边形BDFE 的面积为6,求△ABD 的面积.例5.如图,在□ABCD 中,过点A 作AE ⊥BC,垂足为E,连接DE,F 为线段DE 上一点,且∠AFE=∠B.(1)求证:△ADF ∽△DEC ;(2)若AB=8,3436==AF AD ,,求AE 的长.同步练习:1.用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可选在( )A.原图形的外部B.原图形的内部C.原图形的边上D.任意位置2.下列多边形一定相似的为( )A.两个矩形B.两个菱形C.两个正方形D.两个平行四边形3.下列说法正确的是( )A.两个图形如果是位似图形,那么这两个图形一定全等;B.两个图形如果是位似图形,那么这两个图形不一定相似;C.两个图形如果是相似图形,那么这两个图形一定位似;D.两个图形如果是位似图形,那么这两个图形一定相似。
人教版九年级数学下册位似图形的概念及画法)同步练习题

27.3 位似第1课时 位似图形的概念及画法1.下列说法正确的是( )A. 位似图形一定是相似图形B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D.位似图形中每组对应点所在的直线必相互平行 2.下列说法正确的是( )A. 分别在∆ABC 的边AB.AC 的反向延长线上取点D.E.使DE ∥BC,则∆ADE 是∆ABC 放大后的图形 B.两位似图形的面积之比等于位似比 C. 位似多边形中对应对角线之比等于位似比 D. 位似图形的周长之比等于位似比的平方3.如图,五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形,点A 和点A 1是一对对应点,P 是位似中心,且2 P A =3 P A 1,则五边形ABCDE 和五边形A 1B 1C 1D 1E 1的相似比等于 ( ) A 、32. B 、23. C 、53. D 、35.4.如果两个位似图形的对应线段长分别为3cm 和5cm.且较小图形周长为30cm,则较大图形周长为5.已知∆ABC.以点A 为位似中心.作出∆ADE.使∆ADE 是∆ABC 放大2倍的图形.这样的图形可以作出 个 。
他们之间的关系是6.如左下图,五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形,点O 是位似中心,位似比为2:1. 若五边形ABCDE 的面积为17 cm 2, 周长为20 cm ,那么五边形A ′B ′C ′D ′E ′的面积为______,周长为______.第6题图 第7题图7.如图,A ′B ′∥AB ,B ′C ′∥BC ,且OA ′∶A ′A =4∶3,则△ABC 与_______是位似图形,位似比为______;△OAB 与________是位似图形,位似比为______. 8.如图, ∆OAB 与∆ODC 是位似图形 。
试问:(1) AB 与CD 平行吗?请说明理由 。
(2) 如果OB=3,OC=4,OD=3.5.试求∆OAB 与∆ODC 的相似比及OA 的长 。
2022-2023学年人教版九年级数学下册《27-3位似》同步题型分类练习题(附答案)

2022-2023学年人教版九年级数学下册《27.3位似》同步题型分类练习题(附答案)一.位似变换1.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC的面积与△DEF的面积之比是16:9,则AO:AD的值为()A.4:7B.4:3C.6:4D.9:52.如图平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,点A,B,E在x轴上,若正方形ABCD的边长为3,则F点坐标为()A.(16.5,9)B.(18,12)C.(16.5,12)D.(16,12)3.在如图所示的网格中,以点O为位似中心,能够与四边形ABCD是位似图形的为()A.四边形NGMF B.四边形NGME C.四边形NHMF D.四边形NHME 4.如图所示,在平面直角坐标系中,A(1,0),B(0,2),C(﹣2,1),以A为位似中心,把△ABC在点A同侧按相似比1:2放大,放大后的图形记作△A'B'C',则C'的坐标为()A.(﹣6,2)B.(﹣5,2)C.(﹣4,2)D.(﹣3,2)5.如图,在直角坐标系中,矩形ABCD与矩形EFGO位似,矩形ABCD的边CD在y轴上,点B的坐标为(﹣4,4),矩形EFGO的两边都在坐标轴上,且点F的坐标为(2,1),则矩形ABCD与EFGO的位似中心的坐标是.6.如图,平面直角坐标系中,点A在x轴正半轴上,且OA=4,∠BOA=30°,∠B=90°,以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,则点B的对应点B′的坐标为.7.如图,在平面直角坐标系中,A、B两点的坐标分别为A(﹣1,2)、B(0,2),C、D 两点的坐标分别为C(0,﹣1)、D(2,﹣1).若线段AB和线段CD是位似图形,且位似中心在y轴上,则位似中心的坐标为.8.《墨子•天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为4,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若A'B':AB=2:1,则四边形A'B'C'D'的外接圆的周长为.9.如图,△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,则点A(1,2)在第一象限的对应点A1的坐标是.10.如图,在平面直角坐标系中,O是坐标原点,以点O为位似中心,△A1B1C1和△ABC 相似比为2:1,在网格中画出新图象△A1B1C1,若每个小正方形边长均为1,请写出A1,B1,C1的坐标.11.如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△A n B n∁n组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…A n是OA n﹣1的中点,顶点B2,B3,…,B n.C2,C3,…,∁n都在B1C1边上.(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心;(2)求出第n个三角形△A n B n∁n(n≥2)的周长.12.如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M'在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.(1)求证:四边形PQMN为正方形;(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.13.(1)对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是,若点B′表示的数是2,则点B表示的数是;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是.(2)在平面直角坐标系xOy中,已知△ABC的顶点A(﹣2,0),B(2,0),C(2,4),对△ABC及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同个实数a,将得到的点先向右平移m单位,再向上平移n个单位(m>0,n>0),得到△A′B′C′及其内部的点,其中点A,B的对应点分别为A′(1,2),B′(3,2).△ABC内部是否存在点F,使得点F经过上述操作后得到的对应点F′与点F重合,若存在,求出点F 的坐标;若不存在请说明理由.14.在平面直角坐标系中,抛物线L:y=﹣x2+x+2与y轴交于点C,与x轴交于A、B两点(点A在点B的左侧).(1)求A、B、C三点的坐标;(2)连接AC、BC,以点C为位似中心,将△ABC扩大到原来的2倍得到△A1B1C,其中点A1、B1分别是点A、B的对应点,如何平移抛物线L才能使其同时经过点A1、B1,求出所有的平移方式.二.作图-位似变换15.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是()A.4B.3C.2D.116.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为()A.(0,0),2B.(2,2),C.(2,2),2D.(1,1),17.如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为()A.(m,n+3)B.(m,n﹣3)C.(m,n+2)D.(m,n﹣2)18.如图,以点O为位似中心,把△AOB缩小后得到△COD,使△COD∽△AOB,且相似比为,已知点A(3,6),则点C的坐标为.19.如图,以点O为位似中心,把△ABC放大2倍得到△A'B'C'',①AB∥A'B';②△ABC∽△A'B'C';③AO:AA'=1:2;④点C、O、C'三点在同一直线上.则以上四种说法正确的是.20.如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA =2.OC=1,则矩形AOCB的对称中心的坐标是;在第二象限内,将矩形AOCB 以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是.21.在平面直角坐标系中,△ABC的顶点A的坐标为(2,﹣5),若以原点O为位似中心,作△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为2:1,且点A1和点A 不在同一象限内,则点A1的坐标为.22.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是.23.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C (2,3).请在所给直角坐标系中按要求画图和解答下列问题:(1)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△DEF,△ABC 与△DEF的位似比为;(2)如果△ABC内部一点M的坐标为(a,b),请写出M的对应点M'的坐标(,).24.如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.(1)在平面直角坐标系中画出位似中心;(2)设点P(a,b)为△ABC内一点,确定点P在△A1B1C1内的对应点P1的坐标.25.如图,小明在学习图形的位似时,利用几何画板软件,在平面直角坐标系中画出了△ABC的位似图形△A1B1C1.(1)在图中标出△ABC和△A1B1C1的位似中心M点的位置并写出M点的坐标.(2)若以点A1为位似中心,请你帮小明在图中画出△A1B1C1的位似图形△A2B2C2,且△A1B1C1与△A2B2C2的位似比为2:1.(3)直接写出(2)中C2点的坐标.26.如图,△ABC三个顶点分别为A(0,﹣3),B(3,﹣2),C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC向上平移5个单位得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C2,使得△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并写出A2的坐标.27.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).(1)以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1.(2)画出△ABC绕O点顺时针旋转90°后得到的△A2B2C2.28.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)直接写出△ABC与△A′B′C′的位似比;(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出△A′B′C′各顶点的坐标.参考答案一.位似变换1.解:∵△ABC与△DEF位似,∴△ABC∽△DEF,AC∥DF,∵△ABC的面积与△DEF的面积之比是16:9,∴=,∵AC∥DF,∴△AOC∽△DOF,∴==,∴AO:AD=4:7,故选:A.2.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,∴==,即==,解得:EF=12,OB=4,∴F(16,12).故选:D.3.解:如图,四边形ABCD的位似图形是四边形NGMF.故选:A.4.解:∵以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作△AB'C',∴AC=AC′,∴点C是线段AC′的中点,∵A(1,0),C(﹣2,1),∴C'的坐标为(﹣5,2).故选:B.5.解:连接BF交y轴于点P,∵C和F是对应点,∴点P为位似中心,由题意得,GF=2,AD=4,GC=4﹣1=3,∵BC∥GF,∴△BPC∽△FPG,∴=,即=2,解得,GP=1,∴OP=2,∴位似中心的坐标是(0,2),故答案为:(0,2).6.解:作BE⊥OA于E,则∠BEO=90°,∵∠ABO=90°,∠BOA=30°,∴OB=OA•cos30°=4×=2,∴BE=OB=,OE=OB•cos30°=2×=3,∴点B的坐标为:(3,),∵以点O为位似中心,在第一象限内将△AOB放大,使相似比为2:1,∴点B的对应点B'的坐标为:(3×2,×2),即(6,2),故答案为:(6,2).7.解:连接AD交BC于E,则点E为位似中心,∵A(﹣1,2)、B(0,2),C(0,﹣1)、D(2,﹣1).∴AB=1,CD=2,BC=3,∵线段AB和CD是位似图形,∴AB∥CD,∴=,即=,解得BE=1,∴OE=OB﹣BE=1,∴位似中心点E的坐标为(0,1),故答案为:(0,1).8.解:如图,连接B′D′.设B′D′的中点为O.∵正方形ABCD∽正方形A′B′C′D′,相似比为1:2,又∵正方形ABCD的面积为4,∴正方形A′B′C′D′的面积为16,∴A′B′=A′D′=4,∵∠B′A′D′=90°,∴B′D′=A′B′=4,∴正方形A′B′C′D′的外接圆的周长=4π,故答案为:4π.9.解:∵△ABC与△A1B1C1是以原点O为位似中心的位似图形,且位似比为1:2,∵A(1,2),点A(1,2)在第一象限的对应点是A1,∴点A1的坐标为:(2,4).故答案为:(2,4).10.解:如图,△A1B1C1即为所求,A1(0,8),B1(6,6),C1(6,2).11.解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,∴正△A2B2C2的边长为,正△A3B3C3的边长为()2,正△A10B10C10和的边长为()9,正△A7B7C7的边长为()6,∴正△A10B10C10和正△A7B7C7的相似比==;它们的位似中心为点O;(2)∵第n个三角形△A n B n∁n(n≥2)的边长为()n﹣1,∴第n个三角形△A n B n∁n(n≥2)的周长为.12.(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,∴四边形PQMN为矩形,∵四边形P'Q'M'N'是正方形,∴PN∥P′N′,∴=,∵MN∥M′N′,∴=,∴=,而P′N′=M′N′,∴PN=MN,∴四边形PQMN为正方形;(2)解:作AD⊥BC于D,AD交PN于E,如图,∵△ABC的面积=1.5,∴AB•AC=1.5,∴AB=2,∴BC==2.5,∵BC•AD=1.5,∴AD==,设PN=x,则PQ=DE=x,AE=﹣x,∵PN∥BC,∴△APN∽△ABC,∴=,即=,解得x=,即PN的长为m.13.解:(1)点A′:﹣3×+1=﹣1+1=0,设点B表示的数为a,则a+1=2,解得a=3,设点E表示的数为b,则b+1=b,解得b=;故答案为:0,3,;(2)根据题意,得:,解得:,设点F的坐标为(x,y),∵对应点F′与点F重合,∴x+2=x,y+2=y,解得x=y=4,所以,点F的坐标为(4,4),∵点F的坐标为(4,4)不在△ABC内,故△ABC内部不存在点F,使得点F经过上述操作后得到的对应点F′与点F重合.14.解:(1)在y=﹣x2+x+2中,令y=0,即0=﹣x2+x+2,解得:x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),令x=0,即y=2,∴C(0,2);(2)如图,当抛物线经过A1(2,6),B1(﹣4,6)时,设抛物线的解析式,y=﹣x2+bx+c,则有,解得,,∴抛物线的解析式为y=﹣x2﹣2x+14=﹣(x+1)2+15,当抛物线经过A2(﹣2,﹣2),B2(4,﹣2)时,同法可得抛物线的解析式为:y=﹣x2+2x+6=﹣(x﹣1)2+7.∵原来的抛物线的解析式为y=﹣(x﹣)2+,∴+1=,15﹣=,∴原来抛物线向左平移,再向上平移单位得到y=﹣x2﹣2x+14.1﹣=,7﹣=,原来抛物线向右平移单位,再向上平移单位得到y=﹣x2+2x+6.二.作图-位似变换15.解:第一个图形中的位似中心为A点,第二个图形中的位似中心为AD与BC的交点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.故选:A.16.解:如图所示:位似中心F的坐标为:(2,2),k的值为:=.故选:B.17.解:过点A作x轴的平行线DD′,作CD⊥DD′于D,作C′D′⊥DD′于D′,设C(x,y),则CD=y﹣2、AD=﹣x,C′D′=2﹣n,AD′=m,∵△AB′C′与△ABC的位似比为2:1,∴==,即==,解得:x=﹣m,y=﹣n+3,∴点C的坐标为(﹣m,﹣n+3),故选:A.18.解:由题意得,点A与点C是对应点,△AOB与△COD的相似比是3,∴点C的坐标为(3×,6×),即(1,2),当点C值第三象限时,C(﹣1,﹣2)故答案为:(1,2)或(﹣1,﹣2).19.解:∵以点O为位似中心,把△ABC放大2倍得到△A'B'C'',∴AB∥A'B,△ABC∽△A'B'C';AO:AA'=2:1;点C、O、C'三点在同一直线上,①①②④正确,故答案为:①②④.20.解:∵OA=2.OC=1,∴B(﹣2,1),∴矩形AOCB的对称中心的坐标为(﹣1,),∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,∴B1(﹣3,),同理可得B2(﹣,),B3(﹣,),B4(﹣,),∴矩形A4OC4B4的对称中心的坐标是(﹣,).故答案为(﹣1,),(﹣,).21.解:在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(1,﹣2.5),不在同一象限内,∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),∴则点A′的坐标为:(﹣1,2.5),故答案为:(﹣1,2.5).22.解:如图所示:△A1B1C1和△A′B′C′与△ABC的相似比为2,点B的对应点B1的坐标是:(4,2)或(﹣4,﹣2).故答案为:(4,2)或(﹣4,﹣2).23.解:(1)如图,△DEF即为所求;(2)M′(﹣2a,﹣2b).故答案为:﹣2a,﹣2b.24.解:(1)如图点O即为位似中心;(2)设点P(a,b)为△ABC内一点,则点P在△A1B1C1内的对应点P1的坐标(2a,2b).25.解:(1)如图,点M为所作,M点的坐标为(0,2);(2)如图,△A2B2C2即为所求;(3)C2(﹣4,2).26.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.A2的坐标(﹣2.,﹣2).27.解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.28.解:(1)如图,(2)2:1,(3)A′(﹣6,0),B′(﹣3,2),C′(﹣4,4).。
九年级数学下册27、3位似第2课时平面直角坐标系中的位似变换习题新版新人教版

(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°, 得到△A1B1C1,请画出△A1B1C1; 解:如图,△A1B1C1即为所求.
(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的 位似图形△A2B2C2,使它与△ABC的相似比为2∶1. 解:如图,△A2B2C2即为所求.
10 【教材P49例变式】如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).
人教版 九年级
第二十七章 相似
27.3
位似
第2课时 平面直角坐标系中的位似变换
习题链接
温馨提示:点击 进入讲评
1C 2D 3A 4A
5 6 (4,2) 7D 8
答案呈现
9
10 11 12
1 【中考·辽阳】如图,在由边长为1的小正方形组成的 网格中,建立平面直角坐标系,△ABO与△A′B′O′是 以点P为位似中心的位似图形,它们的顶点均在格点 (网格线的交点)上,则点P的坐标为( C ) A.(0,0) B.(0,1) C.(-3,2) D.(3,-2)
【点拨】 以原点O为位似中心把△AOB放大到原来的2倍,则
点P(m,n)的对应点的坐标为(m×2,n×2)或(m×(-2), n×(-2)),即(2m,2n)或(-2m,-2n).本题易忽略其中 一种情况,应考虑全面.
9 【2020·朝阳】如图所示的平面直角坐标系中, △ABC的三个顶点坐标分别为A(-3,2),B(-1,3), C(-1,1),请按如下要求画图:
(1)若函数y=kx+b的图象过点(3,1),求b的值; 解:由已知得k=-2, 把点(3,1)的坐标和k=-2代入y=kx+b, 得1=-2×3+b, 解得b=7.
人教版九年级数学下册27.3 位似 同步练习附答案【选新】

练习 位 似一、自主学习1.位似图形上某一对对应顶点到位中心的距离分别为5 cm 和15 cm ,则它们的相似比为_________2.如图27-33,蜡烛与成像板之间的距离为3m ,小孔纸板距蜡烛1m ,若蜡烛AB 长20cm ,则所成的像长为_________cm.图27-333.四边形ABCD 和四边形A 'B 'C 'D '是位似图形,O 为位似中心,若OA ∶OA ',=1∶2,那么AB ∶A 'B '=________,S 四边形ABCD ∶S 四边形A 'B 'C 'D '=________. 二、基础巩固4.如图27-34所示,点O 是等边△PQR 的中心,P ,Q ',R '分别是OP 、OQ 、OR 的中点,则△P 'Q 'R '与△PQR 是________,点O 是_____,相似比是________.图27-34 图27-355.如图27-35所示,矩形AOBC 与DOEF 是位似图形,且O 为位似中心,相似比为1∶2,若A(0,1)、B(2,0),则F 点的坐标为________.6.下列两个图形不是位似图形的是( )7.把△ABC 三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A 'B 'C ',的坐标A ',(0,3)、B '(6,0)、C(9,6),那么△ABC 与△A 'B 'C '是______图形,位似中心是_______,相似比为________8.把△ABC 三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以-3,得△A 'B 'C ',的坐标A '(0,-3)、B (-6,0)、C '(-9,-6),那么△ABC 与△A 'B 'C '是_____图形,位似中心是_____,相似比为_____.9.如图27-36所示,按如下方法将△ABC 的三边缩小为原来的21,任取一点O ,连AO 、BO 、CO ,并取它们的中点D 、E 、F ,则下列说法: (1)△ABC 与△DEF 是位似形. (2)△ABC ∽△DEF.(3)△ABC 与△DEF 周长的比为2∶1(4)△ABC 与△DEF 面积的比为4∶1.其中正确的个数是( )图27-36A.1B.2C.3D.410.图27-36中,△ABC 与△DEF 是位似图形.那么,DE 与AB 平行吗?为什么?EF 与BC 呢?DF 与AC 呢?11.如图27-37所示,O 为四边形ABCD 上一点,以O 为位似中心,将四边形ABCD 放大为原来的2倍.12.如图27-38所示,O 为位似中心,将△ABC 缩小为原来的32(要求对应顶点在位似中心的同旁). 13.如图27-39所示,O 为位似中心,将△ABC 放大为原来的2倍(要求对应顶点在位似中心的两旁).图27-37 图27-38 图27-39三、能力提高14.有一个正六边形,将其按比例缩小,使得缩小后的正六边形的面积为原正六边形面积的31,已知原正六边形一边为3,则后来正六边形的边长为( )A.9B.3C.3D.332 15.在任意一个三角形内部,画一个小三角形,使其各边与原三角形各边平行,则它们的位似中心是( )A.一定点B.原三角形三边垂直平分线的交点C.原三角形角平分线的交点D.位置不定的一点 16.下列说法正确的个数是( )①位似图形一定是相似图形; ②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.A.1个B.2个C.3个D.4个17.若两个图形位似,则下列叙述不正确的是( )A.每对对应点所在的直线相交于同一点;B.两个图形上的对应线段之比等于相似比C.两个图形上对应线段必平行D.两个图形的面积比等于相似比的平方18.如图27-40所示,在直角坐标系中,A(1,2),B(2,4),C(4,5),D(3,1)围成四边形ABCD.作出四边形ABCD的位似图形,使得新图形与原图形对应线段的比为2∶1,位似中心是坐标原点.图27-4019.(1)如图27-41所示,作山四边形ABCD的位似图形A'B'C'D',使四边形ABCD与四边形A'B'C'D'的相似比为2∶1;(2)若已知AB=2cm,BC=3cm,∠A=60°,AB⊥BC,CD⊥DA,求四边形A'B'C'D'的面积.图27-4120.正方形ABCD各顶点的坐标分别为A(1,1),B(-1,1),C(-1,2),D(1,2),以坐标原点为位似中心,将正方形ABCD放大,使放大后的正方形A'B'C'D'的边是正方形边的3倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版九年级数学下册平面直角坐标系中的位似同步
练习
基础训练
知识点1 平面直角坐标系中点的位似
1.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A'B'O.若点A的坐标是(1,2),则点A'的坐标是( )
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
3.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,所得到的图形是△A'B'C.设点B的对应点B'的横坐标是a,则点B的横坐标是( )
A.-a
B.-(a+1)
C.-(a-1)
D.-(a+3)
4.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标是_________.
5.如图,已知图中的每个小方格都是边长为1的小正方形,每个
小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是_________.
知识点2 位似在坐标系中的简单应用
6.人们给电脑屏幕也建立了坐标系,如果把电脑屏幕的左上角定为坐标原点(0,0),右下角的点的坐标是(640,-480),则屏幕正中央的点的坐标是_________.
7.如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶
点”的坐标为(a,b) ,那么大“鱼”上对应“顶点”的坐标为( )
A.(-a,-2b)
B.(-2a,-b)
C.(-2a,-2b)
D.(-2b,-2a)
8.如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x 轴﹨y轴的正半轴上,正方形A'B'C'D'与正方形ABCD是以AC 的中点O'为中心的位似图形.已知AC=3,若点A'的坐标为(1,2),则正方形A'B'C'D'与正方形ABCD的相似比是( )
A. B. C. D.
9.如图,将△ABC以点G为位似中心缩小到原来的,得到△A'B'C',写出变化前后两个三角形各顶点的坐标.
10.在13×13的网格中,已知△ABC和点M(1,2).
(1)以点M为位似中心,位似比为2∶1,画出△ABC的位似图形△A'B'C';
(2)写出△A'B'C'的各顶点坐标.
11.如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1). (1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使△A2B2C2与△ABC位似且=.
提升训练
考查角度1 在坐标平面内作位似图形并求其面积(割补法) 12.如图,已知△AB C在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC
位似,且位似比为2∶1,并直接写出C2点的坐标及△A2BC2的面积.
考查角度2 位似图形与一次函数的综合应用(函数思想﹨数形结合思想)
13.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),求这两个正方形的位似中心的坐标.
参考答案
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】(,)
5.【答案】(9,0)
6.【答案】(320,-240)
7.【答案】C
8.【答案】B
9.解:△ABC的各顶点坐标分别为A(0,0),B(5,2),C(0,4),G点坐标为(-2,0).∵△ABC以点G为位似中心缩小到原来的,得到△A'B'C',∴△A'B'C'的各顶点坐标分别为A'(-1,0),B'(1.5,1),C'(-1,2).
误区诊断:应用坐标变化规律时容易忽视前提条件,而以坐标原点为位似中心.在这个问题中,位似中心是点G(-2,0),而非原点,所以不能直接将坐标缩为原来的.
10.解:(1)如图所示,△A'B'C'即为所求;
(2)△A'B'C'的各顶点坐标分别为:A'(3,6),B'(5,2),C'(11,4).
11.解:(1)如图所示,△A1B1C1即为所求.△A1B1C1的各顶点坐标
为:A1(1,-3),B1(4,-2),C1(2,-1).
(2)如图所示,△A2B2C2即为所求.
12.解:(1)△A1B1C1如图所示,C1(2,-2);
(2)△A 2BC2如图所示,C2(1,0),=10.
13.解:①当两个位似图形在位似中心同旁时,连接CF,位似中心就是直线CF与x轴的交点.
设直线CF的解析式为y=kx+b,将点C(4,2),F(1,1)的坐标代入,得
解得
故直线CF的解析式为y=x+.
当y=0时,x=-2,所以直线CF交x轴于点(-2,0),即位似中心为点(-2,0).
②当位似中心在两个正方形之间时,易知直线OC的解析式为y=x,直线BG的解析式为y=-x+1.
联立解得
即位似中心为.
综上所述,这两个正方形的位似中心的坐标为(-2,0)或.。
