双语版材料力学第四章
材料力学(双语)Bending弯曲
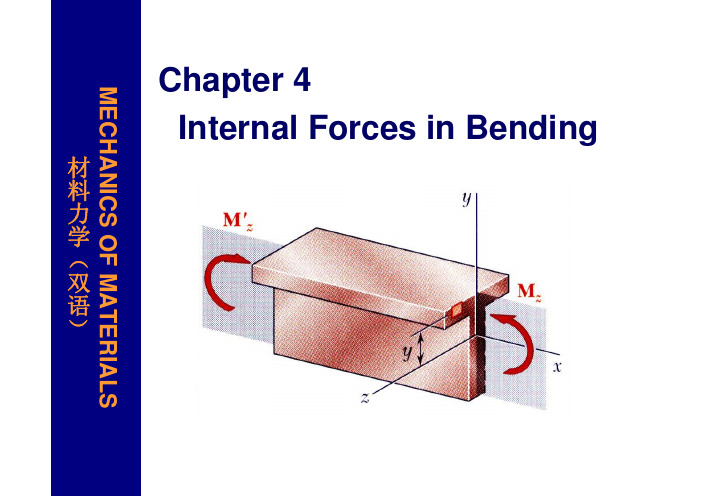
Chapter 4 Internal Forces in BendingMECHANICS OF MATERIALS 材料力学(双语)Content§4.1 Concept of symmetrical bending and calculation sketch of the beam §4.2 The shearing force and bending moment of the beam §4.3 The shearing-force and bending-moment equations · the shearing-force and bending-moment diagrams §4.4 Relations among the shearing force、the bending moment and the density of the distributed load and their applications §4.5 Plot the bending-moment diagram by the theorem of superposition §4.6 The internal-force diagrams of the planar rigid frames and curved rods2目录§4.1 对称弯曲的概念及梁的计算简图 §4.2 梁的剪力和弯矩 §4.3 剪力方程和弯矩方程 ·剪力图和弯矩图 §4.4 剪力、弯矩与分布荷载集度间的关系及应用 §4.5 按叠加原理作弯矩图 §4.6 平面刚架和曲杆的内力图34.1 Concept of symmetrical bending and calculation sketch of the beam1. Concepts of Bending 1). BENDING(弯曲): The action of the external force or the external couple vector perpendicular to the axis of the rod makes the axis of the rod change into curve from original straight lines, this deformation is called bending. 2). BEAM(梁): The member of whose deformation is mainly bending is generally called beam.43). Practical example in engineering about bending564). Symmetric bending(平面弯曲) After deformation the curved axis of the beam is still in the same plane with the external forces. P1 q P2MThe plane of symmetry7Unsymmetrical bending: If a beam does not possess any plane of symmetry, or the external forces do not act in a plane of symmetry of the beam with symmetric planes, this kind of bending is called unsymmetrical bending.82. Calculation sketch of the beamIn general supports and external forces of the beam are very complex. We should do some necessary simplification for them for our convenient calculation and obtain the calculation sketch.1). Simplification(简化) of the beamsIn general case we take the place of the beam by its axis.2). Simplification of the loads (荷载)The loads (including the reaction) acting on the beam may be reduced into three types:concentrated force、concentrated force couple and distributed force.3). Simplification of the supports (支座条件)9①Fixed hinged support固定铰支座2 constraints,1 degree of freedom. Such as the fixed hinged support under bridges.②Movable hinged support可动铰支座1 constraint,2 degree of freedom. Such as the movable hinged support under the bridge.10θA BDB R RA A AB B B0.50.50.5P0.5PP0.50.50.5P0.5PP 0。
材料力学(I)第四章(配孙训方版)

M (x)
距右端为x的任意横截面上的剪力FS(x)和弯矩M(x),根 据截面右侧梁段上的荷载有
FS ( x ) = qx
(0 ≤ x < l ) (0 ≤ x < l )
x qx 2 M ( x ) = − qx ⋅ = − 2 2
29
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
2. 作剪力图和弯矩图 根据剪力方程和弯矩方程作出剪力图和弯矩图分别如 图b和图c。按照习惯,剪力图中正值的剪力值绘于x轴上方, 弯矩图中正值的弯矩值则绘于x轴的下方(即弯矩值绘于梁 弯曲时其受拉的边缘一侧)。 (b) FS ( x ) = qx
)(
)
M A = 96.5 kN ⋅ m
15
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
2. 此梁的约束力亦可将梁在中间铰C处拆开,先利用 CB段梁作为分离体求约束力FBy和AC段梁在中间铰C处作用 在CB段梁上的FCx和FCy,然后利用AC段梁作为分离体求约 束力FAx,FAy和MA。
16
37
Fb (0 < x < a ) FS ( x ) = FA = l Fb M ( x ) = FA x = x (0 ≤ x ≤ a ) l
13
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
于是可求得约束力如下:
∑M
− 20 × 103 N
(
C
=0 m
× 3 m × 2.5 m + 5 ×103 N ⋅ m + FBy × 5 m = 0
FBy = 29 kN
)
14
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
材料力学第四章

二、横截面上的应力 1.圆轴扭转的刚性平面假设:
r s T T r
s
变形前圆轴的横截面,变形后仍保持为同样 大小的圆形平面,半径仍为直线,相邻两截 面间距不变。
§4-2
等直圆杆扭转时的应力和变形
二、横截面上的应力 三关系法则 2.公式推导: 1)几何关系: 1 2
dj A C' dx —单位长度 扭转角
第四章
• §4-1 概 述
扭
转
• §4-2 等直圆杆扭转时的应力和变形 • §4-3 等直圆杆扭转时的强度和刚度计算
• §4-4 非圆截面杆的扭转
• §4-5 螺旋弹簧的计算
• 小 结
§4-1 一、工程实例 1.传动轴:
概
述
§4-1 一、工程实例 2.钻孔:
概
述
3.汽车转向轴,螺丝刀拧螺丝
§4-1
T 180 1.84o /m [ ] GI p
§4-3
等直圆杆扭转时的强度和刚度
例4-2 主传动轴外径D=76mm,壁厚t=2.5mm,传递扭矩 T=1.98kN· m,材料[ ]=100MPa,G=80GPa,[ ]=2o/m, 校核轴的强度与刚度,若采用强度相同的实心轴, 试比较两者使用的材料。 2)采用实心轴时的直径(max=97.5MPa): T 16T max 97.5 MPa d ' 46.9 mm 3 Wp ' (d ' ) 3)空心轴与实心轴的材料比: 2 2 2 1 取相同长度,只需 A空 ( D d ) (d ' ) : 0.334 比较横截面面积 A实 4 4 3 对于相同强度的受扭构件,空心轴较实心轴节省材料;
A
D
材料力学-第4章_576102068

径越小者剪应变越小。
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
设到轴线任意远ρ处的剪应变为γ(ρ),则从图中可得
到如下几何关系:
γ (ρ ) = ρ dϕ
dx
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
圆轴扭转时横截面上的 剪应力分析与强度设计
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
应用平衡方法可以确定圆杆扭转时横截面上的内力分 量——扭矩,但是不能确定横截面上各点剪应力的大小。为 了确定横截面上各点的剪应力,在确定了扭矩后,还必须知 道横截面上的剪应力是怎样分布的。
工程中承受扭转的圆轴
请判断哪一杆件 将发生扭转?
连接汽轮机和发 电机的传动轴将产生 扭转。
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律 圆轴扭转时横截面上的剪应力分析
与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
x
τ =τ′
第4章 圆轴扭转时的强度与刚度计算
剪应力互等定理 剪切胡克定律
y
材料力学第四章习题选及其解答.docx

4-1. 试求图示各梁中截面1、2、3上的剪力和弯矩,这些截面无限接近于截面C或D 。
设p 、q 、a 均为已知。
解:(c )(1)截开1截面,取右段,加内力(22112322qaa qa a P M qaqa P Q -=⨯-⨯-==+=(3)截开2截面,取右段,加内力(4)求内力2222122qaM a qa a P M qaqa P Q -=+⨯-⨯-==+=(d )(1)求约束反力N R N R D A 300 100==(2)截开1截面,取左段,加内力(d)B(f)B(c)M=qa 2M M M=qa 2B(3)求1截面内力NmR M N R Q A A 202.010011-=⨯-=-=-=(4)截开2截面,取左段,加内力(5)求2截面内力NmR M N R Q A A 404.010022-=⨯-=-=-=(6)截开3截面,取右段,加内力(7)求3截面内力NmP M N P Q 402.020023-=⨯-===(f )(1)求约束反力qa R qa R D C 25 21==(2)截开1截面,取左段,加内力Q 1M 12BMB(3)求1截面内力2112121 qa a qa M qa Q -=⨯-=-=(4)截开2截面,取右段,加内力(5)求2截面内力222223qa M a P M qaR P Q D -=-⨯=-=-= 4-3. 已知图示各梁的载荷P 、q 、M0和尺寸a 。
(1)列出梁的剪力方程和弯矩方程;(2)作剪力图和弯矩图;(3)确定∣Q ∣max 和∣M ∣max 。
q(c)M 0=qa 2 (d)(f)(e) (g)q(h)1BM (a)(b) Bq解:(a )(1)求约束反力Pa M P R A A == 2(2)列剪力方程和弯矩方程⎪⎩⎪⎨⎧∈=-⨯-+⨯=∈-=+⨯=⎩⎨⎧∈=-=∈==),0[ )(2)(],0( 2)(]2,( 02)(),0( 2)(2222211111222111a x Pa a x P M x R x M a x Pa Px M x R x M a a x P R x Q a x P R x Q A A A A A A (3)画Q 图和M 图(4)最大剪力和最大弯矩值(i)q(j)BP=20kN(l)q(k)qM xxPa M P Q ==max max 2(b )(1)求约束反力223 qa M qa R B B ==(2)列剪力方程和弯矩方程⎪⎪⎩⎪⎪⎨⎧∈-⨯-=∈-=⎩⎨⎧∈-=∈-=)2,[ )2()(],0[ 21)()2,[ )(],0[ )(2222121112221111a a x a x qa x M a x qx x M a a x qa x Q a x qx x Q (3)画Q 图和M 图(4)最大剪力和最大弯矩值2maxmax 23 qa M qa Q == (c )(1)求约束反力qBxxqM 0=qa 2M2 2qa M qa R A A ==(2)直接画Q 图和M 图(3)最大剪力和最大弯矩值2max max 2qa M qa Q ==(d )(1)求约束反力P R R B A == 0(2)直接画Q 图和M 图(3)最大剪力和最大弯矩值Pa M P Q ==max maxxxxx。
材料力学第四章轴力、剪力与弯矩

x
所以, 又可得到剪力与弯矩图的如下规律: 1) 梁上某段无分布载荷时, 该段剪力图为水平线, 弯矩图为斜线. V>0, M图递 增, V<0, M 图递减. 2) 某段有向下分布载荷时, 该段剪力图递减, 弯矩图为凹向下曲线(concave down); 反之, 则凹向上(concave up). (Vice verse) 3) 在V=0处, M=Mmax or M=Mmin 弯矩取极值. 此外, 弯矩极值也可能发生在 集中力或集中力偶作用处. 此时, 相应的曲线会有突变, 突变值等于集中力 或集中力偶. 利用以上规律可以比较方便的作出剪力图与弯矩图, 并校核其正确性.
4-2 Direct approach: axial force, shear, bending moment
要求得梁上某处的内力, 依然可用截面法. 梁平衡, 局部也平衡. 1. Axial force in beams From ∑Fx= 0 one can get the axial force P
M(x)
3. Draw the P, V, M diagrams
Example 4-2 Plot shear and a bending-moment diagrams for a simple beam with a uniformly distributed load; see Fig.. Solution: 1 Calculate the reactions 2 Calculate V(x), M(x). Study the left segment
Example 4-1 Construct axial-force, shear, and bending-moment diagrams for the cantilever loaded with an inclined force at the end; see the figure. Solution: 1. Calculate reactions 2. Calculate P, V, M. Study left segment: ∑Fx=0 P(x)=P ∑Fy=0 V(x)=P ∑MCz=0, PL-Px+M(x)=0 M(x)=-PL+Px
材料力学第四章

Q1 QC左 R A 4 KN
M 1 M C左 R A 1 4 KN.m
RA
A
10KN.m 2 1
1m 2.5m
RB
B
C 1 C
2
求 2 截面的内力: 右侧
Q2 QC右 RB ( 4) 4 KN
M 2 M C右 RB ( 2.5 1) ( 4) 1.5 6 KN.m
b
RA
记 E 截面处的剪力
A
a E c
P1
C
P2
D
RB
B
为 QE 和弯矩 ME ,
且假设 QE 和弯矩
F
d
l
QE
E
C
ME 的指向和转向
均为 正值。
RA
A
ME
b
y 0, RA QE 0
RA
A
a E c
P1
C
P2
D
RB
B
mE 0, M E R A c 0
F
d
解得
l
第四章
弯曲内力
§4-1(2) 平面弯曲的概念及计算简图 §4-2 梁的剪力和弯矩 §4-3 剪力方程和弯矩方程 · 剪力图和弯矩图
§4-4 弯矩,剪力与分布荷载集度之间的关系及应用
§4-5 平面桁架和曲杆的内力图
§4-1 平面弯曲的概念及梁的计算简图
I. 弯曲的概念 弯曲变形 受力特征:外力是作用线垂直于杆轴线的平衡力系 (有时还包括力偶)。
横截面上的 弯矩 在数值上等于此横截面的 左侧 或 右侧 梁段上的 外力对该截面形心的力矩之代数和 。
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩,而向下 的外力则引起 负值 的弯矩。
工程力学 材料力学 M4弯曲内力

二、梁的简化 梁的支承条件与载荷情况一般都比较复杂,为 了便于分析计算,应进行必要的简化,抽象出计算 简图。 1. 构件本身的简化
通常取梁的轴线来代替梁。 2. 载荷简化 作用于梁上的载荷(包括支座反力)可简化为三 种类型:集中力、集中力偶和分布载荷。 3. 支座简化
《材料力学》 第4章 弯曲内力 14
M(+) M(+) M(–)
《材料力学》 第4章 弯曲内力
M(–)
39
弯曲内力—剪力和弯矩
4.分别取截面左右为研究对象进行计算(验证)
l
a
A
F B A
a
YA
F
B
x
C
x
l
FB
M
YA
x
M
F
Q
F C
y
0 : YA Q 0 Q YA
M
FB
C
0 : M YA x 0 M YA x
第4章 弯曲内力
弯曲的概念和实例 受弯杆件的简化 剪力和弯矩 剪力方程和弯矩方程 剪力图和弯矩图 载荷集度、剪力和弯矩间的关系 平面曲杆的弯曲内力
《材料力学》
第4章 弯曲内力
1
第4章 弯曲内力
弯曲的概念和实例 受弯杆件的简化 剪力和弯矩 剪力方程和弯矩方程 剪力图和弯矩图 载荷集度、剪力和弯矩间的关系 平面曲杆的弯曲内力
《材料力学》 第4章 弯曲内力
例题:计算约束力 q =20kN/m F MA Me=5kN· m C A B FAx D E K FBy FAy 1m 3m 1m 1m
0.5m
F F
x
0, 0,
A
FAx 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称弯曲(如下图)—— 平面弯曲的特例。
P1 q P2
M
纵向对称面
28
Unsymmetrical bending— if a beam does not possess any plane of symmetry, or the external forces do not act in a plane of symmetry of the beam with symmetric planes, this kind of bending is called unsymmetrical bending. In later chapters we will mainly discuss the bending stresses and deformations of the beam under symmetric bending. 29
§4–1 Concepts of planar bending and calculation sketch of the beam
§4–2 The shearing force and bending moment of the beam §4–3 The shearing-force and bending-moment equations
诚实是力量的一种 象征,它显示着一个人 的高琳· 卡瑟
1
走正直诚实的生 活道路,定会有一个 问心无愧的归宿。 ——高尔基
2
Mechanics of Materials
3
第四章
弯曲内力
4
CHAPTER 4
INTERNAL FORCES IN BENDING
9
3. 工程实例
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
4).Planar bending:After deformation the curved axis of the beam is still in the same plane with the external forces.
the shearing-force and the bending-moment diagrams
§4–4 Relations among the shearing force、the bending moment and the density of the distributed load and their applications §4–5 Plot the bending-moment diagram by the theorem of superposition
非对称弯曲—— 若梁不具有纵对称面,或者,梁虽具有纵 对称面但外力并不作用在对称面内,这种
弯曲则统称为非对称弯曲。
下面几章中,将以对称弯曲为主,讨论梁的应力和变 形计算。
30
2、Calculation sketch of the beam In general supports and external forces of the beam are very complex. We should do some necessary simplification for them for our convenient calculation and obtain the calculation sketch. 1). Simplification of the beams
1). BENDING: The action of the external force or the external couple vector perpendicular to the axis of the rod makes the axis of the rod change into curve from original straight lines, this deformation is called bending. 2).BEAM:The member of which the deformation is mainly bending is generally called beam.
§4–4 剪力、弯矩与分布荷载集度间的关系及应用
§4–5 按叠加原理作弯矩图 §4–6 平面刚架和曲杆的内力图 弯曲内力习题课
6
§4–1
CONCEPTS OF PLANAR BENDING AND CALCULATION SKETCH OF THE BEAM
1、CONCEPTS OF BENDING
In general case we take the place of the beam by its axis.
2). Simplification of the loads The loads (including the reaction) acting on the beam may be reduced into three types:
Symmetric bending(as shown in the following figure) — a special example of the planar bending. P1 q
P2
M
The plane of symmetry
27
4. 平面弯曲:杆发生弯曲变形后,轴线仍然和外力在同一 平面内。
7
§4–1 平面弯曲的概念及梁的计算简图
一、弯曲的概念 1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴 线变成了曲线,这种变形称为弯曲。 2. 梁:以弯曲变形为主的 构件通常称为梁。
8
3).Practical examples in engineering about bending
§4–6 The internal-force diagrams of the planar rigid theorem
for frames and curved rods Exercise lessons about the internal force of bending
5
第四章
弯曲内力
§4–1 平面弯曲的概念及梁的计算简图 §4–2 梁的剪力和弯矩 §4–3 剪力方程和弯矩方程 · 剪力图和弯矩图
