高二数学空间向量与立体几何
2024-2025学年上学期高二数学章末(空间向量与立体几何)测试卷

2024-2025学年上学期高二数学章末测试卷选择性必修第一册空间向量与立体几何姓名:___________班级:___________一、单选题1.已知空间向量()6,2,1a =,()2,,3b x =- ,若()2a b a -⊥ ,则x =()A .4B .6C .234D .2142.平面α的一个法向量是1(2n = ,1-,1)3,平面β的一个法向量是(3m =- ,6,2)-,则平面α与平面β的关系是()A .平行B .重合C .平行或重合D .垂直3.如图,四棱锥P OABC -的底面是矩形,设OA a = ,OC b = ,OP c =,E 是棱PC 上一点,且2PE EC =,则BE =()A .111333a b c--+ B .1133a b c--+C .1133a b c-++ D .1133a b c--- 4.如图,在空间直角坐标系O xyz -中,正方形ABCD 与矩形ACEF 所在平面互相垂直(C 与原点O 重合),2,1,AB AF M ==在EF 上,且//AM 平面BDE ,则M 点的坐标为()A .(1,1,1)B .22,,133⎛⎫⎪ ⎪⎝⎭C .22,,122⎛⎫ ⎪ ⎪⎝⎭D .22,,144⎛⎫⎪ ⎪⎝⎭5.在一直角坐标系中,已知(1,6),(3,8)A B --,现沿x 轴将坐标平面折成60︒的二面角,则折叠后,A B 两点间的距离为A .241B .41C .17D .2176.已知平行六面体1111ABCD A B C D -的各棱长均为1,1160A AB A AD ∠=∠=︒,90DAB ∠=︒,则1AC =()A .3B .5C .2D .21+7.鳖臑是指四个面都是直角三角形的三棱锥.如图,在鳖臑P ABC -中,PA ⊥平面ABC ,2AB BC PA ===,D ,E 分别是棱AB ,PC 的中点,点F 是线段DE 的中点,则点F 到直线AC 的距离是()A .38B 4C .118D .48.在下图所示直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,π1,3AB DAB =∠=,12AA =,动点P 在体对角线1BD 上,则顶点B 到平面APC 距离的最大值为()A .12B C D 二、多选题9.(多选)下面关于空间直角坐标系的叙述正确的是()A .点(1,1,0)P -与点(1,1,0)Q 关于z 轴对称B .点(3,1,4)A --与点(3,1,4)B --关于y 轴对称C .点(3,1,4)A --与点(3,1,4)B --关于平面xOz 对称D .空间直角坐标系中的三条坐标轴组成的平面把空间分为八个部分10.已知空间中三点()2,1,1A -,()1,0,2B ,()0,3,1C -,则()A .AB =B .AB AC⊥C .cos 19ABC ∠=D .A ,B ,C 三点共线11.在正方体1111ABCD A B C D -中,1M AD ∈,N BD ∈,且满足113AM AD =,23BN BD =,则下列说法正确的是()A .1AD MN⊥B .1MN A C∥C .MN ∥平面11DCC D D .MN 为1AD 与BD 的公垂线三、填空题12.在Rt ABC △中,90BAC ∠=︒,(2,1,1)A ,(1,1,2)B ,(,0,1)C x ,则x =.13.已知向量()()2,4,5,4,,a b x y ==,分别是直线12l l 、的方向向量,若12//l l ,则x y +=.14.如图所示,若P 为平行四边形ABCD 所在平面外一点,H 为棱PC 上的点,且12PH HC =,点G 在AH 上,且AGm AH=,若G ,B ,P ,D 四点共面,则实数m 的值是.四、解答题15.如图,在棱长为2的正方体中,,E F 分别是1,DD DB 的中点,G 在棱CD 上,且13CG CD =,H 是1C G 的中点.建立适当的空间直角坐标系,解决下列问题:(1)求证:1EF B C ⊥;(2)求异面直线EF 与1C G 所成角的余弦值.16.如图,在直三棱柱111ABC A B C -中,D ,E ,F 分别为AB ,BC ,1B B 的中点.(1)证明:11//AC 平面1B DE ;(2)若1AB =,AB AC ⊥,11B D A F ⊥,求点E 到平面11A FC 的距离.17.在平行六面体1111ABCD A B C D -中,设AB a =,AD b =,1AA c = ,E ,F 分别是1AD ,BD 的中点.(1)用向量a ,b ,c表示1D B ,EF ;(2)若1D F xa yb zc =++,求1D F 在基{},,a b c 下的坐标.18.如图,在平面四边形ABCD 中,//AB DC ,ABD △是边长为2的正三角形,3,DC O =为AB 的中点,将AOD △沿OD 折到POD 的位置,PC =.(1)求证:PO BD ⊥;(2)若E 为PC 的中点,求直线BE 与平面PDC 所成角的正弦值.19.如图,将等腰直角△ABC 沿斜边AC 旋转,使得B 到达B ′的位置,且BB ′=A B .(1)证明:平面AB ′C ⊥平面ABC ;(2)求二面角B -AB ′-C 的余弦值;(3)若在棱CB ′上存在点M ,使得14,,55CM CB μμ⎡⎤'=∈⎢⎥⎣⎦,在棱BB ′上存在点N ,使得BN BB λ'= ,且BM ⊥AN ,求λ的取值范围.参考答案题号12345678910答案C CBCDBBABDAB题号11答案ABD1.【详解】因为()()()26,2,122,,32,22,7a b x x -=--=- ,因为()2a b a -⊥ ,所以124470x +-+=,解得234x =.故选:C.2.【详解】 平面α的一个法向量是1(2n = ,1-,1)3,平面β的一个法向量是(3m =- ,6,2)-,∴6m n =-,∴平面α与平面β的关系是平行或重合.故选:C .3.【详解】由已知2()()3BE OE OB OP PE OA OC OP PC OA OC =-=+-+=+-+2()()3OP OC OP OA OC =+--+ 11113333OP OC OA a b c =--=--+.故选:B .4.【详解】设AC ,BD 交于点O ',连接O E ',因为正方形ABCD 与矩形ACEF 所在的平面互相垂直,点M 在EF 上,且//AM 平面BDE ,又平面BDE ⋂平面ACEF EO =',AM ⊂平面ACEF ,所以//AM O E ',又//AO EM ',所以O AME '是平行四边形,故1122FM O A AC EF '===,所以M 是EF 的中点,因为2,1AB AF ==,所以(0,0,1),(2,2,1)E F ,所以22,,122M ⎛⎫⎪ ⎪⎝⎭.故选:C 5.【详解】如图为折叠后的图形,其中作,AC CD BD CD ⊥⊥则6,8,4AC BD CD ===,∴0,0AC CD BD CD ⋅=⋅=沿x 轴将坐标平面折成60︒的二面角∴两异面直线,CA DB 所成的角为60︒.可得:.cos 6024CA DB CA DB ︒⋅=⋅=故由AB AC CD DB =++ 得22||||AB AC CD DB =++ 2222+22AC CD DB AC CD CD DB AC DB +++⋅⋅+⋅= 2222+22AC CD DB AC CD CD DB CA DB+++⋅⋅-⋅= 36166448=++-68=||AB ∴= D.6.【详解】取{}1,,AB AD AA 为空间向量的基底,因为11AB AD AA === ,90DAB ∠=︒,1160A AB A AD ∠=∠=︒,所以0AB AD ⋅=uuu r uuu r,1112AB AA AD AA ⋅=⋅= .因为11AC AB AD AA =++,所以()2211AC AB AD AA =++ 222111222AB AD AA AB AD AB AA AD AA =+++⋅+⋅+⋅1110115=+++++=,所以1AC =故选:B7.【详解】因为AB BC =,且ABC V 是直角三角形,所以AB BC ⊥.以B 为原点,分别以BC,BA的方向为x ,y 轴的正方向,建立如图所示的空间直角坐标系B xyz -.因为2AB BC PA ===,所以()0,2,0A ,()2,0,0C ,()0,1,0D ,()1,1,1E ,则()2,2,0AC =-,11,1,22AF ⎛⎫=- ⎝⎭ .故点F 到直线AC的距离d =故点F 到直线AC故选:B8.【详解】连接AC 交BD 于点O ,由题意,得AC BD ⊥,1122OB OD AB ===,OA OC ====,如图,以O 为原点建立如图所示的空间直角坐标系,则1110,,,0,0,0,,,0,22222A B C D ⎛⎫⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以()()11,,1,0,22AC AB BD ⎛⎫===- ⎪ ⎪⎝⎭,设()101BP BD λλ=≤≤ ,所以()1111,0,2222AP AB BP AB BD λλλλ⎛⎫⎛⎫=+=+=+-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ,设平面APC 的一个法向量为(),,n x y z = ,则n ACn AP⎧⊥⎪⎨⊥⎪⎩,所以001120222y n AC x n AP x z z λλλλ=⎧⎧⋅==⎪⎪⎪⎛⎫⇒-⎨⎨⎛⎫ ⎪⋅=-+++=⎝⎭⎪⎪ ⎪=⎝⎭⎩⎪⎩ ,取4x λ=,则()4,0,21n λλ=-,设顶点B 到平面APC 距离为d ,则AB n d n ⋅== 当0λ=时0d =,当01λ<≤时,d ===所以当12λ=即12λ=时点B 到平面APC 12=.故选:A.9.【详解】点(1,1,0)P -与点(1,1,0)Q 关于x 轴对称,故A 错误;点(3,1,4)A --与(3,1,4)B --关于y 轴对称,故B 正确;点(3,1,4)A --与(3,1,4)B --不关于平面xOz 对称,故C 错误;空间直角坐标系中的三条坐标轴组成的平面把空间分为八个部分,故D 正确.故选:BD .10.【详解】易得()1,1,3AB =-- ,()2,2,0AC =- ,()1,3,3CB =-,AB ∴= A 正确;因为0AB AC ⋅=,所以AB AC ⊥,B 正确,D 错误;而cos AB CB ABC AB CB⋅∠==⋅,C 错误.故选:AB.11.【详解】设正方体1111ABCD A B C D -的棱长为1,分别以1,,DA DC DD 为,,x y z 轴,建立空间直角坐标系.则()()11,0,0,0,0,1A D ,()1,1,0B ,()0,1,0C ,()11,0,1A 由113AM AD = ,则21,0,33M ⎛⎫⎪⎝⎭由23BN BD = ,则11,,033N ⎛⎫ ⎪⎝⎭所以111,,333MN ⎛⎫=-- ⎪⎝⎭,()11,0,1AD =-,则()11111010333MN AD ⎛⎫⋅=-⨯-+⨯+-⨯= ⎪⎝⎭,所以1AD MN ⊥,选项A 正确.又()11,1,1AC =-- ,则13AC MN = ,所以1//AC MN又1,MN A C 不在同一直线上,所以1//MN A C ,故选项B 正确.平面11DCC D 的一个法向量为()1,0,0n =r ,而1103MN n ⋅=-⨯≠ 所以MN 与平面11DCC D 不平行,故选项C 不正确.由()1,1,0DB = ,有1111100333MN BD ⎛⎫⋅=-⨯+⨯+-⨯= ⎪⎝⎭,所以NM DB ⊥,又1AD MN ⊥,且NM 与1,DB A D 均相交,所以MN 为1AD 与BD 的公垂线,故选项D 正确.故选:ABD12.【详解】||AC ==||BC ==,AB ==90BAC ∠=︒ ,222||||||BC AB AC ∴=+,22(1)22(2)1x x ∴-+=+-+,解得2x =.故答案为:2.13.【详解】12//l l ,//a b ∴,所以存在实数λ,使得b a λ= ,则4245x y λλλ=⎧⎪=⎨⎪=⎩,解得2λ=,8x =,10y =.18x y ∴+=.故答案为:18.14.【详解】连接BD ,BG 因为AB PB PA =- ,AB DC =,所以DC PB PA =- .因为PC PD DC =+,所以PC PD PB PA PA PB PD =+-=-++ .因为12PH HC =,所以13PH PC = ,所以111333PH PA PB PD =-++.又因为AH PH PA =- ,所以411333AH PA PB PD =-++.因为AG m AH=,所以4333m m m AG m AH PA PB PD ==-++ .又因为41333m m m PG PA AG PA PB PD ⎛⎫=+=-++ ⎪⎝⎭,且G ,B ,P ,D 四点共面,所以4103m -=,解得34m =.故答案为:3415.【详解】(1)证明:如图,以D 为原点,以射线DA 、DC 、1DD 分别为x 轴、y 轴、z 轴的正半轴,建立空间直角坐标系D xyz -,则()0,0,0D ,0,0,1,()1,1,0F ,()0,2,0C ,()10,2,2C ,()12,2,2B ,40,,03G ⎛⎫⎪⎝⎭,所以()1,1,1EF =-,()12,0,2B C =-- ,所以()()()()()11,1,12,0,21210120EF B C ⋅=-⋅--=⨯-+⨯+-⨯-=,所以1EF B C ⊥,故1EF B C ⊥.(2)因为120,,23C G ⎛⎫=-- ⎪⎝⎭,所以1C G =因为EF = ()12241,1,10,,22333EF C G ⎛⎫⋅=-⋅--=-+= ⎪⎝⎭ ,所以111443cos ,315EF C GEF C G EF C G⋅==⋅.16.【详解】(1)因为111ABC A B C -为直三棱柱,所以11//A C AC ,又D ,E ,分别为AB ,BC 的中点,所以//DE AC ,所以11//DE A C ,又11A C ⊄平面1B DE ,DE ⊂平面1B DE ,所以11//AC 平面1B DE .(2)因为111ABC A B C -为直三棱柱,且AB AC ⊥,以A 为坐标原点,分别以1,,AB AC AA 所在直线为,,x y z 轴,建立如图所示的空间直角坐标系,设()10AA a a =>,且1AB =,则()()1111,0,,,0,0,0,0,,1,0,22a B a D A a F ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则11,0,2B D a ⎛⎫=-- ⎪⎝⎭,11,0,2a A F ⎛⎫=- ⎪⎝⎭,由11B D A F ⊥可得110B D A F ⋅= ,即21022a -+=,且0a >,解得1a =,设()0AC b b =>,则()10,,1C b ,即()11111,0,,0,,02A F A C b ⎛⎫=-= ⎪⎝⎭,设平面11A FC 的法向量为(),,n x y z =,则1111020n A F x z n AC by ⎧⋅=-=⎪⎨⎪⋅==⎩ ,解得20z x y =⎧⎨=⎩,取1x =,则2z =,所以平面11A FC 的一个法向量为()1,0,2n =,又1,,022b E ⎛⎫ ⎪⎝⎭,即11,,122b A E ⎛⎫=- ⎪⎝⎭,所以点E 到平面11A FC的距离1A E n d n ⋅==17.【详解】(1)在平行六面体1111ABCD A B C D -中,连接AC ,EF ,1D F ,1BD ,如图,11D B D D DB =+ 1AA AB AD =-+- a b c =-- ,11122EF EA AF D A AC =+=+ 1)11()(22AA AD AB AD =-+++ 111112222AB AA a c =-=- .(2)111)1(2D F D D D B =+ 11)1(2AA D B =-+ 1()2c a b c =-+-- 1122a b c =-- xa yb zc =++ ,因此12x =,12y =-,1z =-,所以1D F 在基{},,a b c r r r 下的坐标为11(1)22--,,.18.【详解】(1)依题意ABD △是边长为2的正三角形,O 为AB 的中点,所以OD AB ⊥,所以OD PO ⊥,OD BO ⊥,2PD =,3CD =,PC =则222PD CD PC +=,所以PD CD ⊥,又//AB DC ,即//OB DC ,所以OB PD ⊥,又OD PD D ⋂=,,OD PD ⊂平面POD ,所以OB ⊥平面POD ,因为OP ⊂平面POD ,所以OB OP ⊥,又OB OD O = ,,OB OD ⊂平面BODC ,所以OP ⊥平面BODC ,又BD ⊂平面BODC ,所以PO BD ⊥;(2)如图建立空间直角坐标系,则1,0,0,0,0,1,()D,()C,3122E ⎛⎫ ⎪ ⎪⎝⎭,所以11,222BE ⎛⎫= ⎪ ⎪⎝⎭ ,()3,0,0DC =,()0,DP = ,设平面PDC 的法向量为(),,n x y z =,则300n DC x n DP z ⎧⋅==⎪⎨⋅=+=⎪⎩,令(n = ,设直线BE 与平面PDC 所成角为θ,则sin 5BE n BE nθ⋅===⋅ ,所以直线BE 与平面PDC19.【详解】(1)证明:设AC 的中点为O ,连接OB ,OB ',由题意可得,BB '=AB =AB '=BC =B 'C ,在△AB 'C 中,因为O 为AC 的中点,则OB '⊥AC ,即∠B 'OC =90°,则△OBB '≌△OCB ',所以∠B 'OB =∠B 'OC =90°,即OB '⊥OB ,因为AC ∩OB =O ,AC ,OB ⊂平面ABC ,故OB '⊥平面ABC ,又OB '⊂平面AB 'C ,所以平面AB ′C ⊥平面ABC ;(2)以点O 为坐标原点,建立空间直角坐标系如图所示,不妨设OA =1,则O (0,0,0),A (-1,0,0),B (0,1,0),B '(0,0,1),C (1,0,0),所以(1,1,0),(1,0,1)AB AB '== ,设平面ABB '的法向量为(),,n x y z = ,则00n AB n AB ⎧⋅=⎨⋅=⎩' ,即00x y x z +=⎧⎨+=⎩,令x =1,则y =z =-1,故(1,1,1)n =-- ,因为OB ⊥平面AB 'C ,所以平面AB 'C 的一个法向量为(0,1,0)OB = ,则|||cos ,|||||n OB n OB n OB ⋅〈〉=== 又二面角B -AB ′-C 为锐二面角,所以二面角B -AB ′-C的余弦值为3;(3)结合(2)可得,(1,1,0),(1,0,1),(0,1,1)BC CB BB ''=-=-=- 则(1,1,0)(0,1,1)(1,1,)AN AB BN AB BB λλλλ'=+=+=+-=- ,(1,1,0)(0,1,1)(1,1,)AN AB BN AB BB λλλλ'=+=+=+-=- ,因为BM ⊥AN,则0BM AN ⋅= ,即(1)(1)0μλμλ---+=,所以111λμ=-+,故λ是关于μ的单调递增函数,当14,55μ⎡⎤∈⎢⎣⎦时,14,69λ⎡⎤∈⎢⎥⎣⎦,故λ的取值范围为14,69⎡⎤⎢⎥⎣⎦.。
第一章+空间向量与立体几何-2024-2025学年高二数学上学期期中总结

考点透视 考向5 利用空间向量证明平行、垂直
【例题 5】如图,在四棱锥 P-ABCD 中,PA⊥底面 ABCD,AD⊥AB,AB∥DC, AD=DC=AP=2,AB=1,E 为棱 PC 的中点.证明:
(1)BE⊥DC; (2)BE∥平面 PAD; (3)平面 PCD⊥平面 PAD.
考点透视 考向5 利用空间向量证明平行、垂直
2.二面角与法向量的夹角:利用平面的法向量求二面角的大小时,当求出两个 半平面 α,β 的法向量 n1,n2 时,要根据向量坐标在图形中观察法向量的方向,来确 定二面角与向量 n1,n2 的夹角是相等,还是互补.
02 典例透析
考点透视 考点1.空间向量的线性运算
→
→
【例题 1】如图所示,在平行六面体 ABCD-A1B1C1D1 中,设AA1=a,AB=b,
(2)∵N 是 BC 的中点, ∴A→1N=A→1A+A→B+B→N=-a+b+12B→C=-a+b+12A→D=-a+b +12c.
(3)∵M 是 AA1 的中点, ∴M→P=M→A+A→P=12A→1A+A→P=-12a+a+c+12b=12a+12b+c. 又N→C1=N→C+C→C1=12B→C+A→A1=12A→D+A→A1=12c+a, ∴M→P+N→C1=12a+12b+c+12c+a=32a+12b+32c.
→ |AP·n| 平面 α 的距离为 15 _______|n_|________. (3)线面距和面面距可以转化为点面距求解.
1.线面角 θ 的正弦值等于直线的方向向量 a 与平面的法向量 n 所成角的余弦值 的绝对值,即 sinθ=|cos〈a,n〉|,不要误记为 cosθ=|cos〈a,n〉|.
(2)平面的法向量:直线 l⊥α,取直线 l 的方向向量 a,则向量 a 为平面α的法向 量.
高二数学空间向量与立体几何试题答案及解析

高二数学空间向量与立体几何试题答案及解析1.长方体中,,,,则与所成角的余弦值为.【答案】【解析】以D为空间原点,DA为x轴,D为z轴,DC为y轴,建立空间直角坐标系则=(-1,2,0),=(-1,-2,3)||=,|'|=,·=-3cos<,>==,即为所求。
【考点】本题主要考查空间向量的应用,向量的数量积,向量的坐标运算。
点评:简单题,通过建立空间直角坐标系,将求异面直线的夹角余弦问题,转化成向量的坐标运算。
2.正方体的棱长为1,是底面的中心,则到平面的距离为.【答案】【解析】因为O是A1C1的中点,求O到平面ABC1D1的距离,就是A1到平面ABC1D1的距离的一半,就是A1到AD1的距离的一半.所以,连接A1D与AD1的交点为P,则A1P的距离是:O到平面ABC1D1的距离的2倍O到平面ABC1D1的距离【考点】本题主要考查空间距离的计算。
点评:本题也可以通过建立空间直角坐标系,将求角、求距离问题,转化成向量的坐标运算,是高考典型题目。
3.已知={-4,3,0},则与垂直的单位向量为= .【答案】(,,0)【解析】设与垂直的向量与垂直的向量=(x,y,0),则-4x+3y=0,,解得x= ,y=,所以=(,,0)。
【考点】本题主要考查向量的坐标运算、向量垂直的充要条件、单位向量的概念。
点评:利用向量垂直的充要条件及单位向量的概念。
4.已知向量与向量平行,则()A.B.C.D.【答案】C【解析】因为向量与向量平行,所以,,故选C。
【考点】本题主要考查平行向量及向量的坐标运算。
点评:简单题,按向量平行的充要条件计算。
5.已知点,为线段上一点,且,则的坐标为()A.B.C.D.【答案】C【解析】设C的坐标为(x,y,z)则向量=(x-4,y-1,z-3)向量=(-2,-6,-2),而即=所以x-4=-,y-1=-2,Z-3=-所以x=,y=-1,z=,C的坐标为,选C。
高二数学利用空间向量解决立体几何中的垂直问题

n
g
例2:已知:在空间四边形OABC中,OA⊥BC, OB⊥AC, 证明:由已知 OA B C , OB AC 求证:OC⊥ AB O 所以 OA BC 0 , OB AC 0
OA (OC OB) 0 OB (OC OA) 0
A B C
所以 OA OC OA OB OB OC OB OA 所以 OA OC OB OC 0
M
D
B
N
1 1 2 1 2 2 = ( a + a - a) =0 2 2 2
MN AB
C
同理, MN CD
例3 在平行六面体ABCD ABC D中,底面是菱形,AAB
AAD BAD 60 。 (1)求证:AA BD; AB (2)当AC 平面ABD时,求 的值。 AA
D' A'
D A B B'
C'
C
变式训练(二)
(2)已知在平行六面体ABCD-ABCD中,有AA=AB=AD, 且AAD=AAB=BAD=,求证:AC 平面ABD。
D'
C'
证明: AC AB AD AA
A'
D A B
B'
BD AB AD AB AB AA 所以AC BD (AB AD AA ) (AB AD) 0 AC AB (AB AD AA ) (AB AA ) 0 又因为AB BD=B 所以AC 平面ABD
p xa yb zc
二、数量积的性质
1)数量积性质 对于非零向量 a , b ,有: (1) a e=|a|cos a,e
数学:第三章《空间向量与立体几何》教案(人教版选修2-1)
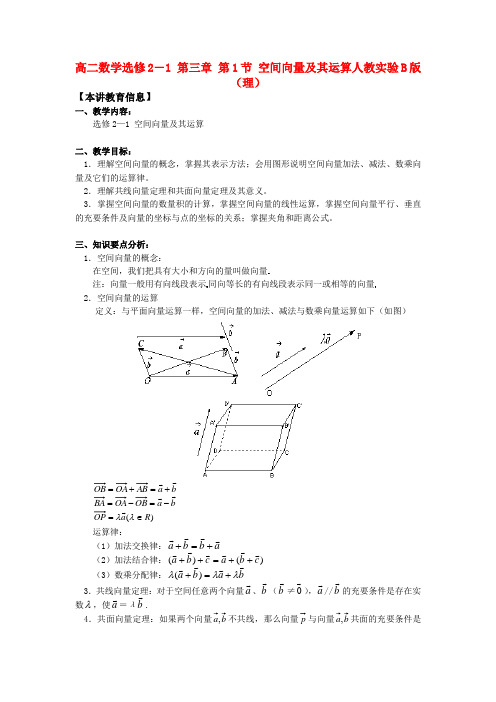
高二数学选修2-1 第三章 第1节 空间向量及其运算人教实验B 版(理)【本讲教育信息】一、教学内容:选修2—1 空间向量及其运算二、教学目标:1.理解空间向量的概念,掌握其表示方法;会用图形说明空间向量加法、减法、数乘向量及它们的运算律。
2.理解共线向量定理和共面向量定理及其意义。
3.掌握空间向量的数量积的计算,掌握空间向量的线性运算,掌握空间向量平行、垂直的充要条件及向量的坐标与点的坐标的关系;掌握夹角和距离公式。
三、知识要点分析: 1.空间向量的概念:在空间,我们把具有大小和方向的量叫做向量注:向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量2.空间向量的运算定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下(如图)b a AB OA OB+=+=b a-=-=)(R a OP ∈=λλ运算律:(1)加法交换律:a b b a+=+(2)加法结合律:)()(c b a c b a++=++(3)数乘分配律:b a b aλλλ+=+)(3.共线向量定理:对于空间任意两个向量a 、b (b ≠0 ),a //b的充要条件是存在实数λ,使a=λb .4.共面向量定理:如果两个向量b a ,不共线,那么向量p 与向量b a ,共面的充要条件是存在有序实数组),(y x ,使得b y a x p +=。
5.空间向量基本定理:如果三个向量c ,b ,a 不共面,那么对空间任一向量p ,存在唯一的有序实数组(x ,y ,z ),使c z b y a x p ++= 6.夹角定义:b a ,是空间两个非零向量,过空间任意一点O ,作b OB a OA ==,,则AOB ∠叫做向量a 与向量b 的夹角,记作><b a , 规定:π>≤≤<b a ,0特别地,如果0,>=<b a ,那么a 与b 同向;如果π>=<b a ,,那么a 与b 反向;如果90b ,a >=<,那么a 与b 垂直,记作b a ⊥。
高二数学-空间向量与立体几何测试题及答案

高二数学空间向量与立体几何测试题第1卷(选择题,共50分)一、选择题:(本大题共10个小题每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 在下列命题中:CD若a、b共线则a、b所在的直线平行;@若a、b所在的直线是异面直线,则a、b一定不共面;@若a、b、c三向量两两共面,则a、b、c三向量一定也共面;@已知三向量a、b、c,则空间任意一个向量p总可以唯一表示为p=a+yb+zc,, y, z R.其中正确命题的个数为( )A. 0B. 1C. 2D. 32. 若三点共线为空间任意一点且则的值为()A. lB.C.D.3. 设,且,则等千()A. B. 9 C. D4. 已知a=(2, —1, 3) , b= C—1, 4, —2) , c= (7, 5, 入),若a、b、c三向量共面,则实数入等千()A. B. C.5.如图1,空间四边形的四条边及对角线长都是,点分别是的中点则等千()D.A.C...BD6. 若a、b均为非零向量,则是a与b共线的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件7. 已知点0是LABC所在平面内一点满足• = • = • '则点0是LABC的()A. 三个内角的角平分线的交点B. 三条边的垂直平分线的交点C. 三条中线的交点8. 已知a+b+c=O,al =2, bl =3,A. 30°B. 45°D.三条高的交点l e = , 则向量a与b之间的夹角为()C. 60°D. 以上都不对9. 已知, ' ,点Q在直线OP上运动,则当取得最小值时,点Q的坐标为()A.B.10. 给出下列命题:CD已知,则C. D.@为空间四点若不构成空间的一个基底,那么共面;@已知则与任何向量都不构成空间的一个基底;@若共线则所在直线或者平行或者重合.正确的结论的个数为()C. 3A.1B.2D.4 第II卷(非选择题,共100分)二、填空题(本大题共6小题,每小题5分,共30分)11.已知LABC的三个顶点为A(3, 3, 2) , B (4, —3, 7) , C (0, 5, 1) , 则BC边上的中线长为12. 已知三点不共线为平面外一点若由向量确定的点与共面,那么13. 已知a,b,c是空间两两垂直且长度相等的基底,m=a+b,n=b-c,则m,n的夹角为14. 在空间四边形ABC D中,AC和B D为对角线G为L:.ABC的重心,E是B D上一点BE=3E D, 以{, , }为基底,则=15. 在平行四边形ABCD中,AB=AC=l,乙ACD=90, 将它沿对角线AC折起,使AB与CD成60角,则B,D两点间的距离为16. 如图二面角a-t -B的棱上有A,B两点直线AC,B D分别在这个二面角的两个半平面内,且都垂直千AB,已知AB=4,AC=6, B D=8, C D= ,二面角Q—t—B的大小三、解答题(本大题共5小题,满分70分),17. C lo分)设试问是否存在实数,使成立?如果存在,求出;如果不存在,请写出证明.18. (12分)如图在四棱锥中,底面ABC D是正方形,侧棱底面ABC D,, 是PC的中点,作交PB千点F.(1)证明PAIi平面EDB:(2)证明PB上平面E F D:(3)求二面角的大小.、、、、、、、、.、19. (12分)如图在直三棱柱ABC—AlBlCl中,底面是等腰直角三角形,乙ACB=90°.侧棱AA1=2, D. E 分别是CCl与AlB的中点点E在平面ABO上的射影是DAB D的重心G.(1)求AlB与平面ABO所成角的大小.(2)求Al到平面ABO的距离1) 20. 12分)如图在三棱柱ABC-AlBlCl中,AB上AC,顶点Al在底面ABC上的射影恰为点B,且AB=AC=A1B=2.2)求棱AA1与BC所成角的大小;在棱BlCl上确定一点P,使AP=, 并求出二面角P—AB—Al的平面角的余弦值A1C1B21. (12分)如图直三棱柱ABC-AlBlCl中AB上AC,D.E分别为AAl.B lC的中点DEl_平面BCCl.C I)证明:A B=ACC II)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小c,22. (12分)P是平面ABC D外的点四边形ABC D是平行四边形,AP= (-1, 2, -1)(1)求证:PA 平面ABC D.(2)对千向量,定义一种运算:,试计算的绝对值;说明其与几何体P—ABC D的体积关系,并由此猜想向量这种运算的绝对值的几何意义(几何体P-ABC D叫四棱锥,锥体体积公式:V= ) .一、选 1 2 择题(本大题土2上、10小题,每3 4空间向量与立体几何(2)参考答案5 6 7 8 9 10小题5/刀\.让,/、50分)题号答案D D D A B C A 二、填空题(本大题共4小题,每小题6分,共24分)11. (0, ,) 12. 0 13. 1, —3 14. 90° l厮—15。
第01讲 空间向量与立体几何-2023年高二数学(人教A版2019选择性必修第一册)(原卷版)

第01讲 空间向量与立体几何知识点1 空间向量的有关概念1.在空间,把具有方向和大小的量叫做空间向量,空间向量的大小叫做空间向量的长度或模.注:数学中讨论的向量与向量的起点无关,只与大小和方向有关,只要不改变大小和方向,空间向量可在空间内任意平移,故我们称之为自由向量。
2. 表示法:(1)几何表示法:空间向量用有向线段表示,有向线段的长度表示空间向量的模(2)字母表示法:用字母表示,若向量a 的起点是A ,终点是B ,则a 也可记作AB →,其模记为|a |或|AB →|. 3.几类特殊的空间向量 名称 定义表示法 零向量 规定长度为0的向量叫做零向量 记为0 单位模为1的向量叫做单位向量|a|=1或【考点目录】【知识梳理】知识点2 空间向量的线性运算(一)空间向量的加减运算共起点的两边为邻边作平行四边形,共起点对角线为和共起点,连终点,方向指向被减向量a+b=b+aλa的长度是a的长度的|λ|倍μa)=(λμ)a知识点3 共线向量与共面向量1.共线向量与共面向量的区别 //0a b b ≠()使得a b λ=;(2)存在唯一实数λ,使得0a b b λ≠=(),则//a b .注意:0b ≠不可丢掉,否则实数就不唯一.―→―→―→1、空间一点实数对→数对(,,)x y z ,使得对空间中任意一点(OP xOA yOB zOC x+=++其中共面向量定理的用途:⇒λ利用向量的线性运算即可,但一定要注意所表示的向量必须有一个公共点。
2.直线l 的方向向量如图O ∥l ,在直线l 上取非零向量a ,设P 为l 上的任意一点,则∥λ∥R 使得OP ―→=λa. 定义:把与a 平行的非零向量称为直线l 的方向向量.知识点4 空间向量的夹角定义如图,已知两个非零向量a ,b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∥AOB 叫做向量a ,b 的夹角,记作〈a ,b 〉范围 0≤〈a ,b 〉≤π向量垂直 如果〈a ,b 〉=π2,那么向量a ,b 互相垂直,记作a ∥b知识点5 空间向量的数量积运算1.(1)空间向量的数量积已知两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做a ,b 的数量积,记作a ·b ,即a ·b =|a ||b |·cos 〈a ,b 〉.零向量与任意向量的数量积为0,即0·a =0.注:a b ⋅等于a 的长度a 与b 在a 的方向上的投影b cos a,b 〈〉的乘积.(2)运算律数乘向量与数量积的结合律(λa )·b =λ(a ·b ),λ∥R交换律 a ·b =b ·a 分配律a ·(b +c )=a ·b +a ·c2.投影向量及直线与平面所成的角(1)如图∥,在空间,向量a 向向量b 投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b 共线的向量c ,c =|a |cos 〈a ,b 〉b|b |,向量c 称为向量a 在向量b 上的投影向量.类似地,可以将向量a 向直线l 投影(如图∥).(2)如图∥,向量a 向平面β投影,就是分别由向量a 的起点A 和终点B 作平面β的垂线,垂足分别为A ′,B ′,得到向量A ′B ′——→,向量A ′B ′——→称为向量a 在平面β上的投影向量.这时,向量a ,A ′B ′——→的夹角就是向量a 所在直线与平面β所成的角.知识点6 空间向量数量积运算律及性质1、数量乘积的运算律:()1a b b a ⋅=⋅; ()2()()()a b a b a b λλλ⋅=⋅=⋅; ()3()a b c a c b c +⋅=⋅+⋅.2、若a ,b 为非零向量,e 为单位向量,则有()1e a a e a cos a,e ⋅=⋅=〈〉;()20a b a b ⊥⇔⋅=;()3()()a b a b a b a b a b ⎧⎪⋅=⎨-⎪⎩与同向与反向,2a a a ⋅=,a a a =⋅;()4a b cos a,b a b ⋅〈〉=;()5a b a b ⋅≤.知识点7 空间向量基本定理1.定理如果三个向量a ,b ,c 不共面,那么对任意一个空间向量p ,存在唯一的有序实数组(x ,y ,z ),使得p =xa+yb+zc .其中{a ,b ,c }叫做空间的一个基底,a ,b ,c 都叫做基向量.如果p =xa+yb+zc ,则称xa+yb+zc 为p 在基底{a ,b ,c }下的分解式. 2.空间向量的正交分解(1)单位正交基底:空间的一个基底中的三个基向量两两垂直,且长度都为1,常用{i ,j ,k }表示. (2)正交分解:由空间向量基本定理可知,对空间中的任意向量a ,均可以分解为三个向量xi ,yj ,zk ,使a =xi +yj +zk .像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量正交分解.知识点8 空间向量基本定理应用1、证明平行、共面问题(1)对于空间任意两个向量a ,b (b ≠0),a ∥b 的充要条件是存在实数λ,使a =λb .(2) 如果两个向量a ,b 不共线,那么向量p 与向量a ,b 共面的充要条件是存在唯一的有序实数对(x ,y ),使p =xa +yb .(3)直线平行和点共线都可以转化为向量共线问题;点线共面可以转化为向量共面问题.2、求夹角、证明垂直问题 (1)θ为a ,b 的夹角,则cos θ=a ·b|a ||b |. (2)若a ,b 是非零向量,则a ∥b ∥a ·b =0. 3、求距离(长度)问题 ||a =a ·a ( ||AB →=AB →·AB→ ).知识点9 空间直角坐标系1.空间直角坐标系(1)空间直角坐标系:在空间选定一点O 和一个单位正交基底{i ,j ,k },以O 为原点,分别以i ,j ,k 的方向为正方向,以它们的长为单位长度建立三条数轴:x 轴、y 轴、z 轴,它们都叫做坐标轴,这时我们就建立了一个空间直角坐标系Oxyz .(2)相关概念:O 叫做原点,i ,j ,k 都叫做坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为Oxy 平面、Oyz 平面、Ozx 平面,它们把空间分成八个部分. 注意点:(1)基向量:|i |=|j |=|k |=1,i ·j =i ·k =j ·k =0.(2)画空间直角坐标系Oxyz 时,一般使∥xOy =135°(或45°),∥yOz =90°.(3)建立的坐标系均为右手直角坐标系.在空间直角坐标系中,让右手拇指指向x 轴的正方向,食指指向y 轴的正方向,如果中指指向z 轴的正方向,则称这个坐标系为右手直角坐标系. 2.空间一点的坐标、向量的坐标 (1)空间点的坐标在空间直角坐标系Oxyz 中,i ,j ,k 为坐标向量,对空间任意一点A ,对应一个向量OA →,且点A 的位置由向量OA →唯一确定,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使OA →=xi +yj +zk .在单位正交基底{i ,j ,k }下与向量OA →对应的有序实数组(x ,y ,z ),叫做点A 在空间直角坐标系中的坐标,记作A (x ,y ,z ),其中x 叫做点A 的横坐标,y 叫做点A 的纵坐标,z 叫做点A 的竖坐标.注:空间直角坐标系中坐标轴、坐标平面上的点的坐标特点(2)空间点的对称问题∥空间点的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.∥对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论. (3)空间向量的坐标向量的坐标:在空间直角坐标系Oxyz 中,给定向量a ,作OA →=a ,由空间向量基本定理,存在唯一的有序实数组(x ,y ,z ),使a =xi +yj +zk .有序实数组(x ,y ,z )叫做a 在空间直角坐标系Oxyz 中的坐标,可简记作a =(x ,y ,z ).知识点10 空间向量的坐标运算1.空间向量的坐标运算法则设向量a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),λ∥R ,那么(1)空间向量运算的坐标表示与平面向量的坐标表示完全一致.(2)设A (x 1,y 1,z 1),B (x 2,y 2,z 2),则AB →=(x 2-x 1,y 2-y 1,z 2-z 1).即一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.(3)运用公式可以简化运算:(a ±b )2=a 2±2a ·b +b 2;(a +b )·(a -b )=a 2-b 2. (4)向量线性运算的结果仍是向量,用坐标表示;数量积的结果为数量.2.空间向量相关结论的坐标表示设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),则有(1)平行关系:当b ≠0时,a ∥b ∥a =λb ∥a 1=λb 1,a 2=λb 2,a 3=λb 3(λ∥R); (2)垂直关系:a ∥b ∥a ·b =0∥a 1b 1+a 2b 2+a 3b 3=0.(3)|a|=a ·a =a 21+a 22+a 23.(4)cos 〈a ,b 〉=a ·b|a ||b |=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 23. 3.空间两点间的距离公式在空间直角坐标系中,设P 1(x 1,y 1,z 1),P 2(x 2,y 2,z 2). (1)P 1P 2――→=(x 2-x 1,y 2-y 1,z 2-z 1).(2)P 1P 2=|P 1P 2――→|=(x 2-x 1)2+(y 2-y 1)2+(z 2-z 1)2. (3)若O (0,0,0),P (x ,y ,z ),则|OP →|=x 2+y 2+z 2.知识点11 空间中点、直线和平面的向量表示1.空间直线的向量表示式设A 是直线上一点,a 是直线l 的方向向量,在直线l 上取AB →=a ,设P 是直线l 上任意一点, (1)点P 在直线l 上的充要条件是存在实数t ,使AP →=ta ,即AP →=tAB →.(2)取定空间中的任意一点O ,点P 在直线l 上的充要条件是存在实数t .使OP →=OA →+ta . (3)取定空间中的任意一点O ,点P 在直线l 上的充要条件是存在实数t ,使OP →=OA →+tAB →.2.空间平面的向量表示式∥如图,设两条直线相交于点O ,它们的方向向量分别为a 和b ,P 为平面α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对(x ,y ),使得OP →=xa +yb .∥如图,取定空间任意一点O ,空间一点P 位于平面ABC 内的充要条件是存在实数x ,y ,使OP →=OA →+xAB →+yAC →.我们把这个式子称为空间平面ABC 的向量表示式.∥由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.如图,直线l ∥α,取直线l 的方向向量a ,我们称向量a 为平面α的法向量.给定一个点A 和一个向量a ,那么过点A ,且以向量a 为法向量的平面完全确定,可以表示为集合{P |a ·AP →=0}.知识点12 空间平行、垂直关系的向量表示知识点13 空间距离及向量求法设u 为直线l 的单位方向向量,A ∥l ,P ∉l ,AP―→=a ,向量AP ―→在直线l 上的投影向量为AQ ―→(AQ ―→=(a ·u )u .), 则PQ =|AP ―→|2-|AQ ―→|2=a 2-a ·u2―→知识点14 空间角及向量求法成锐角的余角.两平面的夹角平面α与平面β相交,形成四个二面角,把不大于π2的二面角称为这两个平面的夹角.设平面α与平面β的夹角为θ,两平面α,β的法向量分别为n 1,n 2,则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|(1)两个平面的夹角的范围是⎣⎡⎦⎤0,π2(2)两平面的夹角是两法向量的夹角或其补角.考点一 空间向量及其线性运算1.(2022·重庆·高二期末)在长方体1111ABCD A B C D -中,1BA BC CC ++=( ) A .11D BB .1D BC .1DBD .1BD2.(2022·湖南益阳·高二期末)在四面体OABC 中,,,,OA a OB b OC c M ===为OA 的中点,N 为棱BC 上的点,且2BN NC =,则MN =( )A .112233a b c -++B .112233a b c --C .121233a b c -++D .111222a b c -++3.(2022·陕西商洛·高二期末(理))在平行六面体1111ABCD A B C D -中,点P 在1A C 上,且1114A P AC =,若1AP xAA yAB zAD =++,则x y z ++=( )A .34B .1C .54D .744.(2022·福建师大附中高二期末)如图所示,在平行六面体ABCD -A 1B 1C 1D 1中,M 为A 1C 1与B 1D 1的交点.若AB a =,AD b =,1AA c =,则下列向量中与BM 相等的向量是( ).【考点剖析】A .1122-++a b cB .1122a b c ++C .1122a b c --+D .1122a b c -+考点二 共线问题5.(2022·全国·高二期末)已知空间向量a ,b ,且2AB a b =+,56BC a b =-+,72CD a b =-,则一定共线的三点是( ) A .、、A B CB .BCD 、、C .A BD 、、D .A C D 、、6.(2022·山西吕梁·高二期末)在平行六面体1111ABCD A B C D -中,点P 在1A C 上,若1311444AP AA AB AD =++,则11A PAC =( ) A .13B .34C .14D .237.(2022·上海松江·高二期末)设O ABC -是正三棱锥,1G 是ABC 的重心,G 是1OG 上的一点,且13OG GG =,若OG xOA yOB zOC =++,则(),,x y z 为( )A .111,,444⎛⎫ ⎪⎝⎭B .333,,444⎛⎫ ⎪⎝⎭C .111,,333⎛⎫ ⎪⎝⎭D .222,,333⎛⎫ ⎪⎝⎭考点三 共面问题8.【多选】(2022·广东江门·高二期末)若{,,}a b c 构成空间的一个基底,则下列向量共面的是( ) A .,,a b a a b -+ B .,,b c b b c -+ C .,,a b c a b -+D .,,a b a b c c +++9.(2022·山东·巨野县第一中学高二期末)对于空间一点O 和不共线三点A ,B ,C ,且有623OP OA OB OC =++,则( )A .O ,A ,B ,C 四点共面 B .P ,A ,B ,C 四点共面 C .O ,P ,B ,C 四点共面D .O ,P ,A ,B ,C 五点共面10.(2022·上海市建平中学高二期末)已知A 、B 、C 、D 、E 是空间中的五个点,其中点A 、B 、C 不共线,则“DE 平面ABC ”是“存在实数x 、y ,使得DE x AB y AC =+的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件11.(2022·福建厦门·高二期末)已知{},,a b c 是空间的一个基底,AB a b =+,AC a c =+,AD b c λ=+,若,,,A B C D 四点共面.则实数λ的值为( )A .1-B .0C .1D .212.(2022·江西·临川一中高二期末(理))已知空间向量()2,1,a m =-,()1,1,2b =-,()1,2,2c t =-,若a ,b ,c 共面,则m +2t =( )A .-1B .0C .1D .-613.(2022·全国·高二期末)已知(2,1,3)PA =-,(1,2,3)PB =-,(7,6,)PC λ=,若P ,A ,B ,C 四点共面,则λ=___________.考点四 空间向量基本定理14.(2022·重庆长寿·高二期末)如图,在斜棱柱1111ABCD A B C D -中,AC 与BD 的交点为点M ,AB a =,AD b =,1AA c =,则1MC =( )A .1122a b c ++B .1122---a b cC .1122-++a b cD .1122a b c --+15.(2022·天津市第九十五中学益中学校高二期末)在四棱锥P ABCD -中,底面ABCD 是正方形,E 为PD 中点,若PA a =,PB b =,PC c =,则BE =( )A .131222a b c ++B .111222a b c --C .131222a b c -+D .131222a b c +-16.(2022·河南郑州·高二期末(理))已知三棱锥O —ABC ,点M ,N 分别为线段AB ,OC 的中点,且OA a =,OB b =,OC c =,用a ,b ,c 表示MN ,则MN 等于( )A .()12c a b -- B .()12b ac -- C .()12a cb -- D .()12c a b ++ 17.(2022·江苏无锡·高二期末)定义:设{}123,,a a a 是空间的一个基底,若向量123p xa ya za =++,则称有序实数组(),,x y z 为向量p 在基底{}123,,a a a 下的坐标.已知{},,a b c 是空间的单位正交基底,{},,2a b a b a c +-+是空间的另一个基底,若向量p 在基底{},,2a b a b a c +-+下的坐标为()1,2,3.(1)求向量p 在基底{},,a b c 下的坐标; (2)求向量p 在基底{},,a b c 下的模.考点五 空间向量的数量积及其性质的应用18.(2022·广西钦州·高二期末(理))如图,正四棱柱是由四个棱长为1的小正方体组成的,AB 是它的一条侧棱,128,,P P P ⋯是它的上底面上其余的八个点,则集合{},1,2,,8i x x AB AP i =⋅=⋯的元素个数( )A .1B .2C .4D .819.(2022·福建省华安县第一中学高二期末)三棱锥A BCD -中,2AB AC AD ===,2BAD π∠=,3BAC π∠=,则AB CD ⋅=______.20.(2022·河南焦作·高二期末(理))已知在四面体ABCD 中,236AB AC AD ===,3BAC CAD DAB π∠=∠=∠=,则BC BD ⋅=______.21.(2022·河南新乡·高二期末(理))已知空间向量()0,1,2AB =-,2AC =,2,3AB AC π=,则AB BC ⋅=( )A .5B 5C .5D 522.(2022·北京昌平·高二期末)已知正三棱锥-P ABC 的底面ABC 的边长为2,M 是空间中任意一点,则()MA MB MC ⋅+的最小值为( )A .32-B .1-C .D .12-23.(2022·江苏省扬州市教育局高二期末)如图,平行六面体1111ABCD A B C D -的底面ABCD 是边长为1的正方形,且1160A AD A AB ∠=∠=︒,12AA =,则线段1AC 的长为( )AB C D .24.(2022·江苏宿迁·高二期末)四面体ABCD 中,2,90,2===∠=︒⋅=-AB AC AD BAD AB CD ,则BAC ∠=( )A .30︒B .45︒C .60︒D .90︒25.(2022·福建厦门·高二期末)在四面体OABC 中,OA OB OC ==,60AOB AOC ∠==︒,90BOC ∠=︒,则OB 与AC 所成角的大小为( ) A .30°B .60°C .120°D .150°26.(2022·全国·高二期末)已知()0,0,0O ,()1,2,3A ,()2,1,2B ,()1,1,2P ,点Q 在直线OP 上运动,当QA QB ⋅取最小值时,点Q 的坐标是______27.【多选】(2022·湖北黄冈·高二期末)棱长为2的正方体1111ABCD A B C D -的侧面11ABB A (含边界)内有一动点P ,则( )A .若1111,1B P mB B nB A m n =++=,则 1110B P B D ⋅= B .若11(01)A P A B λλ=<<,则110C P BD ⋅= C .若()11111111,22B P PA A E AC AD ==+,则 1123E B P A⋅=- D .若()1111112A E AC A D =+,则存在非零向量1B P 使111B P A E ⋅=-考点六 空间向量的运算的坐标表示(一)空间向量坐标的基本运算28.(2022·内蒙古乌兰察布·高二期末(理))已知向量()()2,1,3,1,1,2a b =-=-,则2a b +=( )A .B .()4,1,1-C .()5,1,4-D29.(2022·重庆九龙坡·高二期末)在空间直角坐标系中,若(1,1,0)A ,1(2,0,1)2AB =--,则点B 的坐标为( ) A .(3,1,﹣2)B .(-3,1,2)C .(-3,1,-2)D .(3,-1,2)30.(2022·福建宁德·高二期末)已知()1,2,3A ,()4,5,9B ,13AC AB =,则AC 的坐标为______. 31.(2020·陕西·绥德中学高二期末(理))若(1,1,0)a =,(1,0,2)b =- ,则与a b +同方向的单位向量是_______. 32.【多选】(2022·福建三明·高二期末)已知正方体1111ABCD A B C D -的棱长为2,建立如图所示的空间直角坐标系Dxyz ,则( )A .点1C 的坐标为(2,0,2)B .()12,2,2C A =--C .1BD 的中点坐标为(1,1,1) D .点1B 关于y 轴的对称点为(-2,2,-2)(二)空间向量平行的坐标运算33.(2022·河南焦作·高二期末(理))已知向量()2,1,1a x =---,()2,,2b x x =-,且//a b ,则x 的值为( ) A .2-B .1C .1-或2D .1或2-34.(2022·浙江·杭州四中高二期末)已知向量()1,1,0a =-,()1,0,2b =,且ka b +与2a b -互相平行,则k =( ) A .114-B .15C .35D .12-35.(2022·北京昌平·高二期末)已知(,2,6)a x =-是直线1l 的方向向量,(1,,3)b y =-是直线2l 的方向向量.若直线12l l ∥,则x y +=________.36.(2022·重庆长寿·高二期末)已知()1,2,1u =是直线l 的方向向量,()2,,2v y =为平面α的法向量,若l α⊥,则y 的值为( )A .2-B .12-C .14D .4(三)空间向量垂直的坐标运算37.(2022·广东广州·高二期末)已知向量(1,3,2)a →=-,(2,,4)b m →=--,若a b →→⊥,则实数m 的值是___________. 38.【多选】(2022·福建福州·高二期末)已知空间向量()()1,,2,2,1,2a k k b =+-=-,且a b ⊥,则 ( ) A .6k =-B .6k =C .3b =D .9b =39.(2022·河北保定·高二期末)已知()2,1,3a =-,()1,2,1b =-,若()b a b λ⊥+,则实数λ=______.40.(2022·黑龙江·哈尔滨工业大学附属中学校高二期末(文))已知向量a →=(1,1,k),b →=(−1,0,−1),c →=(0,2,1),且向量2a b -与c 互相垂直,则k 的值是( ) A .1 B .2- C .3- D .4-(四)空间向量模长的坐标运算41.(2021·湖北·黄石市有色第一中学高二期末)若点(1,1,2)A -,(0,3,0)B ,(1,0,1)C -点D 在z 轴上,且AD BC ⊥则||=AD ______.42.(2022·天津市滨海新区塘沽第一中学高二期末)已知向量()2,1,3a →=-,()1,1,b x =-,若a →与b →垂直,则2a b →→+=___________.43.(2022·江苏·南京市大厂高级中学高二期末)向量(),1,1a x =,()1,,1b y =,()2,4,2c =-,且a c ⊥,//b c ,则2a b +=______.44.(2022·江苏·沭阳如东中学高二期末)已知(1,21,0),(3,,)a t t b t t =--=,则||b a -的最小值( )A B C .143D (五)空间向量夹角的坐标运算45.(2022·吉林辽源·高二期末)已知空间向量(3,22)a =-,b 是单位向量,1213a b -=,则向量a 与b 的夹角为______.46.(2022·全国·高二期末)若向量(1,,)a λλ=,(2,1,1)b =-,a ,b 夹角为钝角,则λ的取值范围是______. 47.(2022·江苏淮安·高二期末)如图,在四棱锥P -ABCD 中,底面ABCD 为正方形,P A ⊥平面ABCD ,PA AB =,M 为PC 上一动点,PM tPC =,若⊥BMD 为钝角,则实数t 可能为( )A .15B .14 C .13D .1248.(2022·广东江门·高二期末)若两个单位向量(,,0),(,0,)OA m n OB n p ==与向量(1,1,1)OC =的夹角都等于π4,则cos AOB ∠=__________.(六)空间向量投影的坐标运算49.(2022·上海金山·高二期末)在空间直角坐标系O xyz - 中,已知向量()1,0,3a =,则a 在x 轴上的投影向量为________.50.(2022·天津天津·高二期末)已知空间向量()1,0,1=a ,()2,1,2b =-,则向量a 在向量b 上的投影向量的坐标是__________.51.(2022·广东惠州·高二期末)已知()0,1,1a =,()0,1,0b =,则a 在b 上的投影向量为( )A .1B C .()0,1,0D .110,,22⎛⎫ ⎪⎝⎭考点七 空间向量在立体几何平行、垂直问题中的应用(一)平行问题52.(2022·黑龙江·哈尔滨工业大学附属中学校高二期末(文))如图,已知四棱锥V ABCD -的底面是矩形,VD ⊥平面,222,,,ABCD AB AD VD E F G ===分别是棱,,AB VC CD 的中点.(1)求证:EF ⊥平面VAD ;(2)求平面AVE 与平面VEG 夹角的大小.53.(2022·安徽滁州·高二期末)如图,在多面体ABCDEF 中,AD ⊥平面ABC ,AD //BE //CF ,且AD =1,BE =5,CF =3,⊥ABC 是边长为2的正三角形,G 是AB 的中点.(1)求证:CG //平面DEF ;(2)求二面角E DF A --的余弦值.(二)垂直问题54.(2022·安徽省宿州市第二中学高二期末)如图,边长为2的等边PCD 所在的平面垂直于矩形ABCD 所在的平面,BC =M 为BC 的中点.(1)证明:AM PM ⊥;(2)求平面P AM 与平面ABCD 的夹角的大小;(3)求点D 到平面AMP 的距离.55.(2022·福建福州·高二期末)如图,在正四棱柱1111ABCD A B C D -中,已知2AB AD ==,15AA =,E ,F 分别为1DD ,1BB 上的点,且11DE B F ==.(1)求证:BE ⊥平面ACF :(2)求点B 到平面ACF 的距离.56.(2022·湖北恩施·高二期末)在三棱台ABC -A 1B 1C 1中,C 1C ⊥平面ABC ,AB ⊥BC ,且AB =BC =C 1C =2A 1B 1,O 为AC 的中点,P 是C 1C 的中点.(1)证明:平面A 1BC ⊥平面POB ;(2)求二面角B 1-A 1B -C 的余弦值.(三)综合问题57.(2022·浙江·杭州四中高二期末)已知平面β法向量为()3,1,5m =-,直线l 的方向向量为()6,2,10n =--,则( )A .l 与β平行B .l 与β垂直C .l 与β相交但不垂直D .以上都不对58.【多选】(2022·广东深圳·高二期末)直三棱柱111ABC A B C 中,1,,,,CA CB CA CB CC D E M ⊥==分别为11B C ,11,CC AB 的中点,点N 是棱AC 上一动点,则( )A .对于棱AC 上任意点N ,有1MN BC ⊥B .棱AC 上存在点N ,使得MN ⊥面1BC NC .对于棱AC 上任意点N ,有MN 面1A DED .棱AC 上存在点N ,使得MN DE ∥59.(2022·北京房山·高二期末)如图,正方体1111ABCD A B C D -中,P 是1A D 的中点,则下列说法正确的是( )A .直线PB 与直线1A D 垂直,直线PB ∥平面11B D CB .直线PB 与直线1DC 平行,直线PB ⊥平面11AC DC .直线PB 与直线AC 异面,直线PB ⊥平面11ADC BD .直线PB 与直线11B D 相交,直线PB ⊂平面1ABC考点八 空间角的计算60.(2022·广东江门·高二期末)在直三棱柱111ABC A B C 中,1190,,BCA D F ∠=︒分別是1111,A B AC 的中点,1BC CA CC ==,则1BD 与1AF 所成角的正弦值是( )A B .12 C D 61.(2022·贵州六盘水·高二期末(理))如图是正方体的平面展开图,则在这个正方体中:⊥BM 与ED 平行⊥BM 与CE 垂直⊥CE 与平面ABCD ⊥CN 与BM 所成角为60︒以上四个命题中,正确命题的序号是( )A .⊥⊥B .⊥⊥C .⊥⊥D .⊥⊥62.(2022·黑龙江·双鸭山一中高二期末)如图,在四棱锥S ABCD -中,底面ABCD 为等腰梯形,AD BC ∥,60DAB ∠=,SA ⊥面ABCD ,22SA AD BC ===,点F 为线段SD 中点(1)求证:CF 面SAB ;(2)求异面直线FC 与BD 所成角的大小.63.【多选】(2022·山东·巨野县第一中学高二期末)已知在直三棱柱111ABC A B C 中,底面是一个等腰直角三角形,且1AB BC BB ==,E 、F 、G 、M 分别为1111B C A B AB BC ,,,的中点.则( )A .1GB 与平面11ACC A B .1AB 与1BC 所成角为3π C .1//A M 平面EFBD .平面1AB C ⊥平面1A MC64.(2022·河南南阳·高二期末(理))如图,四边形ABEF 为直角梯形,//AF BE 且BE EF ⊥,CDFE 为正方形,且平面CEFD ⊥平面ABEF ,22EF AF BE ===,13AP AB =,23DQ DC =,则PQ =______,直线PQ 与平面ACD 所成角的正弦值为______.65.(2022·福建省仙游县度尾中学高二期末)如图,在三棱锥-P ABC 中,PAC △是正三角形,AC BC ⊥,2,AC BC PB ===D 是AB 的中点.(1)证明:AC PD ⊥;(2)求直线BC 与平面PAB 所成角的正弦值.66.(2022·甘肃·测试·编辑教研五高二期末(理))如图,在直三棱柱111ABC A B C 中,AC BC ⊥,2AC BC ==,13CC =,点D ,E 分别在棱1AA ,1CC 上,且1AD =,2CE =,M 为棱11A B 的中点.(1)求证:11C M B D ⊥;(2)求直线AB 与平面1DB E 所成角的正弦值.67.(2022·四川绵阳·高二期末(理))如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD ⊥,//BC AD ,2PA AB BC ===,4=AD ,E 为棱PD 的中点,F 是线段PC 上一动点.(1)求证:平面PBC ⊥平面PAB ;(2)若直线BF 与平面ABCD F EA D --的余弦值.(三)平面与平面所成的角(二面角)68.(2022·青海玉树·高二期末(理))如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,2PA AB =,正方形ABCD 的对角线交于点O .(1)求证:BD ⊥平面P AC ;(2)求二面角P BD C --的余弦值.69.(2022·云南曲靖·高二期末)如图所示,AE ⊥平面ABCD ,四边形AEFB 为矩形,,BC AD BA AD ⊥,224AE AD AB BC ====.(1)求证:CF ⊥平面ADE ;(2)求平面CDF 与平面AEFB 所成锐二面角的余弦值.70.(2022·广东中山·高二期末)如图,在四棱锥P ABCD -中,底面四边形ABCD 为直角梯形,π2DAB ∠=,π3ABC ∠=,22AB DC ==,PD PA =CD PD ⊥.(1)求证:平面PAD ⊥平面ABCD ;(2)求平面APB 和平面PBC 的夹角大小.71.(2022·浙江省杭州第九中学高二期末)如图,在三棱锥-P ABC 中,AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,BM BC λ=,且二面角M PA C --为30°,求λ的值.考点九 空间距离的计算(一)点到直线的距离72.(2022·吉林白山·高二期末)已知(3,1,0)A ,(5,2,2)B ,(2,0,3)C ,则点C 到直线AB 的距离为( )A .3BC .D73.(2022·安徽省宿州市第二中学高二期末)已知直线l 经过点()211A ,,,且()101n =,,是l 的方向向量,则点()432P ,,到l 的距离为( )A .12BCD 74.(2022·青海海东·高二期末(理))在正方体1111ABCD A B C D -中,6,3,,AB AB AE PF ==分别是线段11,A C BB 的中点,则点P 到直线EF 的距离是( )A B .125 C D .185(二)点到平面的距离、直线到平面的距离、平面到平面的距离75.(2022·上海市奉贤中学高二期末)经过原点的平面α的一个法向量为(3,1,2)n =,点A 坐标为(0,1,0),则点A 到平面α的距离为______.76.(2022·青海·海南藏族自治州高级中学高二期末(理))设正方体1111ABCD A B C D -的棱长为4,则点1C 到平面1A BD 的距离是( )A B C D77.(2022·江苏·南京师大附中高二期末)在矩形ABCD 中,2==AD AB E 是线段AD 的中点,将⊥ABE 沿BE 折起到⊥PBE 位置(如图),点F 是线段CP 的中点.(1)求证:DF ⊥平面PBE :(2)若二面角P BE C --的大小为2π,求点A 到平面PCD 的距离. 78.(2022·浙江省杭州第九中学高二期末)若两平行平面α、β分别经过坐标原点O 和点()2,1,1A ,且两平面的一个法向量为()1,0,1n =-,则两平面间的距离是______.(三)异面直线的距离79.(2022·福建·厦门外国语学校高二期末)如图,在正方体1111ABCD A B C D -中,AB =1,M ,N 分别是棱AB ,1CC 的中点,E 是BD 的中点,则异面直线1D M ,EN 间的距离为______.80.(2022·浙江宁波·高二期末)如图,正四棱锥P ABCD -的棱长均为2,点E 为侧棱PD 的中点.若点M ,N 分别为直线AB ,CE 上的动点,则MN 的最小值为______.81.(2022·全国·高二期末)在如图所示实验装置中,正方形框架的边长都是1,且平面ABCD ⊥平面ABEF ,活动弹子,M N 分别在正方形对角线AC ,BF 上移动,则MN 长度的最小值是___________.考点十 空间向量与立体几何的综合问题82.【多选】(2022·广东茂名·高二期末)(多选)如图,在长方体1111ABCD A B C D -中,11AA =,AB AD ==E 是侧面11AA D D 的中心,F 是底面ABCD 的中心,以A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则( )A .EF 是单位向量B .三棱锥1A BCD -外接球的表面积为7πC .直线EF 与1A CD .//EF 平面1A BC83.【多选】(2022·辽宁辽阳·高二期末)在空间直角坐标系O xyz -中,(1,0,0),(1,2,2),(0,0,2)---A B C ,则( )A .3⋅=OC ABB .点B 到平面AOC 的距离是2C .异面直线OC 与ABD .点O 到直线AB 84.【多选】(2022·江苏南通·高二期末)在平行六面体1111ABCD A B C D -中,1AB AD AA ==,1160A AB A AD DAB ∠∠∠===,点P 在线段1BC 上,则( ) A .1AP B C ⊥B .P 到11A B 和CD 的距离相等C .AP 与11A BD .AP 与平面ABCD所成角的正弦值最大为13 一、单选题 1.(2022·江苏扬州·高二期中)如图,在平行六面体1111ABCD A B C D -中,M 为AC 和BD 的交点,若AB a =,AD b =,1AA c =,则下列式子中与1MB 相等的是( )A .1122-+a b cB .1122a b c +- C .1122a b c -++ D .1122--+a b c 2.(2022·河北·石家庄二十三中高二阶段练习)设直线1l 、2l 的方向向量分别为a ,b ,能得到12l l ⊥的是( ) A .(1,2,2)a =-,(2,4,4)b =-B .(2,2,1)a =-,(3,2,10)b =-C .(1,0,0)a =,(3,0,0)b =-D .(2,3,5)a =-,(2,3,5)b =3.(2022·全国·高二专题练习)如图所示,空间四边形ABCD 中,点G 为BCD △的重心,E ,F ,H 分别为边CD ,AD 和BC 的中点,则1132AG BE CA ++的化简结果为( )A .AFB .AHC .AED .CF4.(2021·全国·高考真题(理))在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角【过关检测】为( )A .π2B .π3C .π4D .π65.(2022·湖北·武汉市第十七中学高二期中)在正四面体D ABC -中,点E 在棱AB 上,满足2AE EB =,点F 为线段AC 上的动点,则( )A .存在某个位置,使得DE BF ⊥B .存在某个位置,使得π4FDB ∠= C .存在某个位置,使得直线DE 与平面DBFD .存在某个位置,使得平面DEF 与平面DAC二、多选题 6.(2022·广东·普宁市华侨中学高二阶段练习)如图所示,平行六面体1111ABCD A B C D -中,11111A C B D O ⋂=,以顶点A 为端点的三条棱长都为1,且1160BAD DAA BAA ∠=∠=∠=︒,则下列结论正确的是( )A.1BD B .1//CO 平面1BDA C .1AA 与平面ABCDD .四棱锥1B ABCD -7.(2022·全国·高二专题练习)已知直三棱柱111ABC A B C 中,AB BC ⊥,1AB BC BB ==,O 为1A C 的中点.点P 满足1BP BC λ=,其中[0,1]λ∈,则( )A .对[0,1]λ∀∈时,都有11A P OB ⊥B .当13λ=时,直线1A P 与AB 所成的角是30° C .当12λ=时,直线1A P 与平面111A B CD .当12λ=时,直线1A P 与1OB 相交于一点Q ,则112PQ QA = 三、填空题8.(2022·重庆·四川外国语大学附属外国语学校高二阶段练习)在平行六面体1111ABCD A B C D -中,用向量AB ,AD ,1AA 表示1D B =______.9.(2022·江西南昌·高二期末(理))已知正四面体ABCD 中,E ,F 分别是线段BC ,AD 的中点,点G 是线段CD 上靠近D 的四等分点,则直线EF 与AG 所成角的余弦值为______.四、解答题10.(2022·全国·高二课时练习)如图,在三棱柱111ABC A B C 中,AB ⊥平面11BB C C ,122AB BB BC ===,1BC E 为11A C 的中点.(1)求证:1C B ⊥平面ABC ;(2)求点A 到平面BCE 的距离.11.(2022·辽宁实验中学高二阶段练习)如图,在平行六面体1111ABCD A B C D -中,1160A AD A AB BAD ∠=∠=∠=︒,2AB AD ==,11AA =,点P 为线段BC 中点.(1)求1D P ;(2)求直线1AB 与1D P 所成角的余弦值.12.(2022·广东·顺德一中高二阶段练习)如图,在三棱柱111ABC A B C 中,1CC ⊥平面ABC ,,,D E F 分别为111,,AA AC A C 的中点,AB BC ==12AC AA ==.(1)求证:AC ⊥平面BEF ;(2)求二面角1B CD C 的余弦值; 13.(2022·天津·静海一中高二阶段练习)如图,⊥AE 平面ABCD ,//CF AE ,//AD BC ,AD AB ⊥,2AE BC ==,1AB AD ==,87CF =,则(1)求BD 与EC 所成角的余弦值;(2)求直线CE 与平面BDE 所成角的正弦值; (3)求平面EBD 与平面BDF 的夹角的余弦值.。
高二数学寒假作业(5)空间向量与立体几何

高二(上)寒假作业(5)——空间向量与立体几何1.如图所示,在四棱锥P —ABCD 中,侧面P AD 是正三角形,且垂直于底面ABCD ,底面ABCD 是边长为2的菱形,︒=∠60BAD ,M 为PC 上一点,且P A ∥平面BDM .(1)求证:M 为PC 中点;(2)求平面ABCD 与平面PBC 所成的锐二面角的大小.2.如图,平面ABDE ⊥平面ABC ,ABC ∆是等腰直角三角形,AC =BC = 4,四边形ABDE 是直角梯形,BD ∥AE ,BD ⊥BA ,122BD AE ==,O M CE AB 、分别为、的中点,求直线CD 和平面ODM 所成角的正弦值.3.如图,已知四棱锥P —ABCD 的底面为等腰梯形,AB ∥CD , AC ⊥BD ,垂足为H ,PH 是四棱锥的高,E 为AD 的中点.(1)证明:PE ⊥BC ;(2)若∠APB =∠ADB =60°,求直线P A 与平面PEH 所成角的正弦值.A P BC D M AM B C O D E4.如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.(1)证明:AC⊥B1D;(2)求直线B1C1与平面ACD1所成角的正弦值.5.如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=22AB.(1)证明:BC1∥平面A1CD;(2)求二面角D-A1C-E的正弦值.6.如图,在圆锥PO中,已知PO=2,⊙O的直径AB=2,C是AB的中点,D为AC的中点.(1)证明:平面POD⊥平面P AC;(2)求二面角B-P A-C的余弦值.7.如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,点N是BC的中点,点M在CC1上.设二面角A1-DN-M的大小为θ.(1)当θ=90°时,求AM的长;(2)当cos θ=66,求CM的长.8.四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°.(1)求AC1的长;(2)求BD1与AC夹角的余弦值.(完)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学:空间向量与立体几何
1. 空间向量
1.1 定义与性质
在高二数学中,我们学习了平面向量的概念和运算,而空
间向量是在三维空间中的向量。
空间向量也具有和平面向量一样的性质,包括向量的长度、方向、加法与减法等。
1.2 空间向量的表示形式
空间向量可以用多种形式进行表示,最常见的是坐标表示。
对于一个空间向量,我们可以使用一个有序的三元组表示它,如AA=(A,A,A),其中A为向量的起点,A为向量的终点。
1.3 空间向量的加法与减法
与平面向量类似,空间向量的加法与减法也满足平行四边
形法则和三角形法则。
具体计算时,我们只需将向量的对应坐标进行相加或相减即可。
2. 空间向量的数量积与向量积
2.1 数量积
空间向量的数量积是两个向量的长度的乘积与它们之间夹
角的余弦值的乘积,记作$AB\\cdot AC = |AB|\\cdot
|AC|\\cdot \\cos{\\theta}$。
数量积常用来计算两个向量的夹角以及判断两个向量是否垂直或平行。
2.2 向量积
空间向量的向量积是两个向量所构成的平行四边形的面积
的向量,记作$AB\\times AC$。
向量积的模、方向和长度与夹角有关,计算公式为$|AB\\times AC| = |AB|\\cdot |AC|\\cdot \\sin{\\theta}$。
3. 立体几何
3.1 空间几何体的基本概念
在立体几何中,我们学习了各种各样的空间几何体,如点、直线、平面、棱柱、棱锥、球体等,它们在三维空间中具有不同的形状和性质。
3.2 空间几何体的投影
在解决实际问题时,常常需要将三维空间中的几何体投影到一个平面上进行分析。
空间几何体的投影可以根据需要选择不同的投影方式,如平行投影和透视投影。
3.3 立体几何的应用
立体几何在现实生活中具有广泛的应用,如建筑设计、机械制造、地理测量等。
了解立体几何可以帮助我们更好地理解和描述物体的形状和结构。
4. 空间向量与立体几何的关系
4.1 空间向量在立体几何中的应用
空间向量在立体几何中具有重要的应用,如计算点到直线的距离、判断点是否在平面上等。
通过运用空间向量的概念和性质,我们可以更好地解决与立体几何相关的问题。
4.2 空间向量与平行四边形法则
立体几何中的平行四边形法则与空间向量的加法和减法有密切的关系。
通过空间向量的平行四边形法则,我们可以判断平行四边形的性质以及解决相关问题。
总结
高二数学中的空间向量与立体几何是相互关联的。
通过学习空间向量的概念、性质和运算法则,我们可以更好地理解和应用立体几何中的概念和方法。
同时,通过空间向量的应用和立体几何中的几何体分析,我们能够提高解决实际问题的能力和思维能力。
掌握这两个知识点将有助于我们在高中数学学科中取得更好的成绩。
