人教版初中数学《第27章极端原理》竞赛专题复习(含答案)
难点解析:人教版九年级数学下册第二十七章-相似必考点解析试卷(含答案详解)

人教版九年级数学下册第二十七章-相似必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如果线段2cm a =,18cm b =,那么a 和b 的比例中项是( ) A .3cmB .4cmC .6cm ±D .6cm2、如图,点E 是正方形ABCD 的边AB 边上的黄金分割点,且AE >EB ,1S 表示AE 为边长的正方形面积,2S 表示以BC 为长,BE 为宽的矩形面积,3S 表示正方形ABCD 除去1S 和2S 剩余的面积,3S :2S 的值为( )A .12B .23C D 3523、如图,把一张矩形纸片ABCD 沿着AD 和BC 边的中点连线EF 对折,对折后所得的矩形正好与原来的矩形相似,则原矩形纸片长与宽的比为( )A .4:1BC .D .2:14、甲、乙两城市的实际距离为500km ,在比例尺为1:10000000的地图上,则这两城市之间的图上距离为( ) A .0.5cmB .5cmC .50cmD .500cm5、下列四条线段中,成比例的是( ) A .1a =,2b =,3c =,4d = B .1a =,2b =,3c =,6d = C .2a =,3b =,4c =,12d =D .3a =,2b =,5c =,6d =6、已知32a b =,那么下列等式中正确的是( )A .53a b b += B .13a b b -= C .23a b = D .23ab =7、如图,矩形ABCD 的对角线AC 、BD 相交于点E ,DB x ⊥轴于点B ,AC 所在直线交x 轴于点F ,点A 、E 同时在反比例函数()0k y x x =<的图象上,已知直线AC 的解析式为34y x b =+,矩形ABCD 的面积为120,则k 的值是( )A .20-B .452-C .40-D .1603-8、如图,以点O 为位似中心,将△ABC 缩小后得到△A ′B ′C ′,已知BB ′=2OB ′,则△A ′B ′C ′与△ABC的面积之比()A.1:3 B.1:4 C.1:5 D.1:99、如图,点P是▱ABCD边AD上的一点,E,F分别是BP,CP的中点,已知▱ABCD面积为16,那么△PEF的面积为()A.8 B.6 C.4 D.210、如图,Rt△ABC中,∠ACB=90°,分别以AB,BC,AC为边在△ABC外部作正方形ADEB,CBFG,ACHI.将正方形ABED沿直线AB翻折,得到正方形ABE'D',AD'与CH交于点N,点E'在边FG上,D'E'与CG交于点M,记△ANC的面积为S1,四边形'BCME的面积为S2,若CN=2NH,S1+S2=14,则正方形ABED的面积为()A.25 B.26 C.27 D.28第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,AB=5,则BD的长度为_____.2、如图,在矩形ABCD中,AB=30,BC=40,对角线AC与BD相交于点O,点P为边AD上一动点,连接OP,将△OPA沿OP折叠,点A的对应点为点E,线段PE交线段OD于点F.若△PDF为直角三角形,则PD的长为______.3、如图,矩形ABCD中,E是AD的中点,4AB=,6AD=,M是线段CE上的动点,则BM的最小值是___________.4、在△ABC中,AB=8,点D、E分别是AC、BC上点,连接DE,将△CDE沿DE翻折得△FDE,点C的对应点F正好落在AB上,若∠112+∠2=90°,S△ADF12=S△CDE,△BEF的而积为12,则点D到BC的距离为 _____.5、将2020个边长为1的正方形按如图所示的方式排列,点A,A1,A2,A3...A2020和点M,M1,M2 (2019)正方形的顶点,连接AM1,AM2,AM3…AM2019分别交正方形的边A1M,A2M1,A3M2…A2019M2018于点N1,N2,N3…N2019,四边形M1N1A1A2的面积是S1,四边形M2N2A2A3的面积是S2,…,则S2019为 _____.三、解答题(5小题,每小题10分,共计50分)1、在三角形ABC中,AC=AB,∠CAB=α,点D是平面内不与B,C重合的任意一点,连接CD,将线段绕点C逆时针旋转α得到线段CE,连接AD,BE,DE.(1)如图1,当α=60°时,ADBE= ,并求出直线BE 与直线AD 所夹的劣角是多少度? (2)如图2,当α=90°时,若点P ,Q 分别是AC ,AB 的中点,点D 在直线PQ 上,求点A ,D ,E 在同一直线上时CEAD的值. 2、如图,点()3,M m -是一次函数1y x =+与反比例函数ky x=(0k ≠)的图象的一个交点,点E 是一次函数与x 轴的交点. (1)求反比例函数表达式;(2)点P 是x 轴正半轴上的一个动点,设()2OP a a =≠,过点P 作垂直于x 轴的直线,分别交一次函数,反比例函数的图象于点A ,B ,过OP 的中点Q 作x 轴的垂线,交反比例函数的图象于点C ,交一次函数的图象于点F .①当4a =时,求ABC 的面积; ②当a 为何值时,ACF 与EQF 相似.3、定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,ABC 中,点D 是BC 边上一点,连接AD ,若AD 2=BD •CD ,则称点D 是ABC 中BC 边上的“好点”.(1)如图2,ABC 的顶点是4×4网格图的格点,请在图中画出AB 边上的“好点”;(2)如图3,ABC 是⊙O 的内接三角形,点H 在AB 上,连接CH 并延长交⊙O 于点D .若点H 是BCD中CD边上的“好点”.①求证:OH⊥AB;②若OH∥BD,⊙O的半径为r,且r=3OH,求CHDH的值.4、如图,抛物线y=ax2+bx+6与x轴交于A(2,0),B(8,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P是抛物线上一动点,当∠PCB12∠BCO时,求点P的横坐标.5、矩形ABCD的周长为28(AB<BC),对角线AC与BD相交于点O,对角线长为10,过点O作OP⊥BD,且OP=AO,过点P作PE⊥BC,垂足为E,请画出符合题意的图形,并直接写出线段CE的长.---------参考答案-----------一、单选题 1、D 【解析】 【分析】由比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积,即可求解. 【详解】解:设它们的比例中项是x cm ,根据题意得:x 2=2×18,解得:6x =±(线段是正数,负值舍去). 故选:D 【点睛】本题主要考查了比例的基本性质,熟练掌握比例中项的平方等于两条线段的乘积是解题的关键. 2、C 【解析】 【分析】设正方形ABCD 的边长为a ,关键黄金分割点的性质得到512AEAB和BE AE =,用a 表示出1S 、2S 和3S 的面积,再求比例. 【详解】解:设正方形ABCD 的边长为a , ∵点E 是AB 上的黄金分割点,∴512AE AB,BE AE =∴AE AB ==,∴2BE a ==⎝⎭,∵2221S AE ⎫===⎪⎪⎝⎭,22S BE BC =⋅=,∴)222232S a a ==,∴)2232:2S S a ==. 故选C .【点睛】本题考查黄金分割点,解题的关键是掌握黄金分割点的性质. 3、B 【解析】 【分析】根据相似多边形对应边的比相等,设出原来矩形的长,就可得到一个方程,解方程即可求得. 【详解】根据条件可知:矩形AEFB ∽矩形ABCD , ∴AE ABAB AD=, ∵E 为AD 中点 ∴12AE AD =∴12ADAB AB AD=,∴222AD AB=,∴AD=,故选B【点睛】本题考查了相似多边形的性质,根据相似形的对应边的比相等,把几何问题转化为方程问题,正确分清对应边,以及正确解方程是解决本题的关键.4、B【解析】【分析】先将千米换单位为厘米,然后设这两城市之间的图上距离为xcm,根据比例计算即可得.【详解】解:50050000000km cm=,设这两城市之间的图上距离为xcm,则:1 1000000050000000x=,解得:5x cm=,故选:B.【点睛】题目主要考查比例的计算,理解题意,注意单位变换是解题关键.5、B【解析】【分析】通过验证a 、b 、c 、d 中,任意两两一组的比值是否相等,即可判断.【详解】解:A 、a 、b 、c 、d 中,任意两条线段的比值,与其他两个线段的比值都不相等,故错误B 、a 、b 、c 、d 中有:::1:3a c b d ==,故正确C 、a 、b 、c 、d 中,任意两条线段的比值,与其他两个线段的比值都不相等,故错误D 、a 、b 、c 、d 中,任意两条线段的比值,与其他两个线段的比值都不相等,故错误故选:B .【点睛】本题主要是考查了线段长度是否构成比例,直接判断任意两条线段是否与剩余两条比值相等即可解决本题.6、C【解析】【分析】由题意设()30,a k k =≠ 则2,b k = 再逐一代入各选项进行计算与检验即可得到答案.【详解】 解: 32a b =, 设()30,a k k =≠ 则2,b k =∴55,22a b k b k +==故A 不符合题意; 321,22a b k k b k --==故B 不符合题意; 263,a k b ==故C 符合题意;32,,2233a k b k ==则,23a b ≠故D 不符合题意; 故选C【点睛】本题考查的是比例的基本性质,掌握“设参数的方法解决比例问题”是解本题的关键.7、C【解析】【分析】过点A 作AF BD ⊥于点F ,设BC 与y 轴交于点G ,根据题意, EAF EFB ∽,GOF EBF ∽,求得4(0,),(,0)3G b F b -,进而可得4,3OG b OF b ==,即EF GO AF FO =3=4,设3,EF a =则4AF a =,根据面积为120求得a 的值,点A 、E 同时在反比例函数()0k y x x =<的图象上,表示出(,5)5k E a a ,则(4,53)5k A a a a a --,即4,25k A a a a ⎛⎫- ⎪⎝⎭ ,即可求得k 的值 【详解】解:如图,过点A 作AF BD ⊥于点F ,设BC 与y 轴交于点G ,DB x ⊥//AF FB ∴,//DB GOEAF EFB ∴∽,GOF EBF ∽EF EB AF FB ∴=,GO EB FO FB=EF GO AF FO∴= 直线AC 的解析式为34y x b =+,令0x =,y b =,令0y =,43b x =- 4(0,),(,0)3G b F b ∴- 4,3OG b OF b ∴==, EF GO AF FO ∴=3=4设3,EF a =则4AF a =在Rt AEF 中,5AE a =四边形ABCD 是矩形AC BD ∴=5AE EB a ∴==,矩形ABCD 的面积为120,121202BD AF ∴⨯⨯= 即104120a a ⨯=解得23a =根据题意,点A 、E 同时在反比例函数()0k y x x =<的图象上, 设(,5)5k E a a ,则(4,53)5k A a a a a --,即4,25k A a a a ⎛⎫- ⎪⎝⎭∴425k k a a a ⎛⎫=-⨯ ⎪⎝⎭即可240403a k =-=- 故选C【点睛】本题考查了反比例函数与几何图形,相似三角形的性质与判定,一次函数与坐标轴交点问题,矩形的性质,熟练运用以上知识是解题的关键.8、D【解析】【分析】直接根据题意得出位似比,根据位似比等于相似比,进而根据面积比等于相似比的平方求得面积比.【详解】解答:解:∵以点O 为位似中心,将△ABC 缩小后得到△A ′B ′C ′,BB ′=2OB ′,∴OB ′=13OB ,∴△A ′B ′C ′与△ABC 的面积之比为:1:9.故选:D .【点睛】此题主要考查了位似图形的性质,正确得出位似比是解题关键.9、D【解析】【分析】根据平行线间的距离处处相等,得到=8PBC S △,根据EF 是△PBC 的中位线,得到△PEF ∽△PBC ,EF =12BC ,得到1=4PEF PBC S S △△计算即可. 【详解】∵点P 是▱ABCD 边AD 上的一点,且 ▱ABCD 面积为16, ∴1==82PBC ABCD S S △平行四边形;∵E ,F 分别是BP ,CP 的中点,∴EF ∥BC ,EF =12BC ,∴△PEF ∽△PBC , ∴21=()4PEF PBC PBC EF S S S BC =△△△, ∴1=824PEF S ⨯=△,故选D .【点睛】本题考查了平行四边形的性质,三角形中位线定理,三角形相似的判定和性质,熟练掌握中位线定理,灵活运用三角形相似的性质是解题的关键.10、B【解析】【分析】设NH x =,则2CN x =,证明Rt ACN Rt BCA ∽,得出92BC x =,根据2ABED SAB =,再证明'()Rt ABN Rt D AM ASA ≌,得出'Rt ABC CND M S S =四边形,可以得出12''214Rt ABC ABE D S S S S +=-=四边形,得出等式2117192314422x x x -⨯⋅⋅=,求解即可得到. 【详解】解:设NH x =,则2CN x =,由题意知:3CA CH x ==,在Rt ACN 和Rt BCA 中,90ACN BCA ∠=∠=︒,90CAN CNA CAN CAB ∠+∠=∠+∠=︒,CNA CAB ∴∠=∠,Rt ACN Rt BCA ∴∽,2233CN AC x AC BC x ∴===, 92BC x ∴=, 在Rt ABC 中由勾股定理得:22222281117944AB AC BC x x x =+=+=, 2ABED S AB =,2''1174ABED ABE D S S x ∴==四边形, 在Rt ABN △和'Rt D AM 中,'''AB D A ABN D AM BAN AD M =⎧⎪∠=∠⎨⎪∠=∠⎩, '()Rt ABN Rt D AM ASA ∴≌,'Rt ABC CND M S S ∴=四边形,12'''14Rt ABC ABE D CND M S S S S S ∴+=--=四边形四边形,12''214Rt ABC ABE D S S S S ∴∴+=-=四边形,2117192314422x x x ∴-⨯⋅⋅=, 解得:25663x =, 211711756264463ABED S x ∴==⨯=, 故选:B .【点睛】本题考查正方形的性质、三角形相似、三角形全等、勾股定理,解题的关键是掌握相应的判定定理,通过转化的思想及等量代换的思想进行求解.二、填空题1、154【解析】【分析】先利用勾股定理求出BC =3,然后证明△ABC ∽△BDC ,得到AC AB BC BD =,即453BD =,由此求解即可. 【详解】解:在Rt △ABC 中,由勾股定理得,3BC = ,∵∠DBC =∠A ,∠C =∠C ,∴△ABC ∽△BDC , ∴AC AB BC BD =,即453BD=, ∴154BD =,故答案为:154.【点睛】本题主要考查了勾股定理和相似三角形的性质与判定,解题的关键在于能够熟练掌握相似三角形的性质与判定条件.2、5或252【解析】【分析】分情况进行讨论,当∠DPF =90°时,过点O 作OH ⊥AD 于H ,先证△DHO ∽△DAB ,得到1=2OH HD OD AB AD BD ==,求出1152OH AB ==,1202HD AD ==,证明∠HOP =∠HPO =45°,得到OH =PH =15,则PD =HD -PH =5;当∠PFD =90°时,先求出50BD =,得到11=2522OA OB OC OD AC BD =====,从而得到∠DAO =∠ODA ;证明△OFE ∽△BAD ,推出1152OF AB ==,则10DF OD OF =-=,最后证明△PDF ∽△BDA ,则12542PD BD ==. 【详解】解:如图1所示,当∠DPF =90°时,过点O 作OH ⊥AD 于H ,∴∠HPF =90°,∵四边形ABCD 是矩形,∴BD =2OD ,∠BAD =∠OHD =90°,AD =BC =40,∴OH ∥AB ,∴△DHO∽△DAB,∴1=2 OH HD ODAB AD BD==,∴1152OH AB==,1202HD AD==,由折叠的性质可得:1==452HPO FPO HPF∠=∠︒∠,∴∠HOP=45°,∴∠HOP=∠HPO=45°,∴OH=PH=15,∴PD=HD-PH=5;如图2所示,当∠PFD=90°时,∴∠OFE=90°,∵四边形ABCD是矩形,∴∠BCD=90°,CD=AB=30,∴50BD=,∴11=2522OA OB OC OD AC BD=====,∴∠DAO=∠ODA,由折叠的性质可知:AO=EO=25,∠PEO=∠DAO=∠ODA,又∵∠OFE=∠BAD=90°,∴△OFE∽△BAD,∴12 OF OEAB BD==,∴1152OF AB==,∴10DF OD OF=-=,∵∠PFD=∠BAD,∠PDF=∠BDA,∴△PDF∽△BDA,∴14 PD DFBD DA==,∴12542 PD BD==,∴综上所述,当△PDF为直角三角形,则PD的长为5或252,故答案为:5或252.【点睛】本题主要考查了矩形的性质,相似三角形的性质与判定,勾股定理,折叠的性质,解题的关键在于能够熟练掌握相似三角形的性质与判定条件.3、24 5【解析】【分析】先利用勾股定理求出CE 的长,再根据垂线段最短可得当BM CE ⊥时,BM 取得最小值,然后根据相似三角形的判定证出BCM CED ,最后根据相似三角形的性质即可得.【详解】解:矩形ABCD 中,E 是AD 的中点,4AB =,6AD =,3,4,6,90,DE CD BC D AD BC ∴===∠=︒,5,CE BCM CED ∴=∠=∠,由垂线段最短可知,当BM CE ⊥时,BM 取得最小值,在BCM 和CED 中,90BCM CEDBMC D ∠=∠⎧⎨∠=∠=︒⎩,BCMCED ∴,BM BC CD CE ∴=,即645BM =, 解得245=BM , 即BM 的最小值是245, 故答案为:245. 【点睛】本题考查了垂线段最短、矩形的性质、相似三角形的判定与性质等知识点,正确找出两个相似三角形是解题关键. 4、165【解析】 【分析】连接CF ,交DE 于H ,作DG ⊥AB 于G ,通过证明△AGD ≌△FGD ,得AD =DF ,从而可证D 是AC 中点,再证明E 是BC 中点,根据相似三角形的判定与性质,14CDECABS S=△△.设S △CDE =m ,根据△BEF 的而积为12求出m ,然后根据三角形的面积公式和勾股定理求解即可. 【详解】解:连接CF ,交DE 于H ,作DG ⊥AB 于G ,则∠AGD =∠DGF =90°,∵∠112+∠2=90°,∠1+∠GDF =90°,∴∠GDF =12∠2, ∴∠GDF =∠3. 在△AGD 和△FGD 中3AGD DGF DG DGGDF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGD ≌△FGD , ∴DA =DF ,∠A =∠1.由折叠的性质知,△AGD ≌△FGD , ∴FD =CD ,FE =CE , ∴∠4=∠5,AD =CD .∵∠A +∠1+∠4+∠5=180°, ∴∠1+∠4=90°, ∴∠AFC =90°, ∴∠BFC =90°. ∵,FE =CE , ∴∠6=∠7. ∵∠8+∠6=90°, ∴∠B +∠7=90°, ∴∠8=∠B , ∴FE =BE , ∴CE =BE ,∴D 、E 分别为AC 、BC 的中点, ∴DE //AB ,12DE AB =. ∴△CDE ∽△CAB ,∴14CDE CABS S=△△. 设S △CDE =m ,则S △ACB =4m , ∵S △ADF 12=S △CDE ,∴S △ADF 12=m .∵ΔΔΔΔΔ+ADF FDE BFE DEC ABC S S S S S ++=,∴12m +m +m +12=4m ,∴S△CDE=8,S△ACB=32,S△BFE=32-8-8-4=12.∵1322AB CF⋅=,AB=8,∴CF=8.∵DE//AB,∴△ABF与△BFE等高,∴AF:BF=S△ABF:S△BFE=4:12=1:3,∴BF=34AB=6.∵∠BFC=90°,∴BC.∵E为BC中点,∴BE=CE=5.设D到BC的距离为h,∵182CE h⋅=,∴∴h=2816=55⨯.故答案为:165.【点睛】本题考查了折叠的性质,勾股定理,全等三角形的判定与性质,等腰三角形的判定与性质,以及两平行线间的距离等知识,证明、E分别为AC、BC的中点是解答本题的关键.5、40394040【分析】设左边第一个正方形左上角的顶点为O,先判定△M1MN1∽△M1OA,利用相似三角形的性质求出MN1的长,进而得出S1,同理得出S2,按照规律得出Sn,最后n取2019,计算即可得出答案.【详解】解:如图所示,设左边第一个正方形左上角的顶点为O∵将2019个边长为1的正方形按如图所示的方式排列∴OA∥MA1∥M1A2∥M2A3∥…∥M2018A2019∴△M1MN1∽△M1OA∴1111 2MM MNOM OA==∴MN1=12,∴四边形M1N1A1A2的面积是S1=11311224-⨯⨯=;同理可得:121221 3M M M NOM OA==∴四边形M2N2A2A3的面积S2=11511236-⨯⨯=;…∴四边形MnNnAnAn+1的面积Sn=121 12(1)22nn n+ -=++∴S2019=40394040;故答案为:40394040. 【点睛】本题考查了相似三角形的判定与性质在规律型问题中的应用,数形结合并善于发现规律是解题的关键. 三、解答题 1、(1)1;60°(2)√6+√22或√6−√22【解析】 【分析】(1)证明△AAA ≌△AAA 即可求得AAAA =1,延长AA ,AA 交于点F ,设∠AAA =A ,根据三角形内角和即可求得∠A 即直线BE 与直线AD 所夹的劣角;(2)①当点E 在线段AD 上时,根据A ,A 分别为AA ,AA 的中点,可得AA 是ABC 的中位线,进而可得∠AAA =∠AAA =45°=∠AAA ,∠AAA =∠AAA ,证明△AAA ∽△AAA ,设AA =A ,则AA =A ,设AA =2A ,则AA =AA =A ,代入比例式求得A =√2A ,进而证明△AAA ∽△AAA ,设AA =A ,AA =(√3−1)A ,进而即可求得CEAD的值,②当D 在线段AE 上时,同理可得AA =√2A ,AA =(√3−1)A ,进而即可求得CEAD的值 【详解】解:(1)在三角形ABC 中,AC =AB ,∠CAB =60° ∴△AAA 是等边三角形 ∴AA =AA ,60BAC ∠=︒将线段绕点C 逆时针旋转60°得到线段CE ,∴∠AAA =60°,AA =AAADE ∴是等边三角形∴AA =AA ,∠AAA =60°∴∠AAA=∠AAA−∠AAA=∠AAA−∠AAA=∠AAA∴∠AAA=∠AAA∴△AAA≌△AAA∴AA=AA,∠AAA=∠AAA∴AAAA=1如图,延长AA,AA交于点F∵∠AAA=∠AAA,设∠AAA=A则∠AAA=∠AAA−∠AAA=60°−A,∠AAA=∠AAA+∠AAA=60+A 在△AAA中,∠A=180°−∠AAA−∠AAA=60°即直线BE与直线AD所夹的劣角是60°(2)①当点E在线段AD上时,如图,∵△AAA,CDE△是等腰直角三角形,∴∠AAA=45°,∠AAA=45°A,A分别为AA,AA的中点,∴AA∥AA∠AAA=∠AAA=45°∵∠AAA=∠AAA=45°=∠AAA,∠AAA=∠AAA∴△AAA∽△AAA设AA=A,则AA=A,AA=√2A,设AA=2A,则AA=AA=A∴AAAA=AAAA即AA=A2A∵A,A>0∴A=√2A∴AA=√2A=2A∵∠AAA=45°∴∠AAA=180°−∠AAA=135°∵∠AAA=45°∴∠AAA=180°−∠AAA=135°∴∠AAA=∠AAA又∠AAA=∠AAA∴△AAA∽△AAA则AAAA=AAAA设AA=A,∴AA=2A2A+A解得A1=(√3−1)A,A2=−(√3+1)A(舍)∴AA=(√3−1)A∴AAAA =√2A2A+(√3−1)A=√6−√22,②如图,当D在线段AE上时,同理可得AA =√2A ,AA =(√3−1)A∴AA AA =√2A (√3−1)A =√6+√22综上所述CE AD的值为√6−√22或√6+√22【点睛】本题考查了全等三角形的性质与判定,相似三角形的性质与判定,设参数法求解是解题的关键. 2、(1)y =6A ;(2)3.5;(3)当a =3或a =−1+√733【解析】 【分析】(1)由一次函数解析式可得点M 的坐标为(﹣3,﹣2),然后把点M 的坐标代入反比例函数解析式,求得k 的值,可得反比例函数表达式;(2)①作CD ⊥AB 交AB 于点D .当a =4时,利用函数解析式可分别求出点A 、B 、C 、D 的坐标,于是可得AB 和CD 的长度,即可求得△ABC 的面积;②分∠ACF 为直角,∠FAC 为直角两种情况,利用数形结合即可求解.【详解】解:(1)把M (﹣3,m )代入y =x +1,则m =﹣2.将(﹣3,﹣2)代入y =A A ,得k =6,则反比例函数解析式是:y =6A ;(2)①作CD ⊥AB 交AB 于点D .当a =4时,A (4,5),B (4,1.5),则AB =3.5.∵点Q 为OP 的中点,∴Q (2,0),∴C (2,3),则D (4,3),∴CD =2,∴S △ABC 12 AB •CD =12×3.5×2=3.5;②∵点E ,F 在y =x +1上∴点E (-1,0) F (A 2,A 2+1)∵Q (A 2,0)∴EQ=QF∴△ EQF 为等腰直角三角形, ∴当ACF 与EQF 相似时,则ACF 为等腰直角三角形,i 、当∠ACF 为直角时,则点C 和点A 的纵坐标相同,∴AP =CQ =12A ,又∵A 在直线y =x +1上,∴12A =a +1,解得a =3或a =﹣4(舍去),∴当a 的值为3时,ACF 与EQF 相似.ii 、当∠FAC 为直角时,过A 作AN ⊥CQ 如图由题意得A(a,a+1),C(A2,12A)∵△ACF为等腰直角三角形∴N(A2,a+1)∵AN⊥CQ∴AN=CN∴A2=12A-a-1解得:a=−2+2√736=−1+√733或a=−2−2√736=−1−√733(舍去)∴当a=3或a=−1+√733时,ACF与EQF相似.【点睛】本题综合考查了待定系数法求函数解析式,函数图象上点的坐标特征以及相似的性质.难度较大,解题时需要注意数形结合.3、(1)作图见解析;(2)①证明见解析;②2 3【解析】【分析】(1)由“好点”定义知2CD AD BD =⋅;①在Rt ABC 中,D 在线段AB 上;若Rt ADC 与Rt CDB 全等,可得=CD BD AD CD,此时可以得出点D 为Rt ABC 中,垂线CD 与线段AB 的交点,即“好点”;②在Rt ABC 中,由斜边上的中线等于斜边的一半,可知当D 为线段AB 的中点时,AD CD BD ==,有2CD AD BD =⋅,D 为“好点”.进而得出直角三角形的“好点”是斜边上的垂足与斜边的中点.(2)①由同弧所对圆周角相等可知A D ∠=∠ ,ACH DBH ∠=∠, ACH DBH ∽;可得CH DH BH AH ⋅=⋅;点H 为 BCD △中CD 边上的“好点”,故有2BH CH DH =⋅;可知BH AH =,故点H 为AB 边的中点,进而由垂径定理可证OH AB ⊥.②OH BD ∥,90ABD ∠=︒,连接AD ,AD 为直径;设OH m =,33r OH m ==,22BD OH m ==;在Rt AOH ,AH BH ==;在Rt BHD △,DH =;由2BH CH DH =⋅可得CH =CH DH 的值. 【详解】解:(1)如答图1所示①过点C 向线段AB 做垂线,交点为D∴Rt AD C Rt CD B ''∽AD CD CD BD ''∴=''2CD AD BD '''∴=⋅∴斜边上的垂足D 为“好点”②连接C 与线段AB 的中点D∴ CD 为Rt ABC 的中线AD CD BD ∴==2CD BD AD ∴=⋅∴斜边上的中点D 为“好点”∴综上所述,斜边AB 上的垂足D 与斜边AB 上的中点D 为“好点”.(2)①证明:由题意可知A D ∠=∠ ,ACH DBH ∠=∠ACH DBH ∴∽CH AH BH DH∴= CH DH BH AH ∴⋅=⋅ 又点H 为 BCD △中CD 边上的“好点”∴有2BH CH DH =⋅BH AH ∴=∴点H 为AB 边的中点由垂径定理可证OH AB ⊥∴OH AB ⊥②解:如答图2,连接ADOH BD∥90ABD∴∠=︒,AD为直径设OH m=33r OH m∴==,22BD OH m==在Rt AOH,AH BH==在Rt BHD△,DH=又2BH CH DH=⋅CH∴=23CHDH∴==23CHDH∴=.【点睛】本题考察了直角三角形中垂线与中线的性质、三角形相似、垂径定理、圆周角、勾股定理等知识点.解题的关键与难点在于理解新定义与所学知识的连接,是否能灵活运用已有知识.4、(1)2315684y x x =-+;(2)143x =或34633x = 【解析】【分析】(1)由题意代入A (2,0),B (8,0)两点求出a 、b 的值,即可得出抛物线的解析式;(2)根据题意分点P 在BC 下方的抛物线上和点P 在BC 上方的抛物线上两种情况,结合全等三角形的判定与性质以及相似三角形的判定与性质进行分析即可得出答案.【详解】解:(1)由题意代入A (2,0),B (8,0)两点,可得:042606486a b a b =++⎧⎨=++⎩,解得:38154a b ⎧=⎪⎪⎨⎪=-⎪⎩, 所以抛物线的解析式为:2315684y x x =-+; (2)当点P 在BC 下方的抛物线上时,此时∠PCB 12=∠BCO 即CP 平分∠BCO ,如图,作CP 平分∠BCO ,交x 轴于点D ,过D 作DE BC ⊥垂足为E ,∵CP 平分∠BCO ,DE BC ⊥,∴OD DE =,DCO DCE ∠=∠,∵OD DE =,DCO DCE ∠=∠,90COD CED ︒∠=∠=,∴,6,DOC DEC CO CE ≅==∴10,4BC BE BC CE =-=,设OD DE m ==,8BD m =-,勾股定理可得:222DE B D E B +=,即2224(8)m m +=-,解得:3m =,即3OD DE ==,D 的坐标为(3,0),设CD 的解析式为:(0)y kx b k =+≠,代入C 、D 可得:603b k b =⎧⎨=+⎩,解得:26k b =-⎧⎨=⎩,所以CD 的解析式为:26y x =-+, ∵P 为直线CD 与抛物线的交点, ∴联立可得:231526684x x x -+=-+, 解得:0x =(舍去)或143x =,即P 的横坐标为143x =, 当点P 在BC 上方的抛物线上时,此时∠PCB 12=∠BCO ,如图,作∠PCB 12=∠BCO 交抛物线于点P ,延长DE 交CP 于点F ,过E 作EH ⊥x 轴交于点H ,∵∠PCB 12=∠BCO ,DCB DCO ∠=∠,∴,PCB DCB ∠=∠∵,,PCB DCB CE CE DEC FEC ∠=∠=∠=∠,∴,DEC FEC DE DF ≅=,∵,90CBO EBH COB EHB ︒∠=∠∠=∠=,∴EHB COB ∽, ∴4,1068BE EH BH EH BH BC CO BO ====, 可得121624,,555EH BH OH BO BH ===-=, ∴2412(,)55E , 设F 为(,)m n ,由DE DF =可得324012,2525m n ++==,解得:3324,55m n ==, 即F 为3324(,)55, 设CF 的解析式为:(0)y kx b k =+≠,代入C 、F 可得:6243355b k b =⎧⎪⎨=+⎪⎩,解得:2116k b ⎧=-⎪⎨⎪=⎩,所以CD 的解析式为:2611y x =-+, ∵P 为直线CF 与抛物线的交点, ∴联立可得:22315661184x x x -+=-+, 解得:0x =(舍去)或34633x =,即P 的横坐标为34633x =, 综上所述P 的横坐标为143x =或34633x =. 【点睛】 本题考查二次函数的综合问题,熟练掌握待定系数法求二次函数解析式和全等三角形的判定与性质以及相似三角形的判定与性质和角平分线性质是解题的关键.5、见解析,1或7【解析】【分析】根据题意分P 在上方和P 在下方两种情况,进而结合相似三角形的判定与性质以及勾股定理进行分析计算即可得出线段CE 的长.【详解】解:如图,P 在上方时,连接PD ,PO 交AD 于点F ,PE 交AD 于点G ,∵矩形ABCD 的周长为28(AB <BC ),对角线长为10,∴100,AB BC +=解得6,8,AB BC ==∵OP ⊥BD ,90,BAD DOP FDO ADB ︒∠=∠=∠=∠,∴ODF ADB ,OD OF DF AD AB BD==, ∵6,8,AB AD BC ===152OD BD ==, ∴58610OF DF ==, 得1525,44OF DF ==, ∴54PF OP OF =-=,∵PE ⊥BC ,90,PGF DOP PFG DFO ︒∠=∠=∠=∠,∴,PFG DFO ∴54,,2554PG PF PG DO DF ==得1PG =,∵PD∴7CE DG ==; 如图,P 在下方时,连接BP ,OP 交BC 于点H ,同理得1PE=,BP=∴7BE=,∴871=-=-=.CE BC BE综上得线段CE的长为1或7.【点睛】本题考查相似三角形的判定与性质以及勾股定理和矩形的性质,熟练掌握相关知识求解是解题的关键.。
人教版九年级下册数学第二十七章 相似 含答案

人教版九年级下册数学第二十七章相似含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是()A. B. C. ﹣1 D. +12、如图,已知AB∥CD∥EF,那么下列结论正确的是()A. B. C. D.3、如图,树AB在路灯O的照射下形成投影AC,已知路灯高,树影,树AB与路灯O的水平距离,则树的高度AB长是()A. B. C. D.4、如果a=3,b=2,且b是a和c的比例中项,那么c=()A. B. C. D.5、如图,四边形是平行四边形,点在的延长线上,点在的延长线上,连接,分别交,于点,则下列结论错误的是()A. B. C. D.6、如图所示,若△ABC∽△DEF,则∠E的度数为()A.28°B.32°C.42°D.52°7、已知如图,AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB的值()A.2B.3C.4D.58、如图,在矩形ABCD中,AB=2,BC=3,点 E、 F、 G、 H分别在矩形 ABCD 的各边上, EF∥ AC∥ HG , EH∥ BD∥ FG ,则四边形 EFGH的周长是().A. B. C.2 D.29、如图,在等腰Rt△ABC中,∠BAC=90°,BC= ,点D是CB延长线上一点,过AB的中点E作CD的平行线,过点D作AC的平行线,两线相交于点F,则DF的长为( )A. B.4 C.3 D.10、如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于()A.5mB.5.5mC.5.6mD.5.8m11、如图,以A为位似中心,将△ADE放大2倍后,得位似图形△ABC,若 S1表示△ADE的面积,S2表示四边形DBCE的面积,则S 1:S2= ()A.1︰2B.1︰3C.1︰4D.2︰312、如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是()A.∠ADE=∠BB.∠AED=∠CC.D.13、如图,直线a b c,AB=BC,若DF=9,则EF的长度为( )A.9B.5C.4D.314、下列说法不正确的是()A.有一个角等于60°的两个等腰三角形相似B.有一个底角等于30°的两个等腰三角形相似C.有一个锐角相等的两个等腰三角形相似D.有一个锐角相等的两个直角三角形相似15、如图,在一斜边长30cm的直角三角形木板(即Rt△ACB)中截取一个正方形CDEF, 点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为()A.200cm 2B.170cm 2C.150cm 2D.100 cm 2二、填空题(共10题,共计30分)16、如果在比例尺为1∶1000000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是________千米.17、如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC=________.18、如图,在平面直角坐标系中,已知△ABC与△DEF位似,原点O是位似中心,=,若AB=1.5,则DE=________.19、如图,在⊙E中,弦AB与CD相交于坐标原点O,已知B(0,﹣3),C (﹣2,0),D(6,0),则点A的坐标是________.20、如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D是边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,AD的长度为________.21、如图中图形,其中的相似图形有________和________;________和________;________和________;________和________;________和________.22、若,则=________.23、观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.与图形(1)相似的有________;(填序号)与图形(2)相似的有________;与图形(3)相似的有________.24、已知△ABC∽△DEF,且相似比为3:4,S△ABC =12cm2,则S△DEF=________cm2.25、如图,在中,,,D为BC边上的一点,且.若的面积为1,则的面积为________.三、解答题(共5题,共计25分)26、已知xyz≠0且,求k的值.27、如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.28、如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求:(1)求BF和BD的长度.(2)四边形BDEF的周长.29、探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.探究二:如图2,在矩形ABCD中,AB=3,BC=4, E、G分别在边BC、AD上,F、H 分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出的值.探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.30、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.参考答案一、单选题(共15题,共计45分)1、C2、A3、A4、C5、D6、C7、C8、D9、C10、C11、B12、D13、B14、C15、D二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、。
人教版九年级下册数学第二十七章 相似 含答案

人教版九年级下册数学第二十七章相似含答案一、单选题(共15题,共计45分)1、如图,△ABC中,若DE∥BC,EF∥AB,则下列等式①②③④其中正确的是()A.①③④B.②③④C.①②④D.①②③④2、如图,在反比例函数的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足,当点A运动时,点C 始终在函数的图象上运动,若,则的值为()A. B. C. D.3、如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是()A.2 cm 2B.4 cm 2C.8 cm 2D.16 cm 24、如图,以点O为位似中心,把放大为原图形的2倍得到,以下说法中错误的是()A. B.点C,点O、点C′三点在同一直线上 C.D.5、在同一时刻,身高1.6m的小强,在太阳光线下影长是1.2m,旗杆的影长是15m,则旗杆高为()A.22mB.20mC.18mD.16m6、如图,小东用长为3.2 m的竹竿做测量工具测量学校旗杆的高度(竹竿与地面垂直),移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离8 m、与旗杆相距22 m,则旗杆的高为()A.12mB.10mC.8mD.7m7、下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是()A. B. C. D.8、如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为()A. B. C. D.9、如图,已知第一象限内的点A在反比例函数上,第二象限的点B在反比例函数上,且OA⊥OB,,则k的值为()A.-3B.-6C.-4D.10、如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和10米.已知小华的身高为1.6米,那么他所住楼房的高度 ( )A.8米B.16米C.32米D.48米11、如图所示的两个四边形相似,则α的度数是( )A.60°B.75°C.87°D.120°12、如图,内接于,垂直于过点的切线,垂足为.已知的半径为,,那么的值是()A. B. C. D.13、如图,在平面直角坐标系中,已知点E(−4,2),F(−1,−1).以原点O为位似中心,把△EFO扩大到原来的2倍,则点E的对应点E′的坐标为()A.(−8,4)B.(8,−4)C.(8,4)或(−8,−4)D.(−8,4)或(8,−4)14、如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:①△BMD≌△DFE;②△NBE∽△DBC;③AC=2DF;④EF AB=CF BC,其中正确结论的个数是()A.1B.2C.3D.415、某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()A.1.25mB.10mC.20mD.8m二、填空题(共10题,共计30分)16、如图,四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形,若OA:OA'=2:3,则四边形ABCD与四边形A'B'C'D'的面积比为________17、如图所示,,AC、BD相交于点E,若面积为3,的面积为5,则梯形的面积为________.18、如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y =ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B 的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是________.19、如果四条线段m,n,x,y成比例,若m=2 , n=8 , y=4.则线段x的长是________.20、已知△ABC∽△DEF,且BC=5cm,EF=3cm,若S△ABC =25cm2,则S△DEF=________。
人教版九年级下册数学第二十七章测试题含答案

人教版九年级下册数学第二十七章测试题一、单选题1.如果35ba=,则a ba-=()A.23B.85C.25D.832.比例尺为1:800的学校地图上,某条路的长度约为5cm,它的实际长度约为() A.400 cm B.40m C.200 cm D.20 m3.如图,在ABC中,点D、E分别在边AB、AC上,联结DE,如果AD:BD2=:3,那么下列条件中能判断DE//BC的是()A.AE3EC2=B.CE3AC5=C.DE2BC5=D.AB5BD3=4.下列说法中正确的是()A.两个直角三角形一定相似B.两个等腰三角形一定相似C.两个等腰直角三角形一定相似D.两个矩形一定相似5.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是()A.360元B.720元C.1080元D.2160元6.如果两个相似三角形的面积比为1:4,那么它们的相似比为()A.1B.1:2 C.1:4 D.1:167.如图,下列条件不能判定△ADB∽△ABC的是()A.∠ABD=∠ACB B.∠ADB=∠ABCC.AB2=AD•AC D.AD AB AB BC=8.图中的八边形是由10个单位正方形所组成的,在PQ下面的部分包含一个单位正方形与底边为5的三角形.若PQ恰将这八边形平分成两个面积相等的部分,则XQQY之值为()A.25B.12C.35D.239.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是()A.9.3m B.10.5m C.12.4m D.14m10.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=AB=,则CD为()A B C.2 D.3二、填空题11.已知23ab=,则b ab-=_____12.若两个相似六边形的周长比是3∶2,其中较大六边形的面积为81,则较小六边形的面积为________.13.已知△ABC与△DEF相似,且对应边的比为1:2,则△ABC与△DEF的面积比为_________.14.如图,已知∠1=∠2=∠3,图中有_______对相似三角形.15.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.16.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B处有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,则正方形城池的边长为_____步.17.如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点为位似中心,将△ABC缩小,使变换得到的△DEF与△ABC对应边的比为1∶2,则线段AC的中点P变换后对应点的坐标为____.18.如图,在矩形ABCD中,E是边AB的中点,连结DE交对角线AC于点F.若AB=8,AD=6,则CF的长为_____.三、解答题19.已知a:b:c=2:3:4,且a+b﹣c=6.求a、b、c的值.20.如图,AD是△ABC的中线,E是AD上一点,且AE:ED=2:3,CE延长∠AB于F,若AF=3cm,求AB的长.21.如图,在△ABC 中,BC=3,D 为AC 延长线上一点,AC=3CD,过点D 作DH∥AB,交BC 的延长线于点H,求CH 的长.22.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.23.如图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.24.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC 上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.(1)求证:△AEF∽△ABC:(2)求正方形EFMN的边长.25.如图,点P是▱ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交AD于点F,交CD的延长线于点G,已知12 DFFA.(1)求FPBP的值.(2)若四边形ABCD是菱形.①求证:△APB≌△APD;②若DP的长为6,求GF的长.参考答案1.C 【分析】根据两內项之积等于两外项之积用b 表示出a ,然后代入比例式进行计算即可得解. 【详解】 解:∵35b a =, ∴a=53b ,∴a b a -=5b-b35b 3=25.故选C . 【点睛】本题考查了比例的性质,熟记“两內项之积等于两外项之积”,并用b 表示出a 是解题的关键. 2.B 【分析】比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比.根据比例的基本性质即可得出结论. 【详解】解:设实际长度为x ,则:15800x=, 解得:400040x cm m ==, 故答案为B. 【点睛】本题考查比例线段.关键是根据比例尺,利用图上距离求出实际距离,注意单位换算. 3.B 【分析】先求出比例式,再根据相似三角形的判定得出△ADE ∽△ABC ,由相似推出∠ADE=∠B ,再由平行线的判定得出即可. 【详解】解:只有选项B 正确,理由是:∵AD:BD=2:3,∴25 ADAB=,∵35 CEAC=,∴25AEAC=,∴25 AD AEAB AC==,∵∠DAE=∠BAC,∴△ADE∽△ABC,∴∠ADE=∠B,∴DE∥BC,根据选项A、C、D的条件都不能推出DE∥BC,故选B.【点睛】本题考查了相似三角形的判定,能熟练转移比例线段得三角形相似是解此题的关键.4.C【分析】根据三角形、矩形相似的判定方法逐个分析,确定正确答案即可.【详解】解:A、两个直角三角形只有一个直角可以确定相等,其他两个角度未知,故A不正确;B、等腰三角形的角度不一定相等,各边也不一定对应成比例,故B不正确;C、两个等腰直角三角形的对应相等,所以两个等腰直角三角形相似,故C正确;D、两个矩形对应角相等,但对应边的比不一定相等,故D不正确;故选C.【点睛】本题考查了相似图形的知识,解题的关键是了解对应角相等,对应边的比相等的图形相似,难度不大.5.C【分析】根据题意求出长方形广告牌每平方米的成本,根据相似多边形的性质求出扩大后长方形广告牌的面积,计算即可.【详解】3m×2m=6m2,∴长方形广告牌的成本是120÷6=20元/m2,将此广告牌的四边都扩大为原来的3倍,则面积扩大为原来的9倍,∴扩大后长方形广告牌的面积=9×6=54m2,∴扩大后长方形广告牌的成本是54×20=1080元,故选C.【点睛】本题考查的是相似多边形的性质,掌握相似多边形的面积比等于相似比的平方是解题的关键.6.B【分析】根据相似三角形的面积的比等于相似比的平方得到它们的相似比【详解】解:∵两个相似三角形面积的比为1:4,∴它们的相似比1.2故选B.【点睛】本题主要考查了相似三角形的性质,利用相似三角形的面积的比等于相似比的平方是解答此题的关键.7.D【分析】根据有两个角对应相等的三角形相似,以及根据两边对应成比例且夹角相等的两个三角形相似,分别判断得出即可.【详解】解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;C、∵AB2=AD•AC,∴AC ABAB AD=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;D、ADAB=ABBC不能判定△ADB∽△ABC,故此选项符合题意.故选D.【点睛】点评:本题考查了相似三角形的判定,利用了有两个角对应相等的三角形相似,两边对应成比例且夹角相等的两个三角形相似.8.D【分析】首先设QY=x,则XQ=1﹣x,根据题意得到:PQ下面的部分的面积为:S△+S正方形12=⨯5×(1+x)+1=5,解方程即可求得结果.【详解】设QY=x,则XQ=1﹣x.∵PQ恰将这八边形平分成两个面积相等的部分,∴PQ下面的部分的面积为:S△+S正方形1 2 =⨯5×(1+x)+1=5,解得:x35=,∴QY35=,则XQ=1﹣x=13255-=,∴XQ:QY2355==:2:3.故选D.【点睛】本题考查了不规则图形的面积的求解方法:注意将原图形分割求解.此题难度不大,要注意仔细识图.9.B【分析】先证明∴△ABE∽△ACD,则利用相似三角形的性质得1.6 1.21.612.4CD=+,然后利用比例性质求出CD即可.【详解】解:∵EB∥CD,∴△ABE ∽△ACD , ∴AB BEAC CD=,即 1.6 1.21.612.4CD =+,∴CD=10.5(米). 故选B .【点睛】考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.10.C 【分析】根据勾股定理就可求得AB 的长,再根据△ABC 的面积=12•AC•BC=12•AB•CD ,即可求得. 【详解】解:根据题意得:. ∵△ABC 的面积=12•AC•BC=12•AB•CD ,∴CD=•AC BC AB . 故选C . 【点睛】本题主要考查了勾股定理,根据三角形的面积是解决本题的关键. 11.13【分析】根据两內项之积等于两外项之积用b 表示出a ,然后代入比例式进行计算即可得解. 【详解】 解:∵23a b =, ∴a=23b ,∴b a b-==2b-b 3b=13.故答案为:13.【点睛】本题考查了比例的性质,熟记“两內项之积等于两外项之积”,并用b表示出a是解题的关键.12.36【分析】首先根据相似多边形的周长的比求得面积的比,然后根据其中一个六边形的面积求得另一个六边形的面积.【详解】∵两个相似六边形的周长的比是3﹕2,∴它们的面积的比为9:4,∵较大一个六边形的面积为81,∴较小一个六边形的面积为481369⨯=;故答案为36.【点睛】考查相似多边形的性质,相似多边形的周长比等于相似比,面积比等于相似比的平方. 13.1:4【详解】【分析】根据相似三角形的面积比等于相似比的平方这一性质进行解答即可得.【详解】∵△ABC∽△DEF,且ABDE=12,∴S△ABC:S△DEF=211 24⎛⎫=⎪⎝⎭,故答案为1 4 .【点睛】本题考查了相似三角形的性质,熟知相似三角形的面积比等于相似比的平方是解题的关键.14.4【分析】根据已知先判定线段DE∥BC,再根据相似三角形的判定方法进行分析,从而得到答案.【详解】解:由题意的:∠1=∠2=∠3∴DE∥BC∴△ADE~△ABC,DE//BC∴∠EDC=∠DCB,又∠ACD=∠ABC,∴△EDC~△DCB,同理:∠3=∠2,∠A=∠A, ∴△ABC~△ACD,△ADE~ △ABC, △ABC~△ACD,∴△ADE~△ACD∴相似三角形共4对.故答案:4.【点睛】本题考查考查了平行线的判定;及相似三角形的判定:(1)两角对应相等的两个三角形相似;(2)两边对应成比例且夹角相等的两个三角形相似;(3)三边对应成比例的两个三角形相似;(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.15.209.【分析】作AH⊥BC于H,交GF于M,如图,先利用三角形面积公式计算出AH=4,设正方形DEFG 的边长为x,则GF=x,MH=x,AM=4-x,再证明△AGF∽△ABC,则根据相似三角形的性质得方程,然后解关于x的方程即可.【详解】解:如图,作AH⊥BC于H,交GF于M,∵△ABC的面积是10,∴12BC•AH=10,∴AH=4,设正方形DEFG 的边长为x ,则GF=x ,MH=x ,AM=4-x ,∵GF ∥BC ,∴△AGF ∽△ABC , ∴GF AM BC AH= , 454x x -∴= ,解得x=209 . 故答案为:209. 【点睛】 本题考查了相似三角形的判定与性质及正方形的性质,添加合适的辅助线是解题的关键. 16.300.【分析】设正方形城池的边长为x 步,1,2AE CE x ==则Rt BEA Rt EDC 证明∽, 根据比例性质求x . 【详解】解:设正方形城池的边长为x 步,1,2AE CE x ==则 AE CD , BEA EDC ∴∠=∠,Rt BEA Rt EDC ∴∽, 1302,17502x AB AE EC CD x ∴==,即 300x ,∴= 即正方形城池的边长为300步.故答案为300.【点睛】本题考查了相似三角形的应用:构建三角形相似,利用相似比计算对应的线段长.17.(2,32)或(-2,-32) 【分析】位似变换中对应点的坐标的变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或−k.本题中k=2或−2.【详解】解:∵两个图形的位似比是1:(−12)或1:12,AC的中点是(4,3),∴对应点是(2,32)或(−2,−32).【点睛】本题主要考查位似变换中对应点的坐标的变化规律.18.20 3【分析】根据矩形的性质可得出AB∥CD,进而可得出∠F AE=∠FCD,结合∠AFE=∠CFD(对顶角相等)可得出△AFE∽△CFD,利用相似三角形的性质可得出CFAF=CDAE=2,利用勾股定理可求出AC的长度,再结合CF=CFCF AF+•AC,即可求出CF的长.【详解】∵四边形ABCD为矩形,∴AB=CD,AD=BC,AB∥CD,∴∠F AE=∠FCD.又∵∠AFE=∠CFD,∴△AFE∽△CFD,∴CFAF=CDAE=2.∵AC,∴CF=CFCF AF+•AC=221+×10=203.故答案为203.【点睛】本题考查了相似三角形的判定与性质、矩形的性质以及勾股定理,利用相似三角形的性质找出CF:AF=2是解题的关键.19.a=12,b=18,c=24【分析】设a=2k,b=3k,c=4k,代入求出k,即可求出答案.【详解】解:由a:b:c=2:3:4可设a=2k、b=3k、c=4k,∵a+b﹣c=6,∴2k+3k﹣4k=6,解得:k=6,∴a=2k=12、b=3k=18、c=4k=24.【点睛】本题考查了比例的性质的应用,已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来.20.15【分析】作DH∥CF交AB于H,根据平行线分线段成比例定理列出比例式,计算即可.【详解】作DH∥CF交AB于H,则FHHB=CDDB=1,AFFH=23AEED=,∴FH=HB,3FH=23,解得,FH=BH=4.5,∴AH=AF+FH=7.5,∴AB=AH+HB=12.【点睛】本题考查的是平行线分线段成比例定理,灵活运用定理,找准对应关系是解题的关键.21.CH=1.【分析】根据相似三角形的判定得出两三角形相似,得出比例式,代入求出即可.【详解】解:∵DH∥AB,∴△ABC∽△DHC,∴BC ACCH DC=,∵BC=3,AC=3CD,∴CH=1.【点睛】考查了平行线的性质,相似三角形的性质和判定,解直角三角形的应用,能求出△ABC∽△DHC 是解此题的关键.22.10.【分析】根据相似图形的性质进行解答即可.【详解】解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,∴12AB AEDE DC==,∵四边形ABCD为矩形,∴CD=AB=4∴4142AEDE==,∴DE=8,AE=2,∴AD=AE+DE=2+8=10.【点睛】本题主要考查相似图形的性质,相似图形的对应边成比例,比例即为相似比.23.(1)作图见解析;(2)作图见解析;5π(平方单位).【分析】(1)连接AO、BO、CO并延长到2AO、2BO、2CO长度找到各点的对应点,顺次连接即可.(2)△A′B′C′的A′、C′绕点B′顺时针旋转90°得到对应点,顺次连接即可.A′B′在旋转过程中扫过的图形面积是一个扇形,根据扇形的面积公式计算即可.【详解】解:(1)见图中△A′B′C′(2)见图中△A″B′C″ 扇形的面积()22901242053604S πππ=+=⋅=(平方单位). 【点睛】本题主要考查了位似图形及旋转变换作图的方法及扇形的面积公式.24.(1)详见解析;(2)正方形的边长为8cm .【分析】(1)根据两角对应相等的两个三角形相似即可证明;(2)利用相似三角形的性质,构建方程即可解决问题;【详解】(1)证明:∵四边形EFMN 是正方形,∴EF ∥BC ,∴∠AEF=∠B ,∠AFE=∠C ,∴△AEF ∽△ABC .(2)解:设正方形EFMN 的边长为xcm .∴AP=AD-x=12-x(cm)∵△AEF ∽△ABC , AD ⊥BC ,∴EF AP BC AD =, ∴122412x x -=, ∴x=8,∴正方形的边长为8cm .【点睛】本题考查相似三角形的判定和性质、正方形的性质等知识,解题的关键是熟练掌握基本知识.25.(1)23;(2)①见解析,②5【分析】(1)由题意可得AD=BC,AD∥BC,根据题意可设DF=x,则AF=2x,即AD=BC=3x,由平行线分线段成比例可求PFBP=AFBC=2x3x=23;(2)①由菱形的性质可得AB=AD,∠DAP=∠BAP,可证:△APB≌△APD;②由题意可求FP=4,且GFBF=DFAF=12,可求GF的长.【详解】解:∵四边形ABCD是平行四边形∴AD=BC,AD∥BC∵DFAF=12.∴设DF=x,则AF=2x ∴AD=3x∴BC=AD=3x∵AD∥BC∴PFBP=AFBC=2x3x=23;(2)①∵四边形ABCD是菱形∴AC平分∠BAD,AB=AD∴∠DAP=∠BAP又AP=AP∴△APB≌△APD(SAS)②解:∵△APB≌△APD∴DP=BP=6∵PF BP =23, ∴FP =4∵四边形ABCD 是平行四边形∴AB ∥DC ∴GF BF =DF AF =12, ∴10GF =12, ∴GF =5【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行四边形的性质,菱形的性质,熟练运用这些性质进行推理是本题的关键.。
人教版八年级数学上册 第27章 相似章末复习(含答案)
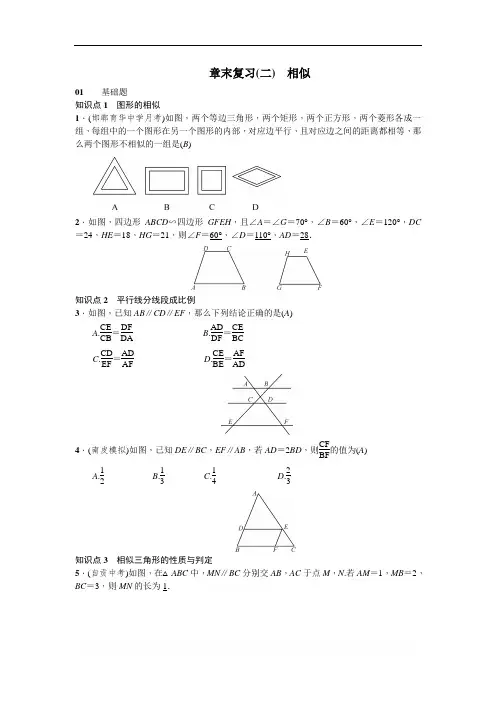
章末复习(二) 相似01 基础题知识点1 图形的相似1.(邯郸育华中学月考)如图,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是(B )2.如图,四边形ABCD ∽四边形GFEH ,且∠A =∠G =70°,∠B =60°,∠E =120°,DC =24,HE =18,HG =21,则∠F =60°,∠D =110°,AD =28.知识点2 平行线分线段成比例3.如图,已知AB ∥CD ∥EF ,那么下列结论正确的是(A )A .CE CB =DF DA B .AD DF =CE BC C .CD EF =AD AF D .CE BE =AF AD4.(南皮模拟)如图,已知DE ∥BC ,EF ∥AB ,若AD =2BD ,则CFBF的值为(A )A .12B .13C .14D .23知识点3 相似三角形的性质与判定5.(自贡中考)如图,在△ABC 中,MN ∥BC 分别交AB ,AC 于点M ,N .若AM =1,MB =2,BC =3,则MN 的长为1.6.(邯郸育华中学月考)如图,已知△ABC 中,CE ⊥AB 于E ,BF ⊥AC 于F .(1)求证:△AFE ∽△ABC ; (2)若∠A =60°时,求△AFE 与△ABC 面积之比.解:(1)证明:∵∠AFB =∠AEC =90°,∠A =∠A , ∴△AFB ∽△AEC . ∴AF AE =AB AC .∴AF AB =AEAC. 又∵∠A =∠A ,∴△AFE ∽△ABC . (2)∵∠A =60°,∠AEC =90°,∴∠ACE =30°. ∴AE =12AC .∵△AFE ∽△ABC .∴S △AFE S △ABC =(AE AC )2=(12)2=14.知识点4 相似三角形的应用7.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD =3 m ,标杆与旗杆的水平距离BD =15 m ,人的眼睛与地面的高度EF =1.6 m ,人与标杆CD 的水平距离DF =2 m ,则旗杆AB 的高度为13.5m .知识点5 位似8.(滨州中考)在平面直角坐标系中,点C ,D 的坐标分别为C (2,3),D (1,0).现以原点为位似中心,将线段CD 放大得到线段AB ,若点D 的对应点B 在x 轴上且OB =2,则点C 的对应点A 的坐标为(4,6)或(-4,-6).02 中档题9.(长沙中考)如图,将正方形ABCD 折叠,使顶点A 与CD 边上的一点M 重合(M 不与端点C ,D 重合),折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与边BC 交于点G ,设正方形ABCD 的周长为m ,△CMG 的周长为n ,则nm的值为(B )A .22 B .12 C .5-12D .随H 点位置的变化而变化10.(枣庄中考)如图,在矩形ABCD 中,∠B 的平分线BE 与AD 交于点E ,∠BED 的平分线EF 与DC 交于点F ,若AB =9,DF =2FC ,则BC =62+3.(结果保留根号)11.(河北中考)如图,在6×8网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均为小正方形的顶点.(1)以O 为位似中心,在网格图中作△A ′B ′C ′,使△A ′B ′C ′和△ABC 位似,且相似比为1∶2; (2)连接(1)中的AA ′,求四边形AA ′C ′C 的周长.(结果保留根号)解:(1)如图所示. (2)AA ′=CC ′=2. 在Rt △OA ′C ′中,OA ′=OC ′=2,得A ′C ′=2 2. 同理可得AC =42,∴四边形AA ′C ′C 的周长为4+6 2.12.如图,矩形ABCD 为台球桌面,AD =260 cm ,AB =130 cm .球目前在E 点位置,AE =60 cm .如果小丁瞄准BC 边上的点F 将球打过去,经过反弹后,球刚好弹到D 点的位置.(1)求证:△BEF ∽△CDF ; (2)求CF 的长.解:(1)证明:由题意,得∠EFG =∠DFG . ∵∠EFG +∠BFE =90°,∠DFG +∠CFD =90°, ∴∠BFE =∠CFD .∴△BEF ∽△CDF .(2)∵△BEF ∽△CDF ,∴BE CD =BF CF ,即70130=260-CF CF.∴CF =169 cm .13.(杭州中考)如图,在锐角△ABC 中,点D ,E 分别在边AC ,AB 上,AG ⊥BC 于点G ,AF ⊥DE 于点F ,∠EAF =∠GAC .(1)求证:△ADE ∽△ABC ; (2)若AD =3,AB =5,求AFAG的值.解:(1)证明:∵AF ⊥DE ,AG ⊥BC , ∴∠AFE =90°,∠AGC =90°. ∴∠AEF =90°-∠EAF ,∠C =90°-∠GAC , 又∵∠EAF =∠GAC ,∴∠AEF =∠C . 又∵∠DAE =∠BAC ,∴△ADE ∽△ABC . (2)∵△ADE ∽△ABC ,∴∠ADE =∠B . 又∵∠AFD =∠AGB =90°, ∴△AFD ∽△AGB .∴AF AG =AD AB. ∵AD =3,AB =5, ∴AF AG =35.03 综合题14.(眉山中考)如图,点E 是正方形ABCD 的边BC 延长线上一点,连接DE ,过顶点B 作BF ⊥DE ,垂足为F ,BF 分别交AC 于H ,交CD 于G .(1)求证:BG =DE ; (2)若点G 为CD 的中点,求HGGF的值.解:(1)证明:∵四边形ABCD 为正方形,∴BC =CD ,∠BCG =∠DCE =90°. ∵BF ⊥DE , ∴∠BFD =90°.∴∠CBF =∠GDF .∴△BCG ≌△DCE .∴BG =DE . (2)设正方形ABCD 的边长为a , ∵点G 是CD 的中点,∴CB =a ,CG =GD =12a .∴BG =52a .∵∠CBG =∠GDF ,∠BGC =∠DGF ,∴△BCG ∽△DFG .∴GF GC =DG BG ,即GF 12a =12a52a .∴GF =510a . 又∵AB ∥CD ,∴CG BA =HG HB =12.∴HG GB =13.∴GH =13GB =56a .∴HG GF =56a510a=53.。
九年级数学下册第二十七章相似知识点汇总(带答案)

九年级数学下册第二十七章相似知识点汇总单选题1、某校开展“展青春风采,树强国信念”科普大阅读活动.小明看到黄金分割比是一种数学上的比例关系,它具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,应用时一般取0.618.特别奇妙的是在正五边形中,如图所示,连接AB,AC,∠ACB的角平分线交边AB于点D,则点D就是线段AB的一个黄金分割点,且AD>BD,已知AC=10cm,那么该正五边形的周长为()A.19.1cmB.25cmC.30.9cmD.40cm答案:C分析:证明BC=CD=AD=6.18(cm),可得结论.解:由题意,点D是线段AB的黄金分割点,∴AD=0.618,AB∵AB=AC=10cm,∴AD=6.18(cm),∵∠ABC=∠ACB=72°,CD平分∠ACB,∴∠ACD=∠BCD=∠CAD=36°,∠CDB=∠CBD=72°,∴BC=CD=AD=6.18(cm),∴五边形的周长为6.18×5=30.90(cm),故选:C.小提示:本题考查正多边形的性质,黄金分割等知识,解题的关键是灵活应用所学知识解决问题.2、如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC 延长线上的动点,当△DCE 和△ABC 相似时线段CE 的长为( )A .3B .43C .3或43D .4或34 答案:C分析:根据∠ACD =∠ABC ,可得∠A =∠DCE ,然后分两种情况讨论,即可求解.解:∵∠ACD =∠ABC ,∠ACD +∠DCE =∠A +∠ABC ,∴∠A =∠DCE ,当 △CDE ∼△ABC 时,∴CD AB =CE AC ,∵AC =6,AB =4,CD =2,∴24=CE 6 ,解得:CE =3 ;当△CED ∼△ABC 时,∴CE AB =CD AC ,∵AC =6,AB =4,CD =2,∴CE 4=26 ,解得:CE =43∴线段CE 的长为3或43.故选:C小提示:本题主要考查了相似三角形的性质,熟练掌握相似三角形的性质定理是解题的关键.3、如图,△ABC 和△A 1B 1C 1中,A 1B 1∥AB ,A 1C 1∥AC ,C 1为OC 的中点,△A 1B 1C 1面积是5,则△ABC 的面积为( )A.10B.20C.25D.50 答案:B分析:利用位似图形的性质得出SΔA1B1C1SΔABC =14,进而求出即可.解:∵A1B1∥AB,A1C1∥AC,∴△ABC和△A1B1C1是以点O为位似中心的位似三角形,∵C1为OC的中点,△A1B1C1面积是5,∴OC1OC =12,∴SΔA1B1C1SΔABC =14,∴5SΔABC =14,解得:S△ABC=20.故选:B.【小提示】此题主要考查了三角形的面积、位似变换,得出位似比是解题关键.4、如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法正确的有()个①S△ABC:S△A′B′C′=1:2②AB:A′B′=1:2③点A,O,A′三点在同一条直线上④BC∥B′C′A.1B.2C.3D.4答案:C分析:根据位似图形的概念和相似三角形的性质判断即可.解:以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则△ABC∽△A′B′C′,且相似比为1:2,∴S△ABC:S△A′B′C′=1:4,故①选项说法错误;∴AB:A′B′=1:2,点A,O,A′三点在同一条直线上,BC∥B′C′,②③④说法正确;故选C.小提示:本题考查的是位似变换的概念和性质、相似三角形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.5、如图,△ABC与△DEF是位似图形,且顶点都在格点上,则位似中心的坐标是()A.(8,2)B.(9,1)C.(9,0)D.(10,0)答案:C分析:延长EB、DA交于点P,根据位似图形的对应点的连线相交于一点解答即可.解:延长EB、DA交于点P,则点P 即为位似中心,位似中心的坐标为(9,0),故选:C .小提示:本题考查的是位似变换的定义,如果两个图形不仅是相似图形,而且对应点的连线相交于一点,对应边互相平行(或共线),那么这样的两个图形叫做位似图形,这个点叫做位似中心.6、已知b a =5,则a−b a+b 的值是( )A .−23B .﹣13C .23D .13答案:A分析:由b a =5,可得b =5a ,然后代入a−b a+b ,即可求出其值.解:∵b a =5 ,∴b =5a ,且 a ≠0 ,则 a−b a+b =a−5a a+5a =−4a 6a =−23 , 故选:A .小提示:本题考查了比例的性质,解题的关键是正确运用基本性质.本题中要先确定a 与b 的关系,再确定a -b 与a +b 的关系.7、《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )A.五丈B.四丈五尺C.一丈D.五尺答案:B分析:根据同一时刻物高与影长成正比可得出结论.设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴x15=1.50.5,解得x=45(尺),即竹竿的长为四丈五尺.故选B小提示:本题考查了相似三角形的应用举例,熟知同一时刻物高与影长成正比是解答此题的关键.8、如图,点A,B的坐标分别为A(√2,0)、B(0,√2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,当OM最大时,M点的坐标为()A.(√22,1+√22)B.(√22,√22)C.(3√24,3√24)D.(1+√24,1+√24)答案:C分析:根据同圆的半径相等可知,点C在半径为1的⊙B上运动,取OD=OA,根据三角形的中位线定理知,点C在BD与⊙B的交点时,OM最小,在DB的延长线与⊙B的交点时,OM最大,根据平行线分线段成比例定理求得C的坐标,进而确定中点M的坐标即可.解:∵点C在坐标平面内,BC=1,∴C在半径为1的⊙B上,如图所示,取OD=OA=√2,连接CD,∵AM=CM,OD=OA,∴OM为△ACD的中位线,∴OM=12CD,当OM最大时,即CD最大,此时D,B,C三点共线,∵OB=OD=√2,∠BOD=90°,∴BD=2,∴CD=2+1=3,作CE⊥x轴于E点,∵CE∥OB,∴OBCE =ODDE=BDCD,即:√2CE=√2DE=23,∴CE=DE=3√22,∴OE=DE−OD=√22,∴C(√22,3√22),∵M是AC的中点,∴M(3√24,3√24),故选:C.小提示:本题考查了坐标与图形的性质,三角形的中位线定理等,确定OM最大时动点C的位置关系是解题关键.9、如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为()A.0.3cm B.0.5cm C.0.7cm D.1cm答案:B分析:求出△AOB和△COD相似,利用相似三角形对应边成比例列式计算求出AB,再根据外径的长度解答.解:∵OA:OC=OB:OD=3,∠AOB=∠COD,∴△AOB∽△COD,∴AB:CD=3,∴AB:3=3,∴AB=9(cm),∵外径为10cm,∴9+2x=10,∴x=0.5(cm).故选:B.小提示:本题考查相似三角形的应用,解题的关键是利用相似三角形的性质求出AB的长.10、已知ab =23,那么下列等式中成立的是()A.2a=3b B.a+1b+1=34C.a+bb=53D.a−bb=13.答案:C分析:比例的性质为两内项之积等于两外项之积,据此可进行解答.解:∵a:b=2:3的两内项是b、2,两外项是a、3,∴3a=2b,A:由以上解释易知A选项错误,不符题意;B:(a+1)×3=(b+1)×4,即3a=4b+1,故错误,不符题意;C:3×(a+b)=5b,即3a=2b,故正确,符合题意;D:3(a−b)=b,即3a=4b,故错误,不符题意;故选C.小提示:本题考查了比例的基本性质,掌握基本性质是解题关键.填空题11、《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为______米.答案:7分析:由题意易得△ACE∽△BDE,则有ACBD =AEBE,然后问题可求解.解:∵AC//BD,∴△ACE∽△BDE,∴ACBD =AEBE,∵AB=1.6米,BD=1米,BE=0.2米,∴AC1=1.6−0.20.2,解得AC=7米,故答案为7.小提示:本题主要考查相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.12、如图,在△ABC中,AB=6,BC=12,点P是AB边的中点,点Q是BC边上一个动点,当BQ=___________时,△BPQ与△BAC相似.答案:1.5或6分析:直接利用△BPQ∽△BAC或△BPQ∽△BCA,分别得出答案.解:∵AB=6,BC=12,点P是AB边的中点,∴BP=3.当△BPQ∽△BAC时,则BPAB =BQBC故36=BQ12解得:BQ=6;当△BPQ∽△BCA时,则BPBC =BQAB,故312=BQ6,解得BQ=1.5.所以答案是:1.5或6.小提示:本题主要考查了相似三角形的判定,正确分类讨论是解题关键.13、已知a6=b5=c4,且a+b−2c=6,则a的值为__________.答案:12分析:直接利用已知比例式假设出a,b,c的值,进而利用a+b-2c=6,得出答案.解:∵a6=b5=c4,∴设a=6x,b=5x,c=4x,∵a+b-2c=6,∴6x+5x-8x=6,解得:x=2,故a=12.故答案为12.小提示:此题主要考查了比例的性质,正确表示出各数是解题关键.14、在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做EF将矩形窗框ABCD分为上下两部分,其中E为边AB的黄金分割点,即BE2=AE⋅AB.已知AB为2米,则线段BE的长为______米.答案:(√5−1)##(−1+√5)分析:根据点E是AB的黄金分割点,可得AEBE =BEAB=√5−12,代入数值得出答案.∵点E是AB的黄金分割点,∴AEBE =BEAB=√5−12.∵AB=2米,∴BE=(√5−1)米.所以答案是:(√5−1).小提示:本题主要考查了黄金分割的应用,掌握黄金比是解题的关键.15、如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且点C与点D在直线AB同侧△ABC和△EDC的周长之比为1:2,点C的坐标为(-2,0),若点A的坐标为(-4,3),则点E的坐标为______.答案:(2,−6)分析:先利用位似的性质得到△ABC和△EDC的位似比为1:2,然后利用平移的方法把位似中心平移到原点解决问题.解:∵△ABC和△EDC是以点C为位似中心的位似图形,而△ABC和△EDC的周长之比为1:2,∴△ABC和△EDC的位似比为1:2,把C点向右平移2个单位到原点,则A点向右平移2个单位的对应点的坐标为(-2,3),点(-2,3)以原点为位似中心的对应点的坐标为(4,-6),把点(4,-6)向左平移2个单位得到(2,-6),∴E点坐标为(2,-6).故填:(2,−6).小提示:本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.也考查了转化的思想.解答题16、如图,在△ABC与△A′B′C′中,点D、D′分别在边BC、B′C′上,且△ACD∽△A′C′D′,若___________,则△ABD∽△A′B′D′.请从①BDCD =B′D′C′D′;②ABCD=A′B′C′D′;③∠BAD=∠B′A′D′这三个选项中选择一个作为条件(写序号),并加以证明.答案:见解析.分析:根据相似三角形的判定定理证明即可.解:若选①BDCD =B′D′C′D′,证明:∵△ACD∽△A′C′D′,∴∠ADC=∠A′D′C′,ADA′D′=CDC′D′,∴∠ADB=∠A′D′B′,∵BDCD =B′D′C′D′,∴BDB′D′=CDC′D′,∴ADA′D′=BDB′D′,又∠ADB=∠A′D′B′,∴△ABD∽△A′B′D′.选择②BACD =B′A′C′D′,不能证明△ABD∽△A′B′D′.若选③∠BAD=∠B′A′D′,证明:∵△ACD∽△A′C′D′,∴∠ADC=A′D′C′,∴∠ADB=∠A′D′B′,又∵∠BAD=∠B′A′D′,∴△ABD∽△A′B′D′.小提示:本题考查相似三角形的判定定理,解题的关键是掌握相似三角形的判定方法.17、如图所示,AB是⊙O的直径,CB,CE分别切⊙O于点B、点D,CE与BA的延长线交于点E,连接OC,OD.已知DE=a,AE=b,BC=c,请选用以上适当的数据,设计出计算⊙O的半径r的一种方案.(1)你选用的已知数据是__________.(2)写出求解过程(结果用字母表示).答案:(1)a,b;(2)r=a2−b22b,其他情况见解析;分析:方案一:选用的已知数据是a,b,根据题意,△EDO是直角三角形,所以在Rt△EDO中,利用勾股定理得到:EO2=DE2+OD2,就可以求出半径的长度;方案二:选用的已知数据是a,b,c,利用△DEO~△BEC,得到ODBC =EDEB,由此可得到半径的长度;方案三:选用的已知数是a,b,c,在Rt△EBC种,利用勾股定理得到:EC2=EB2+BC2,就可以求出半径的长度;方案四:选用的已知数是a,b,c,根据角的关系,得到∠COB=∠DAO,所以AD//OC,由此推出DECD =EAAO,即可求出半径的长度.解:方案一(1)选用的已知数据是a,b.(2)求解过程:∵CE分别切⊙O于点D,∴OD⊥EC.在Rt△EDO中,DE=a,OD=r,EO=b+r,且EO2=DE2+OD2,即(b+r)2=a2+r2,解得r=a2−b22b(舍负值).方案二(1)选用的已知数据是a,b,c.(2)求解过程:∵CB,CE分别切⊙O于点B、点D,∴OD⊥EC,OB⊥BC,∴∠EDO=∠EBC.又∵∠DEO=∠BEC,∴△DEO~△BEC,∴ODBC =EDEB,即rc =ab+2r,解得r=−b+√b2+8ac4(舍负值).说明:在Rt△DEO和Rt△BEC中,分别表示tanE,也可得到上述方程(或等价形式).方案三(1)选用的已知数是a,b,c.(2)求解过程:∵CB,CE分别切⊙O于点B、点D,∴CB=CD=c,OB⊥BC.在Rt△EBC中,EC=ED+CD=a+c,EB=EA+AB=b+2r,BC=C,且EC2=EB2+BC2,即(a+c)2=(b+2r)2+c2,解得r=√a2+2ac−b2(含负值).方案四(1)选用的已知数是a,b,c.(2)求解过程:如图,连接AD.∵CB,CE分别切⊙O于点B、点D,∴CB=CD=c,OB⊥BC,∠DCO=∠BCO.∴∠COB=∠COD=90°−∠BCO,∠DOA=180°−∠DOB=180°−2∠COB=2∠BCO.∵OD=OA,∴∠DAO=90°−12∠DOA=90°−∠BCO.∴∠COB=∠DAO,∴AD//OC,∴DECD =EAAO,即ac=br,∴r=bca.18、如图,a//b//c,直线m,n交于点O,且分别与直线a,b,c交于点A,B,C和点D,E,F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度.答案:154分析:由平行线分线段成比例定理得出比例式,即可得出结果.解:∵b∥c,OB=2,BC=4,∴OEEF =OBBC=24=12.∵EF=5,∴OE=12EF=52.∵a∥c,OA=1∴ODOF =OAOC=12+4=16.∴OD=16OF=16×(52+5)=54.∴DE=OD+OE=54+52=154.小提示:本题考查了平行线分线段成比例定理,熟记平行线分线段成比例定理是解决问题的关键.。
人教版九年级下册数学第二十七章 相似 含答案
人教版九年级下册数学第二十七章相似含答案一、单选题(共15题,共计45分)1、如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D 着地,则捣头点E上升了()A.0.5米B.0.6米C.0.3米D.0.9米2、如图,直线,若,,,则的值为()A. B. C. D.3、如图,能使△ACD∽△BCA全等的条件是()A. B.AC 2=CD•CB C. D.CD 2=AD•BD4、如图,在平行四边形ABCD中,E为AD的中点,△BCF的面积为4,则△DEF 的面积为()A.1B.2C.3D.45、如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为()A.16B.12C.10D.86、如图,AB∥CD,AD与BC相交于O,那么下列比例式正确的是 ( )A. B. C. D.7、如图,过△ABC内任一点P,作DE∥BC,GF∥AC,KH∥AB,则=()A.1B.C.2D.8、如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2 ,则线段CE的长为()A. B.8 C.2 D.99、在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数的图象上,则sin ∠ABO的值为()A. B. C. D.10、如图所示,⊙O中,弦AB,CD相交于P点,则下列结论正确的是()A.PA•AB=PC•PBB.PA•PB=PC•PDC.PA•AB=PC•CDD.PA:PB =PC:PD11、现给出四个命题:①等边三角形既是轴对称图形,又是中心对称图形;②相似三角形的面积比等于它们的相似比;③菱形的面积等于两条对角线的积;④一组数据2,5,4,3,3的中位数是4,众数是3,其中不正确的命题的个数是()A.1个B.2个C.3个D.4个12、如图,直线// // ,若AB=6,BC=9,EF=6,则DE=()A.4B.6C.7D.913、如图,已知点A的坐标为(3,4),⊙A的半径为3,延长OA交⊙A于点B,过点B作⊙A的切线,交y轴于点C,则OC长为()A.8B.9C.10D.1114、如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有()A.△ADE∽△ECFB.△BCF∽△AEFC.△ADE∽△AEFD.△AEF∽△ABF15、已知P是反比例函数图象上一点,点B的坐标为(1,0),A 是y轴正半轴上一点,且AP⊥BP,AP:BP=1:2,那么四边形AOBP的面积为()A.6.5B.8C.10D.7二、填空题(共10题,共计30分)16、如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C;过点B的直线DE分别交l1、l3于点D、E.若AB=2,BC=4,BD=1.5,则线段BE的长为________ .17、如图,矩形ABCD中,AD=1,AB=.将矩形ABCD绕着点B顺时针旋转90°得到矩形.联结,分别交边CD,于E、F.如果AE=,那么=________.18、如图,在△ABC中,∠C=90°,AB=5,BC=3,D是AB的中点,点E在边AC 上,将△ADE沿DE翻折,使点A落在点A'处,当A'E⊥AC时,A'B=________.19、已知△ABC中,∠C=90°,AB=9,,把△ABC 绕着点C旋转,使得点A落在点A′,点B落在点B′.若点A′在边AB上,则点B、B′的距离为________.20、在比例尺为1:2000000的地图上,港珠澳大桥的主桥图上距离为1.48cm,则港珠澳大桥的主桥长度为________km.21、如图,AB是半圆O的直径,AB=10,弦AC长为8,点D是弧BC上一个动点,连接AD,作CP⊥AD,垂足为P,连接BP,则BP的最小值是________.22、如图,点O是△ABC的重心,过点O作DE∥AB,分别交AC、BC于点D、E,如果,那么=________(结果用表示).23、两个相似三角形的周长的比为,它们的面积的比为________.24、在比例尺为1:10000000的地图上,相距7.5cm的两地A、B的实际距离为________千米.25、已知C是线段AB的黄金分割点,若AB=2,则BC=________。
人教版数学九年级下册第27章相似 相似多边形及位似拓展提升与复习过关
人教版数学九年级下册第27章相似相似多边形及位似拓展提升与复习过关知识全面设计合理含答案教师必备相似多边形及位似--知识讲解【学习目标】1、掌握相似多边形的性质及应用;2、了解图形的位似,知道位似变换是特殊的相似变换,能利用位似的方法,将一个图形放大或缩小;3、了解黄金分割值及相关运算.【要点梳理】要点一、相似多边形相似多边形的性质:(1)相似多边形的对应角相等,对应边的比相等.(2)相似多边形的周长比等于相似比.(3)相似多边形的面积比等于相似比的平方.要点诠释:用相似多边形定义判定特殊多边形的相似情况:(1)对应角都相等的两个多边形不一定相似,如:矩形;(2)对应边的比都相等的两个多边形不一定相似,如:菱形;(3)边数相同的正多边形都相似,如:正方形,正五边形.要点二、位似1.位似图形定义:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.2.位似图形的性质:(1)位似图形的对应点和位似中心在同一条直线上;(2) 位似图形的对应点到位似中心的距离之比等于相似比;(3)位似图形中不经过位似中心的对应线段平行.要点诠释:(1)位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.(2)位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.3.平移、轴对称、旋转和位似四种变换的异同:图形经过平移、旋转或轴对称的变换后,虽然对应位置改变了,但大小和形状没有改变,即两个图形是全等的;而位似变换之后图形是放大或缩小的,是相似的.4.作位似图形的步骤第一步:在原图上找若干个关键点,并任取一点作为位似中心;第二步:作位似中心与各关键点连线;第三步:在连线上取关键点的对应点,使之满足放缩比例;第四步:顺次连接各对应点. 要点诠释:位似中心可以取在多边形外、多边形内,或多边形的一边上、或顶点,下面是位似中心不同的画法.要点三、黄金分割定义:如图,将一条线段AB 分割成大小两条线段AP 、PB ,若小段与大段的长度之比等于大段的长度与全长之比,即ABAPAP PB =(此时线段AP 叫作线段PB 、AB 的比例中项),则P 点就是线段AB 的黄金分割点(黄金点),这种分割就叫黄金分割.要点诠释:1.黄金分割值:设AB=1,AP=x ,则BP=x -1 ∵AB APAP PB = ∴11xx x =- ∴x x -=12∴618.0215≈-=x (舍负) 2.黄金三角形:顶角为36°的等腰三角形,它的底角为72°,恰好是顶角的2倍,人们称这种三角形为黄金三角形.黄金三角形性质:底角平分线将其腰黄金分割.【典型例题】类型一、相似多边形1.如图,矩形草坪长20m,宽16m,沿草坪四周有2m宽的环形小路,小路内外边缘所形成的两个矩形相似吗?为什么?【答案与解析】因为矩形的四个角都是直角,所以关键是看矩形ABCD 与矩形EFGH的对应边的比是否相等.542016221616EFAB==++=,652420222020EHAD==++=而6554≠,∴EHADEFAB≠∴矩形ABCD与矩形EFGH的对应边的比不相等,因而它们不相似.【总结升华】两个边数相同的多边形,必须同时满足“对应边的比都相等,对应角都相等”这两个条件才能相似,缺一不可.举一反三【变式】(2015•梧州一模)如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=()A. 2:1B. :1C. 3:D. 3:2【答案】B.提示: ∵矩形纸片对折,折痕为EF,∴AF=AB=a,∵矩形AFED与矩形ABCD相似,∴=,即=,∴()2=2,∴=.故选B.AB CDEF GH2.(2014•甘肃模拟)如图,在长8cm,宽4cm 的矩形中截去一个矩形,使留下的矩形(阴影部分)与原矩形相似,那么留下的矩形的面积为().A. 2cm2B. 4cm2C. 8cm2D. 16cm2【答案】C.【解析】设留下的矩形的宽为x,∵留下的矩形与原矩形相似,∴,∴x=2,∴留下的矩形的面积为:2×4=8(cm2)故答案为:8.故选C.【总结升华】本题主要考查了相似多边形的性质,在解题时要能根据相似多边形的性质列出方程是本题的关键.类型二、位似3. 利用位似图形的方法把五边形ABCDE放大1.5倍.【答案与解析】即是要画一个五边形A′B′C′D′E′,要与五边形ABCDE相似且相似比为1.5.画法是:1.在平面上任取一点O.2.以O为端点作射线OA、OB、OC、OD、OE.3.在射线OA、OB、OC、OD、OE上分别取点A′、B′、C′、D′、E′,使OA′:OA= OB′:OB =OC′:OC=OD′:OD=OE′:OE=1.5.4.连结A′B′、B′C′、C′D′、D′E′、E′A′.这样:A′B′AB=B′C′BC=C′D′CD=D′E′DE=A′E′AE=1.5.则五边形A′B′C′D′E′为所求. 另外一种情况,所画五边形跟原五边形分别在位似中心的两侧.ABC DEA1B1C1D1E1ABC DE【总结升华】由本题可知,利用位似的方法,可以把一个多边形放大或缩小.4. 如图,矩形OABC 的顶点坐标分别为O (0,0),A (6,0),B (6,4),C (0,4).画出以点O 为位似中心,矩形OABC 的位似图形OA ′ B ′ C ′ ,使它的面积等于矩形OABC 面积的41,并分别写出A ′、B ′、C ′三点的坐标.【答案与解析】因为矩形OA ′B ′C ′与矩形OABC 是位似图形,面积比为1:4,所以它 们的位似比为1:2. 连接OB ,(1)分别取线段OA 、OB 、OC 的中点A ′、B ′、C ′,连接O A ′、A ′B ′、B ′C ′、 C ′O ,矩形OA ′B ′C ′就是所求的图形.A ′,B ′,C ′三点的坐标分别为A ′(3,0),B ′(3,2),C ′(0,2). (2)分别在线段OA ,OB ,OC 的反向延长线上截取O A ″、O B ″、O C ″,使OA ″=21OA ,OB ″=21OB ,O C ″=21OC ,连接 A ″B ″、B ″C ″,则矩形O A ″B ″C ″为所求. A ″、B ″、C ″三点的坐标分别为A ″(-3,0),B ″(-3,-2),C ″(0,-2).【总结升华】平面直角坐标系内画位似图形,若没有明确指出只画一个,一定要把两种情况都画在坐标系内,并写出两种坐标.举一反三【变式】在已知三角形内求作内接正方形.【答案】作法:(1)在AB上任取一点G′,作G′D′⊥BC;(2)以G′D′为边,在△ABC内作一正方形D′E′F′G′;(3)连接BF′,延长交AC于F;(4)作FG∥CB,交AB于G,从F、G分别作BC的垂线FE, GD;∴四边形DEFG即为所求.类型三、黄金分割5.求做黄金矩形(写出具体做题步骤)并证明.【答案与解析】宽与长的比是512的矩形叫黄金矩形.(心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.)黄金矩形的作法如下(如图所示):第一步:作一个正方形ABCD;第二步:分别取AD,BC的中点M,N,连接MN;第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;第四步:过E作EF⊥AD,交AD的延长线于F.即矩形DCEF为黄金矩形.证明:在正方形ABCD中,取2AB a=,∵ N为BC的中点,G FF'B CG'∴ 12NC BC a ==. 在Rt DNC △中,2222(2)5ND NC CD a a a =+=+=.又∵ NE ND =,∴ (51)CE NE NC a =-=-.∴5151CE a CD --==(). 故矩形DCEF 为黄金矩形.【总结升华】要求熟练掌握多边形相似的比例关系.会利用相似比,求未知线段的长度或比值.举一反三【变式】美是一种感觉,当人的肚脐是人的身高的黄金分割点时,人的下半身长与身高之比约为0.618,人的身段成为黄金比例,给人一种美感.某女士身高165cm ,下半身长与身高的比值是0.60,为尽可能达到匀称的效果,她应穿高跟鞋的高度大约为( ) A.4cm B.5cm C.6cm D.8cm 【答案】D.∵该女士身高165cm ,下半身长与身高的比值是0.60, ∴此女士下半身长是165×0.60=99cm ,设需要穿的高跟鞋是xcm ,根据黄金分割的定义得:99+=165+xx0.618,解得:x ≈8. 故选D .相似多边形及位似--巩固练习【巩固练习】一. 选择题1.下面给出了相似的一些命题: (1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相 似;(5)正六边形都相似;其中正确的有( ) A .2个 B .3个 C .4个 D .5个2.下列说法错误的是( ). A.位似图形一定是相似图形. B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行. 3.下列说法正确的是( )A.分别在ABC 的边AB 、AC 的反向延长线上取点D 、E ,使DE ∥BC ,则ADE是ABC 放大后的图形.AC D EFM NB.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4.平面直角坐标系中,有一条“鱼,它有六个顶点”,则()A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似.B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似.C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似.D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似.5.(2015•杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是()A. 10B. 12C.D.6.如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是()A. AB:AC=AC:BCB. AC=512AB-C.AB=512AC+D.BC≈0.618AB7.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD 上的F点,若四边形EFDC与矩形ABCD相似,则AD=()A. 512-B.512+C.3D.2二.填空题8. 如果两个位似图形的对应线段长分别为3cm和5cm,且较小图形周长为30cm,则较大图形周长为___ ___.9.已知ABC,以点A为位似中心,作出ADE,使ADE是ABC放大2倍的图形,则这样的图形可以作出______个,它们之间的关系是__________.10.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A B C D E''''',已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A B C D E'''''的周长的比值是__________.11. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.12.(2015春•庆阳校级月考)图中的两个四边形相似,则x+y= ,α= .13.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为__________________.14. 如图,△ABC中,AB=AC=4,∠BAC=36°,∠ABC的平分线与AC边的交点D为边AC的黄金分割点(AD>DC),则BC=______________.三.综合题15.如图,D、E分别AB、AC上的点.(1)如果DE∥BC,那么△ADE和△ABC是位似图形吗?为什么?(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?16.(2014•南通)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形A EFG∽菱形ABCD,连接EB,GD.(1)求证:EB=GD;(2)若∠DAB=60°,AB=2,AG=,求GD的长.17. 如图1,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=43.(1)求矩形ODEF的面积;(2)将图1中的矩形ODEF绕点O逆时针旋转一周,连接EC、EA,△ACE的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.【答案与解析】一、选择题1.【答案】B【解析】(1)菱形的角不一定对应相等,故错误;(2)(3)(5)符合相似的定义,故正确;(4)对应边的比不一定相等.故错误.故正确的是:(2)(3)(5).故选B.2.【答案】D.3.【答案】C.4.【答案】C.5.【答案】C.【解析】∵四边形ABCD∽四边形A1B1C1D1,∴=,∵AB=12,CD=15,A1B1=9,∴C1D1==.6.【答案】D.【解析】∵AC>BC,∴AC是较长的线段,根据黄金分割的定义可知:AB:AC=AC:BC,AC=512AB-, AB=512AC+AC≈0.618AB.故选D.7.【答案】B.【解析】∵AB=1,设AD=x,则FD=x-1,FE=1,∵四边形EFDC与矩形ABCD相似,∴EF AD FD AB=,111xx=-,解得11+5 =2x,21-5 =2x,(负值舍去),经检验11+5 =2x是原方程的解.故选B.二、填空题8.【答案】50cm.9.【答案】2个;全等.10.【答案】1:2.【解析】∵五边形ABCDE与五边形A′B′C′D′E′位似,OA=10cm,OA′=20cm,∴五边形ABCDE∽五边形A′B′C′D′E′,且相似比为:OA:OA′=10:20=1:2,∴五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比为:OA:OA′=1:2.故答案为:1:2.11.【答案】;【解析】由BC ∥DE 可得△ADE ∽△ABC ,所以,故.12.【答案】63,85°.【解析】由于两个四边形相似,它们的对应边成比例,对应角相等,∴ 18:4=x :8=y :6,解得x=36,y=27,则x+y=36+27=63.∴a=360°﹣(77°+83°+115°)=85°.故答案为63,85°.13. 【答案】1256. 【解析】∵A 1、F 1、B 1、D 1、C 1、E 1分别是△ABC 和△DEF 各边中点,∴正六角星形AFBDCE ∽正六角星形A 1F 1B 1D 1C 1E 1,且相似比为2:1,∵正六角星形AFBDCE 的面积为1,∴正六角星形A 1F 1B 1D 1C 1E 1的面积为14, 同理可得,第三个六角形的面积为:314=164, 第四个六角形的面积为:1111=1644256⨯⨯, 故答案为:1256. 14. 【答案】25-2;【解析】∵AB=AC ,∠A=36°,∴∠ABC=∠C=72°,又BD 平分∠ABC ,∴∠ABD=∠CBD=36°,∴∠BDC=72°,∴BC=BD=AD ,∵D 点是AC 的黄金分割点,∴BC=AD=4×5-12=25-2.三.解答题15.【答案与解析】(1)△ADE 和 △ABC 是位似图形.理由是:DE ∥BC ,所以∠ADE=∠B , ∠AED=∠C.所以△ADE ∽△ABC ,所以. 又因为 点A 是△ADE 和 △ABC 的公共点,点D 和点B 是对应点,点E 和点C是对应点,直线BD 与CE 交于点A ,所以△ADE 和 △ABC 是位似图形.(2)DE ∥BC.理由是:因为△ADE 和△ABC 是位似图形,所以△ADE ∽△ABC所以∠ADE=∠B所以DE ∥BC.16.【答案与解析】(1)证明:∵菱形AEFG∽菱形ABCD ,∴∠EAG=∠BAD,∴∠EAG+∠GAB=∠BAD+∠GAB,∴∠EAB=∠GAD,∵AE=AG,AB=AD ,∴△AEB≌△AGD,∴EB=GD;(2)解:连接BD 交AC 于点P ,则BP⊥AC,∵∠DAB=60°,∴∠PAB=30°,∴BP=AB=1,AP==,AE=AG=,∴EP=2, ∴EB===, ∴GD=.17.【答案与解析】(1)∵矩形ODEF ∽矩形ABCO ,其相似比为1:4,∴S 矩形ODEF =116S 矩形ABCO =116×4×43=3; (2)存在.∵OE=所以点E 的轨迹为以点O 为圆心,以2为半径的圆, 设点O 到AC 的距离为h ,AC=()22224438AB BC +=+=∴8h=4×43,。
人教版九年级下册数学第二十七章 相似含答案【直接打印】
人教版九年级下册数学第二十七章相似含答案一、单选题(共15题,共计45分)1、在某一时刻,测得一根高为1.2m的木棍的影长为2m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为()A.15mB. mC.60 mD.24m2、同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则这棵树的高度为()A.2.4米B.9.6米C.2米D.1.6米3、如图,在△ABC中,DE∥BC,若= ,DE=4,则BC的值为()A.9B.10C.11D.124、经过矩形一组对边中点的直线把矩形分成相同的两个矩形,这两个矩形与原矩形的关系()A.一定相似B.一定不相似C.不一定相似D.以上说法都不对5、如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是()A. B. C. D.6、如图,矩形的顶点在反比例函数的图象上,点的坐标为则的值为()A.-18B.8C.9D.187、如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角,窗户的高在教室地面上的影长米,窗户的下檐到教室地面的距离米(点、、在同一直线上),则窗户的高为()A. 米B.3米C.2米D.1.5米8、如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB上的一个动点,过点P画PD⊥AC于点D,PE⊥BC于点E,当点P由A向B移动时,四边形CDPE周长的变化情况是()A.逐渐变小B.逐渐变大C.先变大后变小D.不变9、某同学利用影长测量学校旗杆的高度,在同一时刻,他测得自己的影长0.8米,旗杆的影长7米,已知他的身高1.6米,旗杆的高度为( )米。
A.20B.7C.14D.1210、如图,AD∥BE∥CF ,直线、与这三条平行线分别交于点A、B、C和点D、E、F ,若AB=2,AC=6,DE=1.5,则DF的长为()A.7.5B.6C.4.5D.311、已知两个三角形相似,对应中线之比为1:4,那么对应周长之比为()A.1:2B.1:16C.1:4D.无法确定12、如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为()A.10.8mB.9mC.7.5mD.0.3m13、若两个相似三角形的相似比为1∶2,则它们面积的比为()A.2∶1B.1∶2C.1∶4D.1∶514、如图,抛物线y=x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为()A. 或B. 或C. 或D. 或15、已知四个数,,,成比例的线段,那么m的值是()A.3B.C.D.二、填空题(共10题,共计30分)16、已知点C是AB的黄金分割点(AC<BC),AC=4,则BC的长________ .17、在比例尺为1:8000的城区地图上,人民路的长度约为40cm,它的实际长度约为________km.18、如图,在△ABC中,∠C=90°,点D、E、F分别在边BC、AB、AC上,且四边形CDEF为正方形,若AE=3,BE=5,则S△AEF +S△EDB=________.19、如图,□ABCD中,E是AB中点,F在AD上,且AF=FD,EF交AC于G,则AG︰AC=________ .20、一张等腰三角形纸片,底边长为,底边上的高长.现沿底边依次从下往上数剪宽度均为的矩形纸条,如图所示,已知剪得纸条中有一张是正方形,则这张正方形纸条是第________张21、如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为________.22、如图,小红作出了边长为1的第1个正三角形△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2B2C2,作出了第二个正三角形△A2B2C2,算出第2个正△A2B2C2的面积,用同样的方法作出了第3个正△A3B3C3,算出第3个正△A3B3C3的面积,依此方法作下去,由此可得第n次作出的正△An BnCn的面积是________.23、如图,在四边形中,,,,,若在线段上取一点,使得以为顶点的三角形和以为顶点的三角形相似,则这样的点有________个.24、如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为________.25、已知点在线段上,如果,,那么的长是________.三、解答题(共5题,共计25分)26、已知xyz≠0且,求k的值.27、如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.(1)求证:AB•AF=CB•CD;(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP 的面积为ycm2.①求y关于x的函数关系式.②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.28、如图,证明:三角形一内角平分线分对边所得的两条线段和这个角的两边对应成比例.(要求:在给出的△ABC中用尺规作出∠A的角平分线AD交BC于D,保留作图痕迹,不要求写出作法,并根据图形写出已知、求证和证明.29、如图,∠1=∠2=∠3,试找出图中两对相似三角形,并说明为什么?30、如图,DE∥AB,FD∥BC, ,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?参考答案一、单选题(共15题,共计45分)1、A2、B3、D4、C5、D6、B8、B9、C10、C11、C12、A13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
人教版初中数学《第27章极端原理》竞赛专题复习含答案
第27章极端原理27.1.1** 两人轮流往一个圆桌面上放同样大小的硬币.规定每人每次只能放一枚,硬币平放在桌面上,并且两两不能重叠,谁放完最后一枚.使得对方无法按照规则再放,谁就获胜.问:是先放合算还是后放合算?解析本题的极端情况是:桌面小的只能放下一枚硬币.这时当然是先放的人合算.一般情况下,先放的人把硬币放在圆桌的中心处,每当对手放下一枚硬币后,就在对方硬币关于“圆心”对称位置再放下一枚硬币,这样只要对手还能放硬币,先放的人一定也能放,所以放最后一枚硬币的人一定是先放的人,从而他必能获胜.评注本题解法的独到之处在于考虑最极端的情况,“桌面最小”.这里的极端原理实际是一种“从特殊到一般”的思考方法,并且在极端情况下的结果提示我们解决一般问题的方法,在应用极端原理时,我们要利用如下的事实:1.有限个数中一定有最大数和最小数;2.无限个正整数中有最小数;3.无限个实数不一定有最大数或最小数.27.1.2** 在一次乒乓球循环赛中,n(n≥3)名选手中没有全胜的,证明:一定可以从中找出三名选手A、B、C,使得A胜B,B胜C,C胜A.解析没取胜场数最多的一名选手为A,由于没有一个选手是全胜的,所以在这n名选手中存在一名选手C,C胜A.考虑A击败的选手的全体,其中必有选手B胜C.事实上,若A的手下败将也都负于C,那么C胜的场数比A胜的场数至少要多1,这与A是获胜场数最多的选手矛盾.所以,存在三名选手A、B、C,使得A胜B,B胜C,C胜A.27.1.3** 平面上已给997个点,将连结每两点的线段中点染成红色,证明:至少有1991个红点,能否找到恰有1991个红点的点.解析997个点中每两点都有一个距离,因而共有9979962个距离(其中有可能有些距离是相等的),其中一定有一个最大距离.设AB是最大的距离.分别以A、B为圆心,12AB为半径作圆,如图所示.点A与除点B之外的995个点的连线的中点在圆A的内部或边界上;点B与除点外的995个点的连线的中点在圆B的内部或边界上,这样我们得到了995+995=1990个红点.另外,AB的中点是不同于上述1990个红点的,所以,至少有1991个红点.下面构造一个例子,说明恰好有1991个红点,设997个点在数轴上1,2,3,…,997的位置.这时中点为:32,42,52,…,19922,19932,故红点恰有1991个.27.1.4** 证明:在任意的凸五边形中,都可以找到三条对角线,由这三条对角线可以组成一个三角形.解析如图所示,在凸五边形ABCDE中,一共有5条对角线:AC、AD、BD、BE、CE,所以其中一定有一条是最长的,不妨设AC最长.ABEPD由于ACDE 是凸四边形,设AD 与CE 的交点为P ,则 AC AP PC AD CE <+<+.因为AC 最长,所以,AC 、AD 、CE 这三条对角线可以作为一个三角形的三条边.27.1.5* 平面上给定3个点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第27章极端原理27.1.1** 两人轮流往一个圆桌面上放同样大小的硬币.规定每人每次只能放一枚,硬币平放在桌面上,并且两两不能重叠,谁放完最后一枚.使得对方无法按照规则再放,谁就获胜.问:是先放合算还是后放合算?解析本题的极端情况是:桌面小的只能放下一枚硬币.这时当然是先放的人合算.一般情况下,先放的人把硬币放在圆桌的中心处,每当对手放下一枚硬币后,就在对方硬币关于“圆心”对称位置再放下一枚硬币,这样只要对手还能放硬币,先放的人一定也能放,所以放最后一枚硬币的人一定是先放的人,从而他必能获胜.评注本题解法的独到之处在于考虑最极端的情况,“桌面最小”.这里的极端原理实际是一种“从特殊到一般”的思考方法,并且在极端情况下的结果提示我们解决一般问题的方法,在应用极端原理时,我们要利用如下的事实:1.有限个数中一定有最大数和最小数;2.无限个正整数中有最小数;3.无限个实数不一定有最大数或最小数.27.1.2** 在一次乒乓球循环赛中,n(n≥3)名选手中没有全胜的,证明:一定可以从中找出三名选手A、B、C,使得A胜B,B胜C,C胜A.解析没取胜场数最多的一名选手为A,由于没有一个选手是全胜的,所以在这n名选手中存在一名选手C,C胜A.考虑A击败的选手的全体,其中必有选手B胜C.事实上,若A的手下败将也都负于C,那么C胜的场数比A胜的场数至少要多1,这与A是获胜场数最多的选手矛盾.所以,存在三名选手A、B、C,使得A胜B,B胜C,C胜A.27.1.3** 平面上已给997个点,将连结每两点的线段中点染成红色,证明:至少有1991个红点,能否找到恰有1991个红点的点.解析997个点中每两点都有一个距离,因而共有9979962个距离(其中有可能有些距离是相等的),其中一定有一个最大距离.设AB是最大的距离.分别以A、B为圆心,12AB为半径作圆,如图所示.点A与除点B之外的995个点的连线的中点在圆A的内部或边界上;点B与除点外的995个点的连线的中点在圆B的内部或边界上,这样我们得到了995+995=1990个红点.另外,AB 的中点是不同于上述1990个红点的,所以,至少有1991个红点.下面构造一个例子,说明恰好有1991个红点,设997个点在数轴上1,2,3,…,997的位置.这时中点为:32,42,52,…,19922,19932,故红点恰有1991个. 27.1.4** 证明:在任意的凸五边形中,都可以找到三条对角线,由这三条对角线可以组成一个三角形. 解析 如图所示,在凸五边形ABCDE 中,一共有5条对角线:AC 、AD 、BD 、BE 、CE ,所以其中一定有一条是最长的,不妨设AC 最长.ABEPD由于ACDE 是凸四边形,设AD 与CE 的交点为P ,则AC AP PC AD CE <+<+.因为AC 最长,所以,AC 、AD 、CE 这三条对角线可以作为一个三角形的三条边.27.1.5* 平面上给定3个点。
已知其中任意两点的距离不超过1,证明:这3个点被一个半径为等的圆覆盖.解析 设三点为A 、B 、C ,不妨设BC AB ≥,AC ,当A ∠≥90︒时.易知以删为直径的圆可覆盖ABC △(此圆半径≤2BC ≤12),当90A ∠<︒时,ABC △为锐角三角形,设外心为O 在ABC △内部.由于120BOC ∠︒≥,故外接圆半径,故结论成立. 27.1.6*** 平面上给定2005个点,任意两点距离小于2005,任意三点是某个钝角三角形的顶点.求证:存在直径不超过2005的圆覆盖这2005个点.解析 在这2005个点中,设两两之间距离最大的两点是A 、B 且2005AB <.则以AB 为直径的圆覆盖了这2005个点.这是因为,如图分别过A 、B 作AB 垂线1l 、2l ,则给定的点不能在直线1l 、2l 围成的带形之外.否则这点P 到点B (或A )距离大于AB ,这与AB 的最大性矛盾.同时,给定的点也不能在带形内部的圆外.否则,这点P '与A 、B 不构成钝角三角形,与已知条件矛盾. 故结论成立.评注 此例是组合几何问题中的一类覆盖问题.这些问题的解决往往需借助于极端原理的思想. 27.1.7** 平面上给定()212n n ->个点,其中任意三点都至少有两点距离小于l ,证明:可以找出其中n 个点位于半径为1的圆内.解析 考虑距离最远的两个点A 、B .以A 、B 为圆心、半径为l 作两个圆,若有点C 在这两个圆外或边上,则AC 、BC ≥1,于是由条件知只能有AB <l ,与AB 的定义矛盾,因此没有点在这两个圆外或边上.于是由抽屉原理,至少有n 个点在其中一个圆的内部.27.1.8*** 在平面上任给2n 个点,其中任意三点不共线,并把其中”个点染成红色,n 个点染成蓝色.求证:可以一红一蓝地把它们连成n 条线段,使这些线段互不相交.解析 因为总共只有2n 个点,将红点与蓝点一一配对的方法只有有限种(实际上为()!121n n n ⋯=⋅-⋅⋅⋅种,即第一个红点可与n 个蓝点中的某一个配对,有1n -种可能,第二个红点与剩下的1n -个蓝点中的某一个配对,有1n -种可能……第n 个红点与剩下的一个蓝点配对,有1种可能).对于每一种配对方法,都会得到这n 条线段的长度和,这种和数只有有限个(其实不超过!n 个),所以其中必有一个是最小的,下证这时候n 条线段是互不相交的.用反证法.假定此时有两条线段11R B 和22R B 相交,其中1R 、2R 是红点,1B 、2B 是蓝点,设它们的交点为P (如图).由于()()112112211122R B R B R P PB R P PB R B R B +<+++=+,PR 1R 2B 2B 1所以,当我们将1R 与2B 配对,2R 与1B 配对,其他的保持不变,这时候n 条线段的长度和减少了,矛盾.因此这时n 条线段是互不相交的.评注 本题所要证明的是“存在性”命题,利用极端原理处理存在性命题的基本手法是:取极端制造所存在的东西,然后用反证法证明.27.1.9* 能否在平面上安排有限条线段,使每一条线段都至少有一端点严格地位于其他某条线段的内部?解析 不可能,因为有限条线段中不妨设最长的是AB ,且B 位于另一条线段CD 中,由于180CBA DBA ∠+∠=︒,不妨设90CBA ∠︒≥,于是AC AB >,与AB 的定义矛盾.这个命题即使在空间也是成立的.CBD A27.1.10** 平面上有n 个点,其中任意三点不共线,且任意三点构成的三角形的面积都小于1.证明:存在一个面积小于4的三角形包含这n 个点.解析 我们先通过取极端制造一个面积小于4的三角形,然后用反证法证明这个三角形包含这n 个点.n 个点中任意三点作一个三角形,三角形的个数是有限的(其实为()()1126n n n --个),每一个三角形都有一个面积,取其中面积最大的一个记为123A A A △.由于每个三角形的面积都小于1,所以1231A A A S <△.过顶点1A ,2A ,3A 分别作对边的平行线,得到一个ABC △,如图所示.显然 12344ABC A A A S S =<△△.下面证ABC △包含了这n 个点.用反证法.设ABC △外还有这n 个点中的一点,设为4A (不妨设在AC “外侧”).如图,则123231A A A A A A S S >△△,ACA 1A 2A 3A 4这与123A A A △的面积最大矛盾.于是ABC △即为所求.27.1.11* 设n 是大于2的自然数,12k a a a ⋯<<<是小于n 且与n 互质的全部正整数.证明:这k 个数中必定有一个是质数.解析 显然11a =,又2n >,所以2k >.我们证明2a 是质数.它是异于1、小于n 且和n 互质的最小正整数.如果2a 不是质数,则因为22a >,所以2a xy =,这里x 、y 都是大于1的正整数.既然2a 与n 互质,x 、y 也与n 互质,但21x a <<,这就和上述2a 的最小性矛盾.27.1.12** 考虑一个无限大的棋盘,棋盘的每个方格内有一个正整数.若方格中的每个数是其上下左右四个数的平均值.证明所有的数都相等.解析 若这些正整数不相等,设a 为其中的最小值,则必有某一块与含a 相邻且严格大于a .又含a 方格中的a 等于与之相邻的4块的平均值,每块都不小于a ,有一块大于a .这就得到一个矛盾. 27.1.13** 草场上有15个男孩在玩球,每人手上有一个球.任何两人的距离皆不相等.每个男孩把自己手里的球抛向距离自己最近的那个男孩. (1)证明:结果有一个男孩没有球; (2)证明:没有一个男孩得到的球超过5个.解析 (1)考虑其中距离最近的两个男孩A 、B .他们互相交换了球.若还有其他人传球给他们,则由抽屉原理即证;否则可以忽略A 、B ,这时问题变为13人玩球.我们按照上面的方法同样讨论.因为共有奇数个人,最后一定剩下一人没有人传球给他.(2)若有6个或以上的男孩传球给同一个人O ,不妨设为A 、B 、C 、D 、E 、F .则必有某一个角(不妨记为AOB ∠)小于60︒.这时AB 不会是OAB △的最长边,则OA 、OB 中某条是最长边,即A 、B 中一人不传球给O .27.1.14*** 若干个人聚会,其中某些人彼此认识,已知如果某两人在聚会者中有相同数目的熟人,那么他俩便没有共同的熟人.证明:若聚会者中有人至少有2008个熟人,则必然也有人恰好有2008个熟人.解析 我们考虑(聚会者中)熟人最多的某个人(如果这样的人不止一个,那么任取其中一个),记为A ,设A 共认识n 个人,这些熟人依次记为1B ,2B ,…,n B .由于1B ,2B ,…,n B 中任意两个人i B 与j B 都认识A ,即是他俩的共同熟人,因此(由题设推出)i B 与j B 的熟人数目不等.此外,1B ,2B ,…,n B 的熟人数目均不会超过n (这里用到了n 的“最大性”),于是他们的熟人数目恰好是1,2,…,n .现在已知有人至少认识2008人,这意味着n ≥2008,所以数2008在上述数列中出现,于是1B ,2B ,…,n B 中恰好有人有2008个熟人.27.1.15**** 在圆周上任取21个点.证明:以这些点为端点的所有弧中,不超过120︒的弧不少于100条.解析 本题的出发点在于:圆上任意3点分圆而得的3段弧中至少有一段不超过120︒.为了便于识别,我们将不超过120︒的弧的端点连结成弦.只要证明这样的弦不少于100条.在所有的点中,不妨设以1A 为端点的弦数最小,且记以1A 为端点的弦为12A A ,13A A ,…,1n A A ,共1n -条,而以2A ,3A ,…,n A 为端点的弦都不少于1n -条.故这n 个点至少有()12n n -条.在其余的21n -个点中任取2个点i A 、j A (i j ≠,i ,1j n =+,2n +,…,21).在三点组(1A ,i A ,j A )中一定有一条弦.根据我们对1A 的取法,这条线不会是1i A A 、1j A A 而只能是弦i j A A .所以在这21n-个点任意两点之间连有弦,共()()212112n n ---条.综上,总共有弦至少为 ()()()12121122n n n n y ----=+221210n n =-+ 22139924n ⎛⎫=-+ ⎪⎝⎭.所以当10n =或11时,y 取到最小值100.这就证明了不超过120︒的弧不少于100条.27.1.16*** 某个岛国的每条道路都是单行道,任两个城市之间恰有一条路.证明存在一个这样的城市,从另外每个城市或者可以直接到达该城市,或者可经过至多一个城市到达该城.解析 对每个城市,计算通到这个城市的单行线的条数,其中最大的记为m ,设M 是到达这个数的城市.记D 为有直路通到M 的城市的全体,设R 是除了M 和D 中城市外的其他城市的全体. 如果R 中没有任何城市,则结论当然成立;否则,不妨设X 为R 中的城市,则D 中的有某个城市E 使得道路X E M →→是通的.事实上,如若不然,则D 中所有城市都有直路通到X ,而且M 也直接通到X .这样通到X 的直路至少有1m +条,这与我们对M 的假设矛盾.这样,所有进入的道路数达到最大的城市都满足题中的条件.评注 对于存在性有关的问题,极端原理解题时,有时实际是构造性的,并且常常与反证法结合着使用.27.1.17**** 有23个人,每人的体重都是偶数.他们想进行一场足球比赛,每队11人,剩下的人为裁判.为了公平起见,两个队队员体重之和要求相等.事实上,他们发现不论选谁做裁判,他们都能做到这一点.证明:这23个人的体重都相同.解析 对满足题意的23个数{1x ,2x ,…,23x },当我们把每个数减去一个相同的数或者除以一个相同的数,所得的新数组仍然满足题意.若23人的体重满足条件,则称构成的数组{1x ,2x ,…,23x }为“平衡的”.设S 为23个数的和,若选取1x 为裁判,则1S x -一定是偶数,因为剩余的22名队员体重和能均分成两份.同理,2S x -,3S x -,…,23S x -也都是偶数.所以对于一个平衡的数组,其中的元素具有相同的奇偶性.下面我们证明,平衡数组的每个数都相等.设a 为其中的最小元素,定义i i b x a =-,则新集合{1b ,2b ,…,23b }也是平衡的且每个元素非负,其中某些元素是0.因为0是偶数,所以所有的数都是偶数.取2ii b c =,则{1c ,2c ,…,23c }同样含有一些0,是平衡的.因此,我们仍然可以把每个元素除以2得到新的平衡数组,而且我们可以一直这样做下去.只有0这个整数能够不断除以2且保持是一个整数.所以我们可以推断{1b ,2b ,…,23b }都是0.评注 本题证明中结合使用了奇偶分析和无穷递降法.使用无穷递降法会回到类似的情形. 27.1.18** 证明不定方程33324x y z +=没有正整数解(x ,y ,z ).解析 假设方程有正整数解,设(1x ,1y ,1z )是所有正整数解中使x 最小的一组解.由于 33311124x y z +=,所以31x 是偶数,故1x 是偶数.设122x x =,则333211824x y z +=,即33321142x y z +=, 故1y 是偶数.设122y y =,则333211482x y z +=,即33321124x y z +=, 故1z 是偶数.设122z z =,则333212248x y z +=.所以(2x ,2y ,2z )也是方程的一组正整数解,且21x x <,矛盾. 所以原方程没有正整数解.27.1.19*** 设有n (n ≥7)个圆,其中任意3个圆都不两两相交(包括相切),求证:一定可以找到一个圆,它至多能与5个圆相交.解析 取半径最小的圆(如有多个,取其中一个即可)设为O .若1O 与6个(或多于6个)的圆2O 、3O 、4O 、5O 、6O 、7O 相交,连结12O O ,13O O ,…,17O O ,则1∠,2∠,…,6∠中至少有一个不大于60︒.设213160O O O ∠=∠︒≤,连结23O O ,如图所示.O 7设1O 、2O 、3O 的半径为1R 、2R 、3R ,12R R ≤,13R R ≤.因为1O 、2O 相交,故连心距不超过两圆半径之和,即121223O O R R R R ++≤≤.同理 131323O O R R R R ++≤≤.又在123O O O △中,160∠︒≤,故在2O ∠、3O ∠中必有一个不小于60︒.设2601O ∠︒∠≥≥,则1323O O O O ≥,即2323R R O O +≥,所以2O 、3O 相交,从而1O 、2O 、3O 两两相交.与题设矛盾!27.1.20*** 空间中给出了8个点,其中任意4个点都不在同一平面上,在它们之间连以17条线段.证明:这些线段至少形成了一个三角形.解析 不妨设连出线段数目最多的点为A ,且设它共连出n 条线段.如果所有17条线段都没有形成三角形,那么与A 相连的n 个点之间彼此都没有线段相连,而其余的7n -个点中,每一点所连出的线段条数不多于n 条,因此,线段的总数目不超过()()2878162n n n n n n n +-⎛⎫+-=-= ⎪⎝⎭≤.这与已知的有17条线段矛盾.从而命题成立.评注 其实本题的结论可加强为“三角形的数目不少于4个”,这个问题较难,留给有兴趣的读者思考. 27.1.21**** 在2×n 方格表的每个方格中都写有一个正数,使得每一列中的两个数的和都等于1.证明:可以自每一列中删去一个数,使得每一行中剩下的数的和都不超过14n +. 解析 假设第一行中所放的数为1a ,2a ,…,n a .必要时通过交换列的位置,可以使得1a ≤2a ≤…≤n a ,此时第二行中所写的数就依次分别为111b a =-,221b a =-,…,1n n b a =-.显然1b ≥2b ≥…≥n b .如果1214n n a a a +⋯+++≤,那么就删去第二行中的所有各数即可达到目的.否则,我们可以找到使得1214k n a a a +⋯+++>成立的最小的k .此时我们在第一行中删去k a ,1k a +,…,n a ,在第二行中删去1b ,2b ,…,1k b -由k 的取法,立知12114k n a a a -+⋯+++≤,下面只需证明 114k k n n b b b ++⋯+++≤. 由于1214k k a a a n a k k ⋯++++>≥, 所以1k k n b b b +⋯+++()()()111k k n k b n k a +-=+--≤()()()()221114125144n n k k n k n k+⎛⎫+-- ⎪⎝⎭-+=+-≤()()()212511444n k n n k +++-=≤. 27.1.22*** 平面上有n (>2)个点,它们两两连线都有一个中点,如果重合的中点算一个点,求证:至少有23n -个不同的中点.解析 不妨设n 个点为1A ,2A ,…,n A .且1n A -、n A 为最远两点,记1i n A A -中点为i B (i =1,2,…,2n -),i n A A 中点为i B '(i =1,2,…,2n -). 不存在一个i 与j ,使i j B B '=,否则当i B 不在线段1n n A A -上时,作平行四边形1n n i j A A A A -,不妨设190i n n A A A -∠︒≥,于是11n i n n A A A A -->,这与1n n A A -定义矛盾.A iA jA nA n -1B i当i B 在1n n A A -亦然.于是全部i B 与j B '一共有24n -个中点,加上1n n A A -中点,至少有23n -个不同中点,读者不难构 造出达到此界的例子.27.1.23**** 设正整数a 、b 、k 满足221a b k ab +=-,求证:5k =.解析 对每一个k ,如果有这样的a 、b 存在,可设a b +最小,且a b ≥.a b =时,2221k a =+-,无解,故a b >.关于a 的方程220a bka b k -++=有另一根a ',由两根和知a '为整数,由两根积知a '为正数,故a '为正整数,于是a a '≥,或 22a aa b k '=+≤,即()2222121k a b a a a ---=-≥≥.当1b =时,212111a k a a a +==++--,2a =或3,5k =.当2b ≥时,()()222222121441a a b k ab a a a >+=--=-+≥,故22410a a -+<或()2211a -<,不可能.综上所述,5k =.27.1.24**** 已知正整数a 与b 使得1ab +整除22a b +,求证:221a b ab ++是某个正整数的平方. 解析 用反证法.假设221a b ab ++并不是某个正整数的平方.令 221a b k ab +=+, 220a b kab k +--=.所以,(a ,b )是方程220x y kxy k +--= ①的一组正整数解.设(1a ,1b )是方程①的所有正整数解中,使x y +为最小的一组解,由对称性不妨设11a b ≥. 把①改写成关于x 的二次方程,得()22110x kb x b k -+-=. ②于是1a 就是②的一个正整数解.由韦达定理知②的另一个解211a kb a =-也是整数,由2211a a b k =-知20a ≠(因为k 不是平方数),若20a <,则 222121120a kb a b k kb a k k k -+->---=≥,矛盾.故2a >0.于是(2a ,1b )也是方程①的一组正整数解.但是由2222111121111111b k b a a a a a a a a ---=<<=≤, 得2111a b a b +<+.这与11a b +为最小相矛盾.因此愚为某个正整数的平方.。
