第4章功和能
合集下载
大学物理第四章--功和能
a
a
l
xdx
2l
前已得出：
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时：
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例１一水平放置的弹簧，其一端固定，另一端系一小球，求小
球的位置由A到B的过程中弹力对它所做的功。（在O处弹簧无 形变）
解：根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上．在该质点从坐标原点运动到(0，2R)位
置过程中，力
F
对它所作的功为多少？
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图，水平桌面上有质点 m ，桌面的摩 擦系数为μ 求：两种情况下摩擦力作的功
a
l
xdx
2l
前已得出：
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
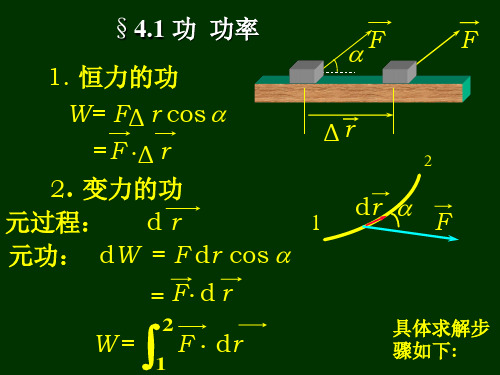
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时：
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例１一水平放置的弹簧，其一端固定，另一端系一小球，求小
球的位置由A到B的过程中弹力对它所做的功。（在O处弹簧无 形变）
解：根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上．在该质点从坐标原点运动到(0，2R)位
置过程中，力
F
对它所作的功为多少？
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图，水平桌面上有质点 m ，桌面的摩 擦系数为μ 求：两种情况下摩擦力作的功
大学物理课件第4章-功和能
如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆，用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时，
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1
v2
v 22
v
v1
v2
由机械能守 恒（ 势能无变化）
v2
v12
v
2 2
v1 v2 0 两球速度总互相垂直
例8：已知半圆柱形光滑木凹槽，放在光滑桌面上，
如图，求质点下滑至最低点时给木块的压力.
解：
mv MV 0
•2.碰撞分类
正碰 斜碰
（从碰撞前后两球中心连线角度分类 ）
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
（从碰撞能量损失角度分类）
例7：在平面上两相同的球做完全弹性碰撞，其中一球开始时处于
大学物理第四章
解：利用功能原理：
A=DE
q
kF
m
Fl0tgq
=
1 2
k (l0 setq
- l0 )2
1 2
mv2
F
m
解得：
v=
2 m
Fl0tgq
-
1 m
k (l0 setq
-
l0
)2
[例13] 作业、p-55 功和能 自-20
一质量为m的球，从质量为M的圆弧
形槽中由A位置静止滑下，设圆弧形槽的半
径为R，(如图)。所有摩擦都略，试求：
+12 MV2
l
L
解得：
vr=
2(m +M) gR M
V= m
2gR M(m +M)
(2)小球到最低点B处时，槽滑行的距离。
∵ SFx = 0 ∴ DPx = 0
mvx = MVx
Am
m vxdt = M Vxdt
R
ml=ML
MB
l+L=R
L
=
mR m+M
lL
(3)小球在最低点B处时，槽对球的作用力；
1、动量： P
P = mv 2、第二定律：
F
=
dP dt
= ma
3、冲量： I
I
=
F t 2
t1
dt
4、动量原理
I = DP
5、力矩 M M = r × F
6、动量矩 L
L = r × P = r × mv
7、角动量原理:
t 2 t1
M dt
=
ω ω
2 1
J
dω
= Jω 2
4.2 保守力及其功
3
4.2 保守力及其功
三、 万有引力的功 为原点， 以 M 为原点， m 的位置矢量为 M 对 m 的万有引力为： 的万有引力为：
第4章 功和能 功能原理
v m a r。 v
M
r (t)
v dr
v m 由 a 点移动到 b 点时 F 作功为： 作功为： v v B Mm v v A = ∫ F ⋅ dr = ∫ − G 3 r ⋅ dr A r
v Mm v F = −G 3 r r
v r (t + dt)
O
b
v v v r ⋅ dr = r dr cos φ = rdr
Mm A = ∫ − G 2 dr ra r
rb
v r (t )
v dr
v r (t + dt ) ϕ
4
4.2 保守力及其功 rb Mm A = ∫ − G 2 dr ra r
2
4.2 保守力及其功
二、弹性力的功
Hale Waihona Puke 第4章 功和能 功能原理xb
A = ∫ F dx = ∫ − kx dx
xa xa
xb
v v F = −kxi
1 2 1 2 A = −( kx b − kx a ) 2 2
v F
o xA xB
x
A = ∫ − kxdx = 0
结论： ） 弹性力的功只与始、末位置有关， 结论： 1） 弹性力的功只与始、末位置有关， 与质点所经过的路径无 而与质点所经过的路径无关。 2） 弹簧的变形减小时，弹性力作正功； ） 弹簧的变形减小时，弹性力作正功； 弹簧的变形增大时，弹性力作负功。 弹簧的变形增大时，弹性力作负功。
4.2 保守力及其功
第4章 功和能 功能原理
4.4 功能原理 机械能守恒定律
30° A o
B
Ep = 0
20
4.4 功能原理 机械能守恒定律 第4章 功和能 功能原理
例：如图所示，轻质弹簧劲度系数为k，两端各固定一 质量均为M的物块A和B，放在水平光滑桌面上静止。 今有一质量为m的子弹沿弹簧的轴线方向以速度υ0射入 A 物块而不复出。求：此后弹簧的最大压缩长度。
解：第一阶段： 子弹射入到相对静止
第4章 功和能 功能原理
人们在总结各种自然过程中发现：
如果一个系统是孤立的、与外界无能量交换，系 统内部各种形式的能量可以相互转换，或由一个物体 传递给另一个物体。但是不论如何转换，这些能量的 总和却保持不变。能量既不能消灭，也不能创造。这 一结论叫做能量守恒定律。
例如：利用水位差推动水轮机转动，能使发电机发 电，将机械能转换为电能。
例：有一轻弹簧, 其一端系在铅直放置的圆环的顶点 P， 另一端系一质量为m 的小球，小球穿过圆环并在 圆环上运动(不计摩擦)。开始小球静止于点 A，弹簧处 于自然状态，其长度为圆环半径R； 当小球运动到圆 环的底端点B时，小球对圆环没有压力。
求：弹簧的劲度系数。
P
解 以弹簧、小球和地球为一系统，
R
Q A → B 只有保守内力做功 ∴系统机械能守恒 EB = EA
υ0
mA
B
于物块中。
由于时间极短，可认为物块还没有移动，
应用动量守恒定律，求得物块A的速度υA
mυ0 = ( M + m )υA
∴ υA
=
m (M +
m)
υ0
21
4.4 功能原理 机械能守恒定律 第4章 功和能 功能原理
第二阶段：A移动，直到当A 和B有相同的速度时，弹簧 压缩最大。应用动量守恒定
大学物理 功和能汇总
0 1
2 动能定理： A 1 2 mv 0
2A v 4 m s m
[思考] 在 x =0 至 x =1m 过程中， F 的冲量？
10
§4.3 质点系的动能定理
Theorem of Kinetic Energy for a system of Particle
对第 i 质点 求和
O 张力不做功，重力做功： 用动能变化定理解：
l
m
T
A mg dl mg dl cos
mgl cos d mgl sin 0 1 2 mgl sin mv 2
ˆn e
v
mg
ˆt e
比直接解牛顿方程简单，但仍作积分运算。
13
§4.4 *柯尼希定理
i
14
一对力 的功
内力总是成对出现 dr1 两质点间的内力 f ij 和 f ji ,
B1
B2
dr2
f 12
称为一对力 f ij f ji
m1
r21
f 21
m2
A1
A2
一对力做的功之和
dA = f12 dr1 + f21 dr2
f 21 dr2 dr1 f 21 dr21
mi ac dri
m i ac
z
y
mi
= ac mi dri
ri
ac
C 质心 O
12
= ac d mi ri = 0 A i
B
x
=
0
【例】柔软细绳长为l，小球质量为m，求摆下至 角时小球的速度和绳的张力。
2 动能定理： A 1 2 mv 0
2A v 4 m s m
[思考] 在 x =0 至 x =1m 过程中， F 的冲量？
10
§4.3 质点系的动能定理
Theorem of Kinetic Energy for a system of Particle
对第 i 质点 求和
O 张力不做功，重力做功： 用动能变化定理解：
l
m
T
A mg dl mg dl cos
mgl cos d mgl sin 0 1 2 mgl sin mv 2
ˆn e
v
mg
ˆt e
比直接解牛顿方程简单，但仍作积分运算。
13
§4.4 *柯尼希定理
i
14
一对力 的功
内力总是成对出现 dr1 两质点间的内力 f ij 和 f ji ,
B1
B2
dr2
f 12
称为一对力 f ij f ji
m1
r21
f 21
m2
A1
A2
一对力做的功之和
dA = f12 dr1 + f21 dr2
f 21 dr2 dr1 f 21 dr21
mi ac dri
m i ac
z
y
mi
= ac mi dri
ri
ac
C 质心 O
12
= ac d mi ri = 0 A i
B
x
=
0
【例】柔软细绳长为l，小球质量为m，求摆下至 角时小球的速度和绳的张力。
八年级下册生物笔记
八年级下册生物笔记第一章植物的生殖1、能够产生花粉粒的结构叫花药2、能够接受花粉粒的结构叫雌蕊3、绿色植物的受精过程为：花粉萌发→→进入胚珠→→与卵细胞结合→→形成受精卵4、绿色植物的受精方式为自花传粉和风媒传粉两种5、胚珠中的卵细胞接受花粉中的精子，完成受精，形成受精卵6、极核细胞与精子结合，形成受精极核7、被子植物的个体发育：由种子萌发→幼苗生长→植株开花、结果→形成种子8、人工授粉的方法有：a.人工点授 b.喷粉 c.戴手套蘸取花粉涂抹在同株异花的花的柱头上第二章昆虫的生殖和发育1、昆虫的发育过程分为：完全变态和不完全变态两类。
完全变态有四个时期：卵→若虫→蛹→成虫（例：蚊、蝇、菜粉蝶、蜜蜂）不完全变态有三个时期：卵→若虫→成虫（例：蝗虫、螳螂、蟋蟀、蝉）2、昆虫在个体发育中，经过卵、幼虫、蛹和成虫等4个时期叫完全变态，经过卵、若虫、成虫等3个时期的叫不完全变态。
3、昆虫在个体发育中，第一条途径是受精卵发育为幼虫，然后幼虫经过蛹期直接发育成为成虫，这条途径叫直接发育，如蚊、蝇、菜粉蝶等。
第二条途径是受精卵发育为幼虫，幼虫经过蛹期不直接发育成成虫，而是通过蛹这一阶段才发育成为成虫，这条途径叫间接发育，如蝗虫、螳螂、蟋蟀、蝉等。
4、昆虫的幼虫在形态结构和生活习性上与成虫差异很大，这样的幼虫叫若虫。
5、昆虫的发育过程与生活环境有密切关系。
第三章两栖动物的生殖和发育1、两栖动物是雌雄异体。
在体外受精。
2、两栖动物的生殖和幼体发育必须在水中进行。
3、两栖动物一般是体外受精，变态发育。
4、两栖动物的幼体是蝌蚪，它用鳃呼吸，必须生活在水中；大多数两栖动物的成体用肺呼吸，可以生活在陆地上。
5、两栖动物的种类有400余种。
常见的有青蛙、蟾蜍和蝾螈等。
它们在人类生产和生活中具有重要的经济意义。
6、两栖动物的生殖和发育过程对水域环境的污染很敏感。
水域污染可能造成两栖动物的不育或死亡。
这是环境监测中判断水域污染程度的一个重要指标。
第四章 机械能和能
2. 单位：焦耳， 简称 焦（ J ）． 单位：焦耳，
1J＝1N×1m ＝ 1N·m ＝ × 3. 功是标量： 只有大小，没有方向。 功是标量： 只有大小，没有方向。 思考： 对物体做的功？ 思考：计算下图中力 F 对物体做的功？
F x
α
W＝Fxcos（π-α） （ ）
（四）求合力的功
求合力功的两种方法 （1） 先求各力的功，再求它们的代数和； W总＝W1 ＋W2 ＋W3 +……+Wn （2）先求合力，再由公式：W＝F合xcosα得出合力做的 功．
（一）做功与能量的变化
举重
瀑布
射箭
1、功：物体受到力的作用，并在力的方向上发生了位移，这个力就对物体做了功。 、 物体受到力的作用，并在力的方向上发生了位移，这个力就对物体做了功。 功的两个必要因素：①作用在物体上的力 ①作用在物体上的力 物体在力的方向上发生的位移 ②物体在力的方向上发生的位移 2、功与能的关系：①做功的过程就是能量转化的过程。 、功与能的关系： 做功的过程就是能量转化的过程。 做了多少功，就有多少能量发生了转化。 ②做了多少功，就有多少能量发生了转化。
功是能量转化的量度
（二）功的计算
思考①：如图，力 F 使滑块发生位移 x ，在这个过程中， F 对滑块做了多少功？
F X
F
思考②：如图，当恒力 F的方向与物体位移 x 的方向成某一夹角 α时，如何计算 力 F 对物体做的功呢？ F α X
W＝Fxcosα
（二）功的计算
1. 力对物体做功等于力的大小、位移的大小、力和位移夹角的余弦这 力对物体做功等于力的大小、位移的大小、 三者的乘积， 三者的乘积，即 (注：适用于恒力做功的计算） W＝Fxcosα
第四章 机械能和能源
1J＝1N×1m ＝ 1N·m ＝ × 3. 功是标量： 只有大小，没有方向。 功是标量： 只有大小，没有方向。 思考： 对物体做的功？ 思考：计算下图中力 F 对物体做的功？
F x
α
W＝Fxcos（π-α） （ ）
（四）求合力的功
求合力功的两种方法 （1） 先求各力的功，再求它们的代数和； W总＝W1 ＋W2 ＋W3 +……+Wn （2）先求合力，再由公式：W＝F合xcosα得出合力做的 功．
（一）做功与能量的变化
举重
瀑布
射箭
1、功：物体受到力的作用，并在力的方向上发生了位移，这个力就对物体做了功。 、 物体受到力的作用，并在力的方向上发生了位移，这个力就对物体做了功。 功的两个必要因素：①作用在物体上的力 ①作用在物体上的力 物体在力的方向上发生的位移 ②物体在力的方向上发生的位移 2、功与能的关系：①做功的过程就是能量转化的过程。 、功与能的关系： 做功的过程就是能量转化的过程。 做了多少功，就有多少能量发生了转化。 ②做了多少功，就有多少能量发生了转化。
功是能量转化的量度
（二）功的计算
思考①：如图，力 F 使滑块发生位移 x ，在这个过程中， F 对滑块做了多少功？
F X
F
思考②：如图，当恒力 F的方向与物体位移 x 的方向成某一夹角 α时，如何计算 力 F 对物体做的功呢？ F α X
W＝Fxcosα
（二）功的计算
1. 力对物体做功等于力的大小、位移的大小、力和位移夹角的余弦这 力对物体做功等于力的大小、位移的大小、 三者的乘积， 三者的乘积，即 (注：适用于恒力做功的计算） W＝Fxcosα
第四章 机械能和能源
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三、弹性势能 F kxi dr dxi
xb W F dr x kxi dxi
a
F dr
xb
xa
1 2 1 2 kxdx kxb kxa 2 2
结论：弹性力的功只与路径始、末位置有关，而与经过 的路径无关。 取弹簧自然长度时为弹性势能零点，弹簧伸长x时的弹性势能
4.3
势能 保守力
4.3.1 势能
一、重力势能
质点在重力场中沿曲线由点a运动到 点b ，求重力做功 rb rb W G dr G dr G (rb ra ) 因为 rb ra ( xb i yb j ) ( xa i y a j ) ( xb xa )i ( yb y a ) j 所以 W G (rb ra ) mgj [( xb xa )i ( yb ya ) j ] mg ( y y ) b a 结论：重力功只与质点运动路径始、末位置有关，而与 经过的路径无关。
这一对力的功之和
注意：
dr j
fj i
j
fi j
i
dri
dW fij drj f ji dri fij drj fij dri fij (drj dri )
fij drji
4.2.3 刚体定轴转动的动能定理
定义式 Wab F dr a 设 F Fx i Fy j Fz k d r dxi dyj dzk F dr Fx i Fy j Fz k dxi dyj dzk Fx dx Fy dy Fz dz
G mgj
ra ra
习惯上将高度记作h
W (mghb mgha )
E p mgh
W mg ( yb ya )
取h＝0 为零势能参照面，则质量为m 的物体，高度为h 时重力势能 重力做的功
W ( E pb E pa ) E p
重力所做的功等于质点重力势能增量的负值
dr dW F F F cos Ft 由功的定义 P dt dt 力与速度 力在切向上的投影量 与速率的乘积 的标积
dW d M M 力矩的功率 P dt dt
功
W Pdt
t1
t2
几个日常活动功率的数量级： 睡觉 70－80W(基础代谢) 闲谈
0 0
3
3
由动能定理
1 2 1 2 W m m0 2 2
解得
2W 2.3 m/s m
a F
x 3m
m
1.5m/s 2
4.2.2 质点系的动能定理
设质点系由n个质点组成 第i 个质点所受外力和内力之和
e F1
F F1 j j 1
e Fj j F ji
e i Fi Fi Fi
Fr sin d
Md
d
W Md
0
若M为常量
W M ( 0 )
说明： （1）如果有多个外力作用于刚体, M为合外力矩
（2）力矩的功实质上仍是力做的功，只不过对于刚体 转动的情况，力的功可以用力矩和角位移的乘积来表示
例4-1 如图，一根长为l 、质量为m的匀质细杆，其一端挂在 一个水平轴O上。求细杆从竖直位置转动到与竖直位置 d
得
Md Jd
1 1 2 2 0 Md 0 J d 2 J 2 J 0
刚体定轴转动的动能定理
刚体定轴转动时，合外力矩的功 等于刚体转动动能的增量
例4-5 应用动能定理求解习题2-14【如图，质量为m 、长为 l 的匀质杆可绕位于杆端的光滑轴O轴在竖直平面内转动，设 杆在水平位置由静止开始自由转下】，求杆转到与水平位置时 成θ角时的 (2)角速度】。 FN l 解 重力对O轴力矩 M mg cos 2 使杆顺时针转动 若杆转动dθ ，则重力矩做功 l dW mg cos d 2 杆从水平位置转动到θ 位置的过程中重力矩做功 G l l W dW mg cos d mg sin 0 2 2 设杆在θ位置时的角速度为ω，根据动能定理，同时考虑 到初始时刻ω0=0 ，以及杆的转动惯量J=ml2/3得 3g sin l
70－80W
听课 70－140W 踢球 630－840W
走路 170－380W 跑步 700－1000W
4.2
动能定理
b
d W Ft ds a m ds m d 0 dt 1 2 1 2 m m0 2 2 1 质点的动能 Ek m 2 2
4.2.1 质点的动能定理
一、刚体定轴转动的转动动能
对 mi ，其动能为
ri
对整个刚体
1 Eki mii2 1 mi ri 2 2 2 2 1 1 2 2 Ek mi ri ( mi ri 2 ) 2 2 2 1 Ek J 2 即 2
mi
i
刚体定轴转动的动能等于刚体的转动惯量与角速度 平方乘积的一半。
RE
(2)质量为m的宇宙飞船返回地球时，将发动机关闭，可以 认为它仅在地球引力场中运动，当它从与地球中心距离为 R1下降至距离为R2时，它的势能改变量为 ，引力 所做的功为 (G为引力恒量，Me为地球质量) GM e m GM e m GM e m GM e m R2 R1 R2 R1
解 当杆与竖直位置方向夹角为θ时，重力矩 l M mg sin 2 “-” 表示力矩有使θ减小的趋势，从θ =0到θ ，重 力矩做的功
W Md 0
0
l l mg sin d mg 1 cos 2 2
4.1.2 功率 （表征力对质点做功的快慢）
Fn
W Ek Ek0 Ek
质点的动能定理：合力对质点做的功，等于质点动能 的增量。
习题4－3 质量为10kg的物体在沿x轴方向的力F=(3+4x)N的 作用下运动了3m，设t=0时，物体位于原点，速率为零。计 算物体处于3m处的速度和加速度。
解
W Fx dx (3 4 x)dx 27J
2 问题4-5 试证明刚体定轴转动动能 Ek 1 J C 2 1 mC
，
JC 是刚体对过质心的轴的转动惯量，υC 是刚体质心的速率， m 是刚体的总质量。 证明
2
2
1 1 2 1 1 2 2 2 2 1 2 2 2 1 Ek J ( J C md ) J C md J C mC 2 2 2 2 2 2
问题4-6 写出下列两种情况下刚体的转动动能：(1) 质量为
m 、长为l 的匀质细杆绕中心或棒端的垂直轴以角速度ω 转动； (2) 质量为m 、半径为R 的匀质薄圆面绕中心垂直轴以角速度 ω 转动。
二、刚体定轴转动的动能定理
由转动定律 M J J d J d d J d
GMm 元功 dW F dr 2 er dr GMm dr r r2 er dr er dr cos dr cos dr
W
rb
ra
GMm GMm GMm 2 dr ( ) ( ) rb ra r
力在元位移方向的投 影与此元位移大小的 乘积 质点从a运动到b时，力对质点所做的功为 b b W F dr F cos dr 功是力对空间的累积效应 a a 元功等于力和 元位移的点积
元位移在力方向 的投影量和力大 小的乘积
说明：
（1）功是标量，只有大小，没有方向，但有正负 （2）功是力对位移的空间积累，是过程量，与路径有关 （3）功是可加量，合力的功等于各分力功的代数和 （4）功的几种计算表示式
说明：
（1）势能属于系统，不为单个物体所具有
（2）势能的多少没有绝对意义，关心的是 势能的变化。
刚体的重力势能
对于一个体积不太大、质量为m 的刚体，它的重力势能 是组成刚体的各个质点的重力势能之和，即
E p mi ghi g mi hi
i i
考虑到刚体质心公式
hC
m h
i
i i
外力的功
内力的功
系统动能的增量
质点系的动能定理：质点系动能的 增量等于作用于质点系内质点上所 有外力和所有内力所做的功。
Wex＋Win Ek 2－Ek1
质点j 在 f ij 的作用下在时间 dt 内 发生了位移 drj ，质点i 在 f ji 的作 用下在时间 dt内发生了位移 dri ，
力对时间的积累效应 F d t 是冲量，反映质点 t1 或质点系在一段过程始末状态下动量的变化 p 。
t2
力矩对时间的积累效应 t 映质点或刚体在一段过程始末状态下角动量的变 化 L 。
1
t2
M d t 是冲量矩，反
力、力矩对空间的积累效应 化 。
r2
是？，反映质点或刚体在一段过程始末状态下?的变
结论：万有引力的功只与质点运动路径始、末位置有关， 而与经过的路径无关。
取 r 处为引力势能零点，当m、M相距r 时的引力势能 GMm Ep r 质点在引力场中从点a运动到点b ，万有引力做功
W ( E pb E pa ) E p
结论：万有引力做的功等于质点引力势能增量的负值 思考题: (1)设地球的质量为M、半径为RE，则质量为m的物 GMm 体在地球表面上的引力势能为 Ep
b