常用弹塑性料模型
弹塑性本构关系简介
松比）。
塑性材料受外部作用的反应和变形的历史有关（可称为历 史相关性或路径相关性），本构关系应写成增量关系。
应力空间表述的弹塑性本构关系
韧性（塑性）金属材料单向拉伸试验曲线如下 图示意
强度极限
b
屈服上限
L y
U y
e
屈服下限
弹性极限
强化段
软化段 卸载
残余变形
弹性变形
y
y
卸载、反向加载 包辛格效应
屈服面随内变量改变的规律称强化规律。由 材料试验的资料可建立各种强化模型，目前广 泛采用的有：等向强化；随动强化两种模型。
等 向 强
初始屈服面
2
B
f 0(ij ) 0 B
2
C A o1
化
o A 1
o
1
C
D
随
弹性
动
f 0 (ij ) 0
强 化
后继屈服面
f
( ij
,
p ij
,
k)
0
等向强化认为屈服面形状不变，只是作均匀
称后继屈服面，f
(
ij
,
p ij
,
k
)
0
。
如果一点应力的 f (ij ,ipj,,则k)此 点0 处于弹性状态，如
果
f (，ij则,处ipj ,于k)塑 0性状态。
式变张中形量的为i量j间应。存ip力j在张如和ip量j 下k，关统系称为ipj为塑内性变应量ip力j 。张其D量i中j，klkkp与l为塑标ipj 性志应永变久
d ij
Dt ijkl
d
kl
式中 Ditjk为l 切线弹性张量，形式上仍可表为
Dt ijkl
常用弹塑性料模型
常用弹塑性材料模型B.2.1. Isotropic Elastic Example: High Carbon Steel MP,ex,1,210e9 ! Pa MP, nu xy,1,.29 ! No units MP,dens,1,7850 ! kg/m 3 例题参看 B.2.7,Bilinear Isotropic Plasticity Example B.2.7. Bil in ear Isotropic Plasticity Example: Nickel AlloyNickel AlloyMP,ex,1,180e9 ! PaMP,n uxy,1,.31 ! No unitsMP,dens,1,8490 ! kg/m 3TB,BISO,1TBDA TA,1,900e6 ! Yield stress （Pa）TBDA TA,2,445e6 ! Tangent modulus （Pa）B.2.10. Bil in ear Kin ematic Plasticity Example: Tita nium AlloyMP,ex,1,100e9! PaMP, nuxy,1,.36! No units! kg/m 3MP,de ns,1,4650TB,BKIN,1TBDA TA,1,70e6! Yield stress （Pa）TBDA TA,2,112e6 ! Tangent modulus （Pa）7.2.3.6 塑性随动模型各向同性、随动硬化或各向同性和随动硬化的混合模型，与应变率相关，可考虑失效。
通过在0 （仅随动硬化）和 1 （仅各向同性硬化）间调整硬化参数B来选择各向同性或随动硬化。
应变率用Cowper-Symo nds模型来考虑，用与应变率有关的因数表示屈服应力，如下所示：1P1 —（0 E P：ff）有效塑性应变， E P —塑性硬化模量，由下式给出:E tan EE PEE tan应力应变特性只能在一个温度条件下给定。
第四讲流体弹塑性模型
❖ 改变的条件 压强或温度。
❖ 相变类型 第一类相变：伴随着相变潜热和体积跃变。如：固固相变、固 夜相变、以及一般的气液相变等。 第二类相变：没有相变潜热和体积跃变，但是有比热等的变化。 如：铁磁体转变为顺磁体，二元合金中的有序无序转变，金属 转变为超导态，液态氦转变为超流态等。
1. 流体弹塑性基本概念（续）
2. 状态方程导引
状态方程的概念
通常是指物体的 PVT关系，即压强P、体积V、温 度T之间的函数关系。有时除上述关系外，还将内能函 数E(V、T)包括在内。
状态方程的建立
理论模型－－通过量子力学和统计物理的概念和方 法从原子、分子运动角度建立模型。
工程理论－－在部分理论模型的基础上确定状态方 程的基本形式，通过实验研究确定参数。
屈服函数
f ( ij , eij ) C
f (I1, I2 , I3) C
3.弹塑性应力应变关系（续）
❖ 初始屈服准则 （续）
应力偏量张量 sij ij p ij
应变偏离张量
应力偏离形式屈服准则（不计静水压效应）
ij
eij
3
ij
f (J2,2
s22 s33
2. 状态方程导引（续）
c) 高温低密度
密度：稍大于常密度至远小于常密度
温度：几个105K至107K 物质状态：由于系统密度较低，温度较高，点阵结 构不存在，分子的离解及原子中电子的电离现象十分显 著。系统中粒子差不多都是带电粒子，需考虑粒子间静 电相互作用。
采用的模型：
用离解电离平衡方程描述分子离解和电离过程。
用Debye－Huckel理论描述静电相互作用
2. 状态方程导引（续）
d) 过渡区（a、b区之间过渡区）
[工学]第五章 弹塑性模型理论
![[工学]第五章 弹塑性模型理论](https://img.taocdn.com/s3/m/2794070ecfc789eb172dc8bc.png)
第五章 弹塑性模型理论5.1 概述弹塑性理论可以分为两种，塑性增量理论和塑性全量理论。
塑性增量理论又称塑性流动理论，塑性全量理论又称塑性形变理论。
在塑性增量理论中，将物体在弹塑性变形阶段的应变ij ε分为两部分：弹性应变e ij ε和塑性应变p ij ε。
塑性应变增量ij d ε的表达式为e p ij ij ij d d d εεε=+ (5.1.1)式中，弹性应变增量d e ij ε可以用广义虎克定律计算，塑性应变增量d p ij ε可以根据塑性增量理论计算。
塑性增量理论主要包括三部分：（1） 屈服面理论；（2） 流动规则理论；（3） 加工硬化（或软化）理论。
在塑性形变理论中是按全量来分析问题的。
它在盈利状态和相应的应变状态之间建立一一对应的关系。
塑性形变理论实质上是把弹塑性变形过程看成是非线性弹性变形过程。
严格说，在弹塑性变形理论的应用是有条件的。
严格讲，只有在等比例加载条件下，应用塑性变形理论可以得到精确解。
所谓等比例加载是指在加载过程中，各应力分量是按同一比例增加的。
严格的等比例加载是很难满足的，在土工问题中可以说是不可能的。
在简单加载条件下应用塑性形变理论分析有时也可以取得较好效果。
近些年来建立的土体弹塑性模型大部分是根据塑性增量理论建立的。
本章主要介绍塑性增量理论，在最后一节简要介绍塑性形变理论。
5.2 屈服面得概念首先讨论理想弹塑性材料。
理想弹塑性材料受力到什么程度才开始发生塑性变形呢？在简单拉伸时，问题是很明显的。
当应力等于屈服应力σs 时，塑性变形开始产生。
σs 值是可以在拉伸试验应力-应变曲线上找到的。
然而在复杂应力状态时，问题就不是这样简单了。
一点的应力状态由六个应力分量确定。
在复杂应力状态下，显然不能任意选取某一个应力分量的数值作为判断材料是否进入塑性状态的标准。
因此需要在应力空间或应变空间来考虑这一问题。
在土塑性力学中，常用的应力空间有三维主应力空间、p 、q （或σm ，σ1-σ3）应力平面、以及132σσ+，132σσ-应力平面等。
弹塑性本构模型理论课件
。
材料屈服强度影响规律
屈服强度定义
材料开始发生明显塑性变形的最小应力值，反映了材料抵抗塑性变 形的能力。
屈服强度对弹塑性行为的影响
屈服强度越大，材料抵抗塑性变形的能力越强，进入塑性阶段所需 的应力水平越高，材料的塑性变形能力越差。
屈服强度的影响因素
材料的晶体结构、化学成分、温度、应变速率等都会影响屈服强度 的大小。
材料弹性模量影响规律
弹性模量定义
01
材料在弹性阶段内，应力与应变之比，反映了材料抵抗弹性变
形的能力。
弹性模量对弹塑性行为的影响
02
弹性模量越大，材料的刚度越大，相同应力作用下产生的弹性
变形越小，进入塑性阶段所需的应力水平越高。
弹性模量的影响因素
03
材料的晶体结构、化学成分、温度等都会影响弹性模量的大小
弹性阶段
材料在受力初期表现出弹性行为，应 力与应变呈线性关系，卸载后无残余 变形。
屈服阶段
当应力达到屈服强度时，材料进入塑 性阶段，应力不再增加但应变继续增 加，卸载后有残余变形。
强化阶段
材料在塑性阶段表现出应变硬化特性 ，随着塑性应变的增加，屈服强度逐 渐提高。
理想弹塑性模型
无强化阶段的弹塑性模型，屈服后应 力保持恒定，应变无限增加。
通过实验测定金属材料的弹性模量、屈服强度、硬化模量等参 数，为模拟提供准确数据。
利用有限元软件建立金属材料的弹塑性行为模型，进行加载、 卸载等模拟过程。
将模拟结果与实验结果进行对比，验证弹塑性本构模型在金属 材料行为模拟中的准确性和可靠性。
实例二：混凝土结构弹塑性损伤评估
损伤模型选择
针对混凝土结构的损伤特点，选择合适 的弹塑性损伤本构模型，如塑性损伤模
《弹塑性力学》第十一章 塑性力学基础
2021/8/9
30
§11-2 一维问题弹塑性分析
s
-
+
+ -
+ +
s
- = +-
s
M I
y
y y0
x
y0s
y
M I
y
y0 y y0
s
M I
y
y y0
2021/8/9
31
§11-2 一维问题弹塑性分析
2.3 梁具有一个对称轴截面的弹塑性弯曲:
M
x
y
b
M
z
h
y
具有一个对称轴截面梁的弹塑性弯曲特点： 随着弯矩的增大，中性轴的位置而变化。
（a段进入塑性屈服，但 b 段仍处于弹性）
N2=P- N1=P-sA 力 P 作用点的伸长取决于b 段杆的变形
b
N2b EA
(P
s A)b
EA
2021/8/9
17
§11-2 一维问题弹塑性分析
b
N2b EA
(P s A)b
EA
Pe s A(1 a b) s A Pe (1 a b)
应力较少）屈服条件是不变的。当应力满足
屈服条件时，卸载将有残余变形，即塑性变
形存在。卸载按线性弹性。
C
s A B
’s s
A
B
C
o
p
e
p
e
o O’
p e
软钢 -
合金钢 -
2021/8/9
5
§11-1 金属材料的力学实验及几种简化力学模型
而对于合金钢，无明显屈服，当 s时进
入强化阶段，在加载即发生弹性变形和塑性变
弹塑性有限元法基本理论与模拟方法
用于模拟流体流动和传热问题 ，如流体机械、航空航天和化 工等领域。
电磁场
用于分析电磁场问题和电气设 备性能，如电机、变压器和天 线等。
声学
用于模拟声音传播和噪声控制 问题，如声学器件和声学环境
等。
04 弹塑性有限元法的基本原 理
弹塑性有限元法的离散化方法
有限元离散化
将连续的物理场或结构体离散为有限个小的单元体， 每个单元体之间通过节点相互连接。
结构强度分析的模拟
结构强度评估
通过弹塑性有限元法模拟，可以对结构的强度进行评估，预测结构在不同载荷下的响应， 确保结构的安全性和稳定性。
疲劳寿命预测
利用弹塑性有限元法，可以模拟结构的疲劳载荷历程，预测结构的疲劳寿命，为结构的维 护和更换提供依据。
结构优化设计
通过模拟结构的应力分布和变形，可以优化结构设计，降低结构重量，提高结构效率。
边界条件和初始条件
在平衡方程中考虑边界条件和初始条件，以确保模拟的准确性和收 敛性。
弹塑性有限元法的边界条件和初始条件
边界条件的处理
01
根据实际情况，将边界条件转化为节点约束或单元载荷的形式。
初始条件的设置
02
在非稳态问题中，需要考虑初始条件的设置，以模拟问题的初
始状态。
边界条件和初始条件的实施
03
随着计算机技术的不断发展，弹塑性 有限元法在各个工程领域中得到了广 泛应用，如机械、航空航械设计中，弹塑性有限元法可用于分析各种复杂结构 的应力分布、变形和疲劳寿命等，提高产品的可靠性和安 全性。
航空航天
在航空航天领域，弹塑性有限元法可用于分析飞行器结构 在各种载荷下的响应，优化结构设计，提高飞行器的性能 和安全性。
弹塑性本构关系简介
2） 势能原理的数学表达
应变能
总势能
Ve=Vε+VP =1/2∫VσijεijdV 外力势能
-∫VFbiuidV- ∫SσFsiuidS = min
2 虚力原理
1）虚力原理的表述
给定位移状态协调的充分必要条件为：对 一切自平衡的虚应力，恒有如下虚功方程成 立（矩阵）
∫V[ε]Tδ[σ]dV=∫Su([L]δ[σ])T [u ]0dS
收敛准则
1、位移模式必须包含单元的刚体位移
2、位移模式必须能包含单元的常应变
3、位移模式在单元内要连续、并使相邻单元间的位移必须协调
满足条件1、2的单元为完备单元
满足条件3的单元为协调单元 多项式位移模式阶次的选择——按照帕斯卡三角形选
几何各向同性：位移模式应与局部坐标系的方位无关
多项式应有偏惠的坐标方向，多项式项数等于单元边界结点的自由度总
变间关系为 octσoct
GKtt
oct 3K s oct oct Gs oct
并有
Gs G
1
a
oct
B c
m
KGss
εoct
oct
K G e s
s (c oct ) p
KG
其中G、K分别为初始切线剪切和体积模量，
B c
为混凝土单轴抗压强度，a、m、c和p为由试验
确定的常数。
POCT
弹性张量Dijkl
ij
Dijkl kl
( 2G 1 2
ij kl
2Giklj ) kl
i 1, j 2, k 1,l 2
12
D1212 12
( 2G 1 2
1212
2G1122 )12
11 1 12 0 22 1
结构计算常用材料模型
Smart Energy Solutions for a Cleaner World
剪切模量是指剪切应力与剪切应变之比。剪切模量G=剪切弹性模量G=切
变弹性模量G；材料的基本物理特性参数之一，与杨氏（压缩、拉伸）弹性模
量E、泊松比V并列称为材料的三项基本物理特性参数，在材料力学、弹性力学
中有广泛的应用。
Smart Energy Solutions for a Cleaner World
4.Engineering Data 模块
Smart Energy Solutions for a Cleaner World
Aluminum Alloy:铝合金；Concrete:混泥土; Copper Alloy:铜合金; Gray Cast Iron:灰口铸铁; Magnesium Alloy:镁合金; Polyethylene: 聚乙烯; Silicon Anisotropic:各向异性硅; Stainless Steel:不锈钢; Structural Steel:结构钢; Titanium Alloy:钛合金
试件拉断为止，试验机的绘图装置会把试件所受的拉力F与试件的拉
长量△l之间的关系自动记录下来，绘出一条曲线F- △l曲线，称为
拉伸图。
除去尺寸因素，变
为应力-应变曲线，
即
曲线
2.应力-应变曲线
Smart Energy Solutions for a Cleaner World
将试件装卡在材料试验机上进行常温、静载拉伸试验，直到把
第一阶段——弹性变形阶段（曲线ob段）。
在此阶段任一时刻时，将载荷慢慢减少（称卸载）为零，变形会消 失。B点对应的应力称材料的弹性极限。即材料处于弹性变形阶段
高等土力学(李广信)2.5 土的弹塑性模型的一般原理
面重合，即f=g。
不相适应（不相关联）的流动（nonassociated
flow rule)：塑性势面不必与屈服面重合fg。
dpij
dij
Drucker 假说：对于稳定材 料：
图2－42 Drucker 假说
认为A与A´在同一屈服面上
图2－41
三轴试验与真三轴试验确定塑性应变增量方向
2.5.3流动规则与硬化定律
1. 流动规则 (flow rule) 2. 硬化定律 (strain-hardening law)
1. 流动规则（flow rule)：用以确定塑性应变增量 向量的方向的规则（或者确定塑性应变增量的 各个分量间的比例关系）－塑性应变增量向量 正交于塑性势面。所以也称为正交规则。
d
ijd
P ij
0
屈服面的外凸 与塑性应变增 量向量的正交
锥形屈服面与帽子屈服面 q
dpij dpij
p 图2－43 与两种屈服面的正交的塑性应变
表现土的塑性剪胀与剪缩，锥形屈服面会使剪胀量过 大，一般采用不相适应的流动规则
2. 加工（应变）硬化定律 (strain-hardening law)： 是确定在一定的应力增量作用下引起的塑性应变增
2.5.2屈服准则与屈服面
1. 屈服准则 2. 屈服函数 3. 屈服面与屈服轨迹 4. 土的屈服面与屈服轨迹的一般形式 5.土的屈服面与屈服轨迹的确定
1. 屈服准则(yield criterion)
判断是否发生塑性变形的准则 －判断加载与卸载的准则
ABBຫໍສະໝຸດ AABA B
A、B在屈服面上， A B不在屈服面上
《弹塑性分析》课件
新材料和新工艺的弹塑性分析
随着新材料和新工艺的出现，对新材料和新工艺的弹塑性分析将成为未来的重要研究方向 ，包括对超弹性、粘弹性、粘塑性等方面的研究。
人工智能在弹塑性分析中的应用
人工智能技术在许多领域都取得了显著的成果，未来可以将人工智能技术应用于弹塑性分 析中，如利用机器学习算法进行模型预测和优化等。
03
建立每个单元的平衡方程，通过求解这些方程得到整个系统的
近似解。
弹塑性分析的有限元模型
材料属性
考虑材料的弹性模量、泊松比、屈服强度等 参数。
初始条件
设定模型在分析开始时的状态，如初始应变 、初始应力等。
边界条件
根据实际情况设定模型的边界条件，如固定 、自由、受压等。
载荷
根据实际情况施加适当的载荷，如集中力、 分布力等。
在建立弹塑性本构模型时，还需要考虑材料的 硬化或软化行为，以及温度、应变速率等对材 料力学行为的影响。
Hale Waihona Puke 03弹塑性分析的有限元方法
有限元方法的基本原理
离散化
01
将连续的物理系统离散成有限个小的单元，每个单元具有特定
的形状和大小。
近似解
02
用数学模型描述每个单元的行为，并使用近似解代替精确解。
平衡方程
弹塑性分析
目 录
• 弹塑性分析概述 • 弹塑性本构模型 • 弹塑性分析的有限元方法 • 弹塑性分析的实例 • 弹塑性分析的展望与挑战
01
弹塑性分析概述
弹塑性材料的定义与特性
弹塑性材料
弹性
塑性
弹塑性材料的特性
弹塑性力学 应力和应变之间的关系
我所认识的应力和应变之间的关系在单向应力状态下，理想弹性材料的应力和应变之间的关系是满足胡克定律的一一对应的关系。
在三维应力状态下描述一点处的应力状态需要9个分量，相应的应变状态也要用9个应变分量来表示。
对于一个具体的理想弹性体来讲，如果在三维应力状态下，应力与应变之间仍然有线性一一对应关系存在，则称这类弹性体为线性弹性体。
所谓各向弹性体，从力学意义上讲，就是弹性体内的每一点沿各个方向的力学性质都完全相同的。
这类线性弹性体独立的唐兴常数只有两个。
各向同性体本构关系特点：1.主应力与主应变方向重合。
2.体积应力与体积应变成比例。
3.应力强度与应变强度成比例。
4.应力偏量与应变偏量成比例。
工程应用中，常把各向同性弹性体的本构方程写下成11()11()11()x y z xy xy y x z yz yz z y x xz xz E G E G E G εσμσσγτεσμσσγτεσμσσγτ⎧⎡⎤=-+=⎣⎦⎪⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩，式中分别为弹性模量、泊松比和剪切模量。
在E G μ、、这三个参数之间，实际上独立的常量只有两个，它们之间存在关系为()21E G μ=+。
屈服条件:弹性和塑性的最主要区别在于变形是可以恢复。
习惯上，根据破坏时变形的大小把工程材料分为脆性材料和塑性材料两类。
对于加载过程如图1OA: 比例阶段；线性弹性阶段AB: 非弹性变形阶段 BC ： 初始屈服阶段 s σσ≤ CDE ：强化阶段；应变强化硬化阶段EF ： 颈缩阶段；应变弱化，软化阶段s σσ≥ C 点为初始屈服点具有唯一性。
在应力超过屈服应力后，如果在曲线上任意一点D 处卸载，应力和应变之间将不再遵循原有的加载曲线规律，而是沿一条接近平行于OA 的直线DO ’变化，直到应力下降为零，这时应变并不为零，即有塑性应变产生。
如果用OD ’表示总应变ε，O ’D ’表示可以恢复的弹性应变eε，OO ’表示不能恢复的塑性应变p ε，则有e p εεε=+，即总应变等于弹性应变加上塑性应变。
08 混凝土的弹塑性本构模型2013
dε
c0 = 9
rbc
ε
ε
rbc a0 − 3 + rbc
(
(
3 − a0 + a0 − 3 / 2
) ( ) (2
σ 2
) (
)
3 − 4 a0
)
39
dσ H '= dε p
10
0 -40 -30 -20 -10 -10 0 10
ε pl 为双轴受压和单轴受压时 ε 11 的比值，一般为 1.28 rbc
启示：胡平的工作
σ σy σt
dσt1
2.
3.
3.
需要迭代求解
增量理论
1. 2. 3.
思考：如何求解？
塑性条件下应力和应变间的增量关系 需要按加载过程积分 适用于计算机分析
ε εt dεt
11 12
8.2.1 增量理论的三个基本假定
1.
8.2.2 屈服面
屈服准则
应力满足什么条件时进入屈服状态
F (σ ij ) = 0
4
问题
已知：
8.1 材料的一维弹塑性行为
加载→卸载
弹性模量200GPa，泊松比为0 von Mises屈服准则，屈服应力200MPa 起始应力{180,0,0,0,0,0}，应变增量{0.002, 0.002, 0,0,0,0}
屈服应力 弹性应变 塑性应变 理想弹塑性 硬化 软化
19
20
8.2.2 屈服面
专用于混凝土的屈服准则
8.2.2 屈服面
专用于混凝土的屈服准则
WF Chen屈服准则 屈服面分区为
Nilson屈服条件 用椭球面来表示
高等土力学(李广信)2.5 土的弹塑性模型的一般原理ppt课件
6
1. 屈服准则(yield criterion)
判断是否发生塑性变形的准则 －判断加载与卸载的准则
A
B
B A
A
B
A B
A、B在屈服面上， A B不在屈服面上
图2－36 屈服－弹塑性应变的判断准则
14
图2－40 试验搜索屈服点 A-1-2-A´
认为A与A´在同一屈服面上
15
图2－41
三轴试验与真三轴试验确定塑性应变增量方向
16
2.5.3流动规则与硬化定律
1. 流动规则 (flow rule) 2. 硬化定律 (strain-hardening law)
17
1. 流动规则（flow rule)：用以确定塑性应变增量 向量的方向的规则（或者确定塑性应变增量的 各个分量间的比例关系）－塑性应变增量向量 正交于塑性势面。所以也称为正交规则。
B 为屈服点；
A´非屈服点 7
2. 屈服函数 (yield function, yield equation)
屈服准则的数学表达式
f (ij , H) 0
对于刚塑性和弹性－塑性模型：H为常数；
对于弹塑性模型：H是塑性应变的函数。
8
加卸载的判断（应变硬化情况）
f
ij
d ij
0
为加载，同时发生弹性、 塑性变形
相适应（相关联）的流动规则（associated flow rule)：根据Drucker假说，塑性势面必须与屈服
面重合，即f=g。
不相适应（不相关联）的流动（nonassociated
钢丝帘线弹塑性材料模型探讨
旦 一 Ａ — Ａ 一 ／ ｏ ｏ
一
（ ）
ｎ （ １＋ 十 ｎ ｅ ｎ ） （ ５ ）
真实 塑性 应变 （ ￡ 。 ） 可 以 由真 实 总 应 变 （ ｅ ） 和
及杨 氏模 量 （ Ｅ） 得 到
ｅ 一 ｅｔ一
关 系［ 引。
而 钢丝 帘线 又是子 午线 轮胎结 构 中的 主要受 力材 料； 因此 ， 对其 进行 受力 分析 已经成 为现 代轮 胎结 构 设计 和分 析 的重要工 作之 一 。 由于轮 胎结 构及
其材 料 的复 杂性 ， 至今 还 没有 有 效 的试 验 手段 来 直观、 定 量地 分析 轮胎 内部材 料 的受力 变形 情况 。 随 着计 算机 和数 学 、 力 学等 自然科 学 的发展 ， 有 限
采用试 验 与 Ａｂ ａ ｑ ｕ ｓ软 件 模 拟 相 结 合 的 方 式， 在 充分 考虑 材料 非线 性 、 多股 加捻钢 丝之 间复 杂 接触 和拉 伸后 截面变 化 的情况 下 ， 较直观 、 简 便
地 获得 了钢 丝帘线 弹 塑性材 料模 型参 数 。结果 表
关键词 ： 钢丝帘线； 有 限 元分 析 ； 材 料 模 型
中 图分 类 号 ： Ｔ Ｑ３ ３ ｏ ． ３ ８ ９
文献 标 志 码 ： Ｂ
文章编号： １ ０ ０ ６ — ８ １ ７ １ （ ２ ０ １ ４ ） １ ０ — ０ ６ ０ ２ — ０ ３
众所 周 知 ， 轮胎 是汽 车安 全 的关键 部件 之一 ，
考虑 塑性 变 形 的不 可 压 缩 性 ， 并 假 设 弹 性 变
形 也是 不可压 缩 的 ， 建 立真 实应 力 （ ） 与 名 义应 力
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
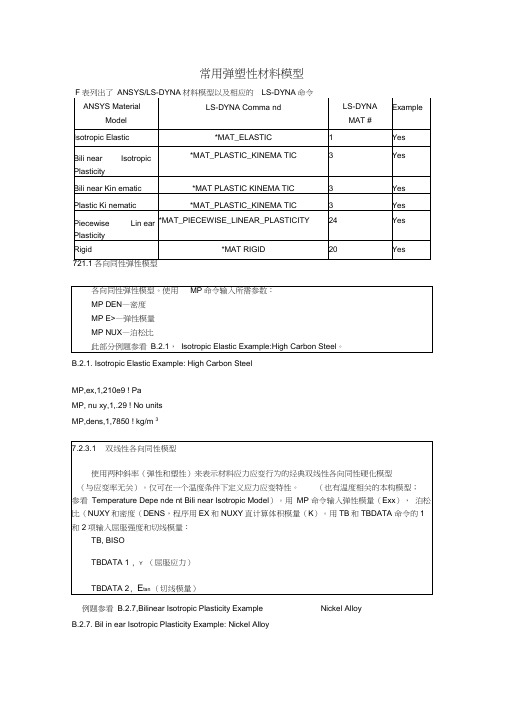
常用弹塑性材料模型下表列出了ANSYS/LS-DYNA材料模型以及相应的LS-DYNA命令
B.2.1. Isotropic Elastic Example: High Carbon Steel
MP,ex,1,210e9 ! Pa
MP,nuxy,1,.29 ! No units
MP,dens,1,7850 ! kg/m3
B.2.7. Bilinear Isotropic Plasticity Example: Nickel Alloy
MP,ex,1,180e9 ! Pa
MP,nuxy,1,.31 ! No units
MP,dens,1,8490 ! kg/m3
TB,BISO,1
TBDA TA,1,900e6 ! Yield stress (Pa)
TBDA TA,2,445e6 ! Tangent modulus (Pa)
B.2.10. Bilinear Kinematic Plasticity Example: Titanium Alloy
MP,ex,1,100e9 ! Pa
MP,nuxy,1,.36 ! No units
MP,dens,1,4650 ! kg/m3
TB,BKIN,1
TBDA TA,1,70e6 ! Yield stress (Pa)
TBDA TA,2,112e6 ! Tangent modulus (Pa)
B.2.11. Plastic Kinematic Example: 1018 Steel
MP,ex,1,200e9 ! Pa
MP,nuxy,1,.27 ! No units
MP,dens,1,7865 ! kg/m3
TB,PLAW,,,,1
TBDA TA,1,310e6 ! Yield stress (Pa)
TBDA TA,2,763e6 ! Tangent modulus (Pa) TBDA TA,4,40.0 ! C (s-1)
TBDA TA,5,5.0 ! P
TBDA TA,6,.75 ! Failure strain
B.2.16. Piecewise Linear Plasticity Example: High Carbon Steel
MP,ex,1,207e9 ! Pa
MP,nuxy,1,.30 ! No units
MP,dens,1,7830 ! kg/m3
TB,PLAW,,,,8
TBDA TA,1,207e6 ! Yield stress (Pa)
TBDA TA,3,.75 ! Failure strain
TBDA TA,4,40.0 ! C (strain rate parameter)
TBDA TA,5,5.0 ! P (strain rate parameter)
TBDA TA,6,1! LCID for true stress vs. true strain (see EDCURVE below) *DIM,TruStran,,5
*DIM,TruStres,,5
TruStran(1)=0,.08,.16,.4,.75
TruStres(1)=207e6,250e6,275e6,290e6,3000e6 EDCURVE,ADD,1,TruStran (1),TruStres(1)
B.2.25. Rigid Material Example: Steel
MP,ex,1,207e9 ! Pa
MP,nuxy,1,.3 ! No units MP,dens,1,7580 ! kg/m3 EDMP,rigid,1,7,7。