弹塑性本构关系简介
合集下载
第11章-弹塑性力学--本构关系
xy c41 x c42 y c43 z c44 xy c45 yz c46 zx yz c51 x c52 y c53 z c54 xy c55 yz c56 zx zx c61 x c62 y c63 z c64 xy c65 yz c66 zx
xy c41 x c42 y c43 z
y y
图4-2
（a）
z
x
x
z
现在引进坐标系 Ox’y’z’, 原坐 标系 Oxyz 绕 y 轴转动 1800 后可与之重合 (图4-2)
新旧坐标轴间的方向余弦
l11 l33 cos180
1 0 0 1 l22 cos 0 1 0 0 l21 l31 l12 l32 l13 l23 cos 90 0
（11-13）
平面应力问题 用应变分量表示 应力分量
E y x 1 2 x E （11-14） y y x 1 2 G
ij ije 2 ij
（11-3’）
以上证明了各向同性的均匀弹性体的弹性常数只有 两个。
现在考虑一种物体各边平行于坐标轴的特殊情况，并 由此导出工程上常用的弹性常数和广义胡克定律。当物 体边界法线方向与 z 轴重合的两对边上有均匀的σz 作 用，其他边均为自由边时，则由材料力学知道
第11章 本构关系
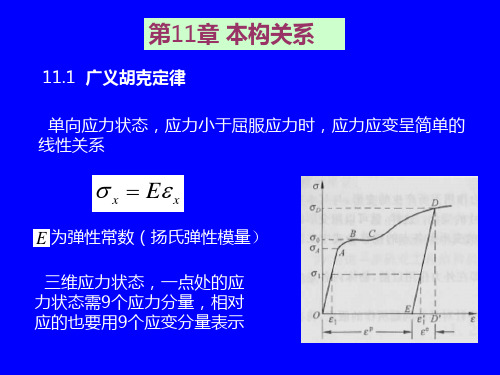
11.1 广义胡克定律 单向应力状态，应力小于屈服应力时，应力应变呈简单的 线性关系
x E x
E 为弹性常数（扬氏弹性模量）
三维应力状态，一点处的应 力状态需9个应力分量，相对 应的也要用9个应变分量表示
xy c41 x c42 y c43 z
y y
图4-2
（a）
z
x
x
z
现在引进坐标系 Ox’y’z’, 原坐 标系 Oxyz 绕 y 轴转动 1800 后可与之重合 (图4-2)
新旧坐标轴间的方向余弦
l11 l33 cos180
1 0 0 1 l22 cos 0 1 0 0 l21 l31 l12 l32 l13 l23 cos 90 0
（11-13）
平面应力问题 用应变分量表示 应力分量
E y x 1 2 x E （11-14） y y x 1 2 G
ij ije 2 ij
（11-3’）
以上证明了各向同性的均匀弹性体的弹性常数只有 两个。
现在考虑一种物体各边平行于坐标轴的特殊情况，并 由此导出工程上常用的弹性常数和广义胡克定律。当物 体边界法线方向与 z 轴重合的两对边上有均匀的σz 作 用，其他边均为自由边时，则由材料力学知道
第11章 本构关系
11.1 广义胡克定律 单向应力状态，应力小于屈服应力时，应力应变呈简单的 线性关系
x E x
E 为弹性常数（扬氏弹性模量）
三维应力状态，一点处的应 力状态需9个应力分量，相对 应的也要用9个应变分量表示
第三章 塑性状态下的本构关系
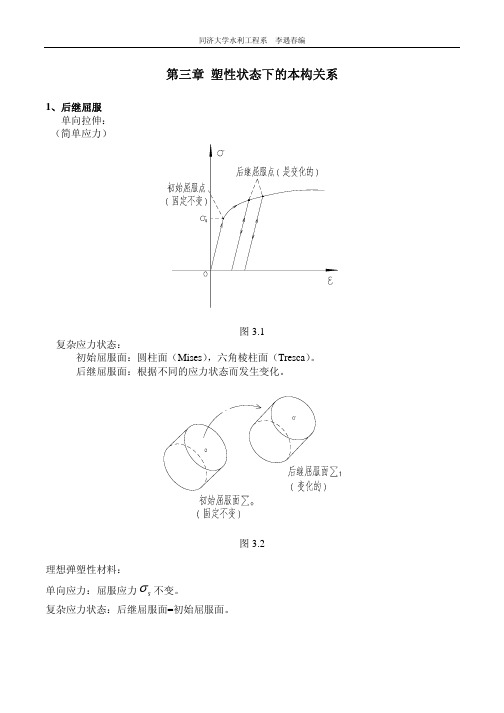
⎧d ε p1 = (σ 1 − σ m ) ⋅ d λ ⎪ p ⎨d ε 2 = (σ 2 − σ m ) ⋅ d λ ⎪ p ⎩d ε 3 = (σ 3 − σ m ) ⋅ d λ
（3.26）
同济大学水利工程系
李遇春编
由（3.26）式得：
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
（初始屈服面）
m ) − c = 0 （后继屈服面） f * (σ ij + σ ij
m ：应力位移 σ ij
， c 不变。见图 3.9,屈服面作平移，位置改变，大小与形状不变。
N
d ε p ij
（塑性应变）
2 产生塑性变形为 d ε 过程○
p ij
，其塑性功为： (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式：
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
（3.26）
同济大学水利工程系
李遇春编
由（3.26）式得：
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
（初始屈服面）
m ) − c = 0 （后继屈服面） f * (σ ij + σ ij
m ：应力位移 σ ij
， c 不变。见图 3.9,屈服面作平移，位置改变，大小与形状不变。
N
d ε p ij
（塑性应变）
2 产生塑性变形为 d ε 过程○
p ij
，其塑性功为： (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式：
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
弹塑性力学讲义—本构关系
例2-1 对Mises屈服条件，证明
f J 2 sij ij ij
证： Mises屈服条件为
2 f J2 s 0 3
J 2 J 2 sk l 1 1 smn smn k l pp k l ij sk l ij sk l 2 3 ij
量是x=，y=0，且x，y，z均为应力的主方向。若材料为理想塑
性，Poisson比<1/2，单轴拉伸屈服极限为s，试利用Mises屈服 条件求出该材料单元达到屈服时的值。记屈服时的值为0，屈服
后加载使得x=0+d，求z方向的应力增量dz。
解：屈服处于弹性阶段，对于平面应变状态，因此根据虎克定律，有 z=(x+y)= 偏应力分量为 1 1 1 sx= (2)，sy= (1+)，sz= (12)，sxy=syz=szx=0 3 3 3
d 3 d ij d ij s 2
sij
2 s diΒιβλιοθήκη 3dij dij d p
p p 2d 2 d1p d 3 p d1p d 3
ud p u
• Tresca屈服条件相关联的流动法则 不规定主应力大小顺序，Tresca屈服条件可写成
例2-4： 有一受内水压p和轴向力共同作用的薄壁圆筒，内半径为r，壁 厚为t，若圆筒保持直径不变，只产生轴向伸长，假设材料是不可压缩的，
在忽略弹性变形的情况下，试求圆筒达到塑性状态时需要多大的内水压力。
解∶ 环向应变=0，轴向伸长靠筒壁变薄实现，各应变分量为 =0 z = r 或 e=0 ez = er Levy-Mises流动理论 s=0 sz = sr
ij
0 p (ij ij )d ij 0
f J 2 sij ij ij
证： Mises屈服条件为
2 f J2 s 0 3
J 2 J 2 sk l 1 1 smn smn k l pp k l ij sk l ij sk l 2 3 ij
量是x=，y=0，且x，y，z均为应力的主方向。若材料为理想塑
性，Poisson比<1/2，单轴拉伸屈服极限为s，试利用Mises屈服 条件求出该材料单元达到屈服时的值。记屈服时的值为0，屈服
后加载使得x=0+d，求z方向的应力增量dz。
解：屈服处于弹性阶段，对于平面应变状态，因此根据虎克定律，有 z=(x+y)= 偏应力分量为 1 1 1 sx= (2)，sy= (1+)，sz= (12)，sxy=syz=szx=0 3 3 3
d 3 d ij d ij s 2
sij
2 s diΒιβλιοθήκη 3dij dij d p
p p 2d 2 d1p d 3 p d1p d 3
ud p u
• Tresca屈服条件相关联的流动法则 不规定主应力大小顺序，Tresca屈服条件可写成
例2-4： 有一受内水压p和轴向力共同作用的薄壁圆筒，内半径为r，壁 厚为t，若圆筒保持直径不变，只产生轴向伸长，假设材料是不可压缩的，
在忽略弹性变形的情况下，试求圆筒达到塑性状态时需要多大的内水压力。
解∶ 环向应变=0，轴向伸长靠筒壁变薄实现，各应变分量为 =0 z = r 或 e=0 ez = er Levy-Mises流动理论 s=0 sz = sr
ij
0 p (ij ij )d ij 0
弹塑性力学第5章—塑性本构关系
3 2
sij
−
Cdε
p ij
sij −
Cdε
p ij
−σs = 0
C表征材料强化的大小，来自单向拉伸
5.3 后继屈服条件
1、等向强化模型
单向拉伸实验曲线中三个方向的塑性主应变为
ε1p
= ε p,
ε
p 2
=
ε
p 3
= − 1ε p
2
其中ε p为单向拉伸方向的塑性应变，由此得到等效塑性应变
( ) ( ) ( ) ε p =
4 3
J
′
2
=
2 9
⎡ ⎢⎣
ε1p
−
ε
p 2
2+
ε
p 2
−
ε
p 3
2+
ε
p 3
最大畸变能是材料屈服的原因
J2 = k2
J 2反映了材料的畸变能（ U0d
=
J2 2G
）
( ) J2
=
1 2
sij sij
=
1 6
(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1)2
k 由实验确定，根据简单拉伸实验，在材料屈服时
[ ] J2
=1 6
(σ 0 − 0)2 + 0 + (0 −σ 0 )2
−0.8
屈服条件类似，主要区别是
−1.0
混凝土的抗压强度比抗拉强
−1.2
度高得多。
5.2 常用的屈服条件
5.2.3 混凝土的莫尔－库仑屈服条件
在实验基础上，提出线性化的莫尔－库仑屈服条件，σ
′
0
,
σ
弹塑性力学第四章弹性本构关系资料
产生的x方向应变：
产生的x方向应变：
叠加
产生的x方向应变：
同理：
剪应变：
物理方程：
说明：
1.方程表示了各向同性材料的应力与应 变的关系，称为广义Hooke定义。也称 为本构关系或物理方程。
2.方程组在线弹性条件下成立。
. 体积应变与体积弹性模量
令： 则： 令：
sm称为平均应力; q 称为体积应变
eij
1 2G
sij
(4.40)
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个
因此应力偏张量形式的广义虎克定律，即
eij
1 2G
sij
em
1 3K
sm
(4.41)
用应变表示应力：
或： ✓ 各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
式（２）中的系数 有３６个．
称为弹性常数，共
由均匀性假设，弹性体各点作用同样应力 时，必产生同样的应变，反之亦然．因此 为 常数，其数值由弹性体材料的性质而定．
式（２）推导过程未引用各向同性假设， 故可适用于极端各向异性体、正交各向异性体、 二维各向同性体以及各向同性体等．
式（２）可用矩阵表示
式(3)可用简写为 称为弹性矩阵.
三、. 弹性常数
1. 极端各向异性体:
物体内的任一点, 沿各个方向的性能都不相 同, 则称为极端各向异性体. (这种物体的材料极 少见)
即使在极端各向异性条件下, 式(2)中的36个 弹性常数也不是全部独立.
产生的x方向应变：
叠加
产生的x方向应变：
同理：
剪应变：
物理方程：
说明：
1.方程表示了各向同性材料的应力与应 变的关系，称为广义Hooke定义。也称 为本构关系或物理方程。
2.方程组在线弹性条件下成立。
. 体积应变与体积弹性模量
令： 则： 令：
sm称为平均应力; q 称为体积应变
eij
1 2G
sij
(4.40)
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个
因此应力偏张量形式的广义虎克定律，即
eij
1 2G
sij
em
1 3K
sm
(4.41)
用应变表示应力：
或： ✓ 各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
式（２）中的系数 有３６个．
称为弹性常数，共
由均匀性假设，弹性体各点作用同样应力 时，必产生同样的应变，反之亦然．因此 为 常数，其数值由弹性体材料的性质而定．
式（２）推导过程未引用各向同性假设， 故可适用于极端各向异性体、正交各向异性体、 二维各向同性体以及各向同性体等．
式（２）可用矩阵表示
式(3)可用简写为 称为弹性矩阵.
三、. 弹性常数
1. 极端各向异性体:
物体内的任一点, 沿各个方向的性能都不相 同, 则称为极端各向异性体. (这种物体的材料极 少见)
即使在极端各向异性条件下, 式(2)中的36个 弹性常数也不是全部独立.
弹塑性本构关系简介
2） 势能原理的数学表达
应变能
总势能
Ve=Vε+VP =1/2∫VσijεijdV 外力势能
-∫VFbiuidV- ∫SσFsiuidS = min
2 虚力原理
1）虚力原理的表述
给定位移状态协调的充分必要条件为：对 一切自平衡的虚应力，恒有如下虚功方程成 立（矩阵）
∫V[ε]Tδ[σ]dV=∫Su([L]δ[σ])T [u ]0dS
收敛准则
1、位移模式必须包含单元的刚体位移
2、位移模式必须能包含单元的常应变
3、位移模式在单元内要连续、并使相邻单元间的位移必须协调
满足条件1、2的单元为完备单元
满足条件3的单元为协调单元 多项式位移模式阶次的选择——按照帕斯卡三角形选
几何各向同性：位移模式应与局部坐标系的方位无关
多项式应有偏惠的坐标方向，多项式项数等于单元边界结点的自由度总
变间关系为 octσoct
GKtt
oct 3K s oct oct Gs oct
并有
Gs G
1
a
oct
B c
m
KGss
εoct
oct
K G e s
s (c oct ) p
KG
其中G、K分别为初始切线剪切和体积模量，
B c
为混凝土单轴抗压强度，a、m、c和p为由试验
确定的常数。
POCT
弹性张量Dijkl
ij
Dijkl kl
( 2G 1 2
ij kl
2Giklj ) kl
i 1, j 2, k 1,l 2
12
D1212 12
( 2G 1 2
1212
2G1122 )12
11 1 12 0 22 1
非线性有限元9弹塑性本构关系ppt课件
单轴试验下材料的弹塑性性态 （1/3）
对塑性变形基本规律的认识来自于实验： • 从实验中找出在应力超出弹性极限后材料的特性; • 将这些特性进行归纳并提出合理的假设和简化模型，
确定应力超过弹性极限后材料的本构关系; • 建立塑性力学的基本方程; 1) 求解这些方程，得到不同塑性状态下物体内的应力和
应变。
• 塑性阶段：继续加载，材料可承受 更大应力，称为材料强化，并伴随 出现塑性应变。至A点以前卸载， 路径接近直线，即处于弹性卸载状 态，其斜率等于加载斜率E。
1) 破坏点：继续加载至可承受的最大 极限应力，试件出现颈缩而破坏，
称为强度极限。
在日常生活中，随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费，也 许你认 为浪费 这一点 点算不 了什么
1913年：泰勒（Taylor）的实验证明，LevyMises本构关系是真实情况的一阶近似。
1924年：提出塑性全量理论，伊柳辛（Ilyushin） 等苏联学者用来解决大量实际问题。
1930年：罗伊斯（Reuss）在普朗特（Prandtle） 的启示下，提出包括弹性应变部分的三维塑性应力 -应变关系。至此，塑性增量理论初步建立。
（屈服点），描写多维问题的屈服条件就需要应力或应变空间的一个临界曲面，该
曲面称为屈服面。
考虑到塑性变形与静
水压力无关的特点
f1,2,3C
FJ2,J3C
至今已出现许多屈服理论。俞茂宏教授在这方面做出了重要贡献。 屈服函数：
是描写屈服条件的函数。不同屈服条件，其屈服函数不尽相同。
在日常生活中，随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费，也 许你认 为浪费 这一点 点算不 了什么
基本实验有两个： • 简单拉伸实验：实验表明，塑性力学研究的应力与应变
对塑性变形基本规律的认识来自于实验： • 从实验中找出在应力超出弹性极限后材料的特性; • 将这些特性进行归纳并提出合理的假设和简化模型，
确定应力超过弹性极限后材料的本构关系; • 建立塑性力学的基本方程; 1) 求解这些方程，得到不同塑性状态下物体内的应力和
应变。
• 塑性阶段：继续加载，材料可承受 更大应力，称为材料强化，并伴随 出现塑性应变。至A点以前卸载， 路径接近直线，即处于弹性卸载状 态，其斜率等于加载斜率E。
1) 破坏点：继续加载至可承受的最大 极限应力，试件出现颈缩而破坏，
称为强度极限。
在日常生活中，随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费，也 许你认 为浪费 这一点 点算不 了什么
1913年：泰勒（Taylor）的实验证明，LevyMises本构关系是真实情况的一阶近似。
1924年：提出塑性全量理论，伊柳辛（Ilyushin） 等苏联学者用来解决大量实际问题。
1930年：罗伊斯（Reuss）在普朗特（Prandtle） 的启示下，提出包括弹性应变部分的三维塑性应力 -应变关系。至此，塑性增量理论初步建立。
（屈服点），描写多维问题的屈服条件就需要应力或应变空间的一个临界曲面，该
曲面称为屈服面。
考虑到塑性变形与静
水压力无关的特点
f1,2,3C
FJ2,J3C
至今已出现许多屈服理论。俞茂宏教授在这方面做出了重要贡献。 屈服函数：
是描写屈服条件的函数。不同屈服条件，其屈服函数不尽相同。
在日常生活中，随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费，也 许你认 为浪费 这一点 点算不 了什么
基本实验有两个： • 简单拉伸实验：实验表明，塑性力学研究的应力与应变
岩石弹塑性本构模型讲课资料
4、弹塑性本构方程
塑性状态时应力-应变关系是多值的，取决材料性质和加载
-卸载历史。
1）全量理论：描述塑性变形中全量关系的理论，称形变
理论或小变性理论。
汉基（Hencky）、依留申等依据类似弹性理论的广义胡克 定律，提出如下公式：
xx m 2Gxx m,xy Gxy
yy m 2G yy m ,yz Gyz
一、非线性弹性理论
在岩石力学中使用弹塑性理论是将岩石介质看作是一 种连续介质，严格来说，岩石介质的应力-应变关系都 是非线性的。
本构关系是关于一个物质质点的力学性质，一般认为 他是与应力和应变有关，而与应力梯度和应变梯度无 关。为了直观的描述质点的状态，引入应力空间和应 变空间两个概念。
用Cauchy方法给出的本构方程
和 dij K t2 3G t dkkij2G tdsij
式 中 ： E t 是 材 料 的 切 线 杨 氏 模 量 ； v t 是 切 线 泊 松 比 ； K t 是 切 线 体 积 模 量 ； G t 是 切 线 剪 切 模 量 ；
二、应力空间表述的弹塑性本构 关系
1、应力-应变关系的多值性 同一应力有多个应变值与它对应，本构关系采用应力
硬化材料的屈服面模型
（1）等向硬化-软化模型：塑性变形发展时，屈服面做均匀 扩大（硬化）或均匀收缩（软化），如果 f * 0是初始屈服面，
那么等向硬化-软化模型的后继屈服面可表示为
ff*ijH 0
（2）随动硬化模型：塑性变形发展时，屈服面的大小和形状
保持不变，仅是整体的在应力空间中做平动，其后继屈服面可
按Cauchy方法可以这样定义弹性介质：在外力作用下， 物体内各点的应力状态和应变状态之间存在着一一对 应的关系，弹性介质的响应仅与当时的状态有关，而 与应力路径或应变路径无关，假设了应力和应变都是 瞬时发生的。
4-3混凝土弹塑性本构关系
x
xy yz zx
i xy 3 i i yz 3 i i zx 3 i
D
ep
K B
v
T
Dep B dv
d11 d 12 d 12 0 0 0
最大偏应力屈服准则，双剪屈服准则
1932年SchmidtR提出最 大偏应力屈服准则，与 后来我国学者俞茂宏提 出的双剪屈服准则相吻 合。 双剪应力屈服条件叙述 为:当两个较大的主剪应 力绝对值之和达到某极 限值时，材料开始屈服。
W F Chen屈服准则
屈服面分区为
Hale Waihona Puke 压－压区,压－拉区, 拉－压区, 拉－拉区
弹塑性矩阵的一般表达形式
硬化模量A
对于作功硬化， A = H'
弹塑性通用矩阵的编制
Tresca条件
Von Mises条件
Mohr-Coulomb条件
Drucker-Prager条件
WF Chen条件
塑性积分计算步骤
显式方法
逐步积分， 不迭代收敛 迭代直至收敛
隐式方法
显式积分方法
加卸载准则
强化材料
对于强化材料其加载面 是不断变化的，为区分 加载面和屈服面，加载 面用f表示，屈服面用必 表示。 加载时，塑性应变变化， H也随着变化，因此有 H=/0;而中性变载和卸载 这两种情况，不产生新 的塑性应变，H也就不 变化，因此有H=0。
强化材料
软化材料
流动法则
弹塑性矩阵的一般表达形式
强化模型
一种新的随动不均匀强( 软) 化砼本构 模型-刘西拉（2002）
弹塑性力学-弹塑性本构关系ppt课件
d
p
|
cos
0
此式限制了屈服面的形状： 对于任意应力状态，应力增量方向
与塑性应变向量之间所成的夹角不应 该大于90°
稳定材料的屈服面必须是凸的.
(a)满足稳定材 料的屈服面
ij
0 ij
(b) 不满足稳定 材料的屈服面
/2
工程弹塑性力学·塑性位势理论
2 塑性应变增量向量与屈服面法向平行
d 必p 与加载面的外法线
p
ij
0
0 ij
WD
(ij
adij
0 ij
)d
p
ij
0
1 a 1 2
当
0 ij
时,略去无穷小量
ij
( ij
0 ij
)d
p ij
0
当
0 ij
ij时，
d
ij
d
p ij
0
屈服面的外凸性
塑性应变增量方向 与加载曲面正交
工程弹塑性力学·塑性位势理论
1 屈服曲面的外凸性
( ij
0 ij
)dijp
|
A0 A||
不小于零，即附加应力的塑性功不出现负值， 则这种材料就是稳定的，这就是德鲁克公设。
工程弹塑性力学·塑性位势理论
在应力循环中，外载所作的 功为：
Ñ W
0 ij
ij
d ij
0
不论材料是不是稳定，上述 总功不可能是负的，不然， 我们可通过应力循环不断从 材料中吸取能量，这是不可 能的。要判断材料稳定必须 依据德鲁克公设，即附加应 力所作的塑性功不小零得出
弹塑性力学本构关系
1
工程弹塑性力学·塑性位势理论
(1) 稳定材料与非稳定材料
弹塑性本构关系
பைடு நூலகம்
F p d kk 3d S；deijp d ij e p p d d G K kk ij 2G eij kk mn 2 mn Sij k
(2) Druker-Prager 模型
Druker-Prager模型采用广义的 Mises屈服函数，其表达式为：
m
3K
ij
弹性变形 + 塑性变形 又可写成：
ij Sij m ij K kk ij 2G eij d d d d e d e
K kk d kk ij 2G eij eijp p d d d F F K kk ij 2G eij d 3K ij 2G d d kk Sij
F σ ij J 2 I1 k 0 +
由
F kk
F Sij 2 Sij J2
得 d ij dSij d m ij d F 2G 3K
F ij Sij kk
Sij m Sij d d d ij 2G 3K ij 2 J2
2G
m为对应于 m体应变
拉梅常数 E (1 )(1 2 )
xy
2
x 3 m 2G x y 3 m 2G y z 3 m 2G z xy 2G xy G xy
yz zx
2 2
2G
G
E 2(1 )
2G
基本方程 yz 2G yz G yz zx 2G zx G zx
张量形式
张量形式
ij ij
F p d kk 3d S；deijp d ij e p p d d G K kk ij 2G eij kk mn 2 mn Sij k
(2) Druker-Prager 模型
Druker-Prager模型采用广义的 Mises屈服函数，其表达式为：
m
3K
ij
弹性变形 + 塑性变形 又可写成：
ij Sij m ij K kk ij 2G eij d d d d e d e
K kk d kk ij 2G eij eijp p d d d F F K kk ij 2G eij d 3K ij 2G d d kk Sij
F σ ij J 2 I1 k 0 +
由
F kk
F Sij 2 Sij J2
得 d ij dSij d m ij d F 2G 3K
F ij Sij kk
Sij m Sij d d d ij 2G 3K ij 2 J2
2G
m为对应于 m体应变
拉梅常数 E (1 )(1 2 )
xy
2
x 3 m 2G x y 3 m 2G y z 3 m 2G z xy 2G xy G xy
yz zx
2 2
2G
G
E 2(1 )
2G
基本方程 yz 2G yz G yz zx 2G zx G zx
张量形式
张量形式
ij ij
弹塑性力学第四章 弹性本构关系
E K 3(1 2 )
(4.36) (4.37) (4.38)
K称为体积弹性模量，简称体积模量。
因此
q
sm
K
,em
sm
3K
1 3 1 1 ex e x e m ( sx sm) sm sx E E 3K 2G
1 ey e y e m sy 2G
1 eij sij 2G
(4.40)
1 eij sij 2G 1 em sm 3K
(4.41)
用应变表示应力：
或：
各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
• 材料的应力与应变关系需通过实验确定的。 • 本构方程实际是应力与应变关系实验结果的数学 描述。 • 由于实验的局限性，通常由简单载荷实验获得应 力与应变关系结果，建立描述相应的数学模型， 再将数学模型用于复杂载荷情况的分析。（用一 定实验验证结果）
• 例如：材料单轴拉伸应力-应变z e m sz 2G
1 1 1 1 yz s yz exy e xy xy sxy eyz e yz 2G 2G 2G 2G
1 1 exz e xz xz sxz 2G 2G
整理以上六个式子，得 整理以上六个式子，得
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个 因此应力偏张量形式的广义虎克定律，即
物理方程：
s ij 3 1 3 e ij s ij s m ij s m ij E E 2G E
(4.36) (4.37) (4.38)
K称为体积弹性模量，简称体积模量。
因此
q
sm
K
,em
sm
3K
1 3 1 1 ex e x e m ( sx sm) sm sx E E 3K 2G
1 ey e y e m sy 2G
1 eij sij 2G
(4.40)
1 eij sij 2G 1 em sm 3K
(4.41)
用应变表示应力：
或：
各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
• 材料的应力与应变关系需通过实验确定的。 • 本构方程实际是应力与应变关系实验结果的数学 描述。 • 由于实验的局限性，通常由简单载荷实验获得应 力与应变关系结果，建立描述相应的数学模型， 再将数学模型用于复杂载荷情况的分析。（用一 定实验验证结果）
• 例如：材料单轴拉伸应力-应变z e m sz 2G
1 1 1 1 yz s yz exy e xy xy sxy eyz e yz 2G 2G 2G 2G
1 1 exz e xz xz sxz 2G 2G
整理以上六个式子，得 整理以上六个式子，得
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个 因此应力偏张量形式的广义虎克定律，即
物理方程：
s ij 3 1 3 e ij s ij s m ij s m ij E E 2G E
金属材料弹性塑性本构关系解析
金属材料弹性塑性本构关系解析金属材料是工程领域中常用的材料之一，具有优良的强度和韧性。
材料的力学行为对设计和制造过程中的性能和可靠性有着重要影响。
因此，对金属材料的力学行为进行解析是非常重要的。
弹性塑性理论是描述金属材料力学行为的基础。
材料的弹性是指在外力作用下，金属可以发生一定的形变，但在去除外力后能够完全恢复原状的性质。
而塑性则是指金属在外力作用下可以发生形变，并保持一定程度的留存。
弹性塑性本构关系是描述金属材料力学行为的数学模型。
本构关系描述了材料的应力-应变关系，即在给定应力下，材料的应变响应。
常见的本构关系有线弹性模型、柯西模型、带硬化的本构模型等。
线弹性模型是最简单的本构模型之一。
它假设应力与应变之间的关系为线性，即材料的应力随应变的变化呈线性关系。
然而，在实际应用中，金属材料的线弹性行为较为有限，只能描述较小的应力应变范围。
相比之下，柯西模型是一种更为复杂的本构模型。
它采用了非线性的弹性本构关系，能更准确地描述金属材料的力学行为。
柯西模型可以考虑材料的应变硬化效应，即当金属材料受到塑性变形时，其硬度会增加，使得应力-应变关系不再是线性的。
带硬化的本构模型是在柯西模型的基础上引入了塑性硬化理论。
塑性硬化理论认为，金属材料在应力作用下会出现晶格滑移和位错运动，导致塑性变形。
这些变形会引起材料内部的晶粒发生变化，使得材料的硬度增加。
带硬化的本构模型可以更好地描述金属材料的变形行为。
解析金属材料的弹性塑性本构关系主要有两种方法：实验法和数值模拟法。
实验法通过对金属材料进行力学试验，如拉伸试验、压缩试验等，测量应力-应变曲线，从而得到材料的弹性塑性本构关系。
数值模拟法则借助计算机软件，通过建立数学模型和力学方程，模拟金属材料的力学行为，从而得到材料的应力-应变关系。
在工程领域中，正确解析金属材料的弹性塑性本构关系对设计和制造过程至关重要。
它不仅可以预测材料在外力作用下的变形行为，还可以指导工程师选择适当的金属材料，并优化材料的成形和加工过程。
塑性力学第五章本构关系
作用，在其原有的应力状态之上，缓慢地施加并卸除一组附加应力，在
这附加应力的施加和卸除的循环内，外部作用所做的功是非负的。
应力循环的过程：
单元体在应力状态 io下j 处于平衡。
ij d ij
ij
在单元体上施加一附加力，使应力达到 ，ij
刚好在加载面上，即开始发生塑性变形。
o ij
继续加载至 ij d i，j 在这期间，将产生
（5-17）
WD
故（5-17）式写成
（
0 ij
ij
i0j）d
e ij
0
WD
（
0 ij
ij
i0j）d
p ij
0
（5-18）
在整个应力循环中，只在应力从 到ij ij d的ij 过程中产生塑性应变。
当 d ij为小量时，上述积分变为：
WD
（ ij
1 2
d ij
i0j）d
p ij
0
（5-19）
由Hooke定律， 由Drucker公设，
d ij
d
e ij
d
p ij
d
e ij
d ij
2G
3
E
d mij
d
p ij
d
ij
（5-30）
（5-31）
（5-32）
精品资料
本构关系
进入塑性阶段后，应变(yìngbiàn)增量可以分解为弹性部分和塑性部分。
d ij
d
e ij
d
p ij
由Hooke定律(dìnglǜd)，iej
p ij
d
ij
（5-23）
精品资料
本构关系
§5.3 加载、卸载(xiè zǎi)准则
弹塑性力学-弹塑性本构关系
0 0 p
W D ( ij ij ) d ij 0
0 p
由图(a)可知，对于弹性性质不随加载面改变的非耦合情况，外 部作用在应变循环内做功WI和应力循环所作的外部功之间仅差 一个正的附加项： 1
d
p
d
p
2
因此可将应变循环所作的外部功，写成
WI WD 1 2 d ij d
d
p
2 3
d e ij d e ij
p
p
m ises : q s H ( d W
p
)[ 或 H ( d
p
p
)] 0
p
tresca : m ax s H ( d W
)[ 或 H ( d
)] 0
在应力空间中，这种后 继屈服面的大小 只与最大 的应力状态有关，而与中 间的加载路径无关。在右 图中，路径1与路径2的最 终应力 状态都刚好对应于 加载过程中最大应力状态， 因此两者的最终后继屈服 是一样的；而路径3的最 终后继屈服面由加载路径 中最大应力状态来定。
0
p
ij
0
ij
0
W D ( ij a d ij ij ) d
0
p
ij
0
1 a
1 2
当 ij ij时 , 略 去 无 穷 小 量
0
( ij ij ) d ij 0
0 p
屈服面的外凸性 塑性应变增量方向 与加载曲面正交
当
0 ij
( ij , H ) F ( I 1 , J 2 , J 3 ) K 0 初始屈服面 硬化系数
p p
t r e s c a 、 vo n m ises 、 M － C K H ( d W ) 或 H ( d
W D ( ij ij ) d ij 0
0 p
由图(a)可知，对于弹性性质不随加载面改变的非耦合情况，外 部作用在应变循环内做功WI和应力循环所作的外部功之间仅差 一个正的附加项： 1
d
p
d
p
2
因此可将应变循环所作的外部功，写成
WI WD 1 2 d ij d
d
p
2 3
d e ij d e ij
p
p
m ises : q s H ( d W
p
)[ 或 H ( d
p
p
)] 0
p
tresca : m ax s H ( d W
)[ 或 H ( d
)] 0
在应力空间中，这种后 继屈服面的大小 只与最大 的应力状态有关，而与中 间的加载路径无关。在右 图中，路径1与路径2的最 终应力 状态都刚好对应于 加载过程中最大应力状态， 因此两者的最终后继屈服 是一样的；而路径3的最 终后继屈服面由加载路径 中最大应力状态来定。
0
p
ij
0
ij
0
W D ( ij a d ij ij ) d
0
p
ij
0
1 a
1 2
当 ij ij时 , 略 去 无 穷 小 量
0
( ij ij ) d ij 0
0 p
屈服面的外凸性 塑性应变增量方向 与加载曲面正交
当
0 ij
( ij , H ) F ( I 1 , J 2 , J 3 ) K 0 初始屈服面 硬化系数
p p
t r e s c a 、 vo n m ises 、 M － C K H ( d W ) 或 H ( d
最新7.弹塑性力学--塑性本构关系汇总
f g J2 k
Cep ijkl
ij kl
ik jl
il jk
k2
sij skl
d ij
C d ep ijkl kl
d x
d
y
d
d z d xy
d
yz
d zx
d x
d y
d
d d
z xy
d
yz
d zx
C ep ijkl
Ce ijkl
Cp ijkl
6
1.理想塑性材料的增量本构关系
f g 相关联流动
塑性应变大小 塑性应变方向
对于强化材料
f
ij
d ij
0
d ij 在
f
ij
方向上的投影，反映了塑性应变增量的大小。
可假设：
d
1 h
f
ij
d ij
d
p ij
1 h
f
ij
f
kl
d kl
如何确定？
f
ij d ij
f ij k
16
2. 硬化材料的增量塑性本构关系
f ij ,ij , k 0
sx2 sysx
Cp ijkl
G k2
szsx
sxy sx
s
yz
sx
szxsx
sxsy
s
2 y
szsy
sxy sy
syz sy
szx sy
sxsz
sysz
s
2 z
sxy sz
syz sz
szx sz
sx sxy sy sxy sz sxy sx2y syz sxy szx sxy
sx syz
第四章 弹塑性体的本构理论
第二部分弹塑性问题的有限元法第四章弹塑性体的本构理论第五章弹塑性体的有限元法第四章弹塑性体的本构理论4-1塑性力学的基本内容和地位塑性力学是有三大部分组成的：1) 塑性本构理论，研究弹塑性体的应力和应变之间的关系；2) 极限分析，研究刚塑性体的应力变形场，包括滑移线理论和上下限法；3) 安定分析，研究弹塑性体在低周交变载荷作用下结构的安定性问题。
塑性力学虽然是建立在实验和假设基础之上的，但其理论本身是优美的，甚至能够以公理化的方法来建立整个塑性力学体系。
塑性力学是最简单的材料非线性学科，有很多其它更复杂的学科，如损伤力学、粘塑性力学等，都是借用塑性本构理论体系而发展起来的。
4-2关于材料性质和变形特性的假定材料性质的假定1)材料是连续介质，即材料内部无细观缺陷；2)非粘性的，即在本构关系中，没有时间效应；3)材料具有无限韧性，即具有无限变形的可能，不会出现断裂。
常常根据材料在单向应力状态下的σ-ε曲线，将弹塑性材料作以下分类：硬化弹塑性材料理想弹塑性材料弹塑性本构理论研究的是前三种类型的材料，但要注意对于应变软化材料，经典弹塑性理论尚存在不少问题。
变形行为假定 1)应力空间中存在一初始屈服面，当应力点位于屈服面以内时，应力和应变增量的是线性的；只有当应力点达到屈服面时，材料才可能开始出现屈服，即开始产生塑性变形。
因此初始屈服面界定了首次屈服的应力组合，可表示为()00=σf(1)2) 随着塑性变形的产生和积累，屈服面可能在应力空间中发生变化而产生后继屈服面，也称作加载面。
对于硬化材料加载面随着塑性变形的积累将不断扩张，对于理想弹塑性材料加载面就是初始屈服面，它始终保持不变，对于软化材料随着塑性变形的积累加载面将不断收缩。
因此加载面实际上界定了曾经发生过屈服的物质点的弹性范围，当该点的应力位于加载面之内变化时，不会产生新的塑性变形，应力增量与应变增量的关系是线性的。
只有当应力点再次达到该加载面时，才可能产生新的塑性变形。
第三章弹塑性本构关系
O
张量（应力偏张量）的主方向保持不变，
这种加载方式称为简单加载或比例加载。 后继屈服曲面
在简单加载过程中，一点的应力状态在
(加载曲面)
应力空间中将沿矢径 移动，如图所示。
在复杂加载时，一点的应力张量各
分量不按比例增加， 在改变，应力张量
和应力偏张量的主方向也随之改变。一
点应力状态在应力空间中的运动轨迹就
第三章 弹塑性本构关系
3.1塑性位势理论 3.2硬化规律 3.3 弹塑性本构关系
3.1 塑性位势理论流动法则
模型三要素
屈服条件 流动法则
硬化规律
判断何时 达到屈服
屈服后塑性应变 增量的方向，也 即各分量的比值
决定给定的应力 增量引起的塑性 应变增量大小
本节内容
3.1.1 加载与卸载准则
1 加载曲面(后继屈服面)
0 ij
)d
e
ij
0
0 ij
于是有：
WD WDp
( ij
0 ij
)d
p
ij
0
0 ij
(3) 德鲁克塑性公设的重要推论
WD WDp
( ij
0 ij
)d
p
ij
化时，称之为卸载过程，如果用φ (σij,Hα)=0表示后继屈服
条件，则：
卸载：ddH
0 0
ij
d ij
0
d
n
0
中性变载：ddH0 0 ijd ij
0
d
n
弹塑性力学本构关系1资料.
在
平面上任取一点，坐标为 (1, 2 , 3 )
它代表一个应力状态，对应的应力张量分量为 ij
相应的平均应力为 m 易见有
m
1 2
3
3
0
将应力张量分解为应力球张量和应力偏张量，即
ij m ij sij sij
上式表明，与此应力状态相应的应力球张量为零，应力张量
等于应力偏张量。 平面上每一点对应的应力张量是应力偏张量。
• Drucker把它引伸到复杂应力 情况,这就是Drucker公设.
0 d p 0
ij
0 ij
d
p ij
0
d d p 0
第二式中的等号适用于理想 塑性材料.
d
ij
d
p ij
0
Drucker公设在塑性力学中有
重要意义.
屈服面的外凸性和塑性应变增量的法向性
•我们如将塑性应变空间与应力空间重合起来,由Drucker公 设的第一式, 把它看成是两个矢量的点积.
在应力空间中代表一曲面，此曲面称为屈服曲面。
屈服曲面内的点满足不等式
f (1, 2,3) c 时，代表弹性状态。 屈服曲面上及屈服曲面外的点满足 f (1, 2,3) c
时，代表塑性状态。因此，屈服曲面是弹、塑性状态的分界面。
4．2．3 等倾线与 平面
1.等倾线 在应力空间中，过坐标原点与三个坐标轴成相同倾角的直线 叫等倾线。
PR线上每一点都代表一个应力状态。 PR线上的点有相同的应力偏张量和不同的应力球张量。
因为应力球张量不影响屈服，所以如果P点在屈服曲面上， 那么PR线上所有点都应该在屈服面上。因此屈服曲面实际上 是一个柱面，并且柱面的母线平行于等倾线OL
P
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
松比）。
塑性材料受外部作用的反应和变形的历史有关（可称为历 史相关性或路径相关性），本构关系应写成增量关系。
应力空间表述的弹塑性本构关系
韧性（塑性）金属材料单向拉伸试验曲线如下 图示意
强度极限
b
屈服上限
L y
U y
e
屈服下限
弹性极限
强化段
软化段 卸载
残余变形
弹性变形
y
y
卸载、反向加载 包辛格效应
屈服面随内变量改变的规律称强化规律。由 材料试验的资料可建立各种强化模型，目前广 泛采用的有：等向强化；随动强化两种模型。
等 向 强
初始屈服面
2
B
f 0(ij ) 0 B
2
C A o1
化
o A 1
o
1
C
D
随
弹性
动
f 0 (ij ) 0
强 化
后继屈服面
f
( ij
,
p ij
,
k)
0
等向强化认为屈服面形状不变，只是作均匀
称后继屈服面，f
(
ij
,
p ij
,
k
)
0
。
如果一点应力的 f (ij ,ipj,,则k)此 点0 处于弹性状态，如
果
f (，ij则,处ipj ,于k)塑 0性状态。
式变张中形量的为i量j间应。存ip力j在张如和ip量j 下k，关统系称为ipj为塑内性变应量ip力j 。张其D量i中j，klkkp与l为塑标ipj 性志应永变久
d ij
Dt ijkl
d
kl
式中 Ditjk为l 切线弹性张量，形式上仍可表为
Dt ijkl
2Gt t 1 2t
ij kl
2Gt ik lj
但其中的弹性系数Gt,μt也不是常数，也是应变或应力的函
数，分别称为切线弹性系数。可将它们看作与一定应力
（或应变）水平对应的切线常数（切线剪切模量和切线泊
在应力增量dσij作用下，应变增量dεij 可分
成弹性和塑性两部分。
d ij
d
p ij
d
e ij
d ij
D d ep ijkl kl
Dt ijkl
2Gt t 1 2t
ij kl
2Gt ik lj
切线弹性张量
e p
d e
A
B
d d
p
p ij
D p ijkl kl
e p p
d e d p d
g
(
ij
,
p ij
,
k
)
0
。塑性应变增量
可由势函数给出：
d
p ij
g,ij
d
因此正交（相d关 ip）j。流对f动正, i准j交d则准。则认，为塑塑性性流势动就方是向屈垂服直面于，
屈服面，加、卸载准则取决于非负的尺度因子dλ， 它大于零，表示加载，等于零，表示其他情况。
4）弹塑性本构关系
在上述概念基础上，下面讨论材料非线性分 析的核心问题——正交流动弹塑性本构关系。
的扩张，后继屈服面仅与一个和内变量有关的
参数 有关，可表为：
f
(
ij
,
p ij
,
k
)
f
0 ( ij ) (k)
0
随动强化则认为屈服面大小和形状不变，仅
是整体地在应力空间中作平动，其后继屈服面
可表为：
f
(
ij
,
p ij
,
k)
f
0 ( ij
p ij
)
0
多数材料的屈服面介于两者间。如果应力空
间中应力方向变化不大，等向强化与实际较符
塑性加载
中性变载 塑性卸载
2-1）理想弹塑性材料
由于此时屈服面大小和形状不随内变量发展
而改变，因此屈服面为 f 0 ( ij。) 用0 公式表示理 想弹塑性材料的加卸载准则为：
0 卸载，弹性 l1 f ,ij d ij 0 加载，塑性
2-2) 具有强化的弹塑性材料
0
l1 f ,ij d ij 0
反向屈服点
1) 屈服准则
判断材料处于弹性还是塑性的准则，称为屈服条件
或塑性条件。弹性和塑性区的分界面称为屈服面。
从自然状态第一次进入屈服的屈服条件称初始屈服
条件，产生塑性变形后的屈服条件称后继屈服条件。
初始屈服条件可表为：f 0 (ij ) 0 ，它只与当前应力状
态有关。初始屈服条件称初始屈服面，后继屈服条件
合。它的数学处理简单，故应用较广。但当需
考虑循环荷载下耗能时，随动强化可反应包辛
格效应，因此应该用它。
2）塑性状态的加载和卸载准则
在外部作用下应变点仍在屈服面上，并有新 的塑性变形发生，此时称这个过程为塑性加载。
如果应变点离开屈服面退回弹性区，反应是 纯弹性的，此过程称塑性卸载。
应变点不离开屈服面，又无新的塑性变形发 生，此时称中性变载。Leabharlann 0卸载，弹性 中性变载，塑性
加载，塑性
塑性加载
中性变载 f ,ij
f ,ij 塑性加载
卸载 f 0
卸载 后继面 f 0
理想弹塑性材料 等向强化弹塑性材料
中性变载 f ,ij 加 载 后继面
f 0卸载 卸载
随动强化弹塑性材料
3）流动准则
在塑性力学中，认为材料进入塑性后存在一个势函
数（简称塑性势）
但其中的弹性系数Gs,μs不再是常数，它们是应变或应力的函数，
分别称为割线弹性系数。可将它们看作与一定应力（或应变）水平
对应的割线常数（割线剪切模量和割线泊松比）。
例如对混凝土，Andenaes等依据实验给出，
八面体正应力、切应力和八面体线应变、角应
变间关系为 octσoct
GKtt
oct 3K s oct oct Gs oct
一般是根据材料的力学试验通过拟合来得到的。
在有限元分析中有两种应用形式：全量形和增量形本构关系。
全量形式本构关系
全量本构关系的表达形式和线性弹性情况相同，也即
ij
Ds ijkl kl
式中
Ds ijkl
为割线弹性张量，形式上它仍可表为
Ds ijkl
2Gs s 1 2s
ij kl
2Gs ik lj
e
e ij
Dijkl kl
d d e d p
d
p ij
Dijkl
d
p kl
d
e ij
Dijkl d kl
应力、应变关系示意d ij
d
e ij
- dipj
Dijkld
e kl
k（又称硬化参数）有多种取法，可以是塑性功、塑性体
并有 Gs G
1
a
oct
B c
m
KGss
K G εoct
s
K G e oct
s
(c oct ) p
OCT
1 3
( 1
2
3)
OCT
2 3
2 12
2 23
2 31
8
其中G、K分别为初始切线剪切和体积模量，
B c
为混凝土单轴抗压强度，a、m、c和p为由试验
确定的常数。
增量形式本构关系
增量本构关系的表达形式为
同济大学土木学院桥梁工程系
有限单元法II
——2012级硕士生课程
同济大学土木工程桥梁工程系
弹塑性本构关系简介
1 弹塑性力学有关内容简介 2 几种常用弹塑性材料模型简介 3 弹塑性矩阵的建立步骤
材料非线性有限元分析
弹塑性问题的有限单元法
本构关系
一般情况下本构关系可表为
ij fij ( kl )