离散系统的状态空间描述状态方程
线性离散系统状态方程的解

Z变换法(2/7)
在Z反变换中对标量函数存在下述公式和性质:
Z 1 1 /(1 az 1 ) a k Z {W1 ( z )W2 ( z )} w1 (k i ) w2 (i )
1 i 0 k
Βιβλιοθήκη 其中W1(z)和W2(z)分别为w1(k)和w2(k)的Z变换。 将上述公式推广到向量函数和矩阵函数,则可得
离散卷积
Z变换法(3/7)—例3-14
因此,离散系统的状态方程的解为:
x(k ) G k x(0) G k j 1Hu( j )
j 0
k 1
该表达式与前面递推法求解结果一致。 例 已知某系统的状态方程和初始状态分别为 1 0 1 1 x(k 1) x( k ) u ( k ) x(0) 0.16 1 1 1
( k 1 , k0 ) G ( k ) ( k , k 0 ) ( k0 , k0 ) I
其解为
(k , k0 ) G(k 1)G(k 2)...G(k0 ) , k k0
线性时变离散系统状态方程的解(3/6)
与线性定常离散系统类似,线性时变离散系统的状态求解公 式可用迭代法证明。 对线性时变离散系统的状态方程,依次令k= k0, k0+1, k0+2, …,从而有
2. 引入状态转移矩阵概念和表示之后,线性连续系统和线 性离散系统的状态方程的求解公式在形式上一致,都由 零输入响应和零状态响应叠加组成, 只是相应的零状态响应在形式上略有不同,一为求 积分(卷积),一为求和(离散卷积),但本质是一致的。 3. 在由输入所引起的状态响应中,第k个时刻的状态只取决 于此采样时刻以前的输入采样值,而与该时刻的输入采 样值u(k)无关。
自动控制原理状态空间法

目录
• 引言 • 状态空间法基础 • 线性系统的状态空间表示 • 状态反馈与极点配置 • 最优控制理论 • 离散系Biblioteka 的状态空间表示01引言
状态空间法的定义
状态空间法是一种基于状态变量描述线性时不变系统的方法,通过建立系 统的状态方程和输出方程来描述系统的动态行为。
状态变量是能够完全描述系统内部状态的变量,可以是系统的物理量或抽 象的数学变量。
最优控制问题
在满足一定约束条件下,寻找一个控制输入, 使得被控系统的某个性能指标达到最优。
性能指标
通常为系统状态或输出函数的积分,如时间加 权或能量加权等。
约束条件
包括系统动态方程、初始状态、控制输入和终端状态等。
线性二次调节器问题
线性二次调节器问题是最优控制问题的一个特例, 其性能指标为系统状态向量的二次范数。
THANKS
状态方程描述了系统内部状态变量之间的动态关系,而输出方程则描述了 系统输出与状态变量之间的关系。
状态空间法的重要性
1
状态空间法提供了系统分析和设计的统一框架, 可以用于线性时不变系统的各种分析和设计问题。
2
通过状态空间法,可以方便地实现系统的状态反 馈控制、最优控制、鲁棒控制等控制策略。
3
状态空间法具有直观性和易于实现的特点,能够 直接反映系统的动态行为,便于理解和分析。
02
状态空间法基础
状态与状态变量
状态
系统在某一时刻的状态是由系统 的所有内部变量共同决定的。
状态变量
描述系统状态的变量,通常选择 系统的输入、输出和内部变量作 为状态变量。
状态方程的建立
根据系统的物理或数学模型,通过适 当的方法建立状态方程。
离散系统的状态空间表达式

(1)连续系统:用微分方程来表示,采用拉 普拉斯变换传递函数进行分析。
离散系统:用差分方程来描述,用Z变 换脉冲传递函数进行分析。
因此,离散系统的状态空间表达式可通过差 分方程或脉冲传递函数。
(2)离散系统的信号采用数字形式,输入和 输出都是脉冲序列或数字序列。计算机控制 系统属离散系统。
试写出其状态方程和输出方程 。
解:
x1 (k 1) 0
1
0 x1(k) 0
x2
(k
1)
0
0
1
x
2
(k
)
0
u(k)
x3 (k 1) 6 5 2x3 (k) 1
x1(k)
y(k) x(k) 1
0
0x2 (k)
x3 (k )
例1.10 已知 y(k+3)+2y(k+2)+5y(k+1) +6y(k)=3u(k+2)+2u(k+1)+6u(k)
脉冲传递函数:
G(z)
Y (z) u(z)
bmzm bm1zm1 b1z b0 zn an1zn1 a1z a0
二 、状态方程的建立
1、由差分方程
设T=1 输入仅有(kT)项,b0=1 整个方程可以写为: y(k+n)+an-1y(k+n-1)+……+a0y(k)=u(k) 设x1(k)=y(k) x2(k)=y(k+1)=x1(k+1) x3(k)=y(k+2)=x2(k+1) ……
xn(k)=y(k+n-1)=xn-1(k+1) xn(k+1)=y(k+n)=-a0 x1(k)-a1 x2(k)-
现代控制原理2-3离散系统

−T −T
−T
)
−T
z 2 − (1 + e −T ) z + e −T
)
0 x( k + 1) = −T -e
0 x ( k ) + u( k ) −T 1+ e 1 1
y( k ) = 1 − e −T − Te − T
T − 1 + e −T x( k )
x(k+1) = [I +TA]x(k) + TBu(k) G = I +TA H =TB
17
0 1 0 & 的近似离散化方程。 例2-13 求 x = x + 1 u 的近似离散化方程。 0 −2
解: G = I + TA = 1 0 + 0 − T = 1 − T 0 1 0 − 2T 0 1 − 2T
x( k + 1) = G ( k ) x( k ) + H ( k )u( k ) y( k ) = C ( k ) x ( k ) + D( k )u( k )
2
2.结构图 2.结构图
3
3.差分方程和脉冲传递函数与离散状态空间表 3.差分方程和脉冲传递函数与离散状态空间表 达式之间的转换 在单变量离散系统中, 在单变量离散系统中,数学模型分为差分方程 和脉冲传递函数两类, 和脉冲传递函数两类,它们与离散状态空间表达式 之间的变换,和连续系统分析相类似。 之间的变换,和连续系统分析相类似。 离散 差分方程 连续 D.E
x1 ( k ) y ( k ) = [1 −4 ] + u( k ) x2 ( k )
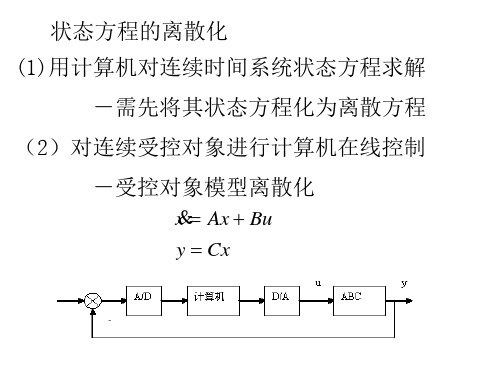
离散系统的状态空间描述

x1(k)
y(k) 1
0
0
x2
(k
)
x3 (k )
4 离散状态方程求解
1. 迭代法
离散状态方程的通式 x(k 1) Fx(k) Gu(k)
已知k=0时系统状态x(0)以及 k 0 k 之间各个时刻的输入量 u(0),u(1), ,u(k)
得到现时刻k的状态
k 1
x(k) F k x(0) F ki1Gu(i) i0
x1(k x2 (k
1) 1)
h1u (k ) h2u(k )
xn (k) xn1(k 1) hn1u(k)
则可得到离散系统状态方程,且有:
式中
h0 b0 h1 b1 a1h0
hh32
b2 b3
a1h1 a1h2
a2h0 a2h1
a3h0
hn bn a1hn1 a2hn2
I
AT
I
AT 2
I
AT 3
I
AT L 1
I
AT L
计算项数L可由精度要求确定。
输入矩阵
G(T ) T eAt Bdt (eAT I ) A1B T AiT i B
0
i0 (i 1)!
T
I
AT 2
I
AT 3IAT L 1 NhomakorabeaI
AT L
B
2. 状态转移阵的求解——(2)拉普拉斯变换
可得方程 (有不同方法)
x3(k 1) 0.9x3(k) e(k)
u(k) 0.01x3(k) 0.9e(k)
(2)广义被控对象部分:
被控对象连 续状态方程
x1 x2
0 0
1 1
x1 x2
离散化的状态方程
T ∫0
I ⋅ B ⋅ dt = BT
结论:上式为近似计算方法 例2.6 已知时变系统
0 5(1 − e −5t ) 5 5e −5t u ɺ x= x + −5t −5t 0 5(e − 1) 0 5(1 − e )
试将它离散化,并求出输入和初始条件分别为
0, x(0) = 0时,方程在采样时刻的近似解 u (t ) = 0 1
1 (3)H(T) = ∫ 0 0
T T 1/ 2(1−e )0 1 dt= ∫0 −2t e 1 0 −2t −2t
x 1 [( k + 1)T] x 1 (kT ) (4) = [G (T)] x (kT ) + [H (kT) U (kT)] x 2 [( k + 1)T] 2
归纳:将连续状态方程离散化步骤
1、求Φ(t )=e = L [ SI − A] 2、G(T ) = Φ(T ) = Φ(t ) t = T T At 3、求H (T ) = ∫0 e Bdt 4、求x[(k + 1)T ] = G(T ) x(kT ) + H (T )u (kT )
At
−1
−1
例2.5已知控制对象满足 1 x + 0u,求其离散化方程 ɺ = 0 x 0 1 −2
系统离散状态方程(T=0.1) 可见T较小时, x1[(k + 1)T ] 0.9 0.1 x1(kT ) 0 = + r (kT ) 两种方法得 x2[(k + 1)T ] − 0.1 0.9 x2 (kT ) 0.1 状态空间表 x1(kT ) 达式近似相 输出y(kT ) = [1 0] 等。 x2 (kT ) 离散方程求解可按2.3递推法或Z变换求解
状态空间表达式

(28) 状态空间方程实现非唯一,书p28, 图1.16b求得其对应的传递函数为: (29)
为求得 令式(29)与式(26)相等,通过对 多项式系数的比较得: 故得: (30)
也可将式(30)写成式(31)的形式,以便记忆。 (31)
将上图a的每个积分器输出选作状念变最,如图所示,得这种结构下的 状态空间表达式:
解:
→
→
u
y
-
+
例: 解: 比例积分环节: → → u y +
例:
解:
综合惯性环节、积分环节模拟结构图得:
u
y
-
+
u
y
解:选积分器的输出为状态变量得:
u
y
状态方程:
输出方程:
状态空间表达式
1.3.2 从系统的机理出发建立状态空间表达式
一般常见的控制系统,按其能量属性,可分为电气、机械、机电、气动 液压、热力等系统。根据其物理规律,如基尔霍夫定律、牛顿定律、能量守 恒定律等,即可建立系统的状态方程。当指定系统的输出时,很容易写出系 统的输出方程。
同一系统,经非奇异变换后,得:
其特征方程为:
(44)
1.5.2 系统特征值的不变性及系统的不变量
1.系统特征值
式(43)与式(44)形式虽然不同,但实际是相等的,即系统的非奇异变换,其特征值是不变的。可以证明如下:
将特征方程写成多项式形式 由于特征 值全由特征多项式的系数 唯一确定,而特征值 经非奇异变换是不变的,那么这些系统 也是不变 的量。所以称特征多项式的系数为系统的不变量。
(3)有共轭复根时,以四阶系统其中有一对共轭复根为例,即 此时
1.6 从状态空间表达式求传递函数阵
1.6.1 传递函数(阵)
现代控制理论知识点汇总

1.状态空间表达式n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯:r n B ⨯:n m C ⨯:rm D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2.状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3.模拟结构图(积分器加法器比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4.状态空间表达式的建立1由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
2由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
③由描述系统的输入输出动态方程式(微分方程)或传递函数,建立系统的状态空间表达式,即实现问题。
实现是非唯一的。
方法:微分方程→系统函数→模拟结构图→状态空间表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u(k) H
D
z x(k 1)
x(k)
1
C
y(k)
G
2019/12/15
单位 如同连续系统中积分器和1/s的关系
迟延
5
3、Z传递函数(矩阵)和特征方程
1)离散系统的Z传递函数为: 零初始条件下,脉冲输出序列的z变换与输入脉冲序列的z 变换之比,称为系统的脉冲传递函数或Z传递函数。
整理上式得: Y (z) [C(zI G)1 H D]U(z) G(z)U(z)
所以Z传递矩阵为:G(z)=C(zI G)1 H D
3)离散系统的特征方程为: zI G 0
而此特征方程的根就是线性离散系统的极点,也是系统矩 阵G的特征值。
2019/12/15
7
4、将差分方程化为状态空间描述:或转换为Z传递函数,再求
c2
cn
x2
(kT
)
Du(kT
)
xn
(
kT
)
(T为采样周期,经常省去不写)
写成矩阵形式,得离散系统的状态空间描述:
x(k 1) Gx (k) Hu(k)
y(k) Cx(k) Du(k)
2019/12/15
4
2、线性定常离散系统状态空间描述的模拟结构图
2)系统中信号既有离散量,也有连续量。 描述方式:离散量部分用一阶差分方程描述 连续量部分用一阶微分方程描述,需要离散化。
2019/12/15
2
一、Z变换及相关理论知识
拉氏变换是分析、设计线性连续系统的主要数学工具。Z变 换是分析、设计线性离散控制系统的主要数学工具。
连续 输入信号
线性 系统
离散
2019/12/15
拉氏变换 S域代数 方程
微分 方程
直接 求解
时域 解
差分 方程
Z变换
Z域代数 方程
S域解 拉
氏 反 变 换
Z 反 变 换
Z域解
3
二、离散系统的状态空间描述
1、线性定常离散系统的状态空间描述为:
x1(k 1)T g11 g12 g1n x1(kT ) h1
输出方程:
选择状态变量:x1(k) y(k)
x2 x3
( (
k k
) )
y(k y(k
1) 2)
xn(k) y(k n 1)
2019/12/15
8
化为一阶差分方程组:
x1(k 1) y(k 1) x2(k)
x2
(
k
1)
y(k
2019/12/15
10
2)差分方程的输入函数中包含高于一阶的差分项 y(k n) an1 y(k n 1) a0 y(k) bnu(k n) b0u(k)
x1(k) y(k) h0u(k)
选择状态变量:
x2 x3
( (
k k
G(z) Y(z) U(z)
用方框图表示为: U(z) G(z) Y (z)
2)MIMO离散系统的Z传递矩阵:
当初始状态 x(0) 0 时,对以下状态空间描述做Z变换:
x(k 1) Gx (k) Hu(k)
y(k) Cx(k) Du(k)
2019/12/15
6
得:
zX (z) GX(z) HU(z) Y(z) CX(z) DU(z)
) )
x1 ( k x2 ( k
1) 1)
h1u( k ) h2u( k )
xn(k) xn1(k 1) hn1u(k)
上式中:
h0 bn
h1 h2
bn1 bn2
an1h0 an1h1
an2h0
离散系统差分方程描述形式:
y(k n) an1 y(k n 1) a1 y(k 1) a0 y(k)
bnu(k n) bn1u(k n 1) b0u(k)
(k 0,1,2)
1)差分方程的输入函数中不包含高于一阶的差分项 y(k n) an1 y(k n 1) a1 y(k 1) a0 y(k) b0u(k)
2)
x3 ( k )
xn1(k 1) y(k n 1) xn(k)
xn
(
k
1)
y(k
n)
a0 y(k) a1 y(k 1) an1 y(k n 1) b0u(k)
a0 x1(k) a1x2(k) an1xn(k) b0u(k)
x2 ( k
1)T
g21
g22
g2n
x2
(
kT
)
h2
u(
kT
)
xn
(
k
1)T
gn1
gn2
gnn
xn
(
kT
)
hn
x1(kT )
状态方程:y(kT ) c1
y(k) x1(k)
2019/12/15
9
写成矩阵形式,得到离散系统的状态空间表达式:
x1(k 1) 0
x2(k 1)
0
10 01
0 x1(k) 0
x2 ( k )
0
0 u(k)
xn1
(
k
1)
0
0 01 来自 xn1(k
)
0
xn(k 1) a0 a1 an2 an1 xn(k) b0
x1(k)
y 1
0
0
x2
(
k
)
xn
(
k
)
第一节 线性离散时间系统 的状态空间描述
1. Z变换及相关理论知识 2. 离散时间系统的状态方程 3. 连续时间系统的离散化
2019/12/15
1
离散系统基本知识:
定义:在系统中,只要有一处信号不是时间t的连续函数,这种 系统就称为离散系统。
分类: 1)系统中所有信号均是离散量。 描述方式:一阶差分方程描述
