2020年最新2020年整理BP神经网络监督控制系统设计
智能控制课设-BP神经网络的简要介绍

智能控制论文BP神经网络的简要介绍学院:电气工程学院专业班级:xxx姓名: xxx 学号:xxxBP神经网络的简要介绍BP(Back Propagation)神经网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP 神经网络模型拓扑结构包括输入层(input)、隐层(hidden layer)和输出层(output layer)。
人工神经网络就是模拟人思维的第二种方式。
这是一个非线性动力学系统,其特色在于信息的分布式存储和并行协同处理。
虽然单个神经元的结构极其简单,功能有限,但大量神经元构成的网络系统所能实现的行为却是极其丰富多彩的。
人工神经网络首先要以一定的学习准则进行学习,然后才能工作。
现以人工神经网络对手写“A”、“B”两个字母的识别为例进行说明,规定当“A”输入网络时,应该输出“1”,而当输入为“B”时,输出为“0”。
所以网络学习的准则应该是:如果网络作出错误的的判决,则通过网络的学习,应使得网络减少下次犯同样错误的可能性。
首先,给网络的各连接权值赋予(0,1)区间内的随机值,将“A”所对应的图象模式输入给网络,网络将输入模式加权求和、与门限比较、再进行非线性运算,得到网络的输出。
在此情况下,网络输出为“1”和“0”的概率各为50%,也就是说是完全随机的。
这时如果输出为“1”(结果正确),则使连接权值增大,以便使网络再次遇到“A”模式输入时,仍然能作出正确的判断。
如果输出为“0”(即结果错误),则把网络连接权值朝着减小综合输入加权值的方向调整,其目的在于使网络下次再遇到“A”模式输入时,减小犯同样错误的可能性。
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID(Proportional-Integral-Derivative)控制器是一种常用的自动控制器,其通过测量系统的输出偏差,根据比例、积分和微分三个因素来控制系统的输出。
然而,传统的PID控制器难以适应复杂、非线性和时变的系统,对于这类系统的控制,神经网络已经被证明是一种有效的方法。
本文将介绍基于BP神经网络的PID控制系统设计。
二、BP神经网络简介BP神经网络(Backpropagation Neural Network)是一种常用的前向反馈型人工神经网络,其通过反向传播算法来训练网络参数,从而实现对输入数据的学习和预测。
BP神经网络拥有多层神经元,每个神经元都与下一层神经元相连,并通过权重和阈值来传递和处理输入信息。
三、PID控制器简介PID控制器由比例(Proportional)、积分(Integral)和微分(Derivative)三个部分组成,其控制输出的公式为:u(t) = Kp * e(t) + Ki * ∑e(t)dt + Kd * de(t)/dt其中,u(t)为控制器的输出,Kp、Ki、Kd为控制器的三个参数,e(t)为系统的输出偏差,∑e(t)dt为偏差的积分项,de(t)/dt为偏差的微分项。
1.数据采集和预处理:首先需要采集系统的输入和输出数据,并对其进行预处理,包括数据归一化和滤波处理等。
2.神经网络设计和训练:根据系统的输入和输出数据,设计BP神经网络的结构,并使用反向传播算法来训练网络参数。
在训练过程中,根据系统的输出偏差来调整比例、积分和微分三个参数。
3.PID控制器实现:根据训练得到的神经网络参数,实现PID控制器的功能。
在每个控制周期内,根据系统的输出偏差来计算PID控制器的输出,将其作为控制信号发送给被控制系统。
4.参数调优和性能评估:根据控制系统的实际情况,对PID控制器的参数进行调优,以提高系统的控制性能。
基于BP神经网络的PID控制器设计

基于BP神经网络的PID控制器设计PID控制器是一种常用的控制器,可以通过根据系统的误差、历史误差和误差的变化率来计算控制信号,从而实现对系统的控制。
传统的PID控制器可以通过调节PID参数来实现对系统动态特性的控制,但是参数调节过程往往需要经验和反复试验,而且很难实现对非线性系统的精确控制。
近年来,基于BP神经网络的PID控制器设计方法得到了广泛的关注。
BP神经网络是一种常用的人工神经网络模型,可以通过训练得到输入与输出之间的映射关系。
在PID控制器设计中,可以将误差、历史误差和误差的变化率作为BP神经网络的输入,将控制信号作为输出,通过训练神经网络来实现对控制信号的合理生成。
1.数据预处理:首先需要采集系统的输入输出数据,包括系统的误差、历史误差和误差的变化率以及相应的控制信号。
对这些数据进行归一化处理,以便神经网络能够更好地学习和训练。
2.网络结构设计:根据系统的特性和要求,设计BP神经网络的输入层、隐藏层和输出层的神经元数量。
通常情况下,隐藏层的神经元数量可以根据经验设置为输入层和输出层神经元数量的平均值。
3.训练网络:采用反向传播算法对神经网络进行训练,以获得输入和输出之间的映射关系。
在训练过程中,需要设置学习率和动量系数,并且根据训练误差的变化情况来确定训练的终止条件。
4.参数调整:将训练得到的神经网络与PID控制器相结合,根据神经网络的输出和系统的误差、历史误差和误差的变化率来计算控制信号,并通过对PID参数的调整来实现对系统的控制。
1.适应能力强:BP神经网络能够通过训练来学习系统的动态特性,从而实现对非线性系统的精确控制。
2.自适应性高:BP神经网络能够根据实时的系统状态来实时调整控制信号,从而实现对系统动态特性的自适应控制。
3.参数调节方便:通过BP神经网络的训练过程,可以直接得到系统的输入和输出之间的映射关系,从而减少了传统PID控制器中参数调节的工作量。
4.系统稳定性好:基于BP神经网络的PID控制器能够根据系统状态及时调整控制信号,从而提高了系统的稳定性和鲁棒性。
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID控制系统是目前工业控制中广泛应用的一种基本控制方法,它通过测量控制系统的偏差来调节系统的输出,以实现对控制对象的稳定控制。
然而,传统的PID控制器需要事先对系统建模,并进行参数调整,工作效果受到控制对象模型的准确性和外部干扰的影响。
而BP神经网络具有非线性映射、自适应性强、鲁棒性好等优点,可以有效地克服传统PID控制器的缺点。
因此,基于BP神经网络的PID控制系统设计成为当前研究的热点之一二、基于BP神经网络的PID控制系统设计理论1.PID控制器设计原理PID控制器是由比例环节(Proportional)、积分环节(Integral)和微分环节(Derivative)组成的控制器,其输出信号可以表示为:u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*(de(t)/dt),其中e(t)为控制系统的输入偏差,t为时间,Kp、Ki和Kd分别为比例系数、积分系数和微分系数。
2.BP神经网络理论BP神经网络是一种前馈型神经网络,通过反向传播算法对输入信号进行学习和训练,从而得到最优的网络结构和参数。
BP神经网络由输入层、隐层和输出层组成,其中每个神经元与上、下相邻层之间的神经元互相连接,并具有非线性的激活函数。
3.基于BP神经网络的PID控制系统设计理论基于BP神经网络的PID控制系统设计的核心思想是将BP神经网络作为PID控制器的自适应调节器,根据控制对象的输入信号和输出信号之间的误差进行训练和学习,通过调整BP神经网络的权重和阈值来实现PID 控制器的参数调节,从而提高控制系统的稳定性和鲁棒性。
三、基于BP神经网络的PID控制系统设计步骤1.系统建模首先,需要对待控制对象进行建模,获取其数学模型。
对于一些复杂的非线性系统,可以采用黑箱建模的方法,利用系统的输入和输出数据进行数据拟合,获取系统的数学模型。
2.BP神经网络训练将系统的数学模型作为BP神经网络的训练集,通过反向传播算法对BP神经网络进行训练,得到最优的网络结构和参数。
自适应神经网络控制系统设计与实现

自适应神经网络控制系统设计与实现随着现代科技的发展,各行各业对自适应神经网络的需求也越来越大。
自适应神经网络控制系统可以自主获取环境信息,根据环境变化实现自调节、自学习和自适应,从而提高系统控制的可靠性、稳定性和鲁棒性。
本文将介绍自适应神经网络控制系统设计的理论基础、实现过程和应用实例。
一、理论基础自适应神经网络控制系统由两大核心部分组成:神经网络和控制器。
神经网络可以根据输入输出数据模型自主学习,实现非线性映射函数的建立和自适应控制;控制器则根据实际系统特点进行参数调整和反馈控制,保证系统控制效果。
具体来说,自适应神经网络控制系统包括以下内容:1.神经网络模型:神经网络是自适应神经网络控制系统的核心部分,它可以处理环境输入的信息,实现对输出信号的调节和控制。
神经网络模型可以分为波形神经网络、径向基神经网络、多层感知器神经网络等多种类型,根据实际控制需要选择合适的模型。
2.控制器:控制器是自适应神经网络控制系统的关键组成部分,通过参数调节和反馈控制实现对神经网络的控制。
控制器的选择和设计应该考虑到受控系统的特点以及系统控制的目标要求。
3.训练算法:自适应神经网络控制系统的训练算法包括反向传播算法、共轭梯度算法、遗传算法等。
根据具体控制场景和神经网络模型的选择,可以选择相应的算法进行网络参数的优化和训练。
4.信号采集和处理:自适应神经网络控制系统需要对有效信号进行采集和处理,实现对环境输入信息的获取和分析。
信号处理可以使用滤波、降噪、去趋势等技术进行处理,以提高神经网络模型的可靠性和精度。
二、实现过程自适应神经网络控制系统的实现可以分为几个阶段:1.系统建模:对受控系统进行建模,确定系统的输入输出特性以及控制目标。
2.神经网络模型选择和建立:根据系统特点和控制目标选择合适的神经网络模型,建立网络结构并进行参数调节和训练。
3.控制器设计:根据实际控制需求,确定控制算法和控制器结构,并完成参数的设置和调节。
基于BP神经网络的网络控制系统调度

基于BP神经网络的网络控制系统调度李建;王亚刚;兰水古【期刊名称】《微型机与应用》【年(卷),期】2012(031)009【摘要】为了在复杂的网络环境下能更合理地分配网络资源,提出了利用BP神经网络,通过对网络调度器产生的历史和当前数据进行训练,预测调度器下周期可能产生的数据,进而对下一调度周期的死区大小进行调整。
实验仿真表明,所设计的反馈调度器能进一步改善网络控制系统的性能,进一步提高应对负载变化的能力。
%In order to allocate network resources in complex network environment, through training historical data and current data produced by network dispatcher, BP neural network is used to predict data probably produced by dispatcher during the next period. Therefore, it can resize the deadband of the next dispatching cycle. Simulation results show that the feedback scheduler can further improve the performance of NCS and the ability to cope with fluctuant workload.【总页数】4页(P50-52,55)【作者】李建;王亚刚;兰水古【作者单位】上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093【正文语种】中文【中图分类】TP273【相关文献】1.基于双参数模糊推理的网络控制系统调度策略 [J], 张明华;贾诺2.基于CAN总线网络控制系统的混合调度算法研究 [J], 李君;徐凤霞3.基于TrueTime的BP神经网络控制系统的仿真平台构建 [J], 高月芳;叶建锋;张薇4.基于BP神经网络的高速动车组网络控制系统时延研究 [J], 宋程; 王元东; 徐滨全5.基于Truetime的网络控制系统调度算法仿真比较 [J], 李君;徐凤霞;陆仲达因版权原因,仅展示原文概要,查看原文内容请购买。
BP神经网络在质量控制中的应用
BP神经网络在质量控制中的应用一、 BP神经网络简介(原理及作用)BP神经网络是一种按误差逆传播算法训练得到的多层前馈神经网络。
BP神经网络能学习和存贮大量的输入-输出模式映射关系,但是无必事前揭示此种映射关系的数学方程。
BP神经网络的学习方法是最速下降法,通过反向传播来不断调整神经网络的权值与阈值,使BP神经网络的误差平方和最小。
BP神经网络模型拓扑结构由输入层、隐层与输出层构成。
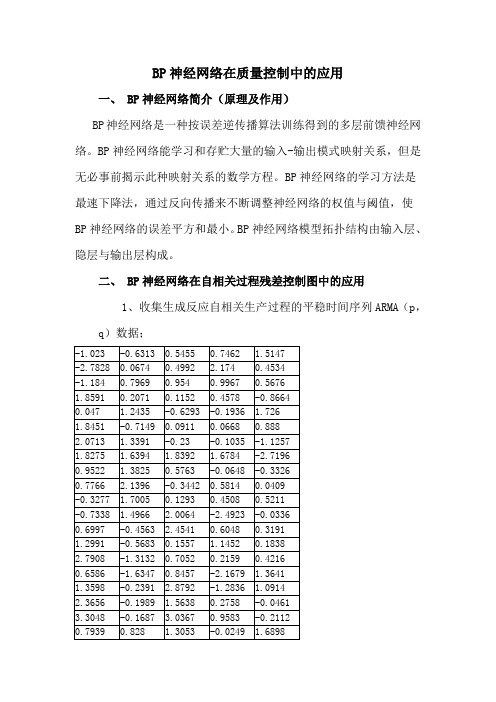
二、 BP神经网络在自相关过程残差控制图中的应用1、收集生成反应自相关生产过程的平稳时间序列ARMA(p,q)数据;-1.023 -0.6313 0.5455 0.7462 1.5147-2.7828 0.0674 0.4992 2.174 0.4534-1.184 0.7969 0.954 0.9967 0.56761.8591 0.2071 0.1152 0.4578 -0.86640.047 1.2435 -0.6293 -0.1936 1.7261.8451 -0.7149 0.0911 0.0668 0.8882.0713 1.3391 -0.23 -0.1035 -1.12571.8275 1.6394 1.8392 1.6784 -2.71960.9522 1.3825 0.5763 -0.0648 -0.33260.7766 2.1396 -0.3442 0.5814 0.0409-0.3277 1.7005 0.1293 0.4508 0.5211-0.7338 1.4966 2.0064 -2.4923 -0.03360.6997 -0.4563 2.4541 0.6048 0.31911.2991 -0.5683 0.1557 1.1452 0.18382.7908 -1.3132 0.7052 0.2159 0.42160.6586 -1.6347 0.8457 -2.1679 1.36411.3598 -0.23912.8792 -1.2836 1.09142.3656 -0.1989 1.5638 0.2758 -0.04613.3048 -0.1687 3.0367 0.9583 -0.21120.7939 0.828 1.3053 -0.0249 1.68982、用自相关或偏自相函数判断其自相性;自相关函数: C3滞后 ACF T LBQ1 0.402804 4.03 16.722 0.101053 0.88 17.783 0.013824 0.12 17.804 0.103236 0.89 18.935 0.010944 0.09 18.946 -0.085554 -0.73 19.747 -0.119216 -1.01 21.308 -0.077815 -0.66 21.979 0.039590 0.33 22.1410 0.144187 1.21 24.5011 0.266638 2.20 32.6512 0.101412 0.80 33.8413 -0.102219 -0.80 35.0714 -0.114110 -0.89 36.6115 -0.036642 -0.28 36.7716 -0.124414 -0.96 38.6517 -0.236740 -1.81 45.5418 -0.194370 -1.44 50.2419 -0.169470 -1.23 53.8520 -0.181176 -1.30 58.0421 -0.021112 -0.15 58.1022 0.031273 0.22 58.2323 -0.005770 -0.04 58.2324 -0.084652 -0.60 59.1925 -0.050194 -0.35 59.53C3 的自相关自相关函数拖尾偏自相关函数: C3滞后 PACF T1 0.402804 4.032 -0.073050 -0.733 -0.000516 -0.014 0.125802 1.265 -0.095023 -0.956 -0.075121 -0.757 -0.049732 -0.508 -0.025613 -0.269 0.100444 1.0010 0.129852 1.3011 0.212013 2.1212 -0.101057 -1.0113 -0.190027 -1.9014 -0.053501 -0.5415 -0.030070 -0.3016 -0.105012 -1.0517 -0.069409 -0.6918 0.014053 0.1419 -0.126045 -1.2620 -0.185761 -1.8621 0.090942 0.9122 -0.042419 -0.4223 -0.023667 -0.2424 0.012443 0.1225 -0.001695 -0.02C3 的偏自相关偏自相关拖尾3、用神经网络建立过程的时间序列模型并计算出残差序列程序如下:clear all;clc;x=randn(100,1);y=zeros(100,1);a(1)=0.2;a(2)=0.6;b=0.3;y(1)=a(1)+x(1);for n=2:100y(n)=a(1)+a(2)*y(n-1)+x(n)-b*x(n-1);endyfor j=1:100y(j)=(y(j)-min(y))/(max(y)-min(y)); %归一化处理endfor i=1:97P(:,i)=[y(i),y(i+1),y(i+2)]endT=y(4:100)T=T'net=newff([0 1;0 1;0 1],[5,1],{'tansig','logsig'},'traingd'); net.trainParam.epochs=15000;net.trainParam.goal=0.01;net.trainParam.lr=0.1;net=train(net,P,T);figure(1);title('原时间序列“+”与预测时间序列“*”')plot(1:length(T),T,'+-',1:length(t1),t1,'-*')e=T-t1e=e'figure(2);%title('残差时间序列')plot(1:length(T),e,'+-')figure(3);title('残差直方图')histfit(e)0.2366 -0.1103 -0.1347 0.0955 -0.2325-0.2022 0.0982 -0.2208 -0.0528 0.4290.1373 -0.3146 0.0455 0.0304 -0.0720.0421 0.141 -0.1098 -0.033 -0.26720.1186 -0.0118 0.2591 0.3786 -0.528-0.0244 0.0773 -0.1636 -0.1394 -0.3301-0.0334 0.2119 -0.2117 0.1149 -0.2868-0.1985 0.106 0.0163 0.0122 0.1711-0.1802 0.102 0.2793 -0.5816 -0.19590.1525 -0.2415 0.2005 0.3676 0.00480.0551 -0.1765 -0.1366 0.0093 -0.34290.2826 -0.2238 -0.0147 0.0284 0.082-0.1092 -0.1699 -0.0041 -0.499 0.42020.0545 0.091 0.3523 -0.0172 -0.06470.1789 -0.0488 0.038 -0.0458 -0.54320.3439 -0.0845 0.3745 0.1863 -0.3494-0.0301 0.1056 0.1167 -0.0359 0.3699-0.2519 -0.059 0.0907 0.3310.061 -0.0509 0.3782 -0.04710.0566 0.0478 0.1333 0.1134、用minitab软件作残差序列的均值-极差控制图三、BP神经网络在过程运行状态监测中的应用,程序如下:clear all;clc;p=load('p.txt')p=p't=load('t.txt');t=t'net=newff(minmax(p),[13,5],{'tansig','purelin'},'trainlm');net.trainParam.epochs=1500;net.trainParam.goal=0.01;net.trainParam.lr=0.1;net=train(net,p,t);t1=sim(net,p)t1=sim(net,p)IW=net.IW{1,1}LW=net.LW{2,1}b1=net.b{1,1}b2=net.b{2,1}[max_t1,index]=max(abs(t1))a=index[max_t,index]=max(t)b=indexc=a-bIW =0.0640 -0.5101 0.2478 -0.4403 -0.8649 0.18960.0006 -0.1196 0.0979 -0.0657 -0.2098 0.0668-0.0053 0.0410 -0.0702 0.8421 0.3494 -0.09370.0094 -0.1322 -0.5518 0.1521 -0.1917 0.27660.0013 0.0185 -0.2406 -0.7263 -0.0901 0.0174-0.0009 -0.0356 0.8021 0.3594 -0.2108 -0.0675 -0.0024 0.0267 0.1138 -1.5195 0.2918 -0.04690.0044 -0.0443 -0.0628 0.2705 -0.4481 0.0552-0.0037 0.0238 1.1816 0.1243 -1.0187 -0.2500-0.0052 0.0371 0.0803 0.1021 0.3516 -0.0855-0.0055 0.0768 0.0038 -1.2757 0.7139 -0.04330.0068 -0.0272 0.3743 -0.1718 0.3354 -0.35750.0344 -0.2047 -0.0930 0.2048 -0.2176 -0.1199LW =Columns 1 through 90.1376 0.0869 -0.1398 0.4112 -0.2075 0.0110 -0.0962 0.5371 0.0239-0.1376 0.0611 1.3396 -0.5504 0.4445 0.9519 0.4120 0.0603 0.00970.3503 -0.1868 -0.9021 0.1470 0.3105 -1.0563 0.8960 -1.0719 -1.51000.0572 0.1904 -0.3101 -1.2424 0.1771 0.1718 -1.0742 -0.32351.5496-0.1858 -0.5161 -0.0474 -0.1411 -0.3059 0.0009 0.0243 -0.2128 -0.0040Columns 10 through 130.4351 0.2808 -0.3877 0.2027-1.4555 0.0508 0.3579 0.10241.9025 -2.3776 -1.2106 -0.3322-1.4560 1.7723 -0.5082 0.2653-0.0842 -0.0927 -0.3173 0.7161b1 =0.99525.36374.57663.265113.45791.44588.72311.8922-5.27307.5620-8.57463.43124.1175b2 =0.7094-0.0903-0.0619-0.0755-0.5540四、总结。
基于BP神经网络的PID控制系统设计汇总

基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法,利用BP神经网络对被控对象进行在线辨识和控制。
基于BP神经网络学习算法设计出两个神经网络模型:一个利用神经网络(NNM)对非线性映射的逼近能力,对被控对象进行辨识,另一个构成具有PID结构的控制器(NNC)。
通过神经网络NNM的在线学习和修正,产生对被控对象输出的预测作用,然后由网络NNC实施控制作用,从而实现对辨识对象的PID控制。
在利用神经网络对系统进行辨识时,选用白噪声信号作为系统的输入信号,以提高系统的辨识精度;另外,为了得到神经网络控制器的初始化权值,本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。
在设计过程中运用MATLAB语言工具箱进行编程,并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。
仿真结果表明了利用神经网络对系统进行辨识的有效性,并用经辨识所得到的输出值取代系统的实际输出值,利用神经网络NNC对系统进行控制,获得了满意的控制效果。
关键词:神经网络,BP学习算法,自适应,参数优化,辨识1 综述PID调节器从问世至今已历经了半个多世纪,在这几十年中,人们为它的发展和推广做出了巨大的努力,使之成为工业过程控制中主要的和可靠的技术工具。
近几十年来,现代控制理论迅速发展,出现了许多先进的控制算法,但到目前为止,即使在微处理技术迅速发展的今天,过程控制中大部分控制规律都未能离开PID,这充分说明PID控制仍具有很强的生命力。
过程工业控制中实际应用最多的仍是常规的PID控制算法,这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点,且PID算法原理简明,参数物理意义明确,理论分析体系完整,为广大控制工程师所熟悉。
但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳,整定的好坏不但会影响到控制质量,而且还会影响到控制器的性能。
PID控制中一个至关重要的问题,就是控制器三参数(比例系数、积分时间、微分时间)的整定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级:控制5班 学号:2111504213 姓名:张睿设计一个神经网络监督控制系统,被控对象为:321000()s 87.35s 10470G s s=++ 采样时间1,输入信号为方波信号,幅值0.5,频率2。
设计一个神经网络监督控制系统,并采用遗传算法进行神经网络参数及权值的优化设计,并进行仿真。
需要说明控制系统结构,遗传算法优化网络的具体步骤,并对仿真结果做出分析。
解决过程及思路如下:1 网络算法以第p 个样本为例,用于训练的网络结构如图1所示。
图1 具有一个隐含层和输出层的神经网络结构网络的学习算法如下: (1)信息的正向传播隐含层神经元的输入为所有输入加权之和,j ij i ix w x =∑隐层神经元的输出'j x 采用S 函数激发j x ,则'1()1j j j x x f x e-==+ '''(1)j j j jx x x x ∂=-∂ 输出层的神经元输出为jk输入层隐含层输出层…j 'jx'k jk j jx w x =∑网络输出与理想输出误差为()k k e k x x =-误差性能指标函数为211()2N p k E e k ==∑上式的N 表示网络输出层的个数。
(2)利用梯度下降法调整各层间权值的反向传播 对从第j 个输入到第k 个输出的权值有:'11()NNp k jk k j k k jkjk E x w e e k x w w ηηη==∂∂∆=-==∂∂∑∑ 其中,η为学习速率,[]0,1η∈。
1时刻网络权值为(1)()jk jk jk w k w k w +=+∆对从第i 个输入到第j 个输出的权值有:1Np kij k k ijijE x w e w w ηη=∂∂∆=-=∂∂∑式中,''''(1)j jk k jk j j i ij j j ijx x x x w x x x w x x w ∂∂∂∂=⋅⋅=⋅⋅-⋅∂∂∂∂ 1时刻网络权值为(1)()ij ij ij w k w k w +=+∆2.网络的监督控制系统结构设计的网络监督控制系统结构如图2所示。
图2 神经网络监督控制在网络结构中,取网络的输入为r (k ),实际输出为y (k ),控制输出为(k ),隐层神经元的输出采用S 函数激发,'1()1j j j x x f x e-==+ 网络的权向量为W1, W2 的网络输出为控制律为u(k)(k)(k)采用梯度下降法调整网络的权值为神经网络权值的调整过程为3.遗传算法对网络权值的优化过程 (1) 取逼近总步骤为100 (2)终止代数:80 (3)样本个数:30 (4)交叉概率:0.70 (5)二进制编码长度:10(6)变异概率:0.001-[1:1]*0.001(7)用于优化的网络结构为:1-4-1 1 1,2,3 ,4 (8)网络权值W1的取值范围为:[-11] (9)网络权值W2的取值范围为:[-0.50.5](10)取网络误差绝对值为参数选择的最小目标函数:∑=jjj x w '2k yn )('222)()(jj k j j x k e w x k e w E w ⋅⋅-=∂∂⋅⋅-=∂∂-=∆ηηηij n ij ij w y k e w E w ∂∂⋅⋅-=∂∂-=∆)(ηη))1()(()()1(22222--+∆+=+k w k w w k w k w j j j j j α))1()(()()1(--+∆+=+k w k w w k w k w ij ij ij ij ij α式中,N 为逼近的总步骤,(i )为第i 步网络逼近误差。
(11)需要优化参数为:],,,,,,,,,,,[p 232221201716151413121110j w w w w w w w w w w w w 4 遗传算法优化网络权值的步骤(1)初始化种群;(2)计算其适应值,保留最优个体,判断是否达到最优解; (3)交叉、变异产生新个体;(4)重新计算种群中每个个体的适应值并保留最优个体;(5)交叉、变异前后的种群放在一起进行二人竞赛选择法,直到填满新的种群;(6)转2)直到找到最优解。
5 仿真结果监督网络遗传算法优化程序包括3部分,即遗传算法优化程序,网络逼近函数程序和网络逼近测试程序。
输入信号为r (t )=0.5*((2*2**k*)采样时间0.001s ,η=0.30,0.0511. 经遗传算法优化后,对象p 的值为[-0.2160,0.7576,0.5230,0.98630.0714,0.2551,0.69110.3627,0.2146,0.3338 ,-0.0875,-0.0582]仿真结果图:790800810820830840850860870880890TimesB e s t J图3 代价函数J 的优化过程00.10.20.30.40.50.60.70.80.91time(s)r a n d y图4 方波位置跟踪0.10.20.30.40.50.60.70.80.91time(s)y n0.10.20.30.40.50.60.70.80.91time(s)u p0.10.20.30.40.50.60.70.80.91time(s)u 00.10.20.30.40.50.60.70.80.91time(s)e r r o r图5 网络及总控制器输出的比较以及误差曲线结论:采用遗专算法可以实现网络参数初始值的优化,节约计算量。
并由仿真结果可知,其误差大部分趋于0,但局部有三个地区的误差比较大,产生原因可能与遗传算法的运行参数有关。
代码:[]()0.001;0.05;0.30;(1000,[1,87.35,10470]);2d(,'z');[](,'v');1=02=0;1=02=0;1=0;0;[0,0]';[0,0,0,0]';[0,0,0,0]';[0,0,0,0]';25;0.3;w1=[p(1)(2)(3)(4)(5)(6)(7)(8)]; w1_111_21;w2=[p(9)(10)(11)(12)];w2_122_22_1;1:1:1000(k)*;1;1r(k)=0.5*((2*2**k*));2r(k)=0.5*((3*2**k*));y(k)(2)*1(3)*2(2)*1(3)*2;e(k)(k)(k);(k);1:1:4I(j)'*w1();(j)=1/(1((j)));(k)2'*; %(k)*x(1)*x(2);2;1u(k)(k);2u(k)(k)(k);u(k)>=10u(k)=10;u(k)<10u(k)10;400u(k)(k)+5.0;(k)(k)(k);w22_1+(*(k))**(w2_12_2);1:1:4(j)((j))/(1((j)))^2;1=0*w1;1:1:21:1:41()(k)**(j)*w2(j)*x(i); w11_11*(w1_11_2);w1_21_11_11;w2_22_12_12;21;1(k);21;x(1)(k); Px(2)=(e(k)1)/0.05; D1(k);0;1:1:100(i)((i));50*(i);;2、;;;0.001;0.05;0.30;25;0.3;(1000,[1,87.35,10470]);2d(,'z');[](,'v');1;1w1=[p(1)(2)(3)(4)(5)(6)(7)(8)]; w2=[p(9)(10)(11)(12)];2w1(2,4);w2(1,4);w1_111_21;w2_122_22_1;1=02=0;1=02=0;[0,0]';[0,0,0,0]';[0,0,0,0]';[0,0,0,0]';0.001;1:1:1000(k)*;1;1r(k)=0.5*((2*2**k*));2r(k)=0.5*((3*2**k*));y(k)(2)*1(3)*2(2)*1(3)*2;e(k)(k)(k);1:1:4I(j)'*w1();(j)=1/(1((j)));(k)2'*; %(k)*x(1)*x(2);2;1u(k)(k);2u(k)(k)(k);u(k)>=10u(k)=10;u(k)<10u(k)10;400u(k)(k)+6.0;(k)(k)(k);w22_1+(*(k))**(w2_12_2);1:1:4(j)((j))/(1((j)))^2;1=0*w1;1:1:21:1:41()(k)**(j)*w2(j)*x(i); w11_11*(w1_11_2);w1_21_11_11;w2_22_12_12;21;1(k);21;1(k);x(1)(k); Px(2)=(e(k)1)/0.05; D1(k);(1);(,'r','b');('(s)')('r y');(2);(411);(,'b');('(s)')('');(412);(,'k');('(s)')('');(413);(,'r');('(s)')('u');(414);(,'b');('(s)')('');3、( );;30; % ȺÌå×ܸöÌåÊýÁ¿80; % ÔÊÐí×î´óµü´ú´ÎÊý10; % ÿ¸ö±äÁ¿ÓµÓеÄȾɫÌåÊýÁ¿1:1:8(i)(1); % Á¬½ÓȨֵµÄ×î´óÖµ(i)(1); % ȨֵµÄ×îСֵ9:1:12(i)=0.5*(1); % ãÐÖµµÄ×î´óÖµ(i)0.5*(1); % ãÐÖµµÄ×îСֵ% ¶ÔËùÇó²ÎÊý½øÐгõʼ¶þ½øÖƱàÂë((,12*)); % ³õʼ»¯¸öÌå´úÂ루ȾɫÌ壩% ÒÅ´«Éñ¾-ÍøÂçѵÁ·¿ªÊ¼0;1:1();1:1(s,:);1:1:12(j)=0;((1)*1:1*);1:1(j)(j)(i)*2^(1);f()=((j)(j))*(j)/1023(j);;(s,:);[]();(s);[]();()(1);();1005;1;[]();(); % ()((),:); % (m), m ()p%****** 2 : ******();()*;();1;1:11:1(i)(,:)((i),:);1;%************ 3 : ************ 0.70;(20*);1:2:(1);>:1:20()(1);(1)();(,:);;%************ 4: **************0.001-[1:1]*(0.001); ,1:11:1:12*;>()0()=1;()=0;(,:)(,:);;%*******************************************************(G)(1);();('')(' J');p;。
