粘弹性滞弹性及高温蠕变
1.2 粘弹性和滞弹性

图l-11所示,当突然施加一应力σo于 拉伸试样时,试样立即沿0A线产生瞬时 应变Oa。如果低于材料的微量塑性变形 抗力,则应变Oa只是材料总弹性应变OH 中的一部分。应变aH只是在σo长期保 持下逐渐产生的,aH对应的时间过程为 图1-11中的ab曲线。
恒定应力σo
卸载时,如果速度也比较大,则当应力下降为零时, 只有应变eH部分立即消逝掉,而应变eO是在卸载后逐渐去 除的,这部分应变对应的时间过程为图中的cd曲线。
三.动态粘弹性(滞后、内耗)
在正弦或其它周期性变化的外力作用下,聚合物粘弹性的表现. 高聚物作为结构材料在实际应用时,往往受到交变力的作 用。如轮胎、传送皮带、橡齿轮。
研究动态力学行为的实际意义?
用作结构材料的聚合物许多是在交变的力场中使用 , 因 此必须掌握作用力频率对材料使用性能的影响。 如外力的作用频率从 0→100~1000 周,对橡胶的力学性 能相当于温度降低 20~40℃,那么在-50℃还保持高弹性 的橡胶,到-20℃就变的脆而硬了。 塑料的玻璃化温度在动态条件下,比静态来的高,就 是说在动态条件下工作的塑料零件要比静态时更耐热 , 因此不能依据静态下的实验数据来估计聚合物制品在动 态条件下的性能。
对于未交联橡胶
Cross-linking polymer Linear polymer
0e
0
t
玻璃态 高弹态
粘流态
不同温度下的应力松弛曲线 t
t
不同聚合物的应力松弛曲线
高分子链的构象重排和分子链滑移是导致材料蠕变和应力松 弛的根本原因。 如果T很高(>>Tg),链运动摩擦阻力很小,应力很快松弛掉了, 所以观察不到,反之,内摩擦阻力很大,链段运动能力差,应力 松弛慢,也观察不到.只有在Tg温度附近的几十度的范围内应 力松弛现象比较明显.(链由蜷曲变为伸展,以消耗外力)
1.2 粘弹性和滞弹性解析

t1
t2
t
0 应力
E1 普弹形变模量
图1 理想弹性体(瞬时蠕变)普弹形变
b.高弹形变
链段运动
(t) 0 (t<t1) t/
(t)
t
外力除去, 逐渐回复
(t)=
E
( 1 e ) 松弛时间
2
=2/E2
0 (t→) E2-高弹模量 特点:高弹形变是逐渐回复的.
t1
t2
图l-11所示,当突然施加一应力σo于 拉伸试样时,试样立即沿0A线产生瞬时 应变Oa。如果低于材料的微量塑性变形 抗力,则应变Oa只是材料总弹性应变OH 中的一部分。应变aH只是在σo长期保 持下逐渐产生的,aH对应的时间过程为 图1-11中的ab曲线。
ห้องสมุดไป่ตู้
恒定应力σo
卸载时,如果速度也比较大,则当应力下降为零时, 只有应变eH部分立即消逝掉,而应变eO是在卸载后逐渐去 除的,这部分应变对应的时间过程为图中的cd曲线。
线形非晶态聚合物在Tg以上单轴 拉伸的典型蠕变及回复曲线
2. 聚合物的蠕变现象
从分子运动和变化的角度来看,蠕变过程分为: a.普弹形变 (t)
从分子运动的角度解释:
材料受到外力的作用,链内的键长和 键角立刻发生变化,产生的形变很小, 我们称它普弹形变.
(t)
t
外力除去, 立即完全回复
0
E1
当聚合物受力时,以上三种形变同时发生聚 合物的总形变方程:
2+3
1 2 3
t
( t ) 1 2 3 -t
1
(1 e ) t E1 E2 3
线形非晶态聚合物的蠕变及回复曲线
粘弹性蠕变松弛

粘弹性蠕变松弛首先想要澄清一下粘弹性的概念,很多人认为粘弹性就是蠕变或者松弛,这不完全对。
描述粘弹性更为准确的方式应该叫做率依赖,就是本构方程中当时刻应力不仅与当时刻的应变有关,还与当时刻应变速率有关(如果还与以往的历史相关的话,就叫做粘弹塑性了)。
而蠕变与松弛只是当应力或者应变维持在定值的时候,产生的应变增加与应力减小的现象。
分清这个概念很重要,因为在aba qus中定义这些行为的方式是截然不同的,具体来说明一下粘弹性与蠕变(松弛)吧。
1粘弹性狭义上来讲粘弹性是材料在加载过程中应力变化与应变,应变率之间关系的描述,也可以称为率依赖问题。
如果你想要实现冲击载荷作用下粘弹性材料的反应,这个问题属于率依赖问题,你可以使用两种方法定义材料的力学响应,这就是微分型与积分性本构,虽然微分型本构比较直观明了,平衡方程也好获得,但是一般常用的还是基于遗传积分的积分性本构,毕竟微分型本构在基于时间或者频率离散的有限元方法中难于准确实现。
一般的粘弹性本构模型就那几个,比如maxwell,kelvin,剩下的就是它们的串联与并联,如果你有个新模型是n个ma xwell串联的,你可以通过遗传积分公式轻易获得松弛模量与蠕变模量。
然而这里又会引出一个新的问题,学过粘弹性力学的人都知道,只要涉及到粘弹性问题势必逃不过一个数学工具——laplace变换,在这里不想多讲laplace变换的内容,大家对于这个数学工具应该都很清楚(如果是初学的话推荐两本书与粘弹性,laplace变化有关的教材,一个是周光泉的粘弹性理论,还有一本南京工学院,即东南大学出版的《积分变化这本书》),只谈谈它的物理意义吧,其实laplace变换的最核心思想在于时域与频域的转化,一个在时域内控制方程为偏微分方程的转化到频域内就是常微分方程了,对于粘弹性的松弛模量与蠕变模量也是这个道理,它存在着时域表示方法与频域表示方法。
它们在abaqus中的关键字为:*VISCOELASTIC, TIME= define1*VISCOELASTIC, FREQUENCY= defi ne2其中define1,define2分别为数据定义方式,详细的可参考Abaqus Analysis User's Manual18.7 Viscoelasticity。
材料在高温下的力学性能(蠕变、松弛)

材料在高温下的力学性能(蠕变、松弛)第7章材料在高温下的力学性能7.1 材料在高温下力学性能的特点有许多机件是在高温下工作的,如高压锅炉,蒸汽轮机、燃气轮机、以及化工厂的反应容器等,对于这些机件的性能要求,就不能以常温下的力学性能来衡量。
材料在高温下的力学性能明显地不同于室温。
首先,材料在高温将发生蠕变现象。
即在应力恒定的情况下,材料在应力的持续作用下不断地发生变形。
这样,材料在高温下的强度便与载荷作用的时间有关了。
载荷作用的时间越长,引起一定变形速率(如)或变形量的形变抗力(蠕变极限)以及断裂抗力(持久强度)就越低。
粗略地说,发生蠕变现象的温度,对金属材料约为T>0.3-0.4TM ;(TM为材料的熔点以绝对温度K计);对陶瓷约为T>0.4-0.5TM ;对高分子材料为T>Tg,Tg为玻璃化温度,多数高分子材料在室温下就发生蠕变。
由于蠕变的产生,我们就不能笼统地说材料在某一高温下其强度是多少,因为高温强度与时间这一因素有关。
而材料在常温下的强度是不考虑时间因素的。
除非试验时加载的应变速率非常高。
材料在高温下不仅强度降低,而且塑性也降低。
应变速率越低,载荷作用时间越长,塑性降低得越显著。
和蠕变现象相伴随的还有高温应力松驰。
一个紧固螺栓在高温长时间作用下,其初始预紧力逐渐下降,这种现象也是由蠕变造成的。
另外,蠕变还会产生疲劳损伤,使高温疲劳强度下降,为此,必须研究蠕变和疲劳的交互作用。
材料在高温下的力学性能特点都是和蠕变过程紧密相连的。
第一,材料在变形时首先总是引起形变强化,蠕变之所以能发生,必然还伴随着一个变形的软化过程,这个软化过程就是高温回复。
第二,蠕变的变形机制必然与在常温下的不同。
材料在常温下的变形可通过位错的滑动产生滑移和孪晶两种变形型式。
而在高温下位错还可通过攀移,使位错遇到障碍时作垂直于滑移面的运动,如图7-0所示。
这样位错便不会阻塞在障碍面前,而使得变形能继续下去,这就是一个变形的软化过程。
1.2 粘弹性和滞弹性
图l-11所示,当突然施加一应力σo于拉 伸试样时,试样立即沿0A线产生瞬时 应变Oa。如果低于材料的微量塑性变 形抗力,则应变Oa只是材料总弹性应 变OH中的一部分。应变aH只是在σo长 期保持下逐渐产生的,aH对应的时间 过程为图1-11中的ab曲线。
恒定应力σo
卸载时,如果速度也比较大,则当应力下降为零时,只 有应变eH部分立即消逝掉,而应变eO是在卸载后逐渐去 除的,这部分应变对应的时间过程为图中的cd曲线。
b.交联:可以防止分子间的相对滑移。如橡胶采用硫化 交联的办法来防止由蠕变产生分子间滑移造成的不可 逆形变。
2. 聚合物的蠕变现象
从分子运动和变化的角度来看,蠕变过程分为: a.普弹形变
(t)
从分子运动的角度解释:
材料受到外力的作用,链内的键长和 键角立刻发生变化,产生的形变很小, 我们称它普弹形变.
(t)
t
外力除去, 立即完全回复
t1
t2 t
图1 理想弹性体(瞬时蠕变)普弹形变
0
E1
0 应力
E1 普弹形变模量
§1-4 粘弹性与滞弹性
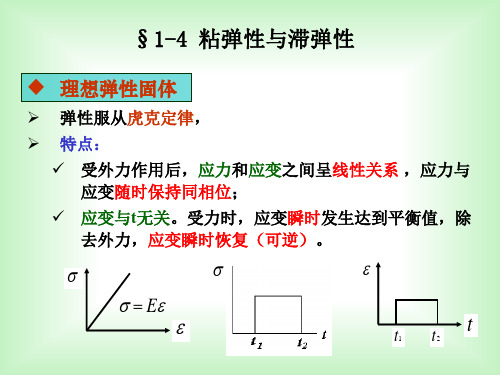
理想弹性固体
➢ 弹性服从虎克定律, ➢ 特点:
✓ 受外力作用后,应力和应变之间呈线性关系 ,应力与 应变随时保持同相位;
✓ 应变与t无关。受力时,应变瞬时发生达到平衡值,除 去外力,应变瞬时恢复(可逆)。
E
t
t1
t2
滞弹性
➢ 实际上,绝大多数固体材料的弹性行为很难满足理想弹 性行为。一般都表现出非理想弹性性质,即实际固体的 应力与应变不是单值对应关系,往往有一个时间的滞后 现象。
(t)
t
不可回复
t1 t2
t
图3 理想粘性流动蠕变
材料力学性能课后答案

1.解释下列名词①滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
②弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
③循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
④包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
⑤塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
⑥韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力⑦加工硬化:金属材料在再结晶温度以下塑性变形时 ,由于晶粒发生滑移 , 出现位错的缠结,使晶粒拉长、破碎和纤维化,使金属的强度和硬度升高,塑性和韧性降低的现象。
⑧解理断裂:解理断裂是在正应力作用产生的一种穿晶断裂,即断裂面沿一定的晶面(即解理面)分离。
2.解释下列力学性能指标的意义弹性模量);(2)ζ p(规定非比例伸长应力)、ζ e(弹性极限)、ζ s(屈服强度)、ζ (屈服强度);(3)ζ b(抗拉强度);(4)n(加工硬化指数); (5)δ (断后伸长率)、ψ (断面收缩率)4.常用的标准试样有 5 倍和10倍,其延伸率分别用δ 5 和δ 10 表示,说明为什么δ 5>δ 10。
答:对于韧性金属材料,它的塑性变形量大于均匀塑性变形量,所以对于它的式样的比例,尺寸越短,它的断后伸长率越大。
5.某汽车弹簧,在未装满时已变形到最大位置,卸载后可完全恢复到原来状态;另一汽车弹簧,使用一段时间后,发现弹簧弓形越来越小,即产生了塑性变形,而且塑性变形量越来越大。
试分析这两种故障的本质及改变措施。
答:(1)未装满载时已变形到最大位置:弹簧弹性极限不够导致弹性比功小;(2)使用一段时间后,发现弹簧弓形越来越小,即产生了塑性变形,这是构件材料的弹性比功不足引起的故障,可以通过热处理或合金化提高材料的弹性极限(或屈服极限),或者更换屈服强度更高的材料。
根据受力应变特征材料分为:脆性材料,延性材料,弹性材料。

1.根据受力应变特征材料分为:脆性材料,延性材料,弹性材料。
2.材料受载荷后形变的三个阶段:弹性形变,塑形形变,断裂3.弹性模量:材料在弹性变形阶段内正应力和对应的正应变的比值。
意义:反映材料抵抗应变的能力,是原子间结合强度的标志。
影响因素(键合方式,晶体结构,温度,复相的弹性模量)。
机理:对于足够小的形变应力与应变成线性关系,系数为弹性模量,物理本质是原子间结合力抵抗外力的宏观表现,弹性系数和弹性模量是反映原子间结合强度的标志。
4.滞弹性:固体材料的应变产生与消除需要有限的时间,这种与时间有关的弹性称为滞弹性。
衡量指标:应力弛豫和应力蠕变。
应力弛豫:在持续外力作用下发生形变的物体在总变形值保持不变的情况下,徐变变形增加使物体的内部应力随时间延续而逐渐减少的现象。
应力蠕变:固体材料在恒定荷载下变形随时间延续而缓慢增加的不平衡过程。
5.塑性形变指一种在外力移去后不能回复的形变。
滑移系统:滑移方向和滑移面。
产生条件:a-(几何条件)面间距大滑移矢量小b(静电条件)每个面上是同种电荷原子,相对滑移面上的电荷相反。
无机非材料不产生原因:a.滑移系统少;b.(位错运动激活能大)位错运动需要克服的势垒比较大,位错运动难以实现。
施加应力,或者由于滑移系统少无法达到临界剪应力,或者在达到临界剪应力之前就导致断裂;c.伯格斯矢量大。
6.高温蠕变定义:材料在高温下长时间受到小应力作用出现蠕变现象。
影响因素:温度和应力。
机理:a晶格机理(位错攀移理论,由于热运动位错线处一列原子移去或移入,位错线向上移一个滑移面。
)b扩散蠕变理论(空位扩散流动,应力造成浓度差,导致晶粒沿受拉方向伸长或缩短引起形变)c晶界机理(多晶体蠕变,高温下晶界相对滑动,剪应力松弛,有利蠕变。
低温下晶界本身是位错源,不利蠕变)7.理论断裂强度:理论下材料所能承受的最大应力。
实际强度:实际情况中材料在外加应力作用下,沿垂直外力方向拉断所需应力。
8.断裂韧性:是材料的固有性能,由材料的组成和显微结构所决定,是材料的本征参数。
粘弹性材料的力学性能研究

粘弹性材料的力学性能研究粘弹性材料是一类具有特殊力学性能的材料,在各个领域都有广泛的应用。
本文将探讨粘弹性材料的力学性能研究,包括其定义、测试方法以及应用领域。
一、粘弹性材料的定义粘弹性材料是指既具有粘性(Viscosity)又具有弹性(Elasticity)的材料。
它们在受到外力作用时,既可以发生形变,又能恢复到原始状态。
粘弹性材料的力学行为常常被描述为粘滞弹性现象。
二、粘弹性材料力学性能的测试方法1. 粘滞性测试:粘滞性是指材料抵抗形变的能力,常用的测试方法包括剪切黏度测试、拉伸黏度测试等。
2. 弹性性测试:弹性是指材料在受力后能够恢复到原始状态的能力。
弹性性测试可以通过应力-应变曲线、弹性模量等进行。
3. 剪切模量测试:剪切模量是指材料在剪切载荷下承受的应力和应变之间的比值。
剪切模量的测试可以通过剪切试验获得。
4. 蠕变测试:蠕变是指材料在持续应力作用下发生的时间依赖性形变。
蠕变测试可以通过施加恒定应力后观察材料的变形情况。
三、粘弹性材料的应用领域1. 医学领域:粘弹性材料在医学领域中应用广泛,常用于仿生组织材料、医疗器械等的研发。
2. 建筑领域:粘弹性材料在建筑领域中的应用主要涉及隔震、减振等方面,可以提高建筑物对地震等外界震动的抵抗能力。
3. 航空航天领域:粘弹性材料常用于飞机、航天器等高性能结构件的制造。
其粘滞性、弹性等特性能够提高材料在复杂环境下的可靠性。
4. 汽车工业:粘弹性材料在汽车工业中的应用主要包括减震、隔声、密封等方面,可以提高汽车的舒适性和安全性。
5. 电子产品:粘弹性材料在电子产品中的应用主要涉及散热、缓冲、保护等方面,可以提高电子产品的性能和可靠性。
结论粘弹性材料的力学性能研究对于材料的开发与应用具有重要意义。
通过合理的测试方法,可以深入了解粘弹性材料的特性,并将其应用于各个领域,为社会的发展和进步做出贡献。
参考文献:1. 李同伟,胡力耀,王香,等. 粘弹性材料力学性能研究进展[J]. 北京航空航天大学学报. 2019(1).2. 李春波,李国强,徐建平. 粘弹性材料力学性能测试方法研究[D]. 东北大学. 2018.3. Ponnurangam R, Sethuraman S, Palsule S. Viscoelastic properties of engineering materials—A review[J]. Materials Science and Engineering: A. 2012, 556: 1-16.4. Zener C. Internal friction in solids: a comprehensive solution of a simple 'beetle's problem[J]. Physical Review. 1948, 73(7): 652-660.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蠕变减速阶段
瞬时发生的和时间没有关系
oa段形变是瞬时发生的和时间没有关系 第一阶段蠕变ab,蠕变减速阶段 A为常数。
低温时n=1, ;
高温时n=2/3, 第二阶段蠕变bc,稳态蠕变阶段 (常数) 成正比 应变与时间
第三阶段蠕变cd,加速蠕变阶段。
应变率随时间增加,最后到d点断裂
高温蠕变理论
标准线性固体的力学行为
蠕变:施加恒定应力, 应变随时间而增加
(b)
驰豫:施加恒定应变, 应力随时间而减小
(c)
标准线性固体应力-应变与时间的关系
§1-3
无机材料的高温变
蠕变:当对材料施加恒定应力σ0时,其
应变随时间而增加的现象
典型的蠕变曲线
加速蠕变阶段。应变率随时 间增加,最后到d点断裂
应变与时间成正比
思考题:
• 高温蠕变的位错运动理论的含义? • 影响蠕变的因素有哪些?怎样影响? • 玻璃相的粘度与哪些因素有关?
粘弹性与滞弹性
理 想弹 性:受到外力后,平衡形变是瞬时达到的与 时间无关。 理想粘弹性:受到外力后,形变是随时间线性发展的。 粘 弹 性:非晶体、多晶体在比较小的应力时可以 同时表现出弹性和粘性 滞 弹 性:无机固体和金属这种与时间有关的弹性
滞弹性或粘弹性的力学模型
σ弹2 ε弹2 E2
σ弹1 ε弹1 E1 σ粘 ε粘 η
粘弹性和滞弹性
• 粘弹性------材料在比较小的应力作用下,可以同时表现出 弹性和粘性。与理想的弹性应变比较,后者应力和应变不 随时间滞后,前者有一定的滞后。 • 滞弹性------与时间有关的弹性,即E(t) 。 • 对于蠕变,应力和应变有 Ec(t)=0/(t) • 对于弛豫,应力和应变有 Er(t)= (t)/ 0 • 也即弹性模量随时间而变化,并不是一个常数。 • 未弛豫模量------测量时间小于松弛时间,随时间的形变还 没有机会发生时的弹性模量; • 弛豫模量------测量的时间大于松弛时间,随时间的形变已 发生的弹性模量。
应力弛豫时间的含义:表达了一种材料在恒定变形下, 势能消失时间的长短,是材料内部结构性质的重要指 标,对于材料变形性质有决定性的影响。 • 松弛时间短,势能消失快,这种材料接近虎克固体. • 两种弛豫时间都表示材料在外力作用下,从不平衡状 态通过内部结构重新调整组合达到平衡状态所需的时 间。 弛豫时间与滞弹性的关系:材料的粘度越大,弹性模量 越小,弛豫时间越长,滞弹性越大。
根据此模型有以下关系: 2=1+3 3= 3 =1+2 1=E1 1 1=3 2=E22 消去各元件的应力和应变,得 (/E1)(E1+E2) + E2 = (/E1) +
设: = /E1 , = (E1+E2)/ E2 = (E1+E2)/ E2 E1 则有 E2( +)=+ 定义: ------ 恒定应变下的应力弛豫时间; ------ 恒定应力下的应变蠕变时间。
高温蠕变主要有以下几种理论:
位错运动理论
扩散蠕变理论 晶界蠕变理论
位错运动理论
高温蠕变理论
位错攀移示意图
扩散蠕变理论
高温蠕变理论
扩散蠕变理论
沿晶粒内部扩散的稳态蠕变速率
高温蠕变理论
ε
沿晶界扩散扩散的稳态蠕变速率
ε
晶界蠕变理论
高温蠕变理论
多晶陶瓷中存在着大量晶界,当晶界 位向差大时,可以把晶界看成是非晶
体。高温时,其粘度变小,从而易发
生粘滞流动,而产生蠕变。
影响蠕变的因素
温度 应力 显微结构 化学组成 晶体结构
§1-4
高温下玻璃相的粘性流动
剪应力与剪切速度梯度成正比
牛顿定律
绝对速率理论模型
流动速度
流体粘度
影响粘度的因素
温度 时间 组成
温 度 影 响
时间的影响
组 成 的 影 响
