海文考研钻石卡系列--容易混淆的概念之数学三.doc
(整理)万学海文钻石卡_高数下册数学(三)计划.
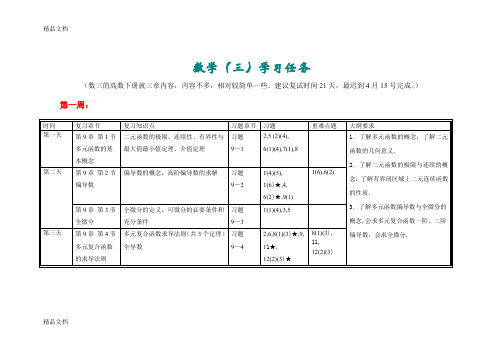
数学(三)学习任务
(数三的高数下册就三章内容,内容不多,相对较简单一些。
建议复试时间21天,最迟到4月15号完成。
)第一周:
精品文档
重点内容:掌握二元函数,偏导和全微分的概念,会求多元隐函数的偏导数.会求简单多元函数的最大值和最小值。
本章的知识不是很难,但也是考试的重点,每年考研都会所涉及。
本周前六天都是学习新的内容,第七天要对以上的内容进行回顾复习,也可以做一下《学习进程监控习题汇编》和《客观题能力特训习题集粹》
精品文档
第二周:
精品文档
重点内容:二重积分的定义式的理解,利用直角坐标计算二重积分很重要。
开始学习的时候要多做练习。
利用极坐标计算二重积分一定要掌握,每年都会考到二重积分的坐标转换。
第三周:
精品文档
:掌握各种级数的重要性质、定理和公式,掌握各种级数的求和方法。
本章每年考试都也会有一道大题。
需要多做练习。
刚开始可以做一下《学习进程监控习题汇编》和《客观题能力特训习题集粹》作为巩固内容。
精品文档
精品文档。
考研数学重要知识点解析——线性代数(三)

钻石卡辅导:2012考研数学重要知识点解析之线性代数(三)万学海文数学虽然属于理科科目,但是仍然有许多重要的知识点需要记忆和运用。
万学海文数学钻石卡考研辅导专家们在此,特别为2012年的广大考生归纳一下高等数学的部分知识点。
这次我们介绍的是线性相关性。
1 线性组合、线性表出(1)线性组合:给定12,,,m ααα,对于任何一组实数12,,,m k k k ,称1122m m k k k ααα+++为向量组12,,,m ααα的一个线性组合,12,,,m k k k 称为这个线性组合的系数.(2)线性表示:给定向量组12,,,m ααα和向量b ,如果存在一组数12,,,m λλλ,使1122m m b λαλαλα=+++,成立,则称向量b 能由向量组12,,,m ααα线性表示.(3)向量组等价:如果向量组中每一个向量可由向量组线性表示,就称前一个向量组可由后一个向量组线性表示.如果两个向量组可以相互线性表示,则称这两个向量组是等价的.【注】(1)向量组中任一向量均可由该向量组本身线性表示.(2)若β可由12,,,m ααα中的部分向量线性表示,则β可由12,,,m ααα线性表示.(3)讨论一个向量能否由一组向量线性表示的一般方法是利用方程组.β能(不能)由12,,,m ααα线性表示 ⇔存在(不存在)12,,,m k k k ,使得1122m m k k k αααβ+++=成立⇔方程组()12,,,m x αααβ=有(无)解(4)向量组等价具有三条性质:①反身性:②对称性: ③传递性. 2 线性相关与线性无关给定m 个向量12,,,m ααα,如果存在m 个不全为零的数12,,,m k k k ,使得11220m m k k k ααα+++=成立,则称12,,,m ααα线性相关,否则,称12,,,mααα线性无关.【注】(1)要注意定义中“否则”一词的含义:没有不全为零的数12,,,m k k k 使11220m m k k k ααα+++=成立⇔对任一组不全为零的数12,,,m k k k ,都有11220m m k k k ααα+++≠⇔只有当12,,,m k k k 全为零时,才有11220m m k k k ααα+++=⇔若11220m m k k k ααα+++=成立,则12,,,m k k k 必须全为零.(2)单个向量α线性相关(无关),当且仅当α为零向量(非零向量). (3)包含零向量的任何向量组都是线性相关的.(4)在一个向量组中,若有两个向量完全相同,则这个向量组线性相关. (5)若向量组中有两个向量成比例,则这个向量组线性相关...............................................................。
数学三考研知识点总结

数学三考研知识点总结一、数学分析1. 集合与映射集合的基本概念,包括子集、并集、交集、补集等;映射的定义和性质,包括单射、满射、双射等。
2. 数列与级数数列的概念,包括常数数列、等差数列、等比数列等;级数的概念,包括收敛级数、发散级数等。
3. 函数与极限函数的定义和性质,包括连续函数、可导函数等;极限的概念,包括极限存在的条件、极限运算法则等。
4. 一元函数微分学导数的定义和性质,包括高阶导数、隐函数求导等;微分的概念和应用,包括微分中值定理、泰勒公式等。
5. 一元函数积分学不定积分的计算方法,包括分部积分、换元积分等;定积分的计算方法,包括定积分的几何意义、定积分的性质等。
6. 定积分的应用定积分在几何、物理等领域的应用,包括求曲线长度、曲线面积、体积等问题。
7. 多元函数微分学偏导数的概念和性质,包括高阶偏导数、全微分等;多元函数的极值和条件极值的判定。
8. 重积分重积分的定义和性质,包括累次积分、极坐标系下的重积分等;重积分的应用,包括质量、质心、转动惯量等问题。
9. 曲线积分与曲面积分曲线积分的概念和计算方法,包括第一类曲线积分和第二类曲线积分;曲面积分的概念和计算方法,包括第一类曲面积分和第二类曲面积分。
10. 常微分方程常微分方程的基本概念,包括初值问题、兼切性、自由度等;常微分方程的解法,包括特征方程法、常数变易法、常系数高阶线性齐次微分方程的特解法等。
11. 泛函分析线性空间和内积空间的定义和性质,包括线性子空间、正交投影等;巴拿赫空间和希尔伯特空间的概念和性质。
12. 牛顿-莱布尼茨公式牛顿-莱布尼茨公式的推导和应用,包括用它来求定积分、用它来求极限等。
二、代数与数论1. 线性代数线性代数的基本概念,包括向量空间、线性变换、矩阵等;线性方程组的解法,包括高斯消元法、矩阵的秩等。
2. 群论群的定义和性质,包括子群、正规子群、循环群等;群的同态映射和同构定理。
3. 环论环的定义和性质,包括理想、素理想、商环等;整环、域的概念和性质。
考研数学三知识点总结

考研数学三知识点总结数学是考研数学教材的一种。
该教材的撰写者都是各大高校的著名数学教师,他们根据多年的教学经验,结合考研数学的特点和难点,编写了这套优秀的教材。
本教材的主要特点是明确、详尽、系统、准确。
接下来我将针对数学三的重点知识点进行总结。
一、导数与微分1.导数的定义及其性质导数的定义:设函数f(x)在x0的某邻域内有定义,若极限lim(x→x0) (f(x)-f(x0))/(x-x0)存在,则称该极限为函数f(x)在点x0处的导数。
记作f'(x0)或dy/dx|_(x=x0) 或df(x)/dx|_(x=x0),称导数的值为函数在该点处的导数值。
导数的性质:(1)可导性与连续性的关系:若函数f(x)在点x0处可导,则在x0处连续;(2)和的导数等于导数的和: (u(x)+v(x))' = u'(x)+v'(x)(3)积的导数等于导数的积: (u(x)v(x))' = u'(x)v(x)+u(x)v'(x)(4)商的导数等于导数的商: (u(x)/v(x))' = [u'(x)v(x)-u(x)v'(x)]/v^2(x)(5)复合函数的导数:(u(v))' = u'(v)v'(x)(6)反函数的导数:(y(x))'=1/(x(y))'2.微分与微分公式微分的定义:设函数f(x)在点x0处有导数,那么函数在这一点的微分为df(x) = f'(x0)dx微分公式:(1)常数微分公式:d(u) = 0(2)幂函数微分公式:d(x^n)=nx^(n-1)dx(3)指数函数微分公式:d(e^x) = e^xdx(4)对数函数微分公式:d(log_a(x)) = (1/ln(a))*1/x dx(5)三角函数微分公式:d(sin(x)) = cos(x)dx, d(cos(x)) = -sin(x)dx, d(tan(x)) = sec^2(x)dx(6)反三角函数微分公式:d(arcsin(x)) = dx/sqrt(1-x^2),d(arccos(x)) = -dx/sqrt(1-x^2), d(arctan(x)) = dx/(1+x^2)(7)反函数的微分:若y=f(x)是可导函数,x=g(y)是其反函数,且在x0处可导,则有dx/dy = 1/dy/dx二、积分与不定积分1.不定积分的概念与性质不定积分的定义:设函数F(x)在区间[a,b]上有原函数f(x),则F(x)是f(x)在区间[a,b]上的不定积分,记作F(x) = ∫ f(x)dx不定积分的性质:(1)线性性质:∫(k*f(x)+g(x))dx = k*∫f(x)dx+∫g(x)dx(2)积分与导数的关系:若f(x)在[a,b]上连续,则∫f(x)dx在[a,b]上可导,且其导函数为f(x)(3)换元积分法:设F'(x) = f(u(x))u'(x),则∫f(u(x))u'(x)dx =∫F'(x)dx = F(x)+C(4)分部积分法:∫(u(x)v'(x))dx = u(x)v(x)-∫(u'(x)v(x))dx2.定积分与其性质定积分的定义:设函数f(x)在区间[a,b]上有界,将区间[a,b]平分成n个小区间,每个小区间长度为Δx = (b-a)/n,设ξ_i为第i个小区间中任意一点,则定积分的极限值为∫_[a]^[b] f(x)dx = lim(n→∞) ∑_[i=1]^n f(ξ_i)Δx定积分的性质:(1)定积分的线性性质:∫_[a]^[b] (k*f(x)+g(x))dx = k*∫_[a]^[b] f(x)dx + ∫_[a]^[b] g(x)dx(2)定积分的保号性:若f(x)在[a,b]上非负,则∫_[a]^[b] f(x)dx ≥ 0(3)定积分的区间可加性:∫_[a]^[b] f(x)dx + ∫_[b]^[c] f(x)dx =∫_[a]^[c] f(x)dx(4)换元积分法:∫_[a]^[b] f(u(x))u'(x)dx = ∫_[u(a)]^[u(b)] f(u)du(5)分部积分法:∫_[a]^[b] u(x)v'(x)dx = [u(x)v(x)]_[a]^[b] -∫_[a]^[b] u'(x)v(x)dx三、级数1.数项级数与部分和数项级数的定义:将给定的数列的各项按一定顺序加起来,得到的和S_n=∑_[n=1]^∞ a_n 称为数项级数的部分和。
海文考研钻石卡学员强化阶段测试卷 数学

y′ = −
6 y + 2x , 两边再对 x 求导,得 ey + 6x
(e y + 6 x( ) 6 y′ + 2)-(6 y + 2 x)(e y y′ + 6) y′′ = − , (e y + 6 x ) 2
-4-
把 x = 0 代入,得 y (0) = 0 , y′(0) = 0 ,代入 y′′ ,得 y′′(0) = −2 (12) 设 y = 1, y = e , y = 2e , y = e +
所以
1 2 1 ax (1 + ax 2 ) 3 − 1 2 = lim 3 =− a. lim x →0 x →0 1 cos x − 1 3 − x2 2
1 2
因为当 x → 0 时, (1 + ax ) 3 − 1 与 cos x − 1 是等价无穷小,所以 −
2 3 a = 1 ,故 a = − . 3 2
y
0
dy ∫ 2 f ( x, y )dx
x
∫
dy ∫
f ( x, y )dx
【答案】 ( D ) 【解析】 由累次积分的积分限可得二重积分的积分区域 D = 然后再交换积分次序即得 ( D ) . (5) 设F ( x ) = (A)为正常数. 【答案】 ( A) 【解析】由于 e 无关. D 错误, 估算
π
0 0
0
π
π
-2-
当 0 < t < π 时, sin t > 0 , e 方法 2:用分部积分法: I =
sin t
− e− sin t > 0, 所以 I > 0 .选 A.
esin t sin tdt = ∫ esin t (− d cos t )
考研数学之容易混淆的知识点

考研数学之容易混淆的知识点考研数学之容易混淆的知识点导语:在考研复习很重要的强化提升阶段,数学对考生们来说可能是最重要的也是最头痛的学科了。
2018考研数学如何复习?考研数学怎么复习?考研数学学科所考内容多、知识面广、综合性强,增加考生复习了数学的难度,很多考生反映即使给数学分配很多的复习时间,做了很多题,还是很难取得突破性的进展,困扰很长时间。
以下是小编为大家精心整理的考研数学之容易混淆的知识点,欢迎大家参考!一、几个易混概念:连续,可导,存在原函数,可积,可微,偏导数存在他们之间的关系式怎么样的?存在极限,导函数连续,左连续,右连续,左极限,右极限,左导数,右导数,导函数的左极限,导函数的右极限。
二、罗尔定理:设函数f(x)在闭区间[a,b]上连续(其中a不等于b),在开区间(a,b)上可导,且 f(a)=f(b),那么至少存在一点ξ∈(a、b),使得f‘(ξ)=0。
罗尔定理是以法国数学家罗尔的名字命名的。
罗尔定理的三个已知条件的意义,①f(x)在[a,b]上连续表明曲线连同端点在内是无缝隙的曲线;②f(x)在内(a,b)可导表明曲线y=f(x)在每一点处有切线存在; ③f(a)=f(b)表明曲线的割线(直线AB)平行于x轴;罗尔定理的结论的直几何意义是:在(a,b)内至少能找到一点ξ,使f’(ξ)=0,表明曲线上至少有一点的切线斜率为0,从而切线平行于割线AB,与x轴平行。
三、.泰勒公式展开的应用专题:相信很多同学看到泰勒公式就哆嗦,因为咋一看很长很恐怖,瞬间大脑空白,身体失重的感觉。
其实在我搞明白一下几点后,原来的症状就没有了。
1.什么情况下要进行泰勒展开;2.以哪一点为中心进行展开;3.把谁展开;4.展开到几阶?四、应用多次中值定理的'专题:大部分的考研题,一般要考察你应用多次中值定理,最重要的就是要培养自己对这种题目的敏感度,要很快反映老师出这题考哪几个中值定理,我的敏感性是靠自己多练习综合题培养出来的。
海文钻石卡讲义(高数)word资料26页

一 函数、极限、连续 1 函数的性质 a 有界性(1) 定义:0M ∃>, x X ∀∈,有Mx f ≤)(.(2) 无界:0M ∀>, x X ∃∈,有 ()f x M >.(3) 无界与无穷:无界的本质是有一个子列趋向于无穷;无穷的本质是任意的子列趋向无穷。
b 奇偶性(1) 定义:偶)()(x f x f =-;奇)()(x f x f =-。
(2) 导函数:奇导偶,偶导奇.(3) 原函数:奇原偶, 偶函数的原函数有且仅有一个为奇函数. c 周期性 (1) 定义:)()(x f T x f =+(2) 导函数:导函数还是周期函数并且周期相同 d 单调性(1) 定义:递增(递减) 当12x x <时,均有()1212()()()()f x f x f x f x <>或(2) 导函数:'()()0()f x f x ≠−−→><←−−单增(减);'()()0()f x f x ≠−−→≥≤←−−单增(减). 一 函数、极限、连续 1 函数的性质 a 有界性(1) 定义:0M ∃>, x X ∀∈,有Mx f ≤)(.(2) 无界:0M ∀>, x X ∃∈,有 ()f x M >.(3) 无界与无穷:无界的本质是有一个子列趋向于无穷;无穷的本质是任意的子列趋向无穷。
b 奇偶性(1) 定义:偶)()(x f x f =-;奇)()(x f x f =-。
(2) 导函数:奇导偶,偶导奇.(3) 原函数:奇原偶, 偶函数的原函数有且仅有一个为奇函数. c 周期性 (1) 定义:)()(x f T x f =+(2) 导函数:导函数还是周期函数并且周期相同 d 单调性(1) 定义:递增(递减) 当12x x <时,均有()1212()()()()f x f x f x f x <>或(2) 导函数:'()()0()f x f x ≠−−→><←−−单增(减);'()()0()f x f x ≠−−→≥≤←−−单增(减). 例1 设2()tan ,()x f x x xe f x =则是(A )(A ) 偶函数 (B )有界函数 (C ) 周期函数 (D )单调函数 分析:(A) 22()()tan()tan ()x x f x x x e x xe f x -=--==则()f x 是偶函数. (B) 取4n x n ππ=+, 则22()tan nnx x n n n n f x x x ex e ==→∞, 故无界.(C) 若为周期函数,设周期为T , ()(0)0f T f ==, 故而tan 0T =, 从而.T k π= 显然22()()()()tan()()tan x k x k f x k x k x k e x k xe ππππππ+++=++=+,当0tan 0x x >≠且, 显然()()f x k f x π+≠, 故而()f x 不是周期函数. (D) 设(0)()0f f π==, 故而()f x 不是单调函数.例2 设()f x 是一个奇的连续函数,则下面必定是奇函数的是( )(A )()0()()x f t f t dt +-⎰ (B )()0()()xf t f t dt --⎰(C )'()f x (D )根据上面条件无法判断分析: 0()()()xx g t dt x ⎧=⎨⎩⎰奇, g 为偶函数偶, g 为奇函数(A) ()()f t f t +-是偶函数, 从而(A)是奇函数. (B) ()()f t f t --是奇函数, 从而(B)是偶函数. (C) ()f x 是奇函数, '()f x 偶函数.例3 设函数()f x 具有二阶导数,并满足()(),f x f x =--且()(1).f x f x =+若'(1)0,f > 则( B )(A)''(5)'(5)(5).f f f -≤-≤- (B)(5)''(5)'(5).f f f =-<- (C) '(5)(5)''(5).f f f -≤-≤- (D) (5)'(5)''(5).f f f -<-=- 分析: 显然(),''()f x f x 是奇函数, 故而(0)''(0)0.f f =='()f x 是偶函数且(),'(),''()f x f x f x 为周期为1的函数, 则 (5)(5)(0)0,'(5)'(1)0,''(5)''(0)0f f f f f f f =-==-=>-==. 2 极限的定义和性质 a 一元函数的极限与性质(1) 0lim ()x xf x A →=:0ε∀>,0δ∃>,当00||x x δ<-<时,有|()|f x A ε-<. (2) 0lim ()lim ()lim ()x x x x x x f x A f x f x A →→+→-=⇔== 推论: 若0lim()lim ()x x x x f x f x →+→-≠, 则0lim ()x xf x →不存在. (3) 0lim ()00,xxf x δ→>⇒∃>当00||,x x δ<-<有()0f x > (4) 四则运算(略). 它的一个重要推论如下: 若0()lim()x xf x Ag x →=,则① 0lim ()0lim ()0;x x x x g x f x →→=⇒= ② 0lim ()0,0lim g()0x x x xf x A x →→=≠⇒=.b 二元函数 (1)00(,)(,)lim(,)x y x y f x y A →=:0ε∀>,0δ∃>,当0δ<<时,有|(,)|f x y A ε-<.(2)0000(,)(,)lim(,)(,)(,),x y x y f x y A x y x y →=⇔以任意路径趋向(,)f x y A →推论:若(,)x y 按两路径趋向于()00,x y 所得极限不同,则()()()00,,lim,x y x y f x y →不存在.(3) 0lim ()00,x xf x δ→>⇒∃>当00||,x x δ<-<有()0f x > 例4 设()221lim 3sin 1x x ax bx →++=-,求a 和b 。
考研数学常见易混知识点整理

考研数学常见易混知识点整理数学作为考研的一科重要科目,其中不乏一些常见但容易混淆的知识点。
为了帮助考生更好地掌握这些知识点,本文将对常见易混知识点进行整理和梳理,以便考生在备考过程中更加有针对性地进行复习和巩固。
一、集合与映射1. 集合的基本概念集合是由对象组成的合集,常用大写字母表示。
子集、真子集、空集等概念需要考生熟悉并能够准确运用。
2. 笛卡尔积笛卡尔积是指两个集合的所有可能有序对组成的集合,可以用来表示多个集合之间的关系。
考生需要理解并能够灵活运用。
3. 映射的概念映射是指一个集合中的每个元素到另一个集合中的唯一元素的对应关系。
函数是一种特殊的映射,是一种有序对的集合。
考生需要注意理解映射的定义及其具体应用。
二、数列与数学归纳法1. 数列的定义和性质数列是按一定顺序排列的数的集合,是数学中研究顺序的一个重要概念。
常见的数列有等差数列和等比数列,考生需要熟悉其定义和基本性质。
2. 数列的通项公式与递推关系式数列的通项公式是指可以用一个公式来表示数列的每一项,递推关系式则是指通过前一项与后一项之间的关系来求解数列。
考生需要掌握如何根据数列的特点求解其通项公式和递推关系式。
3. 数学归纳法数学归纳法是数学中一种常见的证明方法。
通过证明当某个命题在某个特定条件下成立时,它在下一个更一般的条件下也成立,从而得出该命题在所有情况下成立的结论。
考生需要熟悉数学归纳法的基本原理和应用方法。
三、极限与连续1. 函数极限的概念函数极限是指当自变量趋于某个特定值时,函数的取值是否趋于某个确定的值。
考生需要理解函数极限的基本定义和相关性质。
2. 数列极限与函数极限的关系数列极限是函数极限的一种特殊情形,数列极限也可以通过数学归纳法来证明。
考生需要掌握数列极限和函数极限之间的等价关系。
3. 函数的连续性连续性是指函数在某个区间上的无间断性质。
考生需要掌握函数连续性的定义和相关定理,能够灵活运用。
四、导数与微分1. 导数的定义和性质导数是描述函数变化率的重要工具,它表示函数在某一点的瞬时变化率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学部分易混淆概念第一章:函数与极限一、数列极限大小的判断例1:判断命题是否正确.若()n n x y n N <>,且序列,n n x y 的极限存在,lim ,lim ,n n n n x A y B A B →∞→∞==<则解答:不正确.在题设下只能保证A B ≤,不能保证A B <.例如:11,1n n x y n n ==+,,n n x y n <∀,而lim lim 0n n n n x y →∞→∞==.例2.选择题设n n n x z y ≤≤,且lim()0,lim n n n n n y x z →∞→∞-=则( )A .存在且等于零 B. 存在但不一定等于零 C .不一定存在 D. 一定不存在 答:选项C 正确分析:若lim lim 0n n n n x y a →∞→∞==≠,由夹逼定理可得lim 0n n z a →∞=≠,故不选A 与D.取11(1),(1),(1)n n n n n n x y z n n=--=-+=-,则n n n x z y ≤≤,且lim()0n n n y x →∞-=,但lim n n z →∞不存在,所以B 选项不正确,因此选C .例3.设,n n x a y ≤≤且lim()0,{}{}n n n n n y x x y →∞-=则与( )A .都收敛于a B. 都收敛,但不一定收敛于a C .可能收敛,也可能发散 D. 都发散 答:选项A 正确.分析:由于,n n x a y ≤≤,得0n n n a x y x ≤-≤-,又由lim()0n n n y x →∞-=及夹逼定理得lim()0n n a x →∞-=因此,lim n n x a →∞=,再利用lim()0n n n y x →∞-=得lim n n y a →∞=.所以选项A .二、无界与无穷大无界:设函数()f x 的定义域为D ,如果存在正数M ,使得()f x Mx X D ≤∀∈⊂则称函数()f x 在X 上有界,如果这样的M 不存在,就成函数()f x 在X 上无界;也就是说如果对于任何正数M ,总存在1x X ∈,使1()f x M >,那么函数()f x 在X上无界.无穷大:设函数()f x 在0x 的某一去心邻域内有定义(或x 大于某一正数时有定义).如果对于任意给定的正数M (不论它多么大),总存在正数δ(或正数X ),只要x 适合不等式00x x δ<-<(或x X >),对应的函数值()f x 总满足不等式()f x M >则称函数()f x 为当0x x →(或x →∞)时的无穷大. 例4:下列叙述正确的是: ② ① 如果()f x 在0x 某邻域内无界,则0lim ()x x f x →=∞② 如果0lim ()x x f x →=∞,则()f x 在0x 某邻域内无界解析:举反例说明.设11()sin f x x x=,令11,,22n n x y n n πππ==+,当n →+∞时,0,0n n x y →→,而lim ()lim (2)2n n n f x n ππ→+∞→+∞=+=+∞lim ()0n n f y →+∞=故()f x 在0x =邻域无界,但0x →时()f x 不是无穷大量,则①不正确.由定义,无穷大必无界,故②正确.结论:无穷大必无界,而无界未必无穷大.三、函数极限不存在≠极限是无穷大当0x x →(或x →∞)时的无穷大的函数()f x ,按函数极限定义来说,极限是不存在的,但是为了便于叙述函数的性态,我们也说“函数的极限是无穷大”.但极限不存在并不代表其极限是无穷大.例5:函数10()0010x x f x x x x -<⎧⎪==⎨⎪+>⎩,当0x →时()f x 的极限不存在.四、如果0lim()0x xf x →=不能退出01lim()x x f x →=∞ 例6:()0x x f x x ⎧=⎨⎩为有理数为无理数,则0lim ()0x x f x →=,但由于1()f x 在0x =的任一邻域的无理点均没有定义,故无法讨论1()f x 在0x =的极限. 结论:如果0lim ()0x x f x →=,且()f x 在0x 的某一去心邻域内满足()0f x ≠,则1lim()x x f x →=∞.反之,()f x 为无穷大,则1()f x 为无穷小。
五、求函数在某点处极限时要注意其左右极限是否相等,求无穷大处极限要注意自变量取正无穷大和负无穷大时极限是否相等。
例7.求极限10lim ,lim xxx x e e →∞→解:lim ,lim 0x x x x e e →+∞→-∞=+∞=,因而x →∞时x e 极限不存在。
1100lim 0,lim x x x x e e →-→===+∞,因而0x →时1xe 极限不存在。
六、使用等价无穷小求极限时要注意:(1)乘除运算中可以使用等价无穷小因子替换,加减运算中由于用等价无穷小替换是有条件的,故统一不用。
这时,一般可以用泰勒公式来求极限。
(2)注意等价无穷小的条件,即在哪一点可以用等价无穷小因子替换例8:求极限0x →分析一:2写成1)1)+,再用等价无穷小替换就会导致错误。
分析二:用泰勒公式22222211()122(1())22!11()122(1())222!1()4x x x x x x x x οοο-=+++-+-++-=-+原式2221()144x x x ο-+==-。
例9:求极限sin limx xxπ→解:本题切忌将sin x 用x 等价代换,导致结果为1。
sin sin lim 0x x x πππ→== 七、函数连续性的判断(1)设()f x 在0x x =间断,()g x 在0x x =连续,则()()f x g x ±在0x x =间断。
而2()(),(),()f x g x f x f x ⋅在0x x =可能连续。
例10.设0()1x f x x ≠⎧=⎨=⎩,()sin g x x =,则()f x 在0x =间断,()g x 在0x =连续,()()()sin 0f x g x f x x ⋅=⋅=在0x =连续。
若设10()1x f x x ≥⎧=⎨-<⎩,()f x 在0x =间断,但2()()1f x f x =≡在0x =均连续。
(2)“()f x 在0x 点连续”是“()f x 在0x 点连续”的充分不必要条件。
分析:由“若0lim ()x x f x a →=,则0lim ()x x f x a →=”可得“如果00lim ()()x x f x f x →=,则0lim ()()x x f x f x →=”,因此,()f x 在0x 点连续,则()f x 在0x 点连续。
再由例10可得,()f x 在0x 点连续并不能推出()f x 在0x 点连续。
(3)()x ϕ在0x x =连续,()f u 在00()u u x ϕ==连续,则(())f x ϕ在0x x =连续。
其余结论均不一定成立。
第二章 导数与微分一、函数可导性与连续性的关系可导必连续,连续不一定可导。
例11.()f x x =在0x =连读,在0x =处不可导。
二、()f x 与()f x 可导性的关系(1)设0()0f x ≠,()f x 在0x x =连续,则()f x 在0x x =可导是()f x 在0x x =可导的充要条件。
(2)设0()0f x =,则0()0f x '=是()f x 在0x x =可导的充要条件。
三、一元函数可导函数与不可导函数乘积可导性的讨论设()()()F x g x x ϕ=,()x ϕ在x a =连续,但不可导,又()g a '存在,则()0g a =是()F x 在x a =可导的充要条件。
分析:若()0g a =,由定义()()()()()()()()()limlim lim ()()()x a x a x a F x F a g x x g a a g x g a F a x g a a x a x a x aϕϕϕϕ→→→---''====--- 反之,若()F a '存在,则必有()0g a =。
用反证法,假设()0g a ≠,则由商的求导法则知()()()F x x g x ϕ=在x a =可导,与假设矛盾。
利用上述结论,我们可以判断函数中带有绝对值函数的可导性。
四、在某点存在左右导数时原函数的性质(1)设()f x 在0x x =处存在左、右导数,若相等则()f x 在0x x =处可导;若不等,则()f x 在0x x =连续。
(2)如果()f x 在(,)a b 内连续,0(,)x a b ∈,且设00lim ()lim (),x x x x f x f x m →+→-''==则()f x 在0x x =处必可导且0()f x m '=。
若没有如果()f x 在(,)a b 内连续的条件,即设00lim ()lim ()x x x x f x f x a →+→-''==,则得不到任何结论。
例11.20()0x x f x xx +>⎧=⎨≤⎩,显然设00lim ()lim ()1x x f x f x →+→-''==,但0lim ()2x f x →+=,0lim ()0x f x →-=,因此极限0lim ()x f x →不存在,从而()f x 在0x =处不连续不可导。
第三章 微分中值定理与导数的应用一、若lim (),(0,lim ()x x f x A A f x →+∞→+∞'=≠∞=∞可以取), 则若lim ()0x f x A →+∞'=≠,不妨设0A >,则0,()2AX x X f x '∃>≥>时,,再由微分中值定理()()()()(,(,))f x f X f x X x X X x ξξ'=+->∈()()()()lim ()2x Af x f X x X x X f x →+∞⇒≥+->⇒=+∞同理,当0A <时,lim ()x f x →+∞=-∞若lim (),0,()1x f x X x X f x →+∞''=+∞⇒∃>≥>时,,再由微分中值定理()()()()(,(,))f x f X f x X x X X x ξξ'=+->∈()()()()lim ()x f x f X x X x X f x →+∞⇒≥+->⇒=+∞同理可证lim ()x f x →+∞'=-∞时,必有lim ()x f x →+∞=-∞第八章 多元函数微分法及其应用8.1多元函数的基本概念1. 0ε∀f ,12,0δδ∃f ,使得当01x x δ-p ,02y y δ-p 且0,0(,)()x y x y ≠时,有(,)f x y A ε-p ,那么00lim (,)x x y y f x y A →→=成立了吗?成立,与原来的极限差异只是描述动点(,)p x y 与定点000(,)p x y 的接近程度的方法不一样,这里采用的是点的矩形邻域, ,而不是常用的圆邻域,事实上这两种定义是等价的.2. 若上题条件中0,0(,)()x y x y ≠的条件略去,函数(,)f x y 就在0,0()x y 连续吗?为什么?如果0,0(,)()x y x y ≠条件没有,说明0,0()f x y 有定义,并且00(,)x y 包含在该点的任何邻域内,由此对0ε∀f ,都有(,)f x y A ε-p ,从而0,0()A f x y =,因此我们得到00lim (,)x x y y f x y A →→=0,0()f x y =,即函数在0,0()x y 点连续.3. 多元函数的极限计算可以用洛必塔法则吗?为什么? 不可以,因为洛必塔法则的理论基础是柯西中值定理.8.2 偏导数1. 已知2(,)y f x y e x y +=,求(,)f x y令x y u +=,y e v =那么解出x ,y 得ln ln y vx u v =⎧⎨=-⎩,所以22(,)(,).(,)(ln ).ln f u v x u v y u v u v v ==-或者2(,)(ln ).ln f u v u v y =-8.3全微分极其应用1.写出多元函数连续,偏导存在,可微之间的关系偏导数x f ', y f '连续⇒Z 可微⇒ (,)Z f x y =连续⇒ (,)f x y 极限存在 偏导数x f ', y f '连续⇒偏导数x f ', y f '存在2. 判断二元函数(,)f x y=0,00,0(,)()0(,)()x y x y x y x y ≠≠⎩在原点处是否可微.对于函数(,)f x y ,先计算两个偏导数:00(,0)(0,0)00(0,0)lim lim 0x x x f x f f x x∆→∆→∆--'===∆∆0(0,)(0,0)00(0,0)limlim 0y x x f y f f yy ∆→∆→∆--'===∆∆又0005226(,)(0,0)(0,0)(0,0)limlim()()x x x x y y y y f x y f f x f yx yx y →→→→''∆∆--∆-∆∆∆=⎡⎤∆+∆⎣⎦令y k x ∆=∆,则上式为2135550022663()limlim 0(1)(1)x x k x k x k xk ∆→∆→∆=∆=+∆+因而(,)f x y 在原点处可微.8.4多元复合函数的求导法则 1. 设()xyz f x y=+,f 可微,求dz . 22222()()()()()()()()()()()xy xy xy x y d xy xyd x y dz f d f x y x y x y x y xy y xy yf dx f dyx y x y x y x y +-+''==++++''=+++++8.5隐函数的求导1. 设(,)x x y z =,(,)y y x z =,(,)z z x y =都是由方程(,,)0F x y z =所确定的具有连续偏导数的函数,证明..1x y zy z x∂∂∂=-∂∂∂. 对于方程(,,)0F x y z =,如果他满足隐函数条件.例如,具有连续偏导数且0x F '≠,则由方程(,,)0F x y z =可以确定函数(,)x x y z =,即x 是y ,z 的函数,而y ,z 是自变量,此时具有偏导数y xF xy F '∂=-∂',z x F x z F '∂=-∂' 同理, z y F yz F '∂=-∂',所以..1x y z y z x ∂∂∂=-∂∂∂.8.6多元函数的极值及其求法1.设(,)f x y 在点000(,)p x y 处具有偏导数,若(,)0x f x y '=,(,)0y f x y '=则函数(,)f x y 在该点取得极值,命题是否正确?不正确,见多元函数极值存在的充分必要条件.2.如果二元连续函数在有界闭区域内有惟一的极小值点,且无极大值,那么该函数是否在该点取得最小值?不一定,对于一元函数来说上述结论是成立的,但对于多元函数,情况较为复杂,一般来说结论不能简单的推广。
