由质点系的角动量定理得刚体绕定轴转动的角动量定理
合集下载
刚体及其运动规律

解: 设轴反力为 Nx,Ny。
由转动定律: 由质心运动定律:
O c
得: 讨论: 当 l =2l/3 时, Nx =0 。 l > 2l/3 时,Nx >0 ,l < 2l/3 时, Nx <0 。
[例] 半径为 R1 和 R2、转动惯量为 J1 和 J2 的两个圆柱 体,可绕垂直轴转动,最初大圆柱体的角速度为 0,现将 小圆柱体靠近碰到大圆柱体。由于摩擦,小圆柱体被带着 转动,当相对滑动停止时,两圆柱体各以恒定角速度沿相 反方向转动。求小圆柱的最终角速度多大?
M
m
[例] 一质量为m ,长为 l 的均质细杆,转轴在O点,距A 端 l/3 。今使棒从静止开始由水平位置绕O点转动,求(1) 水平位置的角速度和角加速度。(2)垂直位置时的角速度 和角加速度。 c B A 解: O
(1) 方向:
(2)
A
c
Bபைடு நூலகம்
O
[例] 一半径为R,质量为m的均匀圆盘平放在粗糙的水 平面上。若它的初角速度为0,绕中心o旋转,问经过 多长时间圆盘才停止?(设摩擦系数为)
x
转动平面
2. 刚体的角速度 角加速度
角速度
的方向:
角加速度的方向: 加速转动时,两者同方向,减速转动时,两者反方向。
3. 线量与角量的关系:
j
r
匀角加(减)速转动:
匀加(减)速直线平动:
式中:
是 t =0 时刻的角速度和角位置。
说明:作定轴转动时,刚体内各点具有相同的角量, 但不同位置的质点具有不同的线量。
1
2 得:
[例] 均质细棒:m1、 l ,水平轴O,小球:m2与棒 相碰,碰前 碰后 如图,设碰撞时间很短,棒保 持竖直,求碰后棒的角速度。 O 解: 系统对O轴角动量守恒
质点系角动量守恒定律

第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系,在研究物体的运动 时,人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况,并且在这类运动中也存在着某些共同的重要规律。例 如,天文观测表明,行星绕日运动遵从开普勒第二定律,在近 日点附近绕行速度较快,远日点速度较慢,这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
都不守恒,却遵从角动量守恒定律,这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态,在近代物理理 论中仍然是表征微观运动状态的重要物理量,例如原子核的角 动量,通常称为原子核的自旋,就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样,是自然界最基本最
普遍的定律之一。由于角动量这个物理量,从概念到数学表达,
都比动量要难理解,我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念,尽管经典力学中的对称性没
有在微观领域中那么重要,但是介绍一下与本课水平相当的对
称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义; 2. 掌握质点、质点系的角动量定理; 3. 掌握角动量守恒定律; 4. 理解对称性的概念,了解守恒律与对称性的关系。
由上(1)式可以看出,在过程中如果外力对参考点的力矩
的矢量和始终为零,则质点系对该点的角动量保持不变,称为 质点系对该点的角动量守恒定律,即
当τi 0时,
L 常量.
由(2)式可以看出,有时外力矩对参考点虽不为零,但 是,外力矩沿某固定的 z 轴分量为零,则质点系对 z 轴的角动 量保持不变,叫做质点系对 z 轴的角动量守恒定律。即
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系,在研究物体的运动 时,人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况,并且在这类运动中也存在着某些共同的重要规律。例 如,天文观测表明,行星绕日运动遵从开普勒第二定律,在近 日点附近绕行速度较快,远日点速度较慢,这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
都不守恒,却遵从角动量守恒定律,这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态,在近代物理理 论中仍然是表征微观运动状态的重要物理量,例如原子核的角 动量,通常称为原子核的自旋,就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样,是自然界最基本最
普遍的定律之一。由于角动量这个物理量,从概念到数学表达,
都比动量要难理解,我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念,尽管经典力学中的对称性没
有在微观领域中那么重要,但是介绍一下与本课水平相当的对
称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义; 2. 掌握质点、质点系的角动量定理; 3. 掌握角动量守恒定律; 4. 理解对称性的概念,了解守恒律与对称性的关系。
由上(1)式可以看出,在过程中如果外力对参考点的力矩
的矢量和始终为零,则质点系对该点的角动量保持不变,称为 质点系对该点的角动量守恒定律,即
当τi 0时,
L 常量.
由(2)式可以看出,有时外力矩对参考点虽不为零,但 是,外力矩沿某固定的 z 轴分量为零,则质点系对 z 轴的角动 量保持不变,叫做质点系对 z 轴的角动量守恒定律。即
物理-定轴转动刚体的角动量定理和角动量守恒定律

或 Lz = I = 恒量
当刚体相对惯性系中某给定转轴的合外力矩为 零时,该刚体对同一转轴的角动量保持不变。
——对转轴的角动量守恒定律
二、定轴转动中的角动量守恒
说明 1、 关于该守恒定律的条件:
Mz Miz 0
特别地,若每一个力的力矩均为零,即 则
二、定轴转动中的角动量守恒
M iz ri Fi sini 0 的几种情况
10
f
20
O1 R1 A
R2 O2 fB
随堂练习
当两圆柱接触处无相对滑动时,两者转速相反
10
20
O1 R1 A
R2 O2 B
且两者接触点的线速率相等!
二、定轴转动中的角动量守恒
由定轴转动的角动量定理
Mz
dLz dt
若刚体所受对转轴的合外力矩 M z 0,则有
dLz d ( I ) 0
dt
dt
二、定轴转动中的角动量守恒
(3) 对共轴非刚体系(其中各质元到转轴的距离可 变则)系:统的转动惯量可变,此时系统对转轴的角动量守恒,
即:I =恒量
• 特别地,若各质元的 保持一致,
Lz =I =恒量
当 I 增大时, 就减小; 当 I 减小时, 就增大 。
二、定轴转动中的角动量守恒
例如:花样滑冰运动员在冰面上旋转时 运动了角动量守恒定律
(1)
(2)
(3)
二、定轴转动中的角动量守恒
2、对转轴的角动量守恒定律的适用范围: • 不仅适用于刚体, • 也适用于绕同一转轴转动的任意质点系。
二、定轴转动中的角动量守恒
3、对转轴的角动量守恒的几种典型表现 (1) 对定轴刚体:I 不变, 大小和方向均不变;
角动量与刚体转动

这个例子表明,对于一个运动质点,在指定参考 系中,相对不同的固定参考点,有不同的角动量。质 点动量的方向不指向参考点时,它具有绕定点转动的 倾向,角动量不为零。如果质点作惯性运动 ( M 0) , 质点角动量是守恒量。 [例题2] 质点 m 在 z 0平面内以速率 v 绕原点O逆时 针匀速转动。圆周轨道半径为 r ,求它相对于原点O 的角动量。 l 解:质点的动量矢量随时 变化,但它相对于原点O o r 的角动量却是个常矢量。 m v
立即得到
dl M dt
——称为质点的角动量定理
式中 M r F 是合外力相对惯性系中固定参考 点的力矩。
l r mv 是质点 m 相对于同一参考点的角
动量 。
表明相对于同一参考点,质点受到的合(外)力 矩等于质点角动量的时间变化率。
这个定理把质点所受的合外力矩和它角动量的瞬 时变化率联系起来了。 显然,若 M 0 则
r
m
F
在小球与 O点距离缩短的过程中,轨道是缓慢 收缩的螺旋线,径向拉力并不垂直于轨道切线, 正是拉力的切向分量使小球有切向加速度,速率 增加。
小球动能变化
Ek Ek 0 1 2 1 2 1 2 r02 mv mv0 mv0 ( 2 1) 2 2 2 r
小球轨道半径由 r0收缩到 r的过程中,拉力 F 所作的功
i
注意:外力矩与参考点的选择有关。
二、
系统内力性质的小结
⑴ 内力成对出现,所有内力的矢量和为零。 ⑵ 一对内力的功与参考系的选择无关,一对保守 内力的功还与路径无关且等于系统相关势能的减少, 非保守内力的功是系统机械能和其它形式能量转换 的量度。 ⑶ 在任一过程中,所有内力冲量的矢量和为零。 ⑷ 内力不影响系统质心的运动状态,不改变系统 的总动量。内力的冲量使总动量在系统内部重新分 配。 ⑸ 系统内力相对任一固定参考点的力矩矢量和 为零,内力矩不改变系统的总角动量。
刚体定轴转动的角动量定理 角动量守恒定律

典型例子
[例题]如图(a)表示半径为R的放水弧形闸门,可绕图中
左方质点转动,总质量为m,质心在距转轴
7 9
2 处,闸 R 3
门及钢架对质点的总转动惯量为 I mR 2 ,可用钢丝 绳将弧形闸门提起放水,近似认为在开始提升时钢架 部分处于水平,弧形部分的切向加速度为a=0.1g,g为 重力加速度,不计摩擦,不计水浮力.
图(a)
(1)求开始提升时的瞬时,钢丝绳对弧形闸门的拉力 和质点对闸门钢架的支承力. (2)若以同样加速度提升同样重量的平板闸门[图(b)]
需拉力是多少?
FT
W
图(b)
[解](1)以弧形闸门及钢架 为隔离体,受力如图(a)所示. 建立直角坐标系Oxy, 根据质心运动定理 FT FN W mac 向x及y轴投影得
考虑到
t
12v0 dr g 7lg v cos t cos( t) dt 2 24v0 7l
例:圆盘(R,M),人(m)开始静止,人
走一周,求盘相对地转动的角度.
1 I 2 MR 2 2
解: 系统对转轴 角动量守恒
M=0
I11 () I 22 0
I1 mR
2
人— ,盘— (对地的角位移) d d m 1 2 dt dt
I1d I 2 d
1 2 0
2
1 M 2
I d I d
0
2m 2 2m M
例:
圆盘质量M,半径R,J=MR2/2, 转轴光滑,人的质量m,开始时, 两者静止.求:人在盘上沿边 缘走过一周时,盘对地面转过 的角度.
in ex
角动量守恒定律是自然界的一个基本定律.
角动量和角动量守恒定律资料
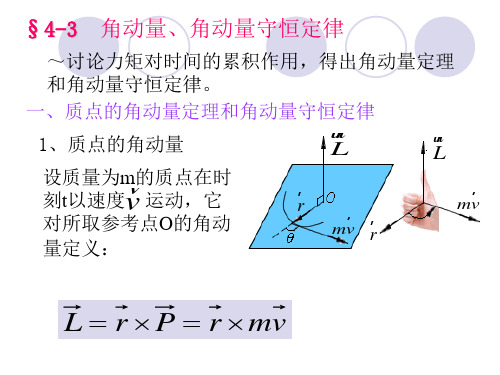
l l0
v0
v
20
解:由角动量守恒和机械能守恒可得
mv 0l0 mvl sin
1 mv 2 1 mv 2 1 k (l l ) 2 0 0 2 2 2
∴
l l0
v0
v
2 k ( l l ) 2 0 v v0 4 m s 1 m
v 0 l0 arcsin( ) 30 vl
4
22
已知
m 1.20 10 kg
4
h 100km
u 1.00 10 m s 2 g 1.62m s
4
1
R 1700km 求 所需消耗燃料的质量 m
vB
R
O B
. 解 设飞船在点 A 的 速度 v0 , 月球质量 mM , 由万有引力和牛顿定律
vA
M
m, v0
l
1 v f 4 v0
l f dt J f ldt
因,
ff
由两式得
3mv 0l 9mv 0 1 这里 J Ml 2 4J 4 Ml 3
例 质量很小长度为l 的均匀细杆,可绕过其中心 O 并与纸面垂直的轴在竖直平面内转动.当细杆静止于水平 位置时, 有一只小虫以速率v0 垂直落在距点O为 l/4 处, 并背离点O 向细杆的端点A 爬行.设小虫与细杆的质量均 为m.问:欲使细杆以恒定的角速度转动, 小虫应以多大速 率向细杆端点爬行? 解 小虫与细杆的碰撞视为完全非弹性碰撞,碰撞 前后系统角动量守恒
L Li mi ri 2 mi ri 2 J
i i i
式中
J mi ri
i
2
5.2 质点的角动量定理与角动量定理定律

21
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
例:质量为M的圆锥摆摆球,以速率 v 运动时, 判断:1)对O参考点的角动量是否守恒?
2)对C参考点的角动量是否守恒?
2)以C为参考点。
重力矩:
r M
=
r l
×
mgr
M = lmg sin θ
张力矩:
r M
=
r l
×
r T
=
0
lθ c
16世纪末至17世纪初,开普勒仔细地分析整理了 前人记录下的大量精确的有关行星运动的资料,总 结出行星运动的规律、即开普勒三定律。
rrr
r M
=
rr ×
r F
=
i x
j y
k
r
r
r
z = Mxi + My j + Mzk
Fx Fy Fz
8
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
rrr
r M
=
rr
×
r F
=
i x
j y
k z
Fx Fy Fz
其中:
⎧ ⎪
M
x
=
yFz
−
zFy
⎨M y = zFx − xFz
r
注意:定理中的力矩和角动量都必须是相对于同 一参考点而言的。
说明: 1)冲量矩是质点角动量变化的原因。
2)质点角动量的变化是力矩对时间的积累结果。 17
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
四、质点的角动量守恒定律
当
v M
=
0
,
时,
(4-2)刚体转动定律、刚体角动量守恒定律
内
外 外 外 质点系的
内
得
内 质点系所受的
内
外 外
冲量矩 质点系的角动量
矩的矢量和 的时间变化率 若各质点的速度或所受外力与参考点共面,则其角动量或力矩只含正 内力矩在求矢 反两种方向,可设顺时针为正向,用代数和代替矢量和。 量和时成对相消 微分形式 称为
外
角动量增量 质点受外力
刚体转动定律、质点系角动量守恒定律
即:
i j k Mo r F x y z Fx F y Fz i yFz zFy j zFx xFz k xFy yFx
M z xFy yFx
Mz为力对 o 点 的力矩在 z 轴方向的分量
注意. 力矩求和只能对同一参考点(或轴)进行。
另一类常见现象
刚体转动定律、质点系角动量守恒定律 ② J 可变,ω亦可变,但 Jω 乘积不变 茹可夫斯基櫈
张臂
大
用外力矩 启动转盘后 撤除外力矩
收臂 小 大
小
花样滑冰常见例
刚体转动定律、质点系角动量守恒定律 忽略脚底摩擦力矩的作用,角动量守恒 J1 J11 J 22 所以 2 1 J2
在冲击等问题中
M 内力 M外力 L 常量
角动量守恒定律是自然界的一个基本定律,有很多实例
刚体转动定律、质点系角动量守恒定律
角动量守恒现象举例 适用于一切转动问题,大至天体,小至粒子...
茹科夫斯基凳实验 为什么银河系呈旋臂盘形结构? 为什么直升飞机的尾翼要安装螺旋桨? 为什么猫从高处落下时总能四脚着地?
1 T1 r T2 r J mr 2 2
T1
r
(3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
J J0
刚体对定轴转动的角 动量守恒定律
4.5刚体定轴转动的角动量定理及角动量守恒
例
如图所示桌面上有一均匀细杆,质量为m、长度为l,它与桌面
之间的摩擦因数为.细杆以初始角速度0绕垂直于杆的质心
轴转动,问细杆经过多长时间停止转动?
解 重力及桌面的支持力的力矩和为零
细杆的质量密度为: m/ l
dx Ox
x
距O为x处的质量元: dm λd x
质元受的摩擦力矩为: dM gxdm
细杆受的摩擦力矩为: M l/2 dM 2 l/2 gxdx 1 mgl
l/2
0
4
L0 J0
L0
t 0
1 4
mgldt
0
J0
t l0 3g
4.5刚体定轴转动的角动量定理及角动量守恒
例
如图所示的两个共轴飞轮,对公共轴OO的转动惯量分别为J1、 J2,角速度分别为 1 、2,求两飞轮啮合后共同的角速度.
解
J1 J2
啮合前后系统角动量守恒
O
O
J11 J22 (J1 J2 )
1 2
J11 J22
J1 J2
4.5刚体定轴转动的角动量定理及角动量守恒
ቤተ መጻሕፍቲ ባይዱ
4.5刚体定轴转动的角动量定理及角动量守恒
由质点系的角动量定理得刚体绕定轴转动的角动量定理
Mz
dLz dt
d(J)
dt
M zdt dLz
力矩的时间累积效应: 冲量矩、角动量、角动量定理.
经历一段时间
t
0 M zdt J J0
刚体在一段时间 内受到的冲量矩 =刚体角动量的 增量
外力对转轴的力矩和为零 M z 0
刚体对定轴转动的角 动量守恒定律
4.5刚体定轴转动的角动量定理及角动量守恒
例
如图所示桌面上有一均匀细杆,质量为m、长度为l,它与桌面
之间的摩擦因数为.细杆以初始角速度0绕垂直于杆的质心
轴转动,问细杆经过多长时间停止转动?
解 重力及桌面的支持力的力矩和为零
细杆的质量密度为: m/ l
dx Ox
x
距O为x处的质量元: dm λd x
质元受的摩擦力矩为: dM gxdm
细杆受的摩擦力矩为: M l/2 dM 2 l/2 gxdx 1 mgl
l/2
0
4
L0 J0
L0
t 0
1 4
mgldt
0
J0
t l0 3g
4.5刚体定轴转动的角动量定理及角动量守恒
例
如图所示的两个共轴飞轮,对公共轴OO的转动惯量分别为J1、 J2,角速度分别为 1 、2,求两飞轮啮合后共同的角速度.
解
J1 J2
啮合前后系统角动量守恒
O
O
J11 J22 (J1 J2 )
1 2
J11 J22
J1 J2
4.5刚体定轴转动的角动量定理及角动量守恒
ቤተ መጻሕፍቲ ባይዱ
4.5刚体定轴转动的角动量定理及角动量守恒
由质点系的角动量定理得刚体绕定轴转动的角动量定理
Mz
dLz dt
d(J)
dt
M zdt dLz
力矩的时间累积效应: 冲量矩、角动量、角动量定理.
经历一段时间
t
0 M zdt J J0
刚体在一段时间 内受到的冲量矩 =刚体角动量的 增量
外力对转轴的力矩和为零 M z 0
