数字信号处理第四次实验报告
数字信号处理上机实验 作业结果与说明 实验三、四、五
上机频谱分析过程及结果图 上机实验三：IIR 低通数字滤波器的设计姓名：赵晓磊 学号：赵晓磊 班级：02311301 科目：数字信号处理B一、实验目的1、熟悉冲激响应不变法、双线性变换法设计IIR 数字滤波器的方法。
2、观察对实际正弦组合信号的滤波作用。
二、实验内容及要求1、分别编制采用冲激响应不变法、双线性变换法设计巴特沃思、切贝雪夫I 型，切贝雪夫II 型低通IIR 数字滤波器的程序。
要求的指标如下：通带内幅度特性在低于πω3.0=的频率衰减在1dB 内，阻带在πω6.0=到π之间的频率上衰减至少为20dB 。
抽样频率为2KHz ，求出滤波器的单位取样响应，幅频和相频响应，绘出它们的图，并比较滤波性能。
（1）巴特沃斯，双线性变换法Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radians frequency in pi unitsa r g (H [e x p (j w )]（2）巴特沃斯，冲激响应不变法（3）切贝雪夫I 型，双线性变换法（4）切贝雪夫Ⅱ型，双线性变换法综合以上实验结果，可以看出，使用不同的模拟滤波器数字化方法时，滤波器的性能可能产生如下差异：使用冲击响应不变法时，使得数字滤波器的冲激响应完全模仿模拟滤波器的冲激响应，也就是时域逼急良好，而且模拟频率和数字频率之间呈线性关系；但频率响应有混叠效应。
frequency in Hz|H [e x p (j w )]|Designed Lowpass Filter Magnitude Response in dBfrequency in pi units|H [e x p (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [e xp (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radiansfrequency in pi unitsa r g (H [e x p (j w )]使用双线性变换法时，克服了多值映射的关系，避免了频率响应的混叠现象；在零频率附近，频率关系接近于线性关系，高频处有较大的非线性失真。
数字信号处理实验四报告
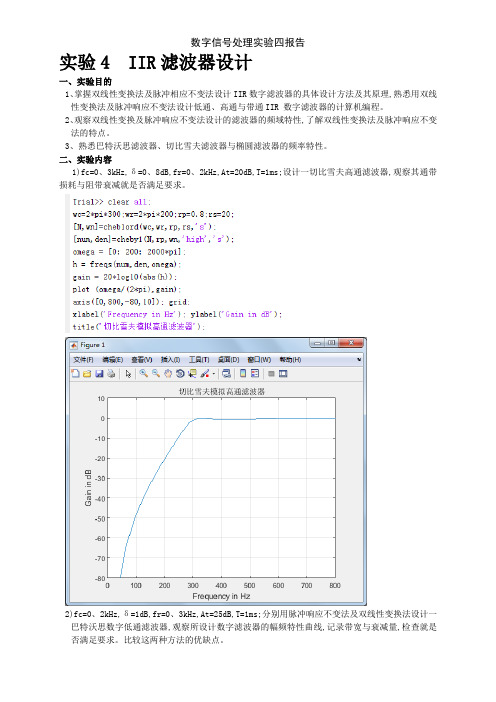
实验4 IIR滤波器设计
一、实验目的
1、掌握双线性变换法及脉冲相应不变法设计IIR数字滤波器的具体设计方法及其原理,熟悉用双线
性变换法及脉冲响应不变法设计低通、高通与带通IIR 数字滤波器的计算机编程。
2、观察双线性变换及脉冲响应不变法设计的滤波器的频域特性,了解双线性变换法及脉冲响应不变
法的特点。
3、熟悉巴特沃思滤波器、切比雪夫滤波器与椭圆滤波器的频率特性。
二、实验内容
1)fc=0、3kHz,δ=0、8dB,fr=0、2kHz,At=20dB,T=1ms;设计一切比雪夫高通滤波器,观察其通带损耗与阻带衰减就是否满足要求。
2)fc=0、2kHz,δ=1dB,fr=0、3kHz,At=25dB,T=1ms;分别用脉冲响应不变法及双线性变换法设计一
巴特沃思数字低通滤波器,观察所设计数字滤波器的幅频特性曲线,记录带宽与衰减量,检查就是否满足要求。
比较这两种方法的优缺点。
3)利用双线性变换法分别设计满足下列指标的巴特沃思型、切比雪夫型与椭圆型数字低通滤波器,并作图验证设计结果: fc =1、2kHz,δ≤0、5dB,fr =2kHz,,At≥40dB,fs =8kHz。
比较这三种滤波器的阶数。
(4) 分别用脉冲响应不变法与双线性变换法设计一巴特沃思型数字带通滤波器,已知fs=30kHz,其等效的模拟滤波器指标为δ＜3dB,2kHz＜f≤3kHz;At≥5dB, f ≥6kHz;At≥20dB,f≤1、5kHz 。
由上图可以瞧出,用脉冲响应不变法由于滤波器的混叠作用在过度带与阻带都衰减的较双线性变换法慢。
数字信号处理EXPIV型教学实验系统实验四常规实验exp4_常规
第四章常规实验指导实验一常用指令实验一、实验目的1、了解DSP开发系统的组成和结构；2、熟悉DSP开发系统的连接；3、熟悉CCS的开发界面；4、熟悉C54X系列的寻址系统；5、熟悉常用C54X系列指令的用法。
二、实验设备计算机，CCS 2.0版软件，DSP仿真器，实验箱。
三、实验步骤与内容1、系统连接进行DSP实验之前，先必须连接好仿真器、实验箱及计算机，连接方法如下所示：2、上电复位在硬件安装完成后，确认安装正确、各实验部件及电源连接正常后，接通仿真器电源，启动计算机，此时，仿真器上的“红色小灯”应点亮，否则DSP开发系统有问题。
3、运行CCS程序待计算机启动成功后，实验箱后面220V输入电源开关置“ON”，实验箱上电，启动CCS，此时仿真器上的“绿色小灯”应点亮，并且CCS正常启动，表明系统连接正常；否则仿真器的连接、JTAG接口或CCS相关设置存在问题，掉电，检查仿真器的连接、JTAG 接口连接，或检查CCS相关设置是否正确。
注：如在此出现问题，可能是系统没有正常复位或连接错误，应重新检查系统硬件并复位；也可能是软件安装或设置有问题，应尝试调整软件系统设置，具体仿真器和仿真软件CCS的应用方法参见第三章。
●成功运行程序后，首先应熟悉CCS的用户界面●学会CCS环境下程序编写、调试、编译、装载，学习如何使用观察窗口等。
4、修改样例程序，尝试DSP其他的指令。
注：实验系统连接及CCS相关设置是以后所有实验的基础，在以下实验中这部分内容将不再复述。
5、填写实验报告。
6、样例程序实验操作说明仿真口选择开关K9拨到右侧，即仿真器选择连接右边的CPU：CPU2；启动CCS 2.0，在Project Open菜单打开exp01_cpu2目录下面的工程文件“exp01.pjt”注意：实验程序所在的目录不能包含中文，目录不能过深，如果想重新编译程序，去掉所有文件的只读属性。
用下拉菜单中Project/Open，打开“exp01.pjt”，双击“Source”，可查看源程序在File Load Program菜单下加载exp01_cpu2\debug目录下的exp01.out文件：加载完毕，单击“Run”运行程序；实验结果：可见指示灯D1定频率闪烁；单击“Halt”暂停程序运行，则指示灯停止闪烁，如再单击“Run”，则指示灯D1又开始闪烁；注：指示灯D1在CPLD单元的右上方关闭所有窗口，本实验完毕。
数字信号处理实验报告(实验1-4)
实验一 MATLAB 仿真软件的基本操作命令和使用方法实验容1、帮助命令使用 help 命令，查找 sqrt （开方）函数的使用方法；2、MATLAB 命令窗口（1）在MATLAB 命令窗口直接输入命令行计算31)5.0sin(21+=πy 的值；（2）求多项式 p(x) = x3 + 2x+ 4的根；3、矩阵运算（1）矩阵的乘法已知 A=[1 2;3 4]， B=[5 5;7 8]，求 A^2*B（2）矩阵的行列式已知 A=[1 2 3;4 5 6;7 8 9]，求A（3）矩阵的转置及共轭转置已知A=[1 2 3;4 5 6;7 8 9]，求A'已知 B=[5+i,2-i,1;6*i,4,9-i], 求 B.' , B'（4）特征值、特征向量、特征多项式已知 A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4] ，求矩阵 A的特征值、特征向量、特征多项式；（5）使用冒号选出指定元素已知： A=[1 2 3;4 5 6;7 8 9]；求 A 中第 3 列前 2 个元素；A 中所有列第 2，3 行的元素；4、Matlab 基本编程方法（1）编写命令文件：计算 1+2+…+n<2000 时的最大 n 值；（2）编写函数文件：分别用 for 和 while 循环结构编写程序，求 2 的 0 到 15 次幂的和。
5、MATLAB基本绘图命令（1）绘制余弦曲线 y=cos(t)，t∈[0，2π]（2）在同一坐标系中绘制余弦曲线 y=cos(t-0.25)和正弦曲线 y=sin(t-0.5)， t∈[0，2π]（3）绘制[0，4π]区间上的 x1=10sint 曲线，并要求：（a）线形为点划线、颜色为红色、数据点标记为加号；（b）坐标轴控制：显示围、刻度线、比例、网络线（c）标注控制：坐标轴名称、标题、相应文本；>> clear;t=0:pi/10:4*pi;y=10*sin(t);plot(t,y);plot(t,y,'-+r');grid>> xlabel('X'),ylabel('Y');>> title('Plot:y=10*sin(t)');>> text(14,10,'完整图形');实验二常见离散信号的MATLAB产生和图形显示实验容与步骤１. 写出延迟了np个单位的单位脉冲函数impseq，单位阶跃函数stepseq, n=ns:nf function [x,n]=impseq[np,ns,nf];function [x,n]=stepseq[np,ns,nf];2. 产生一个单位样本序列x1(n)，起点为ns= -10, 终点为nf=20, 在n0=0时有一单位脉冲并显示它。
重庆大学通信学院数字信号处理实验第四次实验报告
0.511.522.5100150200250300Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.51 1.522.5-30-20-10010Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )0.51 1.522.5-100-50050100Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.51 1.522.5-80-60-40-200Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )0.51 1.522.5-1000-500500Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s)0.51 1.522.5-30-20-10010Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )图1 第一题的频率响应 图2 第二题的频率响应图3 第三题的频率响应图4 第四题的频率响应第五题：零、极点分布图-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.814Real PartI m a g i n a r y P a r t结果单位抽样响应：y =1.0000 0.2000 -0.4000 -0.2000 1.0000 0 012345678910-0.4-0.20.20.40.60.81单位抽样响应用filter 函数： b=[1 0.2 -0.4 -0.2 1];a=1; %注意此处分母的表示 x=zeros(1,10);x(1)=1;%单位抽样脉冲 y=filter(b,a,x) stem(y);title('单位抽样响应')用impz 函数：b=[1 0.2 -0.4 -0.2 1]; a=1;y=impz(b,a);单位阶跃响应：-11234567891000.20.40.60.811.21.41.6单位阶跃响应y =1.0000 1.2000 0.8000 0.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000程序：b=[1 0.2 -0.4 -0.2 1]; a=1;x=ones(1,20);x(1)=1;%单位阶跃信号 y=filter(b,a,x)第六题：零、极点分布图-1-0.50.511.5-1-0.8-0.6-0.4-0.200.20.40.60.81Real PartI m a g i n a r y P a r tB=[0.3 -0.5 0];A=[1 -0.7 0.8];zplane(B,A) %零、极点分布图-101-1-0.500.51Real PartI m a g i n a r y P a r t系统函数极零点分布图-1-0.500.51-1-0.500.51Real PartI m a g i n a r y P a r t最小相移网络零点分布图-11-1-0.500.51Real PartI m a g i n a r y P a r t全通网络零点分布图-11-1-0.500.51Real PartI m a g i n a r y P a r t修正网络零点分布图B=[0.3 -0.5]; A=[1 -0.7 0.8]; subplot(2,2,1);zplane(B,A)title('系统函数极零点分布图') %最小相移网络： B=[1 -0.6];A=[1 -0.7 0.8]; subplot(2,2,2) zplane(B,A);title('最小相移网络零点分布图') %全通网络： B=[-0.6 1];A=[1 -0.6]; subplot(2,2,3); zplane(B,A);title('全通网络零点分布图') %修正网络： B=[-0.6 1]; A=[1 -0.7 0.8]; subplot(2,2,4); zplane(B,A);title('修正网络零点分布图')对比区别：0500100015002000123系统函数极频率响应0500100015002000-4-2024系统函数极频率相位响应500100015002000246修正网络频率响应0500100015002000-4-224修正网络频率相位响应B=[0.3 -0.5]; A=[1 -0.7 0.8]; w=0:0.01:6*pi; h=freqz(B,A,w) subplot(2,2,1); plot(abs(h));title('系统函数极频率响应') subplot(2,2,2); plot(angle(h));title('系统函数极频率相位响应')B=[-0.6 1]; A=[1 -0.7 0.8]; w=0:0.01:6*pi;[h,w]=freqz(B,A,w) subplot(2,2,3); plot(abs(h));title('修正网络频率响应') subplot(2,2,4); plot(angle(h));title('修正网络频率相位响应')第七题：说明grpdelay 的使用方法，计算1和5中的群延时0.51 1.522.53012345678910Normalized Frequency (⨯π rad/sample)G r o u p d e l a y (s a m p l e s )b=[0.2 0 -0.3]; a=[1 -0.4 0.8]; w=0:0.01:3*pi; grpdelay(b,a,w);第五题的群延时00.51 1.522.53-15-10-55101520Normalized Frequency (⨯π rad/sample)G r o u p d e l a y (s a m p l e s )b=[1 0.2 -0.4 -0.2 1]; a=[1];w=0:0.01:3*pi; grpdelay(b,a,w);群延时函数的使用方法： help grpdelayGRPDELAY Group delay of a digital filter.[Gd,W] = GRPDELAY(B,A,N) returns length N vectors Gd and W containing the group delay and the frequencies (in radians) at which it is evaluated. Group delay is -d{angle(w)}/dw. The frequencyresponse is evaluated at N points equally spaced around the upper half of the unit circle. For an FIR filter where N is a power of two, the computation is done faster using FFTs. If you don't specify N, it defaults to 512.GRPDELAY(B,A,N,'whole') uses N points around the whole unit circle.[Gd,F] = GRPDELAY(B,A,N,Fs) and [Gd,F] = GRPDELAY(B,A,N,'whole',Fs) given sampling frequency Fs in Hz return a vector F in Hz.Gd = GRPDELAY(B,A,W) and Gd = GRPDELAY(B,A,F,Fs) return the group delay evaluated at the points in W (in radians/sample) or F (in Hz).GRPDELAY(B,A,...) with no output arguments plots the group delay in the current figure window.提高1：级联后的频率响应0.51 1.522.5-800-600-400-200Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.51 1.522.5-200-150-100-500X: 0.2992Y: -2.991Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )b=0.175*[1 3 3 1]; a=[1];w=0:0.01:3*pi;freqz(b,a,w);最高的点x=0, y=0X=0.2992,y=-2.991Y*pi=0.9400计算的wc= 2*acos(2^(-1/6))=0.9430。
数字信号处理实验报告四IIR数字滤波器设计及软件实现
数字信号处理实验报告四IIR数字滤波器设计及软件实现实验目的：本实验的目的是了解IIR数字滤波器的设计原理和实现方法，通过MATLAB软件进行数字滤波器设计和信号处理实验。
一、实验原理IIR数字滤波器是一种使用有限数量的输入样本和前一次输出值的滤波器。
它通常由差分方程和差分方程的系数表示。
IIR滤波器的特点是递归结构，故其频率响应是无限长的，也就是说它的频率响应在整个频率范围内都是存在的，而不像FIR滤波器那样只有在截止频率处才有响应。
根据设计要求选择合适的滤波器类型和滤波器结构，然后通过对滤波器的模型进行参数化，设计出满足滤波要求的IIR滤波器。
常见的IIR滤波器设计方法有模拟滤波器设计方法和数字滤波器设计方法。
在本实验中，我们主要使用数字滤波器设计方法，即离散时间滤波器设计方法。
二、实验内容（一）设计IIR数字滤波器的步骤：1.确定滤波器类型：根据滤波要求选择合适的滤波器类型，如低通滤波器、高通滤波器、带通滤波器、带阻滤波器等。
2.确定滤波器的阶数：根据滤波要求确定滤波器的阶数。
阶数越高，滤波器的频率响应越陡峭，但计算复杂度也越高。
3. 设计滤波器原型：根据滤波要求，设计滤波器的原型。
可以选择Butterworth滤波器、Chebyshev滤波器、Elliptic滤波器等作为原型。
4.选择滤波器结构：根据计算机实现条件和算法复杂度，选择合适的滤波器结构。
常见的滤波器结构有直接形式I、直接形式II、级联形式等。
5.参数化滤波器模型：根据原型滤波器的差分方程，选择合适的参数化方法。
常见的参数化方法有差分方程法、极点/零点法、增益法等。
6.根据参数化的滤波器模型，计算出所有的滤波器系数。
（二）用MATLAB软件实现IIR数字滤波器设计：1.打开MATLAB软件，并创建新的脚本文件。
2. 在脚本文件中，使用MATLAB提供的滤波器设计函数，如butter、cheby1、ellip等，选择合适的滤波器类型进行设计。
数字信号处理实验报告1-5
实验一时域离散信号的产生及时域处理实验目的：了解Matlab软件数字信号处理工具箱的初步使用方法。
掌握其简单的Matlab语言进行简单的时域信号分析。
实验内容：[1.1]已知两序列x1=[0,1,2,3,4,3,2,1,0];n1=[-2:6];x2=[2,2,0,0,0,-2,-2],n2=[2:8].求他们的和ya及乘积yp. 程序如下：x1=[0,1,2,3,4,3,2,1,0];ns1=-2;x2=[2,2,0,0,0,-2,-2];ns2=2;nf1=ns1+length(x1)-1;nf2=ns2+length(x2)-1;ny=min(ns1,ns2):max(nf1,nf2);xa1=zeros(1,length(ny));xa2=xa1;xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;ya=xa1+xa2yp=xa1.*xa2subplot(4,4,1),stem(ny,xa1,'.')subplot(4,1,2),stem(ny,xa2,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,3),stem(ny,ya,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,4),stem(ny,yp,'.')line([ny(1),ny(end)],[0,0])[1.2]编写产生矩形序列的程序。
并用它截取一个复正弦序列，最后画出波形。
程序如下：clear;close alln0=input('输入序列起点:n0=');N=input('输入序列长度:N=');n1=input('输入位移:n1=');n=n0:n1+N+5;u=[(n-n1)>=0];x1=[(n-n1)>=0]-[(n-n1-N)>=0];x2=[(n>=n1)&(n<(N+n1))];x3=exp(j*n*pi/8).*x2;subplot(2,2,1);stem(n,x1,'.');xlabel('n');ylabel('x1(n)');axis([n0,max(n),0,1]);subplot(2,2,3);stem(n,x2,'.');xlabel('n');ylabel('x2(n)');axis([n0,max(n),0,1]);subplot(2,2,2);stem(n,real(x3),'.'); xlabel('n');ylabel('x3(n)的实部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);subplot(2,2,4);stem(n,imag(x3),'.'); xlabel('n');ylabel('x3(n)的虚部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);[1.3]利用已知条件，利用MATLAB生成图形。
数字信号处理实验报告实验四
物理与电子信息工程学院实验报告实验课程名称：数字信号处理实验名称： IIR数字滤波器设计及软件实现班级： 1012341姓名：严娅学号： 101234153成绩：_______实验时间： 2012年12月13 日一、实验目的（1）熟悉用双线性变换法设计IIR数字滤波器的原理与方法；（2）学会调用MATLAB信号处理工具箱中滤波器设计函数设计各种IIR数字滤波器，学会根据滤波需求确定滤波器指标参数。
（3）掌握IIR数字滤波器的MATLAB实现方法。
（3）通过观察滤波器输入输出信号的时域波形及其频谱，建立数字滤波的概念。
二、实验原理IIR数字滤波器采用递归型结构，即结构上带有反馈环路。
IIR 滤波器运算结构通常由延时、乘以系数和相加等基本运算组成，可以组合成直接型、正准型、级联型、并联型四种结构形式，都具有反馈回路。
由于运算中的舍入处理，使误差不断累积，有时会产生微弱的寄生振荡。
IIR数字滤波器在设计上可以借助成熟的模拟滤波器的成果，如巴特沃斯、契比雪夫和椭圆滤波器等，有现成的设计数据或图表可查，其设计工作量比较小，对计算工具的要求不高。
在设计一个IIR数字滤波器时，我们根据指标先写出模拟滤波器的公式，然后通过一定的变换，将模拟滤波器的公式转换成数字滤波器的公式。
利用MATLAB信号处理工具箱中的滤波器设计和分析工具(FDATool)可以很方便地设计出符合应用要求的未经量化的IIR数字滤波器。
三、实验内容及步骤（1）调用信号产生函数mstg 产生由三路抑制载波调幅信号相加构成的复合信号st ，该函数还会自动绘图显示st 的时域波形和幅频 特性曲线,如图10.4.1所示。
由图可见，图10.4.1 三路调幅信号st 的时域波形和幅频特性曲线三路信号时域混叠无法在时域分离。
但频域是分离的，所以可以通过滤波的方法在频域分离。
（2）通过观察st 的幅频特性曲线，可以用三个滤波器（低通滤波器、带通滤波器、高通滤波器）将它们分离，根据幅频特性曲线分别确定滤波器的通带截止频率和阻带截止频率，并要求滤波器的通带最大衰减为0.1dB,阻带最小衰减为60dB 。
数字信号处理实验报告 (实验四)
实验四 离散时间信号的DTFT一、实验目的１. 运用MA TLAB 计算离散时间系统的频率响应。
２. 运用MA TLAB 验证离散时间傅立叶变换的性质。
二、实验原理（一）、计算离散时间系统的DTFT已知一个离散时间系统∑∑==-=-Nk k N k k k n x b k n y a 00)()(，可以用MATLAB 函数frequz 非常方便地在给定的L 个离散频率点l ωω=处进行计算。
由于)(ωj e H 是ω的连续函数，需要尽可能大地选取L 的值（因为严格说，在MA TLAB 中不使用symbolic 工具箱是不能分析模拟信号的，但是当采样时间间隔充分小的时候，可产生平滑的图形），以使得命令plot 产生的图形和真实离散时间傅立叶变换的图形尽可能一致。
在MA TLAB 中，freqz 计算出序列{M b b b ,,,10 }和{N a a a ,,,10 }的L 点离散傅立叶变换，然后对其离散傅立叶变换值相除得到L l eH l j ,,2,1),( =ω。
为了更加方便快速地运算，应将L 的值选为2的幂，如256或者512。
例3.1 运用MA TLAB 画出以下系统的频率响应。
y(n)-0.6y(n-1)=2x(n)+x(n-1)程序： clf;w=-4*pi:8*pi/511:4*pi;num=[2 1];den=[1 -0.6];h=freqz(num,den,w);subplot(2,1,1)plot(w/pi,real(h));gridtitle(‘H(e^{j\omega}的实部’))xlabel(‘\omega/ \pi ’);ylabel(‘振幅’)；subplot(2,1,1)plot(w/pi,imag(h));gridtitle(‘H(e^{j\omega}的虚部’))xlabel(‘\omega/ \pi ’);ylabel(‘振幅’)；（二）、离散时间傅立叶变换DTFT 的性质。
湘潭大学数字信号处理实验报告(第四次)
湘潭大学数字信号处理实验报告〔第四次〕数字信号处理实验报告〔第四次〕学院：班级：姓名：学号：指导老师：完成日期：内容：实验九、6455表贴键盘控制实验1实验九、6455表贴键盘控制实验一、实验目的了解ICETEK-DM642-AVM板上表贴键盘的使用方法和连接、控制方式。
二、实验设备1、PC兼容机一台，操作系统为Windows2000〔或Windows98，WindowsXP，一下默认为Windows2000〕，安装Code Composer Studio2.21软件。
2、ICETEK-DM642-AVM实验箱。
3、USB连接电缆一条。
三、实验步骤1. 实验准备〔1〕连接开发板+5V的供电电源，连接实验箱220V供电电源连线。
〔2〕翻开实验箱上的开关，给实验箱供电。
上电正常时，ICETEK-DM642-AVM 评估板的上电指示灯常亮，复位灯熄灭。
注意：如果在ICETEK-DM642-AVM评估板上电后，指示灯的亮灯状态不对，请立即关闭实验箱电源开关，检查设备。
拨动仿真选择开关〔J2〕选择DM642仿真方式。
翻开液晶显示屏电源开关，此时液晶显示屏上应显示条状彩条。
如果没有彩条显示，请按下板上的S1复位按钮，再次观察液晶显示屏是否有彩条输出。
提示：如果使用自配的图像输入设备和图像输出设备，请务必保证各设备与DM642-AVM评估板的供电电源共地。
如果不共地，过大的电压差，将击穿DM642评估板。
〔3〕设置Code Composer Studio2.2在硬件仿真〕Emulator〕方式下运行。
〔4〕启动Code Composer Studio2.2.双击桌面上“CCS 2〔‘C60000〕〞，启动Code Composer Studio。
2、翻开工程：project\\open选择C:\\ICETEK-DM642-AVM_V3\\Lab37-KEY\\key.pjt,之后会出现如下列图所示窗口：23、浏览工程中源程序并理解含义。
数字信号处理实验报告完整版[5篇模版]
![数字信号处理实验报告完整版[5篇模版]](https://img.taocdn.com/s3/m/7b21a71bb5daa58da0116c175f0e7cd184251866.png)
数字信号处理实验报告完整版[5篇模版]第一篇：数字信号处理实验报告完整版实验 1利用 T DFT 分析信号频谱一、实验目的1.加深对 DFT 原理的理解。
2.应用 DFT 分析信号的频谱。
3.深刻理解利用DFT 分析信号频谱的原理，分析实现过程中出现的现象及解决方法。
二、实验设备与环境计算机、MATLAB 软件环境三、实验基础理论T 1.DFT 与与 T DTFT 的关系有限长序列的离散时间傅里叶变换在频率区间的N 个等间隔分布的点上的 N 个取样值可以由下式表示：212 /0()|()()0 1Nj knjNk NkX e x n e X k k Nπωωπ--====≤≤-∑由上式可知，序列的 N 点 DFT ,实际上就是序列的 DTFT 在 N 个等间隔频率点上样本。
2.利用 T DFT 求求 DTFT方法 1 1：由恢复出的方法如下：由图 2.1 所示流程可知：101()()()Nj j n kn j nNn n kX e x n e X k W eNωωω∞∞----=-∞=-∞=⎡⎤==⎢⎥⎣⎦∑∑∑由上式可以得到：IDFT DTFT第二篇：数字信号处理实验报告JIANGSUUNIVERSITY OF TECHNOLOGY数字信号处理实验报告学院名称：电气信息工程学院专业：班级：姓名：学号：指导老师：张维玺（教授）2013年12月20日实验一离散时间信号的产生一、实验目的数字信号处理系统中的信号都是以离散时间形态存在的，所以对离散时间信号的研究是数字信号的基本所在。
而要研究离散时间信号，首先需要产生出各种离散时间信号。
使用MATLAB软件可以很方便地产生各种常见的离散时间信号，而且它还具有强大绘图功能，便于用户直观地处理输出结果。
通过本实验，学生将学习如何用MATLAB产生一些常见的离散时间信号，实现信号的卷积运算，并通过MATLAB中的绘图工具对产生的信号进行观察，加深对常用离散信号和信号卷积和运算的理解。
数字信号处理实验报告4
专业： 学号： 姓名： 成绩： 实验题目: 窗函数法设计FIR 数字滤波器实验目的: 了解和掌握线性相位FIR 数字滤波器的设计方法实验原理与内容:1. 设计具有指标ωp =0.2π,R p =0.25dB,ωs =0.3π,A s =50dB 的低通数字滤波器2. 根据指标选择合适的窗函数,确定冲激响应,画出滤波器的频率响应3. 由于在设计过程中,并没有用到Rp=0.25dB 值,因此设计后必须对此进行校验实验结果:1. 绘出理想低通滤波器的冲激响应图12. 绘出Hamming 窗图2010203040506070-0.0500.050.10.150.20.250.3n h d (n )01020304050600.10.20.30.40.50.60.70.80.91n H a m (n )3. 绘出加窗后的滤波器冲激响应图34. 绘出该滤波器的幅频响应图4010203040506070-0.0500.050.10.150.20.250.3Actual Impulse Responsen h (n )00.20.31-100-90-80-70-60-50-40-30-20-10010Magnitude Response in dB w/pi 20l g |H g (w )|思考题:1如果没有给定h(n)的长度N，而是给定了通带边缘截止频率ωc和阻带临界频率ωp，以及相应的衰减，你能根据这些条件用窗函数法设计线性相位FIR低通滤波器吗？2窗函数的傅式变换W(e jω)的主瓣和旁瓣分别决定了H(e jω)的什么特性?程序附录:function hd=ideal_lp(wc,N)alpha=(N-1)/2;n=0:N-1;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);function [db,mag,pha,grd,w]=freqz_m(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);pha=angle(H);db=20*log10((mag+eps)/max(mag));grd=grpdelay(b,a,w);clcwp=0.2*pi;ws=0.3*pi;tr_width=ws-wp;M=ceil(6.6*pi/tr_width);N=0:M-1;wc=(4*ws+6*wp)/10;w_ham=(hamming(M))';hd=ideal_lp(wc,M);h=hd.*w_ham;[db,mag,pha,grd,w]=freqz_m(h,1);delta_w=2*pi/1000;subplot(2,2,1)stem(N,hd,'.');xlabel('n');ylabel('hd(n)');subplot(2,2,2)stem(N,w_ham,'.');axis([0 M-1 0.1 1])xlabel('n');ylabel('Ham(n)');subplot(2,2,3)stem(N,h,'.')title('Actual Impulse Response');xlabel('n');ylabel('h(n)');subplot(2,2,4)plot(w/pi,db)axis([0 1 -100 10])title('Magnitude Response in dB')xlabel('w/pi');ylabel('20lg|Hg(w)|');gridset(gca,'XTickMode','manual','XTick',[0,0.2,0.3 1]) Rp=-(min(db(1:1:wp/delta_w+1)))As=-round(max(db(ws/delta_w+1:1:501)))function hd=ideal_lp(wc,N)alpha=(N-1)/2;n=0:N-1;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);。
数字信号处理实验报告MATLAB
数字信号处理实验报告姓名：班级：09电信一班学号：2)]得下图二，图二图一3．将如下文件另存为：sigadd.m文件function [y,n] = sigadd(x1,n1,x2,n2)% 实现y(n) = x1(n)+x2(n)% -----------------------------% [y,n] = sigadd(x1,n1,x2,n2)% y = 在包含n1 和n2 的n点上求序列和,% x1 = 在n1上的第一序列% x2 = 在n2上的第二序列(n2可与n1不等)n = min(min(n1),min(n2)):max(max(n1),max(n2)); % y(n)的长度y1 = zeros(1,length(n)); y2 = y1; % 初始化y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; % 具有y的长度的x1y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; % 具有y的长度的x2y = y1+y2;在命令窗口输入：x1=[1,0.5,0.3,0.4];n1=-1:2;x2=[0.2,0.3,0.4,0.5,0.8,1];n2=-2:3; [y,n] = sigadd(x1,n1,x2,n2)得：y =n=-1:10;x=sin(0.4*pi*n);y=fliplr(x);n1=-fliplr(n);subplot(2,1,1),stem(n,x) subplot(2,1,2),stem(n1,y在命令窗口键入:n=-1:10; x=sin(0.4*pi*n);n (samples)实验结果：1.（1）在命令窗口输入：tic; [am,pha]=dft1(x)N=length(x);w=exp(-j*2*pi/N);for k=1:Nsum=0;for n=1:Nsum=sum+x(n)*w^((k-1)*(n-1));endam(k)=abs(sum);pha(k)=angle(sum);end;toc得到如下结果：am =Columns 1 through 11120.0000 41.0066 20.9050 14.3996 11.3137 9.6215 8.6591 8.1567 8.0000 8.1567 8.6591Columns 12 through 169.6215 11.3137 14.3996 20.9050 41.0066pha =Columns 1 through 110 1.7671 1.9635 2.1598 2.3562 2.5525 2.7489 2.9452 3.1416 -2.9452 -2.7489Columns 12 through 16-2.5525 -2.3562 -2.1598 -1.9635 -1.7671Elapsed time is 0.047000 seconds.（2）在命令窗口输入：tic;[am,pha]=dft2(x)N=length(x);n=[0:N-1];k=[0:N-1];w=exp(-j*2*pi/N);nk=n’*k;wnk=w.^(nk); Xk=x*wnk; am= abs(Xk); pha=angle(Xk); toc得到下图：figure(1)00.10.20.30.40.50.60.70.80.91signal x(n), 0 <= n <= 99（2）在命令窗口键入：n3=[0:1:99];y3=[x(1:1:10) zeros(1,90)]; ％添90个零。
数字信号处理实验四
实验报告课程名称：数字信号处理实验四：离散系统分析班级：通信1403学生姓名：强亚倩学号：1141210319指导教师：范杰清页脚内容1页脚内容2华北电力大学（北京）一、实验目的深刻理解离散时间系统的系统函数在分析离散系统的时域特性、频域特性以及稳定性中的重要作用及意义，熟练掌握利用MATLAB 分析离散系统的时域响应、频响特性和零极点的方法。
掌握利用DTFT 和DFT 确定系统特性的原理和方法。
二、实验原理MATLAB 提供了许多可用于分析线性时不变连续系统的函数，主要包含有系统函数、系统时域响应、系统频域响应等分析函数。
1. 离散系统的时域响应在调用MATLAB 函数时，需要利用描述该离散系统的系数函数。
对差分方程进行Z 变换即可得系统函数：在MATLAB 中可使用向量a 和向量b 分别保存分母多项式和分子多项式的系数：这些系数均从z 0按z 的降幂排列。
2．离散系统的系统函数零极点分析离散LTI 系统的系统函数H (z )可以表示为零极点形式：))...()(())...()((1)()()(2121)1(111)1(1110N M N N N N M M M M p z p z p z z z z z z z k z a z a z a z b z b z b b z X z Y z H ------=++++++++==---------- )()(1)()()()1(111)1(1110z a z b z a z a z a z b z b z b b z X z Y z H N N N N M M M M =++++++++==---------- ],,,,1[11N N a a a a -= ],,,,[110M M b b b b b -=页脚内容3使用MATLAB 提供的roots 函数计算离散系统的零极点；使用zplane 函数绘制离散系统的零极点分布图。
注意：在利用这些函数时，要求H (z )的分子多项式和分母多项式的系数的个数相等，若不等则需要补零。
数字信号处理实验四报告
实验四离散时间系统的特性和离散傅里叶变换实验报告一.实验内容（一）IIR系统的特性1. 某线性系统用差分方程表示为()()()()()=+-+---y n x n x n y n y n10.910.812求出系统函数，编程调用函数zplane画出系统函数的零极图；①思路：先手动算出差分方程所对应的系统函数，即对方程两边进行z变换，然后根据H(z)=Y(z)/X(z)算出。
然后调用zplane函数作出零极图。
②实验结果：系统函数：H(z)=(z^2+z)/(z^2-0.9*z+0.81);程序：a=[1,-0.9,0.81]; %X(z)按降幂排列时的各项系数b=[1,1,0]; %Y(z)按降幂排列时的各项系数zplane(b,a);xlabel('Re[z])');title('零极图');ylabel('jIm[z])');零极图如图1-1:所示：Re[z])j I m [z ])零极图图1-1 系统函数的零极图2. 调用函数freqz ，画出此系统的频率响应的幅度和相位。
①思路：调用freqz 函数求出频率响应，然后用abs 和angle 分别求幅频和相频。
②实验结果：程序：a=[1,-0.9,0.81];b=[1,1,0];[H,w]=freqz(b,a); %调用freqz 函数求频率响应magH=abs(H); %取模值，即幅度值angH=angle(H); %取相位值subplot(2,1,1);plot(w,magH),grid on %作2行1列的图形，第一个图形为幅度图 xlabel('rad/s');title('频率响应的幅度');ylabel('幅度'); %标注坐标轴的意义subplot(2,1,2);plot(w,angH),grid on %作2行1列的图形，第二个图形为相位图 xlabel('rad/s');title('频率响应的相位');ylabel('相位'); %标注坐标轴的意义作出的频率响应的幅度和相位图如图1-2所示：00.51 1.52 2.53 3.5rad/s频率响应的幅度幅度00.51 1.52 2.53 3.5rad/s 频率响应的相位相位图1-2 频率响应的幅度和相位图3.能否用编写的DTFT 子函数无误差地计算此系统的频率响应特性？不能，dtft 子函数实际上是由不连续的点连起来形成的，不可能做到无误差。
数字信号处理实验报告
《数字信号处理》实验报告实验一：Z 变换及离散时间系统分析给定系统)8.0/(2.0)(2+-=z z H ，编程并绘出系统的单位阶跃响应y(n),频率响应)e (jw H 。
给出实验报告。
实验代码clear;x=ones(100); t=1:100;b=[0 0 -0.2 ]; a=[1 0 0.8]; y=filter(b,a,x); (t,x,'r.',t,y,'k-'); grid on ;ylabel('x(n) and y(n)') xlabel('n')单位阶跃响应单位抽样：b=[0 0 -0.2 ]; a=[1 0 0.8];[h,t]=impz(b,a,70);stem(t,h, '.')幅頻，相频b=[0 0 -0.2 ];a=[1 0 0.8];[H,w]=freqz(b,a,256,1);Hr=abs(H);Hphase=angle(H);Hphase=unwrap(Hphase); subplot(211)plot(w,Hr);grid on;ylabel(' 幅频.')subplot(212)plot(w,Hphase);grid on; ylabel(' 相频')零极点图:b=[0 0 -0.2 ];a=[1 0 0.8];subplot(221);zplane(b,a);实验二：快速傅里叶变换设x(n)由三个实正弦组成，频率分别是8Hz,9Hz,10Hz,抽样频率为60 Hz,时域取256点，作FFT变换，观察波形，给出实验报告。
实验代码：clear all;N=256;f1=8;f2=9;f3=10;fs=60;w=2*pi/fs;x=sin(w*f1*(0:N-1))+sin(w*f2*(0:N-1))+sin(w*f3*(0:N-1)); subplot(3,1,1);plot(x(1:N/4));f=-0.5:1/N:0.5-1/N;X=fft(x);=ifft(X);(3,1,2);plot(f,fftshift(abs(X)));subplot(3,1,3);plot(real(y(1:N/4)));实验三：无限冲击响应数字滤波器设计设计一个数字带通滤波器，参数自定。
数字信号处理第四次实验报告
数字信号处理第四次试验实验报告任务一 IIR 系统的特性某线性系统用差分方程表示为()()()()()10.910.812y n x n x n y n y n =+-+---1、求出系统函数，编程调用函数zplane 画出系统函数的零极图；2、调用函数freqz ，画出此系统的频率响应的幅度和相位。
3、能否用编写的DTFT 子函数无误差地计算此系统的频率响应特性？1.1.1原理及公式()()()()()10.910.812y n x n x n y n y n =+-+---两边进行Z 变化 ()()()()()1120.90.81Y z X z z X z z Y z z Y z ---=++-整理得：()()()12122110.90.810.90.81Y z z z zH z X z z z z z ---++===-+-+ 1.1.2程序脚本clear all ;b=[1 1 0];a=[1 -0.9 0.81]; zplane(b,a);1.1.3程序运行结果Real PartI m a g i n a r y P a r t1.2.1原理和思路在ω的一个周期()~ππ-内取1024个点，用freqz 函数求出系统的频率响应，用1.2.2程序脚本和注释clear all ; M=1024;w=-pi:2*pi/M:pi; b=[1 1 0]; a=[1 -0.9 0.81]; h=freqz(b,a,w); mag=abs(h);pha=phase(h); % 提取滤波器频率响应的幅度mag 和相位pha plot(w,mag); xlabel('w/rad'); ylabel('Magnitude'); title('Magnitude(幅度)'); figure; plot(w,pha); xlabel('w/rad'); ylabel('Phase'); title('Phase （相位）');1.2.3程序运行结果w/rad M a g n i t u d eMagnitude(幅度)w/radP h a s ePhase （相位）1.3不能用编写的DTFT 子函数无误差地计算此系统的频率响应特性。
数字信号实验第四章答案解析
数字信号处理实验报告4线性时不变离散时间系统频域分析一、实验目的通过使用matlab做实验来加强对传输函数的类型和频率响应和稳定性测试来强化理解概念。
4.1 传输函数分析回答:Q4.1 修改程序P3_1去不同的M值，当0<w<2pi时计算并画出式（2.13）所示滑动平均滤波器的幅度和相位谱，代码如下：% Program Q4_1% Frequency response of the causal M-point averager of Eq. (2.13) clear;% User specifies filter lengthM = input('Enter the filter length M: ');% Compute the frequency samples of the DTFTw = 0:2*pi/1023:2*pi;num = (1/M)*ones(1,M);den = [1];% Compute and plot the DTFTh = freqz(num, den, w);subplot(2,1,1)plot(w/pi,abs(h));gridtitle('Magnitude Spectrum |H(e^{j\omega})|')xlabel('\omega /\pi');ylabel('Amplitude');subplot(2,1,2)plot(w/pi,angle(h));gridtitle('Phase Spectrum arg[H(e^{j\omega})]') xlabel('\omega /\pi');ylabel('Phase in radians');所得结果如图示：M=2M=7幅度和相位谱表现出对称性的类型是由于–冲激响应是实数，因此频率响应是周期且对称的，幅度谱是周期甚至对称的，相位响应是周期奇对称。
数字信号处理实验报告——傅里叶变换
B
x(n) sin( 2Mn / N )
M=4时正弦函数序列 代码 ----------------------------------------clear; close all N=20; t=0:1:N-1; syms k; %X=ones(1,N); X=8*((0.4).^t); w=exp(-1i.*2.*pi.*(k-1).*t./N).*X; %W=zeros(1,N); h=sum(w); for i=1:N k=i; W(i)=subs(h); end r=abs(W); r1=dftmtx(20); r1=X*r1; r2=abs(r1); figure; stem(t,X); figure; stem(t,r); figure; stem (t,r2); syms q; w1=exp(1i.*2.*pi.*(q-1).*t./N).*W./N; hw=sum(w1); for i=1:N q=i; x(i)=subs(hw); end
DSP 试验报告（四）
编 写 DFT Ⅰ实验目的 变 换 函 数 ， 并 对 序 列
Ⅳ试验结果
A
给定序列
x(n) sin( 2Mn / N ) 进行 DFT 变换
Ⅱ实验内容
x(n) 8 0.4 n
A 自编实现函数 DFT 与 IDFT。
任给一个时域序列和频域谱线序列，利用 MATLAB已有的dftmtx函数（DFT矩阵函数）,验证你 所编写的DFT与IDFT函数的正确性。
kn H (e j ) n0 x(n)e jn | 2 k / N DFT[ x(n)] n0 x(n)WN N 1 N 1
自己编写IDFT结果
x=abs(x); figure; stem(t,x);
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电子科技大学生命科学与技术学院标准实验报告
（实验）课程名称数字信号处理
2017-2018-第2学期
电子科技大学教务处制表
电子科技大学
实验报告
一、实验室名称：
二、实验名称：
滤波器传输函数的零点和极点对滤波特性的影响
三、实验学时：2学时
四、实验原理：
五、实验目的：
1. 直观地了解滤波器传输函数的零点和极点（的个数和位置）对滤波特性的影响。
2. 利用设计的滤波器进行滤波。
六、实验内容：
H(z):
1、给定某个滤波器的传输函数
2、利用设计滤波器进行滤波，分析滤波器的相位谱特性对滤波结果
的影响
九、实验数据及结果分析：
1. b=conv([0,0.0798],[1,0.6566]);
a=conv([1,-0.5335],[1,-(0.625+0.3773i)]);
a=conv(a,[1,-(0.625-0.3773i)]);
zplane(b,a);
[h,w]=freqz(b,a);
figure(2);plot(w/pi,abs(h))
r=0.5;
w=pi/4;
Rre=r*cos(w);
Rim=r*sin(w);
a1=Rre+i*Rim;
a2=Rre-i*Rim;
b1=0.8*(Rre+i*Rim);
b2=0.8*(Rre-i*Rim);
b=conv(b,[1,b1]);
b=conv(b,[1,b2]);
a=conv(a,[1,a1]);
a=conv(a,[1,a2]);
figure(3)
zplane(b,a);
[h,w]=freqz(b,a);
b=b/max(abs(h));
figure(4);plot(w/pi,abs(h)/max(abs(h)))
clear
x=1:0.01:10;
y=sin(5*x).*exp(0.5*x)+sin(5*x);
ffty=fft(y);
amp=abs(ffty);
pha=angle(ffty);
fliterPha=2*rand(1,length(pha));
phaNew=pha+fliterPha;
cc1=amp.*exp(i*phaNew);
yy1=ifft(cc1,'symmetric');
fliterPha2=linspace(0,-200,length(y));
phaNew2=pha+fliterPha2;
cc2=amp.*exp(i*phaNew2);
yy2=ifft(cc2,'symmetric');
plot(1:length(x),y,'g',1:length(x),yy1,'b',1:length(x),yy2,'r') 原系统图像
新增零极点后的图像
幅度谱对比图
n=0:99;
xs=cos(n*0.1*pi);
xn=sin(n*0.9*pi);
x=xs+xn;
figure(5)
plot(n,xs,'r',n,x,'b');legend('有用信号','加噪声信号');title('信号幅度') [h4,w4]=freqz(x);
figure(6);
plot(w4/pi,abs(h4));title('滤波前信号频谱')
q=filtfilt(b,a,x);
figure(7)
[h3,w3]=freqz(q);
plot(w/pi,abs(h3));title('滤波后信号频谱');
figure(8);
plot(n,q,'r',n,xs,'b');legend('有用信号','滤波后');title('滤波前后')
十、实验结论：（详细填写）
1.添加零点可以将幅度谱曲线向下弯曲
2.合理添加零极点可以更好地滤波
十一、总结及心得体会：（详细填写）
增加了对z变换意义的理解，熟悉了关于z变换的matlab编程方法。
十二、对本实验过程及方法、手段的改进建议：
报告评分：
指导教师签字：。