Ludwik公式中n值计算公式
lichnerowicz 公式

Lichnerowicz公式又称偏微分方程与微分几何之间的通信公式,是微分几何与偏微分方程领域的重要公式之一。
Lichnerowicz公式由法国数学家安德烈·利希纳罗维奇(André Lichnerowicz)于20世纪50年代提出,它描述了曲率与拉普拉斯算子之间的关系,为研究流形上的偏微分方程提供了重要工具。
Lichnerowicz公式在微分几何和相对论等领域有着广泛的应用,它是曲率与拉普拉斯算子间通信的本质。
通过Lichnerowicz公式,我们可以研究曲率与流形上的调和函数、本征值等之间的关系,从而深入理解流形结构与其上的偏微分方程。
为了全面地介绍Lichnerowicz公式,我们将从以下几个方面展开阐述:1. Lichnerowicz公式的基本概念Lichnerowicz公式是指曲率算子与拉普拉斯算子之间的通信。
在Riemannian流形上,曲率算子描述了流形上的几何性质,而拉普拉斯算子则是用来描述函数在该流形上的调和性质。
Lichnerowicz公式揭示了这两者之间的内在通信,通过分析曲率与拉普拉斯算子之间的关系,可以深入理解流形上的几何与微分方程之间的通信。
2. Lichnerowicz公式的数学表达Lichnerowicz公式的数学表达是一个重要的核心内容。
通常情况下,Lichnerowicz公式可以表示为△f + A(f) = 0,其中△为拉普拉斯算子,A为一个与曲率算子有关的算子,f为流形上的调和函数。
这个公式的重要性在于它将曲率算子与拉普拉斯算子之间的关系通过一个简洁而优美的数学形式展现出来。
3. Lichnerowicz公式的应用Lichnerowicz公式在微分几何、相对论等领域有着广泛的应用。
在微分几何领域,Lichnerowicz公式被广泛运用于研究流形上的调和函数、本征值等问题;在相对论领域,Lichnerowicz公式则为广义相对论方程的研究提供了重要的工具。
加工硬化指数n值

加工硬化指数n值加工硬化指数英文名即hardening index。
该指数由真应力应变关系定义,指金属薄板成形时真应力S一真应变ε关系式中的幂指数n,关系式如下:S = Kεn,式中K为强度系数。
亦即双对数坐标系lgS-lgε中,真应力-真应变关系式lgS=lgK+nlgε直线的斜率n是无量纲值,又称加工硬化指数。
(见真应力一真应变曲线)从数值上看,硬化指数n值等于(或近似等于)单向拉伸时材料最大均匀伸长应变的大小,即所谓细颈点应变。
也就是说,n表征了颈缩点位置。
应变分布不均是板材成形中的一个重要特点,n值的大小实际上反映了板材的应变均化能力,主要说明:(1)成形件的应变峰值不同。
n值小的材料产生的应变峰值高,n值大的材料产生的应变峰值低;(2)成形件上的应变分布不同。
n值小的材料应变分布不均匀,n值大的材料应变分布均匀。
硬化指数n值对板材成形极限曲线具有明显的影响,n值大材料的成形极限曲线高,n值小材料的成形极限曲线低。
板材的拉胀性能在很大程度上取决于材料的n值,n值高时,拉胀性能也好。
因此,硬化指数n值是评价板材成形性能的重要指标之一。
-可编辑修改-在双对数的坐标中真应力和真应变成线性关系,直线的斜率即为n,而K相当于ε=1.0时的真应力,见图1-5。
理想的弹性体和理想的塑性体限定了一般材料加工硬化指数n的变化范围,-可编辑修改-1.计算工程应力σ,工程应变ε。
2.计算真应力、真应变。
真应力=σ(1+ε)真应变=ln(1+ε)3.分别对真应力、真应变求Ln对数。
4.Ludwik-Hollomon方程式为:σ=K1+K2εn (σ、ε分别为真应力和真应变)公式变化可以得到:Lnσ= Ln K1+n Ln K2ε再把第3步求得的数据代进去进行Y=B+AX的拟合,斜率即为要求的n。
加工硬化和真应力-真应变曲线-可编辑修改-工程应力工程应变曲线的形状是不变的,并且对试样卸载和重新加载时,应力也没有区别(必须保证卸载和重新加载之间的时间足够短).然而,如果用真应力和真应变来绘制曲线的话就会有区别,例如真应变的定义是长度的增量除以标距瞬时长度,然而工程应变是长度的增量除以原始标距的长度.比较这两种绘制曲线的方法,会发现随着应变的增加,应力应变的数据会发生越来越显著的差.一会儿会给出一些例子.加工硬化率总是从真应力真应变数据中测量得到的.绝大多数应力应变曲线都遵循一个简单的能量表达式,称之为Holloman方程,如下:σt=Kεt n当n 为硬化比率或者硬化系数的时候,这个方程对中断的测试同样适用(但仅适用于立刻重新加载的测试,在室温下被延迟了几个小时后再加载就不适用了).由少量塑性应变,比如1%,引起的应力增加会很显著,在拉伸试验中可以测量出来,从而估计少量塑性应变后屈服强度的增加.对于给定应变,应力增量越大,冷加工屈服强度越大.这个有用的参数被称做加工硬化指数,可以通过绘制如下曲线得到:lnσ=ln K+n.lnε当塑性应变增加时,真应变和工程应变之间的差别也越来越大.一个可以选择的能精确测量 n 值的方法是在给定的应变处,测出真应力应变曲线的斜率:-可编辑修改-dσ/dε=n KεT n−1为了取代εn我们有:-dσ/dε=nσT/εT或者n=dσ/dε.εT/σT这里σT和εT是测量的 dσ/dε处的真应力和真应变.加工硬化指数n的实际意义-可编辑修改--可编辑修改-加工硬化指数n 反应了材料开始屈服以后,继续变形时材料的应变硬化情况,它决定了材料开始发生颈缩时的最大应力。
加工硬化指数n值

加工硬化指数n值加工硬化指数英文名即hardening index。
该指数由真应力应变关系定义,指金属薄板成形时真应力S一真应变ε关系式中的幂指数n,关系式如下:S = Kεn,式中K为强度系数。
亦即双对数坐标系lgS-lgε中,真应力-真应变关系式lgS=lgK+nlgε直线的斜率n是无量纲值,又称加工硬化指数。
(见真应力一真应变曲线)从数值上看,硬化指数n值等于(或近似等于)单向拉伸时材料最大均匀伸长应变的大小,即所谓细颈点应变。
也就是说,n表征了颈缩点位置。
应变分布不均是板材成形中的一个重要特点,n值的大小实际上反映了板材的应变均化能力,主要说明:(1)成形件的应变峰值不同。
n值小的材料产生的应变峰值高,n值大的材料产生的应变峰值低;(2)成形件上的应变分布不同。
n值小的材料应变分布不均匀,n值大的材料应变分布均匀。
硬化指数n值对板材成形极限曲线具有明显的影响,n值大材料的成形极限曲线高,n值小材料的成形极限曲线低。
板材的拉胀性能在很大程度上取决于材料的n值,n值高时,拉胀性能也好。
因此,硬化指数n值是评价板材成形性能的重要指标之一。
在双对数的坐标中真应力和真应变成线性关系,直线的斜率即为n,而K相当于ε=1.0时的真应力,见图1-5。
理想的弹性体和理想的塑性体限定了一般材料加工硬化指数n的变化范围,1.计算工程应力σ,工程应变ε。
2.计算真应力、真应变。
真应力=σ(1+ε)真应变=ln(1+ε)3.分别对真应力、真应变求Ln对数。
4.Ludwik-Hollomon方程式为:σ=K1+K2εn (σ、ε分别为真应力和真应变)公式变化可以得到:Lnσ= Ln K1+n Ln K2ε再把第3步求得的数据代进去进行Y=B+AX的拟合,斜率即为要求的n。
加工硬化和真应力-真应变曲线工程应力工程应变曲线的形状是不变的,并且对试样卸载和重新加载时,应力也没有区别(必须保证卸载和重新加载之间的时间足够短).然而,如果用真应力和真应变来绘制曲线的话就会有区别,例如真应变的定义是长度的增量除以标距瞬时长度,然而工程应变是长度的增量除以原始标距的长度.比较这两种绘制曲线的方法,会发现随着应变的增加,应力应变的数据会发生越来越显著的差.一会儿会给出一些例子.加工硬化率总是从真应力真应变数据中测量得到的.绝大多数应力应变曲线都遵循一个简单的能量表达式,称之为Holloman方程,如下:σt = Kεt n当n 为硬化比率或者硬化系数的时候,这个方程对中断的测试同样适用(但仅适用于立刻重新加载的测试,在室温下被延迟了几个小时后再加载就不适用了).由少量塑性应变,比如1%,引起的应力增加会很显著,在拉伸试验中可以测量出来,从而估计少量塑性应变后屈服强度的增加.对于给定应变,应力增量越大,冷加工屈服强度越大.这个有用的参数被称做加工硬化指数,可以通过绘制如下曲线得到:lnσ = ln K + n.lnε当塑性应变增加时,真应变和工程应变之间的差别也越来越大.一个可以选择的能精确测量 n 值的方法是在给定的应变处,测出真应力应变曲线的斜率:dσ / dε = n KεT n−1为了取代εn我们有:-dσ / dε = nσT / εT或者n = dσ / dε.εT / σT这里σT和εT是测量的dσ/dε处的真应力和真应变.加工硬化指数n的实际意义加工硬化指数n反应了材料开始屈服以后,继续变形时材料的应变硬化情况,它决定了材料开始发生颈缩时的最大应力。
物理化学公式大全

物理化学公式集热力学第一定律功:δW=δW e+δW f(1)膨胀功δW e=p外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f=xdy非膨胀功为广义力乘以广义位移。
如δW(机械功)=fdL,δW(电功)=EdQ,δW(表面功)=rdA。
热Q:体系吸热为正,放热为负。
热力学第一定律:△U=Q—W 焓H=U+pV理想气体的内能和焓只是温度的单值函数。
热容C=δQ/dT(1)等压热容:C p=δQ p/dT=(∂H/∂T)p(2)等容热容:C v=δQ v/dT=(∂U/∂T)v常温下单原子分子:C v,m=C v,m t=3R/2常温下双原子分子:C v,m=C v,m t+C v,m r=5R/2等压热容与等容热容之差:(1)任意体系C p—C v=[p+(∂U/∂V)T](∂V/∂T)p(2)理想气体C p—C v=nR理想气体绝热可逆过程方程:pVγ=常数TVγ-1=常数p1-γTγ=常数γ=C p/ C v理想气体绝热功:W=C v(T1—T2)=(p1V1—p2V2)理想气体多方可逆过程:W=(T1—T2)热机效率:η=冷冻系数:β=-Q1/W可逆制冷机冷冻系数:β=焦汤系数:μJ-T==-实际气体的ΔH和ΔU:ΔU=+ΔH=+化学反应的等压热效应与等容热效应的关系:Q p=Q V+ΔnRT当反应进度ξ=1mol时,Δr H m=Δr U m+RT化学反应热效应与温度的关系:热力学第二定律Clausius不等式:熵函数的定义:dS=δQ R/T Boltzman熵定理:S=klnΩHelmbolz自由能定义:F=U—TS Gibbs自由能定义:G=H-TS热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU=TdS-pdV dH=TdS+VdpdF=-SdT-pdV dG=-SdT+Vdp(2)Maxwell关系:==-(3)热容与T、S、p、V的关系:C V=T C p=TGibbs自由能与温度的关系:Gibbs-Helmholtz公式=-单组分体系的两相平衡:(1)Clapeyron方程式:=式中x代表vap,fus,sub。
初中物理力学公式
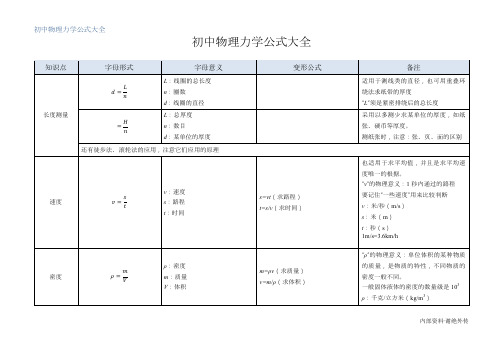
初中物理力学公式大全知识点字母形式字母意义变形公式备注长度测量d=LnL:线圈的总长度n:圈数d:线圈的直径适用于测线类的直径,也可用重叠环绕法求纸带的厚度“L”须是紧密排绕后的总长度=HnL:总厚度n:数目d:某单位的厚度采用以多测少求某单位的厚度,如纸张、硬币等厚度。
测纸张时,注意:张、页、面的区别还有徒步法、滚轮法的应用,注意它们应用的原理速度v=stv:速度s:路程t:时间s=vt(求路程)t=s/v(求时间)也适用于求平均值,并且是求平均速度唯一的根据。
“v”的物理意义:1秒内通过的路程要记住“一些速度”用来比较判断v:米/秒(m/s)s:米(m)t:秒(s)1m/s=3.6km/h密度ρ=mVρ:密度m:质量V:体积m=ρv(求质量)v=m/ρ(求体积)“ρ”的物理意义:单位体积的某种物质的质量,是物质的特性,不同物质的密度一般不同。
一般固体液体的密度的数量级是103ρ:千克/立方米(kg/m3)知识点字母形式字母意义变形公式备注m:千克(kg)V:立方米(m3)1×103kg/m3=1g/cm3重力G=mg G:重力g:重力与质量的比值m=G/g(求质量)重力的施力体是地球G:牛顿(N)g:牛顿/千克(N/kg)g=9.8N/kg是指在地球上。
(g取值要根据题目具体要求)合力方向相同:F合=F1+F2方向相反:F合=∣F1-F2∣方向与两个分力方向相同方向与较大力方向相同压强p=FSp:压强F:压力S:受力面积F=pS(求压力)S=F/p(求面积)适用于任何压强的计算压力:垂直压在物体表面上的力,不是指重力(注意作用点)受力面积:两物体有相互接触的部分p:帕斯卡(Pa)F:牛顿(N)S:平方米(m2)1Pa=1N/m2,表示某物体单位面积上受到的压力p=ρghρ:固体密度h:物体高度ρ=p/gh(求密度)h=p/ρg(求高度)适用于侧面与底面垂直的固体(长方体、正方体、圆柱体)知识点字母形式字母意义变形公式备注h:米(m)p=ρgh ρ:液体的密度h:深度,即所求压强的点到自由液面的竖直距离ρ=p/gh(求密度)h=p/ρg(求深度)适用于液体压强h:米(m)1cm深的水产生的压强是100Pa1标准大气压=760mmHg=1.01×105Pa浮力F浮=G物……①F浮:物体的浮力G物:物体的重力F浮=G船+G货只适用物体漂浮或悬浮F浮=G物-F拉……②F拉:物体在液体中向上的拉力(在液体中时弹簧的示数)用测力计求浮力法F浮=F向上-F向下……③F向上:物体下表面受到的向上液体的压力F向下:物体上表面受到的向下液体的压力压力差法求浮力若F向下=0N,说明此时物体是处于漂浮状态,F=G物若F向上=0N,说明此时物体没有受到浮力,如塞在水池底部的塞子,打入水池底部的木桩等F浮=G排G排:排开液体的重力阿基米德原理,注意V排、V物的关系V排:立方米(m3)F浮=ρ液gV排……④ρ液:液体的密度V排:排开液体的体积(即浸入液体中的体积)浸没在水中100cm3的物体受到水的浮力是1N知识点字母形式字母意义变形公式备注V物V液=ρ液ρ物V物:物体的体积物体处于漂浮状态根据F浮=G和F浮=ρ液g V排得G=ρ液g V排,G=ρ物g V排故ρ物g V物=ρ液g V排。
加工硬化指数n计算方法

1.计算工程应力σ,工程应变ε。
2.计算真应力、真应变。
真应力=σ(1+ε)真应变=ln(1+ε)3.分别对真应力、真应变求Ln对数。
4.Ludwik-Hollomon方程式为:σ=K1+K2εn(σ、ε分别为真应力和真应变)公式变化可以得到:Lnσ= Ln K1+n Ln K2ε再把第3步求得的数据代进去进行Y=B+AX 的拟合,斜率即为要求的n。
加工硬化和真应力-真应变曲线工程应力工程应变曲线的形状是不变的,并且对试样卸载和重新加载时,应力也没有区别(必须保证卸载和重新加载之间的时间足够短).然而,如果用真应力和真应变来绘制曲线的话就会有区别,例如真应变的定义是长度的增量除以标距瞬时长度,然而工程应变是长度的增量除以原始标距的长度.比较这两种绘制曲线的方法,会发现随着应变的增加,应力应变的数据会发生越来越显著的差.一会儿会给出一些例子.加工硬化率总是从真应力真应变数据中测量得到的.绝大多数应力应变曲线都遵循一个简单的能量表达式,称之为Holloman方程,如下:σt = Kεt n当n 为硬化比率或者硬化系数的时候,这个方程对中断的测试同样适用(但仅适用于立刻重新加载的测试,在室温下被延迟了几个小时后再加载就不适用了).由少量塑性应变,比如1%,引起的应力增加会很显著,在拉伸试验中可以测量出来,从而估计少量塑性应变后屈服强度的增加.对于给定应变,应力增量越大,冷加工屈服强度越大.这个有用的参数被称做加工硬化指数,可以通过绘制如下曲线得到:lnσ = ln K + n.lnε当塑性应变增加时,真应变和工程应变之间的差别也越来越大.一个可以选择的能精确测量n 值的方法是在给定的应变处,测出真应力应变曲线的斜率:dσ / dε = n KεT n−1为了取代εn我们有:-dσ / dε = nσT / εT或者n = dσ / dε.εT / σT这里σT和εT是测量的dσ/dε处的真应力和真应变.第1章材料在静载下的力学行为(力学性能)1.1 材料在静拉伸时的力学行为概述静拉伸是材料力学性能试验中最基本的试验方法。
流体主要计算公式

流体主要计算公式-CAL-FENGHAI.-(YICAI)-Company One1主要的流体力学事件有:1738年瑞士数学家:伯努利在名着《流体动力学》中提出了伯努利方程。
1755年欧拉在名着《流体运动的一般原理》中提出理想流体概念,并建立了理想流体基本方程和连续方程,从而提出了流体运动的解析方法,同时提出了速度势的概念。
1781年拉格朗日首先引进了流函数的概念。
1826年法国工程师纳维,1845年英国数学家、物理学家斯托克思提出了着名的N-S方程。
1876年雷诺发现了流体流动的两种流态:层流和紊流。
1858年亥姆霍兹指出了理想流体中旋涡的许多基本性质及旋涡运动理论,并于1887年提出了脱体绕流理论。
19世纪末,相似理论提出,实验和理论分析相结合。
1904年普朗特提出了边界层理论。
20世纪60年代以后,计算流体力学得到了迅速的发展。
流体力学内涵不断地得到了充实与提高。
理想势流伯努利方程(3-14)或(3-15)物理意义:在同一恒定不可压缩流体重力势流中,理想流体各点的总比能相等即在整个势流场中,伯努利常数C 均相等。
(应用条件:“”所示)符号说明物理意义几何意义单位重流体的位能(比位能)位置水头单位重流体的压能(比压能)压强水头单位重流体的动能(比动能)流速水头单位重流体总势能(比势能)测压管水头总比能总水头二、沿流线的积分1.只有重力作用的不可压缩恒定流,有2.恒定流中流线与迹线重合:沿流线(或元流)的能量方程:(3-16)注意:积分常数C,在非粘性、不可压缩恒定流流动中,沿同一流线保持不变。
一般不同流线各不相同(有旋流)。
(应用条件:“”所示,可以是有旋流)流速势函数(势函数)观看录像>>存在条件:不可压缩无旋流,即或必要条件存在全微分d直角坐标(3-19)式中:——无旋运动的流速势函数,简称势函数。
势函数的拉普拉斯方程形式对于不可压缩的平面流体流动中,将(3-19)式代入连续性微分方程(3-18),有:或?(3-20)适用条件:不可压缩流体的有势流动。
AutoForm材质库的建立与生成-2016-03-10-YY

关于这些材料特性及其参数设置将在 13 .2 .3 小 节详细介绍 。
- H幽由唰咆 curve
伽瞄Ined S- H
-'
1
500
400
m:
300 200 100
0.0
0.2
0.4
0. 6
拉伸曲线是由拉伸试验所测定,而 AutoForm 所需的真实应力是塑性应变对数的函数,所
需的拉伸曲线是在轧制方向上测得的。其中方向依赖性是通过厚向异性系数 r 值来描述 。 下
面以图 1 3 -1 2 所示的拉伸试验为例来说明如何用测定的数据来计算真实应力和真实应变的函 数关系 。
午告 : 甲 主斗
Ilfg'I .lPj'&方W
282
}l. uto俨orm 原理 技 巧与战向 军 用手件
后输入对应的拟合参数 。 如图 13 -6 所示,当选定屈服面拟合模型为 Hill 后,在其下方会自动
列出此模型拟合时所 需 的 参 数输入框 。 这些参 数包括与轧制方向夹角为 0 、 45 和 90 度的 三 个
旦旦旦旦三旦旦陆咄咄
1000
..。
‘ 00
"OOi
200
-400
口…
m
0 . 00 . 2
@
、.
..,;
h
设置硬化曲线
f冒--甸回edr...崎
厂厂
参数
o -t! 巾,阳回..
..。
设置屈服面参
1. 0
数
.00 200
。.
@ 才骨一 设置成形极限
