弹性力学有限元法.ppt
合集下载
有限元入门ppt课件

有限体积法 (Finite Volume Method)
其基本思路是:将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,便得出一组离散方程。其中的未知数是网格点上的因变量的数值。为了求出控制体积的积分,必须假定值在网格点之间的变化规律,即假设值的分段的分布的分布剖面。
1-2 应力的概念
作用于弹性体的外力(或称荷载)可能有两种: 表面力,是分布于物体表面的力,如静水压力,一物体与另一物体之间的接触压力等。单位面积上的表面力通常分解为平行于座标轴的三个成分,用记号 来表示。 体力,是分布于物体体积内的外力,如重力、磁力、惯性力等。单位体积内的体力亦可分解为三个成分,用记号X、Y、Z表示。 弹性体受外力以后,其内部将产生应力。
边界元法 (Boundary Element Method)
边界元法是一种继有限元法之后发展起来的一种新的数值方法,与有限元法不同,边界元法仅在定义域的边界划分单元,用满足控制方程的函数去逼近边界条件。所以边界元与有限元相比具有单元和未知数少、数据准备简单等优点,但边界元法解非线性问题时,遇到同非线性项相对应的区域积分,这种积分奇异点处的强烈的奇异性,使求解遇到困难。边界元法在塑性问题中应用还比较少。
弹性力学 — 区别与联系 — 材料力学 弹性力学与材料力学既有联系又有区别。它们都同属于固体力学领域,但弹性力学研究的对象更普遍,分析的方法更严密,研究的结果更精确,因而应用的范围更广泛。 弹性力学 固有弱点: 由于研究对象的变形状态较复杂,处理的方法又较严谨,因而解算问题时,往往需要冗长的数学运算。但为了简化计算,便于数学处理,它仍然保留了材料力学中关于材料性质的假定:
塑性有限元常用软件
弹性力学边值问题及有限元法(PPT)

(2)在边界上给定位移——位移边界条件
(3)在边界上部分给定面力,部分给定位移——混合边界条件
基本解法
弹性力学边值问题——基本方程+边界条件
给定作用在物体全部边界或内部的外界作用(包括温度影响、 外力等),求解物体内由此产生的应力场和位移场。
具体地说,对物体内每一点,当它处在弹性阶段,其应力分 量、应变分量、位移分量等15个未知函数要满足平衡方程、几 何力程、本构方程这15个泛定方程,在边界上并要满足给定的 全部边界条件。
通过与原问题基本方程及边界条件等效的变分原理,建立求 解的代数方程组,求解有限个节点上的场变量值
用有限个节点场变量值插值得到全求解域任意位置的场变量
单元内近似函程形式必须一样 单元内近似函数一般取Lagrange多项式
单元位移函数
对三角形单元,假定单元内的位移分量是坐标的线性函数
x
x
xy
y
xz
z
Fbx
0
yx
x
y
y
yz
z
Fby
0
zx
x
zy
y
z
z
Fbz
0
平衡方程的意义
受力而平衡的弹性体内 各应力之间(及其与体 力之间)的相互制约关 系
几何方程
x
u x
y
v y
z
w z
xy
u y
v x
xy
v z
w y
xy
w x
u z
应变与位移之间的关系, 以及应变之间的关系
物理方程
也叫本构方程
应力应变之间的关系
x
E(1 ) (1 )(1 2)
( x
1
y
(3)在边界上部分给定面力,部分给定位移——混合边界条件
基本解法
弹性力学边值问题——基本方程+边界条件
给定作用在物体全部边界或内部的外界作用(包括温度影响、 外力等),求解物体内由此产生的应力场和位移场。
具体地说,对物体内每一点,当它处在弹性阶段,其应力分 量、应变分量、位移分量等15个未知函数要满足平衡方程、几 何力程、本构方程这15个泛定方程,在边界上并要满足给定的 全部边界条件。
通过与原问题基本方程及边界条件等效的变分原理,建立求 解的代数方程组,求解有限个节点上的场变量值
用有限个节点场变量值插值得到全求解域任意位置的场变量
单元内近似函程形式必须一样 单元内近似函数一般取Lagrange多项式
单元位移函数
对三角形单元,假定单元内的位移分量是坐标的线性函数
x
x
xy
y
xz
z
Fbx
0
yx
x
y
y
yz
z
Fby
0
zx
x
zy
y
z
z
Fbz
0
平衡方程的意义
受力而平衡的弹性体内 各应力之间(及其与体 力之间)的相互制约关 系
几何方程
x
u x
y
v y
z
w z
xy
u y
v x
xy
v z
w y
xy
w x
u z
应变与位移之间的关系, 以及应变之间的关系
物理方程
也叫本构方程
应力应变之间的关系
x
E(1 ) (1 )(1 2)
( x
1
y
有限元经典PPT第4章

Pii Kiiui
Ki1u1 Ki2u2 Kiiui K u i,i1 i1
ui
n
Kiiui Kiiui
Kiju j
4.1.2 平面应力问题有限元的基本思想和瑞雷-里兹法
v3 f3y
3
u3
f3x
f1y v1 u1
1 f1x
v2 f2y u2
2 f2x
给定一个三角形单元和作用在角点上 的六个力,要求得六个角点的位移。 或者是要求三角形角点发生指定的位 移,在三角形三个角点如何加力?
很显然,问题的精确解很困难。采用 瑞雷-里兹法求近似式解
e号单元的三个节点I,j,k的力对应的 力的平衡方程是第2i-1,2i;2j-1,2j;2k1,2k个平衡方程
e号单元的三个节点I,j,k的位移是第 2i-1,2i;2j-1,2j;2k-1,2k个未知数
弹性模量:E 横截面积:A
1
1 L
2
2L
3
局部系单元刚度阵:
k
1
EA L
1 -1
-1
1
2 集成总刚:
0 1
解得:
ux uy
L EA
3.8284L
EA
i
j
第一类位移条件:
Ki1u1 Ki2u2 Kiiui Ki1ui1
ui 0
令: Kij 0 i j
m
vi 0
Kii 1
um 0
Pi 0
ui 0
第二类位移条件:um um
大数
充大数法: Kii Kii
第一步:求转换矩阵
k2
EA 1 2L -1
-1
1
P
cos 0
T sin
弹性力学教学课件-1-有限元位移法的基本概念
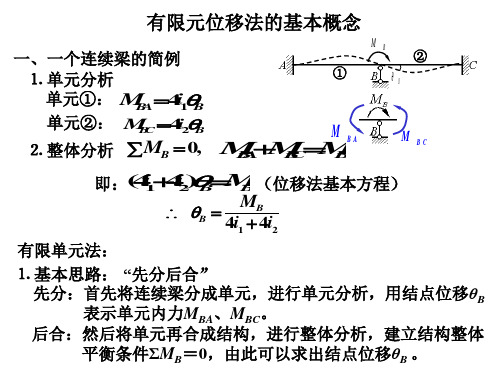
2i1
M3 0
2i1 4i1 4i2
2i2
②
M3
3
0阵:
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22132
m(e) 1 m2
k k1 21 1
k12(e) k22
(e) 1
2
四、支承条件的引入
第一步:暂不引入支承条件,
0
1 1
2
3
2 i1 2
即: M M1242ii11112(4i1i1240i2)322i23 1
M3 012i224i23
0
或:
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22132
1
(4i1 4i2)2 ② 2 i2 2
① 2 2
3
2 i2 3
3 4 i2 3
①2
②
3
M M M123420ii11
2i1 4i1 4i2
2i2
420ii22012M PP123
取出前面两个纯量方程:
4i112i12 P1 2i11(4i14i2)2
P2
即:
4i1 2i1
4i12i14i212P P12
1
①
M2
2
②
M3
3
4 i1 1
2 i1 1 ①
②
0
1 1
2
3
2 i1 2
即: M M1242ii11112(4i1i1240i2)322i23 1
M3 012i224i23
0
或:
M M M123420ii11
2i1 4i1 4i2
有限元 第2讲 有限元法基本理论

•根据问题性质,忽略部分暂时不必考虑的因素,提出一 些基本假设。使问题的研究限定在一个可行的范围。
•基本假设是学科的研究基础。 •超出基本假设的研究领域是固体力学其它学科的研究。
© BIPT
弹性力学的基本假设 1. 连续性假设
•——假设所研究的整个弹性体内部完全由组成物体的 介质所充满,各个质点之间不存在任何空隙。
第2章 有限元法基本理论
张 洪 伟
© BIPT
内容提要
1
弹性力学问题基本描述
弹性问题参量原理
2
3 4
有限元分析基本步骤
有限元解的误差分析
© BIPT
弹性力学问题的基本描述
基本假设的必要性 •工程问题的复杂性是诸多方面因素组成的。如果不分主 次考虑所有因素,则问题的复杂,数学推导的困难,将 使得问题无法求解。
© BIPT
弹性力学的基本假设
5. 小变形假设
——假设在外力或者其他外界因素(如温度等)的影响下, 物体的变形与物体自身几何尺寸相比属于高阶小量。
——在弹性体的平衡等问题讨论时,可以不考虑因变形所 引起的尺寸变化。 ——忽略位移、应变和应力等分量的高阶小量,使基本方 程成为线性的偏微分方程组。
© BIPT
© BIPT
弹性力学的基本假设
4. 完全弹性假设
•——对应一定的温度,如果应力和应变之间存在一一对 应关系,而且这个关系和时间无关,也和变形历史无关, 称为完全弹性材料。 •完全弹性分为线性和非线性弹性,弹性力学研究限于线 性的应力与应变关系。 •研究对象的材料弹性常数不随应力或应变的变化而改变。
符号规定:
应力的概念
图示单元体面的法线为y,称为y面,应力 分量垂直于单元体面的应力称为正应力。 正应力记为 y ,沿y轴的正向为正,其下
(同济大学)第1讲_弹性力学及有限元方法概述

有限元分析
的一般规律物体在空间的位置随时间的改变
对象内容
任务
对象内容
任务
概述
ANSYS 静力分析z起重机械有限元应用
整机模态分析
车辆安全性
工件淬火3.06 min 时的温度、组织分布(NSHT3D)
同济大学
同济大学
金属反挤压成型:温度分布和变化铸造成型:温度变化和气泡
速度
压力导流管分析
超音速飞行压力分布汽车气动分析
高速导弹气动
同济大学
两根热膨胀系数不同的棒焊接在一起,加热后的变形情况
子结构方法分析大型结构的早期应用法
梁单元
建模时充分利用重复性。
有限元ppt课件

15
里兹法:
选择一个定义于整个求解域 并满足边界条件的试探函数
将试探函数代入泛函表 达式,建立线性方程
求解方程 计算系数
16
设有边值问题
d2 y dx2
y
1
0
(1-8)
y(0) 0, y(1) 0
通过数学推导,求得其泛函为
I y(x) 1(1 y2 1 y2 y)dx
39
厚度为1的微分体,在水平方向拉
力F的作用下发生了位移 xdx
拉力表达式:
F xdy 1
x
x dy
拉力做的功:
dx
xdx
dW
1 2
F xdx
将F代入:
dW
1 2
x
x x dy
dU
dW
1 2
x
x
dxdy
单位体积内的应变能:
边值问题的求解
泛函极值的求解
泛函:给定满足一定条件的函数集合A:{y(x)},和实数 集合R。设y(x)是A中的函数,V是R中的变量,若A和V 之间存在一个对应关系,就是A中的每个函数y(x),R 中都有唯一的V值与之对应,则称V是函数y(x)的泛函,
记为V=V(y(x))。
A称为泛函的定义域,可变函数y(x)称为自变函数,依赖 自变函数而变的量V,称为自变函数的泛函。
U T dV V
单位体积内的虚应变能为
U T
U
U
o
43
2.虚位移原理 虚位移原理又称虚功原理,是最基本的能量原理.
虚位移原理:如果在虚位移发生之前弹性体是平衡的, 那么在虚位移发生时,外力在虚位移上所做的功就等 于弹性体的虚应变能,即
里兹法:
选择一个定义于整个求解域 并满足边界条件的试探函数
将试探函数代入泛函表 达式,建立线性方程
求解方程 计算系数
16
设有边值问题
d2 y dx2
y
1
0
(1-8)
y(0) 0, y(1) 0
通过数学推导,求得其泛函为
I y(x) 1(1 y2 1 y2 y)dx
39
厚度为1的微分体,在水平方向拉
力F的作用下发生了位移 xdx
拉力表达式:
F xdy 1
x
x dy
拉力做的功:
dx
xdx
dW
1 2
F xdx
将F代入:
dW
1 2
x
x x dy
dU
dW
1 2
x
x
dxdy
单位体积内的应变能:
边值问题的求解
泛函极值的求解
泛函:给定满足一定条件的函数集合A:{y(x)},和实数 集合R。设y(x)是A中的函数,V是R中的变量,若A和V 之间存在一个对应关系,就是A中的每个函数y(x),R 中都有唯一的V值与之对应,则称V是函数y(x)的泛函,
记为V=V(y(x))。
A称为泛函的定义域,可变函数y(x)称为自变函数,依赖 自变函数而变的量V,称为自变函数的泛函。
U T dV V
单位体积内的虚应变能为
U T
U
U
o
43
2.虚位移原理 虚位移原理又称虚功原理,是最基本的能量原理.
虚位移原理:如果在虚位移发生之前弹性体是平衡的, 那么在虚位移发生时,外力在虚位移上所做的功就等 于弹性体的虚应变能,即
第3讲—弹性力学问题的有限单元法

1 T U d Kd 2
u1 d u 2 u 3
有限单元法
崔向阳
Step 3: 单元集成
单元集成——外力功
整体节点 位移列阵
整体等效节 点力列阵
u1 d u2 u 3
f1 R1 f f 2 0 f F 3
有限单元法
崔向阳
Step 2.单元特征分析
xi
单元节点位移列阵: 单元节点坐标列阵: 单元等效节点力列阵:
II=0
有限单元法 崔向阳
真实位移
6
最小势能原理
1 II ij ij dV bi ui dV pi ui dA 2 Sp 1 II Dijkl ij kl dV bi ui dV pi ui dA Sp 2
ij
ij
dV biui dV piui dA
Sp
弹性问题中等价于最小势能原理!
有限单元法 崔向阳
比较:虚功原理和能量变分原理
虚功原理是理论力学上的一个根本性原理,可以用于
一切非线性力学问题。
最小势能原理只是虚功原理对弹性体导出的一种表述
形式,但是对于线弹性问题,最小势能原理的应用非 常方便。
ij ui ij ui Dijkl ij kl dV bi ui dV pi ui dA Sp ij ij dV bi ui dV pi ui dA Sp
V= – W
弹性势能—弹性体变形后,产生弹性内力,这种力也具有对外作 功的能力,称为弹性势能,或弹性应变能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/11
13
在离散体中任取一个单元,三个节点按逆时针方向顺序编
号为i,j,m。节点坐标分别表示为(xi,yi),(xj,yj), (xm,ym)。
2021/3/11
14
对于弹性力学平面问题,一个三角形单元上的每 个节点应有2个位移分量,则三角形单元共有6个自 由度: ui , vi ,u j , v j ,um , vm 。
u x
K
矩形单元:采用双线性位移模式,单元内的应力是线性
变化的。
u kx2 mx
(kx2 mx) x
3. 薄板弯曲单元和薄板单元
2021/3/11
7
4. 多面体单元
2021/3/11
8
5. 等参数单元:单元内任一点的位移与节点位移之间的关系 恰好和该点的坐标与节点坐标之间的关系相同。
任意四边形的边一般不平行于坐标轴,沿单元边的位 移将按抛物线变化,而不是线性变化。
2021/3/11
2
(2)分析单元的力学性质 列出单元节点和节点位移之间的关系式。应用几何方程和
物理方程来建立力和位移的方程式,导出单元刚度矩阵。
节点载荷和节点位移之间的关系式为:
Fe Kee
K e 为单元刚度矩阵。
(3)计算等效节点力:用等效的节点力来代替所有在单元 上的力。
2021/3/11
元位移模式。
u(x, v(x,
y) y)
Ni
(x, 0
y)
0 N j (x, y) Ni (x, y) 0
0 Nm (x, y) N j (x, y) 0
0
Nm
(
x,
y)
u Ne
2021/3/11
18
• N称为形函数矩阵或插值函数矩阵。
插值函数具有如下性质: (1)在节点上插值函数的值有:
vi a4 a5 xi a6 yi
u j a1 a2 x j a3 y j
v j a4 a5 x j a6 y j
um
a1
a2 xm
a3 ym
2021/3/11 vm a4 a5 xm a176 ym
由上式可以确定 a1, a2,a6 的值。将其带入 (1)式就可以得到用单元节点位移表示的单
以直角坐标系XOY下的任意直边四边形单元单元的形心 为坐标原点,用等分它四个边的两条直线为坐标轴,建立一 个非正交的局部座标系 o1 ,使单元边界上的 、 是1 , 这样在局部坐标系中构成一个矩形单元。矩形单元的节点和 内部任一点都与原总体坐标系中的单元的节点和内部点形成 一一对应关系。总体坐标系适用于整个结构,局部坐标系只 适用于具体某个单元。
第3章 弹性力学有限元法
2021/3/11
1
3.1有限元法求解问题的基本步骤
1. 问题及求解域定义 2. 连续体离散化
即有限元网格划分,将连续体划分为有限个具 有一定形状的单元组合体,相邻单元之间通过节点 相连接。
3. 单元分析 (1)选择位移模式
位移法:选择节点位移作为基本未知量。(应用较多) 力法:选择节点力为基本未知量。 混合法:取一部分力和一部分节点位移作为基本未知量。
将单元的位移分量u,v取为坐标x,y的多项式,且位移 场函数u,v在三个节点处的数值应该等于这三个节点处的六 个位移分量。 即有:
2021/3/11
16
u(x, v(x,
y) y)
a1 a4
a2 a5
x x
a3 a6
y y
在i,j,m三点应该有:
(1)
ui a1 a2 xi a3 yi
Ni (x, y) ij 10当当jj=i(i i,j,m)
(2)在单元内任一点各插值函数的和等于一。
2021/3/11
2021/3/11
9
6. 轴对称单元: 几何形状是回转体,所受约束和外力对称于回转轴的
机械机构称为轴对称问题。对此类问题一般采取柱坐标系 来描述应力和变形。
对于此类问题采用轴对称单元。
划分网格的基本原则: (1)网格数量:网格数量增加,计算精度会有所提高。 (2)网格疏密:在结构不同处采用不同的网格形式。 (3)单元阶次:网格数量较少时,计算精度差别较大,采 用高阶单元。网格数量较多时,采用两种单元的精度相差不 大,采用低阶单元计算量降低。
常用的单元类型: 1. 杆单元
一维单元,位移仅是轴向座标的函数。
2021/3/11
5
2. 平面单元 二维单元,单元内任意点的应力、应变、位移仅与两个
座标方向的变量有关。
2021/3/11
6
三角形单元:采用线性位移模式,在整个单元内各点的 应变值为常数,所以也称为常应变单元或常应力单元。
u kx
2021/3/11
11
3.3 单元分析
1. 单元的插值函数 如果弹性体内的位移分量已知,则应变分量和
应力分量也可以确定了。
F Ku
~ u 几何方程 E 虎克定律
2021/3/11
பைடு நூலகம்
12
对于整体划分单元后,在每个单元的局部范围里可以采 用比较简单的函数来近似地表达单元的真实位移,把各单元 的位移函数连接起来,就可以近似表示整个区域的真实的位 移函数。
2021/3/11
10
(4)网格质量:网格几何形状的合理性,网格质量 的好坏会影响计算精度,对于太差的网格形状程序 将会自动停止计算。 (5)网格分界面和分界点:结构中一些特殊位置的 界面或特殊位置的点应分为网格边界或节点。 (6)位移协调性:一个单元的节点必须也是相邻单 元的节点,只有这样单元上的力和力矩才能够通过 节点传递到相邻单元。 (7)网格布局:对于对称结构应该划分对称单元。 (8)节点和单元编号:一般情况下程序自动编号。
3
4. 组成物体的整体方程组 由单元刚度矩阵构成整体刚度矩阵。对总体建立方程:
F Ku
5. 求解有限元方程和结果解释 根据边界条件和初始条件求解上式,得到节点位移。
2021/3/11
4
3.2 连续体离散化
结构的离散化也称为有限元网格划分,即将求解域近似 为具有不同有限大小和形状且只在节点上彼此相连的有限个 单元组成的离散域。
三角形单元的节点位移矢量是:
e (ui , vi ,u j , vj ,um, vm )T
单元节点力矢量是:
Fe
(
X
e i
,
Yie
,
X
e j
,
Yje
,
X
e m
,
Yme
)T
2021/3/11
15
单元分析的基本任务是建立单元节点力与节点位移之间的 关系式:
Fe Kee
式中 K e 是6*6的矩阵,称为单元刚度矩阵。
