大学物理下册十四章
大学物理第十四章波动光学课后习题答案及复习内容

第十四章波动光学一、基本要求1. 掌握光程的概念以及光程差和相位差的关系。
2. 理解获得相干光的方法,能分析确定杨氏双缝干涉条纹及薄膜等厚干涉条纹的位置,了解迈克尔逊干涉仪的工作原理。
3. 了解惠更斯-菲涅耳原理; 掌握用半波带法分析单缝夫琅和费衍射条纹的产生及其明暗纹位置的计算,会分析缝宽及波长对衍射条纹分布的影响。
4. 掌握光栅衍射公式。
会确定光栅衍射谱线的位置。
会分析光栅常数及波长对光栅衍射谱线分布的影响。
5. 了解自然光和线偏振光。
理解布儒斯特定律和马吕斯定律。
理解线偏振光的获得方法和检验方法。
6. 了解双折射现象。
二、基本内容1. 相干光及其获得方法只有两列光波的振动频率相同、振动方向相同、振动相位差恒定时才会发生干涉加强或减弱的现象,满足上述三个条件的两束光称为相干光。
相应的光源称为相干光源。
获得相干光的基本方法有两种:(1)分波振面法(如杨氏双缝干涉、洛埃镜、菲涅耳双面镜和菲涅耳双棱镜等);(2)分振幅法(如薄膜干涉、劈尖干涉、牛顿环干涉和迈克耳逊干涉仪等)。
2. 光程和光程差(1)光程把光在折射率为n的媒质中通过的几何路程r折合成光在真空x中传播的几何路程x,称x为光程。
nr(2)光程差在处处采用了光程概念以后就可以把由相位差决定的干涉加强,减弱等情况用光程差来表示,为计算带来方便。
即当两光源的振动相位相同时,两列光波在相遇点引起的振动的位相差πλδϕ2⨯=∆ (其中λ为真空中波长,δ为两列光波光程差) 3. 半波损失光由光疏媒质(即折射率相对小的媒质)射到光密媒质发生反射时,反射光的相位较之入射光的相位发生了π的突变,这一变化导致了反射光的光程在反射过程中附加了半个波长,通常称为“半波损失”。
4. 杨氏双缝干涉经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况:(1)位相差为0或2π的整数倍,合成振动最强;(2)位相差π的奇数倍,合成振动最弱或为0。
其对应的光程差()⎪⎩⎪⎨⎧-±±=212λλδk k ()()最弱最强 ,2,1,2,1,0==k k 杨氏的双缝干涉明、暗条纹中心位置:dD k x λ±= ),2,1,0( =k 亮条纹 d D k x 2)12(λ-±= ),2,1( =k 暗条纹 相邻明纹或相邻暗纹间距:λd D x =∆ (D 是双缝到屏的距离,d 为双缝间距) 5. 薄膜干涉以21n n <为例,此时反射光要计“半波损失”, 透射光不计“半波损失”。
大学物理第十四章相对论习题解答

§14.1 ~14. 314.1 狭义相对论的两条基本原理为相对性原理;光速不变原理。
14.2 s ′系相对s 系以速率v=0.8c ( c 为真空中的光速)作匀速直线运动,在S 中观测一事件发生在m x s t 8103,1×==处,在s ′系中测得该事件的时空坐标分别为t =′x 1×108 m 。
分析:洛伦兹变换公式:)t x (x v −=′γ,)x ct (t 2v −=′γ其中γ=,v =β。
14.3 两个电子沿相反方向飞离一个放射性样品,每个电子相对于样品的速度大小为0.67c , 则两个电子的相对速度大小为:【C 】(A )0.67c (B )1.34c (C )0.92c (D )c分析:设两电子分别为a 、b ,如图所示:令样品为相对静止参考系S , 则电子a 相对于S 系的速度为v a = -0.67c (注意负号)。
令电子b 的参考系为动系S '(电子b 相对于参考系S '静止),则S '系相对于S 系的速度v =0.67c 。
求两个电子的相对速度即为求S '系中观察电子a 的速度v'a 的大小。
根据洛伦兹速度变换公式可以得到:a a a v cv v 21v v −−=′,代入已知量可求v'a ,取|v'a |得答案C 。
本题主要考察两个惯性系的选取,并注意速度的方向(正负)。
本题还可选择电子a 为相对静止参考系S ,令样品为动系S '(此时,电子b 相对于参考系S '的速度为v'b = 0.67c )。
那么S '系相对于S 系的速度v =0.67c ,求两个电子的相对速度即为求S 系中观察电子b 的速度v b 的大小。
14.4 两个惯性系存在接近光速的相对运动,相对速率为u (其中u 为正值),根据狭义相对论,在相对运动方向上的坐标满足洛仑兹变换,下列不可能的是:【D 】(A )221c u/)ut x (x −−=′; (B )221cu/)ut x (x −+=′ (C )221c u /)t u x (x −′+′=; (D )ut x x +=′ 分析:既然坐标满足洛仑兹变换(接近光速的运动),则公式中必然含有2211cv −=γ,很明显答案A 、B 、C 均为洛仑兹坐标变换的公式,答案D 为伽利略变换的公式。
大学物理第14章思考题解
《大学物理学》(下册)思考题解第14章 电磁感应14-1 在电磁感应定律i d dtΦ=-¶中,负号的含义是什么? 如何根据负号来判断感应电动势的方向?答:电磁感应定律i d dtΦ=-¶中的负号来自于楞次定律。
由于磁通量Φ变化而引起感应电动势i ¶变化、从而产生感应电流,这个电流的磁场将阻碍原磁通量Φ的变化。
例如原磁通量Φ正在增加,所激发的感应电动势的感应电流的感应磁场将阻碍这个Φ增加。
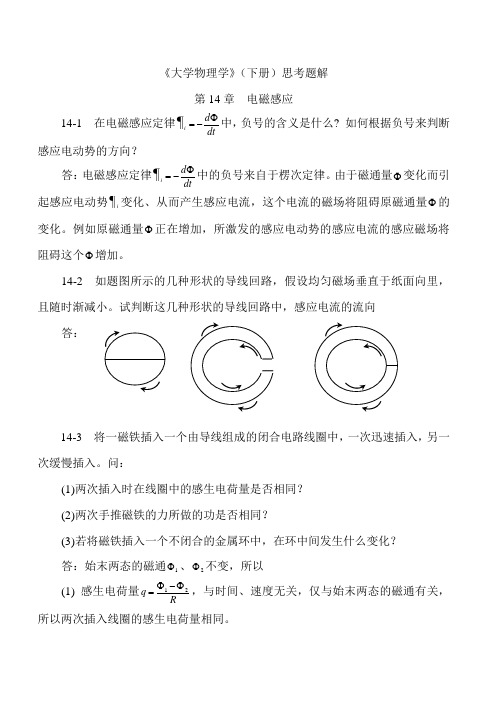
14-2 如题图所示的几种形状的导线回路,假设均匀磁场垂直于纸面向里,且随时渐减小。
试判断这几种形状的导线回路中,感应电流的流向答:14-3 将一磁铁插入一个由导线组成的闭合电路线圈中,一次迅速插入,另一次缓慢插入。
问:(1)两次插入时在线圈中的感生电荷量是否相同? (2)两次手推磁铁的力所做的功是否相同?(3)若将磁铁插入一个不闭合的金属环中,在环中间发生什么变化? 答:始末两态的磁通1Φ、2Φ不变,所以 (1) 感生电荷量12q RΦ-Φ=,与时间、速度无关,仅与始末两态的磁通有关,所以两次插入线圈的感生电荷量相同。
(2)从感应电流作功考虑,W I t =∆¶,定性地判断:两种情况下I t q ∆=不变,12d dttΦ-ΦΦ=∆=-¶分子不变分母有区别,所以两次手推磁铁的力,慢慢插入的作功少,快速插入的作功多。
(3) 若将磁铁插入一个不闭合的金属环中,在环的两端将产生感应电动势。
14-4 让一块很小的磁铁在一根很长的竖直钢管内下落,若不计空气阻力,试定性说明磁铁进入钢管上部、中部和下部的运动情况,并说明理由。
答:把小磁铁看作磁矩为m的磁偶极子,下落至钢管口附近时,由于钢管口所围面积的磁通量发生了变化,管壁将产生感生电动势和感生电流,感生电流将激发感生磁场'1B ,由于磁矩m 自己产生的磁感B 在管口产生的磁通正在增加,根据楞次定律,它所激发的感生磁场'1B 将阻碍这个增加,因此,'1B 与B 反方向。
大学物理-第十四章-波动光学

一部分反射回原介质即光线a1, 另一部分折入另一介质,其中一 部分又在C点反射到B点然后又 折回原介质,即光线a2。因a1,a2是
从同一光线S1A分出的两束,故
满足相干条件。
S
S1
a
a1
iD
e
A
B
C
a2
n1
n2
n1
31
2 薄膜干涉的光程差
n2 n1
CDAD
sin i n2
跃迁 基态
自发辐射
原子能级及发光跃迁
E h
普通光源发光特 点: 原子发光是断续
的,每次发光形成一
长度有限的波列, 各 原子各次发光相互独
立,各波列互不相干.
10
3.相干光的获得:
①原则:将同一光源同一点发出的光波列,即某个原子某次 发出的光波列分成两束,使其经历不同的路程之后相遇叠加。
S2
r2
P
20
为计算方便,引入光程和光程差的概念。
2、光程
光在真空中的速度 光在介质中的速度
c 1 00
u 1
u1 cn
介质的 折射率
真空
u n c
介质中的波长
n
n
n n
21
介质中的波长
n
n
s1 *
r1
P
波程差 r r2 r1
k 0,1,2,
x
d
'
d
(2k
1)
k 0,1,2,
暗纹
d
2
k=0,谓之中央明纹,其它各级明(暗)纹相对0点对称分布
大学物理答案第14章

由分子平均速率公式 ,得:
分子平均速率变为原来的2倍。
17、一定量的理想气体,在容积不变的条件下,当温度降低时,试分析分子的平均碰撞次数和平均自由程变化情况。
解:由碰撞频率气体公式:
而平均速率: 容积不变n不变
当
气体分子平均自由程: n不变
6、我们说分子运动是有规则的,但又说分子运动服从统计规律,这是否有矛盾?应当如何去理解?
解:由于气体分子数目十分庞大,分子之间由于互相碰撞频繁,其运动是无规则的,要根据力学规律对每个分子作计算是不可能的,但是对大量分子整体而言,可用统计平均方法,找出大量分子集体表现出的统计规律性,这与每个分子运动无规则并不矛盾。
第十四章气体动理论
1、如果在封闭容器中,储有处于平衡态的A、B、C三种理想气体。A种气体分子数密度为n1,压强为P1;B种气体分子数密度为2n1;C种气体分子数密度为3n1。求混合气体的压强。
解:由P=nkT,
对于A气体:P1=n1kT;
对于B气体:P2=n2kT=2n1kT;
对于C气体:P3=n3kT=3n1kT;
(4)两种气体内能相等;
解:内能: ,分子的平均动能: 都与自由度i=t+r有关,
平均速率: 与分子量m有关,分子的平均平动动能: 。
而 , ,选
(1)
13、在标准状况下,若氧气(视为刚性双原子分子理想气体)和氦气的体积比为 ,则其内能之比 为多少?
解:O2和He为理想双原子分子气体,标准状况下,压强P和温度T相等。
7、在宏观上理想气体是如何定义的?在微观上应当如何去认识它?其宏观定义与微观假设是否一致?
解:宏观上,理想气体定义为满足三条实验定律的气体,即宏观量(P、V、T)满足状态方程的气体;微观上,理想气体可看成是由许多自由的无规则运动的弹性小球的集合,理想气体是真实气体在低压、高温时的极限情形,分子之间作用力和相互作用势能可忽略,从理想气体微观模型出发,可得到与其宏观性质相符的结论。
大学物理下册课件第十四章光衍射

频率,为波长。
波阵面 dS
S
r
P
en法向
根据惠更斯—菲涅耳原理,P 点的振动等于S
面的所有面积元所引起的振动的叠加
y
S
K cos t
r
2π
r
dS
§14-11 单缝衍射
一. 单缝衍射装置及衍射图样
光屏 y 衍射
单缝
图样
x
z
主光轴方向
焦面位置 透镜L2
透镜L1
对应位置在 BC面上光 程差为 /
狭缝上AB面分成三个半波带
位置P 的衍射角为 时出现亮条纹
3. AC b sin n
2
若n为偶数,各波带发出
B
φ
的光在P点成对相互干涉抵
消,P点出现暗纹。
b
若n为奇数, n-1 个波带 发出的光在P点成对相互干
A
C
涉抵消,剩余一个波带在P
相位相同的 AB 面上各点 发出的子波射线经透镜后 会聚到O 点相位仍相同
相位不同的 BC 面上各点 发出的子波射线经透镜后 会聚到P 点相位差仍等于 位于BC 面处的相位差
二. 菲涅耳半波带法分析单缝衍射条纹分布规律
1. AC b sin 2
2
相邻两波带发出的光 在P 点完全相互抵消
射光栅。光栅常量2.4×10-4cm,透镜焦距0.25m。
问波长为400nm的紫光的第三级谱线和波长为
760nm的红光的第二级谱线分别距离屏中心P0点
多远?
R2
b+b’
V3 x22
φ22 φ13
x13
P0
f
大学物理下下册(马文蔚主编)—第14章例题
(D) ct (1 v / c )
第十四章 相对论
2 1/ 2
8
物理学
第五版
第十四章补充例题
3 下列说法哪种(些)正确: (A) 一切运动物体相对于观察者的速度都不 能大于真空的光速. (B) 质量、长度、时间的测量结果都随物体 与 观察者的相对运动状态而改变. (C) 在一切惯性系中发生于同一时刻、不同地 点的两个事件,在其它惯性系中也同时发生. (D) 惯性系中的观察者观察一个对它作匀速 相对运动的时钟时,会看到该钟走慢了. 答案: (A)(B)(D)
2
(t 2 t1 ) 1 2
这一条件不是任何时候都能满足的!但 在地球这一有限空间内,是可以满足的,虽 然这两事件并不同地,但可近似地套用时间 膨胀公式. 本题求距离,所以可以套用长度缩短公式:
l l 1 2 100 1 0.982 19.9 m
第十四章 相对论
第十四章 相对论
14
物理学
第五版
第十四章补充例题
一电子以0.99c的速率运动(电子静止 质量为9.11×10-31 kg,则电子的总能 5.8×10-13 )J,电子的经典力学的 量是( 动能与相对论动能之比是( 8.04×10-2 ) 质子在加速器中被加速,当其动能为静止 4 能量的3倍时,其质量为静止质量的()倍。
第十四章 相对论
9
物理学
第五版
第十四章补充例题
4 在惯性系S中,相距x=5106m的两地 两事件时间间隔t=10-2 s;在相对S系沿x轴 正向匀速运动的S'系测得这两事件却是同时 发生的,求: S'系中发生这两事件的地点间 距x'. 解设S'系相对于S系的速度大小为 v.
物理14章知识点总结
物理14章知识点总结一、法拉第电磁感应定律1. 当磁感应线与闭合线圈以恒定的速度相对运动时,在闭合线圈中产生感应电动势。
2. 感应电动势的大小与闭合线圈的匝数、磁感应线的改变速度和磁感应线与闭合线圈垂直面积有关。
3. 感应电动势的方向由法拉第电磁感应定律规定,当闭合线圈与磁感应线相对运动时,在闭合线圈中产生的感应电流的方向是的是使感应电动势产生的磁场方向产生的磁场反向作用力。
二、涡流和涡流磁场1. 当导体在磁场中运动时,导体内部会产生感应电流,这种由磁场和感应电流产生的相互作用力称为涡流磁场。
2. 涡流磁场的方向和大小取决于导体的形状、材料、运动状态及磁场的分布,可以根据安培环路定理计算出涡流磁场的分布。
三、恒定磁场中的电动势1. 当导体物体在磁场中匀速运动时,匀速运动的导体的导体内部会有感应电流,感应电流的力作用和感应电动势是由电磁感应定律和洛伦兹力将固定导体定向整理以可确定感应电动势和感应电流的方向。
四、感生电动势的应用1. 感生电动势的应用有电磁感应变压器、感生电动机、感生发电机等。
2. 电磁感应变压器是利用交变电磁场产生的感应电动势而使电能的有效值汽车状均充变压器的。
主要工作原理是变压器以边上的励磁入力能够在副线圈的产生感应电流的时候发生感应电动势产生磁场之量不变留线。
使主线圈在磁场里匀速即使磁感线相对线圈匀速工及变化。
3. 感生电动机是利用感生电动势的原理来转换机械能和电能。
4. 感生发电机是利用感生电动势的原理来转换机械能和电能。
五、洛伦兹力1. 电磁感应定律规定当导体中的电导体在磁场中匀速运动时,在其上将出现感应电动势,而感应电动势产生的感应电流则会受到安培力和洛伦兹力的共同作用,而洛伦兹力是由安培力产生感应电流时所受的电子运动方向、受力的方向和受力的大尺度箍能水平颜料进而使导体受力方向与所对方向成90°。
六、诺依斯定律的原理和应用1. 诺依斯定律指的是自感现象中主线圈和副线圈之间,当主线圈中通电通电磁感应定律产生的副电动势叫衔称触队电动势。
大学物理 马文蔚 第五版 下册 第十四章 课后答案
第十四章 相 对 论14 -1 下列说法中(1) 两个相互作用的粒子系统对某一惯性系满足动量守恒,对另一个惯性系来说,其动量不一定守恒;(2) 在真空中,光的速度与光的频率、光源的运动状态无关;(3) 在任何惯性系中,光在真空中沿任何方向的传播速率都相同.其中哪些说法是正确的? ( )(A) 只有(1)、(2)是正确的 (B) 只有(1)、(3)是正确的(C) 只有(2)、(3)是正确的 (D) 三种说法都是正确的分析与解 物理相对性原理和光速不变原理是相对论的基础.前者是理论基础,后者是实验基础.按照这两个原理,任何物理规律(含题述动量守恒定律)对某一惯性系成立,对另一惯性系也同样成立.而光在真空中的速度与光源频率和运动状态无关,从任何惯性系(相对光源静止还是运动)测得光速均为3×108 m·s -1 .迄今为止,还没有实验能推翻这一事实.由此可见,(2)(3)说法是正确的,故选(C).14 -2 按照相对论的时空观,判断下列叙述中正确的是( )(A) 在一个惯性系中两个同时的事件,在另一惯性系中一定是同时事件(B) 在一个惯性系中两个同时的事件,在另一惯性系中一定是不同时事件(C) 在一个惯性系中两个同时又同地的事件,在另一惯性系中一定是同时同地事件(D) 在一个惯性系中两个同时不同地的事件,在另一惯性系中只可能同时不同地 (E) 在一个惯性系中两个同时不同地事件,在另一惯性系中只可能同地不同时分析与解 设在惯性系S中发生两个事件,其时间和空间间隔分别为Δt 和Δx ,按照洛伦兹坐标变换,在S′系中测得两事件时间和空间间隔分别为221ΔΔΔβx c t t --='v 和 21ΔΔΔβt x x --='v 讨论上述两式,可对题述几种说法的正确性予以判断:说法(A)(B)是不正确的,这是因为在一个惯性系(如S系)发生的同时(Δt =0)事件,在另一个惯性系(如S′系)中是否同时有两种可能,这取决于那两个事件在S 系中发生的地点是同地(Δx =0)还是不同地(Δx≠0).说法(D)(E)也是不正确的,由上述两式可知:在S系发生两个同时(Δt =0)不同地(Δx ≠0)事件,在S′系中一定是既不同时(Δt ′≠0)也不同地(Δx ′≠0),但是在S 系中的两个同时同地事件,在S′系中一定是同时同地的,故只有说法(C)正确.有兴趣的读者,可对上述两式详加讨论,以增加对相对论时空观的深入理解.14 -3 有一细棒固定在S′系中,它与Ox ′轴的夹角θ′=60°,如果S′系以速度u 沿Ox 方向相对于S系运动,S 系中观察者测得细棒与Ox 轴的夹角( )(A) 等于60° (B) 大于60° (C) 小于60°(D) 当S′系沿Ox 正方向运动时大于60°,而当S′系沿Ox 负方向运动时小于60°分析与解 按照相对论的长度收缩效应,静止于S′系的细棒在运动方向的分量(即Ox 轴方向)相对S系观察者来说将会缩短,而在垂直于运动方向上的分量不变,因此S系中观察者测得细棒与Ox 轴夹角将会大于60°,此结论与S′系相对S系沿Ox 轴正向还是负向运动无关.由此可见应选(C).14 -4 一飞船的固有长度为L ,相对于地面以速度v 1 作匀速直线运动,从飞船中的后端向飞船中的前端的一个靶子发射一颗相对于飞船的速度为v 2 的子弹.在飞船上测得子弹从射出到击中靶的时间间隔是( ) (c 表示真空中光速) (A) 21v v +L (B) 12v -v L (C) 2v L (D) ()211/1c L v v - 分析与解 固有长度是指相对测量对象静止的观察者所测,则题中L 、v 2 以及所求时间间隔均为同一参考系(此处指飞船)中的三个相关物理量,求解时与相对论的时空观无关.故选(C). 讨论 从地面测得的上述时间间隔为多少? 建议读者自己求解.注意此处要用到相对论时空观方面的规律了.14 -5 设S′系以速率v =0.60c 相对于S系沿xx′轴运动,且在t =t ′=0时,x =x ′=0.(1)若有一事件,在S系中发生于t =2.0×10-7s,x =50m 处,该事件在S′系中发生于何时刻?(2)如有另一事件发生于S系中t =3.0×10-7 s,x =10m 处,在S′系中测得这两个事件的时间间隔为多少?分析 在相对论中,可用一组时空坐标(x ,y ,z ,t )表示一个事件.因此,本题可直接利用洛伦兹变换把两事件从S系变换到S′系中.解 (1) 由洛伦兹变换可得S′系的观察者测得第一事件发生的时刻为 s 1025.1/1721211-⨯=--='c x c t t 2v v (2) 同理,第二个事件发生的时刻为s 105.3/1722222-⨯=--='c x c t t 2v v 所以,在S′系中两事件的时间间隔为s 1025.2Δ712-⨯='-'='t t t 14 -6 设有两个参考系S 和S′,它们的原点在t =0和t ′=0时重合在一起.有一事件,在S′系中发生在t ′=8.0×10-8 s ,x ′=60m ,y ′=0,z ′=0处若S′系相对于S 系以速率v =0.6c 沿xx′轴运动,问该事件在S系中的时空坐标各为多少?分析 本题可直接由洛伦兹逆变换将该事件从S′系转换到S系.解 由洛伦兹逆变换得该事件在S 系的时空坐标分别为 m 93/12=-'+'=c t x x 2v vy =y′=0z =z′=0s 105.2/1722-⨯=-'+'=c x c t t 2v v 14 -7 一列火车长0.30km(火车上观察者测得),以100km·h -1 的速度行驶,地面上观察者发现有两个闪电同时击中火车的前后两端.问火车上的观察者测得两闪电击中火车前后两端的时间间隔为多少?分析 首先应确定参考系,如设地面为S系,火车为S′系,把两闪电击中火车前后端视为两个事件(即两组不同的时空坐标).地面观察者看到两闪电同时击中,即两闪电在S系中的时间间隔Δt =t 2-t 1=0.火车的长度是相对火车静止的观察者测得的长度(注:物体长度在不指明观察者的情况下,均指相对其静止参考系测得的长度),即两事件在S′系中的空间间隔Δx ′=x ′2 -x ′1=0.30×103m.S′系相对S系的速度即为火车速度(对初学者来说,完成上述基本分析是十分必要的).由洛伦兹变换可得两事件时间间隔之间的关系式为()()21221212/1cx x c t t t t 2v v -'-'+'-'=- (1)()()21221212/1cx x c t t t t 2v v ----='-' (2) 将已知条件代入式(1)可直接解得结果.也可利用式(2)求解,此时应注意,式中12x x -为地面观察者测得两事件的空间间隔,即S系中测得的火车长度,而不是火车原长.根据相对论, 运动物体(火车)有长度收缩效应,即()21212/1c x x x x 2v -'-'=-.考虑这一关系方可利用式(2)求解.解1 根据分析,由式(1)可得火车(S′系)上的观察者测得两闪电击中火车前后端的时间间隔为()s 26.91412212-⨯-='-'='-'x x ct t v 负号说明火车上的观察者测得闪电先击中车头x ′2 处.解2 根据分析,把关系式()21212/1c x x x x 2v -'-'=- 代入式(2)亦可得 与解1 相同的结果.相比之下解1 较简便,这是因为解1中直接利用了12x x '-'=0.30km 这一已知条件.14 -8 在惯性系S中,某事件A 发生在x 1处,经过2.0 ×10-6s后,另一事件B 发生在x 2处,已知x 2-x 1=300m.问:(1) 能否找到一个相对S系作匀速直线运动的参考系S′,在S′系中,两事件发生在同一地点?(2) 在S′系中,上述两事件的时间间隔为多少?分析 在相对论中,从不同惯性系测得两事件的空间间隔和时间间隔有可能是不同的.它与两惯性系之间的相对速度有关.设惯性系S′以速度v 相对S 系沿x 轴正向运动,因在S 系中两事件的时空坐标已知,由洛伦兹时空变换式,可得 ()()2121212/1c t t x x x x 2v v ----='-' (1) ()()2121212/1c x x t t t t 22v c v ----='-' (2)两事件在S′系中发生在同一地点,即x ′2-x ′1=0,代入式(1)可求出v 值以此作匀速直线运动的S′系,即为所寻找的参考系.然后由式(2)可得两事件在S′系中的时间间隔.对于本题第二问,也可从相对论时间延缓效应来分析.因为如果两事件在S′系中发生在同一地点,则Δt ′为固有时间间隔(原时),由时间延缓效应关系式2/1ΔΔc t t 2v -='可直接求得结果. 解 (1) 令x ′2-x ′1=0,由式(1)可得c t t x 50.0s m 1050.11-8121=⋅⨯=--=2x v (2) 将v 值代入式(2),可得()()()s 1073.1/1/162122121212-⨯=--=----='-'c t t c x x t t t t 222v v c v这表明在S′系中事件A 先发生.14 -9 设在正负电子对撞机中,电子和正电子以速度0.90c 相向飞行,它们之间的相对速度为多少?分析 设对撞机为S系,沿x 轴正向飞行的正电子为S′系.S′系相对S系的速度v =0.90c ,则另一电子相对S系速度u x =-0.90c ,该电子相对S′系(即沿x 轴正向飞行的电子)的速度u′x 即为题中所求的相对速度.在明确题目所述已知条件及所求量的物理含义后,即可利用洛伦兹速度变换式进行求解.解 按分析中所选参考系,电子相对S′系的速度为c u cu u u x x x x 994.012-=-'-='v 式中负号表示该电子沿x′轴负向飞行,正好与正电子相向飞行.讨论 若按照伽利略速度变换,它们之间的相对速度为多少?14 -10 设想有一粒子以0.050c 的速率相对实验室参考系运动.此粒子衰变时发射一个电子,电子的速率为0.80c ,电子速度的方向与粒子运动方向相同.试求电子相对实验室参考系的速度.分析 这是相对论的速度变换问题.取实验室为S系,运动粒子为S′系,则S′系相对S系的速度v =0.050c .题中所给的电子速率是电子相对衰变粒子的速率,故u′x =0.80c . 解 根据分析,由洛伦兹速度逆变换式可得电子相对S系的速度为c u cu u x x x 817.012='-+'=v v 14 -11 设在宇航飞船中的观察者测得脱离它而去的航天器相对它的速度为1.2×108m·s-1 i .同时,航天器发射一枚空间火箭,航天器中的观察者测得此火箭相对它的速度为1.0×108m·s-1 i .问:(1) 此火箭相对宇航飞船的速度为多少? (2) 如果以激光光束来替代空间火箭,此激光光束相对宇航飞船的速度又为多少? 请将上述结果与伽利略速度变换所得结果相比较,并理解光速是运动体的极限速度.分析 该题仍是相对论速度变换问题.(2)中用激光束来替代火箭,其区别在于激光束是以光速c 相对航天器运动,因此其速度变换结果应该与光速不变原理相一致.解 设宇航飞船为S系, 航天器为S′系, 则S′系相对S系的速度v =1.2 ×108m·s-1 ,空间火箭相对航天器的速度为u ′x =1.0×108m·s-1,激光束相对航天器的速度为光速c .由洛伦兹变换可得:(1) 空间火箭相对S 系的速度为 1-82s m 1094.11⋅⨯='++'=x x x u cu u v v (2) 激光束相对S 系的速度为 c c c c u x =++=21v v 即激光束相对宇航飞船的速度仍为光速c ,这是光速不变原理所预料的.如用伽利略变换,则有u x =c +v >c .这表明对伽利略变换而言,运动物体没有极限速度,但对相对论的洛伦兹变换来说,光速是运动物体的极限速度.14 -12 以速度v 沿x 方向运动的粒子,在y 方向上发射一光子,求地面观察者所测得光子的速度.分析 设地面为S系,运动粒子为S′系.与上题不同之处在于,光子的运动方向与粒子运动方向不一致,因此应先求出光子相对S系速度u 的分量u x 、u y 和u z ,然后才能求u 的大小和方向.根据所设参考系,光子相对S′系的速度分量分别为u ′x =0,u ′y =c ,u ′z =0. 解 由洛伦兹速度的逆变换式可得光子相对S系的速度分量分别为v v v ='++'=x x x u cu u 21 222/11/1c c u cc u u x y y 22v v v -='+-'= 0=z u所以,光子相对S系速度u 的大小为c u u u u z y x =++=222速度u 与x 轴的夹角为vv 22arctan arctan -==c u u θx y讨论 地面观察者所测得光子的速度仍为c ,这也是光速不变原理的必然结果.但在不同惯性参考系中其速度的方向却发生了变化.14 -13 设想地球上有一观察者测得一宇宙飞船以0.60c 的速率向东飞行,5.0s后该飞船将与一个以0.80c 的速率向西飞行的彗星相碰撞.试问:(1) 飞船中的人测得彗星将以多大的速率向它运动? (2) 从飞船中的钟来看,还有多少时间允许它离开航线,以避免与彗星碰撞?分析 (1) 这是一个相对论速度变换问题.取地球为S系,飞船为S′系,向东为x 轴正向.则S′系相对S系的速度v =0.60c ,彗星相对S系的速度u x =-0.80c ,由洛伦兹速度变换可得所求结果.(2) 可从下面两个角度考虑:a.以地球为S系,飞船为S′系.设x 0=x′0 =0 时t 0=t′0=0,飞船与彗星相碰这一事件在S系中的时空坐标为t =5.0s,x =vt .利用洛伦兹时空变换式可求出t′,则Δt′=t′-t′0表示飞船与彗星相碰所经历的时间.b.把t 0=t′0=0 时的飞船状态视为一个事件,把飞船与彗星相碰视为第二个事件.这两个事件都发生在S′系中的同一地点(即飞船上),飞船上的观察者测得这两个事件的时间间隔Δt′为固有时,而地面观察者所测得上述两事件的时间间隔Δt =5.0s比固有时要长,根据时间延缓效应可求出Δt′.解 (1) 由洛伦兹速度变换得彗星相对S′系的速度为 c u cu u x x x 946.012-=--'='v v 即彗星以0.946c 的速率向飞船靠近. (2) 飞船与彗星相碰这一事件在S′系中的时刻为s 0.4/122=--'='c c t t 2v vx即在飞船上看,飞船与彗星相碰发生在时刻t′=4.0s.也可以根据时间延缓效应s 0.5/1ΔΔ2=-'=c t t 2v ,解得Δt′=4.0 s,即从飞船上的钟来看,尚有4.0 s 时间允许它离开原来的航线.14 -14 在惯性系S 中观察到有两个事件发生在同一地点,其时间间隔为4.0 s ,从另一惯性系S′中观察到这两个事件的时间间隔为6.0 s ,试问从S′系测量到这两个事件的空间间隔是多少? 设S′系以恒定速率相对S系沿xx′轴运动.分析 这是相对论中同地不同时的两事件的时空转换问题.可以根据时间延缓效应的关系式先求出S′系相对S 系的运动速度v ,进而得到两事件在S′系中的空间间隔Δx′=vΔt′(由洛伦兹时空变换同样可得到此结果).解 由题意知在S系中的时间间隔为固有的,即Δt =4.0s,而Δt′=6.0 s.根据时间延缓效应的关系式2/1ΔΔc tt 2v -=',可得S′系相对S系的速度为c c t t 35ΔΔ12/12=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛'-=v 两事件在S′系中的空间间隔为 m 1034.1ΔΔ9⨯='='t x v14 -15 在惯性系S 中, 有两个事件同时发生在xx′轴上相距为1.0×103m 的两处,从惯性系S′观测到这两个事件相距为2.0×103m ,试问由S′系测得此两事件的时间间隔为多少? 分析 这是同时不同地的两事件之间的时空转换问题.由于本题未给出S′系相对S 系的速度v ,故可由不同参考系中两事件空间间隔之间的关系求得v ,再由两事件时间间隔的关系求出两事件在S′系中的时间间隔.解 设此两事件在S 系中的时空坐标为(x 1 ,0,0,t 1 )和(x 2 ,0,0,t 2 ),且有x 2 -x 1 =1.0×103m , t 2 -t 1 =0.而在S′系中, 此两事件的时空坐标为(x′1 ,0,0,t′1 )和(x′2 ,0,0,t′2 ),且|x′2 -x′1| =2.0×103m ,根据洛伦兹变换,有 ()()2121212/1c t t x x x x 2v v ----='-' (1) ()()2121212/1c x x t t t t 22v c v ----='-' (2)由式(1)可得()()c c x x x x 2312/1212212=⎥⎦⎤⎢⎣⎡'-'--=v 将v 值代入式(2),可得 s 1077.5612-⨯='-'t t 14 -16 有一固有长度为l0 的棒在S 系中沿x 轴放置,并以速率u 沿xx′轴运动.若有一S′系以速率v 相对S 系沿xx′轴运动,试问从S′系测得此棒的长度为多少?分析 当棒相对观察者(为S′系)存在相对运动时,观察者测得棒的长度要比棒的固有长度l 0短,即220/1c u l l '-=.式中u′是棒相对观察者的速度,而不要误认为一定是S′系和S 系之间的相对速度v .在本题中,棒并非静止于S系,因而S′系与S 系之间的相对速度v 并不是棒与S′系之间的相对速度u′.所以本题应首先根据洛伦兹速度变换式求u ′,再代入长度收缩公式求l .解 根据分析,有21cu u uv v --=' (1) 220/1c u l l '-= (2)解上述两式,可得()()[]2/1222202v v ---=c u c u c l l14 -17 若从一惯性系中测得宇宙飞船的长度为其固有长度的一半,试问宇宙飞船相对此惯性系的速度为多少? (以光速c 表示)解 设宇宙飞船的固有长度为l 0 ,它相对于惯性系的速率为v ,而从此惯性系测得宇宙飞船的长度为2/0l ,根据洛伦兹长度收缩公式,有200/12/c l l 2v -=可解得v =0.866c14 -18 一固有长度为4.0 m 的物体,若以速率0.60c 沿x 轴相对某惯性系运动,试问从该惯性系来测量,此物体的长度为多少?解 由洛伦兹长度收缩公式m 2.3/120=-=c l l 2v*14 -19 设一宇航飞船以a =9.8 m·s-2 的恒加速度,沿地球径向背离地球而去,试估计由于谱线的红移,经多少时间,飞船的宇航员用肉眼观察不到地球上的霓虹灯发出的红色信号.分析 霓虹灯发出的红色信号所对应的红光波长范围一般为620nm ~760 nm ,当飞船远离地球而去时,由光的多普勒效应可知,宇航员肉眼观察到的信号频率ν <ν0 ,即λ>λ0 ,其中ν0 和λ0 为霓虹灯的发光频率和波长.很显然,当λ0=620 nm ,而对应的红限波长λ=760 nm 时,霓虹灯发出的红色信号,其波长刚好全部进入非可见光范围,即宇航员用肉眼观察不到红色信号.因此,将上述波长的临界值代入多普勒频移公式,即可求得宇航员观察不到红色信号时飞船的最小速率v ,再由运动学关系,可求得飞船到达此速率所需的时间t .解 当光源和观察者背向运动时,由光的多普勒效应频率公式 2/10⎪⎭⎫ ⎝⎛+-=v v v v c c得波长公式 2/10⎪⎭⎫ ⎝⎛-+=v v c c λλ式中v 为飞船相对地球的速率.令λ0 =620 nm ,λ=760 nm ,得宇航员用肉眼观察不到地球上红色信号时飞船的最小速率为1-8202202s m 1060.0⋅⨯=+-=λλλλv 飞船达此速率所需的时间为a 0.20s 101.66≈⨯==at v 14 -20 若一电子的总能量为5.0MeV ,求该电子的静能、动能、动量和速率. 分析 粒子静能E 0 是指粒子在相对静止的参考系中的能量,200c m E =,式中为粒子在相对静止的参考系中的质量.就确定粒子来说,E 0 和m 0均为常数(对于电子,有m 0 =9.1 ×10-31kg,E 0=0.512 MeV).本题中由于电子总能量E >E 0 ,因此,该电子相对观察者所在的参考系还应具有动能,也就具有相应的动量和速率.由相对论动能定义、动量与能量关系式以及质能关系式,即可解出结果.解 电子静能为 MeV 512.0200==c m E电子动能为 E K =E -E 0 =4.488 MeV由20222E c p E +=,得电子动量为 ()1-212/1202s m kg 1066.21⋅⋅⨯=-=-E E c p 由2/12201-⎪⎪⎭⎫ ⎝⎛-=c E E v 可得电子速率为c E E E c 995.02/12202=⎪⎪⎭⎫ ⎝⎛-=v14 -21 一被加速器加速的电子,其能量为3.00 ×109eV.试问:(1) 这个电子的质量是其静质量的多少倍? (2) 这个电子的速率为多少?解 (1) 由相对论质能关系2mc E =和200c m E =可得电子的动质量m 与静质量m 0之比为 320001086.5⨯===cm E E E m m (2) 由相对论质速关系式2/12201-⎪⎪⎭⎫ ⎝⎛-=c m m v 可解得c c m m 999999985.012/120=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=-v可见此时的电子速率已十分接近光速了. 14 -22 在电子偶的湮没过程中,一个电子和一个正电子相碰撞而消失,并产生电磁辐射.假定正负电子在湮没前均静止,由此估算辐射的总能量E .分析 在相对论中,粒子的相互作用过程仍满足能量守恒定律,因此辐射总能量应等于电子偶湮没前两电子总能之和.按题意电子偶湮没前的总能只是它们的静能之和.解 由分析可知,辐射总能量为MeV 1.02J 1064.121320=⨯==-c m E14 -23 若把能量0.50 ×106 eV 给予电子,让电子垂直于磁场运动,其运动径迹是半径为2.0cm 的圆.问:(1) 该磁场的磁感强度B 有多大? (2) 这电子的动质量为静质量的多少倍?分析 (1) 电子在匀强磁场中作匀速圆周运动时,其向心力为洛伦兹力F =evB ,在轨道半径R 确定时,B =B (p ),即磁感强度是电子动量的函数.又由相对论的动能公式和动量与能量的关系可知电子动量p =p (E 0 ,E K ),题中给予电子的能量即电子的动能E K ,在电子静能20c m E =已知的情况下,由上述关系可解得结果.(2) 由相对论的质能关系可得动质量和静质量之比.本题中电子的动能E K =0.50 MeV 与静能E 0=0.512 MeV 接近,已不能用经典力学的方法计算电子的动量或速度,而必须用相对论力学.事实上当E K =0.50 E 0 时,用经典力学处理已出现不可忽略的误差.解 (1) 根据分析,有E =E 0 +E K (1)22202c p E E += (2)Rv m vB 2=e (3) 联立求解上述三式,可得eRcE E E B k k 002+=(2) 由相对论质能关系,可得 98.11000=+==E E E E m m k 本题也可以先求得电子速率v 和电子动质量m ,但求解过程较繁.14 -24 如果将电子由静止加速到速率为0.10c ,需对它作多少功? 如将电子由速率为0.80c 加速到0.90c ,又需对它作多少功?分析 在相对论力学中,动能定理仍然成立,即12ΔΔk k k E E E W -==,但需注意动能E K 不能用2v m 21表示. 解 由相对论性的动能表达式和质速关系可得当电子速率从v1 增加到v2时,电子动能的增量为()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=---=-=--2/1222/12220202120221211ΔΔc c c m c m c m c m c m E E E k k k v v根据动能定理,当v 1 =0,v 2 =0.10c 时,外力所作的功为eV 1058.2Δ3⨯==k E W当v 1 =0.80 c ,v 2=0.90 c 时,外力所作的功为eV 1021.3Δ5⨯='='kE W 由计算结果可知,虽然同样将速率提高0.1 c ,但后者所作的功比前者要大得多,这是因为随着速率的增大,电子的质量也增大.。
大学物理第十四章ppt
2. 平面简谐波的表达式(波函数)
y y ( x, t )
各质点相对平 衡位置的位移
波线上各质点 平衡位置
求解波函数就是求解任意一点的振动表达式 •建立波函数的依据 波的空间、时间周期性 沿波传播方向各质点振动状态(相位)相 继落后(滞后效应)
已知一列波以波速u向右传播,波线上点O的振动方程 为 y A cos(t 0 ) ,求该平面简谐波波函数。
(2)根据传播方向与振动方向的关系 横波:质点振动方向与波的传播方向相垂直的波.
(仅在固体中传播 )
特征:具有交替出现的波峰和波谷.
纵波:质点振动方向与波的传播方向互相平行的波. (可在固体、液体和气体中传播)
特征:具有交替出现的密部和疏部.
2. 波动的特征 (1)波动具有一定传播速度,并伴随着能量的传播。 (2)波动具有可叠加性,在空间同一区域可同时经历两个或两 个以上的波,因而波可以叠加。 (3)波动具有时空周期性,固定空间一点来看,振动随时间的 变化具有时间周期性;而固定一个时刻来看,空间各点的振动 分布也具有空间周期性。 3. 机械波的形成 1)波源 条件: 2)媒质 注意 波是运动状态的传播,介质的质点并不随波传播, 在各自的平衡位置附近作振动. 沿着波的传播方向,相位逐次落后。
流体:纵波 u K 弹性模量
杨氏模量E 切变模量G 体变模量K
波速只决定于媒质 的性质!u弹性 Nhomakorabea量 介质密度
应力 E 应变 F S FL L L SL
G
应力 应变
K
应力 应变
F S FD d D S d
-
P V V
6、波形曲线
描述某时刻,波线上各点位移(广义)分布
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章 气体动理论
1、如果在封闭容器中,储有处于平衡态的A 、B 、C 三种理想气体。
A 种气体分子数密度为n 1,压强为P 1;B 种气体分子数密度为2n 1;C 种气体分子数密度为3n 1。
求混合气体的压强。
解:由P =n k T , 对于A 气体:P 1=n 1 kT ; 对于B 气体:P 2=n 2 kT =2n 1 kT ; 对于C 气体:P 3=n 3 kT =3n 1 kT ; 于是,混合气体:
P =P 1+P 2+P 3=6n 1 k T =6P 1;
2、如果理想气体的体积为V ,压强为P ,温度为T ,一个分子质量为m ,玻耳玆曼常数为k ,气体摩尔常量为R ,求该理想气体分子数。
解:由理想气体状态方程, 或由nkT P =kT V
N
=
气体质量: 得:kT
PV
N =
摩尔质量: 得
所以
3、打开空调后,某房间温度从7℃上升至27℃,计算打开空调前后房间空气密度之比。
(房间内压强可认为不变)
解:由状态方程:
得
开空调前、后:
认为
则
kT
PV N NkT PV k
R N
RT N
N PV m N Nm
M RT M
PV A
A
A =
==
=
===,μμ07
.1273
727327,,1
22
122112
12
22111=++=
=
=====
=
=T T T T P P RT P RT P RT
P V
M RT M
PV ρρρρμ
ρ
μρμ
ρρμ
及
4、室内生起炉子后温度从15℃升到27℃,而室内气压不变,则此时室内的分子数减少了百分之几? 解:由物态方程
温度为T 1和T 2时:
所以分子数减少4%。
5、统计规律与力学规律有什么不同?统计规律存在的前提条件是什么?
解:力学规律表征的是一个物体或几个物体组成的系统的机械运动规律,而统计规律反映的是大量分子热运动的规律,是宏观量与微观量的统计平均值之间的关系,统计规律只对数目非常巨大的粒子系统适用,对于少数几个分子组成的系统不适用。
6、我们说分子运动是有规则的,但又说分子运动服从统计规律,这是否有矛盾?应当如何去理解?
解:由于气体分子数目十分庞大,分子之间由于互相碰撞频繁,其运动是无规则的,要根据力学规律对每个分子作计算是不可能的,但是对大量分子整体而言,可用统计平均方法,找出大量分子集体表现出的统计规律性,这与每个分子运动无规则并不矛盾。
7、在宏观上理想气体是如何定义的?在微观上应当如何去认识它?其宏观定义与微观假设是否一致?
解:宏观上,理想气体定义为满足三条实验定律的气体,即宏观量(P 、V 、T )满足状态方程的气体;微观上,理想气体可看成是由许多自由的无规则运动的弹性小球的集合,理想气体是真实气体在低压、高温时的极限情形,分子之间作用力和相互作用势能可忽略,从理想气体微观模型出发,可得到与其宏观性质相符的结论。
%
4300
12288
3002731527327,,1
1
2212211212
22111-=-=
∆=
++=
==∴==
===
N N T T N N T N T N P P RT m
N V P RT m
N V P Nm M RT M
PV 又μ
μ
μ
8、某人测量一山顶的压强只有地面压强的3/4,问该山顶的相对高度为多少?(设
山顶和地面温度为0℃,空气的摩尔质量为2.89×10-2
kg /mol )。
解:由大气压强公式:
设山高为h
所以,有
9、如果容器中只有少数几个分子,能否用kT i 2
=ε来计算平均动能?为什么?
解:不能用kT i 2
=
ε来计算少数分子的平均动能,因统计规律仅对大量分子适用。
10、如果两种理想气体的温度相等,则其能量关系正确的是: (1)内能必然相等;
(2)分子的平均总能量必然相等;
(3)分子的平均动能相等;
(4)分子的平均平动动能相等。
解:内能:RT i
M E 2μ=,分子的平均总能量(理想气体无势能)即分子的平均动
能:kT i 2
=
ε都与自由度i=t+r 有关。
而分子的平均平动动能:kT k 2
3=
ε。
选(4)
11、储存氧气的容器以速度s m v /100=运动,若该容器突然停止,且全部定向运动的动能均转变成分子热运动的动能,求容器中氧气温度的变化值。
解:设氧气质量为M ,摩尔质量为μ=32×10-3
kg /mol 其内能:
动能: 假设动能全部变为内能,温度变化为ΔT ,则
所以,温度升高7.7K 。
)(103.243ln 8
.91089.227331.8ln ln 3
2
0000m P P g RT h RT
gh
kT mgh P P e P P
e P P kT
mgh kT
mgz ⨯=⨯⨯⨯-=-=-=-===---
μμ2
2
1
252Mv
E RT
M RT M i E k =
=
=
μ
μ)
K (71.731
.85100
10
32525212
3
2
2
=⨯⨯⨯=
⋅=
∆∆=
-R
v
T T R M Mv
μμ
12、两容器中分别盛有H 2和Ne ,若它们的温度和质量分别相等,则正确的是: (1)两种气体分子的平均平动动能相等; (2)两种气体分子的平均动能相等; (3)两种气体的平均速率相等; (4)两种气体内能相等; 解:内能:RT i
M E 2
μ=
,分子的平均动能:kT i 2
=
ε都与自由度i=t+r 有关,
平均速率:m
kT v 60
.1=与分子量m 有关,分子的平均平动动能:kT k 2
3=
ε。
而52
=H i ,3=Ne i ,∴选(1)
13、在标准状况下,若氧气(视为刚性双原子分子理想气体)和氦气的体积比为2
12
1=V V ,则其内能之比
2
1E E 为多少?
解:O 2和H e 为理想双原子分子气体,标准状况下,压强P 和温度T 相等。
设其摩尔数分别为γ1和γ2,有
O 2的内能: H e 的内能:
由PV =γRT ,得
PV 1=γ1RT , PV 2=γ2RT 于是,
所以
14、某气体分子的速率分布曲线如图所示,其中v P 为最可几速率,N P 为处于v P ~v P +Δv P 速率区间的分子数占总分子数的百分比。
若气体温度升高,则v P 、N P 如何变化?
解:理想气体分子的最可几速率:m
kT
v P 2=
当温度升高时:v P 增大,v P 右移,由于f (v )~v 曲线下的面积为1,整个曲线宽度增加。
温度升高后,要维持总面积不变,则曲线高度下降,而Δv P 不变,速率分布在v P ~v P +Δv P 之间的分子数减少。
p p p RT
E RT
E 22112
32
5γγ=
=6
5212
325212
12
121=⨯
=
==E E V V γγ
15、氦、氧两气体在某一相同温度下,分子按速率分布的曲线如图所示。
则:
(1)曲线Ⅰ表示 氧 气分子的速率分布曲线,曲线Ⅱ表示 氦 气分子的速率分布曲线;
(2)画有斜线的小长条面积表示 速度在v ~v +d v 内分子数占总分子数的比率 ;
(3)分布曲线下所包围的面积表示 所有可能速率的分子数占总分子数的比率之和(应为100%) 。
解:(1)由m
kT v P 2=
,温度T 相同,m 不同
又氦氧m m >,氦氧P P v v <∴,曲线Ⅰ表示氧,曲线Ⅱ表示氦气分子的速率分布曲线。
16、假定氧气的热力学温度提高一倍。
氧分子全部离解为氧原子,则氧原子的平均速率是氧分子平均速率的多少倍?
解:氧气(分子)离解为氧原子O 2→2O , 温度T →2T , 分子质量m →m /2, 由分子平均速率公式m
RT
v π8=
,得:
22
/22
==
m m
T T v v O O
分子平均速率变为原来的2倍。
17、一定量的理想气体,在容积不变的条件下,当温度降低时,试分析分子的平均碰撞次数和平均自由程变化情况。
解:由碰撞频率气体公式:v n d Z 2
2⋅=
π
而平均速率:m
RT
v π8=
容积不变→n 不变
∴当↓↓→↓→Z v T 气体分子平均自由程:n
d Z v 2
21⋅=
=
πλ n 不变
温度降低,平均自由程不变。
1p
2
p
f (v )。
