相位测量技术
相位测量技术

相位测量技术
相位测量技术是一种用来测量信号相对时间偏移的技术。
在电气工程、通信工程、物理学、生物医学等领域中广泛应用。
相位测量技术的核心是利用相位差来描述两个信号之间的时间关系,可以用来测量信号的频率、周期、相位、时间延迟等参数。
一般来说,相位测量技术可以分为两类:基于数字信号处理的相位测量和基于模拟电路的相位测量。
基于数字信号处理的相位测量利用数字信号处理器或现场可编程门阵列等硬件设备实现,其优点是可编程性强,精度高;而基于模拟电路的相位测量则利用锁相放大器、相位计等专用电路实现,其优点是响应速度快,适用于高速信号测量。
在实际应用中,相位测量技术被广泛应用于频率合成、相位同步、信号调制与解调、光学测量、雷达测距等领域。
例如,在通信领域中,相位测量技术被用于保证信号的相位同步,从而实现信号的正常传输和接收;在物理学中,相位测量技术可用于测量光的相位,从而实现光的干涉与衍射等重要现象的研究。
总之,相位测量技术是一项重要的测量技术,其在多个领域中发挥着重要的作用,不仅可以提高信号的传输质量和测量精度,而且对于研究复杂的自然现象也具有很大的帮助。
- 1 -。
电力电缆技术及应用 4.4 相位检查

1、电压表指示法
图4-5 核对电缆导线相位的方法
1、电压表指示法
如有相应的直流电压指示,则接电压表正极的导电线芯 为A相,接电压表负极的导电线芯为B相,第三芯为C相。若 电压表没有指示,说明电压表所接的两个导电线芯中,有一 个导电线芯为C相,此时可任意将一个导电线芯换接到电压 表上进行测试,直到电压表有正确的指示为止。
第四章 电力电缆试验
4.4 相位检查
在电缆线路与电力系统接通之前,必须按照电力系统上 的相位进行核相。这项工作对于单个用电设备关系不大,但 对于输电网络、双电源系统和有备用电源的重要用户,以及 有关联的电缆运行系统有重要意义。核对相位的方法很多, 下面介绍几种常见的测试方法。
1、电压表指示法
比较简单的方法是在电缆的一端任意两个导电线芯处接 入一个用干电池2~4节串联的低压直流电,假定接正极的导 电线芯为相,接负极的导电线芯为B相,在电缆的另一端 用直流电压表或万用表的10V电压档测量任意两个导电线芯 ,如图4-5所示。
2、摇表法
接线如图4-6所示。检查的方法是将电缆的一端被试芯 线接地,在另外一端用摇表分别检查三相对地的电阻。
图4-6 摇表法核对电缆导线相位的方法
相位测距中的解模糊技术

1997年3月第24卷 第1期西安电子科技大学学报JOU RNAL O F X I D I AN U N I V ER S IT Y M ar .1997V o l .24 N o.1相位测距中的解模糊技术Ξ沈福民 贾永康(西安电子科技大学电子工程研究所 西安710071)摘要 分析了在连续波(C W )雷达中利用多频率目标回波相位差进行测距时所存在的严重模糊问题.用模糊函数的概念来评价及改善雷达系统的测距(和测速)性能.为减弱测距模糊,文中还对多频C W 雷达的差频值如何按一定参差关系设置进行了探讨.最后,提出和分析了在相位测距中的一种解模糊方法.关键词 相位测距 模糊函数 最大不模糊距离 参差中图分类号 TN 95312连续波(C W )体制雷达因其设备简单、轻便,在不少应用场合仍然受到重视.近年来,由于现代战争环境下反电子干扰的需要,因而又重新产生了对C W 雷达改进和应用的研究兴趣.各种类型的连续波调制雷达能够实现测距功能,但都存在着测距模糊(当然也有测速模糊)问题.解决(或减弱)这种模糊和保证测量精度往往互不兼容.例如,双频发射的C W 雷达,要减弱其测距模糊,必须缩小两个发射频率的频率差值,但这又会使测距精度随之降低.在双频C W 雷达中,目标的距离信息主要依赖于差频的相位关系,而相位值是以2Π为模随距离变化重复出现的,C W 雷达的测距模糊由此而生.解决测距模糊可以采用类似脉冲雷达测距解模糊的方法.在那里,参差脉冲重复周期(R P I )的技术被普遍运用;而对于C W 雷达,可采用多频发射,且相互的差频值按一定的参差关系选择,如此可以有效地解决或减弱测距模图1 目标测量几何关系糊,提高雷达测距性能.1 模型的建立多频C W 雷达直接利用了每个发射频率目标反射回波的多普勒频率相位关系,如图1所示.假设雷达工作频率为f i (i =0,1,2,…,M-1),目标在t 0时刻的距离为R 0,则第i 个频率的目标反射回波信号x i 为x i =A i exp [-j 4Πf i (R 0-V r (t -t 0)) c ](1)其中,A i 为目标回波的振幅,V r 为目标径向速度,c 为光速.将多普勒频率fd i =2V r f i c 代入式(1),则x i =A i exp [j (2Πf d i (t -t 0)-Υoi ]式中 Υoi =4Πf i R 0 c 为t 0时刻由距离R 0引起的目标回波相位滞后.通常由于各工作频率间的差频值远小于工作频率,故目标在不同频率上的多普勒频率差可以忽略不计.(譬如,一般若取f i 为几个GH z,而差频值取为几个M H z,则∃f d i 仅为f d i 的10-3量级).假定f 0为基准发射频率,每个工作频率f i 的反射回波和f 0的回波相位差∃Υi 近似为4Π∃f i R 0c (其中∃f i =f i -f 0),且考虑到振幅A i 近似不变,则接收回波可用矢量表示ΞX (t )=A exp [j (2Πfd (t -t 0)-Υ00)][1,exp (-j ∃Υ1),exp (-j ∃Υ2),…,exp (-j ∃ΥM -1)]T(2)式中 A 、f d 分别表示目标反射回波的振幅和多普勒频率,符号“T ”表示矩阵转置.若有两个或两个以上的目标,C W 雷达必须以它们的不同多普勒频率(即有不同速度)进行区分,接收回波信号需要在通道设置多普勒滤波器组,将不同目标的回波分离开来.这样,均可用式(2)分开表示.2 距离模糊由上面分析可知,相位测距的关系式可表示为R =c ∃Υi 4Π∃f i (i =1,2,…,M -1)(3) 因相位差∃Υi 以2Π为模,即便减小∃f i (不能减小太多,下面还将分析),还会使每个差频∃f i 上的最大不模糊距离远不能满足测距要求,即产生所谓“距离模糊”(或测距模糊).同时采用多个频率发射,且按一定的参差比选择其差频值,利用各个频率上的测距相位信息,就能有效减弱距离模糊的影响.假定以各个差频上的最大不模糊距离a i [=c(2∃f i )]实现参差比,即a 1∶a 2∶…∶a N =m 1∶m 2∶…∶m N (N 一般不大于M -1),则有∃Υi =4ΠFR(c m i ),其中F =m i ∃f i (i =1,2,…,N ).推广应用在脉冲雷达检测中模糊函数的概念,即当两个不同距离上(且有不同速度)的目标回波矢量X a (t )和X b (t ),使下列和式∑K -1k =0X a (k T s )-X b (k T s )2(4)达到最小时,则可认为检测的模糊度[1]最大,即此时两目标在距离(或多普勒速度)上难于区分,产生模糊.式(4)中采用了离散时域信号,T s 为采样周期,K 为观察时间长度,“ ”表示矢量的范数.式(4)还可等价表示为∑K -1k =0R e [XT a (k T s )X 3b (k T s )]式中 “R e [·]”表示取实部,符号“3”表示求共轭.由上式可定义多频C W 雷达检测的模糊函数B (Σ,f d )为35第1期 沈福民等:相位测距中的解模糊技术B (Σ,f d )=∑K -1k =0XT (k T s ,f a )X 3[k (T s +Σ),(f a +f d )](5)式中 Σ、f d 分别表示两目标距离差引起的时延和多普勒频率差;f a 为第一个目标的多普勒频率.将式(2)代入式(5),可得B (Σ,f d )的归一化模值B m (Σ,f d )为B m (Σ,f d )=1K (N +1)sin (ΠK f d T s )sin (Πf d T s)1+∑N i =1exp (j 2Π∃fi Σ)(6)由式(5)容易看出,模糊函数实际上表示矢量X a (t )和X b (t )的互相关,这和在空间域考虑模糊的问题[2]思想是类似的.(a )未参差(b )经参差45 西安电子科技大学学报 第24卷的目标距离和多普勒速度范围内尽可能小;另外,为了提高测距和测速精度,要求B m (Σ,f d )在原点附近有陡的斜率(即有尖锐的峰).图2为两种特定参数(见图中标明)下模糊函数归一化模值的分布情况.图中可明显看出,经参差考虑后的模糊情况要比未参差的减弱得多.精心选择N 个差频值(即各个最大不模糊距离a i 所对应的参差比),可以使模糊减到最弱(考虑整个区域内),使检测性能达到最好.另外,∃f i (i =1,2,…,N )也不能选得太小,否则B m (Σ,f d )在距离维(即Σ)的斜率将不陡,影响距离测量的精度.由式(6)可看出,∃f i 的选择和多普勒频率f d 一维无关,这就使问题得以简化,在f d 维内的考虑主要应选择足够的观测时间长度K .图2(b )中的情况还未达到最佳状况,只是一个例举.选择∃f i ,只须在距离一维内考虑.有关工作频率差频值的最佳选取及对测距性能的影响方面的进一步深入讨论,将另作专门问题考虑,这里不再赘述.图3 多个∃f i 的相位差和距离的关系3 解模糊方法利用经参差考虑的多个差频相位信息,可以有效减弱距离模糊,由此,有可能将目标的真实距离解算出来.用计算机(或微处理器)作参数搜索可容易地实现目标距离的解算功能.图3表示在不同距离上目标回波由各个∃f i 所产生的相位滞后∃Υi 值(以2Π为模),实际上目标距离R 可表示为R =(b i +∃Υi 2Π)a i (i =1,2,…,N )(7)式中 b i 为非负整数,∃Υi 为测量的相位差数据(以弧度为单位).由式(7),可以直接对b i 进行整个测量距离范围内的搜索,以获取目标距离值,但通常由于搜索范围大,显得十分麻烦,且影响处理速度.为了获得简便的搜索方法,不妨先在由第一、二差频组合的最大不模糊距离R (1)m ax 上确定出目标在这组差频上的模糊距离值(并非真实距离),然后再作较少量搜索,得到目标实际距离值.因为R (1)m ax =(m 1m 2 n )a ,其中a =a i m i (i =1,2,…,N ),而n 为m 1、m 2的最大公约数(取m i 为互质时,n =1).假定m 1>m 2(这种假设不失一般性),则有b (1)1(a 1-a 2)+∃Υ12Πa 1=I a 2+∃Υ22Πa 2(8)式中 I =b (1)2-b (1)1,而b (1)1、b (1)2分别表示在R (1)m ax 内目标模糊距离关于a 1和a 2的整段数,容易看出I 亦为非负整数.由于b (1)1≤m 2 n ,b (1)2≤m 1 n ,因而可以确定I 的取值范围为I =a 1-a 2a 2b (1)1+∃R a 2≤m 1-m 2n +∃R a 2(9)式中 ∃R =∃Υ12Πa 1-∃Υ22Πa 2,由上式可对I 的取值范围(即搜索范围)具体分析如下:(1)若∃R <0,I 可以从0至(m 1-m 2) n -1搜索;(2)若∃R >0,I 可以从1至(m 1-m 2) n +I N T [∃Υ1a 1 (2Πa 2)]搜索(其中“I N T [ ]”55第1期 沈福民等:相位测距中的解模糊技术一般情况下,由于m 1、m 2的值比较接近(如图2(b )例),故I 的搜索范围要比b (1)1(或b (1)2)直接搜索时的范围小得多.利用式(8)对I 进行搜索,可以很方便地确定b (1)1值,即当式(8)b (1)1计算恰为整数时的值.确定了在R (1)m ax 内的模糊距离值后,再来解算目标的真实距离.设b 1=J m 2 n +b (1)1,使非负整数J 在雷达作用距离范围内从0开始不断增大搜索(实际上是以R (1)m ax 的整段距离为间隔搜索),由(b 1+∃Υ1 (2Π))m 1 m i =g i (i =3,4,…,N ),找到使所有b i +∃Υi(2Π)与g i 对应相同的b 1值,即为所求目标真实距离关于a 1的整段数,由此得到目标的真实距离.实际测量中,由于雷达通道噪声、杂波背景和测量误差等因素的影响,不可能精确获取多频率目标回波的相位差值.因而在求b (1)1(或b (1)2)和b i (i =3,4,…,N )时,不可能有恰好相符的理想情况,必须依照一定的准则进行最佳估值(或拟合).最简便而有效的估值准则可采用如下形式m in R δi ∑N i =1(R δi -R δ)2(10)式中 R δ=1N ∑N i =1R δi ,Rδi (i =1,2,…,N )为b 1在搜索时所求出的各个∃f i上对应的目标距离估值.图4 目标距离估值的误差计算图4表示目标距离估值由式(10)计算产生的误差(用分贝表示)情况.由图4可清楚看出,在目标真实距离(设为2km )处出现一个最大的零深,说明估计是基本准确的,没有出现误判(模糊段判错,即b i 判错).但由于相位测量误差(Ρp =10°)的影响,这个最大零深的深度已非理想情况下的深度(即估值误差不为零).在实际判决(或估值)中,要求测量误差有一定限制,才能不发生误判,且估值误差也会减小,这种限制对雷达系统和相位测量提出了较为严格的要求,模拟计算和外场测试结果表明,通常要求相位误差值不大于10°.4 结束语多频C W 雷达采用差频按一定参差要求选取,可有效减弱目标的测距模糊.由于仅利用目标回波的相位信息,故测距对相位测量的误差有较高要求.为了提高对目标距离估值的准确65 西安电子科技大学学报 第24卷试表明,通常在低空目标测距中因镜像反射[3]引起的误差对测距影响不大.多个工作频率回波信号的接收致使系统设备显得复杂、庞大,这就失去了原有C W 体制的优越性.可以实行差频分时工作,即如步进频率的脉压雷达那样的工作方式,以解决设备复杂的问题,但由于运动目标距离上的变化,需要对测距进行目标回波的相位补偿,才能较准确地获取目标某一时刻的距离数据.这方面的探索和研究工作尚需进一步进行.参 考 文 献1张有为,李少洪编1雷达系统分析1北京:国防工业出版社,19812L in H C .Spatial Co rrelati on in A dap tive A rrays .IEEE T rans ,1982,A P 230(2)3Barton D K .L ow 2A ngle T rack ing .M icrow ave Jour ,1976,(12)4Eaves J L ,R eedy E K .P rinci p les of M odern R adar .N ew Yo rk :V an N o strand R einho ld Company ,1987(编辑:郭 华) D e 2am b iguous te chnique s in the m e a s urem e nt of ra nge by pha s e sS hen F um in J ia Y ong kang(R esearch In st .of E lectron ic Engineering ,X idian U n iv .,X i πan ,710071)AbstractIn th is pap er ,w e have analyzed the seri ou s am b igu ity that ex ists in range m easu rem en t by u sing the p hase difference betw een targets πechoes of m u lti 2frequency in the C W radar .T he ex tended concep t of the am b igu ity functi on is u sed to criticize and i m p rove the range and speed m easu rem en t p erfo r m ance of the C W radar system .How to select the staggered rati o of frequencies πdifference of the m u lti 2frequency C W radar to reduce the am b igu ity of range m easu rem en t is also discu ssed .F inally ,w e have p resen ted and analyzed a m ethod of de 2am b igu ity of range m easu rem en t .Key W ords range m easu rem en t by phase am b igu ity functi on m ax i m um unam b igu ityrange stagger中国运筹学会第五届全国代表大会在我校召开中国运筹学会第五届全国代表大会暨学术会议于1996年10月11~15日在我校召开.参加会议的有来自全国29个省市自治区及香港的170余名代表.国家科委副主任徐冠华院士、中国科学院副秘书长王玉民教授、陕西省体改委主任李相启、陕西省科协副主席徐任、西安市科委副主任贺昌政等领导出席了大会.国际运筹学联合会主席P .C .Bell 教授(加拿大)、司库Sch rady 博士(美国)、秘书W elling (丹麦)也专程前来参加大会并致了贺词.会议进行了大会报告及分组报告.内容涉及线性与非线性规划、组合优化和排序、图与网络、多目标规划、对策与决策、排队论、系统可靠性数学、计算机模拟、最优控制、马氏决策规划、管理信息系统与决策支持系统等方面的理论与方法以及运筹学在各方面的应用.与会代表进行了热烈的讨论和广泛的交流.75第1期 沈福民等:相位测距中的解模糊技术。
伪距、载波相位测量原理

重建载波
将非连续的载波信号恢复成连续的载波信号。
伪距测量与载波相位测量
载波调制了电文之后 变成了非连续的波
码相关法
将所接收到的调制信号(卫星 信号)与接收机产生的复制码 相乘。
卫 星 信 号 的 生 成
接 收 机 重 建 载 波
(c )2 0 0 2 , 黄 劲 松
码相关法
码相关法
技术要点 卫星信号(弱)与接收机信号(强) 相乘。
3.9 卫星的载波信号及相位测量原理
3.9.1 GPS卫星的载波信号 3.9.2 GPS卫星信号的调制 3.9.3 GPS卫星信号的解调 3.9.4 载波相位测量原理
载波相位测量的特点
优点:测距精度高,可达0.1mm量级 难点: 重建载波 存在整周数不确定问题 存在整周跳变问题
测距码的调制与解调
在数字通讯技术中,为了有效地传播信息, 一般均将低频信号加载到高频的载波上, 这时原低频信号称为调制信号,而加载信 号后的载波就称为已调波。
GPS信号调制,是采用调相技术实现的。
卫星信号的调制
模二和
运算规则
二进制信号:“1”表示二进制“0”,“-1”表示二 进制“1”,则
理(如AS)
每颗GPS卫星都采用特定的 伪随机噪声码
码相关伪距测量
特点 定位速度快,实时定位 精度较高 对信号的强度要求不高
3.9 卫星的载波信号及相位测量原理
3.9.1 GPS卫星的载波信号 3.9.2 GPS卫星信号的调制 3.9.3 GPS卫星信号的解调 3.9.4 载波相位测量原理
6
测距码测距原理①
距离测定的基本思路
ctc
信号传 播时间
信号(测距码)传播时间的测定
相关系数:
激光相位多普勒技术

激光相位多普勒技术
激光相位多普勒技术是一种用于测量目标速度的高精度光学测量方法。
它基于多普勒效应和激光干涉原理,常用于测速、运动检测和遥感等领域。
以下是关于激光相位多普勒技术的一些基本原理和应用:
基本原理:
多普勒效应:
多普勒效应是指当光源和观测者相对运动时,光的频率发生变化。
对于激光相位多普勒技术,激光被用来照射目标,目标反射的光发生多普勒频移,该频移与目标速度成正比。
相位测量:
利用激光干涉原理,测量目标反射光的相位差。
相位差与多普勒频移相关,通过测量这个相位差可以确定目标的速度。
激光干涉:
激光被分成两束,一束直接照射到目标,另一束经过光程延迟器后照射到目标。
两束光在目标处发生干涉,产生干涉图样。
目标的运动导致了相位差的变化,通过测量这个相位差可以计算目标的速度。
高精度测量:
激光相位多普勒技术具有高精度和高分辨率的优点,适用于需要非常精确速度测量的应用,如气象雷达、交通监控、激光雷达等领域。
应用领域:
气象雷达:
用于测量大气中的风速。
激光相位多普勒技术可以提供对风场的高分辨率测量,用于气象研究和天气预测。
交通监控:
用于测量车辆的速度,可应用于交通管理、高速公路监控等领域。
激光雷达:
在激光雷达中,激光相位多普勒技术可用于测量目标的速度,常用于军事、安防和导航系统中。
医学影像:
在医学成像中,激光相位多普勒技术可用于测量血流速度,常应用于超声血流仪等设备。
总体而言,激光相位多普勒技术在需要高精度速度测量的各种应用中发挥着重要作用,提供了一种非常灵敏和精准的测量手段。
零差外差相位测量原理与技术

2014-2-19
一. 相位测量? 相位差变化的连续测量:
ym (t )
2 状态1: 1 0,
yr (t )
2 ym (t ) 状态2: 2 0,
yr (t )
m 2 m1 2 1 N * 2
10
2014-2-19
补充知识 相位测量原理与技术
2014-2-19
<< 激光测量与探测技术>>
补充知识:相位测量原理与技术
哈尔滨工业大学
©HIT
1
2014-2-19
补充知识 相位测量原理与技术
一、 相位测量? 二、中低频信号的相位测量 三、高频信号的相位测量技术
哈尔滨工业大学
©HIT
2
2014-2-19
一. 相位测量?
信号振动方程:
y (t ) A sin 2 ft 0
4
2014-2-19
一. 相位测量? 测量相位差的变化量 (phase h diff difference)
待测信号方程: 参考信号方程:
ym (t )
ym (t ) A sin i 2 ft m
yr (t ) A sin 2 ft f r
ym (t )
yr (t )
高频脉冲计数
t 2 tA
2
N NA
16
2014-2-19
三.高频信号的相位测量
零差解调法 (正交解调 ,零中频)
sin m r
ym y( t, (tf, ,f)m ) m
cos(m r )
yry (rt( ,t f , ,f )r )
17
2014-2-19
知识笔记-7.2用示波器测量相位差
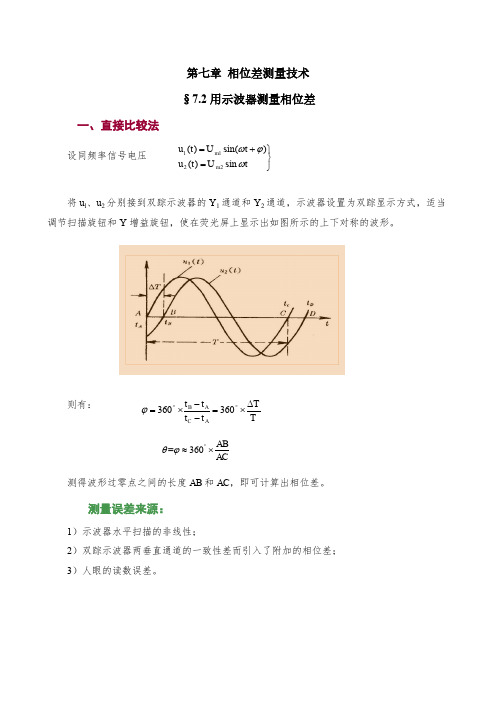
第七章 相位差测量技术§7.2用示波器测量相位差一、直接比较法设同频率信号电压⎭⎬⎫=+=t U t u t U t u m m ωϕωsin )()sin()(2211将u l 、u 2分别接到双踪示波器的Y 1通道和Y 2通道,示波器设置为双踪显示方式,适当调节扫描旋钮和Y 增益旋钮,使在荧光屏上显示出如图所示的上下对称的波形。
则有:=360AB ACθϕ︒≈⨯ 测得波形过零点之间的长度AB 和AC ,即可计算出相位差。
测量误差来源:1)示波器水平扫描的非线性;2)双踪示波器两垂直通道的一致性差而引入了附加的相位差;3)人眼的读数误差。
TT t t t t A C A B ∆⨯=--⨯=︒︒360360ϕ二、椭圆法u 1加于Y 通道,u 2加于X 通道,则光点沿垂直及水平的瞬时位移量y 和x 分别为⎩=⎨⎧=x K u y K u X 2Y 1式中,K Y 、K X 为比例常数。
设u 1、u 2分别为⎩=⎨⎧=+ωωϕu U tu U t m m sin sin()2211整理得=+=+=+ωϕωϕωϕωϕY t Y t y K U t Y t m sin cos cos sin sin()sin()m m Y 1m ==ωωx K U t X t m sin sin X 2m式中,Y m 、X m 分别为光点沿垂直及水平方向的最大位移。
由上式得ω=sin /t x X m则=+-ϕϕX y x X x Y (cos sin )mm m 22 这是一个广义的椭圆方程,其椭圆图形如下图所示,令y =0,x =0,求出椭圆与垂直、水平轴的交点y 0、x 0分别等于⎩=±⎨⎧=±ϕϕx X y Y sin sin 0m 0m可解得相位差为=±=±ϕY X y x arcsin()arcsin()m m00设椭圆的长轴为A ,短轴为B ,可以证明相位差为:ϕ=2arctan B A有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)示波器Y通道、X通道的相频特性一般不会是完全一样的,这要引起附加相位差,又称系统的固有相位差。
电子测量技术频率(时间)与相位测量

电子测量原理
转变为自然基准。
需要指出的是,在电子仪器中常采用石英频率标准。
其原因在于:其一,石英晶体的机械稳定性和热稳定性很 高,它的振荡频率受外界因数的影响较小,因而比较稳定 ;其二,石英频率标准发展快,六十年来将准确度和稳定 度提高了4个数量级;其三,石英晶体振荡器结构简单, 制造、维护、使用均方便,而且准确度能满足大多数测量 的需要。因此,石英频率作为一种次级标准,已成为最常 用的频率标准。 最后还要指出,时间标准就是频率标准,这是因为频 率与时间互为倒数。
第3页
电子测量原理
6.1.2 频率或时间标准
人们早期根据在地球上看到太阳的“运动”较为均匀 这
一现象建立了计时标准,把太阳出现于天顶的平均周期(
即平均太阳日)的86400分之一定为一秒,称零类世界时
(记作UTo),其准确度在10-6量级。考虑到地球受极运 动(即极移引起的经度变化)的影响,可加以修正,修正 后称为第一世界时(记作UT1)。此外,地球的自转不稳 定,进行季节性、年度性变化校正,引出第二世界时(记 作UT2),其稳定度在3×10-8。而公转周期却相当稳定, 于是人们以1900回归年的31556925.9747分之一作为历书时 的秒(记作ET),其标准度可达±1×10-9。
第1页
电子测量原理
所以,频率、时间、相位三个量可归结为一个量的 测量问题。在电子技术领域内,频率是最基本的参数之一 ,它指单位时间内周期变化或振荡的次数,许多电参数的 测量方案及结果都与之密切相关。因此,频率的测量是十 分重要的,而且到目前为止频率的测量在电测量中精确度 是最高的。
第2页
电子测量原理
第11页
电子测量原理
输入信号显示时的位置,则显示第二个输入信号时就可距离,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相位测量技术
相位测量技术是一种用于测量信号相位差的技术。
在通信、雷达、光学等领域中,相位测量技术被广泛应用。
相位测量技术的主要目的是测量两个信号之间的相位差,以便确定它们之间的时间差或距离差。
相位测量技术的基本原理是利用两个信号之间的相位差来计算它们之间的时间差或距离差。
这种技术通常使用两个相位锁定环(PLL)来实现。
一个PLL用于锁定参考信号的相位,另一个PLL用于锁定待测信号的相位。
通过比较这两个PLL的输出,可以计算出两个信号之间的相位差。
相位测量技术的应用非常广泛。
在通信领域中,相位测量技术被用于测量信号的相位差,以便确定信号的时间差或距离差。
在雷达领域中,相位测量技术被用于测量雷达信号的相位差,以便确定目标的距离和速度。
在光学领域中,相位测量技术被用于测量光波的相位差,以便确定物体的形状和表面特征。
相位测量技术的优点是精度高、测量范围广、测量速度快。
相位测量技术的缺点是需要高精度的仪器和复杂的算法,成本较高。
此外,相位测量技术对环境的要求较高,需要在稳定的环境中进行测量。
相位测量技术是一种非常重要的测量技术,被广泛应用于通信、雷达、光学等领域。
随着科技的不断发展,相位测量技术的精度和应
用范围将会不断提高,为人类的生产和生活带来更多的便利和效益。
