材料力学习题解答(拉伸、压缩与剪切)
材料力学习题01拉压剪切

材料力学习题01拉压剪切(共10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--拉伸与压缩一、 选择题 (如果题目有5个备选答案选出其中2—5个正确答案,有4个备选答案选出其中一个正确答案。
)1.若两等直杆的横截面面积为A ,长度为l ,两端所受轴向拉力均相同,但材料不同,那么下列结论正确的是( )。
A .两者轴力相同应力相同B .两者应变和仲长量不同C .两者变形相同D .两者强度相同E .两者刚度不同2.一圆截面直杆,两端承受拉力作用,若将其直径增大一倍,其它条件不变,则( )。
A .其轴力不变B .其应力将是原来的1/4C .其强度将是原来的4倍D .其伸长量将是原来的1/4E .其抗拉强度将是原来的4倍3.设ε和1ε分别表示拉压杆的轴向线应变和横向线应变,μ为材料的泊松比,则下列结论正确的是( )。
A .εεμ1=B .εεμ1-=C .εεμ1= D .εεμ1-= E .常数时,=≤μσσ p 4.钢材经过冷作硬化处理后,其性能的变化是( )。
A .比例极限提高 B .屈服极限提高C .弹性模量降低D .延伸率提高E .塑性变形能力降低5.低碳钢的拉伸σ-ε曲线如图1-19所示若加载至强化阶段的C 点,然后卸载,则应力回到零值的路径是( )。
A .曲线cbaoB .曲线cbf (bf ∥oa )C .直线ce (ce ∥oa )D .直线cd (cd ∥o σ轴)6.低碳钢的拉伸σ-ε曲线如图l —19,若加载至强化阶段的C 点时,试件的弹性应变和塑性应变分别是( )。
A .弹性应变是ofB .弹性应变是oeC .弹性应变是edD .塑性应变是ofE .塑性应变是oe7.图l-2l 表示四种材料的应力—应变曲线,则: (1)弹性模量最大的材料是( );(2)强度最高的材料是( );(3)塑性性能最好的材料是( )。
8.等截面直杆承受拉力,若选用三种不同的截面形状:圆形、正方形、空心圆,比较材料用量,则( )。
材料力学典型题解

1轴向拉伸与压缩例1-1 如图所示的等截面直杆,受轴向力F 1=15kN ,F 2=10kN 的作用。
试分别求出杆件1-1、2-2截面的轴力,并画出轴力图。
F 2F 2C 22 22F 111 11B F 1AF RF RF N1F 1F N2F R F N10kN5kN图1-1解:(1)外力分析 先解除约束,画出杆件的受力图。
120,0xR FF F F = -+=∑得:()121510kN 5kN R F F F =-=-=(2)内力分析 外力F R 、F 1、F 2将杆件分为AB 段和BC 段,在AB 段,用1-1截面将杆件截分为两段,取左段为研究对象,右段对截面的作用力用F N1来代替。
假定内力F N1为正,列平衡方程10,0xN R FF F = +=∑得:15kN N R F F =-=-负号表示F N1的方向和假定方向相反,截面受压。
在BC 这一段,用任意2-2截面将杆件分为两段,取左段为研究对象,右段对左段截面的作用力用F N2来代替。
假定轴力F N2为正,有平衡方程2100xN R FF F F = +-=∑得: ()21515kN N R F F F =-+=-+=10kN (3)画轴力图由以上例题可以总结出求截面轴力的简捷方法:杆件任意截面的轴力F N (x )等于截面一侧所有外力的代数和。
即1nN i i F F ==∑,外力背离该截面的时取正,指向该截面时取负。
例1-2 如图所示为正方形截面阶梯杆,受力及尺寸如图所示。
试分析杆上1截面处和2截面处的正应力。
FF2hh12(a )FFF N 11122N hh σ==F F F N 1222244N h h σ==F F(b ) 图1-2解:先求出杆两截面处的轴力F N 1和F N 2,在用截面上的轴力除以相应的截面面积,如图(b )所示,不难求出σ1=F/h 2,σ2=F/(4h 2)。
例1-3 如图所示,斜杆AB 为直径d =20mm 的钢杆,载荷Q =15kN 。
工程力学:拉伸压缩 习题与答案

一、单选题1、拉压正应力计算公式s=F/A的适用条件是()。
A.应力小于弹性极限B.应力小于屈服极限C.应力小于比例极限D.外力的合力沿杆轴线正确答案:D2、材料经过冷作硬化后,其比例极限和塑性分别()。
A.提高,提高B.下降,不变C.下降,提高D.提高,下降正确答案:D3、假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为()。
A.大于450MPaB.300MPa£s£450MPaC.450MPaD.小于300MPa正确答案:B4、受轴向拉伸的杆件,其最大切应力与轴线的角度为()。
A.30B.90C.45D.0正确答案:C5、一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的()。
A.应力不同,变形相同B.应力不同,变形不同C.应力相同,变形不同D.应力相同,变形相同正确答案:C6、脆性材料与塑性材料相比,其拉伸性能的最大特点是()。
A.没有明显的屈服阶段和塑性变形B.应力应变关系严格遵守虎克定律C.强度低、对应力集中不敏感D.强度极限比塑性材料高正确答案:A7、现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1, 杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为()。
A.2:1B.1:1C.4:1D.1:2正确答案:C8、在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是()。
A.屈服阶段B.颈缩阶段C.强化阶段D.线弹性阶段正确答案:A9、现有两相互接触的平板,在垂直于板平面的方向上打一直径为d的销孔,使用直径d、许用切应力[τ]、许用挤压应力[sbs]的圆柱形销钉进行固定,两板的厚度均为h, 现分别在两板施加大小相同、方向相反的F,使两板有沿接触面相互错动的倾向,若要销钉不失效破坏,则要满足的条件是()。
材料力学 拉伸压缩 习题及参考答案

轴向拉伸和压缩 第二次 作业1. 低碳钢轴向拉伸的整个过程可分为 弹性阶段 、 屈服阶段 、 强化阶段 、 局部变形阶段 四个阶段。
2. 工作段长度100 mm l =,直径10 mm d =的Q235钢拉伸试样,在常温静载下的拉伸图如图所示。
当荷载F = 10kN 时,工作段的伸长∆l = 0.0607mm ,直径的缩小∆d = 0.0017mm 。
则材料弹性模量E = 210 GPa ,强度极限σb = 382 MPa ,泊松比μ = 0.28 ,断后伸长率δ = 25% ,该材料为 塑性 材料。
∆l / mmO0.0607253. 一木柱受力如图所示。
柱的横截面为边长20mm 的正方形,材料的弹性模量E =10GPa 。
不计自重,试求 (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱端A 的位移。
100kN260kN解:(1)轴力图如图所示 (2)AC 段 310010250MPa 2020NAC AC AC F A σ-⨯===-⨯ CB 段 326010650MPa 2020NCB CB CB F A σ-⨯===-⨯ (3)AC 段 69250100.0251010NAC AC AC AC F EA E σε-⨯====-⨯ CB 段 69650100.0651010NCB CB CBCB F EA E σε-⨯====-⨯ (4)AC 段 0.025150037.5mm NAC ACAC AC AC ACF l l l EA ε∆===-⨯=- CB 段 0.065150097.5mm NCB CBCB CB CB CBF l l l EA ε∆===-⨯=- 柱端A 的位移 37.597.5135mm A AC CB l l ∆=∆+∆=--=-(向下)4. 简易起重设备的计算简图如图所示。
已知斜杆AB 用两根63×40×4不等边角钢组成,63×40×4不等边角钢的截面面积为A = 4.058cm 2,钢的许用应力[σ] = 170 MPa 。
材料力学习题解答(拉伸、压缩与剪切)

∑m
C
A
' = 0 NE × 4.5 + N C × 1.5 − P × 3 = 0
(2) 以刚体 BDE 为研究对象
1.5m
NE
E D 0.75m B NB
∑m
D
=0
N E × 1.5 − N B × 0.75 = 0
2
(3) 联立求解
N B = NC
(4) 拉杆内的应力
' NE = NE
∴ N C = 6kN
A B
h
b
解:强度条件为
P ≤ [σ ] A
又因为 A = bh = 1.4b2 , 所以
b≥
P 1100 × 103 = = 116.4mm 1.4 [σ ] 1.4 × ( 58 × 106 ) h = 1.4b ≥ 162.9mm
2.8. 图示夹紧机构需对工件产生一对 20kN的夹紧力,已知水平杆AB及斜杆BC和BD的材料 相同,[σ]=100MPa,α=30o。试求三杆的横截面直径。
D B A1 l1 A2 l2
P
C F l
x
解: (1) 研究 CF,求 BC 和 DF 的受力: NBC P NDF
F l
C
x
∑M
C
=0
− P × x + N DF × l = 0 N DF = x P l
7
∑M
(2) 求 BC 和 DF 杆的变形;
F
=0
P × ( l − x ) − N BC × l = 0 N BC = l−x P l
Δl BC =
N BC l BC l − x Pl1 = × E1 A1 l E1 A1 N DF l DF x Pl2 = × E2 A2 l E2 A2 Δl BC = Δl DF
材料力学练习册答案

第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑x F ,得 01=N F22-截面,取右段如)(b由0=∑x F ,得 P F N -=233-截面,取右段如)(c由0=∑x F ,得 03=N F2.2 图示杆件截面为正方形,边长cm a 20=,杆长m l 4=,kN P 10=,比重3/2m kN =γ。
在考虑杆本身自重时,11-和22-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑xF,得kN la F N 08.04/21==γ22-截面,取右段如)(b由0=∑xF,得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示,已知kN P 20=,kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解:轴力图如图。
杆的总伸长:m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力:MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示,已知直径mm d 40=,杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
(GPa E 80=铜,GPa E 200=钢)。
解:由∑=∆EAl F l N ,得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得: kN P 7.16= 杆内的最大正应力:MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时,在试件的某处分别安装两个杆件变形仪,其放大倍数各为1200=A k ,1000=B k ,标距长为cm s 20=,受压后变形仪的读数增量为mm n A 36-=∆,mm n B 10=∆,试求此材料的横向变形系数ν(即泊松比)。
材料力学例题解析拉伸压缩

指由外力作用所引起的、物体内相邻部分之间分布内力系的合成(附加内力)。
内力的计算是分析构件强度、刚度、稳定性等问题的基础。
求内力的一般方法:
截面法
截面法的基本步骤:
P
A
P
①截
在所求内力的截面处,假想地用截面将杆件截开
P
A
N
② 取 取其中一部分作为研究对象
③ 代 其舍去部分对保留部分的作用,用作用于截面上的内力代替。
④ 平 对保留部分建立平衡方程,由此求得内力
X 0 PN 0 PN
轴力 符号规定: 拉为正、压为负
内力图―轴力图 用横坐标表示截面的位置,用纵坐标表示轴力的大小和符号
N P
+ x
确定出最大内力的数值及其所在横截面的位置,即确 定危险截面位置,为强度计算提供依据。
活塞杆上的力分别简化为Pl=2.62kN,P2=1.3kN,P3=1.32kN。试求活塞杆横截 面1-1和2-2上的轴力,并画出轴力图
某拉伸试验机的示意图如图所示。设试验机的CD杆与试样AB同为低碳钢制成, sp=200MPa,ss=240MPa,sb=400MPa。试验机的最大拉力为10kN。 (1)用这试验机作拉断试验时试样最大直径可达多少? (2)设计时若取安全系数n=2,则CD杆的截面面积为多少? (3)若试样的直径d=10mm,今欲测弹性模量E则所加拉力最大不应超过多少?
10KN
应注意的问题: 应用条件:
直杆 Saint-Venant原理:
离开载荷作用处一定距离,应力分布与大小不受外载荷作用方式的影响
应力集中(Stress Concentration): 在截面尺寸突变处,应力急剧变化。
斜截面上的应力
斜截面上全应力:
材料力学课后答案
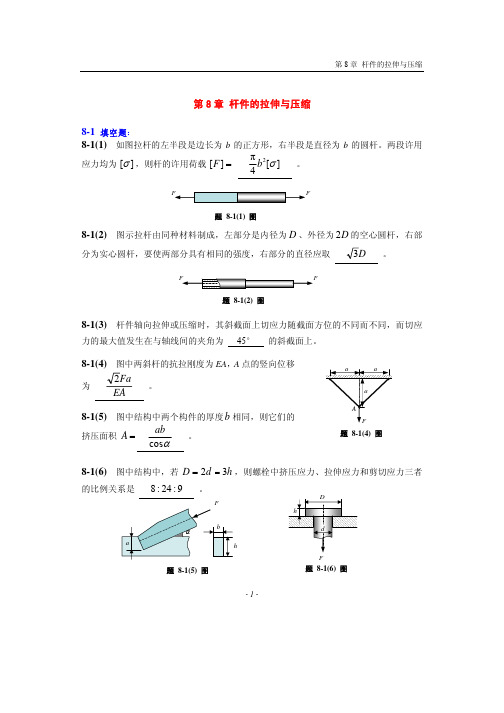
- 1 -第8章 杆件的拉伸与压缩8-1 填空题:8-1(1) 如图拉杆的左半段是边长为b 的正方形,右半段是直径为b 的圆杆。
两段许用应力均为 ][σ,则杆的许用荷载 =][F ][4π2σb 。
8-1(2) 图示拉杆由同种材料制成,左部分是内径为D 、外径为D 2的空心圆杆,右部分为实心圆杆,要使两部分具有相同的强度,右部分的直径应取 D3 。
8-1(3) 杆件轴向拉伸或压缩时,其斜截面上切应力随截面方位的不同而不同,而切应力的最大值发生在与轴线间的夹角为 45° 的斜截面上。
8-1(4) 图中两斜杆的抗拉刚度为EA ,A 点的竖向位移为EAFa 2 。
8-1(5) 图中结构中两个构件的厚度b 相同,则它们的挤压面积 =A αcos ab。
8-1(6) 图中结构中,若 h d D 32==,则螺栓中挤压应力、拉伸应力和剪切应力三者的比例关系是 9:24:8 。
题 8-1(5) 图题 8-1(1) 图题 8-1(2) 图题 8-1(6)图F题 8-1(4) 图- 2 -分析:222bs 3π4)(π4d F d D F =−=σ, 2tπ4d F =σ, 22π3πd F hd F ==τ,故有 9:24:883:1:31::tbs ==τσσ。
8-2 单选题:8-2(1) 图示的等截面杆左端承受集中力,右端承受均布力,杆件处于平衡状态。
1、3两个截面分别靠近两端,2截面则离端部较远。
关于1、2、3这三个截面上的正应力的下列描述中,正确的是 C 。
A .三个截面上的正应力都是均布的 B .1、2两个截面上的正应力才是均布的 C .2、3两个截面上的正应力才是均布的 D .1、3两个截面上的正应力才是均布的8-2(2) 若图示两杆的材料可以在铸铁和钢中选择,那么,综合强度和经济性两方面的因素, C 更为合理。
A .两杆均选钢 B .两杆均选铸铁C .① 号杆选钢,② 号杆选铸铁D .① 号杆选铸铁,② 号杆选钢8-2(3) 图示承受轴向荷载的悬臂梁中,在加载前的一条斜直线KK 在加载过程中所发生的变化是 D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1. 试求图示各杆1-1、2-2、3-3截面的轴力, 并作轴力图。
解: (a)(1)求约束反力kNR R X 500203040 0==-++-=∑(2)求截面1-1的轴力kNN NR X 500011==+-=∑(3)求截面2-2的轴力kNN NR X 10040 022==++-=∑(4)求截面3-3的轴力330 20020X NN kN=--==-∑(5)画轴力图(a)(b)20kNN 220kN(b)(1)求截面1-1的轴力01=N(2)求截面2-2的轴力PN P NX 404022==-=∑(3)求截面3-3的轴力PN P P NX 304 033==-+=∑(4)画轴力图2.3. 作用图示零件上的拉力P=38kN ,试问零件内最大拉应力发生于哪个横截面上?并求其值。
解:(1) 1-1截面上的应力 1613381067.86(5022)2010P MPa A σ-⨯===-⨯⨯ (2) 2-2截面上的应力21333262381063.332152010P MPa A σ-⨯===⨯⨯⨯ (3) 3-3截面上的应力3363381045.24(5022)15210P MPa A σ-⨯===-⨯⨯⨯(4) 最大拉应力在1-1截面上MPa 86.671max ==σσ2.4. 设图示结构的1和2两部分皆为刚体,钢拉杆BC 的横截面直径为10mm ,试求拉杆内的应力。
解:(1) 以刚体CAE 为研究对象∑=⨯-⨯+⨯=035.15.4 0'P N N mC E A (2) 以刚体BDE 为研究对象075.05.1 0=⨯-⨯=∑B E DN N m(3) 联立求解kNN N N N N C EE C B 6 '=∴==NP =7.5kN(4) 拉杆内的应力3261076.40.01/4B N MPa A σπ⨯===⨯2.5.图示结构中,杆1、2的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
解:(1) 以整体为研究对象,易见A 处的水平约束反力为零;(2) 以AB 为研究对象(B 处不带销钉)由平衡方程知0===A B B R Y X(3) 以杆BD 为研究对象由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4) 杆内的应力为311213222210101270.01/4201063.70.02/4N MPaA N MPa A σπσπ⨯===⨯⨯===⨯2.7. 冷镦机的曲柄滑块机构如图所示。
镦压工件时连杆接近水平位置,承受的镦压力P=1100 kN 。
连杆的截面为矩形,高与宽之比为h/b=1.4。
材料为45钢,许用应力为[σ]=58 MPa ,试确定截面尺寸h 和b 。
解:强度条件为][σ≤AP又因为 A = bh = 1.4b2 , 所以116.4141629b mm h .b .mm≥===≥ 2.8. 图示夹紧机构需对工件产生一对20 kN 的夹紧力,已知水平杆AB 及斜杆BC 和BD 的材料相同,[σ]=100MPa ,α=30o 。
试求三杆的横截面直径。
解:(1) 以杆CO 为研究对象013100()0 cos300201023.1cos30cos30o m F N l S l N S kN=⨯-⨯⨯=⨯===∑(2) 以铰B 为研究对象1223.1P S S kN ===(3) 由强度条件得三杆的横截面直径 1217.2AB BC BDd d d mm=====2.10 图示简易吊车的杆BC为钢杆,杆AB为木杆,。
杆AB的横截面面积A1=100 cm2,许用应力[σ]1=7 MPa;杆BC的横截面面积A2=6 cm2,许用应力[σ]2=160 MPa。
求许可吊重P。
解: (1) 以铰B为研究对象,画受力图和封闭的力三角形;12302sin30ooN PctgPN P====(2) 由AB杆的强度条件1111146[][]1001071040.4NAP kNσσ-≤≤⨯⨯⨯∴≤==(3) 由BC杆的强度条件()()2222246222[][]61016010[]4822N PA AAP kNσσσ-≤≤⨯⨯⨯⨯≤==(4) 许可吊重kNP4.40][=注:BC杆受拉,AB杆受压;BC杆的强度比AB杆的强度高。
2.11 拉伸试验机通过杆CD使试件AB受拉,如图所示。
设杆CD与试件AB的材料同为低碳钢,其σp=200 MPa,σs=240 MPa,σb=400 MPa。
试验机的最大拉力为100 kN。
(1) 用这试验机作拉断试验时,试件最大直径可达多少?(2) 设计时若取安全系数n=2,则CD杆的横截面面积为多少?(3) 若欲测弹性模量E,且试样的直径d=10 mm,则所加拉力最大值为多少?PN2N130o解:(1) 试样拉断时2maxmax1417.84bN PA dd mmσπ==∴==(2) 设计时若取安全系数n=2,则CD杆的强度条件为:[]sCDNA nσσ≤=所以CD杆的截面面积为()32610010283324010CDsN nA mmσ⨯⨯⨯≥==⨯(3) 测弹性模量E时,则AB杆内的最大应力为:maxmax PABNAσσ==所加最大拉力为()62max1200100.0115.714P ABN A kNσπ⎛⎫=⨯=⨯⨯⨯⨯=⎪⎝⎭2.13 阶梯杆如图所示。
已知:A1=8 cm2,A2=4 cm2,E=200 GPa。
试求杆件的总伸长。
解: (1) 用截面法求1-1, 2-2截面上的内力:1220 40N kN N kN =-=(2) 求A1段的变形:()()()311194120100.20.025********N L l mm EA --⨯⨯∆===-⨯⨯⨯(3) 求A2段的变形:()()()322294240100.20.120010410N L l mm EA -⨯⨯∆===⨯⨯⨯(4) 杆件的总变形:120.075l l l mm ∆=∆+∆=注:A1段缩短,A2段伸长,总变形为伸长。
2.14 在图示结构中,设CF 为刚体(即CF 的弯曲变形可以不计),BC 为铜杆,DF 为钢杆,两杆的横截面面积分别为A1和A2,弹性模量分别为E1和E2。
如要求CF 始终保持水平位置,试求x 。
解: (1) 研究CF ,求BC 和DF 的受力:0 0CDF DFM P x N l x N P l=-⨯+⨯==∑()0 0FBC BCMP l x N l l x N Pl=⨯--⨯=-=∑(2) 求BC 和DF 杆的变形;DF1111122222BC BC BC DF DF DF N l l x Pl l E A l E A N l x Pl l E A l E A -∆==⨯∆==⨯(3) 变形关系;121122BC DFl l l x Pl x Pl l E A l E A ∆=∆-⨯=⨯122122211l E A x ll E A l E A =+ 2.15 像矿山升降机钢缆这类很长的拉杆,应考虑其自重影响。
设钢缆密度为ρ,许用应力为[σ],下端所受拉力为P ,且截面不变。
试求钢缆的允许长度及其总伸长。
解:(1) 分析钢缆的受力(2) 钢缆重量沿杆长的分布集度为:q gA ρ=(3) 钢缆的内力:max ()N x P qx P gAxN P gAlρρ=+=+=+(4) 钢缆的强度条件:max max [][][]N Pgl A APA P A l g gAσρσσσρρ==+=--== (5) 钢缆的总伸长:()200222222[]2ll N x P gAx Pl gAl l dx dx EA EA EA A P EA gρρσρ++∆===-=⎰⎰2.22 由五根钢杆组成的杆系如图所示。
各杆横截面面积均为500 mm2,E=200 GPa 。
设沿对角线AC 方向作P)用一对20 kN 的力,试求A 、C 两点的距离改变。
解:(1) 分析铰A 的受力2AB AD N N P ==(2) 分析铰B 的受力''BC AB BD ABN N P N P==== 同理可得:2CD N P =(3) 使用功能原理12W P δ=22422i i P a N l U EA EA ⎫⨯⎪⎝⎭==⨯+=∑((396420102220010500106.8310U WPa a EA aδ--=⨯⨯=+=+⨯⨯⨯=⨯2.26 受预拉力10 kN 拉紧的缆索如图所示。
若在C 点再作用向下15 kN 的力,并设缆索不能承受压力。
试P N ADN ABN ’N BCN N BCN ’ABN BD求在h=l/5和h=4l/5两种情况下,AC 和BC 两段内的内力。
解:(1) 分析AB 杆的受力,列平衡方程 150BA Y Y --=(2) 求BC 、AC 段的变形()B BC BC BC AC AC AAC Y l h N l l EA EA N l Y hl EA EA -∆==∆== (3) 根据变形谐调条件()()()1010bC AC B A B B A l l lY l h Y h lEA EA EA Y h Y Y l∆+∆=∆-+=-=-(4) 当h=l/5时 13 2 B A Y kN Y kN ==-缆索只能受拉不能受压,则AC 段的内力为零0 15 0 15 A B AC BC Y Y kN N N kN==∴==(4) 当h=4l/5时7 22 7 22 A B AC BC Y kN Y kN N kN N kN==∴==2.28 在图示结构中,设AC 梁为刚杆,杆件1、2、3的横截面面积相等,材料相同。
试求三杆的轴力。
解:(1) 以刚杆AC 为研究对象,其受力和变形情况如图所示(2) 由平衡方程2 0)(0 032321=+==-++=∑∑a N a N F m P N N N Y A(3) 由变形协调条件 Δ2ΔΔ 231l l l =+(4) 由物理关系Δ Δ Δ332211EAl N l EA lN l EA l N l ===(5) 联立求解得P N P N P N 61 31 65321-===2.31 阶梯形钢杆的两端在T1=5oC 时被固定,如图所示,杆件上、下两段的横截面面积分别是A 上=5 cm2,A 下=10 cm2。
钢材的α=12.5×10-6 /oC ,E=200 GPa 。
若温度升高至T2=25oC ,试求杆内各部分的温度应力。
解:(1) 阶梯杆的受力如图所示,由平衡条件可得21R R =(2) 由温度升高引起的阶梯杆伸长为21()2t l tl T T a αα∆=∆=-由两端反力引起的阶梯杆缩短为ΔL 3A A 22211ΔEA aR EA a R l +=(3) 变形谐调关系122112()2t l l R a R aT T a EA EA α∆-∆=+=- 求得约束力()()()()()()()()12121212964444222001012.5102555101010510101033.3E T T A A R R A A KNα------==+⨯⨯⨯⨯⨯-⨯⨯⨯⨯=⨯+⨯=(4) 计算杆内的应力11121266.7 33.3R RMPA MPa A A σσ=-=-=-=- 2.33 在图示三杆桁架中,1、2两杆的抗拉刚度同为E1A1,杆3为E3A3。
