2019-2020年高三第三次模拟考试(三模)数学 含答案
2020永州三模-数学(文)答案
二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 把答案填在答题卡中对应题号后的
横线上.
13． 3x y 1 0
14．
（写 60 也得分）
15．27
16． 4
3
5
13.解析：由于 f 0 1, f x 4 ex ，所以 f 0 4 1 3，由点斜式可得切线方程
为3x y 1 0 .
即
1 3
SBDE h
1 3
S ABD
DE
………………………………………………10 分
由 1 5 h 1 21 得 h = 4 5
32 3
5
………………………………………11 分
所以 C′ 到平面 B′DE 的距离等于 4 5 5
…………………………………12 分
____________________________________________________________________________________________
5
三、解答题：本大题共 70 分，解答应写出文字说明、证明过程或演算步骤.
17．（本题满分 12 分）
命题意图：第 1 问考查等差、等比数列基本量的运算及等差数列求和；
第 2 问考查累加法求通项公式.
解：（1）由题意可得
(aa1124dd)24
(a1
d
)(a1
10d
)
即
a21d22d
4, a1d.
…………………8 分
所以 bn bn bn1 bn1 bn2 b2 b1 b1
（3 2n 2n1 2n2 L 22） 3 3 2n+1 9(n 2) ． …………………11 分
2020年陕西省宝鸡市高考数学三模试卷(一)(有答案解析)
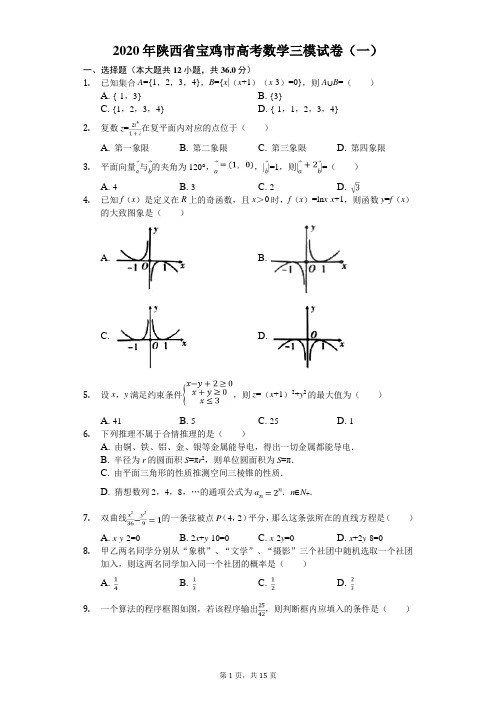
2020年陕西省宝鸡市高考数学三模试卷（一）一、选择题（本大题共12小题，共36.0分）1.已知集合A={1，2，3，4}，B={x|（x+1）（x-3）=0}，则A∪B=（）A. {-1，3}B. {3}C. {1，2，3，4}D. {-1，1，2，3，4}2.复数z=在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.平面向量与的夹角为120°，，||=1，则||=（）A. 4B. 3C. 2D.4.已知f（x）是定义在R上的奇函数，且x＞0时，f（x）=ln x-x+1，则函数y=f（x）的大致图象是（）A. B.C. D.5.设x，y满足约束条件，则z=（x+1）2+y2的最大值为（）A. 41B. 5C. 25D. 16.下列推理不属于合情推理的是（）A. 由铜、铁、铝、金、银等金属能导电，得出一切金属都能导电．B. 半径为r的圆面积S=πr2，则单位圆面积为S=π．C. 由平面三角形的性质推测空间三棱锥的性质．D. 猜想数列2，4，8，…的通项公式为a．n∈N+．7.双曲线的一条弦被点P（4，2）平分，那么这条弦所在的直线方程是（）A. x-y-2=0B. 2x+y-10=0C. x-2y=0D. x+2y-8=08.甲乙两名同学分别从“象棋”、“文学”、“摄影”三个社团中随机选取一个社团加入，则这两名同学加入同一个社团的概率是（）A. B. C. D.9.一个算法的程序框图如图，若该程序输出，则判断框内应填入的条件是（）A. i≤4B. i≤5C. i≤6D. i≥510.已知椭圆，M，N是椭圆上关于原点对称的两点，P是椭圆上任意一点，且直线PM、PN的斜率分别为k1、k2，若，则椭圆的离心率为（）A. B. C. D.11.定义在R上的函数y=f（x）满足以下三个条件：①对于任意的x∈R，都有f（x+1）=f（x-1）；②函数y=f（x+1）的图象关于y轴对称；③对于任意的x1，x2∈[0，1]，都有（f（x1）-f（x2））（x1-x2）＞0则f（）、f（2）、f（3）从小到大的关系是（）A. f（）＞f（2）＞f（3）B. f（3）＞f（2）C. f（）＞f（3）＞f（2）D. f（3）12.异面直线a，b所成的角为，直线a⊥c，则异面直线b与c所成角的范围为（）A. []B. []C. []D. []二、填空题（本大题共4小题，共12.0分）13.若数列{a n}满足a=8n（n∈N*），则a n=______．14.二次函数y=f（x）的图象经过坐标原点，若其导函数为f′（x）=3x-，则f（x）=______．15.已知圆锥的轴截面是一个边长为2的正三角形，则圆锥的侧面积等于______．16.斐波那契数列{a n}前两个数都是1，从第三个数起，每一个数都等于它前面两个数的和．若b n=a n a n+2-a n+12，则b1+b2+b3+…+b2019=______．三、解答题（本大题共7小题，共84.0分）17.已知=（），=（sin x，cos x），函数f（x）=．（1）求f（x）的最小正周期及对称轴方程；（2）当x∈（-π，π]时，求f（x）单调递增区间．18.在如图所示的多面体中，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EC⊥AC，EF∥AC，AB=，EF=EC=1．（1）求证：EC∥平面BFD；（2）求三棱锥D-BEF的体积．19.已知椭圆C：=1（a＞b＞0）的左、右两个焦点分别为F1，F2，上项点A（0，）△AF1F2是正三角形．（1）求椭圆C的标准方程；（2）O为坐标原点，P是直线F1A上的一个动点，求|PF2+|PO|的最小值，并求出此时点P的坐标20.十九大以来，我国新能源产业迅速发展．以下是近几年某新能源产品的年销售量数据：年份20142015201620172018年份代码12345新能源产品年销售y1.6 6.217.733.155.6（万个）（1）请面出上表中年份代码x与年销量y的数据对应的散点图，并根据散点图判断：y=ax+b与y=cx2+d中哪一个更适宜作为年销售量y关于年份代码x的回归方程类型：（2）根据（l）的判断结果及表中数据，建立y关于x的回归方程，并预测2019年某新能源产品的销售量（精确到0.0l）．参考公式：=，=t+参考数据：=3，=22.84，=11，，=374，，其中t i=21.设函数f（x）=a ln x-x（a≠0），f（x）的导函数为f′（x）．（1）当a=1时，求函数f（x）在点（2，f（2））处的切线方程；（2）对于曲线C：y=f（x）上的不同两点A（x1，y1），B（x2，y2），x1＜x2，求证：在（x1，x2）内存在唯一的x0，使直线AB的斜率等于f′（x0）．22.在直角坐标系xoy中，圆C的参数方程为（α为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为．（1）求C的极坐标方程；（2）射线θ=θ1（θ1∈[]，ρ＞0）与圆C的交点为O、P，与直线l的交点为Q，求|OP|•|OQ|的取值范围．23.已知函数f（x）=|x-2|-|x+3|（1）求不等式f（x）≤2的解集；（2）若不等式f（x）＜a2+6a的解集非空，求实数a的取值范围．-------- 答案与解析 --------1.答案：D解析：解：∵集合A={1，2，3，4}，B={x|（x+1）（x-3）=0}={-1，3}，∴A∪B={-1，1，2，3，4}．故选：D．先求出集合A，B，由此能求出A∪B．本题考查并集的求法，考查并集定义等基础知识，考查运算求解能力，是基础题．2.答案：D解析：解：z==，则复数z=在复平面内对应的点的坐标为（1，-1），位于第四象限．故选：D．直接利用复数代数形式的乘除运算化简得答案．本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．3.答案：D解析：解：的夹角为120°；∴；∴；∴．故选：D．根据条件可知，进而求出，从而可以求出，这样即可得出．考查向量夹角的定义，根据向量的坐标求向量长度的方法，以及向量数量积的运算及计算公式，向量长度的求法．4.答案：A解析：解：由f（x）是定义在R上的奇函数，可排除C、D；又x＞0时，f（x）=ln x-x+1，知f′（x）==，则当x＞1时，f′（x）＜0，f（x）单调递减，排除B．故选：A．由函数奇偶性排除C、D；再利用导数研究函数的单调性排除B．本题考查函数的图象与图象变换，考查函数奇偶性的性质及利用导数研究函数的单调性，是中档题．5.答案：A解析：【分析】先根据约束条件画出可行域，再利用z=（x+1）2+y2的几何意义表示点（-1，0）到可行域的点的距离的平方，求最值即可．本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．【解答】解：根据x，y满足约束条件，画出可行域：z=（x+1）2+y2表示D（-1，0）到可行域的距离的平方，由解得A（3，5），当点D与点A（3，5）连线时，AB距离最大，则z=（x+1）2+y2的最大值是A（3，5）到B（-1，0）的距离的平方为：41，故选：A．6.答案：B解析：【分析】本题考查合情推理的定义，关键是掌握合情推理的定义以及分类，属于基础题．根据题意，依次分析选项中推理的类型，综合即可得答案．【解答】解：根据题意，依次分析选项：对于A，是由部分到整体的推理，是归纳推理，属于合情推理；对于B，是演绎推理，不属于合情推理；对于C，是类比推理，属于合情推理；对于D，是由部分到整体的推理，是归纳推理，属于合情推理；故选：B．7.答案：C解析：解：设这条弦的两端点为A（x1，y1），B（x2，y2），斜率为k，则，两式相减再变形得又弦中点为（4，2），故k=，故这条弦所在的直线方程y-2=（x-4），整理得x-2y=0；故选：C．设这条弦的两端点为A（x1，y1），B（x2，y2），则，两式相减再变形得，又由弦中点为（4，2），可得k，由此可求出这条弦所在的直线方程．用“点差法”解题是圆锥曲线问题中常用的方法．8.答案：B解析：【分析】本题考查概率的求法，考查等可能事件概率计算公式等基础知识，是基础题．先求出基本事件总数n=3×3=9，再求出这两名同学加入同一个社团包含的基本事件个数m=3，由此能求出这两名同学加入同一个社团的概率．【解答】解：甲乙两名同学分别从“象棋”、“文学”、“摄影”三个社团中随机选取一个社团加入，基本事件总数n=3×3=9，这两名同学加入同一个社团包含的基本事件个数m=3，∴这两名同学加入同一个社团的概率是p==．故选：B．9.答案：B解析：解：由框图知，此框图的功能是求S=+++…的和，∵S=++++=，∴当i=6时，不满足判断框内的条件，退出循环，输出S的值为，可得判断框内的条件为：i≤5？故选：B．模拟程序的运行判断出程序框图的功能可求判断框内的条件．本题考查会判断程序框图的功能，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．10.答案：C解析：解：根据题意，得∵P是椭圆上任意一点，且直线PM、PN的斜率分别为k1、k2，设M（m，n），N（-m，-n），P（s，t），可得+=1，+=1，两式相减可得+=0，∴k1•k2=•=-，结合，得=，即a2=4b2∵b2=a2-c2，∴a2=4（a2-c2），解得3a2=4c2，得c= a因此，椭圆的离心率e==故选：C．根据题意，结合椭圆的性质得到|k1k2|==，可得a2=4b2，由此解出c=a，即可得到该椭圆的离心率．本题给出椭圆上动点满足的条件，求椭圆的离心率，着重考查了椭圆的基本概念与简单几何性质等知识，属于基础题．11.答案：D解析：解：由①对于任意的x∈R，都有f（x+1）=f（x-1）；得函数为周期函数，且周期为2，由②函数y=f（x+1）的图象关于y轴对称；得函数的图象关于直线x=1对称，由③对于任意的x1，x2∈[0，1]，都有（f（x1）-f（x2））（x1-x2）＞0得函数在[0，1]为增函数，则f（）=f（），f（2）=f（0），f（3）=f（1），又因为0，所以f（0）＜f（）＜f（1），即f（2）＜f（）＜f（3），故选：D．由函数的周期性，对称性及增减性可得：f（）=f（），f（2）=f（0），f（3）=f（1），又因为0，所以f（0）＜f（）＜f（1），即f（2）＜f（）＜f（3），得解．本题考查了函数的周期性，对称性及增减性，属中档题．12.答案：A解析：解：在长方体中，对角线AC表示直线b，棱B1C1表示直线a，则a、b异面，且所成的角为，如图所示；在图中找出与a垂直的平面CDD1C1，显然当DD1为直线c时，异面直线b、c所成的角最大，为；当直线c过DD1、CC1的中点E、F时，异面直线b、c所成的角最小，为；所以异面直线b与c所成角的范围是[，]．故选：A．将异面直线所成的角转化为平面角，根据题意找出与直线a垂直的直线c，判定c与b 的夹角大小．本题考查了异面直线所成角的定义与应用问题，也考查了空间中线线、线面、面面间的位置关系应用问题．13.答案：24-n解析：解：∵a1+2a2+4a3+…+2n-1a n=8n，①∴当n≥2时，a1+2a2+4a3+…+2n-2a n-1=8（n-1），②①-②得，2n-1a n=8，∴a n=24-n，当n=1时，a1=8，符合上式，∴a n=24-n．故答案为：a n=24-n．由条件可得a1=1，当n≥2时，将n换为n-1，两式相减可得数列{a n}的通项公式．本题考查求数列的通项公式，注意运用数列的递推式，考查化简整理的运算能力，属于中档题．14.答案：x2-x解析：解：根据题意，二次函数y=f（x）的图象经过坐标原点，设其解析式为f（x）=ax2+bx，则有f′（x）=2ax+b，又由f′（x）=3x-，则有2ax+b=3x-，则a=，b=-，则f（x）=x2-x，故答案为：x2-x．根据题意，设函数f（x）的解析式为f（x）=ax2+bx，求出其导数f′（x）=2ax+b，结合题意求出a、b的值，即可得答案．本题考查函数的导数计算，涉及二次函数的解析式的求法，属于基础题．15.答案：2π解析：解：∵圆锥的轴截面是一个边长为2的等边三角形，∴底面半径=1，底面周长=2π，∴圆锥的侧面积=×2π×2=2π，故答案为：2π．易得圆锥的底面半径及母线长，那么圆锥的侧面积=底面周长×母线长×．本题利用了圆的周长公式和扇形面积公式、圆锥的轴截面等基础知识，考查运算求解能力、化归与转化思想．属于基础题．16.答案：1解析：解：根据题意，b1=a1a3-a22=1×2-1=1，b2=a2a4-a32=1×3-22=-1，b3=a3a5-a42=2×5-32=1，b4=a4a6-a52=3×8-52=-1…∴b1+b2+b3+…+b2019=（a1a3-a22）+（a2a4-a32）+（a3a5-a42）+…+（a2019•a2021-a20202）=1008×（1-1）+1=1．故答案为：1．利用斐波那契数列的通项公式分析可得，a1a3-a22=1×2-1=1，a2a4-a32=1×3-22=-1，a3a5-a42=2×5-32=1，……，据此分析可得答案．本题考查数列的求和以及归纳推理的应用，涉及斐波那契数列的通项公式及其性质，属于中档题．17.答案：解：（1）根据题意，=（），=（sin x，cos x），则函数f（x）==cos x sinx+cos2x=sin2x+cos2x+=sin（2x+）+，则f（x）的最小正周期T==π，令2x+=kπ+，解可得x=+，则f（x）的对称轴方程为x=+，（k∈Z）；（2）根据题意，由（1）的结论，f（x）=sin（2x+）+，令2kπ-≤2x+≤2kπ+，解可得kπ-≤x≤kπ+，即f（x）在R上的递增区间为（kπ-≤x≤kπ+）又由x∈（-π，π]，则当k=-1时，有-π＜x≤-，当k=0时，有-≤x≤，当k=1时，有≤x≤π，则f（x）在（-π，π]上的单调递增区间（-π，-]，[-，]，[，π）．解析：（1）根据题意，由数量积的计算公式可得化简得f（x）==sin（2x+）+，结合正弦函数的性质分析函数的周期和对称轴方程，即可得答案；（2）根据题意，由正弦函数的性质分析函数在R上的增区间，再给k赋值与定义域求交集得解．本题考查向量数量积的计算以及三角恒等变换，涉及三角函数的周期的求法和对称轴的求法，属于基础题．18.答案：（Ⅰ）证明：连接BD交AC于点O，连接FO，∵正方形ABCD的边长为，∴AC=BD=2，∴CO=1，∵EF∥AC，EF=1，∴四边形EFOC为平行四边形，∴EC∥FO，∵FO⊂平面BFD，EC⊄平面BFD，∴EC∥平面BFD；（Ⅱ）解：∵正方形ABCD⊥直角梯形ACEF，EF∥AC，EC⊥AC，又AC⊂平面ABCD，∴EC⊥平面ABCD；由（1）知EC∥平面BFD，∴V三棱锥D-BEF=V三棱锥E-BDF=V三棱锥C-BDF=V三棱锥F-BCD，且V三棱锥F-BCD=•CE•S△BCD=×1×（××）=，即三棱锥D-BEF的体积为．解析：（1）连接BD交AC于点O，连接FO，先证明EC∥FO，再证明EC∥平面BFD；（2）利用体积变换V三棱锥D-BEF=V三棱锥E-BDF=V三棱锥C-BDF=V三棱锥F-BCD，即可求得三棱锥D-BEF 的体积．本题主要考查空间几何元素平行关系的证明，考查空间几何体体积的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力．19.答案：解：（1）如图所示：由题意得：，解得a=2，b=，c=1，所以椭圆C的标准方程为．（2）因为△AF1F2是正三角形，可得直线AF1的斜率为k=．所以直线AF1的方程为y=（x+1）．设点O关于直线AF1的对称点为M（m，n），则，解得．可得M坐标为（-，）．因为|PO|=|PM|，所以：|PF2|+|PO|=|PF2|+|PM|≥|MF2|．所以：|PF2|+|PO|的最小值=，直线MF2的方程为，即．由．解得：，所以此时点P的坐标为．综上所述，可求的：|PF2|+|PO|的最小值为，此时点P的坐标为．解析：（1）由题得到a，b，c的方程组，解方程组即得椭圆的标准方程；（2）先求出M坐标为．再根据：|PF2|+|PO|=|PF2|+|PM|≥|MF2|．求：|PF2|+|PO|的最小值，再联立直线方程求点P的坐标．本题主要考查椭圆标准方程的求法，考查直线和椭圆的位置关系和最值的求法，意在考查学生对这些知识的理解掌握水平和分析推理计算能力．20.答案：解：（1）以年份代码x为x轴，以年销量y为y轴，作散点图，根据散点图，y=cx2+d更适宜作为年销售量y关于年份代码x的回归方程；（2）依题意=22.84，=11，c==≈2.27，d=-c•2.27×11=-2.13，y=2.27t-2.13=2.27x2-2.13；所以y关于x的回归方程为y=2.27x2-2.13；令x=6，y=2.27×62-2.13=79.59，故预测2019年新能源产品的销售量为79.59万个．解析：（1）以年份代码x为x轴，以年销量y为y轴，作散点图，根据散点图，y=cx2+d 更适宜作为年销售量y关于年份代码x的回归方程；（2）利用最小二乘法求出y关于x的回归方程为y=2.27x2-2.13，再利用回归方程预测2019年某新能源产品的销售量．本题主要考了查散点图和利用最小二乘法求回归方程，以及利用回归方程进行预测应用问题，也考查了对这些知识的理解掌握水平和分析推理能力．21.答案：解：（1）a=1时，f（x）=ln x-x，f′（x）=-1，可得切线的斜率为f′（2）=-，切点为（2，ln2-2），可得f（x）在点（2，f（2））处的切线方程为y-ln2+2=-（x-2），即为x+2y-2ln2+2=0；（2）证明：f（x）=a ln x-x的导数为f′（x）=-1，k AB=f′（x0），等价为=-1，化简得=即x0（ln x2-ln x1）+（x1-x2）=0，因此，要证明原命题成立，只需证明x0（ln x2-ln x1）+（x1-x2）=0，x0∈（x1，x2），且x0唯一．设g（x）=x（ln x2-ln x1）+（x1-x2），g（x0）=0 ①则g（x1）=x1（ln x2-ln x1）+（x1-x2），再设h（x）=x（ln x2-ln x）+（x-x2），0＜x＜x2，∴h′（x）=ln x2-ln x＞0，∴y=h（x）在0＜x＜x2是增函数，又0＜x1＜x2，∴g（x1）=h（x1）＜h（x2）=0 ②同理g（x2）＞0 ③∵一次函数g（x）=x（ln x2-ln x1）+（x1-x2）在（x1，x2）上是增函数，因此由①②③得x（ln x2-ln x1）+（x1-x2）=0在（x1，x2）有唯一解x0，故原命题成立．解析：（1）求得f（x）的导数，可得切线的斜率和切点，由点斜式方程可得切线方程；（2）即证明x0（ln x2-ln x1）+（x1-x2）=0，只需证明x0（ln x2-ln x1）+（x1-x2）=0，x0∈（x1，x2），且x0唯一．再构造函数g（x）=x（ln x2-ln x1）+（x1-x2），用导数判断单调性即可证明．本题主要考查利用导数的几何意义求切线方程，考查利用导数研究函数的零点问题，考查分析法证明数学问题，意在考查学生对这些知识的理解掌握水平和分析推理能力．22.答案：解：（1）圆C的普通方程是（x-2）2+y2=4，又x=ρcosθ，y=ρsinθ，所以圆C的极坐标方程为ρ=4cosθ；（2）设P（ρ1，θ1），则有ρ1=4cosθ1，设Q（ρ2，θ1），且直线l的方程是ρ（sinθ+cosθ）=1，则有ρ2=，所以|OP||OQ|=ρ1ρ2==，θ1∈[，]，所以1≤|OP||OQ|≤2，故|OP||OQ|的范围为[1，2]．解析：（1）先求出圆C的普通方程，再化成极坐标方程；（2）设P（ρ1，θ1），先求出|OP||OQ|=ρ1ρ2=，θ1∈[，]，再求取值范围．本题主要考查参数方程、极坐标方程和普通方程的互化，考查三角函数的图象和性质，考查取值范围的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力．属中档题．23.答案：解：（1）由f（x）=|x-2|-|x+3|≤2可化为：或或不等式解集为：{x|x≥-}（2）因为|f（x）|=≤|x-2-x-3|=5，所以-5≤f（x）≤5，即f（x）min=-5；要使不等式f（x）＜a2+6a解集非空，需f（x）min＜a2+6a，从而a2+6a+5＞0，解得a＜-5或a＞-1，所以a的取值范围为．（-∞，-5）∪（-1，+∞）．解析：（1）利用零点分类讨论法解绝对值不等式得解；（2）先利用绝对值三角不等式求f（x）min=-5，再解不等式＜a2+6a得解．本题主要考查绝对值不等式的解法，考查绝对值三角不等式的应用，考查不等式的有解问题，意在考查学生对这些知识的理解掌握水平和分析推理能力．属中档题．。
2023届福建省南平市(三模)高中毕业班第三次质量检测数学试题及答案
南平市2023届高中毕业班第三次质量检测数学试题〈考试时间：120分钟满分：150分考试形式：闭卷〉注意事项2I.答题前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致－2.回答选择题时，逃出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其官答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3.考试结束后，将本试卷和答题卡一并交回．第I 卷一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的囚个选项中，只有一项是符合题目要求的．l附合A={x l x 2-4<0},B={-2λ以2｝，则AnB=( )A .{-2,2}B {-1,0}c.[-1,0,1]。
｛O,I}2.己知＝= l+i.则i（二I )=()A.-IB.Ic.-l+iD.l+i3. 已知l 正方形ABCD 的边长为I.点Mi削AB+BC=2A页，则｜而｜＝（A .- B.IFG－2C D ..fi.4.2023年3月II 日，“探索一号”科考船搭载11“奋斗者”9载入潜水然因满完成网际首次环大洋洲载人深潜科考任务，顺利jgfnl 三亚．本次航行有两个突出的成就，一是到达了东南印度洋的帮阿受蒂那深渊，二是到达了瓦浆比．热恩！Ur 深渊，并且在这两个海底深渊都:i£行了勘探和采集．如阁l J;h “奋斗者”号楼想阁，其球舱可以抽象为自｜饿和1囚校的组合体，其书h截丽虫al到2所示，则该模型对t舱体和、为〈8con如因l1Jl240ir A.-B .102ir －3c.旦旦3D.旦旦3i已知函数f(x)=2叫{J)X + 王l (C J > 0）的倒象的相邻两条对称轴间的距离为乙型。
（）\.6 )A.f (x ）的Jlill!IJ;I,f8./(x)n:［号音］上叫增c.！（机附于点（号。
2024届浙江省温州市普通高中高三第三次适应性考试(温州三模)数学试卷(含答案详解)
温州市2024届普通高中高三第三次适应性考试高三数学试题卷一、选择题：本题共8小题，每小题5分，共40分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．在ABC 中，三个内角,,A B C 成等差数列，则()sin A C +=（）A ．12B．2CD ．12．平面向量()(),2,2,4a m b ==-，若()a ab - ∥，则m =（）A ．1-B ．1C ．2-D ．23．设,A B 为同一试验中的两个随机事件，则“()()1P A P B +=”是“事件,A B 互为对立事件”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知*m ∈N ，()21mx +和()211m x ++的展开式中二项式系数的最大值分别为a 和b ，则（）A ．a b <B ．a b=C ．a b>D ．,a b 的大小关系与m 有关5．已知5πsin 4⎛⎫β+=-⎪⎝⎭()()sin 2cos cos 2sin αβαβαα---=（）A ．2425-B ．2425C ．35-D ．356．已知函数()223,02,0xx x x f x x ⎧-+>=⎨≤⎩，则关于x 方程()2f x ax =+的根个数不可能是（）A ．0个B ．1个C ．2个D ．3个7．已知12,F F 是椭圆2222:1(0)x y C a b a b +=>>的左右焦点，C 上两点,A B 满足：222AF F B = ，14cos 5AF B ∠=，则椭圆C 的离心率是（）A ．34BC ．23D8．数列{}n a 的前n 项和为()*1,n n n n S S a n a +=∈N ，则5622111i i i i a a -==-∑∑可以是（）A ．18B ．12C ．9D ．6二、选择题：本题共3小题，每小题6分，共18分。
在每小题给出的选项中，有多项符合题目要求。
南京市2020届高三数学三模含答案
南京市2020届高三年级第三次模拟考试数 学注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡． 一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题卡的指定位置．．．．上） 1．已知集合A ＝{x |2＜x ＜4}，B ＝{x |1＜x ＜3}，则A ∪B ＝ ▲ ． 2．若z ＝a 1＋i＋i (i 是虚数单位)是实数，则实数a 的值为 ▲ ．3．某校共有教师300人，男学生1200人，女学生1000人，现用分层抽样从所有师生中抽取一个容量为125的样本，则从男学生中抽取的人数为 ▲ ． 4．如图是一个算法的伪代码，其输出的结果为 ▲ ．5．将甲、乙、丙三人随机排成一行，则甲、乙两人相邻的概率为 ▲ ．6．已知函数f (x )＝2sin(ωx ＋φ) (其中ω＞0，－π2＜φ＜π2)的部分图象如图所示，则f (π2)的值为▲ ．7．已知数列{a n }为等比数列．若a 1＝2，且a 1，a 2，a 3－2成等差数列，则{a n }的前n 项和为 ▲ ．8．在平面直角坐标系xOy 中，已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右焦点为F ．若以F 为圆心，a 为半径的圆交该双曲线的一条渐近线于A ，B 两点，且AB ＝2b ，则该双曲线的离心率为 ▲ ．9．若正方体ABCD －A 1B 1C 1D 1的棱长为2，则三棱锥A －B 1CD 1的体积为 ▲ ．（第6题图）10．已知函数f (x )＝⎩⎨⎧x ＋2， x ≤0，f (－x )，x ＞0，g (x )＝f (x －2)．若g (x －1)≥1，则x 的取值范围为 ▲ ．11．在平面直角坐标系xOy 中，A ，B 是圆O ：x 2＋y 2＝2上两个动点，且OA →⊥OB →．若A ，B 两点到直线l ：3x ＋4y －10＝0的距离分别为d 1，d 2，则d 1＋d 2的最大值为 ▲ ． 12．若对任意a ∈[e ，＋∞) (e 为自然对数的底数) ，不等式x ≤e ax＋b对任意x ∈R 恒成立，则实数b 的取值范围为 ▲ ．13．已知点P 在边长为4的等边三角形ABC 内，满足AP →＝λAB →＋μAC →，且2λ＋3μ＝1，延长AP 交边BC 于点D ．若BD ＝2DC ，则PA →·PB →的值为 ▲ ．14．在△ABC 中，∠A ＝π3，D 是BC 的中点．若AD ≤22BC ，则sin B sin C 的最大值为 ▲ ．二、解答题:本大题共6小题，计90分．解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题卡的指定区域．．．．内． 15．(本小题满分14分)如图，在四棱锥P －ABCD 中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，E ，F 分别为AD ，PB 的中点． 求证：（1）EF ∥平面PCD ；（2）平面PAB ⊥平面PCD ．16．(本小题满分14分)已知向量m ＝(cos x ，sin x )，n ＝(cos x ，－sin x )，函数f (x )＝m ·n ＋12．（1）若f (x 2)＝1，x ∈(0，π)，求tan(x ＋π4)的值；（2）若f (α)＝－110， α∈(π2，3π4)，sin β＝7210，β∈(0，π2)，求2α＋β的值．FEPBDCA(第15题图)17．(本小题满分14分)如图，港口A 在港口O 的正东100海里处，在北偏东方向有一条直线航道OD ，航道和正东方向之间有一片以B 为圆心，半径85海里的圆形暗礁群（在这片海域行船有触礁危险），其中OB ＝2013海里，tan ∠AOB ＝23，cos ∠AOD ＝55．现一艘科考船以105海里/小时的速度从O 出发沿OD 方向行驶，经过2个小时后，一艘快艇以50海里/小时的速度准备从港口A 出发，并沿直线方向行驶与科考船恰好相遇． （1）若快艇立即出发，判断快艇是否有触礁的危险，并说明理由； （2）在无触礁危险的情况下，若快艇再等x 小时出发，求x 的最小值．18．(本小题满分16分)如图，在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)经过点 (－2，0)和 (1，32)，椭圆C 上三点A ，M ，B 与原点O 构成一个平行四边形AMBO ． （1）求椭圆C 的方程；（2）若点B 是椭圆C 的左顶点，求点M 的坐标； （3）若A ，M ，B ，O 四点共圆，求直线AB 的斜率．(第18题图)19．(本小题满分16分)已知函数f(x)＝e xx2－ax＋a(a∈R) ，其中e为自然对数的底数．（1）若a＝1，求函数f(x)的单调减区间；（2）若函数f(x)的定义域为R，且f(2)＞f(a)，求a的取值范围；（3）证明：对任意a∈(2，4)，曲线y＝f(x)上有且仅有三个不同的点，在这三点处的切线经过坐标原点．20．(本小题满分16分)若数列{a n}满足n≥2，n∈N*时，a n≠0，则称数列{a na n＋1}(n∈N*)为{a n}的“L数列”．（1）若a1＝1，且{a n}的“L数列”为{12n}，求数列{a n}的通项公式；（2）若a n＝n＋k－3(k＞0)，且{a n}的“L数列”为递增数列，求k的取值范围；（3）若a n＝1＋p n－1，其中p＞1，记{a n}的“L数列”的前n项和为S n，试判断是否存在等差数列{c n}，对任意n∈N*，都有c n＜S n＜c n＋1成立，并证明你的结论．南京市2020届高三年级第三次模拟考试数学附加题注意事项：1．附加题供选修物理的考生使用． 2．本试卷共40分，考试时间30分钟．3．答题前，考生务必将自己的姓名、学校、班级、学号写在答题卡的密封线内．试题的答案写在答题．．卡．上对应题目的答案空格内．考试结束后，交回答题卡． 21．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共计20分．请在答卷．．卡指定区域内．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—2：矩阵与变换已知矩阵A ＝⎣⎢⎡⎦⎥⎤1 －1a 0，a ∈R ．若点P (1，1)在矩阵A 的变换下得到点P ′(0，－2)．（1）求矩阵A ；（2）求点Q (0，3)经过矩阵A 的2次变换后对应点Q ′的坐标．B ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝1＋cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎨⎧x ＝3t ，y ＝1＋t (t 为参数)，求曲线C 上的点到直线l 的距离的最大值．C ．选修4—5：不等式选讲已知a ，b 为非负实数，求证：a 3＋b 3≥ab (a 2＋b 2)．【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内．．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在直三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，AB ＝3，AC ＝4，B 1C ⊥AC 1． （1）求AA 1的长．（2）试判断在侧棱BB 1上是否存在点P ，使得直线PC 与平面AA 1C 1C 所成角和二面角B －A 1C －A 的大小相等，并说明理由．23．(本小题满分10分)口袋中有大小、形状、质地相同的两个白球和三个黑球．现有一抽奖游戏规则如下：抽奖者每次有放回的从口袋中随机取出一个球，最多取球2n ＋1(n ∈N *)次．若取出白球的累计次数达到n ＋1时，则终止取球且获奖，其它情况均不获奖．记获奖概率为P n ． （1）求P 1；（2）证明：P n ＋1＜P n ．(第22题图)A 1CABB 1C 1P南京市2020届高三年级第三次模拟考试数学参考答案及评分标准说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数，填空题不给中间分数．一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）1．{x |1＜x ＜4} 2．2 3．60 4．10 5．236． 37．2n ＋1－2 8．62 9．8310．[2，4] 11．6 12． [－2，＋∞)13．－9414．38二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．(本小题满分14分)证明：(1)取PC 中点G ，连接DG 、FG ．在△PBC 中，因为F ，G 分别为PB ，PC 的中点，所以GF ∥BC ，GF ＝12BC ．因为底面ABCD 为矩形，且E 为AD 的中点，所以DE ∥BC ，DE ＝12BC ， ······························································ 2分所以GF ∥DE ，GF ＝DE ，所以四边形DEFG 为平行四边形， 所以EF ∥DG ． ············································································· 4分 又因为EF ⊄平面PCD ，DG ⊂平面PCD ，所以EF ∥平面PCD ． ······································································ 6分(2)因为底面ABCD 为矩形，所以CD ⊥AD ．又因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，CD ⊂平面ABCD ， 所以CD ⊥平面PAD ． ·································································· 10分 因为PA ⊂平面PAD ，所以CD ⊥PA ． ················································· 12分 又因为PA ⊥PD ，PD ⊂平面PCD ，CD ⊂平面PCD ，PD ∩CD ＝D ，所以PA ⊥平面PCD ．因为PA ⊂平面PAB ，所以平面PAB ⊥平面PCD ． ································ 14分16．(本小题满分14分)解：(1) 因为向量m ＝(cos x ，sin x )，n ＝(cos x ，－sin x )，所以 f (x )＝m ·n ＋12＝cos 2x －sin 2x ＋12＝cos2x ＋12． ··································· 2分因为f (x 2)＝1，所以cos x ＋12＝1，即cos x ＝12．又因为x ∈(0，π) ，所以x ＝π3， ························································· 4分所以tan(x ＋π4)＝tan(π3＋π4)＝tan π3＋ tan π41－tan π3tanπ4＝－2－3． ······························· 6分(2)若f (α)＝－110，则cos2α＋12＝－110，即cos2α＝－35．因为α∈(π2，3π4)，所以2α∈(π，3π2)，所以sin2α＝－1－cos 22α＝－45． ········ 8分因为sin β＝7210，β∈(0，π2)，所以cos β＝1－sin 2β＝210， ······················ 10分所以cos(2α＋β)＝cos2αcos β－sin2αsin β＝(－35)×210－(－45)×7210＝22． ····· 12分又因为2α∈(π，3π2)，β∈(0，π2)，所以2α＋β∈(π，2π)，所以2α＋β的值为7π4． ····································································· 14分17．(本小题满分14分)解：如图，以O 为原点，正东方向为x 轴，正北方向为y 轴，建立直角坐标系xOy ． 因为OB ＝2013，tan ∠AOB ＝23，OA ＝100，所以点B (60，40)，且A (100，0)． ··············································(1)设快艇立即出发经过t 小时后两船相遇于点C ， 则OC ＝105(t ＋2)，AC ＝50t ．因为OA ＝100，cos ∠AOD ＝55， 所以AC 2＝OA 2＋OC 2－2OA ·OC ·cos ∠AOD ， 即(50t )2＝1002＋[105(t ＋2)]2－2×100×105(t ＋2)×55．化得t 2＝4，解得t 1＝2，t 2＝－2（舍去）， ··············································· 4分 所以OC ＝405．因为cos ∠AOD ＝55，所以sin ∠AOD ＝255，所以C (40，80)，所以直线AC 的方程为y ＝－43(x －100)，即4x ＋3y －400＝0． ······················· 6分因为圆心B 到直线AC 的距离d ＝|4×60＋3×40－400|42＋32＝8，而圆B 的半径r ＝85，所以d ＜r ，此时直线AC 与圆B 相交，所以快艇有触礁的危险．答：若快艇立即出发有触礁的危险． ······················································· 8分 (2)设快艇所走的直线AE 与圆B 相切，且与科考船相遇于点E ． 设直线AE 的方程为y ＝k (x －100)，即kx －y －100k ＝0．因为直线AE 与圆B 相切，所以圆心B 到直线AC 的距离d ＝|60k －40－100k |12＋k2＝85， 即2k 2＋5k ＋2＝0，解得k ＝－2或k ＝－12． ············································ 10分由（1）可知k ＝－12舍去．因为cos ∠AOD ＝55，所以tan ∠AOD ＝2，所以直线OD 的方程为y ＝2x ． 由⎩⎨⎧y ＝2x ， y ＝－2(x －100)，解得⎩⎨⎧x ＝50，y ＝100，所以E (50，100)，所以AE ＝505，OE ＝505， ······························································ 12分此时两船的时间差为505105－50550＝5－5，所以x ≥5－5－2＝3－5．答：x 的最小值为(3－5)小时． ···························································· 14分18．(本小题满分16分)解：(1)因为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点(－2，0)和 (1，32)，所以a ＝2，1a 2＋34b2＝1，解得b 2＝1，所以椭圆C 的方程为x 24＋y 2＝1． ·························································· 2分(2)因为B 为左顶点，所以B (－2，0)．因为四边形AMBO 为平行四边形，所以AM ∥BO ，且AM ＝BO ＝2． ··········· 4分 设点M (x 0，y 0)，则A (x 0＋2，y 0)．因为点M ，A 在椭圆C 上，所以⎩⎨⎧x 024＋y 02＝1， (x 0＋2)24＋y 02＝1，解得⎩⎪⎨⎪⎧x 0＝－1， y 0＝±32，所以M (－1，±32)． ········································································ 6分 (3) 因为直线AB 的斜率存在，所以设直线AB 的方程为y ＝kx ＋m ，A (x 1，y 1)，B (x 2，y 2)． 由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 2＝1，消去y ，得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0， 则有x 1＋x 2＝－8km 1＋4k 2，x 1x 2＝4m 2－41＋4k 2． ···················································· 8分因为平行四边形AMBO ，所以OM →＝OA →＋OB →＝(x 1＋x 2，y 1＋y 2)．因为x 1＋x 2＝－8km 1＋4k 2，所以y 1＋y 2＝k (x 1＋x 2)＋2m ＝k ·－8km 1＋4k 2＋2m ＝2m1＋4k 2， 所以M (－8km 1＋4k 2，2m1＋4k 2)． ································································· 10分因为点M 在椭圆C 上，所以将点M 的坐标代入椭圆C 的方程，化得4m 2＝4k 2＋1．① ········································································ 12分 因为A ，M ，B ，O 四点共圆，所以平行四边形AMBO 是矩形，且OA ⊥OB ， 所以OA →·OB →＝x 1x 2＋y 1y 2＝0．因为y 1y 2＝(kx 1＋m )(kx 1＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2＝m 2－4 k 21＋4k 2，所以x 1x 2＋y 1y 2＝4m 2－41＋4k 2＋m 2－4k 21＋4k 2＝0，化得5m 2＝4k 2＋4．② ················· 14分 由①②解得k 2＝114，m 2＝3，此时△＞0，因此k ＝±112．所以所求直线AB 的斜率为±112． ···················································· 16分 19． (本小题满分16分)解：(1)当a ＝1时，f (x )＝e xx 2－x ＋1，所以函数f (x )的定义域为R ，f'(x )＝e x (x －1)(x －2)(x 2－x ＋1)2．令f'(x )＜0，解得1＜x ＜2，所以函数f (x )的单调减区间为(1，2)． ··················································· 2分(2)由函数f (x )的定义域为R ，得x 2－ax ＋a ≠0恒成立，所以a 2－4a ＜0，解得0＜a ＜4． ·························································· 4分 方法1由f (x )＝e x x 2－ax ＋a ，得f'(x )＝e x (x －a )(x －2)(x 2－ax ＋a )2． ①当a ＝2时，f (2)＝f (a )，不符题意．②当0＜a ＜2时，因为当a ＜x ＜2时，f ′(x )＜0，所以f (x )在(a ，2)上单调递减，所以f (a )＞f (2)，不符题意． ···························································· 6分 ③当2＜a ＜4时，因为当2＜x ＜a 时，f ′(x )＜0，所以f (x )在(2，a )上单调递减，所以f (a )＜f (2)，满足题意．综上，a 的取值范围为(2，4)． ························································· 8分 方法2由f (2)＞f (a )，得e 24－a ＞e a a． 因为0＜a ＜4，所以不等式可化为e 2＞e a a(4－a )． 设函数g (x )＝e x x(4－x )－e 2， 0＜x ＜4． ·················································· 6分 因为g'(x )＝e x·－(x －2)2x 2≤0恒成立，所以g (x )在(0，4)上单调递减． 又因为g (2)＝0，所以g (x )＜0的解集为(2，4)．所以，a 的取值范围为(2，4)． ··························································· 8分(3)证明：设切点为(x 0，f (x 0))，则f'(x 0)＝e x 0(x 0－2)(x 0－a )(x 02－ax 0＋a )2， 所以切线方程为y －e x 0x 02－ax 0＋a ＝e x 0(x 0－2)(x 0－a )(x 02－ax 0＋a )2×(x －x 0)． 由0－e x 0x 02－ax 0＋a ＝e x 0(x 0－2)(x 0－a )(x 02－ax 0＋a )2×(0－x 0)， 化简得x 03－(a ＋3)x 02＋3ax 0－a ＝0． ··················································· 10分 设h (x )＝x 3－(a ＋3)x 2＋3ax －a ，a ∈(2，4)，则只要证明函数h (x )有且仅有三个不同的零点．由(2)可知a ∈(2，4)时，函数h (x )的定义域为R ，h'(x )＝3x 2－2(a ＋3)x ＋3a ．因为△＝4(a ＋3)2－36a ＝4(a －32)2＋27＞0恒成立， 所以h'(x )＝0有两不相等的实数根x 1和x 2，不妨x 1＜x 2．因为所以函数h (x )最多有三个零点． ························································ 12分 因为a ∈(2，4)，所以h (0)＝－a ＜0，h (1)＝a －2＞0，h (2)＝a －4＜0，h (5)＝50－11a ＞0， 所以h (0)h (1)＜0，h (1)h (2)＜0，h (2)h (5)＜0．因为函数的图象不间断，所以函数h (x )在(0，1)，(1，2)，(2，5)上分别至少有一个零点．综上所述，函数h (x )有且仅有三个零点． ············································ 16分20．(本小题满分16分)解：(1) 因为{a n }的“L 数列”为{12n }，所以a n a n ＋1＝12n ，n ∈N *，即a n ＋1a n ＝2n ， 所以n ≥2时，a n ＝a n a n －1·a n －1a n －2·…·a 2a 1·a 1＝2n －1·2n －2·…·2·1＝2(n -1)＋(n －2)＋…＋1＝2n (n －1)2． 又a 1＝1符合上式，所以{a n }的通项公式为a n ＝2n (n －1)2，n ∈N *． ··················· 2分(2)因为a n ＝n ＋k －3(k ＞0)，且n ≥2，n ∈N *时，a n ≠0，所以k ≠1．方法1设b n ＝a n a n ＋1，n ∈N *，所以b n ＝n ＋k －3(n ＋1)＋k －3＝1－1n ＋k －2． 因为{b n }为递增数列，所以b n ＋1－b n ＞0对n ∈N*恒成立，即1n ＋k －2－1n ＋k －1＞0对n ∈N*恒成立． ············································· 4分 因为1n ＋k －2－1n ＋k －1＝1(n ＋k －2)(n ＋k －1)， 所以1n ＋k －2－1n ＋k －1＞0等价于(n ＋k －2)(n ＋k －1)＞0． 当0＜k ＜1时，因为n ＝1时，(n ＋k －2)(n ＋k －1)＜0，不符合题意．············ 6分 当k ＞1时，n ＋k －1>n ＋k －2>0，所以(n ＋k －2)(n ＋k －1)＞0，综上，k 的取值范围是(1，＋∞)． ························································· 8分方法2令f (x )＝1－1x ＋k －2，所以f (x )在区间(－∞，2－k )和区间(2－k ，＋∞)上单调递增． 当0＜k ＜1时，f (1)＝1－1k －1＞1，f (2)＝1－1k ＜1，所以b 2＜b 1，不符合题意． ···················· 6分 当k ＞1时，因为2－k ＜1，所以f (x )在[1，＋∞)上单调递增，所以{b n }单调递增，符合题意．综上，k 的取值范围是(1，＋∞)． ························································· 8分(3)存在满足条件的等差数列{c n }，证明如下：因为a k a k ＋1＝1＋p k －11＋p k ＝1p ＋1－1p 1＋p k ，k ∈N*， ············································· 10分 所以S n ＝n p ＋(1－1p )·(11＋p ＋11＋p 2＋…＋11＋p n －1＋11＋p n)． 又因为p ＞1，所以1－1p ＞0，所以n p ＜S n ＜n p ＋(1－1p ).(1p ＋1p 2＋ (1)n －1＋1p n )， 即n p ＜S n ＜n p ＋1p ·[1－(1p)n ]． ································································· 14分 因为1p ·[1－(1p )n ]＜1p ，所以n p ＜S n ＜n ＋1p． 设c n ＝n p ，则c n ＋1－c n ＝n ＋1p －n p ＝1p，且c n ＜S n ＜c n ＋1， 所以存在等差数列{c n }满足题意． ······················································· 16分南京市2020届高三年级第三次模拟考试数学附加题参考答案及评分标准说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，填空题不给中间分数．21．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共计20分．请在答卷．．纸．指定区域内．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—2：矩阵与变换解：(1) ⎣⎢⎡⎦⎥⎤1 －1a 0 ⎣⎢⎡⎦⎥⎤11＝⎣⎢⎡⎦⎥⎤0a ． ··································································· 2分 因为点P (1，1)在矩阵A 的变换下得到点P ′(0，－2)，所以a ＝－2，所以A ＝⎣⎢⎡⎦⎥⎤1 －1－2 0． ········································································· 4分 (2)因为A ＝⎣⎢⎡⎦⎥⎤1 －1－2 0，所以A 2＝⎣⎢⎡⎦⎥⎤1 －1－2 0 ⎣⎢⎡⎦⎥⎤1 －1－2 0＝⎣⎢⎡⎦⎥⎤3 －1－2 2， ·············· 6分 所以A 2⎣⎡⎦⎤03=⎣⎢⎡⎦⎥⎤3 －1－2 2 ⎣⎡⎦⎤03=⎣⎢⎡⎦⎥⎤－36， 所以，点Q ′的坐标为(－3，6)． ························································ 10分B ．选修4—4：坐标系与参数方程解：由l 的参数方程⎩⎨⎧x ＝3t ，y ＝1＋t(t 为参数)得直线l 方程为x －3y ＋3＝0． ············· 2分 曲线C 上的点到直线l 的距离d ＝|1＋cos θ－ 3 sin θ＋3|2······························· 4分 ＝|2cos(θ＋π3)＋1＋3|2． ········································································ 6分 当θ＋π3＝2k π，即θ＝－π3＋2k π(k ∈Z )时， ··················································· 8分曲线C 上的点到直线l 的距离取最大值3＋32． ········································ 10分 C ．选修4—5：不等式选讲证明：因为a ，b 为非负实数， 所以a 3＋b 3－ab (a 2＋b 2)＝a 2a (a －b )＋b 2b (b －a )＝(a －b )[(a )5－(b )5]． ·································· 4分 若a ≥b 时，a ≥b ，从而(a )5≥(b )5，得(a －b )·[(a )5－(b )5]≥0． ···························································· 6分 若a ＜b 时，a ＜b ，从而(a )5＜(b )5，得(a －b )·[(a )5－(b )5]＞0． ···························································· 8分 综上，a 3＋b 3≥ab (a 2＋b 2)． ····························································· 10分22．（本小题满分10分）解：(1)因为三棱柱ABC －A 1B 1C 1为直三棱柱，所以AA 1⊥平面ABC ，所以AA 1⊥AB ，AA 1⊥AC ．又AB ⊥AC ，所以以{AB →，AC →，AA 1→}为正交基底建立如图所示的空间直角坐标系A —xyz ．设AA 1＝t (t ＞0)，又AB ＝3，AC ＝4，则A (0，0，0)，C 1(0，4，t )，B 1(3，0，t )，C (0，4，0)， 所以AC 1→＝(0，4，t )，B 1C →＝(－3，4，－t )． ·············································· 2分因为B 1C ⊥AC 1，所以B 1C →·AC 1→＝0，即16－t 2＝0，解得t ＝4，所以AA 1的长为4． ·············································································· 4分(2)由(1)知B (3，0，0)，C (0，4，0)，A 1(0，0，4)，所以A 1C →＝(0，4，－4)，BC →＝(－3，4，0)．设n ＝(x ，y ，z )为平面A 1CB 的法向量，则n ·A 1C →＝0，n ·BC →＝0，即⎩⎨⎧4y －4z ＝0，－3x ＋4y ＝0．取y ＝3，解得z ＝3，x ＝4，所以n ＝(4，3，3)为平面A 1CB 的一个法向量．又因为AB ⊥面AA 1C 1C ，所以AB →＝(3，0，0)为平面A 1CA 的一个法向量，。
2023年浙江省温州市高三第三次适应性考试(三模)数学试题及答案解析
2023年浙江省温州市高三第三次适应性考试（三模）数学试题及答案解析2023.5一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设全集{|5}U x x N =∈≤，集合{1,2,3}{2,3,4}A B ==，，则()U A B = ð（）A.{1,5}B.{0,5}C.{1,2,3,4}D.{0,1,4,5}2.已知直线12:0:10l x y l ax by +=++=，，若12l l ⊥，则a b +=（）A.-1B.0C.1D.23.某公司计划租地建仓库，已知每月土地费用与仓库到车站的距离成反比，每月货物的运输费用与仓库到车站的距离成正比.经测算，若在距离车站10km 处建仓库，则每月的土地费用与运输费用分别为2万元和8万元.要使两项费用之和最小，仓库和车站的距离为（）A.4kmB.5kmC.6kmD.7km4.“2>πα”是“sin 12->-παα”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知数列{}n a 各项为正数，{}n b 满足21112n n n n n n a b b a a b +++=+=，，则（）A.{}n b 是等差数列B.{}n b 是等比数列C.{}n b 是等差数列D.{}nb 是等比数列6.四面体OABC 满足90AOB BOC COA ∠=∠=∠= ，123OA OB OC ===，，，点D 在棱OC 上，且3OC OD =，点G 为ABC △的重心，则点G 到直线AD 的距离为（）A.22B.12C.33D.137.如图，A B ，是椭圆2222:1(0)x y C a b a b+=>>的左右顶点，P是圆222a y x O =+：上不同于A B ，的动点，线段PA 与椭圆C 交于点Q ，若tan 3tan PBA QBA ∠=∠，则椭圆的离心率为（）A.13B.23C.33D.638.已知函数()x xx xe ef x a e e ---=-+，存在实数12 n x x x ，，，，使得121()()()()n n f x f x f x f x -+++= 成立，若正整数n 的最大值为6，则实数a 的取值范围为（）A.35,23⎡⎫⎪⎢⎣⎭B.37,25⎛⎤-- ⎥⎝⎦B.C.7337,,5225⎡⎫⎛⎤--⎪ ⎢⎥⎣⎭⎝⎦D.3553,,2332⎡⎫⎛⎤--⎪ ⎢⎥⎣⎭⎝⎦二、多选题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，全部选对的得5分，有选错的得0分，部分选对的得2分．9.已知复数12,z z ，下列命题正确的是（）A.1212z z z z =B.若12z z =，则12z z =C.2111z z z = D.若2211z z =，则1z 为实数10.近年来，网络消费新业态、新应用不断涌现，消费场景也随之加速拓展，某报社开展了网络交易消费者满意度调查，某县人口约为50万人，从该县随机选取5000人进行问卷调查，根据满意度得分分成以下5组:[)[)[]50,60,60,70,,90,100 ，统计结果如图所示.由频率分布直方图可认为满意度得分X (单位:分)近似地服从正态分布()2,N μσ，且()0.6826P X μσμσ-<<+≈,()22P X μσμσ-<<+0.9544≈，()330.9974P x μσμσ-<<+≈，其中μ近似为样本平均数，σ近似为样本的标准差s ，并已求得12s =.则（）A.由直方图可估计样本的平均数约为74.5B.由直方图可估计样本的中位数约为75C.由正态分布可估计全县98.5X ≥的人数约为2.3万人D.由正态分布可估计全县62.598.5X ≤<的人数约为40.9万人11.已知函数()()3104f x x ax a =++<，其中(),0,1,2,3i i i A x y i =，是其图象上四个不重合的点，直线03A A 为函数()f x 在点0A 处的切线，则（）A.函数()f x 的图象关于10,4⎛⎫⎪⎝⎭中心对称B.函数()f x 的极大值有可能小于零C.对任意的100x x >>,直线03A A 的斜率恒大于直线01A A 的斜率D.若123,,A A A 三点共线，则1202x x x +=12.如图，圆柱的轴截面ABCD 是边长为2的正方形，,F H 为圆柱底面圆弧BC 的两个三等分点，EF ,GH 为圆柱的母线，点,P Q 分别为线段,AB GH 上的动点，经过点,,D P Q 的平面α与线段EF 交于点R ，以下结论正确的是（）A ．//QR PDB ．若点R 与点F 重合，则直线PQ 过定点C ．若平面α与平面BCF 所成角为θ，则tan θ233D ．若,P Q 分别为线段,AB GH 的中点，则平面α与圆柱侧面的公共点到平面BCF 距离的最小值为12三、填空题：本题共4小题，每小题5分，共20分.把答案填在题中的横线上.13.在平行四边形ABCD 中，若(1,3),(2,4)AB AC == ，则AB AD ⋅=.14.434log 2log 3x x ⎛⎫+ ⎪⎝⎭展开式的常数项为．（用最简分数表示）15.已知ABC ∆内有一点P ，满足030PAB PBC ∠=∠=，2AB =，3sin 5ABC ∠=，则PB =.16.一位飞镖运动员向一个目标投掷三次，记事件i A =“第i 次命中目标”，（1,2,3i =），()18i P A =，()()1|2i i i P A A P A +=，()()11|1,28i i P A A i +==，则()3P A =.四､解答题：本题共6小题，共70分．解答应写出文字说明､证明过程或演算步骤．17.（本小题满分10分）已知函数()sin 4ωπ⎛⎫=- ⎪⎝⎭f x x 在区间30,2π⎡⎤⎢⎥⎣⎦上恰有3个零点，其中ω为正整数．（1）求函数()f x 的解析式；（2）将函数()f x 的图象向左平移4π个单位得到函数()g x 的图象，求函数()()()=g x F x f x 的单调区间．18.（本小题满分12分）如图，已知四棱台1111-ABCD A B C D 的体积为7316，且满足//DC AB ，⊥BC BA ，11111=====AA A B BB BC CD ，2=AB ，E 为棱AB 上的一点且1//C E 平面11ADD A ．（1）设该棱台的高为h ，求证：1=h A E ；（2）求直线1C E 与平面11BCC B 所成角的正弦值．19.（本小题满分12分）某校开展网络知识竞赛.每人可参加多轮答题活动，每轮答题情况互不影响.每轮比赛共两组题，每组都有两道题，只有第一组的两道题均答对，方可进行第二组答题，否则本轮答题结束.已知甲同学第一组每道题答对的概率均为34，第二组每道题答对的概率均为12，两组题至少答对3题才可获得一枚纪念章.（1）记甲同学在一轮比赛答对的题目数为X ，请写出X 的分布列，并求()E X ；（2）若甲同学进行了10轮答题，试问获得多少枚纪念章的概率最大.20.（本小题满分12分）图中的数阵满足：每一行从左到右成等差数列，每一列从上到下成等比数列，且公比均为实数q ，21,11,32,24,27,5056a a a a a >==-=，，，.（1）设,n n n b a =，求数列{}n b 的通项公式；（2）设1,12,1,1n n S a a a =+++ ，是否存在实数λ，使,1n n a S λ<恒成立，若存在，求出λ的所有值，若不存在，请说明理由.21.（本小题满分12分）已知抛物线21:44C y x =-与双曲线22222:1(12)4x y C a a a -=<<-相交于两点A B F ，，是2C 的右焦点，直线AF 分别交12C C ，于C D ，（不同于A B ，点），直线BC BD ，分别交x 轴于P Q ，两点.（1）设()11,A x y ，()22,C x y ，求证：12y y 是定值；（2）求||||FQ FP 的取值范围.22.（本小题满分12分）已知函数2cos ()(0,)x xf x x x -=∈+∞，.（1）证明：函数()f x 在(0,)+∞上有且只有一个零点;（2）当(0,)x π∈时，求函数()f x 的最小值;（3）设(),1,2i i g x k x b i =+=，若对任意的12,()()()2x g x f x g x π⎡⎫∈+∞≤≤⎪⎢⎣⎭，恒成立，且不等式两端等号均能取到，求12k k +的最大值.答案解析一、单选题12345678BBBCCADC1.解析：{|5}U x x N =∈≤{}5,4,3,2,1,0=且{}4,3,2,1=⋃B A ，则()U A B = ð{}5,0.2.解析：∵12l l ⊥，∴011=⋅+⋅b a ，∴0=+b a 3.解析：不妨设仓库到车站的距离为x ，每月土地费用为1y ，每月货物的运输费用为2y ，两项总费用为21y y y +=，由题意可知，当10=x 时，21=y ,82=y ,则2010211=⇒=k k ，8.010822=⇒=k k .则854202542021=⋅≥+=+=x x x x y y y 当且仅当x x 5420=时，等式成立，即5=x 时，8min =y .4.解析：构造R x x x y ∈-=，sin ，则0cos 1≥-='x y ，y 在R 上单调递增，则2πα>，∴12sin ->-παα，同理，反之也成立.5.解析：∵0>n a ，12+=b n n b b a ，∴1+=n n n b b a ，∵0211>+=++n n n a a b ，∴0>n b ，又112++=+n n n b a a ，∴12112++++=+n n n n n b b b b b ，∴122++=+n n n b b b ，∴{nb 是等差数列.6.解析：如图建系，则⎪⎭⎫ ⎝⎛1,32,31G ，∴⎪⎭⎫⎝⎛-=13232，，AG ，()1,0,1-=AD 故222359172=⎪⎪⎪⎪⎭⎫⎝⎛-==d 7.解析：∵QBA PBA ∠=∠tan 3tan ，∴BQ BP k k 3=，又1-=AP BP k k ，∴22ab k k BQAQ -=.可得3122=a b ，∴321222=-=ab e ，故36=e .8.解析：令()1,11212-∈+-=+-=--xx xx x e e e e e t ，要使提议成立，则1>a 当1-<a 时，()()()min max min 65x f x f x f ≤<，即()()a a a --≤-<--16115，得5723-≤<-a ；当1>a 时，()()()min max min 65x f x f x f ≤<，同理可得2357≤<a 综上可得答案选C.二、多选题9.解析：设()R y x yi x z ∈+=,1，()R b a bi a z ∈+=,2，则()()i bx ay by ax z z ++-=21，则()()222222222221x b y a y b x a bx ay by ax z z +++=++-=，()()=++=222221b a y xz z 2122222222z z x b y a y b x a =+++，故A 正确；若21z z =，例如i z +=11，i z -=12，显然21z z ≠，故B 错误；()()212211z y x yi x yi x z z =+=-+=，故C 正确；若2121z z =，()()22yi x yi x -=+，则xyi xyi 22-=，即0=xy ，当0=x ，0≠y 时，1z 为纯虚数，故D 错误.10.解析：()5.7410010.095025.085030.075020.065015.055=⨯⨯+⨯+⨯+⨯+⨯=X 故A 正确；设中位数为x ，则()5.010030.0107010020.0015.0=⨯⨯-+⨯+x ，75=x ，故B 正确；σμ25.98+=，()()()0228.022215.025.98=+<<--=+≥=≥σμσμσμX P X P X P ,14.10228.050=⨯万人，故C 错误；σμσμ25.985.62+=<≤=-X ，()()()σμσμσμσμ2225.985.62+<≤-=+<≤-=<≤X P X P X P ()()222σμσμσμσμ+<<--+<<--X P X P 9101112ACABDADABD()()222σμσμσμσμ+<<--+<<-=X P X P 8185.0=，925.408185.050=⨯，故D 正确.11.解析：设()()00,x f x A ，则()()02003030341x x a x ax x y A A -+=⎪⎭⎫ ⎝⎛++-：，∵3A 在30A A 上，则()()032003033334141x x a x ax x ax x -+=⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛++，即()()()02030303=-+-x x x x x x ，∵03x x ≠，故0203=+x x .ax x y +=3为奇函数，故()x f 的图象关于⎪⎭⎫⎝⎛410，中心对称，A 正确；∵0<a ，()0>'x f 得⎪⎪⎭⎫ ⎝⎛+∞-⋃⎪⎪⎭⎫ ⎝⎛--∞-∈,33,aa x ；()0<'x f 得⎪⎪⎭⎫⎝⎛---∈3,3a a x ，故()x f 在⎪⎪⎭⎫ ⎝⎛+∞-⎪⎪⎭⎫ ⎝⎛--∞-,33,a a ，单调递增；在⎪⎪⎭⎫⎝⎛---3,3a a 单调递减，故()0413323>+--=⎪⎪⎭⎫ ⎝⎛--=a a a f x f 极大值，故B 错误；a x k A A +=20330，a x x x x x x ax x ax x k A A +++=-⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛++=20012101030131414110，∵001>>x x ，1030A A A A k k <，故C 错误；321,,A A A 三点共线，a x x x x k a x x x x k A A A A +++==+++=2331212*********，故0321=++x x x ，03212x x x x =-=+，故D 正确.12.解析：A 选项，平面ABCD ∥平面EFHG ，平面DPQ ∩平面ABCD DP =，平面DPQ ∩平面EFHG QR =,∴PD QR ∥，A 正确；B 选项，此时PRQD 为梯形，DP QF ∥，∵HQF APD ∆∆∽，相似比为2=FHAD，故2=FQPD，此时PQ 必过DF 上靠近F 额三等分点，B 正确；C 选项，当P 与B 重合，Q 与H 重合，22=BD ,3=BH ,5=DH ,BH DH ⊥，此时DHC ∠为二面角，3322tan >==CH DC θ,C 错误；D 选项，R 为β到面BCF 距离最小值21，D 正确.三、填空题13.4；14.23；15.35；16.204830113.解析：()11，=-==AB AC BC AD ，431=+=⋅AD AB .14.解析：()()()r r r r rrrr x C x x CT 243444344412log 3log 2log 3log ---+=⎪⎭⎫ ⎝⎛=令024=-r 可得2=r ，该项为()()()232log 62log 3log 24232424=⨯=C .15.解析：设θ=∠PBA ,则()5330sin sin =︒+=∠θABC ，由正弦定理：APB AB P AB PB ∠=∠sin sin 得()︒+=︒30sin 30sin θABPB ，即35=PB .16.解析：()()412112==A P A A P ,()()2232A P A A P =，则()8112=A A P ,()8123=A A P ,()8123=A A P 由全概率公式得：()()()()()6498181141811211212=⨯⎪⎭⎫ ⎝⎛-+⨯=+=A A P A P A A P A P A P 得：()()3292223==A P A A P ，即()()()()()20483018164913296492322323=⨯⎪⎭⎫ ⎝⎛-+⨯=+=A A P A P A A P A P A P .四、解答题17.解：（1）∵⎥⎦⎤⎢⎣⎡∈23,0πx ，∴⎦⎤⎢⎣⎡--∈-423,44ππωππωx ，又∵函数()⎪⎭⎫ ⎝⎛-=4sin πωx x f 在区间⎥⎦⎤⎢⎣⎡230π，上恰有3个零点，∴πππωπ34232<-≤，解得61323<≤ω，且ω为正整数，得2=ω，∴()⎪⎭⎫ ⎝⎛-=42sin πx x f ；（2）()⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=442sin ππx x g 得()⎪⎭⎫ ⎝⎛+=42sin πx x g ，∴()()()⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+==42tan 42cos 42sin 24sin 42sin 42sin 42sin πππππππx x x x x x x x f x g x F ，由2422πππππ+<+<-k x k ，解得82832ππππ+<<-k x k ，Z k ∈，∴函数()()()x f x g x F =的单调减区间为⎪⎭⎫⎝⎛+-82832ππππk k ，，Z k ∈.18.解：（1）四棱台1111D C B A ABCD -中有BCC B CD D C AB B A 11111121===，∵1=CD ,1=BC ,可得2111=D C ,2111=C B ,∴()832112121211111111111=⨯⎪⎭⎫ ⎝⎛+⨯=⋅+=C B B AD C S D C B A ,()()231212121=⨯+⨯=⋅+=BC AB CD S ABCD ,()163731111111111111=+⋅+=-h S S S S V ABCD ABCD D C B A D C B A D C B A ABCD ，得23=h ，∵∥E C 1平面11A ADD ，∴A D E C 11∥，又AB B A D C ∥∥1111,即AE D C ∥11，∴四边形AE D C 11是平行四边形，∴2111==D C AE ，∵四边形BA B A 11是等腰梯形，且11111===BB AA B A ,2=AB ,可得AB E A ⊥1,EA A Rt 1∆中，2321122211=⎪⎭⎫⎝⎛-=-=AE A A E A ，∴E A h 1=.（2）过点E 作B B EH 1⊥于H ，由（1）知E A 1⊥平面ABCD ，E AB E A AB BC BC E A =⋂⊥⊥11，，,∴BC ⊥平面B AE 1，⊂EH 平面B AE 1，∴EH BC ⊥，B BB BC =⋂1,∴EH ⊥平面11B BCC ，∴H EC 1∠为直线E C 1与平面11B BCC 所成的角，∵EH B B E A EB S EB B ⋅=⋅=∆1121211，可得343=EH ，22112322221121121211211=⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛=++=+=B C B A E A C A E A E C ,∴6832343sin 11===∠E C EH H EC ,∴直线E C 1与平面11B BCC 所成角的正弦值为683.19.解：（1）X 的可能值为4,3,2,1,0，且()16141410=⨯==X P ，()83414343411=⨯+⨯==X P ，()6492143432202=⎪⎭⎫ ⎝⎛⨯⨯==C X P ，()3292143433212=⎪⎭⎫ ⎝⎛⨯⨯==C X P ，()6492143434222=⎪⎭⎫ ⎝⎛⨯⨯==C X P .∴X 的分布列为∴()16336494329364928311610=⨯+⨯+⨯+⨯+⨯=X E .（2）甲同学在一轮比赛中获得纪念章的概率为6427649329=+=P ,设甲同学进行10轮比赛获得纪念章枚数为Y ，则⎪⎭⎫ ⎝⎛642710~，B Y ,()kkk C k Y P -⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==101064376427，由⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛≥⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛≥⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-++-----kk k k k k kk k k k k C C C C 911101010111110101064376427643764276437642764376427，N k ∈，解得4=k ，即甲同学进行了10轮答题获得4枚纪念章的概率最大.X 01234P1618364932964920.解：（1）设t a =1,1，第一行公差为d ，则由523,1=+=d t a ，()()62,12,2-=+=+=q d t q d a a ，()()()66265,1232,15,722,44q d t q d t q a q a a a +=+⇒=⇒=，联立三式，解得2=d 或10（当10=d 时，01,1<a ，不符题意，舍去），1=t ，2-=q ，∴()[]()()111,11,1,2121----⋅-=-+==n n n n n n n q d n a qa a ，即()()1212--⋅-=n n n b .（2）()111,11,2---==n n n a a ，()()()3212121nnn S --=----=，()()321211,nn n n S a --⋅<-⇔<-λλ，当n 为奇数时，等价于n n n 21232321223+-=+⋅>λ恒成立，得23≥λ；当n 为偶数时，等价于12232312223-+=-⋅<n n n λ恒成立，得23≤λ.综上23=λ，即存在23=λ，使得n n S a λ<1,恒成立.21.解：（1）由()11,y x A ，()22,y x C 是直线AF 与抛物线4421-=x y C ：的两个交点，故设直线AF 的方程为2+=my x ，代入4421-=x y C ：，消去x ，整理得0442=--my y ，∴421-=y y 为定值；（2）由()11,y x B -，则()121212124224y y my my m x x y y k BC -=+-+=-+=，故BC 的直线方程为()11214x x y y y y --=+.令0=y 得()0444442121121=+=++-=y y y y y y x P .设()33,y x D ，联立方程组⎪⎩⎪⎨⎧=--+=1422222a y a x my x 消去x 可得()()()0444422222222=---+--a y a m yaa m m ，()()22222231222223144444m a a m a y y m a a m a m y y -+-=-+-=+，.∴直线BD 的直线方程为()113131x x x x y y y y --+=+，令0=y 得()()22422113131113131+-=+++-=++-=a my y y y y my x y y x x y x Q ∴44222a x FPFQ Q -=-=，∵()2,1∈a ，∴⎪⎭⎫ ⎝⎛∈430，FP FQ .22.解：（1）令()0=x f 得0cos =-x x ，令()x x x g -=cos ，即证()x x x g -=cos 在()∞+，0有唯一零点.()01sin <--='x x g ，故()x g 在()∞+，0上单调递减，066cos 6>-=⎪⎭⎫ ⎝⎛πππg ，022cos 2<-=⎪⎭⎫ ⎝⎛πππg ，∴026<⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛ππg g ，根据零点存在定理得证.（2）()()3cos 2sin 1x x x x x f --='，注意到02=⎪⎭⎫⎝⎛'πf ，当⎪⎭⎫⎝⎛∈ππ,2x 时，显然()0sin 1>-x x ，0cos 2>-x ，故()0>'x f ；当⎪⎭⎫ ⎝⎛∈2,0πx 时，令()()x x x x h cos 2sin 1--=，02=⎪⎭⎫⎝⎛πh ，那么()1cos sin 1>-+='x x x x h ，利用x x x cos sin >，⎪⎭⎫⎝⎛∈2,0πx 放缩，故当⎪⎭⎫ ⎝⎛∈2,0πx ，()x h 在⎪⎭⎫ ⎝⎛2,0π递增，故()02=⎪⎭⎫ ⎝⎛<πh x h ，∴()0<'x f ，⎪⎭⎫ ⎝⎛∈2,0πx ，则()x f 在⎪⎭⎫ ⎝⎛2,0π上单调递减，在⎪⎭⎫ ⎝⎛ππ,2上单调递增，则()ππ22min -=⎪⎭⎫⎝⎛=f x f .（3）由（1）函数()x f 在()∞+，0上有且只有一个零点；由（2）知()x f 在⎪⎭⎫ ⎝⎛2,0π上单调递减，在⎪⎭⎫⎝⎛ππ,2上单调递增，且当+∞→x ，()0→x f ，考虑到()b x k x f +≥1，则01≤k ，则π2-≥b .当b 变大，则2k 减小.考虑到21k k +最大，则01=k ，则π2-=b ，那么等号取到π22-x k 与()x f 相切，设切点为⎪⎪⎭⎫⎝⎛-20000cos ,x x x x ，则()0203000022cos cos 2sin x x x x x x x x x x f k π+-=--='=20000002cos cos 2sin x x x x x x x π+-=--⇒0sin 22cos 3002000=++-⇒x x x x x π230π=⇒x （证明唯一性即可）故229823ππ=⎪⎭⎫⎝⎛'=f k ，∴21k k +的最大值为298π.。
2023届南通三模数学试题及答案
南通市2023届高三第三次调研测试（考前模拟）数 学注意事项：1. 答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2. 作答选择题时，用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑：如需改动，用橡皮擦干净后，再选涂其他答案。
非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；不准使用铅笔和涂改液。
3. 考生必须保持答题卡的整洁。
考试结束后，将试卷和答题卡一并交回。
4. 本试卷共6页，22小题，满分150分。
考试用时120分钟。
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 若“()0,πsin 2sin 0x x k x ∃∈−，＜”为假命题，则k 的取值范围为( ). A. (,2]−∞−B. (,2]−∞C. (,2)−∞−D. (,2)−∞2. 复数22021202212i 3i 2022i 2023i z =+++++的虚部为( ).A. 1012B. 1011−C. 1011D. 20223. 平面向量a ，b 满足，240a a b −⋅−=，||3b =，则||a 最大值是( ).A. 3B. 4C. 5D. 64. 某同学在课外阅读时了解到概率统计中的切比雪夫不等式，该不等式可以使人们在随机变量X 的期望()E X 和方差()D X 存在但其分布未知的情况下，对事件“|()|X E X ε−…”的概率作出上限估计，其中ε为任意正实数．切比雪夫不等式的形式为：(|()|)((),)P X E X f D X εε−厔，其中((),)f D X ε是关于()D X 和ε的表达式．由于记忆模糊，该同学只能确定((),)f D X ε的具体形式是下列四个选项中的某一种．请你根据所学相关知识，确定该形式是( ). A. 2()D X ε⋅B. 21()D X ε⋅C.2()D X ε D.2()D X ε5. 已知三棱锥P ABC −，Q 为BC 中点，2PB PC AB BC AC =====，侧面PBC ⊥底面ABC ，则过点Q 的平面截该三棱锥外接球所得截面面积的取值范围为( ). A. 5ππ,3⎡⎤⎢⎥⎣⎦B. π2π,23⎡⎤⎢⎥⎣⎦C. 2π,2π3⎡⎤⎢⎥⎣⎦D. []π,2π6. 抛物线24y x =的焦点为F ，过点F 的直线l 交抛物线于,A B 两点，以AB 为直径的圆C 交y 轴于,M N 两点，O 为坐标原点，则MNC △的内切圆直径最小值为( ). A. 38B. 36−C. 434−D. 432−7. 已知宽为a 的走廊与另外一条走廊垂直相连，若长为8a 的细杆能水平地通过拐角，则另外一条走廊的宽度至少是( ). A. 2aB. ()421a −C. 23aD. 33a8. 函数()2023f x xx =，若方程()()2sin 0x x f x ax +−=只有三个根123,,x x x ，且123x x x ＜＜，则213sin 2023x x x +的取值范围是( ).A. ()0,+∞B. ()2023,+∞C. (),2023−∞−D. (),0−∞二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9. 直线:20l mx y m +−=与圆224x y +=交于,A B 两点，P 为圆上任意一点，则( ).A. 线段AB 最短长度为22B. AOB △的面积最大值为2C. 无论m 为何值，l 与圆相交D. 不存在m ，使APB ∠取得最大值10. 正方体ABCD A B C D −''''的边长为2，Q 为棱AA '的中点，点,M N 分别为线段,C D CD ''上两动点(含端点)，记直线,QM QN 与面ABB A ''所成角分别为,αβ，且22tan tan 4αβ+=，则( ). A. 存在点,M N 使得//MN AA ' B. DM DN ⋅为定值C. 存在点,M N 使得32MN =D. 存在点,M N 使得MN CQ ⊥11. 椭圆曲线232y ay x bx cx d +=+++是代数几何中一类重要的研究对象.则关于椭圆曲线232:2453W y y x x x +=−+−，下列结论正确的有( ).A. W 关于直线1x =−对称B. W 关于直线1y =−对称C. W 上的点的横坐标的取值范围为[)1,+∞D. W 上的点的横坐标的取值范围为{}[)12,⋃+∞12. 1979年，李政道博土给中国科技大学少年班出过一道智趣题：“5只猴子分一堆桃子.怎么也不能分成5等份，只好先去睡觉.准备第二天再分.夜里1只猴子偷偷爬起来，先吃1个桃子.然后将其分成5等份，藏起自己的一份就去睡觉了;第2只猴子又爬起来，吃掉1个桃子后.也将桃子分成5等份，藏起自己的一份睡觉去了：以后的3只猴子都先后照此办理.问最初至少有多少个桃子?最后至少剩下多少个桃子?”.下列说法正确的是( ).A. 若第n 只猴子分得n b 个桃子(不含吃的)，则1541(2,3,4,5)n n b b n −=−=B. 若第n 只猴子连吃带分共得到n a 个桃子，则{}(1,2,3,4,5)n a n =为等比数列C. 若最初有3121个桃子，则第5只猴子分得256个桃子(不含吃的)D. 若最初有k 个桃子，则4k +必为55的倍数三、填空题：本题共4小题，每小题5分，共20分．13. 随机变量1~2,3X B ⎛⎫ ⎪⎝⎭，则()21X σ+=__________.14. 函数32()(0)f x ax bx cx d a b =++++<在R 上是增函数，则ca b+的最大值为__________. 15. 已知0122C C C C (1)n n nn n n nx x x x ++++=+，则012111C C C C 231n n n n n n ++++=+__________. 16. 将函数()π()2sin 32f x x ϕϕ⎛⎫=+≤ ⎪⎭的图象向右平移2π9个单位长度，得到的函数()g x 的图象关于点11π,018⎛⎫− ⎪⎝⎭对称，且()g x 在区间,m m ϕϕ⎛⎫− ⎪⎝⎭上单调递增，则ϕ=__________,实数m 的取值范围是__________.（本小题答对一空得2分，答对两空得5分）四、解答题：本题共6小题，共70分.请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或演算步骤，只有答案没有过程的不能得分.17. （10分）最新研发的某产品每次试验结果为成功或不成功，且试验成功的概率为(01).p p <<现对该产品进行独立重复试验，若试验成功，试验结束;若试验不成功，则继续试验，且最多试验10次.记X 为试验结束时所进行的试验次数，且每次试验的成本为(0)a a >元. （1）①写出X 的分布列;②证明：1();E X p<（2）某公司意向投资该产品.若0.25p =，且试验成功则获利5a 元，请说明该公司如何决策投资.18. （12分）如图，在三棱柱111ABC A B C −中，14AB AA ==，2BC =，123A C =，AC BC ⊥，160.A AB ︒∠=（1）证明：BC ⊥平面11ACC A ；（2）设点D 为1CC 的中点，求直线1A D 与平面11ABB A 所成角的正弦值．19. （12分）设{}n a 是各项均为正数的等差数列，11a =，且31a +是2a 和8a 的等比中项；记{}n b 的前n 项和为n S ，*22().n n b S n N −=∈（1）求{}n a 和{}n b 的通项公式; （2）设数列{}n c 的通项公式2,,n n n a n c b n +⎧⎪=⎨⎪⎩为奇数为偶数①求数列{}n c 的前21n +项和21n T +；②求(1)21ini i ia c −=∑.20. （12分）已知ABC △，D 为边AC 上一点，1AD =， 2.CD = （1）若34BA BD ⋅=，0BC BD ⋅=，求ABC △的面积； （2）若直线BD 平分ABC ∠，求ABD △与CBD △内切圆半径之比的取值范围.21. （12分）双曲线C ：2213y x −=，点00(,)A x y 是C 上位于第一象限的一点，点A 、B 关于原点O 对称，点A 、D 关于y 轴对称．延长AD 至E 使得1||||3DE AD =，且直线BE 和C 的另一个交点F 位于第二象限中． （1）求0x 的取值范围；（2）证明：AE 不可能是BAF ∠的三等分线．22. （12分）已知函数()e xx f x =. （1）求曲线()y f x =在()()e,e f −−处的切线方程；（2）若120nii i xx ==∑,＞，证明：()212e nni i f x −=≤∑.南通2023高三三模 考前模拟数学1.若“(0,)x π∃∈，”为假命题，则k 的取值范围为( ) A. (,2]−∞− B. (,2]−∞C. (,2)−∞−D. (,2)−∞【答案】 A【解析】 【分析】本题主要考查命题的真假，函数的恒成立问题，求函数的最值，属于中档题． 由题意可得对任意(0,)x π∈，，即，求得2cos x 的范围，可得k 的取值范围． 【解答】 解：“(0,)x π∃∈，”为假命题， ∴对任意(0,)x π∈，，即对任意(0,)x π∈，，，2k ∴−…， 故选：.A2. 已知i 为虚数单位，则复数22021202212i 3i 2022i 2023i z =+++++的虚部为A. 1012B. 1011−C. 1011D. 2022【答案】 A【解析】 【分析】本题考查复数的四则运算，考查错位相减法求和，属于中档题. 利用错位相减法求和求出复数z 求解即可. 【解答】解：22021202212i 3i 2022i 2023i z =+++++， 所以23202220232320222023z i i i i i i ⋅=+++++，所以220222023(1)12023i z i i i i −=++++−20232023120231i i i−=−−20232024i i i=+= 所以2024(2024)(1)1(1)(1)i i i z i i i +==−−+ 20242024101210122i i−==−+ 所以复数z 的虚部为为1012. 故选A3. 平面向量a ，b 满足，，||3b =，则||a 最大值是( )A. 3B. 4C. 5D. 6【答案】 B【解析】 【分析】本题主要考查了平面向量数量积的定义及性质的简单应用，属于中档题．先设向量a ，b 的夹角为θ，由已知结合向量数量积的定义可得2||443cos ||||||a a a a θ−==−，结合向量夹角的范围可求.【解答】解：设向量a ，b 的夹角为θ，240a a b −⋅−=，||3b =，243||cos a a b a θ∴−=⋅=，2||443cos ||||||a a a a θ−∴==−，且0a ≠，0θπ剟，1cos 1θ∴−剟，则，即，解可得，，即||a 最大值是4.故选：.B4. 某同学在课外阅读时了解到概率统计中的切比雪夫不等式，该不等式可以使人们在随机变量X 的期望()E X 和方差()D X 存在但其分布未知的情况下，对事件“|()|X E X ε−…”的概率作出上限估计，其中ε为任意正实数．切比雪夫不等式的形式为：(|()|)((),)P X E X f D X εε−厔，其中((),)f D X ε是关于()D X 和ε的表达式．由于记忆模糊，该同学只能确定((),)f D X ε的具体形式是下列四个选项中的某一种．请你根据所学相关知识，确定该形式是 A. 2()D X ε⋅ B. 21()D X ε⋅C.2()D X ε D.2()D X ε【答案】 D【解析】 【分析】本题主要考查了切比雪夫不等式，属于中档题. 利用期望和方差的关系可得答案. 【解答】解：因为(|()|)((),)P X E X f D X εε−厔， 所以则所以((),)f D X ε的具体形式是2().D X ε故选：.D5. 已知三棱锥P ABC −，Q 为BC 中点，2PB PC AB BC AC =====，侧面PBC ⊥底面ABC ，则过点Q 的平面截该三棱锥外接球所得截面面积的取值范围为( ) A. 5[,]3ππ B. 2[,]23ππC. 2[,2]3ππ D. [,2]ππ【答案】 A【解析】 【分析】本题考查空间几何体的外接球问题和截面问题，考查空间想象能力，难度较大. 【解答】解：连接PQ ，QA ，由2PB PC AB BC AC =====，可知：ABC 和PBC 是等边三角形，设三棱锥P ABC −外接球的球心为O ，所以球心O 到平面ABC 和平面PBC 的射影是ABC 和PBC 的中心F ，E ， PBC 是等边三角形，Q 为BC 中点，所以PQ BC ⊥，又因为侧面PBC ⊥底面ABC ，侧面PBC ⋂底面ABC BC =， 所以PQ ⊥底面ABC ，而AQ ⊂底面ABC ，因此PQ AQ ⊥，所以OFQE 是矩形.ABC 和PBC 是边长为2的等边三角形，所以两个三角形的高2212(2)32h =−⨯=在矩形OFQE 中，1322333OE FQ h AE h =====，连接OA ， 所以22141533OA OE EA =+=+=， 设过点Q 的平面为α，当OQ α⊥时， 此时所得截面的面积最小，该截面为圆形，222211226()()333333OQ OF FQ h h h =+=+===， 因此圆Q 22156199OA OQ −=−=，所以此时面积为21;ππ⋅= 当点Q 在以O 为圆心的大圆上时，此时截面的面积最大，面积为：2155;3ππ⋅= 所以截面的面积范围为：5[,]3ππ，故选.A6. B 【分析】根据抛物线、圆以及导数相关知识求解即可.7. D 【分析】根据解三角以及导数相关知识求解即可.8. D 【分析】根据观察法以及函数奇偶性得到2130,x x x ==−带入即可.9. CD 【分析】斜率一定存在，所以AB 错误，D 正确，直线所过定点在圆内故C 正确。
【附3套模似卷】安徽省安庆市2019-2020学年高考适应性测试卷数学试题(2)含解析.docx
安徽省安庆市2019-2020学年高考适应性测试卷数学试题(2 )一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.若不等式x2+ax + l>0对于一切恒成立，则。
的最小值是()5 。
A.0B. -2C.——D. -32【答案】C【解析】【分析】【详解】试题分析：将参数a与变量x分离，将不等式恒成立问题转化为求函数最值问题，即可得到结论.解：不等式x2+ax+l>0对一切xG(0,上］成立，等价于a>-x-—对于一切-V e ［ 0,^-成立，2 x 12」Vy=-x--在区间f0,」］上是增函数x I 2_. L 1 ° 5・.—X--- S ---- 2 = ---X 2 2a>-—一2.la的最小值为-2故答案为C.2考点：不等式的应用点评：本题综合考查了不等式的应用、不等式的解法等基础知识，考查运算求解能力，考查化归与转化思想，属于中档题2.已知函数/(x) = V^sinx + 〃zcosx,其图象关于直线x = ~对称,为了得到函数= \j3 + m2 cos2x的图象，只需将函数f(x)的图象上的所有点()A.先向左平移£个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变O兀 1B.先向右平移三个单位长度，再把所得各点横坐标缩短为原来的一，纵坐标保持不变6 2C.先向右平移;个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变JI 1D.先向左平移:个单位长度，再把所得各点横坐标缩短为原来的s，纵坐标保持不变【答案】D【解析】【分析】 由函数f ⑴的图象关于直线x = |对称，得秫=1,进而得/(A ) = A /3SIIU - + cosx = 2sin "+ § J = 2cos" - J,再利用图像变换求解即可【详解】由函数f(x)的图象关于直线x = |对称，得/ | =V3W , TT|象上的所有点“先向左平移5个单位长度，得v = 2COSX,再将横坐标缩短为原来的纵坐标保持不变, 得 g (X )=2cos2x ”即可.故选：D 【点睛】本题考查三角函数的图象与性质，考查图像变换，考查运算求解能力，是中档题3. 函数y (x) = 2sin (6K + 9)(口>0,0<0<4)的部分图像如图所示，若AB = 5,点A 的坐标为(-1,2),若将函数f 3)向右平移m(m>0)个单位后函数图像关于y 轴对称，则m 的最小值为()【答案】B 【解析】 【分析】根据图象以及题中所给的条件，求出和们，即可求得f(x)的解析式，再通过平移变换函数图象关于 y 轴对称，求得"？的最小值. 【详解】由于AB = 5,函数最高点与最低点的高度差为4,3 in I即~ + —=右+冰，解得m = l,71所以 f (x) = J^sinx + cosx = 2sin| x + —=2cos x- —I 3g(x) = 2cos2x,故只需将函数f(x)的图1、TC所以函数f(x)的半个周期- = 3,所以T = - = 6^(o = -,2 co 3又 A (—1,2), Q 〈(p< 兀，则有 2sin —lx 三+ 0 =2,可得(p = —将函数f (x)向右平移m 个单位后函数图像关于J 轴对称，即平移后为偶函数, 所以"？的最小值为1, 故选：B. 【点睛】该题主要考查三角函数的图象和性质，根据图象求出函数的解析式是解决该题的关键，要求熟练掌握函数 图象之间的变换关系，属于简单题目.“24.已知函数f(x)=< '+ 1,若关于x 的方程f(x)=kx —：恰有4个不相等的实数根，则实数kIn x, x 〉1 2的取值范围是()【答案】D 【解析】 【分析】由已知可将问题转化为：y=f(x)的图象和直线y=kx-|有4个交点，作出图象，由图可得：点(1,0)必须 在直线y=kx —：的下方，即可求得：k>：；再求得直线y=kx —：和y=lnx 相切时，k=—；结合 图象即可得解.【详解】若关于x 的方程f(x) = kx-:恰有4个不相等的实数根，2则y=f(x)的图象和直线y=kx-|有4个交点.作出函数y=f(x)的图象，如图,5丸所以 /(.x) = 2sin 71571— X~\-------- 3 6=2sin71 71 71 — X~\ ----- 1——3 3 2=2cos §(_v +1),1 5g 1Akxl-->0,解得k>-. 2 2当直线y=kx—：和y=lnx相切时，设切点横坐标为m, [ 1 1. lnm + — 1 . r则k = 2 = , ・• m = Je .m m此时，k=L = *, f(x)的图象和直线y=kx--有3个交点，不满足条件，m e 2故所求k的取值范围是故选D..【点睛】本题主要考查了函数与方程思想及转化能力，还考查了导数的几何意义及计算能力、观察能力，属于难题. (1 、5D. -25. —1= + rnxA. 2【答案】C【解析】【分析】的展开式中r的系数是-10,则实数秫=(B. 1利用通项公式找到r的系数，令其等于一10即可. 【详解】二项式展开式的通项为⑶=C；(Q)J(*)r = 〃D 5 5 —r—— .22 ,令； = 5,得,=3,2 2=rn^Ctx5 = -10A-5 ,所以m3Cl = -10 ,解得m^-1.故选：C【点睛】本题考查求二项展开式中特定项的系数，考查学生的运算求解能力，是一道容易题.6.已知点凡为双曲线。
浙江省名校新高考研究联盟2024届高三第三次联考(三模)数学试题(含答案与解析)_8968
Z 20名校联盟（浙江省名校新高考研究联盟）2024届高三第三次联考数学试题卷本试卷满分150分，考试时间120分钟注意事项：1. 答卷前， 务必将自己的姓名，考生号等填写在答题卡和试卷指定位置上.2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动， 用橡皮擦干净后，再涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在本试卷 上无效.3. 请保持答题卡的整洁.考试结束后， 将试卷和答题卡一并交回.第I 卷一、选择题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 集合{}{}24182A x x B x x x =≤<=-≥-， ，则 A B ⋃=（ ） A [)2,4B. [)3,4C. [)2,∞+D. [)3,∞+2. 复数5ii 2-的虚部是（ ） A. iB. 1C. 2i -D. 2-3. 已知单位向量,a b 满足0a b ⋅=，则cos 34,a b a b ++= （ ）A. 0B.C.D. 14. 设 n S 为等比数列 {}n a 前 n 项和，已知 342322S a S a =-=-， ，则公比 q =（ ） A. 2B. -2C.12D. 12-5. 已知()()2,2,1,3A B --，点P 在圆224x y +=上运动，则22PA PB +的最大值为（ ）A. 16-B. 26+C. 26+D. 326. 若函数 ()()sin cos f x x x ω=+ 最大值为 2，则常数 ω 的取值可以为（ ） A. 1B.12C.13D.14.的的7. 已知 []x 表示不超过 x 的最大整数，若 x t = 为函数1()(0)1e xx f x x -=<-的极值点，则 []()f t =（ ）A. 2e e 1-B. 2231e e -C. 3341e e -D. 4451e e -8. 设O 为原点，12,F F 为双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点，点P 在C 上且满足32OP a =，123cos 7F PF ∠=，则该双曲线的渐近线方程为（ ）A.0y ±= B. 0x ±=C. 0y ±=D. 0x =二、选择题：本大题共3小题，每小题6分，共18分. 在每小题给出的选项中，有多项符合题目要求. 全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 下列说法正确的是（ ）A. 数据7，5，3，10，2的第40百分位数是3B. 已知随机变量X 服从正态分布()2,,Nμσσ越小，表示随机变量X 分布越集中C. 已知一组数据12,,,n x x x 的方差为3，则1231,1,1,,1n x x x x ---- 的方差为3D. 根据一组样本数据的散点图判断出两个变量线性相关，由最小二乘法求得其回归直线方程为ˆ0.3yx m =-，若其中一个散点为(),0.28m -，则4m =10. 已知 ABC 的内角,,A B C 的对边分别为,,a b c 2sin sin 2A Cb A +⋅=⋅，下列结论正确的是（ ） A. π3B =B. 若 45a b ==， ，则 ABC 有两解C. 当a c -=时， ABC 为直角三角形D. 若 ABC 为锐角三角形，则 cos cos A C + 的取值范围是 11. 在棱长为 1 的正方体1111ABCD A B C D -中，已知E F 、分别为线段111B C D C ，的中点，点P 满足[][]10,1,0,1DP DD DB λμλμ=+∈∈，，则（ ）A. 当1λμ+=时，三棱锥D PEF -的体积为定值B. 当12λμ==，四棱锥P ABCD -的外接球的表面积是9π4C. PEF !12D. 若AP =，则点P 的轨迹长为π2第II 卷三、填空题：本题共3小题，每小题5分，共15分.12. 已知圆台的上底面半径为1，下底面半径为5，侧面积为30π，则圆台的高为_________.13. 甲、乙、丙 3 人站到共有 6 级的台阶上， 若每级台阶最多站 2 人且甲、乙不站同一个台阶，同一台阶上的人不区分站的位置，则不同的站法种数是_____________种. (用数字作答)14. 已知关于x 的不等式()()2ln 22110x ax x a x ⎡⎤--++≤⎣⎦对任意 ()0,x ∞∈+ 恒成立，则实数 a 的取值范围是___________________.四、解答题: 本题共 5 小题， 共 77 分. 解答应写出文字说明、证明过程或验算步骤.15. 已知等差数列 {}n a 的公差不为零， 125,,a a a 成等比数列，且 221n n a a =+ . （1）求数列 {}n a 的通项公式; （2）求 13521n a a a a -++++ .16. 已知四面体,2,A BCD AB AD BC CD AC -=====（1）证明：AC BD ⊥;（2）若BD =AB 与平面ACD 所成角的正弦值.17. 为了增强身体素质，寒假期间小王每天坚持在 “跑步20 分钟”和“跳绳20 分钟” 中选择一项进行锻炼. 在不下雪的时候，他跑步的概率为80%，跳绳的概率为20%，在下雪天他跑步的概率为20%，跳绳的概率为80%. 若前一天不下雪，则第二天下雪的概率为60%，若前一天下雪，则第二天仍下雪的概率为40%. 已知寒假第一天不下雪，跑步20分钟大约消耗能量300卡路里，跳绳20分钟大约消耗能量200卡路里. 记寒假第n 天不下雪的概率为n P . （1）求123P P P 、、的值，并求n P; （2）设小王寒假第n 天通过运动消耗的能量为X ，求X 的数学期望.18. 已知椭圆2222:1(0)x y C a b a b +=>>左、右焦点分别为 12F F 、 ，焦距为直线 :l y x m =+ 与椭圆交于 A B 、 两点 （其中点 A 在 x 轴上方，点 B 在 x 轴下方）. （1）求椭圆 C 的标准方程;（2）如图，将平面 xOy 沿 x 轴折叠，使 y 轴正半轴和 x 轴所确定半平面（平面 12A F F '）与 y 轴 负半轴和 x 轴所确定的半平面 (平面 12B F F ' ) 垂直.①若折叠后 OA OB '⊥' ，求 m 的值;②是否存在 m ，使折叠后 A B ''、 两点间的距离与折叠前 A B 、 两点间的距离之比为34 ? 19. 在平面直角坐标系中，如果将函数()y f x =的图象绕坐标原点逆时针旋转π(0)2αα<£后，所得曲线仍然是某个函数的图象，则称()f x 为“α旋转函数”. （1）判断函数y =是否为“π6旋转函数”，并说明理由；（2）已知函数()()()ln 210f x x x =+>是“α旋转函数”，求tan α的最大值；（3）若函数()()21e ln 2xx g x m x x x =---是“π4旋转函数”，求m 的取值范围.的的参考答案一、选择题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 集合{}{}24182A x x B x x x =≤<=-≥-， ，则 A B ⋃=（ ） A. [)2,4 B. [)3,4C. [)2,∞+D. [)3,∞+【答案】C 【解析】【分析】先解集合B 中的不等式182x x -≥-，解出x 的范围，再求得A B ⋃即可. 【详解】由182x x -≥-，解得3x ≥，即{}3B x x =≥，{}24A x x =≤< ，{}2A B x x ∴⋃=≥.故选：C2. 复数5ii 2-的虚部是（ ） A. iB. 1C. 2i -D. 2-【答案】D 【解析】【分析】根据复数代数形式的除法运算化简，再判断其虚部.【详解】因为()()()5i 2i 5i 12i i 2i 22i --==-----， 所以复数5ii 2-的虚部是2-. 故选：D3. 已知单位向量,a b 满足0a b ⋅=，则cos 34,a b a b ++= （ ）A. 0B.C.D. 1【答案】B 【解析】【分析】计算出()()347a b a b +⋅+=，345a b +=r r，a b += ，利用向量夹角余弦公式求出答案..【详解】()()22343743047a b a b a a b b +⋅+=+⋅+=++= ，()2223492416901625a ba ab b +=+⋅+=++= ，故345a b +=r r ，()2222112a b a a b b +=+⋅+=+=，故a b += ，所以()()34cos 34,34a b a b a b a b a b a b+⋅+++===+⋅+ . 故选：B4. 设 n S 为等比数列 {}n a 的前 n 项和，已知 342322S a S a =-=-， ，则公比 q =（ ） A. 2 B. -2C.12D. 12-【答案】A 【解析】【分析】根据数列的前n 项和与n a 的关系，两式相减，即可求解. 【详解】由已知，342322S a S a =-=-，，两式相减得，32343S S a a a -==-，即342a a =，即432a q a ==. 故选：A5. 已知()()2,2,1,3A B --，点P 在圆224x y +=上运动，则22PA PB +的最大值为（）A. 16- B. 26+ C. 26+D. 32【答案】C 【解析】【分析】设()2cos ,2sin P θθ，根据两点间的距离公式结合三角函数的性质即可得解. 【详解】设()2cos ,2sin P θθ，则()()()()2222222cos 22sin 22cos 12sin 3PA PB θθθθ+=++++-+-22224cos 8cos 44sin 8sin 44cos 4cos 14sin 12sin 9θθθθθθθθ=++++++-++-+π4cos 4sin 26264θθθ⎛⎫=-+=++ ⎪⎝⎭，当πcos 14θ⎛⎫+= ⎪⎝⎭时，22PA PB +取得最大值26+. 故选：C.6. 若函数 ()()sin cos f x x x ω=+ 的最大值为 2，则常数 ω 的取值可以为（ ） A. 1 B.12C.13D.14【答案】D 【解析】【分析】首先分别分析函数cos y x =和()sin y x ω=的最大值，再根据三角函数的性质，即可求解. 【详解】因为函数cos y x =的最大值为1，()sin y x ω=的最大值为1， 由题意可知，cos y x =取得最大值1时，()sin y x ω=也取得最大值1， 即当2π,Z x k k =∈时，π2π2π2k k ω'⋅=+，,Z k k '∈， 得14k k kω'=+，,Z k k '∈，0k ≠， 当1,0k k '==时，14ω=，其他值不满足等式.故选：D7. 已知 []x 表示不超过 x 的最大整数，若 x t = 为函数1()(0)1e x xf x x -=<-的极值点，则 []()f t =（ ）A. 2e e 1-B. 2231e e -C. 3341e e -D. 4451e e -【答案】B 【解析】【分析】求导后，构造()e 2e 1x xg x x =-+-，分别求出()()10,20g g ->-<，由零点存在定理得到零点范围，再结合题意求出结果即可.【详解】由题意可得()()2e 2e 1e 1x x xx f x -+-¢=-，令()e 2e 1x xg x x =-+-， 则()1313e 110e g --=-=->，()22424e 110eg --=-=-<，所以存在021x -<<-，使得()00g x =，即()00f x '=，当02x x -<<时，()0f x '<，()f x 单调递减；当01x x <<-时，()0f x ¢>，()f x 单调递增， 所以0x x =为函数()f x 的极值点， 所以[][]02t x ==-，所以[]()()22222133e 21e 1e 11e ft f ----=-===---，故选：B.8. 设O 为原点，12,F F 为双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点，点P 在C 上且满足32OP a =，123cos 7F PF ∠=，则该双曲线的渐近线方程为（ ）A.0y ±=B. 0x ±=C. 0y ±=D. 0x =【答案】B 【解析】【分析】设12,PF m PF n ==，由题意列出含,m n 的方程组，解出,a b 的关系式，进而求出双曲线的渐近线即可.【详解】设12,PF m PF n == ，由双曲线的定义知 2m n a -= ①， 在 12F PF △ 中，由余弦定理得：2221242cos c m n mn F PF ∠=+-⋅， 所以222647c m n mn =+- ②， 再由32OP a =，O 为12,F F 的中点，延长PO 至Q ，使OQ OP =， 所以四边形12PF F Q 为平行四边形，且3232PQ a a =⨯=，在12PF F △中，由余弦定理知：2221242cos c m n mn F PF ∠=+-⋅， 在1PF Q △中，由余弦定理知：222192cos a m n mn PF Q =+-∠， 因为121πF PF PF Q ∠+∠=，则121cos cos 0F PF PF Q ∠+∠=， 可知()()()2222232m na c +=+，所以2222942a c m n ++=③， 由①③得2214mn a c =+④， 把③④代入②得2222294614274a c c a c +⎛⎫=-+ ⎪⎝⎭，化简得222222*********c a a b a a =∴+=∴=， ，所以渐近线方程0x =. 故选：B.【点睛】关键点点睛：由四点共圆的四边形四个边的平方和等于两条对角线的平方和()()()2222232m n a c +=+是解决本题的关键.二、选择题：本大题共3小题，每小题6分，共18分. 在每小题给出的选项中，有多项符合题目要求. 全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 下列说法正确的是（ ）A. 数据7，5，3，10，2的第40百分位数是3B. 已知随机变量X 服从正态分布()2,,Nμσσ越小，表示随机变量X 分布越集中C. 已知一组数据12,,,n x x x 的方差为3，则1231,1,1,,1n x x x x ---- 的方差为3D. 根据一组样本数据的散点图判断出两个变量线性相关，由最小二乘法求得其回归直线方程为ˆ0.3yx m =-，若其中一个散点为(),0.28m -，则4m = 【答案】BC 【解析】【分析】根据百分位数的定义即可判断A ；根据正态曲线的性质即可判断B ；根据方差的性质即可判断C ；根据观测值与预测值的区别即可判断D.【详解】对于A ，数据按照从小到大的顺序排列为2,3,5,7,10，为因为540%2⨯=，所以数据7，5，3，10，2的第40百分位数是3542+=，故A 错误； 对于B ，σ越小，即方差越小，随机变量X 分布越集中，故B 正确； 对于C ，已知一组数据12,,,n x x x 的方差为3，则1231,1,1,,1n x x x x ---- 的方差为2133⨯=，故C 正确；对于D ，散点(),0.28m -不一定在回归直线为ˆ0.3yx m =-上， 所以由散点(),0.28m -无法求出m 值，故D 错误. 故选：BC.10. 已知 ABC 的内角,,A B C 的对边分别为,,a b c2sin sin 2A Cb A +⋅=⋅，下列结论正确的是（ ） A. π3B =B. 若 45a b ==， ，则 ABC 有两解C.当a c -=时， ABC 为直角三角形 D. 若 ABC 为锐角三角形，则 cos cos A C +的取值范围是 【答案】ACD 【解析】【分析】通过正弦定理、诱导公式、二倍角公式及辅助角公式即可判断A ；通过余弦定理即可判断B ；通过余弦定理及a c -=可得2a c =或2c a =，即可判断C ；通过求A 的取值范围ππ62A <<，并将πcos cos sin(6A C A +=+即可判断D.【详解】对于A2sin sin 2A C b A +⋅=⋅，所以由πA B C ++=2πsin sin sin 2BA B A -⋅=⋅，2cos sin sin 2BA B A ⋅=⋅，的因为(0,π)A ∈，故sin 0A ≠22sin cos 222B B B =，化解得coscos )0222B B B -=，即πcos sin()0226B B -=， 所以cos 02B =或πsin(026B -=，即B π=（舍）或π3B =，故A 正确； 对于B ，由余弦定理得2222cos b a c ac B =+-，即21251682c c =+-⨯⨯，得2490c c --=， 由2(4)4(9)520∆=--⨯-=>，所以2c =+负值舍)，即ABC 有一解，故B 错误；对于C，因为a c -=，两边平方得22223b a ac c -+=， 由余弦定理得222222cos b a c ac B a c ac =+-=+-，由两式消2b 得，222520a ac c -+=，解得2a c =或2c a =，由π23B a c b ===，，解得π2A ∠=，由π23B c a b ===，，解得π2C ∠=; 故ABC 为直角三角形，故C 正确；对于D ，因为ABC 为锐角三角形，且π3B =， 所以ππ00ππ222πππ6200322A A A AC ⎧⎧<<<<⎪⎪⎪⎪⇒⇒<<⎨⎨⎪⎪<-<<<⎪⎪⎩⎩，即2π1πcos cos cos cos()cos sin()326A C A A A A A +=+-=+=+， 所以ππ2π(,)633A +∈，所以πsin()6A +∈，故D 正确. 故选：ACD.11. 在棱长为 1 的正方体1111ABCD A B C D -中，已知E F 、分别为线段111B C D C ，的中点，点P 满足[][]10,1,0,1DP DD DB λμλμ=+∈∈ ，，则（ ）A. 当1λμ+=时，三棱锥D PEF -的体积为定值B. 当12λμ==，四棱锥P ABCD -的外接球的表面积是9π4C. PEF !12D. 若AP =，则点P 的轨迹长为π2 【答案】ABD【解析】【分析】A 选项，先得到1BP BD λ= ，故点P 在线段1D B 上，证明出1//D B EF ，所以三棱锥D PEF-为定值；B 选项，点P 为线段1D B 的中点，作出辅助线，找到外接球球心，从而得到外接球半径和外接球面积；C 选项，取线段11A D 的中点1F ，由对称性知，1PF PF =，数形结合得到11PF PE PF PE F E ∴+=+≥=，从而得到周长的最小值；D 选项，由AP =得到点P 的轨迹为以Q 为圆心，半径为1的圆的一部分，求出圆的半径，得到轨迹长度.【详解】A 选项，当1λμ+=时，()111DP DD DB DP DD DB λμλλ=+⇒=+- ，故()1DP DB DD DB λ-=- ，即1BP BD λ= ， 故点P 在线段1D B 上，连接1BC ，与1B C 相交于点E ，则E 为1BC 的中点，连接EF ，因为F 为11D C 的中点，所以1//D B EF ，故三棱锥D PEF -的体积为定值，A 正确；B 选项，当12λμ==时，由A 选项可知，112BP BD = ，点P 为线段1D B 的中点，连接,AC BD 相交于点Q ，则PQ ⊥平面ABCD ，设正四棱锥P ABCD -的外接球的球心为T ，则,,P Q T 三点共线，其中1,2PQ CQ ==，设PT TC r ==，则12TQ r =-， 由勾股定理得222TC TQ CQ =+，即221122r r ⎛⎫=-+ ⎪⎝⎭， 解得34r =， 则表面积是29π4r =，B 正确； C 选项，点P 在矩形11D B BD 及其内部，取线段11A D 的中点1F ， 由对称性知，1PF PF =，11PF PE PF PE F E ∴+=+≥=，此时1,,E F P 三点共线，又112EF BD ==PF PE FE ∴++≥，C 错误；D 选项，因为AP = ，又点P 在矩形11D B BD 及其内部，∴点P 的轨迹为点A 11D B BD 截且在矩形11D B BD 及其内部的图形，又AQ ⊥平面11BDD B ，且AQ =，故1PQ == ， 所以点P 的轨迹为以Q 为圆心，半径为1的圆的一部分，如图，其中1JQ MQ ==，DQ DB ==故JD MB === 则45JQD MQB ∠=∠=︒，则90JQM ∠=︒，则轨迹长为1π2π142⨯⋅=，D 正确. 故选：ABD【点睛】解决与球有关的内切或外接的问题时，解题的关键是确定球心的位置．对于外切的问题要注意球心到各个面的距离相等且都为球半径；对于球的内接几何体的问题，注意球心到各个顶点的距离相等，解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形，利用勾股定理求得球的半径第II 卷三、填空题：本题共3小题，每小题5分，共15分.12. 已知圆台的上底面半径为1，下底面半径为5，侧面积为30π，则圆台的高为_________.【答案】3【解析】【分析】根据圆台的侧面积求圆台的母线，再根据圆台轴截面求出高即可.【详解】因为圆台的上底面半径为1，下底面半径为5，侧面积为30π ，设母线长为l ，高为h .则π(15)30πl +⨯=，解得5l =.如图所示圆台的轴截面，在BED 中，||4,||5ED BD ==，由勾股定理得：圆台的高3h =.故答案为：3.13. 甲、乙、丙 3 人站到共有 6 级的台阶上， 若每级台阶最多站 2 人且甲、乙不站同一个台阶，同一台阶上的人不区分站的位置，则不同的站法种数是_____________种. (用数字作答)【答案】180【解析】【分析】采用分步乘法计数原理计算即可.【详解】易知甲有6种站法，则乙有5种站法，丙有6种站法，总共有656180⨯⨯=种.故答案为：18014. 已知关于x 的不等式()()2ln 22110x ax x a x ⎡⎤--++≤⎣⎦对任意 ()0,x ∞∈+ 恒成立，则实数 a 的取值范围是___________________. 【答案】11,2e 2⎡⎤⎢⎥⎣⎦ 【解析】【分析】将原不等式转化为2ln 21x ax x x ≤≤-+恒成立，画出函数ln y x =与21,0y x x x =-+>的图像，求出过原点且与函数ln y x =，21,0y x x x =-+>分别相切时直线的斜率，根据数形结合可得结果.【详解】不等式可化为()()22ln 210ax x ax x x ⎡⎤---+≤⎣⎦，令()2ln 1,0y x x x x =--+>，因为()()211121x x y x x x+-'=-+=-， 令001y x >⇒<<'，所以函数()2ln 1y x x x =--+在()0,1上为增函数， 令01y x '<⇒>，所以函数()2ln 1y x x x =--+在()1,+∞上为减函数， 所以当1x =时max 10y =-<，即当()0,x ∈+∞时0y <，所以()2ln 1x x x <-+， 所以2ln 21x ax x x ≤≤-+设1k 为过原点且与ln y x =相切的直线的斜率，设切点()00,x y ， 则001001x x y k y x x ===='，所以01y =，又00ln 1y x ==，所以0e x =，所以11ek =， 设2k 为过原点且与21,0y x x x =-+>相切的直线的斜率，设切点()11,x y ， 则1121121x x y k y x x ===-'=，且21111y x x =-+，解得11x =或11x =-（舍去），所以21k =， 画出函数ln y x =与21,0y x x x =-+>的图像，如图：数形结合可得，121221e k a k a ≤≤⇒≤≤，所以112e 2a ≤≤， 故答案为：11,2e 2⎡⎤⎢⎥⎣⎦. .【点睛】关键点点睛：本题关键点是将原不等式转化为2ln 21x ax x x ≤≤-+恒成立，根据数形结合，将问题转化为过原点且与函数ln y x =，21,0y x x x =-+>分别相切时直线的斜率，从而得结果.四、解答题: 本题共 5 小题， 共 77 分. 解答应写出文字说明、证明过程或验算步骤. 15. 已知等差数列 {}n a 的公差不为零， 125,,a a a 成等比数列，且 221n n a a =+ .（1）求数列 {}n a 的通项公式;（2）求 13521n a a a a -++++ .【答案】（1）21n a n =-（2）22n n -【解析】【分析】（1）根据等差数列基本量的计算即可求解，（2）根据等差数列求和公式即可求解.【小问1详解】由题意 221121211n n a a a a d a =+⇒=+⇒=+ (1)()()()222151111422.a a a a d a a d d a =⋅⇒+=+⇒= 由(1)(2)可得 112a d ==，所以 ()11221n a n n =+-⋅=-【小问2详解】()21221143n a n n -=--=-，2347n a n -=-，21234n n a a ---=，故{}21n a -为等差数列， ()12121352122n n n a a n a a a a n a n n --+⋅++++==⋅=- .16. 已知四面体,2,A BCD AB AD BC CD AC -=====（1）证明：AC BD ⊥;（2）若BD =AB 与平面ACD 所成角的正弦值.【答案】（1）证明见解析（2【解析】【分析】（1）根据题意可知,BD AM BD CM ⊥⊥，结合线面垂直的判定定理分析证明；（2）方法1：根据题意可知：平面BCD ⊥平面ACM ，作辅助线，可知AH ⊥平面BCD ，利用等体积法求点B 到平面ACD 的距离为，结合线面夹角的定义分析求解；方法2：根据题意可知：平面BCD ⊥平面ACM ，作辅助线，可知AH ⊥平面BCD ，建系，利用空间向量求线面夹角.【小问1详解】取BD 的中点M ，连,AM CM ，由AB AD BC BD ===，可得,BD AM BD CM ⊥⊥，又因为AM CM M ⋂=，AM CM ⊂、平面ACM ，所以BD ⊥ 平面 ACM ，因为AC ⊂平面ACM ，所以AC BD ⊥.【小问2详解】方法1：因为BD =，所以1AM CM ==，又因为AC =120AMC ∠= ，由（1）可得BD ⊥平面ACM ，所以平面BCD ⊥平面ACM ，作AH CM ⊥交CM 延长线于点H ，则AH ⊥平面BCD 且AH =，设点B 到平面ACD 的距离为h ，因为B ACD A BCD V V --=，则1133ACD BCD S h S ⋅= ，可得h ==， 设直线AB 与平面ACD 所成角为θ，可得sin h AB θ==， 所以直线AB 与平面ACD 取成线面角； 方法2：因为BD =，所以1AM CM ==，又因为AC =120AMC ∠= ，由（1）可得BD ⊥平面ACM ，且BD ⊂平面BCD ，所以平面BCD ⊥平面ACM ，作AH CM ⊥交CM 延长线于点H ，则AH ⊥平面BCD且AH =， 如图，以MB 为x 轴，MC 为y 轴，z 轴//AH 建立空间直角坐标系，的则)()()10,,,0,1,0,2A B C D ⎛- ⎝，可得)310,,,,,22AC DC AB ⎛=== ⎝ ，设平面ACD 的一个法向量为(),,n x y z =，则3020n AC y z n DC y ⎧⋅==⎪⎨⎪⋅=+=⎩ ， 令1x =，则3==-y z，可得()1,3n =- ， 设直线AB 与平面ACD 所成角为θ，可得sin cos ,AB n AB n AB nθ⋅====⋅ ， 所以直线AB 与平面ACD. 17. 为了增强身体素质，寒假期间小王每天坚持在 “跑步20 分钟”和“跳绳20 分钟” 中选择一项进行锻炼. 在不下雪的时候，他跑步的概率为80%，跳绳的概率为20%，在下雪天他跑步的概率为20%，跳绳的概率为80%. 若前一天不下雪，则第二天下雪的概率为60%，若前一天下雪，则第二天仍下雪的概率为40%. 已知寒假第一天不下雪，跑步20分钟大约消耗能量300卡路里，跳绳20分钟大约消耗能量200卡路里. 记寒假第n 天不下雪的概率为n P .（1）求123P P P 、、的值，并求n P; （2）设小王寒假第n 天通过运动消耗的能量为X ，求X 的数学期望.【答案】（1）12310.40.52P P P ===，，，1111225n n P -⎛⎫=+⋅- ⎪⎝⎭（2）11250305n -⎛⎫+- ⎪⎝⎭【解析】 【分析】（1）由题意得到123,,P P P ，且得到()110.40.61n n n P P P --=+-，利用构造法得到12n P⎧-⎫⎨⎬⎩⎭为等比数列，从而求出通项公式；（2）求出200300X =，，及对应的概率，得到X 的数学期望.【小问1详解】由题意得121,10.40.4P P ==⨯=，第3天不下雪，分为两种情况，第2天不下雪且第三天不下雪，第2天下雪且第3天不下雪，故30.40.40.60.60.52P =⨯+⨯=，依题意()111130.40.6155n n n n P P P P ---=+-=-+， 整理得1111252n n P P -⎛⎫-=-- ⎪⎝⎭， 所以12n P ⎧-⎫⎨⎬⎩⎭是以11122P -=为首项，15-为公比的等比数列， 即1111225n n P -⎛⎫-=⋅- ⎪⎝⎭，所以1111225n n P -⎛⎫=+⋅- ⎪⎝⎭；【小问2详解】 200300X =，，由（1）得()()3000.80.210.60.2n n n P X P P P ==+-=+，则他第n 天通过运动锻炼消耗的能量X 的期望为()()()3003002001300P X P X =+-=()1120010030022060250305n n P X P -⎛⎫=+==+=+- ⎪⎝⎭ .18. 已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为 12F F 、 ，焦距为 直线 :l y x m =+ 与椭圆交于 A B 、 两点 （其中点 A 在 x 轴上方，点 B 在 x 轴下方）.（1）求椭圆 C 的标准方程;（2）如图，将平面 xOy 沿 x 轴折叠，使 y 轴正半轴和 x 轴所确定的半平面（平面 12A F F '）与 y 轴 负半轴和 x 轴所确定的半平面 (平面 12B F F ' ) 垂直.①若折叠后 OA OB '⊥' ，求 m 的值;②是否存在 m ，使折叠后 A B ''、 两点间的距离与折叠前 A B 、 两点间的距离之比为34? 【答案】（1）2214x y += （2）①1m =±；②不存在【解析】【分析】（1）由焦距为，可得出c和222a b c =+可得出a 与b 的值，从而求得椭圆的标准方程；（2）①联立直线方程与椭圆方程，由直线和椭圆有两个交点且两个交点在x 轴两侧，利用韦达定理求出m 范围，然后建立空间直角坐标系，根据条件OA OB '⊥'，得出0OA OB ''⋅= ，即可得出m 值；②分别表示出折叠前A B 、间的距离和折叠后A B ''、间的距离，根据题目中距离的比值列方程求解m ，再判断其是否满足条件即可.【小问1详解】由题意222c a a c b c =+==，解得：21a b ==，， 所以椭圆 C 的标准方程为 2214x y += 【小问2详解】折叠前设 ()()1122A x y B x y ，，， ，联立2214y x m x y =+⎧⎪⎨+=⎪⎩ 可得()2258410x mx m ++-=的由直线 y kx m =+ 与椭圆交于不同两点，所以 0∆> ，解得 25m < ， 由韦达定理得：()221212418,55m m x x x x -+=-⋅=，因为 AB 位于 x 轴两侧，所以120y y ⋅<，化简得 24m < ，从而 22m -<< ，以 O 为坐标原点，折叠后，分别以原 y 轴负半轴，原 x 轴，原 y 轴正半轴所在直线为 x y z ，， 轴建立空间直角坐标系，则折叠后()()11220,,,,,0A x y B y x ''-①折叠后 OA OB '⊥' ，则 0OA OB ''⋅= ，即120x x ⋅= ，所以21,1m m ==±②折叠前2AB x =-==，折叠后A B '=='==34=，解得 2152m = ，此时直线 l 与椭圆无交点， 故不存在 m ，使折叠后的 A B '' 与折叠前的 AB 长度之比为 34.【点睛】关键点点睛：本题解题的关键是找到折叠前后的联系，建立空间直角坐标系，设出点的坐标，利用空间向量的知识求解.19. 在平面直角坐标系中，如果将函数()y f x =的图象绕坐标原点逆时针旋转π(0)2αα<£后，所得曲线仍然是某个函数的图象，则称()f x 为“α旋转函数”.（1）判断函数y =是否为“π6旋转函数”，并说明理由； （2）已知函数()()()ln 210f x x x =+>是“α旋转函数”，求tan α的最大值；（3）若函数()()21e ln 2xx g x m x x x =---是“π4旋转函数”，求m 的取值范围. 【答案】（1）不是，理由见解析（2）12（3）e m ≥【解析】【分析】（1）根据函数的定义直接判断即可.（2）将已知条件转化为函数与直线y kx b =+最多一个交点，利用两个函数图象的交点与对应方程根的关系，分离b ，构造新函数，转化为新函数在()0+∞，上单调，进而求解. （3）同问题（2）根据已知条件构造新函数，转化为新函数在()0+∞，上单调，求导，分离参数，转化为恒成立问题求最值即可.【小问1详解】函数y =不是“π6旋转函数”，理由如下：y =逆时针旋转π6后与y 轴重合， 当0x =时，有无数个y 与之对应，与函数的概念矛盾，因此函数y =不是“π6旋转函数”. 【小问2详解】由题意可得函数()()()ln 210f x x x =+>与函数y kx b =+最多有1个交点， 且πtan 2k α⎛⎫=- ⎪⎝⎭， 所以()()ln 210x kx b x +=+>最多有一个根，即()()ln 210x kx b x +-=>最多有一个根，因此函数()()ln 210y x kx x =+->与函数(y b b =∈R )最多有1个交点，即函数()ln 21y x kx =+-在()0,∞+上单调，因为221y k x =-+'，且()20,0,221x x >∈+， 所以220,2121y k k x x =-≤≥++'，所以2k ≥， 即πtan 22α⎛⎫-≥ ⎪⎝⎭，1tan 2α≤，即tan α的最大值为12. 【小问3详解】由题意可得函数()()21e ln 2xx g x m x x x =---与函数y x b =+最多有1个交点， 即()()221e ln 1e ln 22xx x x m x x x x b m x x x x b ---=+⇒----=， 即函数()21e ln 2xx y m x x x x =----与函数y b =最多有1个交点， 即函数()21e ln 2xx y m x x x x =----在()0,∞+上单调， e ln 2x y mx x x =---'，当0x →时，y '→+∞，所以maxln 20e x x x y m x '++⎛⎫≥⇒≥ ⎪⎝⎭， 令()ln 2e x x x x x ϕ++=，则()()()2n e 1l 1xx x x x x ϕ+-'--=， 因为ln 1t x x =---在()0,∞+上单调减，且()10104t t ⎛⎫><⎪⎝⎭，， 所以存在01,14x ⎛⎫∈ ⎪⎝⎭，使()00t x =， 即()0000001ln 1ln e 1e ex x x x x x +=-⇒⋅=-⇒⋅=， 所以()x ϕ在()00,x 单调递增，()0,x +∞单调递减，所以()()0000max 000ln 21e e ex x x x x x x x ϕϕ++====， 即e m ≥.【点睛】方法点睛：利用函数的零点与对应方程的根的关系，我们经常进行灵活转化：函数()()y f x g x =-的零点个数⇔方程()()0f x g x -=的根的个数⇔函数()y f x =与()y g x =图象的交点的个数；另外，恒成立求参数范围问题往往分离参数，构造函数，通过求构造函数的最值来求出参数范围，例：若(,),()x a b m f x ∀∈≥恒成立，只需max ()m f x ≥，(,),()x a b m f x ∀∈≤恒成立，只需min ()m f x ≤.。
2020届河南省郑州市高考数学三模试卷(理科)有答案(加精)
2019年河南省郑州市高考第三次模拟考试数学试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设命题p：∀x＞0，log2x＜2x+3，则￢p为（）A．∀x＞0，log2x≥2x+3 B．∃x＞0，log2x≥2x+3C．∃x＞0，log2x＜2x+3 D．∀x＜0，log2x≥2x+32．已知复数m=4﹣xi，n=3+2i，若复数∈R，则实数x的值为（）A．﹣6 B．6 C．D．﹣3．已知双曲线+=1，焦点在y轴上，若焦距为4，则a等于（）A．B．5 C．7 D．4．已知，则的值等于（）A．B．C．D．5．设集合A={x1，x2，x3，x4}，x i∈{﹣1，0，1}，i={1，2，3，4}，那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为（）A．60 B．65 C．80 D．816．如图是某个几何体的三视图，则这个几何体体积是（）A．B．C．D．7．设实数x，y满足，则2xy的最大值为（）A．25 B．49 C．12 D．248．已知等比数列{a n}，且a6+a8=，则a8（a4+2a6+a8）的值为（）A．π2B．4π2C．8π2D．16π29．若实数a、b、c∈R+，且ab+ac+bc+2，则2a+b+c的最小值为（）A．B．C．D．10．椭圆+=1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（）A．B．C．D．11．四面体A﹣BCD中，AB=CD=10，AC=BD=2，AD=BC=2，则四面体A﹣BCD外接球的表面积为（）A．50π B．100πC．200πD．300π12．设函数f（x）满足2x2f（x）+x3f'（x）=e x，f（2）=，则x∈，求函数h（x）的最小值；（2）对任意x∈=﹣cos（+2θ）=﹣cos2（+θ）=﹣=﹣，解得：sin2（+θ）=，∴=±．故选：B．5．设集合A={x1，x2，x3，x4}，x i∈{﹣1，0，1}，i={1，2，3，4}，那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为（）A．60 B．65 C．80 D．81【考点】1A：集合中元素个数的最值．【分析】将x的取值分为两组：M={0}，N={﹣1，1}，A中的四个元素中有1个取值为0，2个取值为0，个取值为0，4个取值为0，进行分类讨论，由此能求出集合A中满足条件“x12+x22+x32+x42≤3”的元素个数．【解答】解：集合A={x1，x2，x3，x4}，x i∈{﹣1，0，1}，i={1，2，3，4}，集合A满足条件“x12+x22+x32+x42≤3”，设M={0}，N={﹣1，1}，①A中的四个元素中有1个取值为0，另外3个从M中取，取法总数有： =32，②A中的四个元素中有2个取值为0，另外2个从M中取，取法总数有： =24，③A中的四个元素中有3个取值为0，另外1个从M中取，取法总数有： =8，④A中的四个元素中有4个取值为0，取法总数有： =1，∴集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为：32+24+8+1=65．故选：B．6．如图是某个几何体的三视图，则这个几何体体积是（）A．B．C．D．【考点】L!：由三视图求面积、体积．【分析】由三视图可知：该几何体由一个半圆柱与三棱柱组成的几何体．【解答】解：由三视图可知：该几何体由一个半圆柱与三棱柱组成的几何体．这个几何体体积V=+×（）2×2=2+．故选：A．7．设实数x，y满足，则2xy的最大值为（）A．25 B．49 C．12 D．24【考点】7C：简单线性规划．【分析】作出不等式组对应的平面区域，利用基本不等式进行求解即可．【解答】解：作出不等式组对应的平面区域如图：由图象知y≤10﹣2x，则2xy≤2x（10﹣2x）=4x（5﹣x））≤4（）2=25，当且仅当x=，y=5时，取等号，经检验（，5）在可行域内，故2xy的最大值为25，故选：A．8．已知等比数列{a n}，且a6+a8=，则a8（a4+2a6+a8）的值为（）A．π2B．4π2C．8π2D．16π2【考点】67：定积分．【分析】先根据定积分的几何意义求出a6+a8==4π，再根据等比数列的性质即可求出．【解答】解：表示以原点为圆心以4为半径的圆的面积的四分之一，故a6+a8==4π，∴a8（a4+2a6+a8）=a8a4+2a8a6+a82=a62+2a8a6+a82=（a6+a8）2=16π2．故选：D9．若实数a、b、c∈R+，且ab+ac+bc+2，则2a+b+c的最小值为（）A．B．C．D．【考点】RB：一般形式的柯西不等式．【分析】因为（2a+b+c）2=4a2+b2+c2+4ab+2bc+4ca，与已知等式比较发现，只要利用均值不等式b2+c2≥2bc 即可求出结果．【解答】解：∵ab+ac+bc+2，∴a2+ab+ac+bc=6﹣2（6﹣2）×4=（a2+ab+ac+bc）×4=4a2+4ab+4ac+4bc≤4a2+4ab+b2+c2+4ca+2bc=（2a+b+c）2，所以2a+b+c≥2﹣2，故选D．10．椭圆+=1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（）A．B．C．D．【考点】K4：椭圆的简单性质．【分析】设右焦点为F′，连接MF′，NF′，由于|MF′|+|NF′|≥|MN|，可得当直线x=a过右焦点时，△FMN的周长最大．c==1．把c=1代入椭圆标准方程可得： =1，解得y，即可得出此时△FMN的面积S．【解答】解：设右焦点为F′，连接MF′，NF′，∵|MF′|+|NF′|≥|MN|，∴当直线x=a过右焦点时，△FMN的周长最大．由椭圆的定义可得：△FMN的周长的最大值=4a=4．c==1．把c=1代入椭圆标准方程可得： =1，解得y=±．∴此时△FMN的面积S==．故选：C．11．四面体A﹣BCD中，AB=CD=10，AC=BD=2，AD=BC=2，则四面体A﹣BCD外接球的表面积为（）A．50π B．100πC．200πD．300π【考点】LE：棱柱、棱锥、棱台的侧面积和表面积．【分析】由题意可采用割补法，考虑到四面体ABCD的四个面为全等的三角形，所以可在其每个面补上一个以10，2，2为三边的三角形作为底面，且以分别为x，y，z，长、两两垂直的侧棱的三棱锥，从而可得到一个长、宽、高分别为x，y，z的长方体，由此能求出球的半径，进而求出球的表面积．【解答】解：由题意可采用割补法，考虑到四面体ABCD的四个面为全等的三角形，所以可在其每个面补上一个以10，2，2为三边的三角形作为底面，且以分别为x，y，z，长、两两垂直的侧棱的三棱锥，从而可得到一个长、宽、高分别为x，y，z的长方体，并且x2+y2=100，x2+z2=136，y2+z2=164，设球半径为R，则有（2R）2=x2+y2+z2=200，∴4R2=200，∴球的表面积为S=4πR2=200π．故选C．12．设函数f（x）满足2x2f（x）+x3f'（x）=e x，f（2）=，则x∈=e2﹣=（x﹣2），当x∈．【考点】9H：平面向量的基本定理及其意义．【分析】根据题意画出图形，结合图形，设外接圆的半径为r，对=p+q两边平方，建立p、q的解析式，利用基本不等式求出p+q的取值范围．【解答】解：如图所示，△ABC中，∠A=，∴∠BOC=；设|=r，则O为△ABC外接圆圆心；∵=p+q，∴==r2，即p2r2+q2r2+2pqr2cos=r2，∴p2+q2﹣pq=1，∴（p+q）2=3pq+1；又M为劣弧AC上一动点，∴0≤p≤1，0≤q≤1，∴p+q≥2，∴pq≤=，∴1≤（p+q）2≤（p+q）2+1，解得1≤（p+q）2≤4，∴1≤p+q≤2；即p+q的取值范围是．故答案为：．三、解答题（本大题共7小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．在△ABC中，角A、B、C所对的边分别是a、b、c，已知sinB+sinC=msinA（m∈R），且a2﹣4bc=0．（1）当a=2，时，求b、c的值；（2）若角A为锐角，求m的取值范围．【考点】HR：余弦定理．【分析】（1）sinB+sinC=msinA（m∈R），利用正弦定理可得：b+c=ma，且a2﹣4bc=0．a=2，时，代入解出即可得出．（2）利用余弦定理、不等式的解法即可得出．【解答】解：（1）由题意得b+c=ma，a2﹣4bc=0．当时，，bc=1．解得．（2）．∴，又由b+c=ma可得m＞0，所以．18．为了研究学生的数学核素养与抽象（能力指标x）、推理（能力指标y）、建模（能力指标z）的相关性，并将它们各自量化为1、2、3三个等级，再用综合指标w=x+y+z的值评定学生的数学核心素养；若w≥7，则数学核心素养为一级；若5≤w≤6，则数学核心素养为二级；若3≤w≤4，则数学核心素养为三级，为了了解某校学生的数学核素养，调查人员随机访问了某校10名学生，得到如下结果：（2）从数学核心素养等级是一级的学生中任取一人，其综合指标为a，从数学核心素养等级不是一级的学生中任取一人，其综合指标为b，记随机变量X=a﹣b，求随机变量X的分布列及其数学期望．【考点】CH：离散型随机变量的期望与方差；CG：离散型随机变量及其分布列．【分析】（1）由题可知：建模能力一级的学生是A9；建模能力二级的学生是A2，A4，A5，A7，A10；建模能力三级的学生是A1，A3，A6，A8．记“所取的两人的建模能力指标相同”为事件A，利用互斥事件与古典概率计算公式即可得出，P（A）．（2）由题可知，数学核心素养一级：A1，A2，A3，A5，A6，A8，数学核心素养不是一级的：A4，A7，A9，A10；X 的可能取值为1，2，3，4，5．利用相互独立事件、互斥事件与古典概率计算公式即可得出P（X=k）及其分布列与数学期望．【解答】解：（1）由题可知：建模能力一级的学生是A9；建模能力二级的学生是A2，A4，A5，A7，A10；建模能力三级的学生是A1，A3，A6，A8．记“所取的两人的建模能力指标相同”为事件A，则．（2）由题可知，数学核心素养一级：A1，A2，A3，A5，A6，A8，数学核心素养不是一级的：A4，A7，A9，A10；X的可能取值为1，2，3，4， 5.；；；；．∴随机变量X的分布列为：∴=．19．如图，在四边形ABCD中，AB∥CD，∠BCD=，四边形ACFE为矩形，且CF⊥平面ABCD，AD=CD=BC=CF．（1）求证：EF⊥平面BCF；（2）点M在线段EF上运动，当点M在什么位置时，平面MAB与平面FCB所成锐二面角最大，并求此时二面角的余弦值．【考点】MT：二面角的平面角及求法；LW：直线与平面垂直的判定．【分析】（1）在梯形ABCD中，设AD=CD=BC=1，由题意求得AB=2，再由余弦定理求得AC2=3，满足AB2=AC2+BC2，得则BC⊥AC．再由CF⊥平面ABCD得AC⊥CF，由线面垂直的判定可得AC⊥平面BCF．进一步得到EF⊥平面BCF；（2）分别以直线CA，CB，CF为x轴，y轴，z轴建立如图所示的空间直角坐标系，设AD=CD=BC=CF=1，令FM=λ（），得到C，A，B，M的坐标，求出平面MAB的一个法向量，由题意可得平面FCB的一个法向量，求出两法向量所成角的余弦值，可得当λ=0时，cosθ有最小值为，此时点M与点F重合．【解答】（1）证明：在梯形ABCD中，∵AB∥CD，设AD=CD=BC=1，又∵，∴AB=2，∴AC2=AB2+BC2﹣2AB•BC•cos60°=3．∴AB2=AC2+BC2．则BC⊥AC．∵CF⊥平面ABCD，AC⊂平面ABCD，∴AC⊥CF，而CF∩BC=C，∴AC⊥平面BCF．∵EF∥AC，∴EF⊥平面BCF；（2）解：分别以直线CA，CB，CF为x轴，y轴，z轴建立如图所示的空间直角坐标系，设AD=CD=BC=CF=1，令FM=λ（），则C（0，0，0），A（，0，0），B（0，1，0），M（λ，0，1），∴=（﹣，1，0），=（λ，﹣1，1），设=（x，y，z）为平面MAB的一个法向量，由得，取x=1，则=（1，，），∵=（1，0，0）是平面FCB的一个法向量，∴cos＜＞==．∵，∴当λ=0时，cosθ有最小值为，∴点M与点F重合时，平面MAB与平面FCB所成二面角最大，此时二面角的余弦值为．20．已知圆C1：x2+y2=r2（r＞0）与直线l0：y=相切，点A为圆C1上一动点，AN⊥x轴于点N，且动点M满足，设动点M的轨迹为曲线C．（1）求动点M的轨迹曲线C的方程；（2）若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O，求线段PQ长度的取值范围．【考点】KP：圆锥曲线的范围问题；J3：轨迹方程；KL：直线与椭圆的位置关系．【分析】（1）设动点M（x，y），A（x0，y0），由于AN⊥x轴于点N．推出N（x0，0）．通过直线与圆相切，求出圆的方程，然后转化求解曲线C的方程．（2）①假设直线l的斜率存在，设其方程为y=kx+m，设P（x1，y1），Q（x2，y2），联立直线与椭圆方程，结合韦达定理，通过，以及弦长公式，利用基本不等式求出范围．②若直线l的斜率不存在，设OP所在直线方程为y=x，类似①求解即可．【解答】解：（I）设动点M（x，y），A（x0，y0），由于AN⊥x轴于点N．∴N（x0，0）．又圆与直线即相切，∴．∴圆．由题意，，得，∴．∴，即∴将代入x2+y2=9，得曲线C的方程为．（II）（1）假设直线l的斜率存在，设其方程为y=kx+m，设P（x1，y1），Q（x2，y2），联立，可得（1+2k2）x2+4kmx+2m2﹣8=0．由求根公式得．（*）∵以PQ为直径的圆过坐标原点O，∴．即．∴x1x2+y1y2=0．即∴x1x2+（kx1+m）（kx2+m）=0．化简可得，．将（*）代入可得，即3m2﹣8k2﹣8=0．即，又．将代入，可得=．∴当且仅当，即时等号成立．又由，∴，∴．（2）若直线l的斜率不存在，因以PQ为直径的圆过坐标原点O，故可设OP所在直线方程为y=x，联立解得，同理求得，故．综上，得．21．已知函数f（x）=（x+a）ln（x+a），g（x）=﹣+ax．（1）函数h（x）=f（e x﹣a）+g'（e x），x∈，求函数h（x）的最小值；（2）对任意x∈上h'（x）≥0，h（x）递增，h（x）的最小值为．②当﹣1＜a﹣1＜1即0＜a＜2时，在x∈上h'（x）≤0，h（x）为减函数，在在x∈上h'（x）≥0，h（x）为增函数．∴h（x）的最小值为h（a﹣1）=﹣e a﹣1+a．③当a﹣1≥1即a≥2时，在上h'（x）≤0，h（x）递减，h（x）的最小值为h（1）=（1﹣a）e+a．综上所述，当a≤0时h（x）的最小值为，当0＜a＜2时h（x）的最小值为﹣e a﹣1+a，当a≥2时，h （x）最小值为（1﹣a）e+a．（II）设，F'（x）=ln（x﹣1）+1+a（x﹣1）（x≥2）．①当a≥0时，在x∈[2，+∞）上F'（x）＞0，F（x）在x∈[2，+∞）递增，F（x）的最小值为F（2）=0，不可能有f（x﹣a﹣1）﹣g（x）≤0．②当a≤﹣1时，令，解得：，此时∴．∴F'（x）在[2，+∞）上递减．∵F'（x）的最大值为F'（2）=a+1≤0，∴F（x）递减．∴F（x）的最大值为F（2）=0，即f（x﹣a﹣1）﹣g（x）≤0成立．③当﹣1＜a＜0时，此时，当时，F''（x）＞0，F'（x）递增，当时，F''（x）＜0，F'（x）递减．∴=﹣ln（﹣a）＞0，又由于F'（2）=a+1＞0，∴在上F'（x）＞0，F（x）递增，又∵F（2）=0，所以在上F（x）＞0，显然不合题意．综上所述：a≤﹣1．22．以直角坐标系的原点O为极点，x轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线l的参数方程为，（t为参数，0＜θ＜π），曲线C的极坐标方程为ρsin2θ﹣2cosθ=0．（1）求曲线C的直角坐标方程；（2）设直线l与曲线C相交于A，B两点，当θ变化时，求|AB|的最小值．【考点】QH：参数方程化成普通方程；Q4：简单曲线的极坐标方程．【分析】（1）利用极坐标与直角坐标的转化方法，求曲线C的直角坐标方程；（2）将直线l的参数方程代入y2=2x，得t2sin2θ﹣2tcosθ﹣1=0，利用参数的几何意义，求|AB|的最小值．【解答】解：（1）由ρsin2θ﹣2cosθ=0，得ρ2sin2θ=2ρcosθ．∴曲线C的直角坐标方程为y2=2x；（2）将直线l的参数方程代入y2=2x，得t2sin2θ﹣2tcosθ﹣1=0．设A，B两点对应的参数分别为t1，t2，则，，==．当时，|AB|的最小值为2．23．已知函数f（x）=|x﹣5|﹣|x﹣2|．（1）若∃x∈R，使得f（x）≤m成立，求m的范围；（2）求不等式x2﹣8x+15+f（x）≤0的解集．【考点】R5：绝对值不等式的解法．【分析】（1）通过讨论x的范围，求出f（x）的分段函数的形式，求出m的范围即可；（2）通过讨论x的范围，求出不等式的解集即可．【解答】解：（1），当2＜x＜5时，﹣3＜7﹣2x＜3，所以﹣3≤f（x）≤3，∴m≥﹣3；（2）不等式x2﹣8x+15+f（x）≤0，即﹣f（x）≥x2﹣8x+15由（1）可知，当x≤2时，﹣f（x）≥x2﹣8x+15的解集为空集；当2＜x＜5时，﹣f（x）≥x2﹣8x+15，即x2﹣10x+22≤0，∴；当x≥5时，﹣f（x）≥x2﹣8x+15，即x2﹣8x+12≤0，∴5≤x≤6；综上，原不等式的解集为．。
2020年湖南省邵阳市高考数学第三次联考试卷（三模）（含答案解析）
2020年湖南省邵阳市高考数学第三次联考试卷（三模）一、选择题（本大题共12小题，共60.0分）1.复数z满足(l-i)z= |2+2i|,则z=()A.l-iB.1+ i CZ-回 D. ^2+yj2i2.设集合A=(%|x2<2%),B=(x|l<x<4),则AU B=()A.(一8,4)B.[0,4]C. (1,2]D.(1,+co)3.已知&是等差数列｛%｝的前项和，若ag.=S2ois=2015,则首项角=()A.2015B.-2015C.2013D. -20134.己知双的线。
§一荃=1的左、右焦点分别为F19F29P为C上一点,瓦6=亦・。
为坐标原点,若|PFJ=10,则\OQ\=()5.A.10 B.1或9执行如图所示的程序框图，若输出的S=A.i>2014B.i>2014c.i>2015D.i >2017026.函数了。
）=j的大致图象为（）7.命题“任意向量a, b. \a^b\>\a\\b\"的否定为（）A. 任意向量X E ，B. 存在向Ma. b.C. 任意向量，D. 存在向量由正\a b\ > |a||b|\a-b\> |a || b||a-b| > |a||b||淑引 < |a||b|8.己知函数/（对=也云，若f （々）= b・则f （一。
）等于（）AM B. -b C. | D •-匕o b 9.己知正四面体的棱长为2,则它的外接球的表面枳为（）A.顼yrB. 2>/3nC. 3jtD. 6兀10.某学校需要把6名实习老师安排到A, B, C 三个班级去听课，每个班级安排2名老师，已知甲不能安排到A 班，乙和丙不能安排到同一班级，则安排方案的种数有（）A. 24B. 36C. 48D. 7211. 旦、旦是椭圆W + S=l （a>b>0）的左，右焦点，8是该椭圆短轴的一个端点.直线BF ］与椭圆C 交于点A,若\AB\.届F2I ，|4月I 成等差数列,则该怖圆的离心率为A 上B.爽C.| D .竺4 2 2 212. 己知函数/•（》）=伫；2 _心 x <o >Q 若方程/\x ）=x + a 有2个不同的实根，则实数〃的取值范围是（）A.(a|0<a<1>1}B.{a|a>1)C. {a|a=—1或。
安徽省宣城市2019-2020学年高考数学三模考试卷含解析
安徽省宣城市2019-2020学年高考数学三模考试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．若双曲线22214x y b -=的离心率e =）A ．B ．2C D ．1【答案】C 【解析】 【分析】根据双曲线的解析式及离心率，可求得,,a b c 的值；得渐近线方程后，由点到直线距离公式即可求解. 【详解】双曲线22214x y b -=的离心率2e =，则2a =，2c e a ==，解得c =()，所以b ===则双曲线渐近线方程为2y x =±20y ±=，不妨取右焦点，则由点到直线距离公式可得d ==故选：C. 【点睛】本题考查了双曲线的几何性质及简单应用，渐近线方程的求法，点到直线距离公式的简单应用，属于基础题.2．已知[]2240a b a b +=⋅∈-r r r r ，，，则a r的取值范围是（ ） A ．[0，1] B ．112⎡⎤⎢⎥⎣⎦，C ．[1，2]D ．[0，2]【答案】D 【解析】 【分析】设2m a b =+r r r ，可得[]2240a b a m a ⋅=⋅-∈-r r r r r ，，构造（14a m -r r ）2≤22116m +r ，结合2m =r ，可得113422a m ⎡⎤-∈⎢⎥⎣⎦r r ，，根据向量减法的模长不等式可得解.【详解】设2m a b =+r r r ，则2m =r ，[]22240b m a a b a m a =-⋅=⋅-∈-r r r r r r r r，，，∴（14a m -rr ）2212a a =-r r •2116m m +≤r r 22116m +r|m r |2m r =2＝4，所以可得：2182m =r，配方可得222111192()428482m a m m =≤-≤+=r r rr ， 所以113422a m ⎡⎤-∈⎢⎥⎣⎦rr ，， 又111||||||||||||444a m a m a m -≤-≤+r r r r r r 则a ∈r[0，2]． 故选：D ． 【点睛】本题考查了向量的运算综合，考查了学生综合分析，转化划归，数学运算的能力，属于中档题. 3．在平面直角坐标系xOy 中，锐角θ顶点在坐标原点，始边为x 轴正半轴，终边与单位圆交于点5P m ⎛⎫ ⎪ ⎪⎝⎭，则sin 24πθ⎛⎫+= ⎪⎝⎭（ ）A ．10B C ．10D 【答案】A 【解析】 【分析】根据单位圆以及角度范围，可得m ，然后根据三角函数定义，可得sin ,cos θθ，最后根据两角和的正弦公式，二倍角公式，简单计算，可得结果. 【详解】由题可知：221m +=⎝⎭，又θ为锐角所以0m >，5m =根据三角函数的定义：sin θθ==所以4sin 22sin cos 5θθθ==223cos 2cos sin 5θθθ=-=-由sin 2sin 2cos cos 2sin 444πππθθθ⎛⎫+=+ ⎪⎝⎭所以43sin 24525210πθ⎛⎫+=⨯-⨯= ⎪⎝⎭ 故选：A 【点睛】本题考查三角函数的定义以及两角和正弦公式，还考查二倍角的正弦、余弦公式，难点在于公式的计算，识记公式，简单计算，属基础题.4．盒中有6个小球，其中4个白球，2个黑球，从中任取()1,2i i =个球，在取出的球中，黑球放回，白球则涂黑后放回，此时盒中黑球的个数()1,2i X i =，则( )A ．()()1233P X P X =>=，12EX EX >B ．()()1233P X P X =<=，12EX EX >C ．()()1233P X P X =>=，12EX EX <D ．()()1233P X P X =<=，12EX EX < 【答案】C 【解析】 【分析】根据古典概型概率计算公式，计算出概率并求得数学期望，由此判断出正确选项. 【详解】13X =表示取出的为一个白球，所以()14116233C P X C ===.12X =表示取出一个黑球，()12116123C P X C ===，所以()121832333E X =⨯+⨯=.23X =表示取出两个球，其中一黑一白，()11422268315C C P X C ===，22X =表示取出两个球为黑球，()22226115C P X C ==，24X =表示取出两个球为白球，()242266415C P X C ===，所以()2816103241515153E X =⨯+⨯+⨯=.所以()()1233P X P X =>=，12EX EX <. 故选：C 【点睛】本小题主要考查离散型随机变量分布列和数学期望的计算，属于中档题.5．如图所示，网络纸上小正方形的边长为1，粗线画出的是某四棱锥的三视图，则该几何体的体积为（ ）A ．2B ．83C ．6D ．8【答案】A 【解析】 【分析】先由三视图确定该四棱锥的底面形状，以及四棱锥的高，再由体积公式即可求出结果. 【详解】由三视图可知，该四棱锥为斜着放置的四棱锥，四棱锥的底面为直角梯形，上底为1，下底为2，高为2，四棱锥的高为2， 所以该四棱锥的体积为()11V 1222232=⨯⨯+⨯⨯=. 故选A 【点睛】本题主要考查几何的三视图，由几何体的三视图先还原几何体，再由体积公式即可求解，属于常考题型.6．622x x ⎛⎫- ⎪⎝⎭的展开式中，含3x 项的系数为（ ） A ．60- B ．12-C ．12D ．60【答案】B 【解析】 【分析】在二项展开式的通项公式中，令x 的幂指数等于3，求出r 的值，即可求得含3x 项的系数． 【详解】622x x ⎛⎫- ⎪⎝⎭的展开式通项为()663166222rr r r rr r T C x C x x --+⎛⎫=⋅⋅-=⋅-⋅ ⎪⎝⎭， 令633r -=，得1r =，可得含3x 项的系数为()16212C ⨯-=-.故选：B. 【点睛】本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．7．中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”人们把此类题目称为“中国剩余定理”，若正整数N 除以正整数m 后的余数为n ，则记为(mod )N n m =，例如112(mod3)=．现将该问题以程序框图的算法给出，执行该程序框图，则输出的n等于（ ）．A ．21B ．22C ．23D ．24【答案】C 【解析】从21开始，输出的数是除以3余2，除以5余3，满足条件的是23，故选C.8．已知平面向量,a b r r 满足||||a b =r r，且2)a b b -⊥r r ，则,a b r r 所夹的锐角为（ ）A ．6π B ．4π C ．3π D ．0【答案】B 【解析】 【分析】根据题意可得2)0a b b -⋅=r r，利用向量的数量积即可求解夹角.因为))0b b b b -⊥⇒-⋅=r r r r2||b b ⋅=r r而2cos ,2||||||a b a b a b a b b ⋅⋅===⋅r r r r r r r r r所以,a b rr 夹角为4π故选：B 【点睛】本题考查了向量数量积求夹角，需掌握向量数量积的定义求法，属于基础题. 9．在正项等比数列{a n }中，a 5-a 1=15，a 4-a 2 =6，则a 3=（ ） A ．2 B ．4 C ．12D ．8【答案】B 【解析】 【分析】根据题意得到4511115a a a q a -=-=，342116a a a q a q -=-=，解得答案.【详解】4511115a a a q a -=-=，342116a a a q a q -=-=，解得112a q =⎧⎨=⎩或11612a q =-⎧⎪⎨=⎪⎩（舍去）.故2314a a q ==.故选：B . 【点睛】本题考查了等比数列的计算，意在考查学生的计算能力. 10．已知定义在[)0,+∞上的函数()f x 满足1()(2)2f x f x =+，且当[)0,2x ∈时，2()2f x x x =-+.设()f x 在[)22,2n n -上的最大值为n a （*n N ∈），且数列{}n a 的前n 项的和为n S .若对于任意正整数n 不等式()129n k S n +≥-恒成立，则实数k 的取值范围为（ ） A ．[)0,+∞ B ．1,32⎡⎫+∞⎪⎢⎣⎭C ．3,64⎡⎫+∞⎪⎢⎣⎭D ．7,64⎡⎫+∞⎪⎢⎣⎭【答案】C 【解析】由已知先求出1max ()2n f x -=，即12n n a -=，进一步可得21nn S =-，再将所求问题转化为292nn k -≥对于任意正整数n 恒成立，设n c =292nn -，只需找到数列{}n c 的最大值即可. 【详解】当222n x n -≤<时，则0222x n ≤+-<，(22)(22)(2)f x n x n x n +-=-+--， 所以，11()2[2(1)]2n n f x f x n --=--=-(22)(2)x n x n +--，显然当21x n =-时，1max ()2n f x -=，故12n n a -=，1(12)2112n n n S ⨯-==--，若对于任意正整数n 不等式 ()129n k S n +≥-恒成立，即229n k n ≥-对于任意正整数n 恒成立，即292nn k -≥对于任 意正整数n 恒成立，设n c =292n n -，111122n n n n c c ++--=，令111202n n +->，解得112n <， 令111202n n +-<，解得112n >，考虑到*n N ∈，故有当5n ≤时，{}n c 单调递增， 当6n ≥时，有{}n c 单调递减，故数列{}n c 的最大值为6633264c ==，所以364k ≥. 故选：C. 【点睛】本题考查数列中的不等式恒成立问题，涉及到求函数解析、等比数列前n 项和、数列单调性的判断等知识，是一道较为综合的数列题.11．已知定义在R 上的函数()f x ，若函数()2y f x =+为偶函数，且()f x 对任意1x ，[)22,x ∈+∞()12x x ≠，都有()()21210f x f x x x -<-，若()()31f a f a ≤+，则实数a 的取值范围是（ ）A ．13,24⎡⎤-⎢⎥⎣⎦B ．[]2,1--C ．1,2⎛⎤-∞- ⎥⎝⎦D ．3,4⎛⎫+∞⎪⎝⎭【答案】A 【解析】 【分析】根据题意，分析可得函数()f x 的图象关于2x =对称且在[)2,+∞上为减函数，则不等式()()31f a f a ≤+等价于231a a -≥-，解得a 的取值范围，即可得答案. 【详解】解:因为函数()2y f x =+为偶函数，所以函数()f x 的图象关于2x =对称，因为()f x 对任意1x ，[)22,x ∈+∞ ()12x x ≠，都有()()21210f x f x x x -<-，所以函数()f x 在[)2,+∞上为减函数，则()()()()312312231f a f a f a f a a a ≤+⇔-≤+-⇔-≥-， 解得：1324a -≤≤. 即实数a 的取值范围是13,24⎡⎤-⎢⎥⎣⎦.故选：A. 【点睛】本题考查函数的对称性与单调性的综合应用，涉及不等式的解法，属于综合题.12．已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，1,03A ⎛⎫ ⎪⎝⎭为()f x 图象的对称中心，若图象上相邻两个极值点1x ，2x 满足121x x -=，则下列区间中存在极值点的是（ ） A ．,06π⎛⎫-⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,3π⎛⎫⎪⎝⎭D ．,32ππ⎛⎫⎪⎝⎭【答案】A 【解析】 【分析】结合已知可知，112T =可求T ，进而可求ω，代入()f x ，结合1()03f =，可求ϕ，即可判断．【详解】Q 图象上相邻两个极值点1x ，2x 满足12||1x x -=，∴112T =即2T =，ωπ∴=，()sin()f x x πϕ=+，且11()sin()033f πϕ=+=，∴13k πϕπ+=，k Z ∈，1||2ϕπ<Q ，13ϕπ∴=-，1()sin()3f x x ππ=-，当16x =-时，1()16f -=-为函数的一个极小值点，而1(,0)66π-∈-．故选：A ． 【点睛】本题主要考查了正弦函数的图象及性质的简单应用，解题的关键是性质的灵活应用．二、填空题：本题共4小题，每小题5分，共20分。
2019-2020学年江西省九江市高考数学三模试卷(理科)(有答案)
江西省九江市高考数学三模试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合M={x|x＜1}，N={x|2x＞1}，则M∩N=（）A．∅B．{x|x＜0} C．{x|x＜1} D．{x|0＜x＜1}2．复数﹣在复平面内所对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3．在Rt△ABC中，∠A=90°，AB=2，AC=4，E，F分别为AB，BC的中点，则=（）A．9 B．﹣9 C．7 D．﹣74．已知直线l经过圆C：x2+y2﹣2x﹣4y=0的圆心，且坐标原点到直线l的距离为，则直线l的方程为（）A．x+2y+5=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+3=05．设Sn 是等差数列{an}的前n项和，若S672=2，S1344=12，则S2016=（）A．22 B．26 C．30 D．346．设x1=18，x2=19，x3=20，x4=21，x5=22，将这五个数据依次输入如图所示的程序框进行计算，则输出的S值及其统计意义分别是（）A．S=2，即5个数据的方差为2B．S=2，即5个数据的标准差为2C．S=10，即5个数据的方差为10D．S=10，即5个数据的标准差为107．如图所示，有一条长度为1的线段MN，其端点M，N在边长为3的正方形ABCD的四边上滑动，当点N绕着正方形的四边滑动一周时，MN的中点P所形成轨迹的长度为（）A．B．8+π C．D．12+π）满足f（n）=，则f（1）=（）8．已知函数f（n）（n∈N+A．97 B．98 C．99 D．1009．高中数学联赛期间，某宾馆随机安排A、B、C、D、E五名男生入住3个标间（每个标间至多住2人），则A、B入住同一标间的概率为（）A．B．C．D．10．如图所示，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则此多面体的体积等于（）A．B．16 C．D．3211．若函数f（x）=cosx+axsinx，x∈（﹣，）存在零点，则实数a的取值范围是（）A．（0，+∞）B．（1，+∞）C．（﹣∞，﹣1） D．（﹣∞，0）12．如图所示，已知椭圆C： =1（a＞b＞0），⊙O：x2+y2=b2，点A、F分别是椭圆C的左顶点和左焦点，点P是⊙O上的动点，且为定值，则椭圆C的离心率为（）A．B．C．D．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．若二项展开式的第三项系数为80，则实数a=_______．14．若函数f（x）的定义域为[﹣2，2]，则函数y=f（2x）•ln（2x+1）的定义域为_______．15．已知数列{a n }各项均不为0，其前n 项和为S n ，且a 1=1，2S n =a n a n+1，则S n =_______．16．如图所示，半径为1的球内切于正三棱锥P ﹣ABC 中，则此正三棱锥体积的最小值为_______．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．在△ABC 中，三边a ，b ，c 所对应的角分别是A ，B ，C ，已知a ，b ，c 成等比数列． （1）若+=，求角B 的值；（2）若△ABC 外接圆的面积为4π，求△ABC 面积的取值范围．18．某工厂为了对新研发的产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组检测数据（x 1，y 1）（i=1，2，…6）如表所示： 试销价格x （元） 4 5 6 7 a 9 产品销量y （件） b8483 807568已知变量x ，y 具有线性负相关关系，且x i =39，y i =480，现有甲、乙、丙三位同学通过计算求得其归直线方程分别为：甲y=4x+54；乙y=﹣4x+106；丙y=﹣4.2x+105，其中有且仅有一位同学的计算结果是正确的．（1）试判断谁的计算结果正确？并求出a ，b 的值；（2）若由线性回归方程得到的估计数据与检测数据的误差不超过1，则该检测数据是“理想数据“，现从检测数据中随机抽取3个，求“理想数据“的个数ξ的分布列和数学期望．19．如图所示，四棱锥P ﹣ABCD 中，底面ABCD 为菱形，∠ABC=60°，PA=PC ，PB=PD=AB ． （1）求证：平面PAC ⊥平面ABCD ；（2）求直线PB 与平面PCD 所成角的正弦值．20．如图所示，已知抛物线C ：y 2=2px （p ＞0）的焦点为F ，过点F 垂直于x 轴的直线与抛物线C 相交于A ，B 两点，抛物线C 在A ，B 两点处的切线及直线AB 所围成的三角形面积为4． （1）求抛物线C 的方程；（2）设M ，N 是抛物线C 上异于原点O 的两个动点，且满足k OM •k ON =k OA •k OB ，求△OMN 面积的取值范围．21．已知函数f （x ）=x 2+ax ﹣lnx ，g （x ）=e x （a ∈R ）．（1）是否存在a 及过原点的直线l ，使得直线l 与曲线y=f （x ），y=g （x ）均相切？若存在，求a 的值及直线l 的方程；若不存在，请说明理由； （2）若函数F （x ）=在区间（0，1]上是单调函数，求a 的取值范围．四.请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-1：几何证明选讲]22．如图所示，直线AB 为圆O 的切线，切点为B ，点C 在圆O 上，∠ABC 的平分线BE 交圆O 于点E ，DB 垂直BE 交圆O 于点D ． （1）证明：DB=DC ； （2）设圆O 的半径为1，BC=，延长CE 交AB 于点F ，求线段BF 的长．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy 中，直线l 的参数方程为（t 为参数，α∈（0，）），以原点O为极点，x 轴非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ=4cosθ． （1）若直线l 与曲线C 有且仅有一个公共点M ，求点M 的直角坐标；（2）若直线l与曲线C相交于A，B两点，线段AB的中点横坐标为，求直线l的普通方程．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|﹣|x+1|．（1）求不等式|f（x）|＜1的解集；（2）若不等式|a|f（x）≥|f（a）|对任意a∈R恒成立，求实数x的取值范围．江西省九江市高考数学三模试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合M={x|x＜1}，N={x|2x＞1}，则M∩N=（）A．∅B．{x|x＜0} C．{x|x＜1} D．{x|0＜x＜1}【考点】交集及其运算．【分析】利用指数函数的单调性求出集合N中的解集；利用交集的定义求出M∩N．【解答】解：N={x|2x＞1}={x|x＞0}∵M={x|x＜1}，∴M∩N={X|0＜X＜1}故选D2．复数﹣在复平面内所对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数代数形式的乘除运算．【分析】化简复数为：a+bi的形式，求出对应点的坐标即可．【解答】解：．对应点的坐标（）在第三象限．故选：C．3．在Rt△ABC中，∠A=90°，AB=2，AC=4，E，F分别为AB，BC的中点，则=（）A．9 B．﹣9 C．7 D．﹣7【考点】平面向量数量积的运算．【分析】结合向量的加法与减法法则把表示出来，并根据向量的数量积运算法则计算即可．【解答】解：，故选：D．4．已知直线l经过圆C：x2+y2﹣2x﹣4y=0的圆心，且坐标原点到直线l的距离为，则直线l的方程为（）A．x+2y+5=0 B．2x+y﹣5=0 C．x+2y﹣5=0 D．x﹣2y+3=0【考点】直线与圆的位置关系．【分析】求出圆C 的圆心C （1，2），设直线l 的方程为y=k （x ﹣1）+2，由坐标原点到直线l 的距离为，求出直线的斜率，由此能求出直线l 的方程．【解答】解：圆C ：x 2+y 2﹣2x ﹣4y=0的圆心C （1，2），∵直线l 经过圆C ：x 2+y 2﹣2x ﹣4y=0的圆心，且坐标原点到直线l 的距离为，∴当直线l 的斜率不存在时，直线l 的方程为x=1，此时坐标原点到直线l 的距离为1，不成立； 当直线l 的斜率存在时，直线l 的方程为y=k （x ﹣1）+2， 且=，解得k=﹣，∴直线l 的方程为y=﹣（x ﹣1）+2，即x+2y ﹣5=0． 故选：C ．5．设S n 是等差数列{a n }的前n 项和，若S 672=2，S 1344=12，则S 2016=（ ） A ．22 B ．26 C ．30 D ．34 【考点】等差数列的前n 项和．【分析】由等差数列的性质得S 672，S 1344﹣S 672，S 2016﹣S 1344成等差数列，由此能求出S 2016． 【解答】解：∵S n 是等差数列{a n }的前n 项和，S 672=2，S 1344=12， 由等差数列的性质得S 672，S 1344﹣S 672，S 2016﹣S 1344成等差数列， 得到：2×10=2+S 2016﹣12， 解得S 2016=30． 故选：C ．6．设x 1=18，x 2=19，x 3=20，x 4=21，x 5=22，将这五个数据依次输入如图所示的程序框进行计算，则输出的S 值及其统计意义分别是（ ）A ．S=2，即5个数据的方差为2B ．S=2，即5个数据的标准差为2C ．S=10，即5个数据的方差为10D ．S=10，即5个数据的标准差为10【考点】程序框图．【分析】算法的功能是求S=++…+的值，根据条件确定跳出循环的i 值，计算输出S的值．【解答】解：由程序框图知：算法的功能是求S=++…+的值，∵跳出循环的i值为5，∴输出S=×[（18﹣20）2+（19﹣20）2+（20﹣20）2+（21﹣20）2+（22﹣20）2]=×（4+1+0+1+4）=2．故选：A．7．如图所示，有一条长度为1的线段MN，其端点M，N在边长为3的正方形ABCD的四边上滑动，当点N绕着正方形的四边滑动一周时，MN的中点P所形成轨迹的长度为（）A．B．8+π C．D．12+π【考点】轨迹方程．【分析】根据题意判断出轨迹是四个角处的四个直角扇形与正方形的四条边上的四条线段组成，然后根据圆的周长公式进行计算即可求解．【解答】解：由题意，轨迹为四条线段加四个四分之一的圆．如图，四个角上的图形合起来刚好是一个半径为0.5的圆，周长为：2π×0.5=π，再加上四个边上滑动为四个等长的线段，长度均为2，合起来就是：2×4+π=8+π．故选：B．8．已知函数f（n）（n∈N）满足f（n）=，则f（1）=（）+A．97 B．98 C．99 D．100【考点】函数的值．【分析】由已知条件，利用分段函数的性质推导出f（96）=f[f=97，由此能求出f（1）的值．【解答】解：∵函数f（n）（n∈N）满足f（n）=，+∴f=f[f=98，f（98）=f[f=97，f（97）=f[f=98，f（96）=f[f=97，依此类推，得f（99）=f（97）=…=f（1）=98．故选：B．9．高中数学联赛期间，某宾馆随机安排A、B、C、D、E五名男生入住3个标间（每个标间至多住2人），则A、B入住同一标间的概率为（）A．B．C．D．【考点】古典概型及其概率计算公式．【分析】先求出基本事件总数，再求出A、B入住同一标间包含的基本事件个数，由此能求出A、B入住同一标间的概率．【解答】解：某宾馆随机安排A、B、C、D、E五名男生入住3个标间，共有种情形，A、B入住同一标间有种情形，∴A、B入住同一标间的概率为．故选：B．10．如图所示，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则此多面体的体积等于（）A．B．16 C．D．32【考点】由三视图求面积、体积．【分析】如图所示，该多面体的直观图为直三棱柱ABC ﹣A 1B 1C 1截去一个三棱锥A ﹣A 1B 1C 1，即四棱锥A ﹣BB 1C 1C ，即可得出．【解答】解：如图所示，该多面体的直观图为直三棱柱ABC ﹣A 1B 1C 1截去一个三棱锥A ﹣A 1B 1C 1， 即四棱锥A ﹣BB 1C 1C ， ∴．故选：C ．11．若函数f （x ）=cosx+axsinx ，x ∈（﹣，）存在零点，则实数a 的取值范围是（ ）A ．（0，+∞）B ．（1，+∞）C ．（﹣∞，﹣1）D ．（﹣∞，0）【考点】函数零点的判定定理． 【分析】确定函数是偶函数，a ＜0，f （x ）在上只有一个零点，即可得出结论．【解答】解：∵f （﹣x ）=cos （﹣x ）﹣axsin （﹣x ）=cosx+axsinx=f （x ）， ∴函数是偶函数，当a ≥0时，恒成立，函数无零点，当a ＜0时，，∴函数f （x ）在上单调递减，∵，∴f （x ）在上只有一个零点，由f （x ）是偶函数可知，函数恰有两个零点．故选：D ．12．如图所示，已知椭圆C ：=1（a ＞b ＞0），⊙O ：x 2+y 2=b 2，点A 、F 分别是椭圆C 的左顶点和左焦点，点P 是⊙O 上的动点，且为定值，则椭圆C 的离心率为（ ）A ．B ．C ．D ．【考点】椭圆的简单性质． 【分析】设P （x 1，y 1），由是常数，得，然后利用，转化为关于x 1 的方程，由系数相等可得a ，c 的关系式，从而求得椭圆C 的离心率． 【解答】解：设F （﹣c ，0），c 2=a 2﹣b 2， 设P （x 1，y 1），要使得是常数，则有，λ是常数，∵，∴，比较两边系数得b 2a 2=λ（b 2+c 2），a=λc， 故c （b 2+a 2）=a （b 2+c 2），即2ca 2﹣c 3=a 3， 即e 3﹣2e+1=0，即（e ﹣1）（e 2+e ﹣1）=0， 又0＜e ＜1， ∴．故选：D ．二、填空题（每题5分，满分20分，将答案填在答题纸上） 13．若二项展开式的第三项系数为80，则实数a=2．【考点】二项式定理的应用．【分析】由条件利用二项展开式的通项公式，求得实数a 的值． 【解答】解：由题意可得二项展开式的第三项系数为，∴10a 3=80，解得a=2， 故答案为：2．14．若函数f （x ）的定义域为[﹣2，2]，则函数y=f （2x ）•ln（2x+1）的定义域为．【考点】函数的定义域及其求法．【分析】由函数f （x ）的定义域为[﹣2，2]，可得f （2x ）的定义域为满足﹣2≤2x ≤2的x 的取值集合，再与2x+1＞0的解集取交集即可得到函数y=f （2x ）•ln（2x+1）的定义域． 【解答】解：要使原函数有意义，则，解得．∴函数y=f （2x ）•ln（2x+1）的定义域为．故答案为：．15．已知数列{a n }各项均不为0，其前n 项和为S n ，且a 1=1，2S n =a n a n+1，则S n =．【考点】数列递推式．【分析】利用递推关系、等差数列的通项公式及其前n 项和公式即可得出． 【解答】解：当n=1时，2S 1=a 1a 2，即2a 1=a 1a 2，∴a 2=2．当n ≥2时，2S n =a n a n+1，2S n ﹣1=a n ﹣1a n ，两式相减得2a n =a n （a n+1﹣a n ﹣1）， ∵a n ≠0，∴a n+1﹣a n ﹣1=2，∴{a 2k ﹣1}，{a 2k }都是公差为2的等差数列，又a 1=1，a 2=2， ∴{a n }是公差为1的等差数列， ∴a n =1+（n ﹣1）×1=n ， ∴S n =．故答案为：．16．如图所示，半径为1的球内切于正三棱锥P ﹣ABC 中，则此正三棱锥体积的最小值为8．【考点】棱柱、棱锥、棱台的体积．【分析】设棱锥底面边长为a，高为h，作过棱锥的高和斜高的截面，根据三角形相似得出a，h的关系，代入棱锥的体积公式，利用导数求出体积的最小值．【解答】解：设正三棱锥P﹣ABC的底面边长AB=a，高为PO=h．设内切球球心为M，与平面PAC的切点为N，D为AC的中点，则MN⊥PD．DO==．MN=1，PM=h﹣1，∴PN===．∵Rt△PMN∽Rt△PDO，∴，即，∴a=．∴，，令V'=0得h=4，故当h=4时，．故答案为8．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．在△ABC中，三边a，b，c所对应的角分别是A，B，C，已知a，b，c成等比数列．（1）若+=，求角B的值；（2）若△ABC外接圆的面积为4π，求△ABC面积的取值范围．【考点】正弦定理；余弦定理．【分析】（1）由切化弦、两角和的正弦公式化简式子，由等比中项的性质、正弦定理列出方程，即可求出sinB，由内角的范围和特殊角的三角函数值求出B；（2）由余弦定理和不等式求出cosB的范围，由余弦函数的性质求出B的范围，由正弦定理和三角形的面积公式表示出△ABC面积，利用B的范围和正弦函数的性质求出△ABC面积的范围．【解答】解：（1）由题意得，，∵a，b，c成等比数列，∴b2=ac，○由正弦定理有sin2B=sinAsinC，∵A+C=π﹣B，∴sin（A+C）=sinB，得，即，由b2=ac知，b不是最大边，∴．（2）∵△ABC外接圆的面积为4π，∴△ABC的外接圆的半径R=2，由余弦定理b2=a2+c2﹣2accosB，得，又b2=ac，∴，当且仅当a=c时取等号，∵B为△ABC的内角，∴，由正弦定理，得b=4sinB，∴△ABC的面积，∵，∴，∴．18．某工厂为了对新研发的产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组检测数据（x1，y1）（i=1，2，…6）如表所示：试销价格x（元） 4 5 6 7 a 9 产品销量y（件） b 84 83 80 75 68已知变量x，y具有线性负相关关系，且xi =39， yi=480，现有甲、乙、丙三位同学通过计算求得其归直线方程分别为：甲y=4x+54；乙y=﹣4x+106；丙y=﹣4.2x+105，其中有且仅有一位同学的计算结果是正确的．（1）试判断谁的计算结果正确？并求出a，b的值；（2）若由线性回归方程得到的估计数据与检测数据的误差不超过1，则该检测数据是“理想数据“，现从检测数据中随机抽取3个，求“理想数据“的个数ξ的分布列和数学期望．【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．【分析】（1）xi =39， yi=480，x的和为39，y的和为480，解得a和b的值，并求得，，由x，y具有线性负相关关系，甲同学的不对，将，，代入验证，乙同学的正确；（2）分别求出有回归方程求得y值，与实际的y相比较，判断是否为“理想数据“，并求得ξ的取值，分别求得其概率，写出分布列和数学期望．【解答】解：（1）已知变量x，y具有线性负相关关系，故甲不对，且xi=39，4+5+6+7+a+9=39，a=8，y=480，b+84+83+80+75+68=480，b=90，i∵=6.5，=80，将，，代入两个回归方程，验证乙同学正确，故回归方程为：y=﹣4x+106；（2）X 4 5 6 7 8 9y 90 84 83 80 75 68y 92 88 84 80 76 72“理想数据“的个数ξ取值为：0，1，2，3；P（X=0）==，P（X=1）==，P（X=2）==，P（X=3）==．“理想数据“的个数ξ的分布列：X 0 1 2 3P =数学期望E（X）=0×+1×+2×+3×=1.5．19．如图所示，四棱锥P﹣ABCD中，底面ABCD为菱形，∠ABC=60°，PA=PC，PB=PD=AB．（1）求证：平面PAC⊥平面ABCD；（2）求直线PB与平面PCD所成角的正弦值．【考点】直线与平面所成的角；平面与平面垂直的判定．【分析】（1）设AC与BD相交于点O，连接PO，根据三线合一得出PO⊥AC，PO⊥BD，故而PO⊥平面ABCD，得出平面PAC⊥平面ABCD；（2）以O为原点，以OB，OD，OP为坐标轴建立空间直角坐标系，设AB=2，求出和平面PCD的法向量，则|cos＜＞|即为所求．【解答】（1）证明：设AC与BD相交于点O，连接PO，∵ABCD为菱形，∴O为AC，BD的中点．∵PA=PC，PB=PD，∴PO⊥AC，PO⊥BD．又AC∩BD=O，AC，BD⊂平面ABCD，∴PO⊥平面ABCD，又PO⊂平面PAC，∴平面PAC⊥平面ABCD．（2）解：∵ABCD为菱形，∠ABC=60°，∴△ABC为正三角形，AC⊥BD，不妨设PB=PD=AB=2，则BO=，∴PO=1．以O为原点，以OB，OD，OP为坐标轴建立如图所示的空间直角坐标系O﹣xyz，∴P（0，0，1），B（，0，0），C（0，1，0），D（﹣，0，0）．∴=（，0，﹣1），=（0，1，﹣1），=（﹣，0，﹣1）．设平面PCD的法向量为=（x，y，z），则，即．令x=1得=（1，﹣，﹣）．∴cos＜＞===．∴直线PB与平面PCD所成角的正弦值为．20．如图所示，已知抛物线C ：y 2=2px （p ＞0）的焦点为F ，过点F 垂直于x 轴的直线与抛物线C 相交于A ，B 两点，抛物线C 在A ，B 两点处的切线及直线AB 所围成的三角形面积为4． （1）求抛物线C 的方程；（2）设M ，N 是抛物线C 上异于原点O 的两个动点，且满足k OM •k ON =k OA •k OB ，求△OMN 面积的取值范围．【考点】抛物线的简单性质．【分析】（1）求出A ，B 坐标，利用导数解出切线方程，求出切线与x 轴的交点，利用三角形的面积列方程解出p ；（2）计算k OA •k OB =﹣4，设出MN 方程，求出MN 与x 轴的交点，联立方程组，根据根与系数的关系计算|y M ﹣y N |，得出△OMN 面积S 关于t 的函数，解出函数的最值． 【解答】解：（1）抛物线的焦点坐标为F （，0），∴，由，得，∴抛物线C 在A 处的切线斜率为1，由抛物线C 的对称性，知抛物线C 在B 处的切线卸斜率为﹣1， ∴抛物线过A 点的切线方程为y ﹣p=x ﹣，令y=0得x=﹣． ∴，解得p=2．∴抛物线C 的方程为y 2=4x ．（2）k OA =2，k OB =﹣2，∴k OA •k OB =﹣4，设，则，∴y 1y 2=﹣4．令直线MN 的方程为x=ty+n ， 联立方程组消去x 得：y 2﹣4ty ﹣4n=0，则y 1y 2=﹣4n ，y 1+y 2=4t ，∵y 1y 2=﹣4，∴n=1．即直线MN 过点（1，0）． ∴．∵t 2≥0，∴S △OMN ≥2．综上所示，△OMN 面积的取值范围是[2，+∞）．21．已知函数f （x ）=x 2+ax ﹣lnx ，g （x ）=e x （a ∈R ）．（1）是否存在a 及过原点的直线l ，使得直线l 与曲线y=f （x ），y=g （x ）均相切？若存在，求a 的值及直线l 的方程；若不存在，请说明理由； （2）若函数F （x ）=在区间（0，1]上是单调函数，求a 的取值范围．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【分析】（1）求出f （x ），g （x ）的导数，设出切点，求得切线的斜率，运用点斜式方程可得切线的方程，即可判断存在a=e ﹣1及l ：y=ex ； （2）求出F （x ）的解析式和导数，令，求出导数，判断单调性，再对a 讨论，分a ≤2，a ＞2，判断h （x ）的单调性，进而得到F （x ）的单调性，即可得到所求范围． 【解答】解：（1）g （x ）的导数为g'（x ）=e x ， 设曲线y=g （x ）在点处切线过原点，则切线方程为，由点在切线上，可得，解得x 1=1，即有切线方程为y=ex ，设直线y=ex 与曲线y=f （x ）切于点（x 2，y 2）， 由f （x ）的导数为，可得，即有，又，则，可得，解得x 2=1，a=e ﹣1．故存在a=e ﹣1及l ：y=ex ，使得直线l 与曲线y=f （x ），y=g （x ）均相切． （2），，令，则，易知h'（x ）在（0，1]上单调递减，从而h'（x ）≥h'（1）=2﹣a ．①当2﹣a ≥0时，即a ≤2时，h'（x ）≥0，h （x ）在区间（0，1]上单调递增， 由h （1）=0，可得h （x ）≤0在（0，1]上恒成立， 即F'（x ）≤0在（0，1]上恒成立．即F （x ）在区间（0，1]上单调递减，则a ≤2满足题意；②当2﹣a ＜0时，即a ＞2时，由h'（1）=2﹣a ＜0，当x ＞0且x→0时，h'（x ）→+∞， 故函数h'（x ）存在唯一零点x 0∈（0，1]，且h （x ）在（0，x 0）上单调递增， 在（x 0，1）上单调递减，又h （1）=0，可得F （x ）在（x 0，1）上单调递增．注意到h （e ﹣a ）＜0，e ﹣a ∈（0，x 0），即有F （x ）在（0，e ﹣a ）上单调递减， 这与F （x ）在区间（0，1]上是单调函数矛盾，则a ＞2不合题意． 综合①②得，a 的取值范围是（﹣∞，2]．四.请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-1：几何证明选讲]22．如图所示，直线AB 为圆O 的切线，切点为B ，点C 在圆O 上，∠ABC 的平分线BE 交圆O 于点E ，DB 垂直BE 交圆O 于点D ． （1）证明：DB=DC ； （2）设圆O 的半径为1，BC=，延长CE 交AB 于点F ，求线段BF 的长．【考点】与圆有关的比例线段．【分析】（1）连接DE交BC于点G，由弦切角定理可得∠ABE=∠BCE，由已知角平分线可得∠ABE=∠CBE，于是得到∠CBE=∠BCE，BE=CE．由已知DB⊥BE，可知DE为⊙O的直径，Rt△DBE≌Rt△DCE，利用三角形全等的性质即可得到DC=DB．（2）由（1）可知：DG是BC的垂直平分线，即可得到BG=．设DE的中点为O，连接BO，可得∠BOG=60°．从而∠ABE=∠BCE=∠CBE=30°．得到CF⊥BF．进而得到线段BF的长【解答】（1）证明：连接DE交BC于点G，由弦切角定理得，∠ABE=∠BCE．∵∠ABE=∠CBE，∴∠CBE=∠BCE，BE=CE．又∵DE⊥BE，∴DE是直径，∠DCE=90°．∴△DBE≌△DCE，∴DC=DB．（2）解：设DE与BC相交于点G，由（1）知，∠CDE=∠BDE，DB=DC，故DG是BC的中垂线．∵，∴．连接BO，∵圆O的半径为1，∴∠BOG=60°，∠ABE=∠BCE=∠CBE=30°，∴CF⊥BF．，∴．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy中，直线l的参数方程为（t为参数，α∈（0，）），以原点O 为极点，x轴非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4cosθ．（1）若直线l与曲线C有且仅有一个公共点M，求点M的直角坐标；（2）若直线l与曲线C相交于A，B两点，线段AB的中点横坐标为，求直线l的普通方程．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（1）曲线C的极坐标方程为ρ=4cosθ，即ρ2=4ρcosθ，把ρ2=x2+y2，x=ρcosθ，代入可得C 的直角坐标方程．把直线l的参数方程代入上式并整理得t2﹣6tcosα+5=0．令△=0，解出即可得出点M的直角坐标．（2）设A，B两点对应的参数分别为t1，t2，则t1+t2=6cosα．利用中点坐标公式即可得出．【解答】解：（1）曲线C的极坐标方程为ρ=4cosθ，即ρ2=4ρcosθ，把ρ2=x2+y2，x=ρcosθ，代入可得C的直角坐标方程为：x2﹣4x+y2=0，即（x﹣2）2+y2=4．把直线l的参数方程代入上式并整理得t2﹣6tcosα+5=0．令△=（6cosα）2﹣20=0，解得．∴点M的直角坐标为．（2）设A，B两点对应的参数分别为t1，t2，则t1+t2=6cosα．线段AB的中点对应的参数为．则，解得．∴直线l的普通方程为x﹣y+1=0．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|﹣|x+1|．（1）求不等式|f（x）|＜1的解集；（2）若不等式|a|f（x）≥|f（a）|对任意a∈R恒成立，求实数x的取值范围．【考点】绝对值三角不等式；绝对值不等式的解法．【分析】（1）利用绝对值的几何意义，求不等式|f（x）|＜1的解集；（2）若不等式|a|f（x）≥|f（a）|对任意a∈R恒成立，分类讨论，转化为|f（x）|≥2，求实数x的取值范围．【解答】解：（1）x＜﹣1时，f（x）=﹣x+1+x+1=2＜1，不成立；﹣1≤x≤1时，f（x）=﹣x+1﹣x﹣1=﹣2x，|﹣2x|＜1，∴﹣＜x＜；x＞1时，f（x）=x﹣1﹣x﹣1=﹣2，|f（x）|＞1，不成立，综上所述不等式|f（x）|＜1的解集为{x|﹣＜x＜}；（2）a=0时，不等式成立，a≠0时，|f（x）|≥||1﹣|﹣|1+||∵||1﹣|﹣|1+||＜2，∴|f（x）|≥2，x＜﹣1时，f（x）=﹣x+1+x+1=2，成立；﹣1≤x≤1时，f（x）=﹣x+1﹣x﹣1=﹣2x，|﹣2x|≥2，∴x=±1；x＞1时，f（x）=x﹣1﹣x﹣1=﹣2，|f（x）|=2，成立，综上所述实数x的取值范围为{x|x≤﹣1或x≥1}．。
2020年高考数学三模试题 理(含解析)
2019高考数学三模试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．若复数（a∈R，i是虚数单位）是纯虚数，则实数a的值为（）A．﹣2 B．﹣6 C．4 D．62．设[x]表示不大于x（x∈R）的最大整数，集合A={x|[x]=1}，B={1，2}，则A∪B=（）A．{1} B．{1，2} C．[1，2）D．[1，2]3．某学生一个学期的数学测试成绩一共记录了6个数据：x1=52，x2=70，x3=68，x4=55，x5=85，x6=90，执行如图所示的程序框图，那么输出的S是（）A．1 B．2 C．3 D．44．若函数的图象上某一点处的切线过点（2，1），则切线的斜率为（）A．0 B．0或C．D．5．已知x，y满足，若存在x，y使得2x+y≤a成立，则a的取值范围是（）A．（2，+∞）B．[2，+∞）C．[4，+∞）D．[10，+∞）6．某几何体的三视图如图所示，则该几何体的体积为（）A．4 B．2 C．6 D．7．数列{a n}满足a n+1（a n﹣1﹣a n）=a n﹣1（a n﹣a n+1），若a1=2，a2=1，则a20=（）A． B．C．D．8．长为的线段AB在双曲线x2﹣y2=1的一条渐近线上移动，C为抛物线y=﹣x2﹣2上的点，则△ABC面积的最小值是（）A．B．C．D．79．在区间[0，4]上随机取两个数x，y，则xy∈[0，4]的概率是（）A．B．C．D．10．将函数的图象向右平移θ（θ＞0）个单位长度后关于y轴对称，则θ的最小值是（）A．B．C．D．11．已知三棱锥S﹣ABC的底面△ABC为正三角形，顶点在底面上的射影为底面的中心，M，N分别是棱SC，BC的中点，且MN⊥AM，若侧棱，则三棱锥S﹣ABC的外接球的表面积是（）A．12π B．32π C．36π D．48π12．已知函数f（x），g（x）满足关系式f（x）=g（|x﹣1|）（x∈R）．若方程f（x）﹣cosπx=0恰有7个根，则7个根之和为（）A．3 B．5 C．7 D．9二、填空题：本大题共4小题，每小题5分，共20分.13．已知，若存在向量使，则= ．14．若展开式中存在常数项，则n的最小值为．15．非零实数a，b满足tanx=x，且a2≠b2，则（a﹣b）sin（a+b）﹣（a+b）sin（a﹣b）= ．16．已知椭圆的左、右焦点分别为F1，F2，左右顶点分别为A1，A2，P为椭圆上任意一点（不包括椭圆的顶点），则以线段PF i（i=1，2）为直径的圆与以A1A2为直径的圆的位置关系为．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．已知三角形ABC中，角A，B，C成等差数列，且为角A的内角平分线，．（1）求三角形内角C的大小；（2）求△ABC面积的S．18．如图，ABC﹣A'B'C'为三棱柱，M为CC的中点，N为AB的中点，AA'=2，AB=2，BC=1，∠ABC=60°．（1）求证：CN∥平面AB'M；（2）求平面AB'M与平面BB'C所成的锐二面角的余弦值．19．为推行“新课改”教学法，某数学老师分别用传统教学和“新课改”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中个随机抽取20名学生的成绩进行统计，结果如表：记成绩不低于105分者为“成绩优良”．分数[0，90）[90，105）[105，1200）[120，135）[135，150）甲班频数 5 6 4 4 1乙班频数 1 3 6 5（1）由以上统计数据填写下面的2×2列联表，并判断能否有97.5%的把握认为“成绩优良”与教学方式有关？（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为X，求X的分布列和数学期望．甲班乙班总计成绩优良成绩不优良总计附：K2=，（n=a+b+c+d）临界值表：P（K2≥k0） 0.10 0.050 0.025 0.010k0 2.706 3.841 5.024 6.63520．一张坐标纸上涂着圆E：（x+1）2+y2=8及点P（1，0），折叠此纸片，使P与圆周上某点P'重合，每次折叠都会留下折痕，设折痕与EP'的交点为M．（1）求M的轨迹C的方程；（2）直线l：y=kx+m与C的两个不同交点为A，B，且l与以EP为直径的圆相切，若，求△ABO的面积的取值范围．21．已知f（x）=且a≠1），f（x）是增函数，导函数f'（x）存在零点．（1）求a的值；（2）设A（x1，y1），B（x2，y2）（x1＜x2）是函数f（x）图象上的两点，x0是AB中点的横坐标，是否存在x0，使得f'（x0）=成立？若存在，请证明；若不存在，请说明理由．[选修4-4：参数方程与极坐标系]22．在平面直角坐标系xoy中，以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为，且曲线C在极坐标系中过点（2，π）．（1）求曲线C的直角坐标方程；（2）设直线（t为参数）与曲线C相交于A，B两点，直线m过线段AB的中点，且倾斜角是直线l的倾斜角的2倍，求m的极坐标方程．[选修4-5：不等式选讲]23．已知函数f（x）=|x﹣1|+|x﹣a|（a＞0），其最小值为3．（1）求实数a的值；（2）若关于x的不等式f（x）+|x|＞m2﹣2m对于任意的x∈R恒成立，求实数m的取值范围．2017年河南省八市中评高考数学三模试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1．若复数（a∈R，i是虚数单位）是纯虚数，则实数a的值为（）A．﹣2 B．﹣6 C．4 D．6【考点】A5：复数代数形式的乘除运算．【分析】复数==+i是纯虚数，可得=0，≠0，解出即可得出．【解答】解：复数==+i是纯虚数，则=0，≠0，解得a=﹣2．故选：A．2．设[x]表示不大于x（x∈R）的最大整数，集合A={x|[x]=1}，B={1，2}，则A∪B=（）A．{1} B．{1，2} C．[1，2）D．[1，2]【考点】1D：并集及其运算．【分析】根据[x]的定义用区间表示集合A，再根据并集的定义写出A∪B．【解答】解：根据题意，集合A={x|[x]=1}={x|1≤x＜2}=[1，2），集合B={1，2}，所以A∪B=[1，2]．故选：D．3．某学生一个学期的数学测试成绩一共记录了6个数据：x1=52，x2=70，x3=68，x4=55，x5=85，x6=90，执行如图所示的程序框图，那么输出的S是（）A．1 B．2 C．3 D．4【考点】EF：程序框图．【分析】由模拟程序框图的运行过程，得出输出的S是记录六次数学测试成绩中得分60以上的次数，由数据得出S的值．【解答】解：模拟程序框图的运行过程，知输出的S是记录六次数学测试成绩中得分60以上的次数；∴比较数据：x1=52，x2=70，x3=68，x4=55，x5=85，x6=90，得出S=4；故选：D．4．若函数的图象上某一点处的切线过点（2，1），则切线的斜率为（）A．0 B．0或C．D．【考点】6H：利用导数研究曲线上某点切线方程．【分析】设切点为（m，n），（﹣1≤m≤1，n≥0），由于f（x）的图象为单位圆的上半圆，求得切线的斜率和方程，代入（2，1），解方程可得m，n，进而得到所求切线的斜率．【解答】解：设切点为（m，n），（﹣1≤m≤1，n≥0），由于函数的图象为单位圆的上半圆，可得切线的斜率为﹣，即有切线的方程为y﹣n=﹣（x﹣m），代入m2+n2=1，可得mx+ny=1，代入（2，1），可得2m+n=1，解得m=，n=﹣，（舍去）或m=0，n=1，即为切线的斜率为﹣=0．故选：A．5．已知x，y满足，若存在x，y使得2x+y≤a成立，则a的取值范围是（）A．（2，+∞）B．[2，+∞）C．[4，+∞）D．[10，+∞）【考点】7C：简单线性规划．【分析】画出x，y满足的平面区域，求出可行域各角点的坐标，然后利用角点法，求出目标函数的最大值和最小值，即可得到a的取值范围．【解答】解：令z=2x+y，画出x，y满足，的可行域，由可行域知：目标函数过点A时取最大值，由，可得x=3，y=4，可得A（3，4）时，z的最大值为：10．所以要使2x+y≤a恒成立，只需使目标函数的最大值小于等于a 即可，所以a的取值范围为a≥10．故答案为：a≥10．故选：D．6．某几何体的三视图如图所示，则该几何体的体积为（）A．4 B．2 C．6 D．【考点】L!：由三视图求面积、体积．【分析】由三视图还原原几何体，该几何体为四棱锥，底面ABCD为直角梯形，AB∥CD，AB⊥BC，PC⊥平面ABCD．然后由棱锥体积公式得答案．【解答】解：由三视图还原原几何体如图：该几何体为四棱锥，底面ABCD为直角梯形，AB∥CD，AB⊥BC，PC⊥平面ABCD．∴该几何体的体积V=．故选：B．7．数列{a n}满足a n+1（a n﹣1﹣a n）=a n﹣1（a n﹣a n+1），若a1=2，a2=1，则a20=（）A． B．C．D．【考点】8H：数列递推式．【分析】数列{a n}满足a n+1（a n﹣1﹣a n）=a n﹣1（a n﹣a n+1），展开化为： +=．利用等差数列的通项公式得出．【解答】解：数列{a n}满足a n+1（a n﹣1﹣a n）=a n﹣1（a n﹣a n+1），展开化为： +=．∴数列是等差数列，公差为=，首项为1．∴=1+=，解得a20=．故选：C．8．长为的线段AB在双曲线x2﹣y2=1的一条渐近线上移动，C为抛物线y=﹣x2﹣2上的点，则△ABC面积的最小值是（）A．B．C．D．7【考点】KC：双曲线的简单性质．【分析】求出双曲线的渐近线方程，设C（m，﹣m2﹣2），运用点到直线的距离公式，以及二次函数的最值的求法，再由三角形的面积公式，即可得到三角形的面积的最小值．【解答】解：双曲线x2﹣y2=1的一条渐近线方程为y=x，C为抛物线y=﹣x2﹣2上的点，设C（m，﹣m2﹣2），C到直线y=x的距离为d==≥，当m=﹣时，d的最小值为，可得△ABC的面积的最小值为S=×4×=．故选：A．9．在区间[0，4]上随机取两个数x，y，则xy∈[0，4]的概率是（）A．B．C．D．【考点】CF：几何概型．【分析】由题意把两个数为x，y看作点P（x，y），作出Ω={（x，y）|}表示的平面区域，把xy∈[0，4]转化为0≤y≤，求出满足0≤y≤的区域面积，计算所求的概率值．【解答】解：由题意把两个数为x，y看作点P（x，y），则Ω={（x，y）|}，它所表示的平面区域是边长为4的正方形，面积为42=16；xy∈[0，4]转化为0≤y≤，如图所示；且满足0≤y≤的区域面积是：16﹣（4﹣）dx=16﹣（4x﹣4lnx）=4+4ln4，则xy∈[0，4]的概率为：P==．故选：C．10．将函数的图象向右平移θ（θ＞0）个单位长度后关于y轴对称，则θ的最小值是（）A．B．C．D．【考点】GL：三角函数中的恒等变换应用；HJ：函数y=Asin（ωx+φ）的图象变换．【分析】将函数f（x）化简，根据三角函数的平移变换规律即可求解．【解答】解：函数=sin（x+），图象向右平移θ（θ＞0）个单位长度后，可得sin（x ﹣θ+），关于y轴对称，∴，k∈Z．即θ=﹣∵θ＞0，当k=﹣1时，可得θ的最小值为，故选：D．11．已知三棱锥S﹣ABC的底面△ABC为正三角形，顶点在底面上的射影为底面的中心，M，N分别是棱SC，BC的中点，且MN⊥AM，若侧棱，则三棱锥S﹣ABC的外接球的表面积是（）A．12π B．32π C．36π D．48π【考点】LG：球的体积和表面积．【分析】由题意推出MN⊥平面SAC，即SB⊥平面SAC，∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，正方体的对角线就是球的直径，求出直径即可求出球的表面积积．【解答】解：∵M，N分别为棱SC，BC的中点，∴MN∥SB∵三棱锥S﹣ABC为正棱锥，∴SB⊥AC（对棱互相垂直），∴MN⊥AC又∵MN⊥AM，而AM∩AC=A，∴MN⊥平面SAC，∴SB⊥平面SAC∴∠ASB=∠BSC=∠ASC=90°以SA，SB，SC为从同一定点S出发的正方体三条棱，将此三棱锥补成以正方体，则它们有相同的外接球，正方体的对角线就是球的直径．∴2R=SA=6，∴R=3，∴S=4πR2=36π．故选：C12．已知函数f（x），g（x）满足关系式f（x）=g（|x﹣1|）（x∈R）．若方程f（x）﹣cosπx=0恰有7个根，则7个根之和为（）A．3 B．5 C．7 D．9【考点】54：根的存在性及根的个数判断．【分析】函数y=g（|x|）是偶函数，y=g（|x﹣1|）是把y=g（|x|）向右平移1个单位得到的，可得y=f（x）的图象关于直线x=1对称．再由x=1是f（x）=cosπx的一条对称轴，可得y=f（x）的图象与y=cosπx的图象有3对交点关于直线x=1对称，有1个交点为（1，1）．结合中点坐标公式得答案．【解答】解：函数y=g（|x|）是偶函数，其图象关于直线x=0对称，而y=g（|x﹣1|）是把y=g（|x|）向右平移1个单位得到的，∴y=g（|x﹣1|）的图象关于直线x=1对称．即y=f（x）的图象关于直线x=1对称．方程f（x）﹣cosπx=0恰有7个根，即方程f（x）=cosπx恰有7个根，也就是y=f（x）的图象与y=cosπx的图象有7个交点，而x=1是f（x）=cosπx的一条对称轴，∴y=f（x）的图象与y=cosπx的图象有3对交点关于直线x=1对称，有1个交点为（1，1）．由中点坐标公式可得：y=f（x）的图象与y=cosπx的图象交点的横坐标和为3×2+1=7．故选：C．二、填空题：本大题共4小题，每小题5分，共20分.13．已知，若存在向量使，则= ．【考点】9J：平面向量的坐标运算．【分析】设=（x，y），由，可得，解出x，y．即可得出．【解答】解：设=（x，y），∵，∴，解得x=3，y=﹣2．则==．故答案为：14．若展开式中存在常数项，则n的最小值为 5 ．【考点】DB：二项式系数的性质．【分析】根据二项式展开式的通项公式，令x的指数等于0，求出n、r的关系，即可求出n的最小值．【解答】解：展开式中通项公式为T r+1=••=•（﹣1）r•，令=0，解得n=，其中r=0，1，2，…，n；当r=3时，n=5；所以n的最小值为5．故答案为：5．15．非零实数a，b满足tanx=x，且a2≠b2，则（a﹣b）sin（a+b）﹣（a+b）sin（a﹣b）= 0 ．【考点】HP：正弦定理；HR：余弦定理．【分析】由已知可得b=tanb，a=tana，利用两角和与差的正弦函数公式化简所求可得2acosasinb﹣2bsinacosb，利用同角三角函数基本关系式化简即可得解．【解答】解：∵非零实数a，b满足tanx=x，且a2≠b2，∴可得：b=tanb，a=tana，∴原式=（a﹣b）（sinacosb+cosasinb）﹣（a+b）（sinacosb﹣cosasinb）=2acosasinb﹣2bsinacosb=2tanacosasinb﹣2tanbsinacosb=2sinasinb﹣2sinasinb=0．故答案为：0．16．已知椭圆的左、右焦点分别为F1，F2，左右顶点分别为A1，A2，P为椭圆上任意一点（不包括椭圆的顶点），则以线段PF i（i=1，2）为直径的圆与以A1A2为直径的圆的位置关系为内切．【考点】K4：椭圆的简单性质．【分析】设PF1的中点为M，可得以线段PF i（i=1，2）为直径的圆与以A1A2为直径的圆的圆心距为OM，根据中位线的性质得OM==a﹣，即可【解答】解：如图，设PF1的中点为M，可得以线段PF i（i=1，2）为直径的圆与以A1A2为直径的圆的圆心距为OM，根据中位线的性质得OM==a﹣，a﹣就是两圆的半径之差，故两圆内切．故答案为：内切．三、解答题：本大题共5小题，共70分.解答应写出必要的文字说明或推理、验算过程.17．已知三角形ABC中，角A，B，C成等差数列，且为角A的内角平分线，．（1）求三角形内角C的大小；（2）求△ABC面积的S．【考点】HT：三角形中的几何计算．【分析】（1）根据角A，B，C成等差数列，可得2B=A+C，利用三角形内角和定理带入化简可得C的大小；（2）根据C的大小和2B=A+C，可得A，B的大小．利用正弦定理即可求解．【解答】解：（1）∵角A，B，C成等差数列，∴2B=A+C，∴B=，∵=2sin（A+C），∴2sinCcosA+sinA=2sinAcosC+2cosAsinC，∴sinA=2sinAcosC，∵A∈（0，π），sinA≠0，∴cosC=，∵C∈（0，π），∴．（2）．由（1）值A=，C=，由正弦定理得，得AB=，同理得AC=，∴△ABC面积的S=．18．如图，ABC﹣A'B'C'为三棱柱，M为CC的中点，N为AB的中点，AA'=2，AB=2，BC=1，∠ABC=60°．（1）求证：CN∥平面AB'M；（2）求平面AB'M与平面BB'C所成的锐二面角的余弦值．【考点】MT：二面角的平面角及求法；LS：直线与平面平行的判定．【分析】（1）取A′B′的中点E，连接EC′，EN，由已知可得AB′，EN共面，设AB′∩EN=F，连接FM，可得NF∥CM，NF=CM，从而得到CN∥FM，然后利用线面平行的判定可得CN∥平面AB'M；（2）在三角形ABC中，由余弦定理可得AC2，由AC2+BC2=AB2，得AC⊥CB，建立如图所示空间直角坐标系，求出所用点的坐标，得到平面AB′M与平面BCC′B′的一个法向量，利用两法向量所成角的余弦值可得平面AB'M与平面BB'C所成的锐二面角的余弦值．【解答】（1）证明：如图，取A′B′的中点E，连接EC′，EN，∵ABC﹣A′B′C′为直三棱柱，∴ABB′A′为矩形，则AB′，EN共面，设AB′∩EN=F，连接FM，则EN∥BB′∥CC′，且F为AB′的中点．又∵M为CC′的中点，∴NF∥CM，NF=CM，则CN∥FM，而MF⊂平面AB'M，CN⊄平面AB'M，∴CN∥平面AB'M；（2）解：在三角形ABC中，由余弦定理可得：AC2=AB2+BC2﹣2AB×BC×cosB=22+12﹣2×2×1×cos60°=3．∴AC2+BC2=AB2，则AC⊥CB．建立如图所示空间直角坐标系，则C（0，0，0），A（），B′（0，1，2），M（0，0，1），∴，，设平面AB′M的一个法向量为．由，取x=1，得．∵AC⊥平面BCC′B′，∴可取平面BCC′B′的一个法向量．∴cos＜＞=∴平面AB'M与平面BB'C所成的锐二面角的余弦值为．19．为推行“新课改”教学法，某数学老师分别用传统教学和“新课改”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中个随机抽取20名学生的成绩进行统计，结果如表：记成绩不低于105分者为“成绩优良”．分数[0，90）[90，105）[105，1200）[120，135）[135，150）甲班频数 5 6 4 4 1乙班频数 1 3 6 5（1）由以上统计数据填写下面的2×2列联表，并判断能否有97.5%的把握认为“成绩优良”与教学方式有关？（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为X，求X的分布列和数学期望．甲班乙班总计成绩优良成绩不优良总计附：K2=，（n=a+b+c+d）临界值表：P（K2≥k0） 0.10 0.050 0.025 0.010k0 2.706 3.841 5.024 6.635【考点】CG：离散型随机变量及其分布列；BO：独立性检验的应用；CH：离散型随机变量的期望与方差．【分析】（1）根据以上统计数据填写2×2列联表，根据列联表计算K2，对照临界值得出结论；（2）由题意知X的可能取值，计算对应的概率值，写出X的分布列，计算数学期望值．【解答】解：（1）根据以上统计数据填写2×2列联表，如下；甲班乙班总计成绩优良 9 16 25成绩不优良 11 4 15总计 20 20 40根据列联表，计算K2==≈5.227＞5.024，对照临界值知，有97.5%的把握认为“成绩优良”与教学方式有关；（2）由表可知，8人中成绩不优良的人数为3，则X的可能取值为0、1、2、3，则P（X=0）==，P（X=1）==，P（X=2）==，P（X=3）==；所以X的分布列为：X 0 1 2 3P数学期望为E（X）=0×+1×+2×+3×==．20．一张坐标纸上涂着圆E：（x+1）2+y2=8及点P（1，0），折叠此纸片，使P与圆周上某点P'重合，每次折叠都会留下折痕，设折痕与EP'的交点为M．（1）求M的轨迹C的方程；（2）直线l：y=kx+m与C的两个不同交点为A，B，且l与以EP为直径的圆相切，若，求△ABO的面积的取值范围．【考点】J9：直线与圆的位置关系．【分析】（1）折痕为PP′的垂直平分线，则|MP|=|MP′|，推导出E的轨迹是以E、P为焦点的椭圆，且a=，c=1，由此能求出M的轨迹C的方程．（2）l与以EP为直径的圆x2+y2=1相切，从而m2=k2+1，由，得（1+2k2）x2+4kmx+2m2﹣2=0，由此利用根的判别式、韦达定理、向量的数量积、弦长公式、三角形面积公式，能求出△AOB的面积的取值范围．【解答】解：（1）折痕为PP′的垂直平分线，则|MP|=|MP′|，由题意知圆E的半径为2，∴|ME|+|MP|=|ME|+|MP′|=2＞|EP|，∴E的轨迹是以E、P为焦点的椭圆，且a=，c=1，∴b2=a2﹣c2=1，∴M的轨迹C的方程为=1．（2）l与以EP为直径的圆x2+y2=1相切，则O到l即直线AB的距离：=1，即m2=k2+1，由，消去y，得（1+2k2）x2+4kmx+2m2﹣2=0，∵直线l与椭圆交于两个不同点，∴△=16k2m2﹣8（1+2k2）（m2﹣1）=8k2＞0，k2＞0，设A（x1，y1），B（x2，y2），则，，y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2=，又=x1x2+y1y2=，∴，∴，==，设μ=k4+k2，则，∴=，，∵S△AOB关于μ在[，2]单调递增，∴，∴△AOB的面积的取值范围是[，]．21．已知f（x）=且a≠1），f（x）是增函数，导函数f'（x）存在零点．（1）求a的值；（2）设A（x1，y1），B（x2，y2）（x1＜x2）是函数f（x）图象上的两点，x0是AB中点的横坐标，是否存在x0，使得f'（x0）=成立？若存在，请证明；若不存在，请说明理由．【考点】6B：利用导数研究函数的单调性；6D：利用导数研究函数的极值．【分析】（1）求出函数的导数，从而可得△=4ln2a﹣4lna=0，从而解得；（2）求导，得到（x2+x1）﹣2+=（x2+x1）﹣2+，化简得ln﹣=0，即ln﹣=0，令t=＞1，g（t）=lnt﹣，根据函数的单调性判断即可．【解答】解：（1）∵f（x）=x2﹣2x+log a x，∴f′（x）=x﹣2+=，∵f（x）在（0，+∞）上是增函数，且f′（x）存在零点，∴△=4ln2a﹣4lna=0，解得，lna=1或lna=0；故a=e或a=1（舍去）；故a=e；（2）假设存在x0，使得f′（x0）=成立，由（1）得：f（x）=x2﹣2x+lnx，（x＞0），f′（x）=x﹣2+，f′（x0）=x0﹣2+=（x2+x1）﹣2+，又==（x2+x1）﹣2+，故（x2+x1）﹣2+=（x2+x1）﹣2+，化简得ln﹣=0，即ln﹣=0，令t=＞1，g（t）=lnt﹣，则g′（t）=﹣=＞0，g（t）在（1，+∞）递增，则g（t）＞g（1）=0，故不存在x0，使得f'（x0）=成立．[选修4-4：参数方程与极坐标系]22．在平面直角坐标系xoy中，以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为，且曲线C在极坐标系中过点（2，π）．（1）求曲线C的直角坐标方程；（2）设直线（t为参数）与曲线C相交于A，B两点，直线m过线段AB的中点，且倾斜角是直线l的倾斜角的2倍，求m的极坐标方程．【考点】Q4：简单曲线的极坐标方程；QH：参数方程化成普通方程．【分析】（1）由曲线C在极坐标系中过点（2，π），得到曲线C的极坐标方程为4ρ2sin2θ+ρ2cos2θ=4，由此能求出曲线C的直角坐标方程．（2）直线l消去参数t，得直线l的普通方程为x﹣2y+2=0，联立，得x2+2x=0，求出AB的中点为M（﹣1，），从而直线l的斜率为，由此求出直线m的斜率为．从而求出直线m的直角坐标方程，进而求出m的极坐标方程．【解答】解：（1）∵曲线C在极坐标系中过点（2，π），∴把（2，π）代入曲线C的极坐标方程，得：4=，解得a=4，∴曲线C的极坐标方程为，即4ρ2sin2θ+ρ2cos2θ=4，∴曲线C的直角坐标方程为x2+4y2=4，即=1．（2）∵直线（t为参数），∴消去参数t，得直线l的普通方程为x﹣2y+2=0，联立，得x2+2x=0，解得x=﹣2或x=0，∴A（﹣2，0），B（0，1），∴AB的中点为M（﹣1，），∵直线l的斜率为，即tanα=，∴tan2α==．∴直线m的方程为y﹣=（x+1），即8x﹣6y+11=0，∴m的极坐标方程为8ρcosθ﹣6ρsinθ+11=0．[选修4-5：不等式选讲]23．已知函数f（x）=|x﹣1|+|x﹣a|（a＞0），其最小值为3．（1）求实数a的值；（2）若关于x的不等式f（x）+|x|＞m2﹣2m对于任意的x∈R恒成立，求实数m的取值范围．【考点】R4：绝对值三角不等式；R5：绝对值不等式的解法．【分析】（1）求出f（x）的最小值，得到关于a的方程，求出a的值即可；（2）根据不等式的性质，问题转化为m2﹣2m＜3，解出即可．【解答】解：（1）f（x）=|x﹣1|+|x﹣a|≥|a﹣1|，故|a﹣1|=3，解得：a=﹣2或4，由a＞0，得a=4；（2）由（1）得f（x）=|x﹣1|+|x﹣4|，x≥4时，f（x）=x﹣1+x﹣4=2x﹣5≥3，1＜x＜4时，f（x）=x﹣1﹣x+4=3，x≤1时，f（x）=1﹣x﹣x+4=﹣2x+5≥3，∴f（x）+|x|≥3，当x=0时”=“成立，故m2﹣2m＜3即（m+1）（m﹣3）＜0，解得：﹣1＜m＜3，故m的范围是（﹣1，3）．。
安徽省宿州市2019-2020学年高考数学三模考试卷含解析
安徽省宿州市2019-2020学年高考数学三模考试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知(1,3),(2,2),(,1)a b c n ===-r r r ，若()a c b -⊥r r r，则n 等于（ ）A ．3B ．4C ．5D ．6【答案】C 【解析】 【分析】先求出(1,4)a c n -=-r r ，再由()a c b -⊥r r r，利用向量数量积等于0，从而求得n .【详解】由题可知(1,4)a c n -=-r r，因为()a c b -⊥r r r，所以有()12240n -⨯+⨯=，得5n =，故选：C. 【点睛】该题考查的是有关向量的问题，涉及到的知识点有向量的减法坐标运算公式，向量垂直的坐标表示，属于基础题目.2．执行如图所示的程序框图若输入12n =，则输出的n 的值为（ ）A ．32B ．2C ．52D ．3【答案】C 【解析】 【分析】由程序语言依次计算，直到a b <时输出即可【详解】 程序的运行过程为n12132 252a522 32112b1ln 23ln 2ln 25ln 2当n=2时，51ln 22n >=；时，15ln 22<，此时输出2n =. 故选：C 【点睛】本题考查由程序框图计算输出结果，属于基础题3．某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是( )A ．28cmB ．212cmC ．()2452cmD ．()2454cm【答案】D 【解析】 【分析】根据三视图判断出几何体为正四棱锥，由此计算出几何体的表面积. 【详解】根据三视图可知，该几何体为正四棱锥.底面积为224⨯=.22215+1425452⨯⨯=所以该几何体的表面积是()2454cm .故选：D 【点睛】本小题主要考查由三视图判断原图，考查锥体表面积的计算，属于基础题.4．函数()()sin f x A x =+ωϕ（其中0A >，0>ω，2πϕ<）的图象如图，则此函数表达式为（ ）A ．()3sin 24f x x π⎛⎫=+⎪⎝⎭B ．()13sin 24f x x π⎛⎫=+⎪⎝⎭C ．()3sin 24f x x π⎛⎫=- ⎪⎝⎭D ．()13sin 24πf x x ⎛⎫=- ⎪⎝⎭【答案】B 【解析】 【分析】由图象的顶点坐标求出A ，由周期求出ω，通过图象经过点3,02π⎛⎫⎪⎝⎭，求出ϕ，从而得出函数解析式. 【详解】解：由图象知3A =，534422T πππ⎛⎫=-=⎪⎝⎭，则2142ωπ==π， 图中的点3,02π⎛⎫⎪⎝⎭应对应正弦曲线中的点(,0)π， 所以1322πϕπ⨯+=，解得4πϕ=，故函数表达式为()13sin 24f x x π⎛⎫=+ ⎪⎝⎭．故选：B. 【点睛】本题主要考查三角函数图象及性质，三角函数的解析式等基础知识；考查考生的化归与转化思想，数形结合思想，属于基础题.5．已知函数()f x 满足()()11f x f x -=+，当1x ≥时，()2f x x x=-，则()}{21x f x +>=（ ）A ．{3x x <-或}0x > B ．{0x x <或}2x > C ．{2x x <-或}0x > D ．{2x x <或}4x >【答案】C【解析】 【分析】简单判断可知函数关于1x =对称，然后根据函数()2f x x x =-的单调性，并计算21x xx ⎧-=⎪⎨⎪≥⎩，结合对称性，可得结果. 【详解】由()()11f x f x -=+， 可知函数()f x 关于1x =对称 当1x ≥时，()2f x x x=-， 可知()2f x x x=-在[)1,+∞单调递增 则2120x x xx ⎧-=⎪⇒=⎨⎪≥⎩ 又函数()f x 关于1x =对称，所以()01f = 且()f x 在(),1-∞单调递减，所以20x +<或22x +>，故2x <-或0x > 所以()}{21x f x +>={2x x <-或}0x > 故选：C 【点睛】本题考查函数的对称性以及单调性求解不等式，抽象函数给出式子的意义，比如：()()11f x f x -=+，()()110f x f x -++=，考验分析能力，属中档题.6．过抛物线C 的焦点且与C 的对称轴垂直的直线l 与C 交于A ，B 两点，||4AB =，P 为C 的准线上的一点，则ABP ∆的面积为（ ） A ．1 B ．2 C ．4 D ．8【答案】C 【解析】 【分析】设抛物线的解析式22(0)y px p =>，得焦点为,02p F ⎛⎫⎪⎝⎭，对称轴为x 轴，准线为2p x =-，这样可设A点坐标为,22p ⎛⎫⎪⎝⎭，代入抛物线方程可求得p ，而P 到直线AB 的距离为p ，从而可求得三角形面积． 【详解】设抛物线的解析式22(0)y px p =>， 则焦点为,02p F ⎛⎫⎪⎝⎭，对称轴为x 轴，准线为2p x =-，∵ 直线l 经过抛物线的焦点，A ，B 是l 与C 的交点， 又AB x ⊥轴，∴可设A 点坐标为,22p ⎛⎫⎪⎝⎭， 代入22y px =，解得2p =，又∵点P 在准线上，设过点P 的AB 的垂线与AB 交于点D ，||222p pDP p =+-==， ∴11||||24422ABP S DP AB ∆=⋅=⨯⨯=. 故应选C. 【点睛】本题考查抛物线的性质，解题时只要设出抛物线的标准方程，就能得出A 点坐标，从而求得参数p 的值．本题难度一般．7．已知数列{}n a 满足11a =,1n n a a n --=(2n ≥),则数列{}n a 的通项公式n a =( ) A ．()112n n + B ．()1312n n - C ．2n n 1-+ D ．222n n -+【答案】A 【解析】 【分析】利用数列的递推关系式，通过累加法求解即可． 【详解】数列{}n a 满足：11a =，*1(2,)n n a a n n n N --=∈…， 可得11a =212a a -= 323a a -= 434a a -=⋯1n n a a n --=以上各式相加可得：1123(1)2n a n n n =+++⋯+=+， 故选：A ． 【点睛】本题考查数列的递推关系式的应用，数列累加法以及通项公式的求法，考查计算能力．8．某人2018年的家庭总收人为80000元，各种用途占比如图中的折线图，2019年家庭总收入的各种用途占比统计如图中的条形图，已知2019年的就医费用比2018年的就医费用增加了4750元，则该人2019年的储畜费用为（ ）A ．21250元B ．28000元C ．29750元D ．85000元【答案】A 【解析】 【分析】根据 2018年的家庭总收人为80000元，且就医费用占10% 得到就医费用8000010%8000⨯=，再根据2019年的就医费用比2018年的就医费用增加了4750元，得到2019年的就医费用，然后由2019年的就医费用占总收人15%，得到2019年的家庭总收人再根据储畜费用占总收人25%求解. 【详解】因为2018年的家庭总收人为80000元，且就医费用占10% 所以就医费用8000010%8000⨯=因为2019年的就医费用比2018年的就医费用增加了4750元， 所以2019年的就医费用12750元， 而2019年的就医费用占总收人15%所以2019年的家庭总收人为127501585000÷%= 而储畜费用占总收人25%所以储畜费用：850002521250⨯%= 故选：A【点睛】本题主要考查统计中的折线图和条形图的应用，还考查了建模解模的能力，属于基础题.9．已知12,F F 是双曲线22221(0,0)x y a b a b-=>>的左右焦点，过1F 的直线与双曲线的两支分别交于,A B 两点（A 在右支，B 在左支）若2ABF ∆为等边三角形，则双曲线的离心率为（ ）A B ．C D【答案】D 【解析】 【分析】根据双曲线的定义可得2ABF ∆的边长为4a ，然后在12AF F ∆中应用余弦定理得,a c 的等式，从而求得离心率． 【详解】由题意122AF AF a -=，212BF BF a -=，又22AF BF AB ==， ∴114AF BF AB a -==，∴12BF a =， 在12AF F ∆中2221212122cos60F F AF AF AF AF =+-︒，即22214(6)(4)2642c a a a a =+-⨯⨯⨯228a =，∴． 故选：D ． 【点睛】本题考查求双曲线的离心率，解题关键是应用双曲线的定义把A 到两焦点距离用a 表示，然后用余弦定理建立关系式．10．已知函数()2x f x x x ln a ⎛⎫=- ⎪⎝⎭，关于x 的方程f （x ）＝a 存在四个不同实数根，则实数a 的取值范围是（ ）A ．（0，1）∪（1，e ）B ．10e ⎛⎫⎪⎝⎭，C ．11e ⎛⎫⎪⎝⎭，D ．（0，1）【答案】D 【解析】 【分析】原问题转化为221x x a a =有四个不同的实根，换元处理令t =，对g （t）21lnt t t ⎫=--⎪⎭进行零点个数讨论. 【详解】由题意，a ＞2，令t =， 则f （x ）＝a ⇔2x x x ln a a ⎛⎫-= ⎪⎝⎭⇔221x x a a -=⇔221t -=⇔210lnt t t ⎫-=⎪⎭． 记g （t）21lnt t t ⎫=-⎪⎭．当t ＜2时，g （t ）＝2ln （﹣t）t 1t-）单调递减，且g （﹣2）＝2， 又g （2）＝2，∴只需g （t ）＝2在（2，+∞）上有两个不等于2的不等根．则210lnt t t ⎫--=⎪⎭221tlntt =-， 记h （t ）221tlntt =-（t ＞2且t≠2）， 则h′（t ）()()()22222222212122141(1)(1)t t lnt lnt t t lnt t t t ⎛⎫-+- ⎪+--+⎝⎭==--．令φ（t ）2211t lnt t -=-+，则φ′（t ）()()2222222221211(1)(1)(1)t t t t t t t t t +---=-=-++＜2． ∵φ（2）＝2，∴φ（t ）2211t lnt t -=-+在（2，2）大于2，在（2，+∞）上小于2．∴h′（t ）在（2，2）上大于2，在（2，+∞）上小于2， 则h （t ）在（2，2）上单调递增，在（2，+∞）上单调递减． 由211222112t t tlnt lnt limlim t →→+==-1，即a ＜2．∴实数a 的取值范围是（2，2）． 故选：D ． 【点睛】此题考查方程的根与函数零点问题，关键在于等价转化，将问题转化为通过导函数讨论函数单调性解决问题.11．如图，正方体1111ABCD A B C D -中，E ，F ，G ，H 分别为棱1AA 、1CC 、11B C 、11A B 的中点，则下列各直线中，不与平面1ACD 平行的是（ ）A ．直线EFB ．直线GHC ．直线EHD ．直线1A B【答案】C 【解析】 【分析】充分利用正方体的几何特征，利用线面平行的判定定理，根据//EF AC 判断A 的正误.根据1111//,//GH A C A C AC ，判断B 的正误.根据11//,EH C D C D 与 1D C 相交，判断C 的正误.根据11//A B D C ，判断D 的正误.【详解】在正方体中，因为//EF AC ，所以//EF 平面1ACD ，故A 正确.因为1111//,//GH A C A C AC ，所以//GH AC ，所以//GH 平面1ACD 故B 正确. 因为11//A B D C ，所以1//A B 平面1ACD ，故D 正确.因为11//,EH C D C D 与 1D C 相交，所以 EH 与平面1ACD 相交，故C 错误. 故选：C 【点睛】本题主要考查正方体的几何特征，线面平行的判定定理，还考查了推理论证的能力，属中档题.12．已知12,F F 分别为双曲线2222:1x y C a b-=的左、右焦点，点P 是其一条渐近线上一点，且以12F F 为直径的圆经过点P ，若12PF F ∆223，则双曲线的离心率为（ ） A 3 B ．2C 5D ．3【答案】B 【解析】 【分析】根据题意，设点()00,P x y 在第一象限，求出此坐标，再利用三角形的面积即可得到结论. 【详解】由题意，设点()00,P x y 在第一象限，双曲线的一条渐近线方程为by x a=， 所以，00by x a=， 又以12F F 为直径的圆经过点P ，则OP c =，即22200x y c +=，解得0x a =，0y b =，所以，1220122PF F S c y c b ∆=⋅⋅=⋅=，即c =，即()22243c c a =-，所以，双曲线的离心率为2e =. 故选：B. 【点睛】本题主要考查双曲线的离心率，解决本题的关键在于求出a 与c 的关系，属于基础题. 二、填空题：本题共4小题，每小题5分，共20分。
【最新】湖南省衡阳市高三第三次联考(三模)数学(理)试题(含答案)
理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知i 为虚数单位，则12i z i =-在复平面内的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2.若01cos(75)3α+=，则0cos(302)α-的值为（ ） A ．429 B ．429- C ．79 D ．79- 3.在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C 为正态分布(1,1)N -的密度曲线）的点的个数大约为（ ）A ．1193B ．1359C ．2718D ．3413附：若X ～2(,)N μσ，()0.6826P X μσμσ-<<+=，(22)0.9544P X μσμσ-<<+=.4.有下列三个结论：①命题“,ln 0x R x x ∀∈->”的否定是“000,ln 0x R x x ∃∈-≤”；②“1a =”是“直线10x ay -+=与直线20x ay +-=互相垂直”的充要条件； ③命题“角α的终边在第一象限，则α为锐角”的逆否命题为真命题；其中正确结论的个数为（ ）A ．0个B ．1个C ．2个D ．3个5.某产品在某零售摊位的零售价x （单位：元）与每天的销售量y （单位：个）的统计资料如下表所示，由表可得回归直线^^^y b x a =+中的4b =-，据此模型预测零售价为20元时，每天的销售量为（ ）16 17 18 19 y 50 34 41 31 A ．23个 B ．25个 C ．27个 D ．29个6.将()sin 2f x x =的图象右移(0)2πϕϕ<<个单位后得到()g x 的图象，若对于满足12|()()|2f x g x -=的12,x x 有12||x x -的最小值为3π，则ϕ的值为（ ） A ．12π B ．6π C ．4π D ．3π 7.某程序框图如图所示，执行该程序，若输入的3N =，则输出的i 等于（ ）A ．6B ．7C ．8D ．98.棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（ ）A ．143B ．4C ．103D ．39.双曲线:M 22221(0,0)x y a b a b-=>>的左、右焦点为12,F F ，抛物线2:2(0)N y px p =>的焦点为2F ，点P 为双曲线M 与抛物线N 的一个交点，若线段1PF 的中点在y 轴上，则该双曲线的离心率为（ ）A 31B 21C 31+D 21+ 10.将4名大学生分配到,,A B C 三个不同的学校实习，每个学校至少分配一人，若甲要求不到A 学校，则不同的分配方案共有（ ）A ．36种B ．30种C ．24种D ．20种11.设,M N 为抛物线2:2(0)C y px p =>上任意两点，点E 的坐标为(,0)(0)λλ-≥，若EM EN •u u u u r u u u r 的最小值为0，则λ等于（ ）A ．2pB ．pC ．2p D ．0 12.已知()||x f x x e =•，又2()()()()g x f x tf x t R =+∈，若满足()1g x =-的x 有四个，则t 的取值范围为（ ）A ．21(,)e e +-∞-B ．21(,)e e ++∞C ．21(,2)e e +--D ．21(2,)e e+ 第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.在ABC ∆中，||||AB AC AB AC +=-u u u r u u u r u u u r u u u r ，2,1AB AC ==，,E F 为BC 边的两个三等分点，则AE AF •=u u u r u u u r .14.已知(2,1),(0,0)A O ，点(,)M x y 满足12222x y x y ≤≤⎧⎪≤⎨⎪-≤⎩，则Z OA AM =•u u u r u u u u r 的最大值为 .15.已知,,,P A B C 为球O 球面上四点，其中ABC ∆为正三角形，三棱锥P ABC -的体积为4，且30APO BPO CPO ∠=∠=∠=o ，则球O 的表面积为 . 16.若函数2()ln()f x x x a =++与21()(0)2x g x x e x =+-<的图象上存在关于y 轴对称的点，则实数a 的取值范围为 . 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （本小题满分12分） 设函数21()(0)3f x x x=+>，数列{}n a 满足1111,()n n a a f a -==，其中*n N ∈，且2n ≥. （1）求数列{}n a 的通项公式；（2）对*n N ∈，设12233411111n n n S a a a a a a a a +=++++L ，若34n t S n≥恒成立，求实数t 的取值范围.18. （本小题满分12分）某校为了解一个英语教改班的情况，举行了一次测试，将该班60位学生的英语成绩进行统计，得频率分布直方图如图，其中成绩分组区间为[50,60)，[60,70)，[70,80)，[80,90)，[90,100].（1）求出该班英语成绩的众数和平均数；（2）从成绩低于80分的学生中随机抽取2人，规定抽到的学生成绩在[50,60)的记1绩点分，在[60,80)的记2绩点分，设抽取2人的总绩点分为ξ，求ξ的分布列和数学期望.19. （本小题满分12分）如图，在四棱锥S ABCD -中，底面ABCD 为正方形，SD ⊥面ABCD ，点,E F 分别为,AB SC 的中点.（1）求证：//EF 平面SAD ；（2）设2SD DA =，求二面角A EF D --的余弦值.20. （本小题满分12分）已知椭圆1:C 22221(0)x y a b a b+=>>的一个焦点与抛物线22:2(0)C y px p =>的焦点F 重合，且点F 到直线10x y -+=2，1C 与2C 的公共弦长为26.（1）求椭圆1C 的方程及点F 的坐标；（2）过点F 的直线l 与1C 交于,A B 两点，与2C 交于,C D 两点，求11||||AB CD +的取值范围.21. （本小题满分12分）已知函数32()()f x x x x R =-+∈，()g x 满足'()(,0)a g x a R x x =∈>，且()g e a =，其中e 为自然对数的底数.（1）已知1()()x h x e f x -=•，求()h x 在(1,(1))h 处的切线方程；（2）设函数(),1()(),1f x x F xg x x <⎧=⎨≥⎩，O 为坐标原点，若对于()y F x =在1x ≤-时的图象上的任一点P ，在曲线()y F x =()x R ∈上，总存在一点Q ，使得0OP OQ •<u u u r u u u r ，且PQ uuu r 的中点在y 轴上，求实数a 的取值范围.请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，过圆O 外一点作圆O 的两条切线,EA EB ，其中,A B 为切点，BC 为圆O 的一条直径，连CA 并延长交BE 的延长线于D 点.（1）证明：BE ED =；（2）若3AD AC =，求:AE AC 的值.23. （本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系xoy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知在极坐标系中，(33,)2A π，(3,)3B π，圆C 的方程为2cos ρθ=. （1）求在平面直角坐标系xoy 中圆C 的标准方程；（2）已知P 为圆C 上的动点，求ABP ∆面积的最大值.24. （本小题满分10分）选修4-5：不等式选讲已知函数()|||21|f x x x =--，记()1f x >-的解集为M .（1）求M ；（2）已知a M ∈，比较21a a -+与1a 的大小. 答案与解析 1.B 525)21(i i i Z +-=+= 2.C 31)15sin()75cos(=-︒=+︒αα 979121)15(sin 21)230cos(2=⨯-=-︒-=-︒∴αα 3.B 1,1=-=σμΘ 1359.026826.09544.0=-=∴s 1359.0=∴μ 4.B 只有①对 5.D 由39,5.17==y x 代入方程可知a=109，∴当20=x 时，29109204=+⨯-=y6.B 由图可知，6323434πφπφπππφπ=⇒=-⇒=-+7.C →=→=→=→=→=→=→=→=8416352103n i n i n i n n 8172645=→=→=→=→=→=→=i n i n i n i8.B 如图，所求几何体的体积为42=正方体V 9.B 如图，由题意可知：∴=,2pc 抛物线方程为12.4PF cx y Θ=的中点在y 轴上，c x p =∴，带入抛物线方程可得c y p 2±=，又点P 在双曲线上，12)21(22314222222+=⇒+=+=⇒=-∴e e b c a c10.C ①：甲单独一人，则12222312=⋅⋅A C C ，②：甲与另一人一起，则：12221213=⋅⋅A C C11.C 由图可知，0)(min =⋅EN EM Θ ∴图中此时的︒=∠90MEN故此时EM 与抛物线相切，且1=EM k12.A 012=++tx x 一根在)1,0(e 中间，一根在),1(+∞e ，0)1(<∴ey 即：01112<+⋅+e t e ，1112--<⋅∴e e t ，e e e e t 112+-=--<∴13.91014.1 52-+=⋅=y x AM OA Z ，如图，15222max =-+⨯=Z15.π16 令BC=a ，则a AH 33=，又AHP Δ中，︒=∠30APH Θ，a a PH =⋅=∴333，4391232321313==⨯⨯⨯=∴-a a a a V ABC P 3=⇒a 从而，3PH 3==，AH ，令球O 的半径为R ，则在O ΔAH 中可知：2)3()3(222=⇒=-+R R R ，πR πS 1642==∴球表面积16.),(e -∞ 令)0)(,(000<x y x P 为)(x g 图象上满足条件的对称点，则),-('00y x P 在)(x f 的图象上，210200-+=∴x e x y ，)ln(0200a x x y +-+=，∴方程)0,()ln(21-∞+-=-在a x e x 上有解，)21,21(21)0,(-∈--∞∈x e x 时，Θ，且函数)ln()(a x x +-=ϕ为定义域上的减函数，又当+∞→+--∞→)ln(,a x x 时，e a a <<<∴,21ln ,21)0(即只需ϕ 17.解：(1)由11()n n a f a -=可得，123n n a a --=，n *∈N ，2n ≥. 所以{}n a 是等差数列，因为11a =，所以2211(1)33n n a n +=+-⋅=，n *∈N . …4分 (2)因为213n n a +=，所以1233n n a ++=， 所以119911()(21)(23)22123n n a a n n n n +==-++++. 122334*********()232323n n n n S a a a a a a a a n n +=++++=-=++L . …8分 34n t S n ≥恒成立等价于33234n t n n ≥+，即2423n t n ≤+恒成立．…9分令24()(0)23x g x x x =>+，则28(3)()0(23)x x g x x +'=>+，18.解：（1）由频率分布直方图可知：众数为85；24610855657585953030303030⨯+⨯+⨯+⨯+⨯ 1(5526547568510958)30=⨯⨯+⨯+⨯+⨯+⨯ 81=∴该班学生英语成绩的平均数为81.（2）依题意，成绩在[50,60)的学生数为230(10)2300⨯⨯=， 成绩在[60,80)的学生数为4630(1010)10300300⨯⨯+⨯=， ∴成绩低于80分的学生总人数为12， ∴ξ可取的值为2,3,4，222121(2)66C P C ξ===， 1121021220(3)66C C P C ξ===， 21021245(4)66C P C ξ===， ∴ξ的分布列为：∴ξ的数学期望1204511()2346666663E ξ=⨯+⨯+⨯=. 19.（解法一）（1）证明：如图1，取SD 的中点G ，连接,GF GA ， 因为,G F 分别是,SD SC 的中点，所以//GF DC ，且12GF DC =. 又底面ABCD 为正方形，且E 是AB 的中点，所以//AE DC ，且12AE DC =. 于是//AE GF ，且AE GF =，所以AEFG 是平行四边形，所以//EF AG . 又EF ⊄平面SAD ，AG ⊂平面SAD ，故//EF 平面SAD . （2）如图2，取,AG EF 的中点分别为,M N ，连接,,DM MN DN .因22SD DA DG ==，得DA DG =，又M 是AG 的中点，所以DM AG ⊥.又因为SD ⊥平面ABCD ，所以SD AB ⊥，由底面ABCD 为正方形，可得AB AD ⊥， 而SD AD D =I ，所以AB ⊥平面SAD ，又,M N 分别为,AG EF 的中点， 则//MN AB ，所以MN ⊥平面SAD ，又AG ⊂平面SAD ，则MN AG ⊥. 由于DM MN M =I ，所以AG ⊥平面MND . 又由（1）知，//EF AG ，故EF ⊥平面MND . 因此MND ∠是二面角A EF D --的平面角.设2DA =，由22SD DA DG ==，得2,DG DM ==112MN AB ==，又MN ⊥平面SAD ，DM ⊂平面SAD ，得MN DM ⊥，所以DN =从而cos 3MN MND DN ∠==，故所求二面角A EF D --的余弦值为3. （解法二）以D 为原点，射线,,DA DC DS 分别为,,x y z 的正半轴建立空间直角坐标系， （1）设2,2AB a SD b ==，则(2,,0),(0,0,2),(0,2,0)E a a S b C a ，所以(0,,)F a b ，(2,0,),(0,2,0)EF a b DC a =-=u u u r u u u r ，于是(0,2,0)(2,0,)0EF DC a a b •=•-=u u u r u u u r.则EF DC ⊥u u u r u u u r ，又DC u u u r是平面SAD 的一个法向量，所以//EF 平面SAD .（2）设2DC =，有24SD DC ==，则(0,0,0),(2,0,0),(2,2,0),(0,2,0),(0,0,4)D A B C S ，(2,1,0),(0,1,2)E F ，则(2,1,0)DE =u u u r ，(0,1,2)DF =u u u r ，(0,1,0)AE =u u u r ，(2,0,2)EF =-u u u r，设平面DEF 的法向量为(,,)n x y z =r ，则n DEn DF⎧⊥⎪⎨⊥⎪⎩r u u u rr u u u r ，所以2020x y y z +=⎧⎨+=⎩，取(1,2,1)n =-r . 同理可得面AEF 的一个法向量为(1,0,1)m =u r ，所以3cos ||||||26n m n m θ•===•⨯r u rr u r 故所求二面角A EF D --320. （1）∵22:2C y px =的焦点F 的坐标为(,0)2p . 由点F 到直线10x y -+=2|1|222p +=. ∵0p >，解得2p =， 又(1,0)F 为椭圆的一个焦点，∴221a b -=①∵1C 与2C的公共弦长为，1C 与2C 都关于x 轴对称，而2C 的方程为24y x =，从而1C 与2C的公共点的坐标为3(,2， ∴229614a b+=② 联立①②解得229,8a b ==，∴1C 的方程为22198x y +=，点F 的坐标为(1,0). （2）当l 过点F 且垂直于x 轴时，l 的方程为1x =，代入22198x y +=，求得83y =±， ∴16||3AB =，把1x =代入22:4C y x =求得2y =±. ∴||4CD =，此时，11317||||16416AB CD +=+=， 当l 与x 轴不垂直时，要使l 与2C 有两个交点，可设l 的方程为(1)(0)y k x k =-≠， 此时设11223344(,),(,),(,),(,),A x y B x y C x y D x y把直线l 的方程与椭圆1C 的方程联立得22(1)198y k x x y =-⎧⎪⎨+=⎪⎩，消去y 化简得2222(89)189720k x k x k +-+-=，可得21221889k x x k +=+，212297289k x x k-=+，213664(1)0k ∆=⨯+>，∴||AB =2248(1)89k k +==+ 把直线l 的方程与抛物线2C 的方程联立得24(1)y xy k x ⎧=⎨=-⎩，消去y 化简得2222(24)0k x k x k -++=，可得234224k x x k ++=，2216(1)0k ∆=+>， ∴223422244(1)||22k k CD x x k k ++=++=+=， ∴22221189||||48(1)4(1)k k AB CD k k ++=+++ 222222891221871348(1)48(1)1648(1)k k k k k k +++===-+++ ∵20k >，∴211k +>， ∴2131304848(1)k -<-<+， ∴1117(,)||||616AB CD +∈， 综上可得11||||AB CD +的取值范围是17(,]616. 21、解：（1）Q 321()()xh x x x e -=-+，321()(42)xh x x x x e-'=-+，(1)0h ∴=，(1)1h '=-。
2019长春高三三模数学理科
长春市普通高中2019届高三质量监测(三)数学试题卷(理科)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项就是符合题目要求的、1、 sin 210︒= A 、 12-B 、 3-C 、 12D 、 32、已知集合{1,0,1,2},{|(1)(2)0}A B x x x =-=+-<,则A B =A 、 {1,0,1,2}-B 、 {1,0,1}-C 、 {0,1,2}D 、 {0,1} 3、 若复数1a ii++的实部与虚部相等,则实数a 的值为 A 、 0 B 、 1 C 、 2 D 、 3 4、执行如图所示的程序框图,如果输入=4N ,则输出p 为A 、 6B 、 24C 、 120D 、 7205、 已知等差数列{}n a 的前n 项与为n S ,且24a =,42a =,则6S = A 、 0 B 、 10 C 、 15 D 、 306、 已知1e 、2e 就是两个单位向量,且夹角为3π,则1212(2)(2)-⋅-+=e e e e A 、 32-B 、 36- C 、 12D 、 337、 若 8 件产品中包含 6 件一等品,在其中任取 2 件,则在已知取出的 2 件中有 1 件不就是一等品的条件下,另 1 件就是一等品的概率为 A 、37 B 、 45 C 、 67D 、 1213 8、 已知,m n 为两条不重合直线,α,β为两个不重合平面,下列条件中,一定能推出α//β的就是A 、 //,,m n m n αβ⊂⊂B 、 //,,m n m n αβ⊥⊥C 、 ,//,//m n m n αβ⊥D 、 ,,m n m n αβ⊥⊥⊥9.“科技引领,布局未来”科技研发就是企业发展的驱动力量、 2007 年至 2018 年,某企业连续 12 年累计研发投入达 4100 亿元,我们将研发投入与经营收入的比值记为研发投入占营收比、 这 12 年间的研发投入(单位:十亿元)用下图中的条形图表示,研发投入占营收比用下图中的折线图表示、根据折线图与条形图,下列结论错误．．的就是 A 、 2012-2013 年研发投入占营收比增量相比 2017-2018 年增量大 B 、 该企业连续 12 年研发投入逐年增加 C 、 2015-2016 年研发投入增值最大D 、 该企业连续 12 年研发投入占营收比逐年增加10、 函数2()()41x x x e e f x x --=-的部分图象大致就是11、 已知O 为坐标原点,抛物线2:8C y x =上一点A 到焦点F 的距离为 6,若点P 为抛物线C 准线上的动点,则||||OP AP +的最小值为A 、 4B 、 43C 、 46D 、 6312、 已知函数1ln ,1()11,122x x f x x x +⎧⎪=⎨+<⎪⎩≥,若12x x ≠,且12()()2f x f x +=,则12x x +的取值范围就是A 、 [32ln 3,)-+∞B 、 [1,)e -+∞C 、 [32ln 2,)-+∞D 、[2,)+∞二、填空题:本题共4小题,每小题5分、 13、 已知函数()sin()(0)4f x x πωω=+>的最小正周期为π,则ω=_____________,若2()210f α=,则sin 2α=____________、 14、 已知矩形ABCD ,12AB =,5BC =,以,A B 为焦点,且过,C D 两点的双曲线的离心率为 、15、 我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两堑堵、 斜解堑堵,其一为阳马,一为鳖臑、 阳马居二,鳖臑居一,不易之率也、 合两鳖臑三而一,验之以棊,其形露矣、”若 称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为 1,对该几何体有如下描述:① 四个侧面都就是直角三角形; ② 最长的侧棱长为26;③ 四个侧面中有三个侧面就是全等的直角三角形; ④ 外接球的表面积为24π、其中正确的描述为 、16、已知数列{}n a 中,12a =,1(N )12n n n na a n n a *+=∈++,则11nk ka ==∑ 、 三、解答题:共70份,解答应写出文字说明、证明过程或演算步骤、第17~21题为必考题,每个试题考生都必须作答,第22~23选考题,考生根据要求作答、 (一)必考题:共60分 17、(本小题满分12分)在ABC ∆中,6AB =,42AC =、 (1)若22sin 3B =,求ABC ∆的面积; (2)若点D 在BC 边上且2,BD DC AD BD ==,求BC 的长、18、 (本小题满分12分)某工厂有两个车间生产同一种产品,第一车间有工人 200 人,第二车间有工400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对她们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照 [55,65),[65,75) ,[75,85),[85,95]进行分组)、(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min 的人数;(Ⅱ)分别估计两个车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高？(同一组中的数据以这组数据所在的区间中点的值作代表)(Ⅲ)从第一车间样本中生产时间小于 75min 的工人中随机抽取3人,记抽取的生产时间小于 65min 的工人人数为随机变量X ,求X 的分布列及数学期望、 19、 (本小题满分12分)如图,等腰梯形ABCD 中,AB CD ∥, 1AD AB BC ===,2CD =, E 为CD 中点, AE 与BD 交于点O ,将ADE ∆沿AE 折起,使点D 到达点P 的位置(P ∉平面ABCE )、 (1)证明: 平面POB ⊥平面ABCE ; (2)若直线PB 与平面ABCE 所成的角为4π,求二面角A PE C --的余弦值、20、 (本小题满分12分)如图所示,椭圆2222:1(0)x y C a b a b +=>>离心率为22,1B 、2B 就是椭圆C 的短轴端点,且1B 到焦点的距离为32,点M 在椭圆C 上运动,且点M 不与1B 、2B 重合,点N 满足11NB MB ⊥,22NB MB ⊥、(1)求椭圆C 的方程;(2)求四边形21MB NB 面积的最大值、 21、 (本小题满分12分) 已知a R ∈,函数2()ln f x a x x=+、 (1)讨论函数()f x 的单调性;(2)若2x =就是()f x 的极值点,且曲线()y f x =在两点1122(,()),(,())P x f x Q x f x12(6)x x <<处的切线互相平行,这两条切线在y 轴上的截距分别为1b 、2b ,求12b b -的取值范围、(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做则按所做的第一题计分、 22、 (本小题满分10分)选修4-4 坐标系与参数方程选讲在直角坐标系xOy 中,直线1l 的倾斜角为30︒且经过点(2,1)A 、 以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线2:l cos 3ρθ=,从原点O 作射线交2l 于点M ,点N为射线OM 上的点,满足||||12OM ON ⋅=,记点N 的轨迹为曲线C 、 (1)求出直线1l 的参数方程与曲线C 的直角坐标方程; (2)设直线1l 与曲线C 交于P ,Q 两点,求||||AP AQ ⋅的值、23、 (本小题满分10分) 选修4-5 不等式选讲已知函数()|21||1|f x x x =-+-、 (1)求不等式()4f x ≤的解集;(2) 设函数()f x 的最小值为m ,当,,a b c R +∈,且a b c m ++=时, 212121a b c +++长春市2019年高三质量监测(三) 数学(理科)试题参考答案及评分标准一、选择题(本大题共12小题,每小题5分,共60分) 1、 A 【命题意图】本题考查诱导公式、【试题解析】A 1sin 2102︒=-、故选A 、 2、 D 【命题意图】本题考查集合运算、 【试题解析】D {|12},{0,1}B x x A B =-<<=、故选D 、3、 A 【命题意图】本题考查复数的运算、【试题解析】A 1(1),02a a iz a ++-==、故选A 、4、 B 【命题意图】本题考查程序框图、【试题解析】B 可知、 故选B 、5、C 【命题意图】本题主要考查等差数列的相关知识、【试题解析】C 161,5,15d a S =-==、故选C 、6、 A 【命题意图】本题主要考查平面向量、 【试题解析】A 可知、 故选A 、7、 D 【命题意图】本题考查条件概率的相关知识、【试题解析】D 可知、 故选D 、8、 B 【命题意图】本题主要考查空间直线与平面位置关系、【试题解析】B 可知、 故选B9、 D 【命题意图】本题考查统计识图能力、【试题解析】D 可知ABC 正确、故选D 、10、 B 【命题意图】本题主要考查函数性质的相关知识、【试题解析】B 确定函数为偶函数,代入特殊值,可排除A,C,当,()x f x →+∞→-∞、故选B 、11、 C 【命题意图】本题主要考查抛物线的相关知识、【试题解析】C 做O 点关于准线的对称点M,则所求距离与的最小值为|AM|、故选C 、 12、 C 【命题意图】本题主要考查函数与导数的相关知识、【试题解析】C 先确定121x x <<,借助条件等式,用2x 表示1x ,1212ln x x =-,得到关于2x 的函数关系式122212ln x x x x +=-+,通过构造函数并求导确定该函数的单调性求出答案、故选C 、二、填空题(本大题共4小题,每小题5分,13题对一个给3分,共20分)13、 242,25-【试题解析】由周期公式2=T ππω=得=2ω,由()210f α=得sin()410πα+=所以1sin cos 5αα+=,平方得11+2sin cos 25αα=∴24sin 225α=-14、32【试题解析】在焦点ABC ∆中,12,5,13AB BC AC === ∴离心率2||1232||||1352c AB e a AC BC ====-- 15、 ①②④ 【试题解析】如图长宽高分别为4,2,2,易得①②④正确、16、 2534n n-【试题解析】由112n n n na a n a +=++得112n n n a n a na +++=（）,即112(1)n n n n a a n a na ++++=,两边同时除以1(1)n n n n a a ++得1211(1)(1)n n n n na n a ++=++ 由累加法得154=2nn na n-∴154=2nn a -为等差数列所以2111(154)53224nk kn n n n a =+--=⋅=∑三、解答题17、(本小题满分12分)【命题意图】本题考查解三角形的相关知识、【试题解析】解:(Ⅰ)由正弦定理得426sinC22=,所以sin 1C =,2C π∠=, 所以226(42)2BC =-=,所以1242422S =⨯⨯= (6分)(Ⅱ)设DC x =,则2BD x =,则2AD x =,所以222222(2)(2)6(2)(42)22222x x x x x x x x +-+-=-⋅⋅⋅⋅ 解得:52x =所以352BC DC == (12分)18、(本小题满分12分)【命题意图】本题考查统计知识及概率相关知识、 【试题解析】(Ⅰ)由题意得,第一车间样本工人20人,其中在75min 内(不含75min) 生产完成一件产品的有6人,第二车间样本工人40人,其中在75min 内(不含75min) 生产完成一件产品的有40(0.0250.05)1030⨯+⨯=人,故第一车间工人中有60人, 第二车间工人中有300名工人中在75min 内生产完成一件产品;(4分)(II)第一车间样本平均时间为60270480109047820x ⨯+⨯+⨯+⨯==甲(min),第二车间样本平均时间为 600.25700.5800.2900.0570.5x =⨯+⨯+⨯+⨯=乙(min),∵x x >甲乙,∴乙车间工人生产效率更高;(8分)(III)由题意得,第一车间样本生产时间小于75min 的工人有6人,从中抽取3人, 其中生产时间小于65min 的有2人,随机变量X 服从超几何分布, X 可取值为0,1,2,03243641(0)205C C P X C ====,122436123(1)205C C P X C ====,21243641(2)205C C P X C ====X 的分布列为:X 012P15 35 15数学期望131()0121555E X =⨯+⨯+⨯=、 (12分)19、 (本小题满分12分)【命题意图】本小题以四棱锥为载体,考查立体几何的基础知识、 本题考查学生的空 间想象能力、推理论证能力与运算求解能力、 【试题解析】(Ⅰ)证明:在PAE △中,OP AE ⊥,在BAE △中,OB AE ⊥, AE POB ∴⊥平面,AE ABCE ⊂平面, 所以平面POB ⊥平面ABCE ;(4分) (Ⅱ)在平面POB 内作PQ OB Q ⊥=,PQ ABCE ∴⊥平面、 ∴直线PB 与平面ABCE 夹角为4PBQ π∠=,又OP OB =,OP OB ∴⊥,O 、Q 两点重合, 即OP ABCE ⊥平面,以O 为原点,OE 为x 轴,OB 为y 轴,OP 为z 轴, 建立空间直角坐标系,由题意得,各点坐标为P ,1(,0,0)2E,C ,∴1(,0,2PE =,1(2EC =, 设平面PCE 的一个法向量为1(,,)n x y z =,则1100PE n EC n ⎧⋅=⎪⎨⋅=⎪⎩,即102102x x y ⎧=⎪⎪⎨⎪+=⎪⎩,设x 则1y =-,1z =,∴1(3,1,1)n =-,由题意得平面P AE 的一个法向量2(0,1,0)n =, 设二面角A-P-EC 为α,1212|||cos |||||1n n n n α⋅===⋅即二面角A-P-EC为α的余弦值为5-、(12分) 20、(本小题满分12分)【命题意图】本小题考查直线与椭圆的位置关系,考查椭圆的相关知识、 【试题解析】解:(Ⅰ)2e =,a ∴=,又a =且222a b c =+, 218a ∴=,29b =,因此椭圆C 的方程为221189x y +=、 (4分)(Ⅱ)法一:设000(,)(0)M x y x ≠,11(,)N x y ,11MB NB ⊥,22MB NB ⊥,∴直线1NB :0033x y x y +=-+……①直线2NB :0033xy x y -=--……②由①,②解得:20109y x x -=,又22001189x y +=,012x x ∴=-,四边形21MB NB 的面积1212013||(||||)3||22S B B x x x =+=⨯,Q P OECBA20018x <≤,∴当2018x =时,S、 (12分)法二:设直线1MB :3(0)y kx k =-≠,则直线1NB :13y x k=--……①直线1MB 与椭圆C :221189x y +=的交点M 的坐标为2221263(,)2121k k k k -++,则直线2MB 的斜率为222263312112221MB k k k k k k --+==-+,∴直线2NB :23y kx =+……②由①,②解得N 点的横坐标为2621N kx k =-+,四边形21MB NB 的面积12222112||6||54||54||(||||)3()122121212||||M N k k k S B B x x k k k k k =+=⨯+==++++,当且仅当||k =,S、 (12分)21、(本小题满分12分)【命题意图】本小题主要考查函数与导数的相关知识,以导数为工具研究函数的方法,考查学生解决问题的综合能力、【试题解析】(Ⅰ)2222()a ax f x x x x -'=-+=,①当0a ≤时,()0f x '<在(0,)x ∈+∞上恒成立,∴()f x 在(0,)+∞上单调递减;②当0a >时, 2(0,)x a ∈时()0f x '<,2[,)x a ∈+∞时,()0f x '>,即()f x 在2(0,)x a ∈上单调递减,在2[,)x a∈+∞单调递增; (4分)(Ⅱ)∵2x =就是()f x 的极值点, ∴由(1)可知22a=, ∴1a = 设在()11,()P x f x 处的切线方程为112111221(ln )()()y x x x x x x -+=-+-,在()22,()Q x f x 处的切线方程为222222221(ln )()()y x x x x x x -+=-+-∴若这两条切线互相平行,则2211222121x x x x -+=-+,∴121112x x +=∵211112x x =-,且1206x x <<<,∴11111162x x <-<,∴111143x <<,∴1(3,4)x ∈令0x =,则1114ln 1b x x =+-,同理,2224ln 1b x x =+-、【解法一】∵211112x x =-,∴1212121111121111=4()ln ln =4()ln ln()22b b x x x x x x x --+---+- 设1()82ln ln()2g x x x x =--+-,11(,)43x ∈∴2222111681(41)()801222x x x g x x x x x xx -+-'=--==<---∴()g x 在区间11(,)43上单调递减,∴2()(ln 2,0)3g x ∈-即12b b -的取值范围就是2(ln 2,0)3-、 (12分) 【解法二】∵12122x x x =-, ∴11212121118=4()ln ln =2ln(1)2x b b x x x x x --+--+-令8()ln(1)22xg x x =+--,其中(3,4)x ∈ ∴2222281816(4)()02(2)(2)x x x g x x x x x x x -+-'=-+==>---∴函数()g x 在区间(3,4)上单调递增, ∴2()(ln 2,0)3g x ∈- ∴12b b -的取值范围就是2(ln 2,0)3-、 (12分)【解法三】∵()12122x x x x ⋅=+,()1212211111212112122122222124()44ln ln ln =ln ln 1x x x x x x x x x b b x x x x x x x x x x x x x ⎛⎫- ⎪--⎝⎭-=-+-=+=+=+⋅++设()21()ln 1x g x x x -=++,则()222141()(1)(1)x g x x x x x --'=+=++ ∵1121=1(,1)22x x x -∈,∴()0g x '>,∴函数()g x 在区间1(,1)2上单调递增, ∴2()(ln 2,0)3g x ∈-,∴12b b -的取值范围就是2(ln 2,0)3-、 (12分)22、 (本小题满分10分)【命题意图】本小题主要考查极坐标与参数方程的相关知识、【试题解析】解:(Ⅰ)2112x y t ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数) 设()()11,,,N M ρθρθ,()10,0ρρ>>1112ρρθθ=⎧⎨=⎩,即312cos ρθ=,即4cos ρθ=,所以()22400x x y x -+=≠、 (5分) (Ⅱ)将1l 的参数方程代入C 的直角坐标方程中,221(2)4(2)(1)02t -+++=即230t t +-=,12,t t 为方程的两个根,所以123t t =-, 所以1233AP AQ t t ⋅==-=、 (10分)23、(本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及到绝对值不等式等内容、 本小题重点考查化归与转化思想、【试题解析】解:(1)①当12x <时,21()324,32f x x x =-+≤∴-≤< ②当112x ≤<时,1()4,12f x x x =≤∴≤< ③当1x ≥时,()324,f x x =-≤∴12x ≤≤综上:()4f x ≤的解集为2{|2}3x x -≤≤、 (5分) (II)法一:由(I)可知13+221(),1232,1x x f x x x x x ⎧-<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩，,min 1(),2f x ∴=即12m =、 又,,,a b c R +∈且12a b c ++=,则2221a b c ++=,设x =,y =,z =, 222x y xy +≥,2222121222xy x y a b a b ∴≤+=+++=++,同理:2222yz b c ≤++,2222zx c a ≤++,2222222222228xy yz zx a b b c c a ∴++≤++++++++=,2222()222212121812x y z x y z xy yz zxa b c ∴++=+++++≤++++++=,x y z ∴++≤≤当且仅当16a b c ===时,取得最大值 (10分) 法二:由(I)可知13+221(),1232,1x x f x x x x x ⎧-<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩，,min 1(),2f x ∴=即12m =, ∴,,,a b c R +∈且12a b c ++=, 2444212121333()222a a a =++++++≤++=当且仅当16a b c ===时,取得最大值 (10分) 法三:由(I)可知13+221(),1232,1x x f x x x x x ⎧-<⎪⎪⎪=≤<⎨⎪-≥⎪⎪⎩，,min 1(),2f x ∴=即12m = 12a b c ∴++=,(21)(21)(21)4a b c ∴+++++= 由柯西不等式可知2222222)(111)111)++⋅++≥+≤ 当且仅当212121a b c +=+=+,即16a b c ===时。
江西师大附中2024年高三第三次适应性测试数学试题试卷
江西师大附中2024年高三第三次适应性测试数学试题试卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。
考试结束后，请将本试卷和答题卡一并交回。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．从装有除颜色外完全相同的3个白球和m 个黑球的布袋中随机摸取一球，有放回的摸取5次，设摸得白球数为X ，已知()3E X =，则()(D X = )A ．85B ．65C ．45D ．252．已知(1)nx +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（ ）． A ．122B ．112C ．102D ．923．已知向量a 与向量()4,6m =平行，()5,1b =-，且14a b ⋅=，则a =（ ） A ．()4,6 B ．()4,6-- C ．213313,1313⎛⎫⎪⎪⎝⎭ D ．213313,1313⎛⎫-- ⎪ ⎪⎝⎭ 4．已知集合{}{}2|1,|31x A x x B x ==<，则()RAB =（ ）A ．{|0}x x <B ．{|01}x xC ．{|10}x x -<D ．{|1}x x -5．如图，在ABC ∆中，点M ，N 分别为CA ，CB 的中点，若5AB =，1CB =，且满足223AG MB CA CB ⋅=+，则AG AC ⋅等于（ ）A ．2B 5C ．23D ．836．已知0x =是函数()(tan )f x x ax x =-的极大值点，则a 的取值范围是 A ．(,1)-∞- B ．(,1]-∞ C ．[0,)+∞D ．[1,)+∞7．若变量,x y ，满足22390x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则22x y +的最大值为（ ）A ．3B ．2C ．8113D ．108．如图，长方体1111ABCD A B C D -中，1236AB AA ==，112A P PB =，点T 在棱1AA 上，若TP ⊥平面PBC .则1TP B B ⋅=（ ）A ．1B ．1-C ．2D ．2-9．若不等式210x ax ++≥对于一切10,2x ⎛⎤∈ ⎥⎝⎦恒成立，则a 的最小值是 （ ）A ．0B ．2-C ．52-D ．3-10．已知抛物线C ：22y px =（0p >）的焦点为F ，01,2M y ⎛⎫ ⎪⎝⎭为该抛物线上一点，以M 为圆心的圆与C 的准线相切于点A ，120AMF ∠=︒，则抛物线方程为（ ） A ．22y x =B ．24y x =C ．26y x =D ．28y x =11．要得到函数()sin(3)3f x x π=+的导函数()f x '的图像，只需将()f x 的图像（ ）A ．向右平移3π个单位长度，再把各点的纵坐标伸长到原来的3倍 B ．向右平移6π个单位长度，再把各点的纵坐标缩短到原来的13倍 C ．向左平移3π个单位长度，再把各点的纵坐标缩短到原来的13倍 D ．向左平移6π个单位长度，再把各点的纵坐标伸长到原来的3倍 12．用数学归纳法证明，则当时，左端应在的基础上加上（ ）A ．B ．C ．D ．二、填空题：本题共4小题，每小题5分，共20分。
浙江省杭州北斗联盟2024年高三三模数学试题
浙江省杭州北斗联盟2024年高三三模数学试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知定义在[)1,+∞上的函数()f x 满足()()33f x f x =，且当13x ≤≤时，()12f x x =--，则方程()()2019f x f =的最小实根的值为（ ）A ．168B ．249C ．411D ．5612．甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.①甲同学成绩的中位数大于乙同学成绩的中位数； ②甲同学的平均分比乙同学的平均分高； ③甲同学的平均分比乙同学的平均分低； ④甲同学成绩的方差小于乙同学成绩的方差. 以上说法正确的是（ ） A ．③④B ．①②C ．②④D ．①③④3．五行学说是华夏民族创造的哲学思想，是华夏文明重要组成部分.古人认为，天下万物皆由金、木、水、火、土五类元素组成，如图，分别是金、木、水、火、土彼此之间存在的相生相克的关系.若从5类元素中任选2类元素，则2类元素相生的概率为（ ）A ．12B ．13C ．14D ．154．已知AB 是过抛物线24y x =焦点F 的弦，O 是原点，则OA OB ⋅=（ ） A ．－2B ．－4C ．3D ．－35．已知正项等比数列{}n a 的前n 项和为2317,,927n S S S ==，则12n a a a 的最小值为（ ） A ．24()27B ．34()27C ．44()27D ．54()276．如图，矩形ABCD 中，1AB =，2BC =，E 是AD 的中点，将ABE △沿BE 折起至A BE '，记二面角A BE D '--的平面角为α，直线A E '与平面BCDE 所成的角为β，A E '与BC 所成的角为γ，有如下两个命题：①对满足题意的任意的A '的位置，αβπ+≤；②对满足题意的任意的A '的位置，αγπ+≤，则( )A ．命题①和命题②都成立B ．命题①和命题②都不成立C ．命题①成立，命题②不成立D ．命题①不成立，命题②成立7．已知抛物线2:4C y x =和点()2,0D ，直线2x ty =-与抛物线C 交于不同两点A ，B ，直线BD 与抛物线C 交于另一点E ．给出以下判断：①直线OB 与直线OE 的斜率乘积为2-； ②//AE y 轴；③以BE 为直径的圆与抛物线准线相切. 其中，所有正确判断的序号是（ ） A ．①②③B ．①②C ．①③D ．②③8．已知函数31()sin ln 1x f x x x x +⎛⎫=++⎪-⎝⎭，若(21)(0)f a f ->，则a 的取值范围为（ ） A ．1,2⎛⎫+∞ ⎪⎝⎭B ．()0,1C ．1,12⎛⎫⎪⎝⎭D ．10,2⎛⎫⎪⎝⎭9．已知函数()ln f x x ax b =++的图象在点(1,)a b +处的切线方程是32y x =-，则a b -=（ ） A ．2B ．3C ．-2D ．-310． “幻方”最早记载于我国公元前500年的春秋时期《大戴礼》中．“n 阶幻方()*3,n n ≥∈N ”是由前2n 个正整数组成的—个n 阶方阵，其各行各列及两条对角线所含的n 个数之和（简称幻和）相等，例如“3阶幻方”的幻和为15（如图所示）．则“5阶幻方”的幻和为（ ）A ．75B ．65C ．55D ．4511．若函数()f x 的图象如图所示，则()f x 的解析式可能是（ ）A ．()x e x f x x +=B ．()21x f x x-=C ．()x e xf x x-=D ．()21x f x x +=12．已知函数()2121f x ax x ax =+++-（a R ∈）的最小值为0，则a =（ ） A ．12B ．1-C ．±1D ．12±二、填空题：本题共4小题，每小题5分，共20分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020年高三第三次模拟考试（三模）数学 含答案注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内．试题的答案写在答题纸．．．上对应题目的答案空格内．考试结束后，交回答题纸． 参考公式样本数据x 1，x 2，…，x n 的方差s 2＝1n i ＝1∑n (x i －－x )2，其中－x ＝1n i ＝1∑n x i ．一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）1．已知全集U ＝{－1，2，3，a }，集合M ＝{－1，3}．若∁U M ＝{2，5}，则实数a 的值为▲________．2．设复数z 满足z (1＋i)＝2＋4i ，其中i 为虚数单位，则复数的共轭复数为 ▲ ． 3．甲、乙两位选手参加射击选拔赛，其中连续5轮比赛的成绩（单位：环）如下表：则甲、乙两位选手中成绩最稳定的选手的方差是▲________．4．从2个白球，2个红球，1个黄球这5个球中随机取出两个球，则取出的两球中恰有一个红球的概率是▲________．5．执行如图所示的伪代码，输出的结果是 ▲ ．6．已知α，β是两个不同的平面，l ，m 是两条不同直线，l ⊥α，m ⊂β．给出下列命题：①α∥β⇒l ⊥m ； ②α⊥β⇒l ∥m ； ③m ∥α⇒l ⊥β； ④l ⊥β⇒m ∥α．其中正确的命题是▲________． (填．写．所有正确命题的．．．．．．．序号．．)．7．设数列{a n }的前n 项和为S n ，满足S n ＝2a n －2，则a 8a 6＝ ▲ ．8．设F 是双曲线的一个焦点，点P 在双曲线上，且线段PF 的中点恰为双曲线虚轴的一（第5题图）个端点，则双曲线的离心率为▲________．9．如图，已知A ，B 分别是函数f (x )＝3sin ωx (ω＞0)在y 轴右侧图象上的第一个最高点和第一个最低点，且∠AOB ＝π2，则该函数的周期是▲________．10．已知f (x )是定义在R 上的偶函数，当x ≥0时，f (x )＝2x －2，则不等式f (x －1)≤2的解集是▲________．11．如图，在梯形ABCD 中，AB ∥CD ，AB ＝4，AD ＝3，CD ＝2，AM →＝2MD →．若AC →·BM →＝－3，则AB →·AD →＝▲________．12．在平面直角坐标系xOy 中，圆M ：(x －a )2＋(y ＋a －3)2＝1(a ＞0)，点N 为圆M 上任意一点．若以N 为圆心，ON 为半径的圆与圆M 至多有一个公共点，则a 的最小值为▲________． 13．设函数f (x )＝⎩⎪⎨⎪⎧x －1e x ，x ≥a ，－x －1，x ＜a ，g (x )＝f (x )－b ．若存在实数b ，使得函数g (x )恰有3个零点，则实数a 的取值范围为▲________．14．若实数x ，y 满足2x 2＋xy －y 2＝1，则x －2y5x 2－2xy ＋2y 2的最大值为▲________．二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．(本小题满分14分)在△ABC 中，已知a ，b ，c 分别为角A ，B ，C 的对边．若向量m ＝(a ，cos A )，向量n ＝(cos C ，c )，且m ·n ＝3b cos B ． （1）求cos B 的值；（2）若a ，b ，c 成等比数列，求1tan A ＋1tan C 的值．（第11题图）如图，在直三棱柱ABC －A 1B 1C 1中，D 为棱BC 上一点．（1）若AB ＝AC ，D 为棱BC 的中点，求证：平面ADC 1⊥平面BCC 1B 1； （2）若A 1B ∥平面ADC 1，求BDDC的值．17． (本小题满分14分)如图，在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，点(2，1)在椭圆C 上． （1）求椭圆C 的方程；（2）设直线l 与圆O ：x 2＋y 2＝2相切，与椭圆C 相交于P ，Q 两点．①若直线l 过椭圆C 的右焦点F ，求△OPQ 的面积； ②求证： OP ⊥OQ ．（第16题图）ABCDA 1B 1C1（第17题图）如图，某森林公园有一直角梯形区域ABCD ，其四条边均为道路，AD ∥BC ，∠ADC ＝90°，AB ＝5千米，BC ＝8千米，CD ＝3千米．现甲、乙两管理员同时从地出发匀速前往D 地，甲的路线是AD ，速度为6千米/小时，乙的路线是ABCD ，速度为v 千米/小时．（1）若甲、乙两管理员到达D 的时间相差不超过15分钟，求乙的速度v 的取值范围； （2）已知对讲机有效通话的最大距离是5千米．若乙先到达D ，且乙从A 到D 的过程中始终能用对讲机与甲保持有效通话，求乙的速度v 的取值范围．19．(本小题满分16分)设函数f (x )＝－x 3＋mx 2－m (m ＞0)． （1）当m ＝1时，求函数f (x )的单调减区间；（2）设g (x )＝|f (x )|，求函数g (x )在区间[0，m ]上的最大值；（3）若存在t ≤0，使得函数f (x )图象上有且仅有两个不同的点，且函数f (x )的图象在这两点处的两条切线都经过点(2，t )，试求m 的取值范围．20．(本小题满分16分)已知数列{a n }的前n 项的和为S n ，记b n ＝S n +1n．（1）若{a n }是首项为a ，公差为d 的等差数列，其中a ，d 均为正数． ①当3b 1，2b 2，b 3成等差数列时，求ad的值；②求证：存在唯一的正整数n ，使得a n +1≤b n ＜a n +2．（2）设数列{a n }是公比为q (q ＞2)的等比数列，若存在r ，t (r ，t ∈N *，r ＜t )使得b t b r ＝t ＋2r ＋2，求q 的值．（第18题图）CB AD南京市xx 届高三年级第三次模拟考试数学附加题 xx.05注意事项：1．附加题供选修物理的考生使用． 2．本试卷共40分，考试时间30分钟．3．答题前，考生务必将自己的姓名、学校、班级、学号写在答题纸的密封线内．试题的答案写在答题纸．．．上对应题目的答案空格内．考试结束后，交回答题纸． 21．【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共计20分．请在答．卷．纸指定区域内．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲如图，已知半圆O 的半径为2，P 是直径BC 延长线上的一点，P A 与半圆O 相切于点A ， H 是OC 的中点，AH ⊥BC ． （1）求证：AC 是∠P AH 的平分线； （2）求PC 的长．B ．选修4—2：矩阵与变换已知曲线C ：x 2＋2xy ＋2y 2＝1，矩阵A ＝⎣⎢⎡⎦⎥⎤1 2 1 0 所对应的变换T 把曲线C 变成曲线C 1，求曲线C 1的方程．C ．选修4—4：坐标系与参数方程设极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合．已知椭圆C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝sin θ（θ为参数），点M 的极坐标为(1，π2)．若P 是椭圆C 上任意一点，试求PM 的最大值，并求出此时点P 的直角坐标．D ．选修4—5：不等式选讲求函数f (x )＝5x ＋8－2x 的最大值．【必做题】第22题、第23题，每题10分，共计20分．请在答．卷卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）从0，1，2，3，4这五个数中任选三个不同的数组成一个三位数，记X 为所组成的三位数各位数字之和．（1）求X 是奇数的概率；（2）求X 的概率分布列及数学期望．23．（本小题满分10分）在平面直角坐标系xOy 中，点P (x 0，y 0)在曲线y ＝x 2(x ＞0)上．已知A (0，－1)，P n (x n 0，y n0)，n ∈N *．记直线AP n 的斜率为k n ． （1）若k 1＝2，求P 1的坐标； （2）若 k 1为偶数，求证：k n 为偶数．南京市xx 届高三年级第三次模拟考试数学参考答案及评分标准说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数，填空题不给中间分数．一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）1．5 2．3－i 3．0.02 4．35 5．8 6．①④7．4 8． 5 9．4 10．[－1，3] 11．32 12．313．(－1－1e 2，2) 14．24二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．(本小题满分14分)解：（1）因为m ·n ＝3b cos B ，所以a cos C ＋c cos A ＝3b cos B ． 由正弦定理，得sin A cos C＋sin C cos A＝3sin B cos B ，···························································3分所以sin(A ＋C )＝3sin B cos B ，所以sin B ＝3sin B cos B ． 因为B是△ABC的内角，所以sin B ≠0，所以cos B ＝13．····················································7分 （2）因为a ，b ，c 成等比数列，所以b 2＝ac ． 由正弦定理，得sin 2B＝sin A·sin C．···············································································9分因为cos B＝13，B是△ABC的内角，所以sin B＝22 3．······················································11分又1tan A＋1tan C＝cos Asin A＋cos Csin C＝cos A·sin C＋sin A·cos Csin A·sin C＝sin(A＋C)sin A·sin C＝sin Bsin A·sin C＝sin Bsin2B＝1sin B＝32 4．·································································14分16．(本小题满分14分)证明：（1）因为AB＝AC，点D为BC中点，所以AD⊥BC．·················································2分因为ABC－A1B1C1 是直三棱柱，所以BB1⊥平面ABC．因为AD⊂平面ABC，所以BB1⊥AD．···················································4分因为BC∩BB1＝B，BC⊂平面BCC1B1，BB1⊂平面BCC1B1，所以AD⊥平面BCC1B1．因为AD⊂平面ADC1，所以平面ADC1⊥平面BCC1B1．·············································6分(2)连结A1C，交AC1于O，连结OD，所以O为AC1中点．·············································8分因为A1B∥平面ADC1，A1B⊂平面A1BC，平面ADC1∩平面A1BC＝OD，所以A1B∥OD．··················································12分因为O为AC1中点，所以D为BC中点，所以BDDC＝1．··································································14分17．(本小题满分14分)解：（1）由题意，得ca＝22，4a2＋1b2＝1，解得a2＝6，b2＝3．所以椭圆的方程为x26＋y23＝1． ··································································2分（2）①解法一 椭圆C 的右焦点F (3，0)． 设切线方程为y ＝k (x －3)，即kx －y －3k ＝0， 所以|－3k |k 2＋1＝2，解得k ＝±2，所以切线方程为y ＝±2(x －3)．······························4分由方程组⎩⎪⎨⎪⎧y ＝2(x －3)，x 26＋y 23＝1，解得⎩⎨⎧x ＝43＋325，y ＝－6＋65，或⎩⎨⎧x ＝43－325，y ＝－6－65．所以点P ，Q 的坐标分别为(43＋325，－6＋65)，(43－325，－6－65)，所以PQ＝665． ·································6分 因为O 到直线PQ 的距离为2，所以△O PQ 的面积为635．因为椭圆的对称性，当切线方程为y ＝－2(x －3)时，△O PQ 的面积也为635．综上所述，△O PQ的面积为635． ·································8分 ②解法二 椭圆C 的右焦点F (3，0)． 设切线方程为y ＝k (x －3)，即kx －y －3k ＝0， 所以|－3k |k 2＋1＝2，解得k ＝±2，所以切线方程为y ＝±2(x －3)．·······························4分把切线方程 y ＝2(x －3)代入椭圆C 的方程，消去y 得5x 2－83x ＋6＝0．设P (x 1，y 1) ，Q (x 2，y 2)，则有x 1＋x 2＝835．由椭圆定义可得，PQ ＝PF ＋FQ ＝2a －e( x 1＋x 2)＝2×6－22×835＝665．·····················6分 因为O 到直线PQ 的距离为2，所以△O PQ 的面积为635．因为椭圆的对称性，当切线方程为y ＝－2(x －3)时，所以△O PQ 的面积为635．综上所述，△O PQ的面积为635． ·································8分 ②解法一：(i)若直线PQ 的斜率不存在，则直线PQ 的方程为x ＝2或x ＝－2．当x ＝2时，P (2，2)，Q (2，－2)．因为OP →·OQ →＝0，所以OP ⊥OQ ． 当x＝－2时，同理可得OP ⊥OQ ． ·································10分(ii) 若直线PQ 的斜率存在，设直线PQ 的方程为y ＝kx ＋m ，即kx －y ＋m ＝0． 因为直线与圆相切，所以|m |1＋k2＝2，即m 2＝2k 2＋2． 将直线PQ 方程代入椭圆方程，得(1＋2k 2) x 2＋4kmx ＋2m 2－6＝0.设P (x 1，y 1) ，Q (x 2，y 2)，则有x 1＋x 2＝－4km1＋2k 2，x 1x 2＝2m 2－61＋2k 2． (12)分因为OP →·OQ →＝x 1x 2＋y 1y 2＝x 1x 2＋(kx 1＋m )(kx 2＋m )＝(1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝(1＋k 2)×2m 2－61＋2k 2＋km ×(－4km 1＋2k2)＋m 2．将m 2＝2k 2＋2代入上式可得OP →·OQ →＝0，所以OP ⊥OQ ． 综上所述，OP ⊥OQ ． ·····································14分解法二：设切点T (x 0，y 0)，则其切线方程为x 0x ＋y 0y －2＝0，且x 20＋y 20＝2．(i)当y 0＝0时，则直线PQ 的直线方程为x ＝2或x ＝－2．当x ＝2时，P (2，2)，Q (2，－2)．因为OP →·OQ →＝0，所以OP ⊥OQ ． 当x＝－2时，同理可得OP ⊥OQ ． ··································10分(ii) 当y 0≠0时，由方程组⎩⎪⎨⎪⎧x 0x ＋y 0y －2＝0，x 26＋y 23＝1，消去y 得(2x 20＋y 20)x 2－8x 0x ＋8－6y 20＝0．设P (x 1，y 1) ，Q (x 2，y 2)，则有x 1＋x 2＝8x 02x 20＋y 20，x 1x 2＝8－6y 202x 20＋y 20． (12)分所以OP →·OQ →＝x 1x 2＋y 1y 2＝x 1x 2＋(2－x 0x 1)( 2－x 0x 2)y 02＝－8(x 02＋y 20)＋16y 02(2x 20＋y 20)． 因为x 20＋y 20＝2，代入上式可得OP →·OQ →＝0，所以OP ⊥OQ ． 综上所述，OP ⊥OQ ． ·····································14分 18．(本小题满分16分)解：(1)由题意，可得AD ＝12千米． 由题可知|126－16v|≤14， ··············································2分 解得649≤v ≤647． ··············································4分(2) 解法一：经过t 小时，甲、乙之间的距离的平方为f (t )． 由于先乙到达D地，故16v＜2，即v＞8． ················································6分①当0＜vt ≤5，即0＜t ≤5v时，f (t )＝(6t )2＋(vt )2－2×6t ×vt ×cos ∠DAB ＝(v 2－485v ＋36) t 2．因为v 2－485v ＋36＞0，所以当t ＝5v时，f (t )取最大值，所以(v 2－485v ＋36)×(5v )2≤25，解得v ≥154． (9)分②当5＜vt ≤13，即5v ＜t ≤13v 时，f (t )＝(vt －1－6t )2＋9＝(v －6) 2 (t －1v －6)2＋9． 因为v ＞8，所以1v －6＜5v，(v －6) 2＞0，所以当t ＝13v 时，f (t )取最大值，所以(v －6) 2 (13v －1v －6)2＋9≤25，解得398≤v ≤394． (13)分③当13≤vt ≤16， 13v ≤t ≤16v 时，f (t )＝(12－6t )2＋(16－vt )2，因为12－6t ＞0，16－vt ＞0，所以当f (t )在(13v ，16v )递减，所以当t ＝13v 时，f (t )取最大值，(12－6×13v )2＋(16－v ×13v )2≤25，解得398≤v ≤394．因为v ＞8，所以 8＜v ≤394． (16)分解法二：设经过t 小时，甲、乙之间的距离的平方为f (t )．由于先乙到达D 地，故16v ＜2，即v ＞8． (6)分以A 点为原点，AD 为x 轴建立直角坐标系， ①当0＜vt ≤5时，f (t )＝(45vt －6t )2＋(35vt )2．由于(45vt －6t )2＋(35vt )2≤25，所以(45v －6)2＋(35v )2≤25t 2对任意0＜t ≤5v都成立，所以(45v －6)2＋(35v )2≤v 2，解得v ≥154． (9)分②当5＜vt ＜13时，f (t )＝(vt －1－6t )2＋32．由于(vt －1－6t )2＋32≤25，所以－4≤vt －1－6t ≤4对任意5v ＜t ＜13v 都成立，即⎩⎨⎧v －6≤5t ，－3t≤v －6，对任意5v ≤t ≤13v 都成立，所以⎩⎨⎧v －6≤5v 13，－3v13≤v －6，解得398≤v ≤394． ···············································13分③当13≤vt ≤16即13v ≤t ≤16v ，此时f (t )＝(12－6t )2＋(16－vt )2．由①及②知：8＜v ≤394，于是0＜12－6t ≤12－78v ≤12－78394＝4，又因为0≤16－vt ≤3，所以f (t )＝(12－6t )2＋(16－vt )2≤42＋32＝25恒成立．综上①②③可知8＜v ≤394． (16)分19．(本小题满分16分)解：（1）当m ＝1时，f (x )＝－x 3＋x 2－1．f ′(x )＝－3x 2＋2x ＝－x (3x －2)． 由f ′(x )＜0，解得x ＜0或x ＞23．所以函数f (x )的减区间是(－∞，0)和(23，＋∞)． ······································2分（2）依题意m ＞0．因为f (x )＝－x 3＋mx 2－m ，所以f ′(x )＝－3x 2＋2mx ＝－x (3x －2m )． 由f ′(x )＝0，得x ＝2m3或x ＝0．当0＜x ＜2m 3时，f ′(x )＞0，所以f (x )在上为增函数；所以，f (···············································4分． (6)分． (8)分（3）设两切点的横坐标分别是x 1，x 2．则函数f (x )在这两点的切线的方程分别为 y －(－x 13＋mx 12－m )＝(－3x 12＋2mx 1)(x －x 1)，y －(－x 23＋mx 22－m )＝(－3x 22＋2mx 2)(x －x 2)． (10)分将(2，t )代入两条切线方程，得t －(－x 13＋mx 12－m )＝(－3x 12＋2mx 1)(2－x 1)，t －(－x 23＋mx 22－m )＝(－3x 22＋2mx 2)(2－x 2)．因为函数f (x )图象上有且仅有两个不同的切点，所以方程t －(－x 3＋mx 2－m )＝(－3x 2＋2mx )(2－x )有且仅有不相等的两个实根． (12)分整理得t ＝2x 3－(6＋m )x 2＋4mx －m ．设h (x )＝2x 3－(6＋m )x 2＋4mx －m ，h ′(x )＝6x 2－2(6＋m )x ＋4m ＝2(3x －m )(x －2)． ①当m ＝6时，h ′(x )＝6(x －2)2≥0，所以h (x )单调递增，显然不成立． ②当m ≠6时， h ′(x )＝0，解得x ＝2或x ＝m 3．列表可判断单调性，可得当x ＝2或x ＝m3，h (x )取得极值分别为h (2)＝3m －8，或h (m 3)＝－127m 3＋23m 2－m ．要使得关于x 的方程t ＝2x 3－(6＋m )x 2＋4mx －m 有且仅有两个不相等的实根，则t ＝3m －8，或t ＝－127m 3＋23m 2－m ． (14)分因为t ≤0，所以3m －8≤0，（*），或－127m 3＋23m 2－m ≤0．（**）解（*），得m ** (16)分20．(本小题满分16分)解：（1）①因为3b 1，2b 2，b 3成等差数列，所以4b 2＝3b 1＋b 3，即4×3a ＋3d 2＝3(2a ＋d )＋4a ＋6d 3，解得，a d ＝34． (4)分② 由a n ＋1≤b n ＜a n ＋2，得a ＋nd ≤(n ＋1)a ＋(n ＋1)nd2n＜a ＋(n ＋1)d ，整理得⎩⎨⎧n 2－n －2ad≤0，n 2＋n －2a d＞0，········································6分解得－1＋1＋8a d2＜n ≤1＋1＋8a d2， (8)分由于1＋1＋8ad2－－1＋1＋8a d2＝1且－1＋1＋8a d2＞0．因此存在唯一的正整数n ，使得a n ＋1≤b n ＜a n ＋2． ·········································10分（2）因为b tb r ＝a 1(1－q t ＋1)t (1－q )a 1(1－q r ＋1)r (1－q )＝t ＋2r ＋2，所以q t ＋1－1t (t ＋2)＝q r ＋1－1r (r ＋2)．设f (n )＝q n ＋1－1n (n ＋2)，n ≥2，n ∈N *．则f (n ＋1)－f (n )＝q n ＋2－1(n ＋1)(n ＋3)－q n ＋1－1n (n ＋2)＝q n ＋1[(q －1)n 2＋2(q －2)n －3]＋2n ＋3n (n ＋1)(n ＋2)(n ＋3)，因为q ＞2，n ≥2，所以(q －1)n 2＋2(q －2)n －3＞n 2－3≥1＞0，所以f (n ＋1)－f (n )＞0，即f (n ＋1)＞f (n )，即f (n )单调递增．··································12分所以当r ≥2时，t ＞r ≥2，则f (t )＞f (r )，即q t ＋1－1t (t ＋2)＞q r ＋1－1r (r ＋2)，这与q t ＋1－1t (t ＋2)＝q r ＋1－1r (r ＋2)互相矛盾．所以r ＝1，即q t ＋1－1t (t ＋2)＝q 2－13． (14)分若t ≥3，则f (t )≥f (3)＝q 4－115 ＝q 2－13·q 2＋15＞q 2－13，即q t ＋1－1t (t ＋2)＞q 2－13，与q t ＋1－1t (t ＋2)＝q 2－13相矛盾．于是t ＝2，所以q 3－18＝q 2－13，即3q 2－5q －5＝0．又q ＞2，所以q ＝5＋856． ···········································16分南京市xx 届高三年级第三次模拟考试 数学附加题参考答案及评分标准xx.05说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数，填空题不给中间分数．21．【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共计20分．请在答．卷．卡指定区域内．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲证明：(1)连接AB ．因为P A 是半圆O 的切线，所以∠P AC ＝∠ABC ． 因为BC 是圆O 的直径，所以AB ⊥AC ．又因为AH ⊥BC ，所以∠CAH ＝∠ABC ，所以∠P AC ＝∠CAH ，所以AC 是∠P AH 的平分线． ···········································5分(2)因为H 是OC 中点，半圆O 的半径为2，所以BH ＝3，CH ＝1． 又因为AH ⊥BC ，所以AH 2＝BH ·HC ＝3，所以AH ＝3．在Rt △AHC 中，AH ＝3，CH ＝1，所以∠CAH ＝30°．由(1)可得∠P AH ＝2∠CAH ＝60°，所以P A ＝23．由P A 是半圆O 的切线，所以P A 2＝PC ·PB ，所以PC .(PC ＋BC )＝(23)2＝12，所以PC ＝2． (10)分B ．选修4—2：矩阵与变换解：设曲线C 上的任意一点P (x ，y )，P 在矩阵A ＝⎣⎢⎡⎦⎥⎤1 2 1 0 对应的变换下得到点Q (x ′，y ′)．则⎣⎢⎡⎦⎥⎤1 2 1 0 ⎣⎡⎦⎤x y ＝⎣⎡⎦⎤x ′y ′， 即x ＋2y ＝x ′，x ＝y ′，所以x ＝y ′，y ＝x ′－y ′2． (5)分代入x 2＋2xy ＋2y 2＝1，得y ′2＋2y ′·x ′－y ′2＋2(x ′－y ′2)2＝1，即x ′2＋y ′2＝2， 所以曲线C 1的方程为x 2＋y 2＝2． ···········································10分 C ．选修4—4：坐标系与参数方程解：M 的极坐标为(1，π2)，故直角坐标为M (0，1)，且P (2cos θ，sin θ)，所以PM ＝(2cos θ)2＋(sin θ－1)2＝－3sin 2θ－2sin θ＋5，sin θ∈[－1，1]． (5)分当sin θ＝－13时，PM max ＝433，此时cos θ＝±223．所以，PM 的最大值是433，此时点P 的坐标是(±423，－13)． (10)分D ．选修4—5：不等式选讲解：函数定义域为[0，4]，且f (x )≥0．由柯西不等式得[52＋(2)2][(x )2＋(4－x )2)]≥(5·x ＋2·4－x )2，······················5分即27×4≥(5·x ＋2·4－x )2，所以5x ＋8－2x ≤63． 当且仅当2x ＝54－x ，即x ＝10027时，取等号．所以，函数f (x )＝5x ＋8－2x 的最大值为63． ··································10分【必做题】第22题、第23题，每题10分，共计20分． 22．（本小题满分10分）解：（1）记“X 是奇数”为事件A ，能组成的三位数的个数是48． ·································2分 X 是奇数的个数有28，所以P (A )＝2848＝712．答：X 是奇数的概率为712． ·································4分（2） X 的可能取值为3，4，5，6，7，8，9．当 X ＝3时，组成的三位数只能是由0，1，2三个数字组成，所以P (X ＝3)＝448＝112；当 X ＝4时，组成的三位数只能是由0，1，3三个数字组成，所以P (X ＝4)＝448＝112；当 X ＝5时，组成的三位数只能是由0，1，4或0，2，3三个数字组成，所以P (X ＝5)＝848＝16； 当 X ＝6时，组成的三位数只能是由0，2，4或1，2，3三个数字组成，所以P (X ＝6)＝1048＝524； 当 X ＝7时，组成的三位数只能是由0，3，4或1，2，4三个数字组成，所以P (X ＝7)＝1048＝524； 当 X ＝8时，组成的三位数只能是由1，3，4三个数字组成，所以P (X ＝8)＝648＝18；当 X ＝9时，组成的三位数只能是由2，3，4三个数字组成，所以P (X ＝9)＝648＝18； (8)分所以X 的概率分布列为：E (X )＝3×112＋4×112＋5×16＋6×524＋7×524＋8×18＋9×18＝254． (10)分23．（本小题满分10分）解：（1）因为k 1＝2，所以y 0＋1x 0＝x 20＋1x 0＝2，解得x 0＝1，y 0＝1，所以P 1的坐标为(1，1)． ····································2分（2）设k 1＝2p (p ∈N *)，即y 0＋1x 0＝x 20＋1x 0＝2p ，所以x 20－2px 0＋1＝0，所以x 0＝p ±p 2－1． (4)分因为y 0＝x 02，所以k n ＝y n 0＋1x n 0＝x 2n 0＋1x n 0＝x n 0＋1x n 0，所以当x 0＝p ＋p 2－1时， k n ＝(p ＋p 2－1)n ＋(1p ＋p 2－1)n ＝(p ＋p 2－1)n ＋(p －p 2－1)n ．····························6分同理，当 x 0＝p －p 2－1时，k n ＝(p ＋p 2－1)n ＋(p －p 2－1)n ． ①当n ＝2m (m ∈N *)时， k n ＝2k =0∑mC 2k n p n－2k(p 2－1)k ，所以 k n 为偶数． ②当n ＝2m ＋1(m ∈N )时，k n ＝2k =0∑mC 2k n p n－2k(p 2－1)k ，所以 k n 为偶数．综上， k n 为偶数． ································10分。