小学四年级奥数 第39讲:统筹与最优化_PDF压缩
四年级数学统筹与最优化知识点分析与例题解析

四年级数学统筹与最优化主要内容及解题思路一、时间统筹1、排队问题:等候最短,先快后慢2、过河问题:1)快的来回走;2)接近的一起走二、地点统筹1、人数相同1)奇数点,中间点2)偶数点,中间段2、人数不同两头相比较,小的往大靠三、调运问题1、无冲突,直接运2、有冲突,比较差值例题:1、车间里有五台车床同时出现故障,已知第一台到第五台修复时间依次为18,30,17,25,20分钟,每台车床停产一分钟造成经济损失5元。
1)现有一名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元?2)现有两名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元?解题思路:本题是排队问题,应采用先快后慢的方式,才能使等候时间最短。
1)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
17×5+18×4+20×3+25×2+30×1=85+72+60+50+30=297(分钟)第三步:计算损失297×5=1485(元)2)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
甲17,乙18,甲20,乙25,甲30,即甲:17,20,30乙:18,25甲修机器等待时间17×3+20×2+30甲修机器等待时间18×2+25即:17×3+(20+18)×2+25+30=51+76+25+30=182(分钟)第三步:计算损失182×5=910(元)2、小明骑在牛背上赶牛过河。
共有甲乙丙丁4头牛,甲牛过河需要1分钟,乙牛过河需要2分钟,丙牛过河需要5分钟,丁牛过河需要6分钟。
每次只能赶两头牛过河,那么小明要把这4头牛都赶到对岸,最少要用多少分钟?解题思路:本题是过河问题,应采用1)快的来回走;2)接近的一起走。
四年级数学统筹与最优化知识点分析与例题解析

四年级数学统筹与最优化主要内容及解题思路一、时间统筹1、排队问题:等候最短,先快后慢2、过河问题:1)快的来回走;2)接近的一起走二、地点统筹1、人数相同1)奇数点,中间点2)偶数点,中间段2、人数不同两头相比较,小的往大靠三、调运问题1、无冲突,直接运2、有冲突,比较差值例题:1、车间里有五台车床同时出现故障,已知第一台到第五台修复时间依次为18,30,17,25,20分钟,每台车床停产一分钟造成经济损失5元。
1)现有一名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元2)现有两名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元解题思路:本题是排队问题,应采用先快后慢的方式,才能使等候时间最短。
1)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
17×5+18×4+20×3+25×2+30×1=85+72+60+50+30=297(分钟)第三步:计算损失297×5=1485(元)2)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
甲17,乙18,甲20,乙25,甲30,即甲:17,20,30乙:18,25甲修机器等待时间17×3+20×2+30甲修机器等待时间18×2+25即:17×3+(20+18)×2+25+30=51+76+25+30=182(分钟)第三步:计算损失182×5=910(元)2、小明骑在牛背上赶牛过河。
共有甲乙丙丁4头牛,甲牛过河需要1分钟,乙牛过河需要2分钟,丙牛过河需要5分钟,丁牛过河需要6分钟。
每次只能赶两头牛过河,那么小明要把这4头牛都赶到对岸,最少要用多少分钟解题思路:本题是过河问题,应采用1)快的来回走;2)接近的一起走。
统筹与最优化
庄有 50 人,B 村庄有 500 人,C 村庄有 5000 人
(E 度论坛)
四年级春季知识点精讲
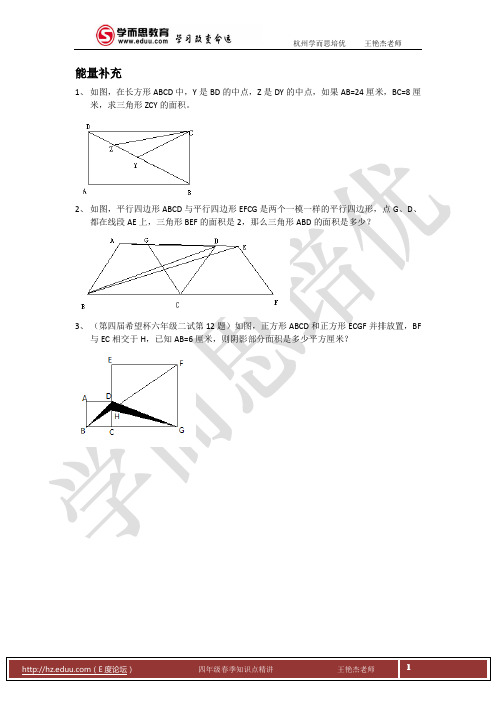
3、 (第四届希望杯六年级二试第 12 题)如图,正方形 ABCD 和正方形 ECGF 并排放置,BF 与 EC 相交于 H,已知 AB=6 厘米,则阴影部分面积是多少平方厘米?
(E 度论坛)
四年级春季知识点精讲
王艳杰老师
1
杭州学而思培优 王艳杰老师
第三讲 统筹与最优化
想想练练 2
① A 村或 B 村都一样 ② B村 ③ B村 ④ C村
(E 度论坛)
四年级春季知识点精讲
王艳杰老师
3
学习目标
1、 体会合理安排,可以节约时间,提高效率。希望大家逐渐养成合理安排时间的良好习惯 2、 从解决问题的不同方案中找到最佳方案,理解优化思想,逐步培养解决实际问题的能力 3、 体会解决问题途径的多样性以及方案策略的最优性
想想练练
1、 逗逗是个懂事的孩子,每天早上起来给妈妈蒸鸡蛋糕,过程为 ① 打鸡蛋,花 1 分钟 ② 切葱花,花 2 分钟 ③ 搅蛋,花 1 分钟 ④ 洗锅,花 2 分钟 ⑤ 烧热水,花 6 分钟 ⑥ 蒸 鸡蛋,花 11 分钟。每天完成这个过程需要 1+2+1+2+6+11=23 分钟。聪明的同学,你能 不能想出办法帮助逗逗更快地完成这 6 个步骤?如何完成?
杭州学而思培优 王艳杰老师
能量补充
1、 如图,在长方形 ABCD 中,Y 是 BD 的中点,Z 是 DY 的中点,如果 AB=24 厘米,BC=8 厘 米,求三角形 ZCY 的面积。
四年级数学统筹与最优化知识点分析与例题解析讲课稿

四年级数学统筹与最优化主要内容及解题思路一、时间统筹1、排队问题:等候最短,先快后慢2、过河问题:1)快的来回走;2)接近的一起走二、地点统筹1、人数相同1)奇数点,中间点2)偶数点,中间段2、人数不同两头相比较,小的往大靠三、调运问题1、无冲突,直接运2、有冲突,比较差值例题:1、车间里有五台车床同时出现故障,已知第一台到第五台修复时间依次为18,30,17,25,20分钟,每台车床停产一分钟造成经济损失5元。
1)现有一名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元?2)现有两名工作效率相同的修理工,问怎样安排才能使得经济损失最少,最少为多少元?解题思路:本题是排队问题,应采用先快后慢的方式,才能使等候时间最短。
1)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
17×5+18×4+20×3+25×2+30×1=85+72+60+50+30=297(分钟)第三步:计算损失297×5=1485(元)2)第一步:排序,17,18,20,25,30第二步:采用由快到慢的方式修理机器,并且计算其它机器的等待时间(包括自身等待)。
甲17,乙18,甲20,乙25,甲30,即甲:17,20,30乙:18,25甲修机器等待时间17×3+20×2+30甲修机器等待时间18×2+25即:17×3+(20+18)×2+25+30=51+76+25+30=182(分钟)第三步:计算损失182×5=910(元)2、小明骑在牛背上赶牛过河。
共有甲乙丙丁4头牛,甲牛过河需要1分钟,乙牛过河需要2分钟,丙牛过河需要5分钟,丁牛过河需要6分钟。
每次只能赶两头牛过河,那么小明要把这4头牛都赶到对岸,最少要用多少分钟?解题思路:本题是过河问题,应采用1)快的来回走;2)接近的一起走。
小学四年级奥数竞赛班作业第39讲:统筹与最优化

5. 有一家五口人要在夜晚过一座独木桥.他们家里的老爷爷行动非常不便,过桥需要 12 分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8 分钟; 母亲则一直坚持劳作,动作还算敏捷,过桥要 6 分钟;两个孩子中姐姐需要 3 分钟,弟
1
弟只要 1 分钟.当时正是初一夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓 伸手不见五指.所幸的是他们有一盏油灯,同时可以有两个人借助灯光过桥.但要命的 灯油将尽,这盏灯只能再维持 30 分钟了!他们焦急万分,该怎样过桥呢?
A1 C
B
A2
A5
A6
D
F
E
公路
A3 A4 A7
5
答案: 1. 在不浪费时间的情况下:两张饼可同时煎完,三张饼也可以:首先 A,B 的正面,然后拿
走 A,煎 B 的反面和 C 的正面,然后拿走 B,煎 A,C 的反面. 2009 21003 3,完全可 以不浪费时间煎完,从而所需时间为: 2009 2 2 2009 分钟.
小学四年级奥数竞赛班作业第39讲:统筹与最优化

8. 五个基地人员总数为17 4 16 14 9 60 (人). 依题意,调整后每个基地应各有 60 5 12 (人). 因此,需要从多于 12 人的基地 A,C, D 向不足 12 人的基地 B, E 调人.为了避免对流,经 试验容易得到调整方案如下: 先从 D 调 2 人到 E,这样 E 尚缺 1 人;再由 A 调 1 人给 E ,则 E 达到要求.此时, A 尚 多余 4 人, C 也多余 4 人,总共 8 人全部调到 B ,则 B 亦符合要求. 调动示意图如下所示,这样的图形叫做物资流向图.用流向图代替调运方案,能直观地 看出调运状况及有无对流现象,又可避免列表和计算的麻烦.图中箭头表示流向,箭杆 上的数字表示流量.
14. 有十个村庄,座落在从县城出发的一条公路上,现要安装水管,从县城供各村自来水.可 以用粗、细两种水管,粗管每千米 7000 元,细管每千米 2000 元.粗管足够供应所有各 村用水,细管只能供应一个村用水,各村与县城间距离如下图所示(图中单位是千米), 现要求按最节约的方法铺设,总费用是多少?
6. 5 所学校 A,B,C,D,E 之间有公路相通,图中标出了各段公路的千米数,现在想在某所学 校召开一次学生代表会议,应出席会议的 A,B,C,D,E 校分别有 6 人,4 人,8 人,7 人, 10 人,为使参加会议的代表所走的路程总和最小,会议应选在哪个学校召开?
A
2
B
3
C
2
2
D
E
4
二. 拓展提高:
3. 第一个人接水时,包括他本人在内,共有 6 个人等候,第二个人接水时,有 5 个人等候; 第 6 个人接水时,只有他 1 个人等候.可见,等候的人越多(一开始时),接水时间
应当越短,这样总的等候时间才会最少,因此,应当把接水时间按从少到多顺序排列等 候接水,这个最短时间是 36 45 5 4 63 7 2 10 100 (分).
四年级奥数统筹规划最优解

统筹规划知识框架统筹学是一门数学学科,但它在许多的领域都在使用,在生活中有很多事情要去做时,科学的安排好先后顺序,能够提高我们的工作效率.我国著名数学家华罗庚教授生前十分重视数学的应用,并亲自带领小分队推广优选法、统筹法,使数学直接为国民经济发展服务,他在中学语文课本中,曾有一篇名为《统筹原理》的文章详,细介绍了统筹方法和指导意义.运筹学是利用数学来研究人力、物力的运用和筹划,使它们能发挥最大效率的科学。
它包含的内容非常广泛,例如物资调运、场地设置、工作分配、排队、对策、实验最优等等,每类问题都有特定的解法。
运筹学作为一门科学,要运用各种初等的和高等的数学知识及方法,但是其中分析问题的某些朴素的思想方法,如高效率优先的原则、调整比较的思想、尝试探索的方法等,都是我们小学生能够掌握的。
这些来源于生活实际的问题,正是启发同学们学数学、用数学最好的思维锻炼题目。
本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
“节省跑空车的距离”是物资调运问题的一个原则。
“发生对流的调运方案”不可能是最优方案。
“小往大靠,支往干靠”。
例题精讲一、合理安排时间【例 1】星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间?【考点】统筹规划【难度】2星【题型】解答【解析】如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共需60分钟(见下图)。
【答案】60分钟【巩固】妈妈让小明给客人烧水沏茶。
统筹与最优化
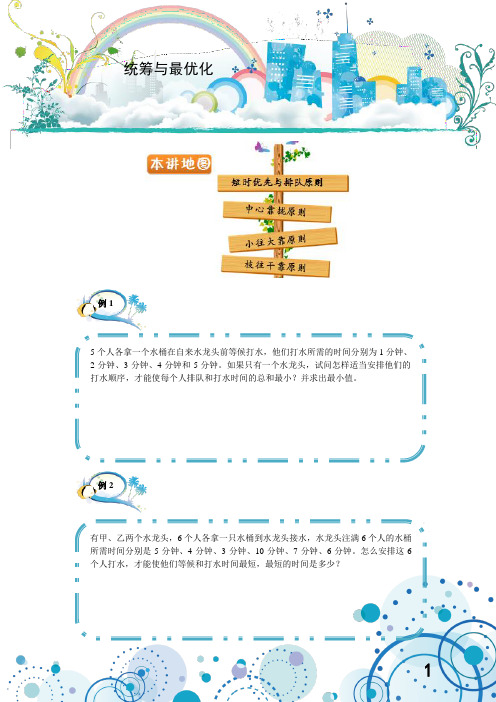
统筹与最优化例15个人各拿一个水桶在自来水龙头前等候打水,他们打水所需的时间分别为1分钟、2分钟、3分钟、4分钟和5分钟。
如果只有一个水龙头,试问怎样适当安排他们的打水顺序,才能使每个人排队和打水时间的总和最小?并求出最小值。
例2有甲、乙两个水龙头,6个人各拿一只水桶到水龙头接水,水龙头注满6个人的水桶所需时间分别是5分钟、4分钟、3分钟、10分钟、7分钟、6分钟。
怎么安排这6个人打水,才能使他们等候和打水时间最短,最短的时间是多少?在一条公路上每隔100千米有一个仓库(如图),共有5个仓库,一号仓库存有10吨货物,二号仓库有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。
现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要0.5元运输费,那么最少要多少运费才行?⑴如图,在街道上有A 、B 、C 、D 、E 五栋居民楼,现在设立一个公交站,为使这五栋楼到车站的距离之和最短,车站应立于何处?⑵如图,在街道上有A 、B 、C 、D 、E 、F 六栋居民楼,现在设立一个公交站,要想每栋楼到达车站的距离之和最短,车站应该设在何处?⑶有1993名少先队员分散在一条公路上执勤宣传交通法规,问完成任务后应该在公路的什么地点集合,可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小?例3例4某乡共有六块甘蔗地,每块地的产量如下图所示。
现在准备建设一座糖厂,问糖厂建于何处总运费最省?下图是A ,B ,C ,D ,E 五个村之间的道路示意图,○中数字是各村要上学的学生人数,道路上的数表示两村之间的距离(单位:千米)。
现在要在五村之中选一个村建立一所小学。
为使所有学生到学校的总距离最短,试确定最合理的方案。
例5例6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例4】(★★★) 在一条公路上,每隔10千米有一座仓库(如图),共有五座,图中数字表示各仓库库存货物的重量。
现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要运费0.9元,那么集中到哪个仓库运费最少?
【例5】(★★★)
下图是A ,B ,C ,D ,E 五个村之间的道路示意图,○中数字是各村要上学的学生人数,道路上的数表示两村之间的距离(单位:千米)。
现在要在五村之中选一个村建立一所小学。
为使所有学生到学校的总距离最短,试确定最合理的方案。
【例6】(★★★) 某乡共有六块甘蔗地,每块地的产量如下图所示。
现在准备建设一座糖厂,问糖厂建于何处总运费最省?
【例7】(★★★★)
A 、
B 、
C 、
D 四人带着一个手电筒,要通过一个黑暗的只容2人走的隧道,每次先让2人带着手电筒通过,再由一人送回手电筒,又由2人带着手电筒通过…。
若A 、B 、C 、D 四人单独通过隧道分别需要2,3,5,6分钟,则他们4人通过隧道至少需要________分钟。
本讲总结 短时优先原则 中心靠拢原则 小往大靠原则 优劣比较原则
2。
