北师大数学七下第二章单元练习题
第二章 相交线与平行线——2022-2023学年北师大版数学七年级下册单元测试
第二章 相交线与平行线一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.如图，1∠和2∠是同位角的图形有( )A.③④B.①③⑤C.①②⑤D.①②③2.同一平面内三条直线互不重合，那么交点的个数可能是( )A.0，1，2B.0，1，3C.1，2，3D.0，1，2，33.如图，给出下列条件：①12∠=∠；②34∠=∠；③//AD BE ，且D B ∠=∠.其中能推出//AB DC 的条件为( )A.①②B.①③C.②③D.①②③4.下列说法正确的有( )①两点之间的所有连线中，线段最短②相等的角叫对顶角③过一点有且只有一条直线与已知直线平行④不相交的两条直线叫做平行线⑤直线外一点到该直线的所有线段中垂线最短⑥在同一平面内，过一点有且只有一条直线与已知直线垂直A.1个B.2个C.3个D.4个5.如图，快艇从P 处向正北航行到A 处时，向左转50°航行到B 处，再向右转80°继续航行，此时的航行方向为( )A.北偏东30°B.北偏东80°C.北偏西30°D.北偏西50°6.如图，直线AB ，CD 相交于点O ，EO AB ⊥，垂足为O ，若30EOC ∠=︒，则AOD ∠的度数为( )A.115°B.120°C.125°D.130°7.如图木条a 、b 、c 用螺丝固定在木板a 上，且50ABM ∠=︒，70DEM ∠=︒，将木条a 、木条b 、木条c 看作是在同一平面a 内的三条直线AC 、DF 、MN ，若使直线AC 、直线DF 达到平行的位置关系则下列描述错误的是( )A.木条b 、c 固定不动，木条a 绕点B 顺时针旋转20°B.木条b 、c 固定不动，木条a 绕点B 逆时针旋转160°C.木条a 、c 固定不动，木条b 绕点E 逆时针旋转20°D.木条a 、c 固定不动，木条b 绕点E 顺时针旋转110°8.如图，//AB CD .62AEF ∠=︒，FG 平分EFC ∠，则1∠的度数为( )A.62°B.60°C.59°D.50°9.如图，AC 、BD 相交于点O ，连接AB 、BC 、CD 、DA ，能判定//AD BC 的条件是( )A.CDB ABD ∠=∠B.180ADC DAB ∠+∠=︒C.DCA BAC ∠=∠D.DAC BCA ∠=∠10.如图，//AB CD ，α∠=( )A.70°B.75°C.80°D.85°二、填空题（每小题4分，共20分）11.如图，用一个钉子（点O ）将两根木条AB ，CD 钉在一起，已知2AOC BOC ∠=∠.（1）AOC ∠的度数为______；（2）调整AOC ∠的大小，使45AOC ∠=︒，则图中的BOD ∠的度数减少______.12.如图，直线1l ，2l 被3l 所截，下列条件：①12∠=∠；②34∠=∠；③12//l l ，其中能判断//AC BD 的一个条件是_________.13.光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射.如图，水面AB 与水杯下沿CD 平行，光线EF 从水中射向空气时发生折射，光线变成FH ，点G 在射线EF 上，已知20HFB ∠=︒，45FED ∠=︒，则GFH ∠的度数为___________.14.如图，AE 平分BAC ∠，CE 平分ACD ∠，要使//AB CD ，则E ∠的大小为___________.15.已知：如图，直线EF 、GH 被直线MN 所截，AB GH ⊥，B 为垂足，12∠=∠.求证：AB EF ⊥.证明：12∠=∠(_____)，//EF ∴___________(_____)，FAB HBA ∴∠+∠=___________(_____)，AB GH ∴⊥（已知），90HBA ∴∠=︒(_____)，1801809090FAB HBA ∴∠=︒-∠=-︒=︒，AB EF ∴⊥(_____).三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）如图，在一张半透明的纸上画一条直线l ，在l 上任取一点P ，在l 外任取一点Q ，折出过点P 且与l 垂直的直线.这样的直线能折出几条？为什么？过点Q 呢？17.（8分）如图，已知//AB CD ，线段GH 交AB 于点J ，直线EF 分别交AB ，CD ，GH 于点L ，M ，H ，且148243∠=︒∠=︒，.（1）找出图中1∠的所有同位角；（2）求GHF ∠的度数.18.（10分）如图，AF 分别与BD 、CE 交于点G 、H ，155∠=︒.若A F ∠=∠，C D ∠=∠，求2∠的度数.19.（10分）如图，直线AB ，CD 相交于点O ，OE 平分BOD ∠，OF 平分COE ∠，:4:1AOD BOE ∠∠=，求AOF ∠的度数.20.（12分）如图，在四边形ABCD 中，180ADC ABC ∠+∠=︒，90ADF AFD ∠+∠=︒，点E 、F 分别在DC 、AB 上，且BE 、DF 分别平分ABC ∠、ADC ∠，判断BE 、DF 是否平行，并说明理由.21.（12分）如图1，直线MN 与直线AB 、CD 分别交于点E 、F ，MEB ∠与NFD ∠互补.(1)试判断直线AB 与直线CD 的位置关系，并说明理由；(2)如图2，BEF ∠与EFD ∠的角平分线交于点P ，EP 与CD 交于点G ，点H 是MN 上一点，且GH EG ⊥，求证：//PF GH ；(3)如图3，在(2)的条件下，连接PH ，K 是GH 上一点，使PHK HPK ∠=∠，作PQ 平分EPK ∠，问HPQ ∠的大小是否发生变化，若不变，请求出其值；若变化，说明理由.答案以及解析1.答案：C解析：根据同位角定义可得①②⑤是同位角，故选：C.2.答案：D 解析：三条直线位置不明确，所以分情况讨论：①三条直线互相平行，有0个交点；②一条直线与两平行线相交，有2个交点；③三条直线都不平行，有1个或3个交点，故选D.3.答案：C解析：①12∠=∠，可判定//AD BC ，不能判定//AB CD ，故①错误，不符合题意； ②34∠=∠，可判定//AB CD ，故②正确，符合题意；③由//AD BE 可得D DCE ∠=∠，再由D B ∠=∠可得B DCE ∠=∠，可判定//AB CD ，故③正确，符合题意；故选：C.4.答案：B解析：①两点之间的所有连线中，线段最短，正确；②相等的角叫对顶角，错误，应该是对顶角相等；③过一点有且只有一条直线与已知直线平行，错误，应该强调在直线外一点； ④不相交的两条直线叫做平行线，错误，应该强调在同一平面内；⑤直线外一点到该直线的所有线段中垂线最短，错误，应该是垂线段最短； ⑥在同一平面内，过一点有且只有一条直线与已知直线垂直，正确，正确的有2个，故选：B.5.答案：A解析：如图，过点B 作//BC PA ，则50CBD ∠=︒，805030CBE ∴∠=︒-︒=︒，故此时快艇的航行方向为北偏东30°.故选A.6.答案：B解析：EO AB ⊥，90EOB ∴∠=︒.又30EOC ∠=︒，120COB EOC BOE ∴∠=∠+∠=︒.AOD COB ∠=∠（对顶角相等），120AOD ∴∠=︒.故选B.7.答案：D解析：A 、木条b 、c 固定不动，木条a 绕点B 顺时针旋转20°，此时502070ABM ∠=︒+︒=︒，则ABM DEM ∠=∠，有//AC DF ，故本选项正确，不符合题意；B 、木条b 、c 固定不动，木条a 绕点B 逆时针旋转160°，此时()5018016070ABM ∠=︒+︒-︒=︒，则ABM DEM ∠=∠，有//AC DF ，故本选项正确，不符合题意；C 、木条a 、c 固定不动，木条b 绕点E 逆时针旋转20°，此时702050DEM ∠=︒-︒=︒，则ABM DEM ∠=∠，有//AC DF ，故本选项正确，不符合题意；D 、木条a 、c 固定不动，木条b 绕点E 顺时针旋转110°，木条b 、c 重合，则180DEM ABM ∠=︒≠∠，故本选项错误，符合题意.故选：D.8.答案：C解析：//AB CD ，180AEF CFE ∴∠+∠=︒，62AEF ∠=︒，180118CFE AEF ∠=︒-∠=︒，FG 平分EFC ∠，1592CFG CFE ∴∠=∠=︒， //AB CD ，159CFG ∴∠=∠=︒，故选：C.9.答案：D解析：A.CDB ABD ∠=∠，可得//AB CD ，不合题意，故此选项错误；B.180ADC DAB ∠+∠=，可得//AB CD ，不合题意，故此选项错误；C.DCA BAC ∠=∠，可得//AB CD ，不合题意，故此选项错误；D.DAC BCA ∠=∠，可得//AD BC ，符合题意，故此选项正确；故选：D.10.答案：D解析：如图，过点E 作//EF AB ，120B ∠=︒，18060BEF B ∴∠=︒-∠=︒，//AB CD ，//EF CD ∴，25C ∠=︒，25CEF C ∴∠=∠=︒，85BEF CEF α∴∠=∠+∠=︒，故选：D.11.答案：（1）120°（2）75°解析：（1）2AOC BOC ∠=∠，=180AOC BOC ∠+∠︒，1=1802AOC AOC ∴∠+∠︒， 120AOC ∴∠=︒，故答案：120°；（2）AOC ∠与BOD ∠为对顶角，45AOC BOD ∴∠=∠=︒，BOD ∴∠的度数减少：1204575︒-︒=︒，故答案为：75°.12.答案：①解析：12∠=∠，//AC BD ∴（同位角相等，两直线平行），而34∠=∠或12//l l 均不能判定//AC BD ，故答案为：①.13.答案：25°解析：//AB CD ，45GFB FED ∴∠=∠=︒，20HFB ∠=︒，452025GFH GFB HFB ∴∠=∠-︒-︒∠==︒，故答案为：25°.14.答案：90︒解析：若//AB CD ，180BAC DCA ∴∠+∠=︒，AE 平分BAC ∠，CE 平分ACD ∠，180121809090E ∴∠=-∠-∠=︒-︒=︒.故答案为：90°.15.答案：已知；GH ；内错角相等，两直线平行；两直线平行，同旁内角互补；垂直的定义；垂直的定义解析：证明：12∠=∠（已知），//EF GH ∴（内错角相等，两直线平行）180FAB HBA ∴∠+∠=︒（两直线平行，同旁内角互补）AB GH ⊥（已知），90HBA ∴∠=︒（垂直的定义）1801809090FAB HBA ∴∠=︒-∠=-︒=︒，AB EF ∴⊥（垂直的定义），故答案为：已知；GH ；内错角相等，两直线平行；两直线平行，同旁内角互补；垂直的定义；垂直的定义.16.答案：都只能折出一条，理由见解析解析：折出过点P 且与l 垂直的直线，这样的直线只能折出一条，理由是：过直线上的一点有且只有一条直线与已知直线垂直；过点Q 且与l 垂直的直线，这样的直线也只能折出一条，理由是：过直线外的一点有且只有一条直线与已知直线垂直.17.答案：（1）由图可得，1∠的同位角是ELB JHM ∠∠，.（2）如图，过点H 作//HN AB ，则//HN CD ，故12GHN FHN ∠=∠∠=∠，.因为148243∠=︒∠=︒，，所以1291∠+∠=︒，所以91GHN FHN ∠+∠=︒，所以91GHF GHN FHN ∠=∠+∠=︒，即91GHF ∠=︒.18.答案：125°解析：证明：1180BGF ∠+∠=︒，155∠=︒，180118055125BGF ∴∠=︒-∠=︒-︒=︒，A F ∠=∠，//AC DF ∴，C CEF ∴∠=∠，C D ∠=∠，CEF D ∴∠=∠，//CE BD ∴，2125BGF ∴∠=∠=︒.19.答案：135AOF ∠=︒解析：因为:4:1AOD BOE ∠∠=，所以设4AOD x ∠=，则BOE x ∠=.因为OE 平分BOD ∠，所以22BOD BOE x ∠=∠=.因为180AOD BOD ∠+∠=︒，所以42180x x +=︒，解得30x =︒. 所以120AOD ∠=︒，60BOD ∠=︒，30BOE DOE ∠=∠=︒，所以150COE ∠=︒. 因为OF 平分COE ∠，所以1752EOF COE ∠=∠=︒.所以45BOF EOF BOE ∠=∠-∠=︒.所以180135AOF BOF ∠=-∠=︒︒.20.答案：平行，理由见解析解析：//BE DF ，理由如下：BE ，DF 分别平分ABC ∠，ADC ∠，12ABE ABC ∴∠=∠，12ADF ADC ∠=∠， 180ADC ABC ∠+∠=︒，()1902ADF ABE ADC ABC ∴∠+∠=∠+∠=︒， 又90ADF AFD ∠+∠=︒，ABE AFD ∴∠=∠，//BE DF ∴.21.答案：(1)//AB CD(2)证明见解析(3)HPQ ∠的大小不会发生变化，其值为45°解析：(1)如图1，//AB CD ， 1∠与2∠互补，12180∴∠+∠=︒. 又1AEF ∠=∠，2CFE ∠=∠，180AEF CFE ∴∠+∠=︒， //AB CD ∴；(2)如图2，由(1)知，//AB CD ，180BEF EFD ∴∠+∠=︒.又BEF ∠与EFD ∠的角平分线交于点P ，1()902FEP EFP BEF EFD ∴∠+∠=∠+∠=︒， 90EPF ∴∠=︒，即EG PF ⊥. GH EG ⊥， //PF GH ∴；(3)HPQ ∠的大小不会发生变化，理由如下： PHK HPK ∠=∠，2PKG HPK ∴∠=∠， GH EG ⊥，90902KPG PKG HPK ∴∠=︒-∠=︒-∠， 180902EPK KPG HPK ∴∠=︒-∠=︒+∠， PQ 平分EPK ∠，1452QPK EPK HPK ∴∠=∠=︒+∠， 45HPQ QPK HPK ∴∠=∠-∠=︒，HPQ ∴∠的大小不会发生变化，其值为45°.。
七级数学下册第二章单元测试题及答案
北师大版七年级数学下册第二章 相交线与平行线单元测试卷（一）班级 姓名 学号 得分一、单选题(注释)1、如图，直线a 、b 、c 、d ，已知c ⊥a ，c ⊥b ，直线b 、c 、d 交于一点，若∠1=500，则∠2等于【 】A ．600B ．500C ．400 D ．3002、如图，AB ⊥BC ，BC ⊥CD ，∠EBC ＝∠BCF ，那么，∠ABE 与∠DCF 的位置与大小关系是 （ ）A ．是同位角且相等B ．不是同位角但相等。
C ．是同位角但不等D ．不是同位角也不等3、如果两个角的一边在同一直线上，另一边互相平行，那么这两个角只能（ ） A ．相等 B ．互补 C ．相等或互补 D ．相等且互补4、下列说法中，为平行线特征的是（ ）①两条直线平行，同旁内角互补。
②同位角相等, 两条直线平行。
③内错角相等, 两条直线平行。
④垂直于同一条直线的两条直线平行. A ．① B ．②③ C ．④ D ．②和④5、如图，AB∥CD∥EF，若∠ABC＝50°，∠CEF＝150°，则∠BCE＝（）A．60°B．50°C．30°D．20°6、如图，如果AB∥CD，则角α、β、γ之间的关系为（）A．α+β+γ＝360°B．α-β+γ＝180°C．α+β-γ＝180°D．α+β+γ＝180°7、如图，由A到B 的方向是（）A．南偏东30°B．南偏东60°C．北偏西30°D．北偏西60°8、如图，由AC∥ED，可知相等的角有（）A．6对B．5对C．4对D．3对9、如图，直线AB、CD交于O，EO⊥AB于O，∠1与∠2的关系是( )更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余，∠1与∠3互补，∠3=120°，则∠1与∠2的度数分别为( ) A．50°、40°B．60°、30°C．50°、130°D．60°、120°11、下列语句正确的是( )A．一个角小于它的补角B．相等的角是对顶角C．同位角互补，两直线平行D．同旁内角互补，两直线平行12、图中与∠1是内错角的角的个数是( )A．2个B．3个C．4个D．5个13、如图，直线AB和CD相交于点O，∠AOD和∠BOC的和为202°，那么∠AOC的度数为( )A．89°B．101°C．79°D．110°14、如图，∠1和∠2是对顶角的图形的个数有( )A．1个B．2个C．3个D．0个15、如图，直线a、b被直线c所截，现给出下列四个条件：①∠1=∠5，②∠1=∠7，③∠2+∠3=180°，④∠4=∠7，其中能判定a∥b的条件的序号是( )A．①②B．①③C．①④D．③④二、填空题(注释)16、如图，∠ACD＝∠BCD，DE∥BC交AC于E，若∠ACB＝60°，∠B＝74°，则∠EDC＝___°，∠CDB＝____°。
(完整版)北师大版七年级下学期数学第二单元测试题及答案
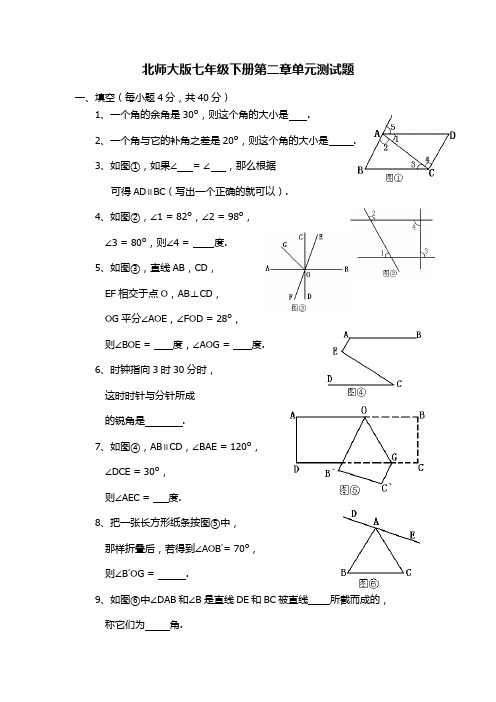
北师大版七年级下册第二章单元测试题一、填空（每小题4分，共40分）1、一个角的余角是30º，则这个角的大小是 .2、一个角与它的补角之差是20º，则这个角的大小是 .3、如图①，如果∠ = ∠ ，那么根据可得AD ∥BC （写出一个正确的就可以）.4、如图②，∠1 = 82º，∠2 = 98º，∠3 = 80º，则∠4 = 度.5、如图③，直线AB ，CD ，EF 相交于点O ，AB ⊥CD ，OG 平分∠AOE ，∠FOD = 28º，则∠BOE = 度，∠AOG = 度.6、时钟指向3时30分时，这时时针与分针所成的锐角是 .7、如图④，AB ∥CD ，∠BAE = 120º，∠DCE = 30º，则∠AEC = 度.8、把一张长方形纸条按图⑤中，那样折叠后，若得到∠AOB ′= 70º，则∠B ′OG = .9、如图⑥中∠DAB 和∠B 是直线DE 和BC 被直线 所截而成的，称它们为 角.10、如图⑦，正方形ABCD 边长为8，M 在DC 上，且DM = 2，N 是AC上一动点，则DN + MN 的最小值为 .二、选择题（每小题3分，共18分）11、下列正确说法的个数是（ ）①同位角相等 ②对顶角相等③等角的补角相等 ④两直线平行，同旁内角相等A . 1， B. 2， C. 3， D. 412、如图⑧，在△ABC 中，AB = AC ，∠A = 36º，BD平分∠ABC ，DE ∥BC ，那么在图中与△ABC 相似的三角形的个数是（ ）A. 0，B. 1，C. 2，D. 313、下列图中∠1和∠2是同位角的是（ ）A. ⑴、⑵、⑶，B. ⑵、⑶、⑷，C. ⑶、⑷、⑸，D.⑴、⑵、⑸14、下列说法正确的是（ ）A.两点之间，直线最短；B.过一点有一条直线平行于已知直线；C.和已知直线垂直的直线有且只有一条；D.在平面内过一点有且只有一条直线垂直于已知直线.15、一束光线垂直照射在水平地面，在地面上放一个平面镜，欲使这束光线经过平面镜反射后成水平光线，则平面镜与地面所成锐角的度数为（）A. 45º，B. 60º，C. 75º，D. 80º16、如图⑨，DH ∥EG ∥EF ，且DC ∥EF ，那么图中和∠1相等的角的个数是（ ）A. 2，B. 4，C. 5，D. 6三、解答题：17、按要求作图（不写作法，但要保留作图痕迹）（3分）已知点P 、Q 分别在∠AOB 的边OA ，OB 上（如图 ）.）①作直线PQ ，②过点P 作OB 的垂线，③过点Q 作OA 的平行线.18、已知线段AB，延长AB到C，使BC∶AB=1∶3，D为AC中点，若DC = 2cm，求AB的长. （7分）分）19、如图，，已知AB∥CD，∠1 = ∠2．求证.：∠E＝∠F （620、如图所示，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个判断：⑴ AD = CB⑵ AE = FC⑶∠B = ∠D⑷ AD∥BC请用其中三个作为已知条件，余下一个作为结论，编一道数学问题，并写出解答过程. （8分）21、如图，ABCD是一块釉面砖，居室装修时需要一块梯形APCD的釉面砖，且使∠APC＝120º.请在长方形AB边上找一点P，使∠APC＝120º.然后把多余部分割下来，试着叙述怎样选取P点及其选取P点的理由.（8分）22、如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E =分）140º，求∠BFD的度数. （10第二单元答案一、填空题：1．60°；２．100°；３．∠5= ∠B，同位角相等，两直线平行；４．80°；５．62°，59°；６．75°；７．90°；８．55°；９．AB，内错；１０．10.二、选择题：11．B； 1２．C； 1３．D； 1４．D； 1５．A； 1６．C.三、解答题：17. 略；18. AB＝3cm；19.略；20. 比如：已知：⑴⑵⑷.求证：⑶；求证过程略；21. 以C为顶点，CD为一边，在∠DCB内画∠DCP＝60°，交AB于P，则P点为所选取的点.证明略；22.∠BFD＝70°；。
北师大版七年级数学下册第二章《相交线与平行线》考试卷附解析版)
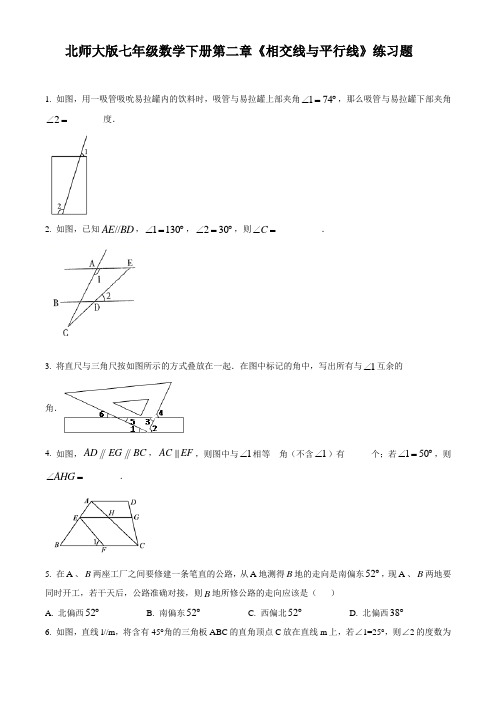
（3）利用上述结论解决问题：如图已知 ， 和 的平分线相交于 ， ，求 的度数．
22.实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．
（1）如图，一束光线 射到平面镜 上，被 反射到平面镜 上，又被 反射，若被 反射出的光线 与光线 平行，且 ，则 _________， ________．
4.如图， ， ，则图中与 相等 角（不含 ）有______个；若 ，则 ________．
5.在 、 两座工厂之间要修建一条笔直的公路，从 地测得 地的走向是南偏东 ，现 、 两地要同时开工，若干天后，公路准确对接，则 地所修公路的走向应该是（ ）
A.北偏西 B.南偏东 C.西偏北 D.北偏西
6.如图，直线l//m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1=25°，则∠2的度数为（）
【答案】95°
【解析】
【详解】如图，作EF∥AB，则EF∥CD，
∴∠ABE+∠BEF=180°，∵∠ABE=120°，∴∠BEF=60°，
∵∠DCE=∠FEC=35°，∴∠BEC=∠BEF+∠FEC=95°.
故答案为95°.
点睛：本题关键在于构造平行线，再利用平行线的性质解题.
13.某人在练车场上练习驾驶汽车，两次拐弯后的行驶方向与原来的方向相反，则这两次拐弯的角度可能是________．①第一次向左拐 ，第二次向右拐 ；②第一次向右拐 ，第二次向左拐 ；③第一次向右拐 ，第二次向左拐 ；④第一次向左拐 ，第二次向左拐 ．
A. 20°B. 25°C. 30°D. 35°
【答案】A
【解析】
【详解】如图，过点B作BD//l，
北师大版七年级数学下册第二章《相交线与平行线》单元同步练习题(含答案)
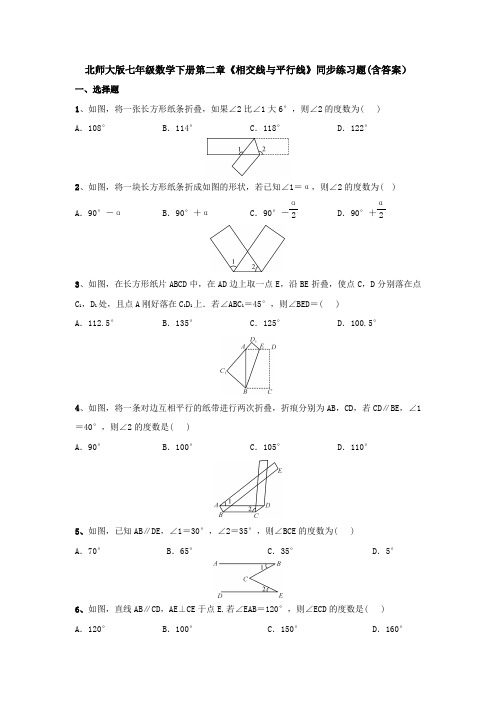
北师大版七年级数学下册第二章《相交线与平行线》同步练习题(含答案）一、选择题1、如图，将一张长方形纸条折叠，如果∠2比∠1大6°，则∠2的度数为( ) A ．108°B ．114°C ．118°D ．122°2、如图，将一块长方形纸条折成如图的形状，若已知∠1＝α，则∠2的度数为( ) A ．90°－αB ．90°＋αC ．90°－α2D ．90°＋α23、如图，在长方形纸片ABCD 中，在AD 边上取一点E ，沿BE 折叠，使点C ，D 分别落在点C 1，D 1处，且点A 刚好落在C 1D 1上．若∠ABC 1＝45°，则∠BED ＝( ) A ．112.5°B ．135°C ．125°D ．100.5°4、如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB ，CD ，若CD ∥BE ，∠1＝40°，则∠2的度数是( ) A ．90°B ．100°C ．105°D ．110°5、如图，已知AB ∥DE ，∠1＝30°，∠2＝35°，则∠BCE 的度数为( ) A ．70°B ．65°C ．35°D ．5°6、如图，直线AB ∥CD ，AE ⊥CE 于点E.若∠EAB ＝120°，则∠ECD 的度数是( ) A ．120°B ．100°C ．150°D ．160°二、填空题7、如图，将长方形ABCD沿EF折叠，点D落在AB边上的H点处，点C落在点G处．若∠AEH ＝30°，则∠EFC等于______.8、如图a是长方形纸带，∠DEF＝15°，将纸带沿EF折叠成图b，则∠AEG＝______.度，再沿BF折叠成图c.则图中的∠CFE＝______度．9、已知：如图，AB∥EF，∠ABC＝75°，∠CDF＝135°，则∠BCD＝______度．10、如图，直线l1∥l2，∠α＝∠β，∠1＝40°，则∠2＝______．11、如图，AB∥CD，∠BED＝110°，BF平分∠ABE，DF平分∠CDE，则∠BFD＝______.12、如图是我们生活中经常接触的小刀，刀片的外壳是一个直角梯形，刀片上、下是平行的，转动刀片时会形成∠1和∠2，则∠1＋∠2＝______.三、解答题13、如图，在Rt△AOB和Rt△COD中，∠AOB＝∠COD＝90°，∠B＝40°，∠C＝60°.点D 在边OA上，将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周，当旋转了多少秒时，边CD恰好与边AB平行？14、问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC.(1)按小明的思路，易求得∠APC的度数为______度；(2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P 在B，D两点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；(3)在(2)的条件下，如果点P在B，D两点外侧运动时(点P与点O，B，D三点不重合)，请直接写出∠APC与α，β之间的数量关系．15、已知AM∥CN，点B为平面内一点，AB⊥BC于点B.(1)如图1，直接写出∠A和∠C之间的数量关系；(2)如图2，过点B作BD⊥AM于点D，∠BAD与∠C有何数量关系，并说明理由；(3)如图3，在(2)问的条件下，点E，F在DM上，连接BE，BF，CF，BF平分∠DBC，BE平分∠ABD.若∠FCB＋∠NCF＝180°，∠BFC＝5∠DBE，求∠EBC的度数．参考答案一、选择题1、如图，将一张长方形纸条折叠，如果∠2比∠1大6°，则∠2的度数为(D) A ．108°B ．114°C ．118°D ．122°2、如图，将一块长方形纸条折成如图的形状，若已知∠1＝α，则∠2的度数为(C) A ．90°－αB ．90°＋αC ．90°－α2D ．90°＋α23、如图，在长方形纸片ABCD 中，在AD 边上取一点E ，沿BE 折叠，使点C ，D 分别落在点C 1，D 1处，且点A 刚好落在C 1D 1上．若∠ABC 1＝45°，则∠BED ＝(A) A ．112.5°B ．135°C ．125°D ．100.5°4、如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB ，CD ，若CD ∥BE ，∠1＝40°，则∠2的度数是(B) A ．90°B ．100°C ．105°D ．110°5、如图，已知AB ∥DE ，∠1＝30°，∠2＝35°，则∠BCE 的度数为(B) A ．70°B ．65°C ．35°D ．5°6、如图，直线AB ∥CD ，AE ⊥CE 于点E.若∠EAB ＝120°，则∠ECD 的度数是(C) A ．120°B ．100°C ．150°D ．160°二、填空题7、如图，将长方形ABCD沿EF折叠，点D落在AB边上的H点处，点C落在点G处．若∠AEH ＝30°，则∠EFC等于105°.8、如图a是长方形纸带，∠DEF＝15°，将纸带沿EF折叠成图b，则∠AEG＝150度，再沿BF折叠成图c.则图中的∠CFE＝135度．9、已知：如图，AB∥EF，∠ABC＝75°，∠CDF＝135°，则∠BCD＝30度．10、如图，直线l1∥l2，∠α＝∠β，∠1＝40°，则∠2＝140°．11、如图，AB∥CD，∠BED＝110°，BF平分∠ABE，DF平分∠CDE，则∠BFD＝125°．12、如图是我们生活中经常接触的小刀，刀片的外壳是一个直角梯形，刀片上、下是平行的，转动刀片时会形成∠1和∠2，则∠1＋∠2＝90°．三、解答题13、如图，在Rt△AOB和Rt△COD中，∠AOB＝∠COD＝90°，∠B＝40°，∠C＝60°.点D 在边OA上，将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周，当旋转了多少秒时，边CD恰好与边AB平行？解：分两种情况：当两三角形在点O的同侧时，如图1，设CD与OB相交于点E.∵AB∥CD，∴∠CEO＝∠B＝40°.∵∠C＝60°，∴∠OOE＝180°－60°－40°－80°.∴∠DOE＝∠COD－∠COE＝10°.∴旋转角∠AOD＝∠AOB＋∠DOE＝90°＋10°＝100°.∵每秒旋转10°，∴旋转的时间为100÷10＝10(秒)．当两三角形在点O的异侧时，如图2，延长BO与CD相交于点E.∵AB∥CD，∴∠CEO＝∠B＝40°.∵∠C＝60°，∴∠COE＝180°－60°－40°＝80°.∴旋转角为360°－∠COE＝360°－80°＝280°.∵每秒旋转10°，∴旋转的时间为280÷10＝28(秒)．综上所述，当旋转了10秒或28秒时，边CD恰好与边AB平行．14、问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC.(1)按小明的思路，易求得∠APC的度数为110度；(2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P 在B，D两点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；(3)在(2)的条件下，如果点P在B，D两点外侧运动时(点P与点O，B，D三点不重合)，请直接写出∠APC与α，β之间的数量关系．图1 图2解：∠APC＝α＋β.理由：过点P作PE∥AB交AC于点E，∵AB∥CD，∴AB∥PE∥CD.∴α＝∠APE，β＝∠CPE.∴∠APC＝∠APE＋∠CPE＝α＋β.(3)如图3，当P在BD延长线上时，∠CPA＝α－β；如图4，当P在DB延长线上时，∠CPA＝β－α.图3 图415、已知AM∥CN，点B为平面内一点，AB⊥BC于点B.(1)如图1，直接写出∠A和∠C之间的数量关系；(2)如图2，过点B作BD⊥AM于点D，∠BAD与∠C有何数量关系，并说明理由；(3)如图3，在(2)问的条件下，点E，F在DM上，连接BE，BF，CF，BF平分∠DBC，BE平分∠ABD.若∠FCB＋∠NCF＝180°，∠BFC＝5∠DBE，求∠EBC的度数．解：(1)∠A＋∠C＝90°(2)过点B作BG∥DM，∵BD⊥AM，∴∠ABD＋∠BAD＝90°，DB⊥BG，即∠ABD＋∠ABG＝90°.又∵AB⊥BC，∴∠CBG＋∠ABG＝90°.∴∠ABD＝∠CBG.∵AM∥CN，BG∥AM，∴CN∥BG.∴∠C＝∠CBG.∴∠ABD＝∠C.∴∠C＋∠BAD＝90°.(3)过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF＝∠CBF，∠DBE＝∠ABE，由(2)可得∠ABD＝∠CBG.∴∠ABF＝∠GBF.设∠DBE＝α，∠ABF＝β，则∠ABE＝α，∠ABD＝2α＝∠CBG，∠GBF＝β＝∠AFB，∠BFC ＝5∠DBE＝5α，∴∠AFC＝5α＋β.∵∠AFC＋∠NCF＝180°，∠FCB＋∠NCF＝180°，∴∠FCB＝∠AFC＝5α＋β.在△BCF中，由∠CBF＋∠BFC＋∠BCF＝180°，可得(2α＋β)＋5α＋(5α＋β)＝180°.①由AB⊥BC，可得β＋β＋2α＝90°.②由①②联立方程组，解得α＝9°.∴∠ABE＝9°.∴∠EBC＝∠ABE＋∠ABC＝9°＋90°＝99°.。
北师大版七年级数学下册第二章相交线与平行线专项测试题 附答案解析(一)
第二章相交线与平行线专项测试题(一)一、单项选择题（本大题共有15小题，每小题3分，共45分）1）.2、在下列命题中，一定正确的是( ).A. 对顶角相等B. 同旁内角互补C. 内错角相等D. 同位角相等3（）4、过一点画已知直线的平行线（）A. 不存在或有且只有一条B. 有两条C. 不存在D. 有且只有一条5、平面内三条直线的交点个数可能有（）6）7、画一条线段的垂线，垂足在（）A. 以上都有可能B. 线段的延长线上C. 线段的端点D. 线段上8）9、在同一平面内，两条直线的位置关系是（）A. 平行，垂直或相交B. 垂直或相交C. 平行或相交D. 平行或垂直10）A. 垂直B. 相交或平行C. 平行D. 相交11）12、下列说法中：①棱柱的上、下底面的形状相同；③相等的两个角一定是对顶角；④不相交的两条直线叫做平行线；⑤直线外一点与直线上各点连接的所有线段中，垂线段最短．正确的有（）13、下列语句：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；④如果两个角是邻补角，那么这两个角的平分线组成的图形是直角．其中错误的有（）14、用一把带有刻度的直角尺，（1）可以画出两条平行线；（2）可以画出一个角的平分线；（3）可以确定一个圆的圆心、以上三个判断中正确的个数是（）15、尺规作图的画图工具是（）A. 没有刻度的直尺和圆规B. 直尺、量角器C. 三角板、量角器D. 刻度尺、量角器二、填空题（本大题共有5小题，每小题5分，共25分）16、已知两条直线相交，有一组邻补角相等，则这两条直线的位置关系为 .17．18、三条直线相交，最多有个交点．19米，则小明从起跳点到落脚点的距离于”）20、作图题的书写步骤是_______、________、_______，而且要画出_______和_______，保留________．三、解答题（本大题共有3小题，每小题10分，共30分）21、如图，在铁路旁有一城镇，现在要建一火车站，为使城镇的人乘车方便（即距离最近），①请你在铁路边选一点建火车站,②说明理由．2223、如图，用数字标出的八个角中，同位角、内错角、同旁内角分别有哪些？请把它们一一写出来．第二章相交线与平行线专项测试题(一) 答案部分一、单项选择题（本大题共有15小题，每小题3分，共45分）1）.【答案】D所以这两个角互为同位角．2、在下列命题中，一定正确的是( ).A. 对顶角相等B. 同旁内角互补C. 内错角相等D. 同位角相等【答案】A【解析】解：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；所以只说同位角相等，内错角相等，同旁内角互补都是错误的，对顶角相等是正确的.故答案应选：对顶角相等.3（）【答案】A4、过一点画已知直线的平行线（）A. 不存在或有且只有一条B. 有两条C. 不存在D. 有且只有一条【答案】A【解析】解：若点在直线上，过这点不能画已知直线的平行线；若点在直线外，根据平行公理，有且只有一条直线与已知直线平行．5、平面内三条直线的交点个数可能有（）【答案】A【解析】解：如图所示，6）【答案】A7、画一条线段的垂线，垂足在（）A. 以上都有可能B. 线段的延长线上C. 线段的端点D. 线段上【答案】A【解析】解：由垂线的定义可知，画一条线段的垂线，垂足可以在线段上，可以是线段的端点，也可以在线段的延长线上．8）【答案】B9、在同一平面内，两条直线的位置关系是（）A. 平行，垂直或相交B. 垂直或相交C. 平行或相交D. 平行或垂直【答案】C【解析】在同一个平面内，两条直线只有两种位置关系，即平行或相交。
北师大版七年级数学下册第二章单元测试卷
第二章评估测试卷(时间：120分钟满分：120分)一、选择题(下列各题的备选答案中，只有一个答案是正确的，每小题2分，共20分)1．如图，有一个破损的扇形零件，小明利用图中的量角器量出这个扇形零件的圆心角度数为50°，你认为小明测量的依据是(B)A．垂线段最短B．对顶角相等C．圆的定义D．三角形内角和等于180°2．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是(B)A．∠4，∠2 B．∠2，∠6 C．∠5，∠4 D．∠2，∠43．如图，∠1＝∠2＝∠3＝55°，则∠4的度数为(C)A．115° B．120° C．125° D．135°4．如图，下列条件中，不能判定直线l1∥l2的是(D)A．∠1＝∠3 B．∠2＋∠4＝180°C．∠4＝∠5 D．∠2＝∠35．如图，将直角三角尺的直角顶点落在直尺上，且斜边与直尺平行，那么在形成的这个图中与∠α互余的角共有(C)A．4个B．3个C．2个D．1个6．如图，点E在AB的延长线上，下列条件中能判断AD∥BC的是(B)A．∠1＝∠3 B．∠2＝∠4C．∠C＝∠CBE D．∠C＋∠ABC＝180°7．如图，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1＝15.5°，则下列结论不正确的是(D)A．∠2＝45° B．∠1＝∠3C．∠AOD与∠1互为补角D．∠1的余角等于75.5°8．如图是赛车跑道的一段示意图，其中AB∥DE，测得∠B＝140°，∠D＝120°，则∠C的度数为(B)A．120° B．100° C．140° D．90°9．如图，AB∥CD，EF平分∠AEG，若∠FGE＝40°，那么∠EFG 的度数为(C)A．35° B．40° C．70° D．140°10．如果两个角的一边在同一直线上，另一边互相平行，那么这两个角只能(C)A．相等B．互补C．相等或互补D．相等且互补二、填空题(每小题3分，共18分)11．如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是直线外一点与直线上各点连接的所有线段中，垂线段最短．12．如图，已知直线AB与CD交于点O，ON平分∠DOB，若∠BOC＝110°，则∠AON的度数为145度．13．如图，∠BDE的同位角是∠BGC，∠BDE的内错角是∠FGD，∠BDE的同旁内角是∠DGC，∠ADE与∠DGC是两条直线ED和CF 被直线AB所截成的同位角．14．如图，AC∥DF，AB∥EF，点D，E分别在AB，AC上，若∠2＝50°，则∠1的大小是50°.15．如图是我们常用的折叠式小刀，刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成∠1与∠2，若∠1＝75°，则∠2的度数为15°.16．如图所示，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯的∠A是120°，第二次拐弯的∠B是150°，第三次拐弯的角是∠C，这时的道路恰好与拐弯前的道路平行，则∠C等于150°.三、解答题(第17小题6分，第18、19小题各8分，共22分)17．完成下列证明：如图所示，已知AD⊥BC，EF⊥BC，∠1＝∠2.求证：DG∥BA.证明：因为AD⊥BC，EF⊥BC(已知)，所以∠EFB＝90°，∠ADB＝90°(垂直的定义)，所以∠EFB＝∠ADB(等量代换)，所以EF∥AD(同位角相等，两直线平行)，所以∠1＝∠BAD(两直线平行，同位角相等)，又∠1＝∠2(已知)，所以∠BAD＝∠2(等量代换)，所以DG∥BA(内错角相等，两直线平行)．18．如图，a ∥b ∥c ，∠1＝40°，∠2＝100°，BD 平分∠ABC ，求∠DBE 的度数．解：因为a ∥b ，所以∠ABE ＝∠1＝40°.因为b ∥c ，所以∠EBC ＋∠2＝180°.因为∠2＝100°，所以∠EBC ＝80°.所以∠ABC ＝∠ABE ＋∠EBC ＝40°＋80°＝120°.因为BD 平分∠ABC ，所以∠DBC ＝12∠ABC ＝60°，所以∠DBE ＝∠EBC －∠DBC ＝80°－60°＝20°.19．如图，已知AD ⊥BC ，EF ⊥BC ，∠3＝∠C ，求证：∠1＝∠2.证明：因为AD ⊥BC ，EF ⊥BC (已知)，所以∠BDA ＝90°，∠BFE ＝90°，所以∠BDA ＝∠BFE ，所以AD ∥EF (同位角相等，两直线平行)，所以∠1＝∠4(两直线平行，同位角相等)，又∠3＝∠C (已知)，所以AC ∥DG (同位角相等，两直线平行)，所以∠2＝∠4(两直线平行，内错角相等)，所以∠1＝∠2(等量代换)．四、(每小题8分，共16分)20．如图，直线AB，CD相交于点O，OE⊥AB于点O，且∠DOE ＝3∠COE，求∠AOD的度数．解：因为∠DOE＋∠COE＝180°，且∠DOE＝3∠COE，所以∠COE＝45°，所以∠BOC＝90°＋45°＝135°，所以∠AOD＝∠BOC＝135°(对顶角相等)．21．(2020·四平模拟)如图，AB∥CD，∠ADC＝∠ABC.求证：∠E ＝∠F.证明：因为AB∥CD，所以∠ABC＝∠DCF.又因为∠ADC＝∠ABC，所以∠ADC＝∠DCF.所以DE∥BF.所以∠E＝∠F.五、(本题10分)22．已知，如图，AB∥CD，BD平分∠ABC，CE平分∠DCF，∠ACE＝90°.(1)判断BD和CE的位置关系并说明理由；(2)判断AC和BD是否垂直并说明理由．解：(1)BD ∥CE .理由：因为AB ∥CD ，所以∠ABC ＝∠DCF ，所以BD 平分∠ABC ，CE 平分∠DCF ，所以∠2＝12∠ABC ，∠4＝12∠DCF ，所以∠2＝∠4，所以BD ∥CE (同位角相等，两直线平行)．(2)AC ⊥BD ，理由：由(1)知BD ∥CE ，所以∠DGC ＋∠ACE ＝180°， 因为∠ACE ＝90°，所以∠DGC ＝180°－90°＝90°，即AC ⊥BD .六、(本题10分)23．如图，已知∠ABC ＝63°，∠ECB ＝117°，∠P ＝∠Q .(1)AB 与ED 平行吗？为什么？(2)∠1与∠2是否相等？说说你的理由．解：(1)平行．理由：因为∠ABC ＝63°，∠ECB ＝117°， 所以∠ABC ＋∠ECB ＝180°，所以AB ∥ED (同旁内角互补，两直线平行)．(2)相等．理由：因为∠P＝∠Q(已知)，所以PB∥CQ(内错角相等，两直线平行)，所以∠PBC＝∠QCB(两直线平行，内错角相等)．因为AB∥CD(已证)，所以∠ABC＝∠DCB(两直线平行，内错角相等)，所以∠ABC－∠PBC＝∠DCB－∠QCB(等式的性质)，即∠1＝∠2.七、(本题12分)24．如图，AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BFD ＝55°，求∠BED的度数．题图解：如图，过点E，F分别作EG∥AB，FH∥AB，答图则有∠5＝∠ABE，∠3＝∠1.又因为AB∥CD，所以EG∥CD，FH∥CD，所以∠6＝∠CDE，∠4＝∠2，所以∠1＋∠2＝∠3＋∠4＝∠BFD＝55°.因为BF 平分∠ABE ，DF 平分∠CDE ，所以∠ABE ＝2∠1，∠CDE ＝2∠2，所以∠BED ＝∠5＋∠6＝2∠1＋2∠2＝2(∠1＋∠2)＝2×55°＝110°.八、(本题12分)25．如图，直线AB ，CD 相交于点O ，OE 平分∠BOD .(1)若∠AOC ＝70°，∠DOF ＝90°，求∠EOF 的度数；(2)若OF 平分∠COE ，∠BOF ＝15°，求∠AOC 的度数．解：(1)因为∠DOB 与∠AOC 互为对顶角，所以∠DOB ＝∠AOC ＝70°，因为OE 平分∠BOD ，所以∠DOE ＝12∠BOD ＝35°，所以∠EOF ＝∠DOF －∠DOE ＝55°.(2)设∠AOC ＝x ，则∠DOB ＝∠AOC ＝x .因为OE 平分∠BOD ，所以∠DOE ＝∠EOB ＝12∠BOD ＝12x ，所以∠EOC ＝180°－∠DOE ＝180°－x 2，因为∠EOF ＝∠EOB ＋∠BOF ，所以∠EOF ＝x 2＋15°.因为OF 平分∠COE ，所以∠EOC ＝2∠EOF ，所以180°－x 2＝2⎝ ⎛⎭⎪⎫x 2＋15°， 解得x ＝100°，即∠AOC ＝100°.。
北师大版七年级数学下册第二章《相交线与平行线》单元检测练习及答案
七年级数学下册第二章《相交线与平行线》单元检测练习命题人：家长签名：班级：______________ 姓名：________________ 座位号：________ 总分一. 选择题(每小题3分，共10小题，答案写在表格内，否则答案无效)题号 1 2 3 4 5 6 7 8 9 10 答案1．已知∠α=35°,那么∠α的余角等于( )A．35°B．55°C．65°D．145°2．下面四个图形中，∠1与∠2是对顶角的图形（）A．B．C．D．3．下列四幅图中，∠1和∠2是同位角的是（）A．⑴⑵B．⑶⑷C．⑴⑵⑶D．⑵⑶⑷4．下列说法：①在同一平面内，不相交的两条线段叫做平行线；②过一点，有且只有一条直线平行于已知直线；③两条平行直线被第三条直线所截，同位角相等；④同旁内角相等，两直线平行．正确的个数有（）个．A．1 B．2 C．3 D．45．如图，已知直线a∥b，直线c与a，b相交，∠1＝110°，则∠2的度数为( )（第5题图）（第6题图）A．60°B．70°C．80°D．110°6．如图，直线AB、CD相交于点E，DF∥AB．若∠AEC=100°，则∠D等于（）A．70°B．80°C．90°D．100°7．如图所示，直线l 1，l 2被直线l 所截形成八个角．由下列哪一个选项中的条件可判定l 1∥l 2 ( )（第7题图） （第8题图） A ．∠2＋∠4＝180° B ．∠3＋∠8＝180° C ．∠5＋∠6＝180° D ．∠7＋∠8＝180° 8．如图，AB∥CD，则图中∠1、∠2、∠3关系一定成立的是 ( )A ．∠1＋∠2＋∠3＝180°B ．∠1＋∠2＋∠3＝360°C ．∠1＋∠3＝2∠2D ．∠1＋∠3＝∠29．如图，A B∥CD，∠1=58°，FG 平分∠EFD，则∠FGB 的度数等于（ ）（第9题图） （第10题图） A ．122°B ．151°C ．116°D ．97°10．如图，已知//AB CD ．直线EF 分别交,AB CD 于点,,E F EG 平分BEF ∠．若1 50∠=︒．则2∠的度数为（ ） A ．50︒B ．65︒C ．60︒D ．70︒二．填空题（每小题4分，共7小题）11．一个角的度数为20°，则它的补角的度数为_____________12．如图，图①是装修工人装修的一部分，图②是一活动角工具(∠1的度数可大可小)，利用活动角工具，装修工人能检测出a 与b 是否平行，其中的依据是_______________________________________________________13．如图，已知AB∥CD，∠1=130°，则∠2=_____________14．如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2=_______（第14题图）（第15题图）15．如图，直线a，b与直线c，d相交，若∠1=∠2，∠3=70°，则∠4的度数是16．如图，∠1＝80°，∠2＝100°，∠3＝76°，则∠4的度数是___________（第16题图）（第17题图）17．如图，直线a，b与直线c相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4+∠7=180°；④∠5+∠3=180°；⑤∠6=∠8，其中能判断a∥b的是_______________________________ (填序号)三．解答题（18-20每题6分，21-23每题8分，24-25每题10分）18．如图，∠1＝∠2，DE⊥BC，AB⊥BC，试说明：∠A＝∠3.解：因为DE⊥BC，AB⊥BC(已知)，所以∠DEC＝∠ABC＝90°(____________________________________)，所以DE∥AB(____________________________________________)，所以∠2＝________ (____________________________________)，∠1＝________ (____________________________________)．因为∠1＝∠2(已知)，所以∠A＝∠3(等量代换)．19．如图,已知AC∥DF,直线AF分别与直线BD、CE相交于点G，H,∠1=∠2.求证：∠C=∠D解：∵∠1=∠2（已知）∠1=∠DGH（），∴∠2=_______（等量代换）∴_______∥_______（同位角相等，两直线平行）∴∠C=_______（两直线平行，同位角相等）又∵AC∥DF（）∴∠D=∠ABG （）∴∠C=∠D （）20．已知：如图：∠1=∠2，∠3+∠4= 180°；确定直线a，c的位置关系，并说明理由；解：a c；理由：∵∠1=∠2（）,∴ a // ( )；∵ ∠3+∠4= 180°（）,∴ c // ( )；∵ a // , c // ,∴ // ( )；21．如图，E 点为DF 上的点，B 为AC 上的点，12∠=∠，C D ∠=∠，求证：DF∥AC．证明：∵ 12∠=∠（已知），∠1=∠3，∠2=∠4（ ），∴∠3=∠4（等量代换）．∴ // ( )；∴∠C=∠ABD（ ）∵∠C=∠D（ ）∴∠D=__________（ ）∴AC∥DF （ ）22．已知：如图，DE∥BC，∠ADE＝64°，BE 平分∠DBC，求∠DEB 的度数．23．如图，直线EF∥GH，点A 在EF 上，AC 交GH 于点B ，若∠FAC=72°，∠ACD=58°，点D 在GH 上，求∠BDC 的度数．24．按要求作图（不写作法，但要保留作图痕迹）已知点P、Q分别在∠AOB的边OA，OB上（如图所示）①作直线PQ；②过点P作OB的垂线；③过点Q作OA的平行线．25．已知：如图，直线a∥b，直线c与直线a、b分别相交于C、D两点，直线d与直线a、b分别相交于A、B两点．（1）如图1，当点P在线段AB上（不与A、B两点重合）运动时，∠1、∠2、∠3之间有怎样的大小关系？请说明理由；（2）如图2，当点P在线段AB的延长线上运动时，∠1、∠2、∠3之间的大小关系为________；（3）如图3，当点P在线段BA的延长线上运动时，∠1、∠2、∠3之间的大小关系为________．七年级数学下册第二章《相交线与平行线》单元检测练习参考答案一. 选择题(每小题3分，共10小题)二．填空题（每小题4分，共7小题）11. 160°12. 同位角相等，两直线平行. 13. 50°14.60° 15.110°16. 76°17. ①③④⑤三．解答题（共8小题）18. 垂直的定义同位角相等，两直线平行∠3两直线平行，内错角相等∠A两直线平行，同位角相等19. 对顶角相等，∠DGH，BD∥CE ，∠ABG，已知，两直线平行，内错角相等，等量代换，20. 解：a // c；理由：∵∠1=∠2（已知）,∴ a // b ( 内错角相等，两直线平行)；∵ ∠3+∠4= 180°（已知）,∴ c // b ( 同旁内角互补，两直线平行)；∵ a // b ,c // b ,∴ a // c ( 平行于同一条直线的两条直线平行)；21. 对顶角相等；DB；CE；内错角相等，两直线平行；两直线平行，同位角相等；已知；等量代换；内错角相等，两直线平行.22.解：因为DE∥BC，所以∠DBC＝∠ADE＝64°.因为BE平分∠DBC，所以∠CBE＝12∠DBC＝12×64°＝32°.因为DE∥BC，所以∠DEB＝∠CBE＝32°.23.解：∵EF∥GH，∴∠ABD+∠FAC=180°，∴∠ABD=180°﹣72°=108°，∵∠ABD=∠ACD+∠BDC，∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°．24.解：如图所示：25. （1）解：如图1，过点P作PE∥a，则∠1=∠CPE．∵a∥b，PE∥a，∴PE∥b，∴∠2=∠DPE，∴∠3=∠1+∠2；（2）解：如图2，过点P作PE∥b，则∠2=∠EPD，∵直线a∥b，∴a∥PE，∴∠1=∠3+∠EPD，即∠1=∠2+∠3．故答案为∠1=∠2+∠3;（3）解：如图3，设直线AC与DP交于点F，∵∠PFA是△PC F的外角，∴∠PFA=∠1+∠3，∵a∥b，∴∠2=∠PFA，即∠2=∠1+∠3．故答案为∠2=∠1+∠3．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相交线与平行线单元测试题
一、相信你的选择（每小题3分，共30分）
1、在下面A、B、C、D四幅图案中，能通过左边的叶片图案平移得到的是( )。
叶片图案 A B C D
￥
2、下列语句不是命题的是（）。
A、有理数的混合运算
B、对顶角相等
C、若∠1＝∠2，∠2＝∠3，则∠1＝∠3
D、任何数的平方都是非负数
3、如图，下列说法错误的是（）。
A、∠A与∠C是同旁内角
B、∠1与∠3是同位角
C、∠2与∠3是内错角
D、∠3与∠B是同旁内角
'
4、三条直线相交于一点，构成的对顶角共有（）。
A、3对
B、4对
C、5对
D、6对
5、如图，∠1＝20°，AO⊥CO，点B、O、D在同一直
线上，则∠2的度数为（）。
A、70°
B、20°
C、110°
D、160°
`
6、如图，△ABC沿BC方向平移得到△DEF，如果∠B＝35°，
∠A＝75°，则∠F＝（）。
A、60°
B、65°
C、70°
D、75°
7、如图，AB∥EF∥DC，EG∥BD，则图中与∠1相等
的角有（）个。
A、2个
B、4个
C、5个
D、6个
/
8、如图，AB∥DE，∠1＝∠2，则AE与DC的位置关系
是（）。
A、相交
B、平行
C、垂直
D、不能确定
9、下列命题正确的是（）。
A、互相垂直的两条线段一定相交
B、从直线外一点到这条直线的垂线段是点到这条直线的距离
C、有且只有一条直线平行于已知直线
?
D、若直线c外一点P与直线c上各点连接而成的所有线段中最短线段的长为4cm，则点P到直线c的距离为4cm。
10、如图，直线a、b都与直线c相交，给出下列条件：①∠1＝∠2；
②∠3＝∠6；③∠4＋∠7＝180°；④∠5＋∠8＝180°。
其中能判断
a∥b的条件是（）。
A、①②
B、②④
C、①③④
D、①②③④
二、试试你的身手（每小题3分，共30分）
11、命题“如果x≠y，那么x2≠y2”的题设是，结论是。
!
12、如图，AB∥CD，∠B＝58°，则∠DFE的度数
为。
13、把命题“同角的补角相等”改写成“如果……那么……”的形式，正确的改写应为。
[
14、一辆汽车在公路上行驶，两次拐弯后仍在原来的方向上平行前进，如果第一次向右拐60°，则第二次向_____拐_______。
15、如图，直线a∥b，且∠1＝28°，∠2＝50°，则
∠ABC＝_______。
*
16、如图，已知AB∥CD，EF⊥CD，FG平分∠EFD，
则∠1与∠2的大小关系为。
17、如图，AB∥CD，直线EF分别交AB、CD于点E、F，
EG平分∠BEF，若∠EFG＝72°，则∠EGF＝_______。
@
18、如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是_______。
19、每天小刚上学时，需要先由家向东走150米到公共汽车站点，然后再乘车向西900米到学校，每天小刚由家到学校移动的方向是_______，移动的距离是_______。
*
20、如图，CD⊥AB于D，DE∥BC，∠1＝∠2，则
FG与AB的位置关系是_____。
三、挑战你的技能（共40分）
21、（6分）如图，字母“X”上的点A平移到了点B，
试画出平移后的图形。
、
22、（6分）如图、A、B之间是一座山，一条高速公路要通过
A、B两点，在A地测得公路走向是北偏西111°32′。
如果A、
B两地同时开工，那么在B地按北偏东多少度施工，才能使公路
在山腹中准确接通为什么
;
23、（6分）如图，△DEF沿CB方向平移得到△ABC，指
出图中平行的线段，相等的线段，相等的角。
@
24、（6分）如图，已知∠AED＝60°，∠2＝30°，EF平分
∠AED，可以判断EF∥BD吗为什么
25、（8分）如图，DE∥AC，DF∥AB，试问∠A＋∠B
＋∠C＝180°这个结论成立吗若成立，试说明理由；若不
）
成立，也请说明理由。
26、（8分）如图，AOB是一条直线，∠AOD∶∠DOB＝3∶1，
OD平分∠COB。
（1）求∠DOC的度数；
（2）判断AB与OC的位置关系。
四、拓广与探索（共20分）
27、（规律开放，结论探究题，8分）如图，（1）已知AB∥CD，
EF∥MN，∠1＝115°，求∠2和∠4的度数；
（2）本题隐含着一个规律，请你根据（1）的结果进行归
纳，试着用文字表述出来；
（3）利用（2）的结论解答：如果两个角的两边分别平行，
其中一角是另一个角的两倍，求这两个角的大小。
]
28、（操作探究题，12分）如图（a），木杆EB与PC平行，木杆的两端B、C用一橡皮筋连接。
"
（1）在图（a）中，∠B与∠C有何关系
（2）若将橡皮筋拉成图（b）的形状，则∠A、∠B、∠C之间有何关系
（3）若将橡皮筋拉成图（c）的形状，则∠A、∠B、∠C之间有何关系
（4）若将橡皮筋拉成图（d）的形状，则∠A、∠B、∠C之间有何关系
)
（5）若将橡皮筋拉成图（e）的形状，则∠A、∠B、∠C之间有何关系
参考答案
一、1、C 2、A 3、B 4、D 5、C 6、C 7、C 8、B 9、D 10、D
二、11、x≠y，x2≠y2；12、122°；
13、如果两个角是同一个角的补角，那么这两个角相等；
14、左，60°；15、78°；16、∠1＝∠2；
17、54°（提示：利用平行线的性质求得∠BEF＝108°，又由角平分线的定义求得∠BEF＝54°，再根据平行线的性质求得∠EGF＝54°）；
18、60°；19、向西，750米；
【
20、FG⊥AB（提示：因为DE∥BC，所以∠2＝∠BCD；又∠1＝∠2，所以∠1＝∠BCD，所以CD∥FG，又因CD⊥AB，故FG⊥AB）。
三、21、如图所示：
【
22、在B地按北偏东68°28′施工，就能使公路在山腹中准确接通。
因为A、B两地公路走向要形成一条直线，根据两正北线平行，同旁内角互补即得。
23、平行的线段有：AB∥DE，AC∥DF；相等的线段有：AB＝DE，AC＝DF，BC＝EF，BE＝CF；相等的角有：∠A＝∠D，∠B＝∠DEF，∠ACB＝∠F。
24、可以判断EF∥BD。
因为∠AED＝60°，EF平分∠AED，所以∠1＝30°，又知∠2＝30°，所以∠1＝∠2。
利用内错角相等两直线平行能得EF∥BD。
25、成立。
因为DE∥AC，所以∠C＝∠EDB，∠EDF＝∠DFC；又因为DF∥AB，所以∠B＝∠FDC，∠A＝∠DFC＝∠EDF；即∠A＋∠B＋∠C＝∠EDF＋∠FDC＋∠EDB，而∠EDF ＋∠FDC＋∠EDB＝180°，故∠A＋∠B＋∠C＝180°。
26、（1）∠DOC＝45°；
（2）易得∠AOC＝90°，故AB⊥OC。
四、
27、（1）∠2＝115°，∠4＝∠3＝65°；
（2）如果一个角两边分别平行于另一个角的两边，那么，这两个角相等或互补；
（3）根据（2）设其中一个角为x，则另一个角为2x，x＋2x＝180°，x＝60°，故这两个角的大小为60°，120°。
28、过点A分别作EB、FC的平行线，将图形转化成两种平行线的基础图形，再结合平行线的性质，进行∠A、∠B、∠C之间数量关系的探索。
（1）∠B＋∠C＝180°，或∠B＝180°－∠C，或∠C＝180°－∠B；
（2）∠A＝∠B＋∠C，或∠B＝∠A－∠C，或∠C＝∠A－∠B。
（3）∠A＋∠B＋∠C＝360°
（4）∠C＝∠A＋∠B，或∠A＝∠C－∠B，或∠B＝∠C－∠A。
（5）∠B＝∠A＋∠C，或∠A＝∠B－∠C，或∠C＝∠B－∠A。