第14章 全等三角形复习课件 ppt
合集下载
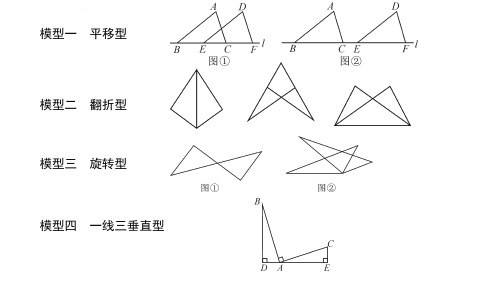
全等三角形的基本模型复习正式经典ppt课件
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
模型三 旋转型 模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全 重合,则称这两个三角形为旋转型三角形.识别旋转型三角形时,如图①, 涉及对顶角相等;如图②,涉及等角加(减)公共角的条件.
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解:∵AB⊥CD,∴∠EBC=∠DBA=90°.在 Rt△CEB 与 Rt△ADB 中 CBEE= =ABDD,,∴Rt△CEB≌Rt△ADB(HL),∴∠C=∠A,又∵∠C+∠CEB= 90°,∠CEB=∠AEF,∴∠A+∠AEF=90°,∴CF⊥AD
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解:∵AD⊥AB,BE⊥AB,CD⊥CE,∴∠DAC=∠CBE=∠DCE=90 °,又∵∠DCB=∠D+∠DAC=∠DCE+∠ECB,∴∠D=∠ECB.在△ACD
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
八年级数学上册 第14章 全等三角形 14.1 全等三角形教学课件 (新版)沪科版

D
⑵.找出对应边,它们有什么关系?(口答)
对应边:_O__A_=__O_B_ _O__D__=__O_C_ _A__D__=_B_C_
⑶.找出对应角,它们有什么关系? (口答)
A
对应角:∠__A__=_∠__B_ _∠__D__=_∠__C_
∠__D__O_A__=_∠__C_O__B_
A
⑷.如果∠A=35°,∠D=75°,那么
∠COB=__7_0_° 2、如图2,如果△ADE ≌ △CBF,那
DB
么AE∥CF吗? _是__ (口答“是”或“不是”) 精选ppt
C
O
B
图1
C
EF
图2 12
五、布置作业
习题14.1
精选ppt
13
本课结束
精选ppt
14
对应角:∠A和∠A1,∠B精和选pp∠t B1,∠C和∠C1
10
三、归纳小结
这节课我们学到了什么?
1、全等形定义及全等三角形; 2、全等三角形的性质.
精选ppt
11
四、强化训练
1、⑴. 已知:如图1,△OAD与△OBC全等, 请用式子表示出这种关系:_△__O__A_D__≌___△__O_B_C_
精选ppt
8
二、新课讲解
A1
A1
B1
C1
B1
C1
能够完全重合的两个三角形称为全等三角形. 记作:△ABC≌△A1B1C1
精选ppt
9
二、新课讲解
全等三角形的对应边相等,对应角相等.
A
A1
B
C
B1
C1
对应顶点:点A和点A1,点B和点B1,点C和点C1
对应边:AB和A1B1,AC和A1C1 ,BC和B1C1
沪科版数学八年级上册14.1全等三角形课件(共19张PPT)

如图,按同一底版印制的两枚邮票,它们的形状相同、大小一样。
全等形定义:能够完全重合的两个图形,叫做全等形.
全等形性质:如果两个图形全等,它们的形状相同,大小相等.
1.与下左图所示图形全等的是 .
①、④
2.下列说法:①用一张底片冲洗出来的2张1寸相片是全等的; ②所有正三角形是全等形; ③面积相等的图形一定是全等形.其中正确的是 .
两个三角形全等是通过什么方法验证的?
平移
解:对应边是:__________________________________
对应角是:__________________________________
AC与DF,AB与DE,BC与EF
∠A与∠D,∠B与∠E,∠C与∠F
A
C
B
如图△AOC≌△BOD
1.对应边是:________________________
2.∠AOC的对应角是________
∠A的对应角是________
OC与OD,AC与BD
∠BOD
∠B
O
D
小结:有对顶角的,对顶角也是对应角.
想一想: 有什么办法判断两个三角形全等?用数学式子表示两个三角形全等,并指出对应角、对应边.
旋转
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
同学们再见!
授课老师:
时间:2024年9月1日
第十四章 全等三角形
14.1 全等三角形
学习目标
学习重难点
重点
难点
1.了解全等形,明确全等三角形的概念.2.掌握全等三角形的性质,识别全等三角形的对应边和对应角.
全等形定义:能够完全重合的两个图形,叫做全等形.
全等形性质:如果两个图形全等,它们的形状相同,大小相等.
1.与下左图所示图形全等的是 .
①、④
2.下列说法:①用一张底片冲洗出来的2张1寸相片是全等的; ②所有正三角形是全等形; ③面积相等的图形一定是全等形.其中正确的是 .
两个三角形全等是通过什么方法验证的?
平移
解:对应边是:__________________________________
对应角是:__________________________________
AC与DF,AB与DE,BC与EF
∠A与∠D,∠B与∠E,∠C与∠F
A
C
B
如图△AOC≌△BOD
1.对应边是:________________________
2.∠AOC的对应角是________
∠A的对应角是________
OC与OD,AC与BD
∠BOD
∠B
O
D
小结:有对顶角的,对顶角也是对应角.
想一想: 有什么办法判断两个三角形全等?用数学式子表示两个三角形全等,并指出对应角、对应边.
旋转
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
同学们再见!
授课老师:
时间:2024年9月1日
第十四章 全等三角形
14.1 全等三角形
学习目标
学习重难点
重点
难点
1.了解全等形,明确全等三角形的概念.2.掌握全等三角形的性质,识别全等三角形的对应边和对应角.
人教版《全等三角形》PPT精品课件

练一练
一、挖掘“隐含条件”判全等
AD
1.如图(1),AB=CD,AC=BD,
则△ABC≌△DCB吗? 说说理由.
B 图(1) C
2.如图(2),点D在AB上,点E在AC B
D
上,CD与BE相交于点O,且
O
A
AD=AE,AB=AC.∠B=20°,CD=5cm,则 C ∠C= 20°,BE= 5c.m说说理由.
全等三角形的性质: 全等三角形的对应边、对应角相等.
全等三角形的判定 SAS、ASA、AAS、SSS、HL
角平分线的性质、判定:
三个角对应相等的两个三角形全等吗?
三个角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三 角形全等吗?
\
==
两边和其中一边的对角对应相等的两个三
角形不一定全等
3、全等三角形的性质?
例1: 如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是
.
要使△ABD≌△ACD,
两边和其中一边的对角对应相等的两个三角形全等吗?
证明题的方法①要证什么
B
添加条件判定全等
A
D
2. 如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
C
根据“SAS”需要添加条件AB=AC ;
12 A
EB
典例分析: 基本图形变式探究 例3:已知如图,AB⊥DC于B,且BD=BA,
BE=BC. 问:AC与DE有什么关系呢?
F
变式练习: 基本图形变式探究 变式1.将上题中的△DBE沿DC方向平移
A EE
DD
BF C
变式练习: 基本图形变式探究
初二数学《全等三角形完整复习》PPT课件

A O E C F
B
D
8、两块含30°角的相同直角三角板,按如图位置摆放,使得两条 相等的直角边AC、C1A1共线 (1)图中有多少对全等三角形?并将它们写出来; (2)选择其中一对(⊿ABC≌⊿A1B1C1除外)进行证明。
B1 O E F B
(1)3对
(2)⊿AEC1≌⊿A1FC
A
C1
C
A1
AC1=A1C
)
延长AD到E,使得AD=DE ⊿ABD≌⊿ECD AB=CE AE-AC<CE<AE+AC 8-5<CE<8+5 3<CE<13
B
A
D
C
E
(三角形中两边之和大于第三 边,两边之差小于第三边)
(2)当⊿DEF旋转至如图③位置时,(1)中的结论还成立吗?请说 A 明理由; A
C A E
O B
F B(E) C
⊿ABF≌⊿DBC
∠AFD=∠DCA
(3)在图③中,连接BO、AD,探索BO、AD之间有怎样的位置关系, A 并证明。
1 3
连接BO,AD
由(2)知:⊿ABC≌⊿DBF ∴∠1=∠2,AB=DB,AC=DF ∴∠3=∠4 AO=DO ∴AO=DO BA=BD BO=BO
B(E)
F C
O
4
2
D
⊿BAO≌⊿BDO ∠ABO=∠DBO
三角形全等
完整复习
知识点
三角形全等的证题思路:
找夹角 SAS 已知两边找直角 HL 找另一边 SSS 边为角的对边 找任一角 AAS 找夹角的另一边 SAS 已知一边一角 边为角的邻边找夹角的另一角 ASA 找边的对角 AAS
第14章全等三角形期末复习PPT课件(沪科版)

第14章 全等三角形的判定
复习要点 1.全等三角形的定义
能够完全重合的两个三角形称为全等三角形. 2.全等三角形的性质:
全等三角形的对应边相等. 全等三角形的对应角相等. 全等三角形的对应边上的高相等. 全等三角形的对应边上的中线相等. 全等三角形的对应角的平分线相等.
复习要点 3.全等三角形的判定方法
C
D
∴BC=DC.
16. 如图,已知AC=BD, BC、AD相交于点E,且
BC⊥AC,BD⊥AD. AD 是∠BAC的平分线. 求证:BC
是∠ABD的平分线.
C
证明:∵ BC⊥AC,BD⊥AD,
D
∴∠C=∠D=90°.
在△RtABC和Rt△BAD中
AB=BA
A
B
AC=BD
∴ △RtABC ≌ Rt△BAD (HL)
要证:DE=AE-DC A 要证:AE=BD DC=BE 要证: △ABE≌△BCD
D 1E
∠ABE=∠BCD.
B
C
∠ABC=120° ∠D=60°
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,
BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是
线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
一般三角形:SSS SAS ASA AAS 直角三角形:HL SAS ASA AAS
结论:判定两个三角形全等的条件中 至少有一组边对应相等.
复习要点
判定两个三角形全等的条件中至少有
一组边对应相等.
4. 判
S SSS
定
S
SAS
全 第一
等 的
找边S
A HL ASA
思
复习要点 1.全等三角形的定义
能够完全重合的两个三角形称为全等三角形. 2.全等三角形的性质:
全等三角形的对应边相等. 全等三角形的对应角相等. 全等三角形的对应边上的高相等. 全等三角形的对应边上的中线相等. 全等三角形的对应角的平分线相等.
复习要点 3.全等三角形的判定方法
C
D
∴BC=DC.
16. 如图,已知AC=BD, BC、AD相交于点E,且
BC⊥AC,BD⊥AD. AD 是∠BAC的平分线. 求证:BC
是∠ABD的平分线.
C
证明:∵ BC⊥AC,BD⊥AD,
D
∴∠C=∠D=90°.
在△RtABC和Rt△BAD中
AB=BA
A
B
AC=BD
∴ △RtABC ≌ Rt△BAD (HL)
要证:DE=AE-DC A 要证:AE=BD DC=BE 要证: △ABE≌△BCD
D 1E
∠ABE=∠BCD.
B
C
∠ABC=120° ∠D=60°
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,
BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是
线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
一般三角形:SSS SAS ASA AAS 直角三角形:HL SAS ASA AAS
结论:判定两个三角形全等的条件中 至少有一组边对应相等.
复习要点
判定两个三角形全等的条件中至少有
一组边对应相等.
4. 判
S SSS
定
S
SAS
全 第一
等 的
找边S
A HL ASA
思
沪科版八年级数学上册 第14章 全等三角形 复习课件 (共22张PPT)

第14章 全等三角形
复习题
要点梳理
一、全等三角形的性质 能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形. 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点, 重合的边叫做对应边, 重合的角叫做对应角.
D B和 点E ,点C和_点F _是对应顶点. 其中点A和 点 ,点 AB和 DE ,BC和EF ,AC和 DF 是对应边.
∠BAO =∠CAO吗?为什么?
解: ∠BAO=∠CAO, 理由:∵ OB⊥AB,OC⊥AC,
B A C O
∴ ∠B=∠C=90°.
在Rt△ABO和Rt△ACO中,
OB=OC,AO=AO,
∴ Rt△ABO≌Rt△ACO ,(HL)
∴ ∠BAO=∠CAO.
热点四 利用全等三角形解决实际问题
例4 如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面垂 直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离 相等吗? 【分析】将本题中的实际问题转化为数学问题 就是证明BD=CD.由已知条件可知AB=AC,
D.AB=DE,BC=EF, ∠ C= ∠ F
3.如图所示,AB与CD相交于点O, ∠A=∠B,OA=OB 添加 或∠AOC=∠BOD , 所以 条件 ∠C=∠D △AOC≌△BOD 理由是 AAS . 或ASA
C O A D
B
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC 交AC于点F, 求证:∠DEC=∠FEC.
A
D
BC=CB(公共边),
∠ACB=∠DBC(已知), ∴△ABC≌△DCB(ASA ).
B
C
复习题
要点梳理
一、全等三角形的性质 能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形. 把两个全等的三角形重合到一起,重合的顶点叫做对应顶点, 重合的边叫做对应边, 重合的角叫做对应角.
D B和 点E ,点C和_点F _是对应顶点. 其中点A和 点 ,点 AB和 DE ,BC和EF ,AC和 DF 是对应边.
∠BAO =∠CAO吗?为什么?
解: ∠BAO=∠CAO, 理由:∵ OB⊥AB,OC⊥AC,
B A C O
∴ ∠B=∠C=90°.
在Rt△ABO和Rt△ACO中,
OB=OC,AO=AO,
∴ Rt△ABO≌Rt△ACO ,(HL)
∴ ∠BAO=∠CAO.
热点四 利用全等三角形解决实际问题
例4 如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面垂 直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离 相等吗? 【分析】将本题中的实际问题转化为数学问题 就是证明BD=CD.由已知条件可知AB=AC,
D.AB=DE,BC=EF, ∠ C= ∠ F
3.如图所示,AB与CD相交于点O, ∠A=∠B,OA=OB 添加 或∠AOC=∠BOD , 所以 条件 ∠C=∠D △AOC≌△BOD 理由是 AAS . 或ASA
C O A D
B
考点三 全等三角形的性质与判定的综合应用
例3 如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC 交AC于点F, 求证:∠DEC=∠FEC.
A
D
BC=CB(公共边),
∠ACB=∠DBC(已知), ∴△ABC≌△DCB(ASA ).
B
C
最新沪科版八年级数学上第14章全等三角形复习课件

___________________________ _______________________
1、证明两个三角形全等 分析:现在我们已知
A→∠CAB=∠DAB
例1 :如图,点B在AE上 ,∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的一 个条件是 ∠∠∠CACCBDB=A=E∠A==∠CD∠.DDBBAE
C
A
B E
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AD=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件
∠CBE=∠DBE也可以 D___________________________
_______________________
1:如图,△AOB≌△COD,AB=7,∠C=60°则
CD= 7
,∠A= 60°
.
B
C
O
A
D
___________________________ _______________________
一、全等三角形性质应用
2:已知△ABC≌△DEF, ∠ A=60°,∠C=50°则
∠E= 70̊
.
A
D
B
(?)
练习1:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一
个条件是
.
E A
D
B C
C
E 1 A 2
B
D
练习2:如图,已知∠1=∠2,AC=AD,增加下列件:①
AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使
ΔABC≌ΔAED的条件有( )个. B
B.3 C.2 D.1
1、证明两个三角形全等 分析:现在我们已知
A→∠CAB=∠DAB
例1 :如图,点B在AE上 ,∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的一 个条件是 ∠∠∠CACCBDB=A=E∠A==∠CD∠.DDBBAE
C
A
B E
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AD=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件
∠CBE=∠DBE也可以 D___________________________
_______________________
1:如图,△AOB≌△COD,AB=7,∠C=60°则
CD= 7
,∠A= 60°
.
B
C
O
A
D
___________________________ _______________________
一、全等三角形性质应用
2:已知△ABC≌△DEF, ∠ A=60°,∠C=50°则
∠E= 70̊
.
A
D
B
(?)
练习1:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一
个条件是
.
E A
D
B C
C
E 1 A 2
B
D
练习2:如图,已知∠1=∠2,AC=AD,增加下列件:①
AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使
ΔABC≌ΔAED的条件有( )个. B
B.3 C.2 D.1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:BC∥E
拓展题
练习8.如图,已知AC∥BD,EA、EB分别平分∠CAB和 ∠DBA,CD过点E,则AB与AC+BD相等吗?
要证明两条线段的和与一条线段 相等时常用的两种方法: C E D A B
1、可在长线段上截取与两条线段 中一条相等的一段,然后证明剩 余的线段与另一条线段相等。 (割)
交流平台
本节课你还有不理解的地方吗?
E
C
D
变式:以上条件不变,将 △ABC绕点C旋转一定角 度(大于零度而小于六十 度),以上的结论仍成立 吗?
∴ BE=AD
练习4:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
C 3 A E 4 D 1 2 B
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2 ∠3=∠4
证明: ∵ AB∥DE
A
练习6:如图,已知,EG∥AF,请你从下面三个条件中, 再选出两个作为已知条件,另一个作为结论,推出一个 正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF 已知: EG∥AF
求证:
E B G
A
D
C F
高
拓展题
练习7.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
2、把一个三角形移到另一位置, 使两线段补成一条线段,再证明 它与长线段相等。(补)
练习9.如图:在四边形ABCD中,点E在边CD上,连接AE、 BE并延长AE交BC的延长线于点F,给出下列5个关系 式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4, ⑤AD+BC=AB。将其中三个关系式作为已知,另外两个 作为结论,构成正确的命题。请用序号写出两个正确 的命题:(书写形式:如果……那么……) (1) ;(2) ;
方法指引
证明两个三角形全等的基本思路:
找第三边 (SSS) (1):已知两边---- 找夹角 (SAS) 找是否有直角 (HL) 找这边的另一个邻角(ASA) 已知一边和它的邻角 (2):已知一边一角--已知一边和它的对角 找这个角的另一个边(SAS) 找这边的对角 (AAS) 找一角(AAS) 已知角是直角,找一边(HL) 找两角的夹边(ASA) 找夹边外的任意边(AAS) 练习
(3):全等三角形的对应边上的对应中线、角平分线、 高线分别相等。
知识回顾:
包括直角三角形
一般三角形 全等的条件:
解题 中常 用的 4种 方法
1.定义(重合)法; 2.SSS; 3.SAS; 不包括其它形 状的三角形 4.ASA; 5.AAS. 直角三角形 全等特有的条件: HL.
回顾知识点:
边边边:三边对应相等的两个三角形全等(可简写成
练习3.已知,△ABC和△ECD都是等边三角形, 且点B,C,D在一条直线上求证:BE=ADA
证明:
∵ △ABC和△ECD都是等边三角形 ∴ AC=BC DC=EC ∠BCA=∠DCE=60° ∴ ∠BCA+∠ACE=∠DCE+ ∠ACE 即∠BCE=∠DCA 在△ACD和△BCE中 AC=BC ∠BCE=∠DCA DC=EC ∴ △ACD≌△BCE (SAS) B
G F H B D E
C
练习12.已知:如图,AD∠BAC, DE⊥AB于E,DF⊥AC于F,DB=DC, 求证:EB=FC
总结提高
学习全等三角形应注意以下几个问题: (1):要正确区分“对应边”与“对边”,“对应 角”与 “对角”的不同含义; (2):表示两个三角形全等时,表示对应顶点的 字母要写在对应的位置上; (3):要记住“有三个角对应相等”或“有两边及 其中一边的对角对应相等”的两个三角形不一定全等; (4):时刻注意图形中的隐含条件,如 “公共角” 、 “公共边”、“对顶角”
B
_ (5)若∠B=∠DEF=90°要以“HL” 为依据,还缺条 件_____
练习2、如图,AE=AD,要使Δ ABD≌Δ ACE,请你增加一 个条件是 .
B
E C 1 A
E A D C
B D
2
练习3、如图,已知∠1=∠2,AC=AD,增加下列件:① AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使 Δ ABC≌Δ AED的条件有( A.4 B.3 C.2 D.1 ) 个.
EB=EB
∴ △EBC≌△EBD (AAS) ∴ BC=BD 在△ABC和△ABD中 AB=AB ∠1=∠2 BC=BD ∴ △ABC≌△ABD (SAS) ∴ AC=AD
练习5:如图,已知,AB∥DE,AB=DE,AF=DC。 请问图中有那几对全等三角形?请任选一对给予证明。
E F
C B
解:
D
△ABC≌△DEF ∴ ∠A=∠D ∵ AF=DC ∴ AF+FC=DC+FC ∴ AC=DF 在△ABC和△DEF中 AC=DF ∠A=∠D AB=DE ∴ △ABC≌△DEF (SAS)
A 2 1 D
E
3 B 4 C F
练习10.如图,在R△ABC中,∠ACB=450, ∠BAC=900,AB=AC,点D是AB的中点,AF⊥CD 于H交BC于F,BE∥AC交AF的延长线于E, 求证:BC垂直且平分DE.
练习11.已知:如图:在△ABC中,BE、CF分别是 AC、AB两边上的高,在BE上截取BD=AC,在CF 的延长线上截取CG=AB,连结AD、AG、DG。 A 求证:△ ADG 为等腰直角三角形。
“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可 简写成“SAS”) 角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全 等(可简写成“AAS”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”)
(3):已知两角---
练习1:已知,如图∠B=∠DEF,BC=EF,补充条 件求证:ΔABC≌ ΔDEF A D
E C F (1)若要以“SAS”为依据,还缺条件 ____ (2) 若要以“ASA”为依据,还缺条件____ (3) 若要以“AAS”为依据,还缺条件____ _ (4)若要以“SSS” 为依据,还缺条件__
第14章 全等三角形(复习)
一.全等三角形:
1:什么是全等三角形?一个三角形经过 哪些变化可以得到它的全等形? 能够完全重合的两个三角形叫做全等三角形。 一个三角形经过平移、翻折、旋转可以得到 它的全等形。 2:全等三角形有哪些性质?
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
拓展题
练习8.如图,已知AC∥BD,EA、EB分别平分∠CAB和 ∠DBA,CD过点E,则AB与AC+BD相等吗?
要证明两条线段的和与一条线段 相等时常用的两种方法: C E D A B
1、可在长线段上截取与两条线段 中一条相等的一段,然后证明剩 余的线段与另一条线段相等。 (割)
交流平台
本节课你还有不理解的地方吗?
E
C
D
变式:以上条件不变,将 △ABC绕点C旋转一定角 度(大于零度而小于六十 度),以上的结论仍成立 吗?
∴ BE=AD
练习4:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
C 3 A E 4 D 1 2 B
解:AC=AD
理由:在△EBC和△EBD中
∠1=∠2 ∠3=∠4
证明: ∵ AB∥DE
A
练习6:如图,已知,EG∥AF,请你从下面三个条件中, 再选出两个作为已知条件,另一个作为结论,推出一个 正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF 已知: EG∥AF
求证:
E B G
A
D
C F
高
拓展题
练习7.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.
2、把一个三角形移到另一位置, 使两线段补成一条线段,再证明 它与长线段相等。(补)
练习9.如图:在四边形ABCD中,点E在边CD上,连接AE、 BE并延长AE交BC的延长线于点F,给出下列5个关系 式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4, ⑤AD+BC=AB。将其中三个关系式作为已知,另外两个 作为结论,构成正确的命题。请用序号写出两个正确 的命题:(书写形式:如果……那么……) (1) ;(2) ;
方法指引
证明两个三角形全等的基本思路:
找第三边 (SSS) (1):已知两边---- 找夹角 (SAS) 找是否有直角 (HL) 找这边的另一个邻角(ASA) 已知一边和它的邻角 (2):已知一边一角--已知一边和它的对角 找这个角的另一个边(SAS) 找这边的对角 (AAS) 找一角(AAS) 已知角是直角,找一边(HL) 找两角的夹边(ASA) 找夹边外的任意边(AAS) 练习
(3):全等三角形的对应边上的对应中线、角平分线、 高线分别相等。
知识回顾:
包括直角三角形
一般三角形 全等的条件:
解题 中常 用的 4种 方法
1.定义(重合)法; 2.SSS; 3.SAS; 不包括其它形 状的三角形 4.ASA; 5.AAS. 直角三角形 全等特有的条件: HL.
回顾知识点:
边边边:三边对应相等的两个三角形全等(可简写成
练习3.已知,△ABC和△ECD都是等边三角形, 且点B,C,D在一条直线上求证:BE=ADA
证明:
∵ △ABC和△ECD都是等边三角形 ∴ AC=BC DC=EC ∠BCA=∠DCE=60° ∴ ∠BCA+∠ACE=∠DCE+ ∠ACE 即∠BCE=∠DCA 在△ACD和△BCE中 AC=BC ∠BCE=∠DCA DC=EC ∴ △ACD≌△BCE (SAS) B
G F H B D E
C
练习12.已知:如图,AD∠BAC, DE⊥AB于E,DF⊥AC于F,DB=DC, 求证:EB=FC
总结提高
学习全等三角形应注意以下几个问题: (1):要正确区分“对应边”与“对边”,“对应 角”与 “对角”的不同含义; (2):表示两个三角形全等时,表示对应顶点的 字母要写在对应的位置上; (3):要记住“有三个角对应相等”或“有两边及 其中一边的对角对应相等”的两个三角形不一定全等; (4):时刻注意图形中的隐含条件,如 “公共角” 、 “公共边”、“对顶角”
B
_ (5)若∠B=∠DEF=90°要以“HL” 为依据,还缺条 件_____
练习2、如图,AE=AD,要使Δ ABD≌Δ ACE,请你增加一 个条件是 .
B
E C 1 A
E A D C
B D
2
练习3、如图,已知∠1=∠2,AC=AD,增加下列件:① AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使 Δ ABC≌Δ AED的条件有( A.4 B.3 C.2 D.1 ) 个.
EB=EB
∴ △EBC≌△EBD (AAS) ∴ BC=BD 在△ABC和△ABD中 AB=AB ∠1=∠2 BC=BD ∴ △ABC≌△ABD (SAS) ∴ AC=AD
练习5:如图,已知,AB∥DE,AB=DE,AF=DC。 请问图中有那几对全等三角形?请任选一对给予证明。
E F
C B
解:
D
△ABC≌△DEF ∴ ∠A=∠D ∵ AF=DC ∴ AF+FC=DC+FC ∴ AC=DF 在△ABC和△DEF中 AC=DF ∠A=∠D AB=DE ∴ △ABC≌△DEF (SAS)
A 2 1 D
E
3 B 4 C F
练习10.如图,在R△ABC中,∠ACB=450, ∠BAC=900,AB=AC,点D是AB的中点,AF⊥CD 于H交BC于F,BE∥AC交AF的延长线于E, 求证:BC垂直且平分DE.
练习11.已知:如图:在△ABC中,BE、CF分别是 AC、AB两边上的高,在BE上截取BD=AC,在CF 的延长线上截取CG=AB,连结AD、AG、DG。 A 求证:△ ADG 为等腰直角三角形。
“SSS”)
边角边:两边和它们的夹角对应相等两个三角形全等(可 简写成“SAS”) 角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”)
角角边:两角和其中一角的对边对应相等的两个三角形全 等(可简写成“AAS”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”)
(3):已知两角---
练习1:已知,如图∠B=∠DEF,BC=EF,补充条 件求证:ΔABC≌ ΔDEF A D
E C F (1)若要以“SAS”为依据,还缺条件 ____ (2) 若要以“ASA”为依据,还缺条件____ (3) 若要以“AAS”为依据,还缺条件____ _ (4)若要以“SSS” 为依据,还缺条件__
第14章 全等三角形(复习)
一.全等三角形:
1:什么是全等三角形?一个三角形经过 哪些变化可以得到它的全等形? 能够完全重合的两个三角形叫做全等三角形。 一个三角形经过平移、翻折、旋转可以得到 它的全等形。 2:全等三角形有哪些性质?
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
