2015年数学二模理科(含答案)
2015年上海市十三校联考高考数学二模试卷(理科)含详解

2015年上海市十三校联考高考数学二模试卷(理科)一、填空题(本大题满分56分)本大题共有14题,每个空格填对4分,否则一律得零分.1.(4分)幂函数y=x(m∈N)在区间(0,+∞)上是减函数,则m=.2.(4分)函数的定义域是.3.(4分)在△ABC中,已知BC=8,AC=5,三角形面积为12,则cos2C=.4.(4分)设i为虚数单位,若关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,则m=.5.(4分)若椭圆的方程为+=1,且此椭圆的焦距为4,则实数a=.6.(4分)若一个圆锥的侧面展开如圆心角为120°、半径为3 的扇形,则这个圆锥的表面积是.7.(4分)若关于x的方程lg(x2+ax)=1在x∈[1,5]上有解,则实数a的取值范围为.8.(4分)《孙子算经》卷下第二十六题:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?.(只需写出一个答案即可)9.(4分)在极坐标系中,某直线的极坐标方程为ρsin(θ+)=,则极点O 到这条直线的距离为.10.(4分)设口袋中有黑球、白球共7 个,从中任取两个球,令取到白球的个数为ξ,且ξ的数学期望Eξ=,则口袋中白球的个数为.11.(4分)如图所示,一个确定的凸五边形ABCDE,令x=•,y=•,z=•,则x、y、z 的大小顺序为.12.(4分)设函数f(x)的定义域为D,D⊆[0,4π],它的对应法则为f:x→sin x,现已知f(x)的值域为{0,﹣,1},则这样的函数共有个.13.(4分)若多项式(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,则a1+a3+…+a2015=.14.(4分)在平面直角坐标系中有两点A(﹣1,3)、B(1,),以原点为圆心,r>0为半径作一个圆,与射线y=﹣x(x<0)交于点M,与x轴正半轴交于N,则当r变化时,|AM|+|BN|的最小值为.二、选择题(本大题满分20分)本大题共有4题,每题有且仅有一个正确答案,选对得5分,否则一律得零分.15.(5分)若非空集合A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若A⊊B,则命题α是命题β的()条件.A.充分非必要B.必要非充分C.充分必要D.既非充分又非必要16.(5分)用反证法证明命题:“已知a、b∈N+,如果ab可被 5 整除,那么a、b 中至少有一个能被5 整除”时,假设的内容应为()A.a、b 都能被5 整除B.a、b 都不能被5 整除C.a、b 不都能被5 整除D.a 不能被5 整除17.(5分)实数x、y满足x2+2xy+y2+4x2y2=4,则x﹣y的最大值为()A.B.C.D.218.(5分)直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是()A.[,]B.[2﹣2,2+2]C.[,]D.[3﹣2,3+2]三、解答题(本大题满分74分)本大题共5题,解答下列各题须写出必要的步骤.19.(12分)已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.20.(14分)已知数列{b n}满足b1=1,且b n+1=16b n(n∈N),设数列{}的前n 项和是T n.(1)比较T n+12与T n•T n+2的大小;(2)若数列{a n}的前n项和S n=2n2+2n+2,数列{c n}=a n﹣log d b n(d>0,d≠1),求d的取值范围使得{c n}是递增数列.21.(14分)某种波的传播是由曲线f(x)=Asin(ωx+φ)(A>0)来实现的,我们把函数解析式f(x)=Asin(ωx+φ)称为“波”,把振幅都是A 的波称为“A 类波”,把两个解析式相加称为波的叠加.(1)已知“1 类波”中的两个波f1(x)=sin(x+φ1)与f2(x)=sin(x+φ2)叠加后仍是“1类波”,求φ2﹣φ1的值;(2)在“A 类波“中有一个是f1(x)=Asinx,从A类波中再找出两个不同的波f2(x),f3(x),使得这三个不同的波叠加之后是平波,即叠加后f1(x)+f2(x)+f3(x),并说明理由.(3)在n(n∈N,n≥2)个“A类波”的情况下对(2)进行推广,使得(2)是推广后命题的一个特例.只需写出推广的结论,而不需证明.22.(16分)设函数f(x)=ax2+(2b+1)x﹣a﹣2(a,b∈R).(1)若a=0,当x∈[,1]时恒有f(x)≥0,求b的取值范围;(2)若a≠0且b=﹣1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.23.(18分)设有二元关系f(x,y)=(x﹣y)2+a(x﹣y)﹣1,已知曲线Γ:f (x,y)=0(1)若a=2时,正方形ABCD的四个顶点均在曲线上Γ,求正方形ABCD的面积;(2)设曲线Γ与x轴的交点是M、N,抛物线Γ′:y=x2+1与y轴的交点是G,直线MG与曲线Γ′交于点P,直线NG与曲线Γ′交于Q,求证:直线PQ过定点,并求出该定点的坐标.(3)设曲线Γ与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线Γ在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Y i(i=1,2,…,255),将Y i中的所有元素相加(若iY中只有一个元素,则其是其自身)得到255个数y1,y2,…,y255求所有的正整数n的值,使得y1n+y2n+…+y255n是与变数a及变数x i(i=1,2,…8)均无关的常数.2015年上海市十三校联考高考数学二模试卷(理科)参考答案与试题解析一、填空题(本大题满分56分)本大题共有14题,每个空格填对4分,否则一律得零分.1.(4分)幂函数y=x(m∈N)在区间(0,+∞)上是减函数,则m= 0.【考点】4U:幂函数的概念、解析式、定义域、值域;4Y:幂函数的单调性、奇偶性及其应用.【专题】11:计算题;51:函数的性质及应用;59:不等式的解法及应用.【分析】根据幂函数的性质,可得m2+2m﹣3<0,解不等式求得自然数解,即可得到m=0.【解答】解:由幂函数y=x m2+2m﹣3在(0,+∞)为减函数,则m2+2m﹣3<0,解得﹣3<m<1.由于m∈N,则m=0.故答案为:0.【点评】本题考查幂函数的性质,主要考查二次不等式的解法,属于基础题.2.(4分)函数的定义域是(0,1] .【考点】33:函数的定义域及其求法;4K:对数函数的定义域.【专题】11:计算题.【分析】令被开方数大于等于0,然后利用对数函数的单调性及真数大于0求出x的范围,写出集合区间形式即为函数的定义域.【解答】解:∴0<x≤1∴函数的定义域为(0,1]故答案为:(0,1]【点评】求解析式已知的函数的定义域应该考虑:开偶次方根的被开方数大于等于0;对数函数的真数大于0底数大于0小于1;分母非0.3.(4分)在△ABC中,已知BC=8,AC=5,三角形面积为12,则cos2C=.【考点】HR:余弦定理.【专题】11:计算题.【分析】先通过BC=8,AC=5,三角形面积为12求出sinC的值,再通过余弦函数的二倍角公式求出答案.【解答】解:∵已知BC=8,AC=5,三角形面积为12,∴•BC•ACsinC=12∴sinC=∴cos2C=1﹣2sin2C=1﹣2×=故答案为:【点评】本题主要考查通过正弦求三角形面积及倍角公式的应用.属基础题.4.(4分)设i为虚数单位,若关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,则m=1.【考点】A1:虚数单位i、复数.【专题】5N:数系的扩充和复数.【分析】把n代入方程,利用复数相等的条件,求出m,n,即可.【解答】解:关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,可得n2﹣(2+i)n+1+mi=0所以,所以m=n=1,故答案为:1.【点评】本题考查复数相等的条件,考查计算能力,是基础题.5.(4分)若椭圆的方程为+=1,且此椭圆的焦距为4,则实数a=4或8.【考点】K4:椭圆的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】首先分两种情况:①焦点在x轴上.②焦点在y轴上,分别求出a的值即可.【解答】解:∵椭圆的焦距为4.∴2c=4,即c=2∵在椭圆中,a2=b2+c2①焦点在x轴上时:10﹣a﹣(a﹣2)=4解得:a=4.②焦点在y轴上时a﹣2﹣(10﹣a)=4解得:a=8故答案为:4或8.【点评】本题考查的知识要点:椭圆方程的两种情况:焦点在x轴或y轴上,考察a、b、c的关系式,及相关的运算问题.6.(4分)若一个圆锥的侧面展开如圆心角为120°、半径为3 的扇形,则这个圆锥的表面积是4π.【考点】LE:棱柱、棱锥、棱台的侧面积和表面积.【专题】5F:空间位置关系与距离.【分析】易得圆锥侧面展开图的弧长,除以2π即为圆锥的底面半径,圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长,把相关数值代入即可求解.【解答】解:圆锥的侧面展开图的弧长为:=2π,∴圆锥的底面半径为2π÷2π=1,∴此圆锥的表面积=π×(1)2+π×1×3=4π.故答案为:4π.【点评】本题考查扇形的弧长公式为;圆锥的侧面展开图的弧长等于圆锥的底面周长,圆锥的表面积的求法.7.(4分)若关于x的方程lg(x2+ax)=1在x∈[1,5]上有解,则实数a的取值范围为﹣3≤a≤9.【考点】51:函数的零点.【专题】11:计算题;51:函数的性质及应用.【分析】由题意,x2+ax﹣10=0在x∈[1,5]上有解,可得a=﹣x在x∈[1,5]上有解,利用a=﹣x在x∈[1,5]上单调递减,即可求出实数a的取值范围.【解答】解:由题意,x2+ax﹣10=0在x∈[1,5]上有解,所以a=﹣x在x∈[1,5]上有解,因为a=﹣x在x∈[1,5]上单调递减,所以﹣3≤a≤9,故答案为:﹣3≤a≤9.【点评】本题主要考查方程的根与函数之间的关系,考查由单调性求函数的值域,比较基础.8.(4分)《孙子算经》卷下第二十六题:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?23,或105k+23(k为正整数)..(只需写出一个答案即可)【考点】F4:进行简单的合情推理.【专题】5M:推理和证明.【分析】根据“三三数之剩二,五五数之剩三,七七数之剩二”找到三个数:第一个数能同时被3和5整除;第二个数能同时被3和7整除;第三个数能同时被5和7整除,将这三个数分别乘以被7、5、3除的余数再相加即可求出答案.【解答】解:我们首先需要先求出三个数:第一个数能同时被3和5整除,但除以7余1,即15;第二个数能同时被3和7整除,但除以5余1,即21;第三个数能同时被5和7整除,但除以3余1,即70;然后将这三个数分别乘以被7、5、3除的余数再相加,即:15×2+21×3+70×2=233.最后,再减去3、5、7最小公倍数的整数倍,可得:233﹣105×2=23.或105k+23(k为正整数).故答案为:23,或105k+23(k为正整数).【点评】本题考查的是带余数的除法,简单的合情推理的应用,根据题意下求出15、21、70这三个数是解答此题的关键.[可以原文理解为:三个三个的数余二,七个七个的数也余二,那么,总数可能是三乘七加二,等于二十三.二十三用五去除余数又恰好是三]9.(4分)在极坐标系中,某直线的极坐标方程为ρsin(θ+)=,则极点O 到这条直线的距离为.【考点】Q4:简单曲线的极坐标方程.【专题】5S:坐标系和参数方程.【分析】由直线的极坐标方程为ρsin(θ+)=,展开并利用即可得出直角坐标方程,再利用点到直线的距离公式即可得出.【解答】解:由直线的极坐标方程为ρsin(θ+)=,展开为,化为x+y﹣1=0,∴极点O到这条直线的距离d==.故答案为:.【点评】本题考查了直线的极坐标方程化为直角坐标方程、点到直线的距离公式、两角和差的正弦公式,考查了推理能力与计算能力,属于基础题.10.(4分)设口袋中有黑球、白球共7 个,从中任取两个球,令取到白球的个数为ξ,且ξ的数学期望Eξ=,则口袋中白球的个数为3.【考点】CH:离散型随机变量的期望与方差.【专题】5I:概率与统计.【分析】设口袋中有白球x个,由已知得ξ的可能取值为0,1,2,由Eξ=,得×,由此能求出口袋中白球的个数.【解答】解:设口袋中有白球x个,由已知得ξ的可能取值为0,1,2,P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,∵Eξ=,∴×,解得x=3.∴口袋中白球的个数为3.故答案为:3.【点评】本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.11.(4分)如图所示,一个确定的凸五边形ABCDE,令x=•,y=•,z=•,则x、y、z 的大小顺序为x>y>z.【考点】9O:平面向量数量积的性质及其运算;9S:数量积表示两个向量的夹角.【专题】5A:平面向量及应用.【分析】根据向量的数量积公式分别判断x,y,z的符号,得到大小关系.【解答】解:由题意,x=•=AB×ACcos∠BAC>0,y=•=AB×ADcos∠BAD≈AB×ACcos∠BAD,又∠BAD>∠BAC所以cos∠BAD<cos∠BAC,所以x>y>0z=•=AB×AEcos∠BAE<0,所以x>y>z.故答案为:x>y>z.【点评】本题考查了向量的数量积的公式;属于基础题.12.(4分)设函数f(x)的定义域为D,D⊆[0,4π],它的对应法则为f:x→sin x,现已知f(x)的值域为{0,﹣,1},则这样的函数共有1395个.【考点】3C:映射.【专题】51:函数的性质及应用;5J:集合.【分析】分别求出sinx=0,x=0,π,2π,3π,4π,sinx=,x=,x=,x=,x=,sinx=1,x=,x=利用排列组合知识求解得出这样的函数共有:(C+C)()()即可.【解答】解:∵函数f(x)的定义域为D,D⊆[0,4π],∴它的对应法则为f:x→sin x,f(x)的值域为{0,﹣,1},sinx=0,x=0,π,2π,3π,4π,sinx=,x=,x=,x=,x=,sinx=1,x=,x=这样的函数共有:(C+C)()()=31×15×3=1395故答案为:1395【点评】本题考查了映射,函数的概念,排列组合的知识,难度不大,但是综合性较强.13.(4分)若多项式(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,则a1+a3+…+a2015=0.【考点】DA:二项式定理.【专题】5P:二项式定理.【分析】根据等式,确定a1=﹣2000×2001+2001×2000=0,a3=0,a5=0,…,即可得出结论.【解答】解:根据(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,可得x1999•x2000的系数a1=﹣2000×2001+2001×2000=0,a3=0,a5=0,…,所以a1+a3+a5+…+a2011+a2013+a2015=0,故答案为:0.【点评】本题考查二项式定理的运用,考查学生分析解决问题的能力,属于中档题.14.(4分)在平面直角坐标系中有两点A(﹣1,3)、B(1,),以原点为圆心,r>0为半径作一个圆,与射线y=﹣x(x<0)交于点M,与x轴正半轴交于N,则当r变化时,|AM|+|BN|的最小值为2.【考点】IR:两点间的距离公式.【专题】11:计算题;35:转化思想;5M:推理和证明.【分析】由题意,设M(a,﹣a)(a<0),则r=﹣2a,N(﹣2a,0).可得|AM|+|BN|=+,设2a=x,进而可以理解为(x,0)与(﹣,)和(﹣1,)的距离和,即可得出结论.【解答】解:由题意,设M(a,﹣a)(a<0),则r=﹣2a,N(﹣2a,0).∴|AM|+|BN|=+设2a=x,则|AM|+|BN|=+,可以理解为(x,0)与(﹣5,)和(﹣1,)的距离和,∴|AM|+|BN|的最小值为(﹣5,)和(﹣1,﹣)的距离,即2.故答案为:2.【点评】本题考查两点间距离公式的应用,考查学生分析解决问题的能力,有难度.二、选择题(本大题满分20分)本大题共有4题,每题有且仅有一个正确答案,选对得5分,否则一律得零分.15.(5分)若非空集合A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若A⊊B,则命题α是命题β的()条件.A.充分非必要B.必要非充分C.充分必要D.既非充分又非必要【考点】29:充分条件、必要条件、充要条件.【专题】5J:集合;5L:简易逻辑.【分析】可举个例子来判断:比如A={1},B={1,2},α:x>0,β:x<3,容易说明此时命题α是命题β的既非充分又非必要条件.【解答】解:命题α是命题β的既非充分又非必要条件;比如A={1},α:x>0;B={1,2},β:x<3;显然α成立得不到β成立,β成立得不到α成立;∴此时,α是β的既非充分又非必要条件.故选:D.【点评】考查真子集的概念,以及充分条件、必要条件、既不充分又不必要条件的概念,以及找一个例子来说明问题的方法.16.(5分)用反证法证明命题:“已知a、b∈N+,如果ab可被 5 整除,那么a、b 中至少有一个能被5 整除”时,假设的内容应为()A.a、b 都能被5 整除B.a、b 都不能被5 整除C.a、b 不都能被5 整除D.a 不能被5 整除【考点】FC:反证法.【专题】5M:推理和证明.【分析】反设是一种对立性假设,即想证明一个命题成立时,可以证明其否定不成立,由此得出此命题是成立的.【解答】解:由于反证法是命题的否定的一个运用,故用反证法证明命题时,可以设其否定成立进行推证.命题“a,b∈N,如果ab可被5整除,那么a,b至少有1个能被5整除.”的否定是“a,b都不能被5整除”.故选:B.【点评】反证法是命题的否定的一个重要运用,用反证法证明问题大大拓展了解决证明问题的技巧.17.(5分)实数x、y满足x2+2xy+y2+4x2y2=4,则x﹣y的最大值为()A.B.C.D.2【考点】7F:基本不等式及其应用.【专题】56:三角函数的求值.【分析】x2+2xy+y2+4x2y2=4,变形为(x+y)2+(2xy)2=4,设x+y=2cosθ,2xy=2sinθ,θ∈[0,2π).化简利用三角函数的单调性即可得出.【解答】解:x2+2xy+y2+4x2y2=4,变形为(x+y)2+(2xy)2=4,设x+y=2cosθ,2xy=2sinθ,θ∈[0,2π).则(x﹣y)2=(x+y)2﹣4xy=4cos2θ﹣4sinθ=5﹣4(sinθ+)2≤5,∴x﹣y.故选:C.【点评】本题考查了平方法、三角函数代换方法、三角函数的单调性,考查了推理能力与计算能力,属于中档题.18.(5分)直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是()A.[,]B.[2﹣2,2+2]C.[,]D.[3﹣2,3+2]【考点】MK:点、线、面间的距离计算.【专题】5F:空间位置关系与距离.【分析】确定直线BC与动点O的空间关系,得到最大距离为AD到球心的距离+半径,最小距离为AD到球心的距离﹣半径.【解答】解:由题意,直线BC与动点O的空间关系:点O是以BC为直径的球面上的点,所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离,最大距离为AD到球心的距离(即BC与AD的公垂线)+半径=2+2.最小距离为AD到球心的距离(即BC与AD的公垂线)﹣半径=2﹣2.∴点O到直线AD的距离的取值范围是:[2﹣2,2+2].故选:B.【点评】本题考查点、线、面间的距离计算,考查学生分析解决问题的能力,属于中档题,解题时要注意空间思维能力的培养.三、解答题(本大题满分74分)本大题共5题,解答下列各题须写出必要的步骤.19.(12分)已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.【专题】5F:空间位置关系与距离;5G:空间角.【分析】(1)由已知得AB⊥平面B1BCC1,从而PQ⊥平面B1BCC1,进而C1Q⊥PQ,又C1Q⊥QR,由此能证明C1Q⊥平面PQR.(2)由已知得B1Q=1,BQ=1,△B1C1Q∽△BQR,从而BR=,QR=,由C1Q、QR、QP两两垂直,能求出四面体C1PQR 的体积.【解答】(1)证明:∵四棱柱ABCD﹣A1B1C1D1是正四棱柱,∴AB⊥平面B1BCC1,又PQ∥AB,∴PQ⊥平面B1BCC1,∴C1Q⊥PQ,又已知C1Q⊥QR,且QR∩QP=Q,∴C1Q⊥平面PQR.(2)解:∵B1C1=,,∴B1Q=1,∴BQ=1,∵Q是BB1中点,C1Q⊥QR,∴∠B1C1Q=∠BQR,∠C1B1Q=∠QBR,∴△B1C1Q∽△BQR,∴BR=,∴QR=,∵C1Q、QR、QP两两垂直,∴四面体C1PQR 的体积V=.【点评】本小题主要考查空间线面关系、线面垂直的证明、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.20.(14分)已知数列{b n}满足b1=1,且b n+1=16b n(n∈N),设数列{}的前n 项和是T n.(1)比较T n+12与T n•T n+2的大小;(2)若数列{a n}的前n项和S n=2n2+2n+2,数列{c n}=a n﹣log d b n(d>0,d≠1),求d的取值范围使得{c n}是递增数列.【考点】82:数列的函数特性;8H:数列递推式.【专题】11:计算题;54:等差数列与等比数列.【分析】(1)由数列递推式可得数列{b n}为公比是16的等比数列,求出其通项公式后可得,然后由等比数列的前n项和求得T n,再由作差法证明T n+12>T n•T n+2;(2)由S n=2n2+2n+2求出首项,进一步得到n≥2时的通项公式,再把数列{a n},{b n}的通项公式代入c n=a n﹣log d b n=4n+(4﹣4n)log d2=(4﹣4log d2)n+4log d2,然后由一次项系数大于0求得d的取值范围.【解答】解:(1)由b n+1=16b n,得数列{b n}为公比是16的等比数列,又b1=1,∴,因此,则=,∵T n+12﹣T n•T n+2=.于是T n+12>T n•T n+2;(2)由S n=2n2+2n+2,当n=1时求得a1=S1=6;当n≥2时,=4n.a1=6不满足上式,∴a n=.当n=1时,c1=a1﹣log d b1=6﹣log d1=6,当n≥2时,可得c n=a n﹣log d b n=4n+(4﹣4n)log d2=(4﹣4log d2)n+4log d2,要使数列{c n}是递增数列,则,解得:0<d<1或d>4.综上,d∈(0,1)∪(4,+∞).【点评】本题考查了等比关系的确定,考查了数列的函数特性,考查了对数不等式的解法,是中档题.21.(14分)某种波的传播是由曲线f(x)=Asin(ωx+φ)(A>0)来实现的,我们把函数解析式f(x)=Asin(ωx+φ)称为“波”,把振幅都是A 的波称为“A 类波”,把两个解析式相加称为波的叠加.(1)已知“1 类波”中的两个波f1(x)=sin(x+φ1)与f2(x)=sin(x+φ2)叠加后仍是“1类波”,求φ2﹣φ1的值;(2)在“A 类波“中有一个是f1(x)=Asinx,从A类波中再找出两个不同的波f2(x),f3(x),使得这三个不同的波叠加之后是平波,即叠加后f1(x)+f2(x)+f3(x),并说明理由.(3)在n(n∈N,n≥2)个“A类波”的情况下对(2)进行推广,使得(2)是推广后命题的一个特例.只需写出推广的结论,而不需证明.【考点】F1:归纳推理;GP:两角和与差的三角函数.【专题】15:综合题;57:三角函数的图像与性质;5M:推理和证明.【分析】(1)根据定义可求得f1(x)+f2(x)=(cosφ1+cosφ2)sinx+(sinφ1+sinφ2)cosx,则振幅是=,由=1,即可求得φ1﹣φ1的值.(2)设f2(x)=Asin(x+φ1),f3(x)=Asin(x+φ2),则f1(x)+f2(x)+f3(x)=0恒成立,可解得cosφ1=﹣,可取φ2=(或φ2=﹣等),证明f1(x)+f2(x)+f3(x)=0.(3)由题意可得f1(x)=Asinx,f2(x)=Asin(x+),f3(x)=Asin(x+),…,从而可求f n(x)=Asin(x+),这n个波叠加后是平波.【解答】解:(1)f1(x)+f2(x)=sin(x+φ1)+sin(x+φ2)=(cosφ1+cosφ2)sinx+(sinφ1+sinφ2)cosx,振幅是=则=1,即cos(φ1﹣φ2)=﹣,所以φ1﹣φ2=2kπ±,k ∈Z.(2)设f2(x)=Asin(x+φ1),f3(x)=Asin(x+φ2),则f1(x)+f2(x)+f3(x)=Asinx+Asin(x+φ1)+Asin(x+φ2)=Asinx(1+cosφ1+cosφ2)+Acosx(sinφ1+sinφ2)=0恒成立,则1+cosφ1+cosφ2=0且sinφ1+sinφ2=0,即有:cosφ2=﹣cosφ1﹣1且sinφ2=﹣sinφ1,消去φ2可解得cosφ1=﹣,若取φ1=,可取φ2=(或φ2=﹣等),此时,f2(x)=Asin(x+),f3(x)=Asin(x+)(或f3(x)=Asin(x﹣)等),则:f1(x)+f2(x)+f3(x)=A[sinx+(sinx+cosx)+(﹣sinx﹣cosx)]=0,所以是平波.(3)f1(x)=Asinx,f2(x)=Asin(x+),f3(x)=Asin(x+),…,f n(x)=Asin(x+),这n个波叠加后是平波.【点评】本题主要考查了两角和与差的正弦函数公式的应用,考查了归纳推理的常用方法,综合性较强,考查了转化思想,属于中档题.22.(16分)设函数f(x)=ax2+(2b+1)x﹣a﹣2(a,b∈R).(1)若a=0,当x∈[,1]时恒有f(x)≥0,求b的取值范围;(2)若a≠0且b=﹣1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.【考点】3H:函数的最值及其几何意义;53:函数的零点与方程根的关系.【专题】15:综合题;51:函数的性质及应用.【分析】(1)求出a=0的解析式,再由一次函数的单调性,得到不等式,即可得到范围;(2)b=﹣1时,y=a(x2﹣1)﹣x﹣2,当x2=1时,无论a取任何值,y=﹣x﹣2为定值,y=f(x)图象一定过点(1,﹣3)和(﹣1,﹣1),运用函数的定义即可得到结论;(3)由题意,存在t∈[3,4],使得at2+(2b+1)t﹣a﹣2=0,即(t2﹣1)a+(2t)b+t﹣2=0,由点到直线的距离意义可知≥=,由此只要求,t∈[3,4]的最小值.【解答】解:(1)当a=0时,f(x)=(2b+1)x﹣2,当x∈[,1]时恒有f(x)≥0,则f()≥0且f(1)≥0,即b﹣≥0且2b﹣1≥0,解得b≥;(2)b=﹣1时,y=a(x2﹣1)﹣x﹣2,当x2=1时,无论a取任何值,y=﹣x﹣2为定值,y=f(x)图象一定过点(1,﹣3)和(﹣1,﹣1)由函数定义可知函数图象一定不过A(1,y1)(y1≠﹣3)和B(﹣1,y2)(y2≠﹣1);(3)由题意,存在t∈[3,4],使得at2+(2b+1)t﹣a﹣2=0即(t2﹣1)a+(2t)b+t﹣2=0,由点到直线的距离意义可知≥=,由此只要求,t∈[3,4]的最小值.令g(t)=,t∈[3,4]设u=t﹣2,u∈[1,2],则g(t)=f(u)==∴u=1,即t=3时,g(t)取最小值,∴t=3时,a2+b2的最小值为.【点评】本题考查不等式的恒成立问题转化为求函数的值域问题,主要考查一次函数的单调性,运用主元法和直线和圆有交点的条件是解题的关键.23.(18分)设有二元关系f(x,y)=(x﹣y)2+a(x﹣y)﹣1,已知曲线Γ:f (x,y)=0(1)若a=2时,正方形ABCD的四个顶点均在曲线上Γ,求正方形ABCD的面积;(2)设曲线Γ与x轴的交点是M、N,抛物线Γ′:y=x2+1与y轴的交点是G,直线MG与曲线Γ′交于点P,直线NG与曲线Γ′交于Q,求证:直线PQ过定点,并求出该定点的坐标.(3)设曲线Γ与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线Γ在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Y i(i=1,2,…,255),将Y i中的所有元素相加(若iY中只有一个元素,则其是其自身)得到255个数y1,y2,…,y255求所有的正整数n的值,使得y1n+y2n+…+y255n是与变数a及变数x i(i=1,2,…8)均无关的常数.【考点】KH:直线与圆锥曲线的综合.【专题】5E:圆锥曲线中的最值与范围问题.【分析】(1)令f(x,y)=(x﹣y)2+2(x﹣y)﹣1=0,解得x﹣y=﹣1±,由于f(x,y)表示两条平行线,之间的距离是2,为一个正方形,即可得出面积S.(2):在曲线C中,令y=0,则x2+ax﹣1=0,设M(m,0),N(n,0),则mn=﹣1,G(0,1),则直线MG:y=﹣x+1,NG:y=﹣x+1.分别与抛物线方程联立可得P,Q.直线PQ的方程为:,令x=0,可得y=3,因此直线PQ过定点(0,3).(3)令y=0,则x2+ax﹣1=0,则mn=﹣1,即点R(u,v)在曲线xy=﹣1上,又曲线C:f(x,y)=0.恒表示平行线x﹣y=,A(x1,x2),B(x3,x4)关于直线y=﹣x对称,即x1+x2+x3+x4=0,同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,集合X={x1,x2,…,x8}的所有非空子集设为Y i=1,2,…,255),取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,=0,对X的其它子集,把它们配成集合“对”(Y p,Y q),Y p∪Y q=X,Y p∩Y q=∅,这样的集合“对”共有127对,且对每一个集合“对”都满足y p+y q=0.可以利用扇形归纳法证明:对于Y p的元素和y p与Y q的元素和y q,当n为奇数时,=0.即可得出.【解答】解:(1)令f(x,y)=(x﹣y)2+2(x﹣y)﹣1=0,解得x﹣y=﹣1±,∴f(x,y)=0表示两条平行线,之间的距离是2,此为一个正方形的一个边长,其面积S=4.(2)证明:在曲线C中,令y=0,则x2+ax﹣1=0,设M(m,0),N(n,0),则mn=﹣1,G(0,1),则直线MG:y=﹣x+1,NG:y=﹣x+1.联立,解得P,同理可得Q.∴直线PQ的方程为:令x=0,则y===3,因此直线PQ过定点(0,3).(3)令y=0,则x2+ax﹣1=0,则mn=﹣1,即点R(u,v)在曲线xy=﹣1上,又曲线C:f(x,y)=(x﹣y)2+a(x﹣y)﹣1=0.恒表示平行线x﹣y=,如图所示,A(x1,x2),B(x3,x4)关于直线y=﹣x对称,则=,即x1+x2+x3+x4=0,同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,集合X={x1,x2,…,x8}的所有非空子集设为Y i,取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,=0,对X的其它子集,把它们配成集合“对”(Y p,Y q),Y p∪Y q=X,Y p∩Y q=∅,这样的集合“对”共有127对,且对每一个集合“对”都满足y p+y q=0.以下证明:对于Y p的元素和y p与Y q的元素和y q,当n为奇数时,=0.先证明:n为奇数时,x+y能够整除x n+y n,用数学归纳法证明.1°当n=1时,成立;2°假设当n=k(奇数)时,x+y能够整除x k+y k,则当n=k+2时,x k+2+y k+2=x k+2﹣x k y2+x k y2+y k+2=x k(x2﹣y2)+y2(x k+y k),因此上式可被x+y整除.由1°,2°可知:n为奇数时,x+y能够整除x n+y n.又∵当n为奇数时,=(y p+y q)M,其中M是关于y p,y q的整式,∵Y p∪Y q=X,Y p∩Y q=∅,∴每一个集合“对”(Y p,Y q)都满足y p+y q=0.则一定有=(x+y)M=0,M∈N*,于是可得y1n+y2n+…+y255n=0是常数.【点评】本题考查了平行直线系、直线的交点、一元二次方程的根与系数的关系、集合的性质、中点坐标公式、对称性、扇形归纳法,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.。
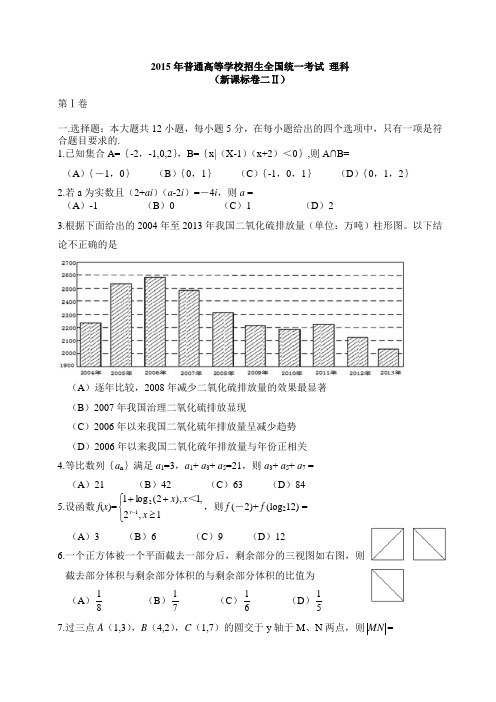
2015年山东省青岛市二模理科数学试题及答案word版

高三自主诊断试题 数学(理科)第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知11abi i=-+,其中,a b 是实数,i 是虚数单位,则||a bi -= A .3 B .2 C .5 D2. 已知集合2{|lg(2)}M x y x x ==-,22{|1}N x x y =+=,则M N = A .[1,2)- B .(0,1) C .(0,1] D .∅3. 高三(3)班共有学生56人,座号分别为1,2,3,,56 ,现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知3号、17号、45号同学在样本中,那么样本中还有一个同学的座号是A .30B .31C .32D .334. 已知函数22, 0,()|log |,0,x x f x x x ⎧≤=⎨>⎩,则使()2f x =的x 的集合是A .1{,4}4B .{1,4}C .1{1,}4D .1{1,,4}45. 已知MOD 函数是一个求余函数,其格式为其结果为n 除以m 的余数,例如(8,3)2MOD =. 右面是一个算法的程序框图, 当输入的值为25时, 则输出的结果为A .4B .5C .6D .76. 设,x y 满足约束条件2311x x y y x ≥⎧⎪-≥⎨⎪≥+⎩,则下列不等式恒成立的是A .3x ≥B .4y ≥C .280x y +-≥D .210x y -+≥7. “2-≤a ”是“函数a x x f -=)(在[1,)-+∞上单调递增”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件8. 将甲、乙等5名交警分配到三个不同路口疏导交通,每个路口至少一人,且甲、乙在同一路口的分配方案共有 A .18种 B .24种 C .36种 D .72种9. 定义在R 上的奇函数()f x 满足(1)()f x f x +=-,当1(0,]2x ∈时,)1(log )(2+=x x f ,则()f x 在区间3(1,)2内是 A .减函数且()0f x >B .减函数且()0f x <C .增函数且()0f x >D .增函数且()0f x <10. 已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,过F 作斜率为1-的直线交双曲线的渐近线于点P ,点P 在第一象限,O 为坐标原点,若OFP ∆的面积为228a b +,则该双曲线的离心率为 A.3 B.3C.3 D.3 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.11. 已知不共线的平面向量a ,b满足(2,2)a =- ,()()a b a b +⊥- ,那么||b = ;12. 某班有50名同学,一次数学考试的成绩X 服从正态分布2(110,10)N ,已知(100110)0.3P X ≤≤=,估计该班学生数学成绩在120分以上的有 人; 13. 某三棱锥的三视图如图所示,该三棱锥的体积是 ;第14题图正(主)视图侧(左)视图第13题图14. 若函数()sin()(0,0)6f x A x A πωω=->>的图象如图所示,则图中的阴影部分的面积为 ;15. 若不等式2222()y x c x xy -≥-对任意满足0x y >>的实数,x y 恒成立,则实数c 的最大值为 .三、解答题:本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤. 16. (本小题满分12分)已知向量2(s i n,c o s )33xx a k = ,(cos ,)3xb k =- ,实数k 为大于零的常数,函数()f x a b =⋅ ,R x ∈,且函数()f x 的最大值为12.(Ⅰ)求k 的值;(Ⅱ)在ABC ∆中,,,a b c 分别为内角,,A B C 所对的边,若2A ππ<<,()0f A =,且a =,求AB AC ⋅的最小值.17.(本小题满分12分)为了分流地铁高峰的压力,某市发改委通过听众会,决定实施低峰优惠票价制度.不超过22公里的地铁票价如下表:现有甲、乙两位乘客,他们乘坐的里程都不超过22公里.已知甲、乙乘车不超过6公里 的概率分别为14,13,甲、乙乘车超过6公里且不超过12公里的概率分别为12,13. (Ⅰ)求甲、乙两人所付乘车费用不相同的概率;(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望. 18.(本小题满分12分)如图,在正四棱台1111ABCD A BC D -中,11A B a =,2AB a =,1AA ,E 、F 分别是AD 、AB 的中点. (Ⅰ)求证:平面11EFB D ∥平面1BDC ;(Ⅱ)求二面角1D BC C --的余弦值的大小.注:底面为正方形,从顶点向底面作垂线,垂足是底面中心, 这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的 平面去截该棱锥,底面与截面之间的部分叫做正四棱台.19.(本小题满分12分)设{}n a 是等差数列,{}n b 是各项都为正整数的等比数列,且111a b ==,13250a b =,82345a b a a +=++,*N n ∈.(Ⅰ)求{}n a ,{}n b 的通项公式; (Ⅱ)若数列{}n d 满足218log 11()2n b n n d d +-++=(*N n ∈),且116d =,试求{}n d 的通项公式及其前n 项和n S .20.(本小题满分13分)已知抛物线1:C 22(0)y px p =>的焦点为F ,抛物线上存在一点G 到焦点的距离为3,且点G 在圆:C 229x y +=上.(Ⅰ)求抛物线1C 的方程;(Ⅱ)已知椭圆2:C 2222 1 (0)x y m n m n+=>>的一个焦点与抛物线1C 的焦点重合,若椭圆2C 上存在关于直线:l 1143y x =+对称的两个不同的点,求椭圆2C 的离心率e 的取值范围. 21.(本小题满分14分)已知函数1()1ln a f x x x=-+(a 为实数). (Ⅰ)当1a =时,求函数()f x 的图象在点11(,())22f 处的切线方程;(Ⅱ)设函数2()32h a a a λ=-(其中λ为常数),若函数()f x 在区间(0,2)上不存在极值,且存在a 满足()≥h a 18+λ,求λ的取值范围; C1BE D FAB1A1D 1C(Ⅲ)已知*N n ∈,求证:11111ln(1)12345n n+<++++++ . 高三自主诊断试题数学(理科)参考答案及评分标准一、选择题:本大题共10小题.每小题5分,共50分.D C B A B C A C B C二、填空题:本大题共5小题,每小题5分,共25分. 11.12. 8 13.32 14.232- 15.4 三、解答题:本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤. 16. (本小题满分12分)解:(Ⅰ)由已知2()(sin ,cos )(cos ,)333x x x f x a b k k =⋅=⋅-221cos12223sin cos cos sin (sin cos )3332322332x x x x x k x x k k k k k +=-=-=--……2分222)sin()3342x x k x k π=-=-- ……………………5分因为R x ∈,所以()f x 的最大值为1)122k=,则1k = …………………6分 (Ⅱ)由(Ⅰ)知,21()sin()2342xf x π=--,所以21()sin()02342A f A π=--= 化简得2sin()34A π-= 因为2A ππ<<,所以25123412Aπππ<-< 则2344A ππ-=,解得34A π=…………………………………………………8分因为2222240cos222b c a b c A bc bc+-+-=-==,所以2240b c ++= 则22402b c bc +=≥,所以20(2bc ≤= ……………10分则3cos 20(142AB AC AB AC π⋅==-≥所以AB AC ⋅的最小值为20(1 …………………………………………………12分17.(本小题满分12分)解:(Ⅰ)由题意可知,甲、乙乘车超过12公里且不超过22公里的概率分别为14,13则甲、乙两人所付乘车费用相同的概率111111114323433P =⨯+⨯+⨯= ……………2分 所以甲、乙两人所付乘车费用不相同的概率1121133P P =-=-= …………………4分 (Ⅱ)由题意可知,6,7,8,9,10ξ= 则111(6)4312P ξ==⨯= 11111(7)43234P ξ==⨯+⨯=1111111(8)4343233P ξ==⨯+⨯+⨯=11111(9)23434P ξ==⨯+⨯=111(10)4312P ξ==⨯= ………………………………………………………………10分所以ξ的分布列为则11111()67891081243412E ξ=⨯+⨯+⨯+⨯+⨯= ……………………………………12分 18.(本小题满分12分)证明:(Ⅰ)连接11AC ,AC ,分别交11,,B D EF BD 于,,M N P ,连接1,MN C P 由题意,BD ∥11B D因为BD ⊄平面11EFB D ,11B D ⊂平面11EFB D ,所以BD ∥平面11EFB D …………2分又因为11,2A B a AB a ==,所以111122MC AC a == 又因为E 、F 分别是AD 、AB 的中点,所以14NP AC == 所以1MC NP =又因为AC ∥11AC ,所以1MC ∥NP 所以四边形1MC PN 为平行四边形 所以1PC ∥MN因为1PC ⊄平面11EFB D ,MN ⊂平面11EFB D ,所以1PC ∥平面11EFB D因为1PC BD P =I ,所以平面11EFB D ∥平面1BDC …………………………………5分 (Ⅱ)连接1A N ,因为11A M MC NP ==,又1A M ∥NP 所以四边形1A NPM 为平行四边形,所以PM ∥1A N由题意M P ⊥平面ABCD ,1A N ∴⊥平面ABCD ,1A N AN ∴⊥ 因为11A B a =,2AB a =,1AA =,所以12A N MP === 因为ABCD 为正方形,所以AC BD ⊥所以,以,,PA PB PM 分别为,,x y z 轴建立如图所示的坐标系则,0)B,(0,,0)D,(,0,0)C,1()2C a -所以(0,,0)BD =-u u u r,1(,)BC =uuu r,(,,0)BC =u u u r ………………………………………………………7分设1111(,,)n x y z =u u r 是平面1BDC 的法向量,则1110n BC n BD ⎧⋅=⎪⎨⋅=⎪⎩u u r uuu ru u r uu u r111100⎧-=⎪∴⎨⎪-=⎩,10y ∴=, 令11z =,则1x1n =u u r……………………………………………9分设2222(,,)n x y z =uu r 是平面1BCC 的法向量,则2120n BC n BC ⎧⋅=⎪⎨⋅=⎪⎩uu r uuu r uu r uu u r2222200⎧=⎪∴⎨⎪=⎩令21y =,则21x =-,23z =所以2(3n =-uu r ………………………………11分所以1212120cos ,3n n n n n n +⋅<>===u u r uu r u r u u r u u r uu r 所以二面角1D BC C --………………………………………12分 ,则依题意有0q >2分4分(Ⅱ) 12n n b -= 21log n b n +∴=811()2n n n d d -++∴= , 7121()2n n n d d -+++=两式相除:212n n d d +=, 由116d =,81121()1282d d -+==可得:28d =135,,,d d d ∴ 是以116d =为首项,以12为公比的等比数列;246,,,d d d 是以28d =为首项,以12为公比的等比数列 ……………………………………………………………6分 ∴当n 为偶数时,1218()16(22n n n d -=⨯= ……………………………………………………………7分13124()()n n n S d d d d d d -=+++++++22221116[1()]8[1()]112232[1()]16[1()]4811221122n nn n n ⨯-⨯-=+=-+-=--- …………9分∴当n 为奇数时,112116()2(22n n n d +-=⨯=…………………………………………………………10分13241()()n n n S d d d d d d -=+++++++112211221116[1()]8[1()]112232[1()]16[1()]4811221122n n n n n +-+-⨯-⨯-=+=-+-=---∴,,nn n d ⎧⎪⎪=⎨⎪⎪⎩,48,48,n n n S ⎧-⎪⎪=⎨⎪-⎪⎩ …………………12分20.(本小题满分13分)n 为奇数 n 为偶数n 为偶数 n 为奇数解:(Ⅰ)设点G 的坐标为00(,)x y ,由题意可知022002003292p x x y y px⎧+=⎪⎪+=⎨⎪=⎪⎩………………………2分解得:001,4,x y p ==±=所以抛物线1C 的方程为:28y x = ………………………………………………………4分 (Ⅱ)由(Ⅰ)得抛物线1C 的焦点(2,0)F椭圆2C 的一个焦点与抛物线1C 的焦点重合∴椭圆2C 半焦距2222, 4c m n c =-==……①…………………………………………5分设1122(,),(,)M x y N x y 是椭圆2C 上关于直线:l 1143y x =+对称的两点, :4MN y x λ=-+ 由2222 1 4x y m n y x λ⎧+=⎪⎨⎪=-+⎩22222222(16)80m n x m x m m n λλ⇒+-+-=……(*) 则42222222644(16)()0m m n m m n λλ∆=-+->,得:222160m n λ+->……②………………………………………………………………7分对于(*),由韦达定理得:21222816m x x m n λ+=+ 212122224()216n y y x x m n λλ∴+=-++=+ MN 中点Q 的坐标为2222224(,)1616m n m n m n λλ++将其代入直线:l 1143y x =+得:222222141164163n m m n m n λλ=⨯+++……③……9分 由①②③消去λ,可得:217m <<, 椭圆2C 的离心率2c e m m ==,∴137e << ………13分21.(本小题满分14分)解:(Ⅰ)当1a =时,11()1ln f x x x =-+,211()f x x x'=-, 则1()4222f '=-=,1()12ln 2ln 212f =-+=-∴函数()f x 的图象在点11(,())22f 的切线方程为:1(ln 21)2()2y x --=-, 即2ln 220x y -+-= …………………………………………………………………4分 (Ⅱ)221()a a x f x x x x-'=-=,由()0f x '=x a ⇒= 由于函数()f x 在区间(0,2)上不存在极值,所以0≤a 或2≥a ………………………5分由于存在a 满足()≥h a 18+λ,所以max ()≥h a 18+λ……………………………………6分 对于函数2()32h a a a λ=-,对称轴34a λ= ①当304λ≤或324λ≥,即0λ≤或83λ≥时,2max 39()()48h a h λλ==, 由max ()≥h a 18+λ29188⇒≥+λλ,结合0λ≤或83λ≥可得:19≤-λ或83λ≥ ②当3014λ<≤,即403λ<≤时,max ()(0)0h a h ==, 由max ()≥h a 18+λ108⇒≥+λ,结合403λ<≤可知:λ不存在; ③当3124λ<<,即4833λ<<时,max ()(2)68h a h λ==-; 由max ()≥h a 18+λ1688⇒-≥+λλ,结合4833λ<<可知:13883≤<λ 综上可知:19≤-λ 或138≥λ………………………………………………………………9分 (Ⅲ)当1a =时,21()x f x x-'=,当(0,1)x ∈时,()0f x '>,()f x 单调递增;当(1,)∈+∞时,()0f x '<,()f x 单调递减,∴11()1ln f x x x=-+在1x =处取得最大值(1)0f = 即11()1ln (1)0f x f x x =-+≤=,∴11ln x x x-≤,……………………………………11分 令 1n x n =+,则11ln n n n +<,即1ln(1)ln n n n +-<, ∴ln(1)ln(1)ln1[ln(1)ln ][ln ln(1)](ln 2ln1)n n n n n n +=+-=+-+--++-1111121n n n <++++-- . 故11111ln(1)12345n n +<++++++ . ………………………………………………14分。
二模理科数学试题及答案.docx

桑水试卷类型:A2015年广州市普通高中毕业班综合测试(二)数学(理科)2015.4本试卷共4页,21小题, 满分150分.考试用时120分钟 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号.用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:球的表面积公式24S R =π,其中R 是球的半径.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“若2x =,则2320x x -+=”的逆否命题是A .若2x ≠,则2320x x -+≠B .若2320x x -+=,则2x = C .若2320x x -+≠,则2x ≠ D .若2x ≠,则2320x x -+=桑水2.已知0a b >>,则下列不等关系式中正确的是A .sin sin a b >B .22log log a b <C .1122a b < D .1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭3.已知函数()4,0,1,0,x x f x x x x ⎧-≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩则()2f f =⎡⎤⎣⎦ A .14 B .12C .2D .44.函数()sin y A x ωϕ=+()0,0,0A ωϕ>><<π的图象的一部分如图1所示, 则此函数的解析式为A .3sin y x ππ⎛⎫=+ ⎪44⎝⎭B .3sin y x π3π⎛⎫=+ ⎪44⎝⎭C .3sin y x ππ⎛⎫=+ ⎪24⎝⎭D .3sin y x π3π⎛⎫=+ ⎪24⎝⎭5.已知函数()223f x x x =-++,若在区间[]4,4-上任取一个实数0x ,则使()00f x ≥成立的概率为A .425B .12C .23 D .16.如图2,圆锥的底面直径2AB =,母线长3VA =,点C 在母线VB 上,且1VC =, 有一只蚂蚁沿圆锥的侧面从点A 到达点C ,则这只蚂蚁爬行的最短距离是A .13B .7C .433D .3327.已知两定点()1,0A -,()1,0B ,若直线l 上存在点M ,使得3MA MB +=,则称直线l 为“M 型直线”.给出下列直线:①2x =;②3y x =+;③21y x =--;④1y =;⑤23y x =+.其中是“M 型直线”的条数为A .1B .2C .3D .48.设(),P x y 是函数()y f x =的图象上一点,向量()()51,2x =-a ,()1,2y x =-b ,且//a b .数列{}na 是公差不为0的等差数列,且()()()12936f a f a f a ++⋅⋅⋅+=,则129a a a ++⋅⋅⋅+= A .0 B .9 C .18 D .36二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.y xO 1 5 3 -3图1AV CB图2桑水(一)必做题(9~13题)9.已知i 为虚数单位,复数1i1iz -=+,则z = . 10.执行如图3所示的程序框图,则输出的z 的值是 .11.已知()sin 6f x x π⎛⎫=+⎪⎝⎭,若3cos 5α=02απ⎛⎫<< ⎪⎝⎭,则12f απ⎛⎫+= ⎪⎝⎭ .12.5名志愿者中安排4人在周六、周日两天参加社区公益活动.若每天安排2人,则不同的安排方案共有_________种(用数字作答). 13.在边长为1的正方形ABCD 中,以A 为起点,其余顶点为终点的向量分别为1a ,2a ,3a ;以C 为起点,其余顶点为终点的向量分别为1c ,2c ,3c .若m 为()()i j s t +∙+a a c c 的最小值,其中{}{},1,2,3i j ⊆,{}{},1,2,3s t ⊆,则m = .(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图4,在平行四边形ABCD 中,4AB =,点E 为边DC 的中点, AE 与BC 的延长线交于点F ,且AE 平分BAD ∠,作DG AE ⊥,垂足为G ,若1DG =,则AF 的长为 . 15.(坐标系与参数方程选做题)在平面直角坐标系中,已知曲线1C 和2C 的方程分别为32,12x t y t =-⎧⎨=-⎩(t 为参数)和24,2x t y t=⎧⎨=⎩(t 为参数),则曲线1C 和2C 的交点有 个.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知△ABC 的三边a ,b ,c 所对的角分别为A ,B ,C ,且::7:5:3a b c =. (1)求cos A 的值;(2)若△ABC 的面积为453,求△ABC 外接圆半径的大小. 17.(本小题满分12分)某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了n 份,统计结果如下面的图表所示. 组号 年龄 答对全卷 答对全卷的人数x=1, y=2z=xy是z<20? x =yy =z输出z结束否开始图3BACDE FG 图4年龄频率/组距 20 30 40 50 600.010c 0.0350.025 0桑水分组 的人数 占本组的概率1 [20,30) 28 b2 [30,40) 27 0.93 [40,50) 5 0.5 4[50,60]a0.4(1)分别求出a ,b ,c ,n 的值;(2)从第3,4组答对全卷的人中用分层抽样的方法抽取6人,在所抽取的6人中随机抽取2人授予“环保之星”,记X 为第3组被授予“环保之星”的人数,求X 的分布列与数学期望.18.(本小题满分14分) 如图5,已知六棱柱111111ABCDEF A B C D E F -的侧棱 垂直于底面,侧棱长与底面边长都为3,M ,N 分别 是棱AB ,1AA 上的点,且1AM AN ==. (1)证明:M ,N ,1E ,D 四点共面;(2)求直线BC 与平面1MNE D 所成角的正弦值. 19.(本小题满分14分)已知点(),n n n P a b ()n ∈*N在直线l :31y x =+上,1P 是直线l 与y 轴的交点,数列{}n a 是公差为1的等差数列.(1)求数列{}n a ,{}n b 的通项公式; (2)求证:22212131111116n PP PP PP ++++<. 20.(本小题满分14分)已知圆心在x 轴上的圆C 过点()0,0和()1,1-,圆D 的方程为()2244x y -+=.(1)求圆C 的方程;(2)由圆D 上的动点P 向圆C 作两条切线分别交y 轴于A ,B 两点,求AB 的取值范围. 21.(本小题满分14分)已知函数()ln f x a x =-11x x -+,()e xg x =(其中e 为自然对数的底数). C 1ABA 1B 1D 1 CDMNEFE 1F 1图5桑水(1)若函数()f x 在区间()0,1内是增函数,求实数a 的取值范围;(2)当0b >时,函数()g x 的图象C 上有两点(),e b P b ,(),e b Q b --,过点P ,Q 作图象C 的切线分别记为1l ,2l ,设1l 与2l 的交点为()00,M x y ,证明00x >.2015年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题,满分40分.题号 12 3 4 56 7 8答案 C D A A B B C C二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题,满分30分.其中14~15题是选做题,考生只能选做一题.题号 9 10 1112 131415答案1327210305- 43 116.(本小题满分12分) 解:(1)因为::7:5:3a b c =,所以可设7a k =,5b k =,3c k =()0k >,…………………………………………………………2分 由余弦定理得,222cos 2b c a A bc +-=()()()222537253k k k k k+-=⨯⨯…………………………………………………………3分桑水12=-.………………………………………………………………………………………………4分 (2)由(1)知,1cos 2A =-,因为A 是△ABC 的内角,所以2sin 1cos A A =-32=.………………………………………………………………………6分 由(1)知5b k =,3c k =, 因为△ABC 的面积为453,所以1sin 4532bc A =,……………………………………………8分 即135345322k k ⨯⨯⨯=, 解得23k =.…………………………………………………………………………………………10分由正弦定理2sin a R A =,即71432sin 32k R A ==,…………………………………………………11分 解得14R =.所以△ABC 外接圆半径的大小为14.…………………………………………………………………12分 17.(本小题满分12分)解:(1)根据频率直方分布图,得()0.0100.0250.035101c +++⨯=,解得0.03c =.……………………………………………………………………………………………1分 第3组人数为105.05=÷,所以1001.010=÷=n .…………………………………………………2分 第1组人数为1000.3535⨯=,所以28350.8b =÷=.……………………………………………3分 第4组人数为2525.0100=⨯,所以250.410a =⨯=.……………………………………………4分 (2)因为第3,4组答对全卷的人的比为5:101:2=,所以第3,4组应依次抽取2人,4人.…………………………………………………………………5分 依题意X 的取值为0,1,2.……………………………………………………………………………6分()022426C C 20C 5P X ===,…………………………………………………………………………………7分 ()112426C C 81C 15P X ===,………………………………………………………………………………8分桑水()202426C C 12C 15P X ===,………………………………………………………………………………9分所以X 的分布列为:X 0 12 P25 815 115所以2812012515153EX =⨯+⨯+⨯=. ………………………………………………………………12分 18.(本小题满分14分)第(1)问用几何法,第(2)问用向量法: (1)证明:连接1A B ,11B D ,BD ,11A E ,在四边形1111A B D E 中,1111A E B D 且1111=A E B D , 在四边形11BB D D 中,11BD B D 且11=BD B D ,所以11A E BD 且11=A E BD ,所以四边形11A BDE 是平行四边形. 所以11A BE D .………………………………2分在△1ABA 中,1AM AN ==,13AB AA ==, 所以1AM ANAB AA =, 所以1MN BA .…………………………………………………………………………………………4分 所以1MNDE .所以M ,N ,1E ,D 四点共面.………………………………………………………………………6分 (2)解:以点E 为坐标原点,EA ,ED ,1EE 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系, 则()33,3,0B ,339,,022C ⎛⎫⎪ ⎪⎝⎭,()0,3,0D , ()10,0,3E ,()33,1,0M ,…………………………8分………………………………………10分 xzyC 1A BA 1B 1D 1CDMNEFE 1F 1 C 1A BA 1B 1D 1CDMNEFE 1F 1桑水则333,,022BC ⎛⎫=- ⎪⎪⎝⎭,()10,3,3DE =-,()33,2,0DM =-.……………………………………………………………………………………10分设(),,x y z =n 是平面1MNE D 的法向量,则10,0.DE DM ⎧=⎪⎨=⎪⎩n n 即330,3320.y z x y -+=⎧⎪⎨-=⎪⎩取33y =,则2x =,33z =.所以()2,33,33=n 是平面1MNE D 的一个法向量.………………………………………………12分 设直线BC 与平面1MNE D 所成的角为θ, 则sin BC BCθ=n n()()2222223332333302217411633323333022⎛⎫⨯-+⨯+⨯ ⎪⎝⎭==⎛⎫⎛⎫++⨯-++ ⎪ ⎪⎝⎭⎝⎭. 故直线BC 与平面1MNE D 所成角的正弦值为174116.………………………………………………14分 第(1)(2)问均用向量法:(1)证明:以点E 为坐标原点,EA ,ED ,1EE 所在的直线分别为x 轴,y 轴,z 轴,建立如图的空间直角坐标系,则()33,3,0B ,339,,022C ⎛⎫⎪ ⎪⎝⎭,()0,3,0D ,()10,0,3E ,()33,1,0M ,()33,0,1N ,……………2分所以()10,3,3DE =-,()0,1,1MN =-. ………………3分 因为13DE MN =,且MN 与1DE 不重合,xzyC 1A BA 1B 1D 1CDMNEFE 1F 1桑水所以1DE MN .…………………………………………5分所以M ,N ,1E ,D 四点共面.………………………………………………………………………6分 (2)解:由(1)知333,,022BC ⎛⎫=- ⎪⎪⎝⎭,()10,3,3DE =-,()33,2,0DM =-.………………10分(特别说明:由于给分板(1)6分(2)8分,相当于把(1)中建系与写点坐标只给2分在此加2分)设(),,x y z =n 是平面1MNE D 的法向量, 则10,0.DE DM ⎧=⎪⎨=⎪⎩n n即330,3320.y z x y -+=⎧⎪⎨-=⎪⎩ 取33y =,则2x =,33z =.所以()2,33,33=n 是平面1MNE D 的一个法向量.………………………………………………12分 设直线1BC 与平面1MNE D 所成的角为θ, 则sin BC BCθ=n n()()2222223332333302217411633323333022⎛⎫⨯-+⨯+⨯ ⎪⎝⎭==⎛⎫⎛⎫++⨯-++ ⎪ ⎪⎝⎭⎝⎭. 故直线BC 与平面1MNE D 所成角的正弦值为174116.………………………………………………14分 第(1)(2)问均用几何法:(1)证明:连接1A B ,11B D ,BD ,11A E ,在四边形1111A B D E 中,1111A E B D 且1111=A E B D , 在四边形11BB D D 中,11BD B D 且11=BD B D ,所以11A E BD 且11=A E BD ,C 1A 1B 1D 1DEE 1F 1桑水所以四边形11A BDE 是平行四边形. 所以11A BE D .………………………………2分在△1ABA 中,1AM AN ==,13AB AA ==, 所以1AM ANAB AA =, 所以1MN BA .…………………………………………………………………………………………4分 所以1MNDE .所以M ,N ,1E ,D 四点共面.………………………………………………………………………6分 (2)连接AD ,因为BCAD ,所以直线AD 与平面1MNE D 所成的角即为直线BC 与平面1MNE D 所成的角.…………………7分 连接DN ,设点A 到平面DMN 的距离为h ,直线AD 与平面1MNE D 所成的角为θ,则sin hADθ=.……………………………………………………………………………………………8分 因为A DMN D AMN V V --=,即1133DMN AMN S h S DB ∆∆⨯⨯=⨯⨯.…………………………………………9分在边长为3的正六边形ABCDEF 中,33DB =,6DA =, 在△ADM 中,6DA =,1AM =,60DAM ∠=, 由余弦定理可得,31DM =.在Rt △DAN 中,6DA =,1AN =,所以37DN =. 在Rt △AMN 中,1AM =,1AN =,所以2MN =. 在△DMN 中,31DM =,37DN =,2MN =,由余弦定理可得,2cos 31DMN ∠=-,所以29sin 31DMN ∠=.所以158sin 22DMN S MN DM DMN ∆=⨯⨯⨯∠=.…………………………………………………11分桑水 又12AMN S ∆=,……………………………………………………………………………………………12分 所以3358AMN DMN S DB h S ∆∆⨯==.…………………………………………………………………………13分 所以174sin 116h AD θ==. 故直线BC 与平面1MNE D 所成角的正弦值为174116.………………………………………………14分19.(本小题满分14分)(1)解:因为()111,P a b 是直线l :31y x =+与y 轴的交点()0,1,所以10a =,11b =.……………………………………………………………………………………2分 因为数列{}n a 是公差为1的等差数列,所以1n a n =-.……………………………………………………………………………………………4分 因为点(),n n n P a b 在直线l :31y x =+上,所以31n n b a =+32n =-.所以数列{}n a ,{}n b 的通项公式分别为1n a n =-,32n b n =-()*n ∈N .………………………6分(2)证明:因为()10,1P ,()1,32n P n n --,所以()1,31n P n n ++. 所以()222211310n PP n n n +=+=.………………………………………………………………………7分 所以222121311111n PP PP PP ++++22211111012n ⎛⎫=+++ ⎪⎝⎭.……………………………………8分 因为()()2221144112141212121214n n n n n n n ⎛⎫<===- ⎪--+-+⎝⎭-,……………………………10分 所以,当2n ≥时,222121311111n PP PP PP ++++桑水111111210352121n n ⎡⎤⎛⎫<+-++- ⎪⎢⎥-+⎝⎭⎣⎦……………………………………………………………11分 15110321n ⎛⎫=- ⎪+⎝⎭………………………………………………………………………………………12分 16<. 又当1n =时,212111106PP =<.………………………………………………………………………13分 所以22212131+111116n PP PP PP +++<.……………………………………………………………14分 20.(本小题满分14分)解:(1)方法一:设圆C 的方程为:()222x a y r -+=()0r >,………………………………………1分因为圆C 过点()0,0和()1,1-,所以()22222,11.a r a r ⎧=⎪⎨--+=⎪⎩………………………………………………………………………………3分 解得1a =-,1r =.所以圆C 的方程为()2211x y ++=.…………………………………………………………………4分 方法二:设()0,0O ,()1,1A -,依题意得,圆C 的圆心为线段OA 的垂直平分线l 与x 轴的交点C .………………………………1分 因为直线l 的方程为1122y x -=+,即1y x =+,……………………………………………………2分 所以圆心C 的坐标为()1,0-.…………………………………………………………………………3分 所以圆C 的方程为()2211x y ++=.…………………………………………………………………4分 (2)方法一:设圆D 上的动点P 的坐标为()00,x y ,则()220044x y -+=, 即()2200440y x =--≥, 解得026x ≤≤.…………………………………………………………………………………………5分 由圆C 与圆D 的方程可知,过点P 向圆C 所作两条切线的斜率必存在,桑水设PA 的方程为:()010y y k x x -=-,则点A 的坐标为()0100,y k x -,同理可得点B 的坐标为()0200,y k x -, 所以120AB k k x =-,因为PA ,PB 是圆C 的切线,所以1k ,2k 满足00211k y kx k -+-=+,即1k ,2k 是方程()()2220000022110x x k y x k y +-++-=的两根,………………………………7分 即()0012200201220021,21.2y x k k x x y k k x x ⎧++=⎪+⎪⎨-⎪=⎪+⎩所以120AB k k x =-()()220000220000412122y y x x x x x x -+⎡⎤=-⎢⎥++⎣⎦……………………………………………9分 因为()220044y x =--, 所以()02056222x AB x -=+.…………………………………………………………………………10分 设()()0020562x f x x -=+,则()()00305222x f x x -+'=+.………………………………………………………………………………11分由026x ≤≤,可知()0f x 在222,5⎡⎫⎪⎢⎣⎭上是增函数,在22,65⎛⎤ ⎥⎝⎦上是减函数,……………………12分 所以()0max 2225564f x f ⎛⎫==⎡⎤ ⎪⎣⎦⎝⎭, ()()(){}min 0131min 2,6min ,484f x f f ⎧⎫===⎡⎤⎨⎬⎣⎦⎩⎭, 所以AB 的取值范围为522,4⎡⎤⎢⎥⎣⎦.…………………………………………………………………14分桑水方法二:设圆D 上的动点P 的坐标为()00,x y ,则()220044x y -+=, 即()2200440y x =--≥, 解得026x ≤≤.…………………………………………………………………………………………5分 设点()0,A a ,()0,B b ,则直线PA :00y a y a x x --=,即()0000y a x x y ax --+=, 因为直线PA 与圆C 相切,所以()0022001a y ax y a x -+=-+,化简得()2000220x a y a x +--=. ①同理得()2000220x b y b x +--=, ②由①②知a ,b 为方程()2000220x x y x x +--=的两根,…………………………………………7分即00002,2.2y a b x x ab x ⎧+=⎪+⎪⎨-⎪=⎪+⎩所以()24AB a b a b ab =-=+- 200002422y x x x ⎛⎫=+ ⎪++⎝⎭ ()()2000204422y x x x ++=+.……………………………………………………………………9分 因为()220044y x =--, 所以()02056222x AB x -=+……………………………………………………………………………10分 ()2001652222x x =-+++.………………………………………………………………11分桑水 令012t x =+,因为026x ≤≤,所以1184t ≤≤. 所以222165AB t t =-+252522163264t ⎛⎫=--+ ⎪⎝⎭,………………………………………12分 当532t =时,max 524AB =, 当14t =时,min 2AB =. 所以AB 的取值范围为522,4⎡⎤⎢⎥⎣⎦.…………………………………………………………………14分 21.(本小题满分14分)(1)解法一:因为函数()ln f x a x =-11x x -+在区间()0,1内是增函数, 所以()()2201a f x x x '=-≥+()01x <<.……………………………………………………………1分 即()2120a x x +-≥()01x <<,即()221xa x ≥+……………………………………………………………………………………………2分212x x=++()01x <<, 因为21122x x<++在()0,1x ∈内恒成立, 所以12a ≥. 故实数a 的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.……………………………………………………………………4分 解法二:因为函数()ln f x a x =-11x x -+在区间()0,1内是增函数, 所以()()2201a f x x x '-+≥=()01x <<.……………………………………………………………1分 即()2120a x x +-≥()01x <<,桑水即()2210ax a x a +-+≥()01x <<,…………………………………………………………………2分 设()()221g x ax a x a =+-+,当0a =时,得20x -≥,此时不合题意.当0a <时,需满足()()00,10,g g ≥⎧⎪⎨≥⎪⎩即()0,210,a a a a ≥⎧⎪⎨+-+≥⎪⎩解得12a ≥,此时不合题意. 当0a >时,需满足()222140a a --≤⎡⎤⎣⎦或()()00,10,10,g g a a ⎧⎪≥⎪≥⎨⎪-⎪-<⎩或()()00,10,11,g g a a⎧⎪≥⎪≥⎨⎪-⎪->⎩ 解得12a ≥或1a >, 所以12a ≥. 综上所述,实数a 的取值范围为1,2⎡⎫+∞⎪⎢⎣⎭.……………………………………………………………4分(2)证明:因为函数()e x g x =,所以()e x g x '=. 过点(),e b P b ,(),e b Q b --作曲线C 的切线方程为: 1l :()e e b b y x b =-+,2l :()e e b b y x b --=++,因为1l 与2l 的交点为()00,M x y ,由()()e e ,e e ,b b b b y x b y x b --⎧=-+⎪⎨=++⎪⎩ ………………………………………………………………………………6分 消去y ,解得()()()0e +e e e e e b b b b b b b x -----=-. ①…………………………………………7分 下面给出判定00x >的两种方法:方法一:设e bt =,………………………………………………………………………………………8分 因为0b >,所以1t >,且ln b t =.桑水所以()()2202+1ln 11t t t x t --=-.…………………………………………………………………………9分设()()()22+1ln 1h t t t t =--()1t >, 则()12ln h t t t t t'=-+()1t >.………………………………………………………………………10分 令()12ln u t t t t t=-+()1t >, 则()212ln 1u t t t'=+-. 当1t >时,ln 0t >,2110t ->,所以()212ln 10u t t t'=+->,………………………………11分 所以函数()u t 在()1,+∞上是增函数,所以()()10u t u >=,即()0h t '>,…………………………………………………………………12分 所以函数()h t 在()1,+∞上是增函数,所以()()10h t h >=.…………………………………………………………………………………13分 因为当1t >时,210t ->, 所以()()2202+1ln 101t t t x t --=>-.…………………………………………………………………14分方法二:由①得0x ()221+e 11e b b b --=--. 设2e b t -=,…………………………………………………………………………………………………8分 因为0b >,所以01t <<,且ln 2t b =-. 于是21ln b t -=,……………………………………………………………………………………………9分 所以()01+221ln 1ln 1b t b t x b t t t t +⎛⎫=+=+ ⎪--⎝⎭.…………………………………………………………10分 由(1)知当12a =时,()1ln 2f x x =-11x x -+在区间()0,1上是增函数,…………………………11分 所以()ln 2t f t =-()1101t f t -<=+, 即ln 2t <11t t -+. …………………………………………………………………………………………12分桑水 即210ln 1t t t++>-,………………………………………………………………………………………13分 已知0b >, 所以0210ln 1t x b t t +⎛⎫=+> ⎪-⎝⎭.…………………………………………………………………………14分。
2015年普通高中高三第二次联合考试理科数学附答案

BA BC 2 ,则 ABC 的面积为 (
A. 2
2
) C. 2 2 D. 4 2
B.
3 2
(10)已知抛物线 y =2px(p>0)与双曲线 2- 2=1(a>0,b>0)有相同的焦点 F,点 A 是两曲线的一个交点,且 AF⊥x 轴,则双曲线的离心率为( ( ) A. 2+2 B. 5+1 C. 3+1
2015 年普通高中高三第二次联合考试理科数学
注意事项: 1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的 姓名、准考证号填写在答题卡上。 2. 回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号框 涂黑。如 需改动,用橡皮擦干净后,再选涂其它答案标号框。写在本试卷上无效。 3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。 4. 考试结束后,将本试卷和答题卡一并交回。
D. 1,1
第Ⅱ卷
本卷包括必考题和选考题两部分。 第 13 题~第 21 题为必考题, 每个试题考生都必须做 答。第 22 题~第 24 题为选考题,考生根据要求做答。 二、填空题:本大题共 4 小题,每小题 5 分。
(13)若复数 z
(a 2 4) (a 2)i 为纯虚数,则
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只 有一项是符合题目要求的。
(1)设集合 A
x y lg(3 2x),集合 B y y
B. (﹣∞,1] C.
)
A. [ 0, )
3 2
(2) 若命题 p 为真命题,命题 q 为假命题,则以下为真命题的是(
A. p q
2015年高考数学全国卷二理科真题+答案解析
2015年普通高等学校招生全国统一考试 理科(新课标卷二Ⅱ)第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-2,-1,0,2},B={x|(X-1)(x+2)<0},则A∩B= (A ){-1,0} (B ){0,1} (C ){-1,0,1} (D ){0,1,2}2.若a 为实数且(2+ai )(a -2i )=-4i ,则a =(A )-1 (B )0 (C )1 (D )23.根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图。
以下结论不正确的是(A )逐年比较,2008年减少二氧化硫排放量的效果最显著 (B )2007年我国治理二氧化硫排放显现(C )2006年以来我国二氧化硫年排放量呈减少趋势 (D )2006年以来我国二氧化硫年排放量与年份正相关 4.等比数列{a n }满足a 1=3,a 1+ a 3+ a 5=21,则a 3+ a 5+ a 7 = (A )21 (B )42 (C )63 (D )845.设函数f (x )=⎩⎨⎧≥++-1,2,1),2(log 112x x x x <,则f (-2)+ f (log 212) =(A )3 (B )6 (C )9 (D )126.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则 截去部分体积与剩余部分体积的与剩余部分体积的比值为(A )81 (B )71 (C )61(D )517.过三点A (1,3),B (4,2),C (1,7)的圆交于y 轴于M 、N 两点,则MN=(A )26 (B )8 (C )46 (D )10 8.右边程序抗土的算法思路源于我国古代数学名著《九章算术》 中的“更相减损术”。
执行该程序框图,若输入a,b 分别为14,18, 则输出的a= (A )0 (B )2 (C )4 (D )149.已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体 积的最大值为36,则球O 的表面积为(A )36π (B )64π (C )144π (D )256π10.如图,长方形ABCD 的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC ,CD 与 DA 运动,∠BOP=x 。
2015市二模理科数学

理科数学试题(二)参考答案一、选择题(本大题共12小题,每小题5分,共60分.)CBDA A BCBAD CC. 二、填空题:(本大题共4小题,每小题5分,共20分.) 13.23π. 14. 23n n a =. 15.14. 16. 2016 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 解:(Ⅰ)11sincos 2222ααα-=,11c o s 22αα-=,所以1sin()62πα-=,又因为α为锐角,所以3πα=. ………………6分(Ⅱ)2()cos 22sin 2sin 2sin 1f x x x x x =+=-++,令sin t x =,则2221(11)y t t t =-++-≤≤,由二次函数的图像知:当12t =时,max 32y =;当1t =-时,min 3y =-, 所以函数()f x 的值域为3[3,]2-. ………………12分18.(本小题满分12分) 解:(Ⅰ)证明:PD ⊥平面ABCD ,BC Ü平面ABCD ,BC PD ∴⊥,又,BC CD CD PD D ⊥=,BC PCD ∴⊥面,又PC PCD 面Ü,∴BC PC ⊥. …………6分(Ⅱ)因为,//BC CD AD BC ⊥,所以AD DC ⊥,以D 为原点建立空间直角坐标系D xyz -,不妨设1AD =,则(1,0,0)A ,(0,0,2)P ,(0,2,0)C ,(2,2,0)B ,设平面PBC 的一个法向量为(,,)m x y z =,又(2,0,0)BC =-,(0,2,2)PC =-,由00m BC m PC ⎧⋅=⎪⎨⋅=⎪⎩得20220x y z -=⎧⎨-=⎩,不妨取1y =,则(0,1,1)m =,(1,0,2)PA =-,∴PA 与平面PBC 所成角θ的正弦值sin cos ,52PA m PA m PA mθ⋅=<>===⋅. ……………12分19.(本小题满分12分)解:(Ⅰ)由图知,m 名学生中星期日运动时间少于60分钟的频率为:111()30750300020+⨯=,所以1520m ⨯=,所以100m =;设星期日运动时间在[)90,120内的频率为x ,则1111111()3013000750300100200300600x ++++++⨯+=,所以14x =.所以星期日运动时间在[)90,120内的频率为14. ……………6分 (Ⅱ)由图知,第一组有1人、第二组有4人、第七组有10人,第八组有5人,四组共20人,其中星期日运动时间少于60分钟的有5人.所以ξ可能取值为0,1,2,3,且3515320()(0,1,2,3)i i C C P i i C ξ-⋅===.所以ξ的分布列为所以ξ的期望=0+1+2+3==2282282282282284E ξ⨯⨯⨯⨯. …………12分20.(本小题满分12分) 解:(Ⅰ)由c a =,及222a b c =+,设2,,(0)a k c b k k ===>,则由四个顶点构成的四边形面积为4得12242a b ⋅⋅=,即14242k k ⋅⋅=,解得1k =, ∴椭圆22:14x C y +=. ……………5分 (Ⅱ)设直线:l x ty m =+,即0x ty m --=,1m ≥,则由直线l 与圆221x y +=相切得1=,即221t m =-, 由222244()44x y ty m y x ty m⎧+=⇒++=⎨=+⎩,即222(4)240t y tmy m +++-=,易知0∆>恒成立,设1122(,),(,)A x y B x y ,由韦达定理知:12221222444tm y y t m y y t -⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩,∴由弦长公式得12AB y =-21212)4]y y y y =+-⋅==,∵1m ≥,∴23AB m m ==≤=+,当且仅当3m m =,即m =时等号成立,所以max 2AB =,所以OAB ∆的面积最大值为12112⨯⨯=. ……………12分21.(本小题满分12分) 解:(Ⅰ)由已知得,221ln ln ()=ex xf x x x--'=.由()0f x '>得01x <<;由()0f x '<得1x >.所以函数()y f x =的单调增区间为:(0,1),单调减区间为(1,)+∞.……………5分(Ⅱ)不等式()()f x g x ≥恒成立⇔不等式1+ln 1x kx x ≥+恒成立 ⇔不等式(1)(1+ln )x x k x+≤恒成立,令(1)(1+ln )1()1(1+ln )(1)x x h x x x x x +⎛⎫==+≥ ⎪⎝⎭,则min ()k h x ≤.因为2ln ()x x h x x-'=,令()l n (1)x x xx ϕ=-≥,则()h x '与()x ϕ同号,因为1()0x x x ϕ-'=≥(当且仅当1x =时取等号),所以()x ϕ在[1,)+∞上递增,所以()(1)10x ϕϕ≥=>,所以()0h x '>,所以()h x 在[1,)+∞上递增,所以min ()(1)2h x h ==,所以 2.k ≤ ……………12分22.证明:(Ⅰ)因为A C B D =,所以ABC BCD ∠=∠.又因为EC 与圆相切于点C ,故ACE ABC∠=∠,所以ACE BCD ∠=∠. ………………5分 (Ⅱ)因为ECB CDB ∠=∠,EBC BCD ∠=∠,所以BDCECB ∆∆,故B C C DB E B C=.即2BC BE CD =⋅.又82BE ,CD ,==所以=4BC . ………………10分23.解:(Ⅰ)曲线1:2cos C ρθ=化为普通方程为:22(1)1x y -+=;直线2C的参数方程x ty =⎧⎪⎨=⎪⎩ (t 为参数).0y -=.所以曲线1C 是以1C ()1,0为圆心,1r =为半径的圆.所以圆心1C ()1,00y -=的距离为:d ==.所以1AB ==.………………5分 (Ⅱ)由(Ⅰ)知,圆10分 24.解: 1,1()1223,121,2x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩(Ⅰ)不等式()2f x x >,即112x x ≤⎧⎨->⎩或12232x x x <<⎧⎨->⎩或212x x≥⎧⎨>⎩,解得12x <-,所以不等式()2f x x >的解集为12x x ⎧⎫<-⎨⎬⎩⎭. ……………5分(Ⅱ)存在x R ∈,使得2()1f x t t >-+,即2max ()1f x t t >-+∵max ()1f x =, ∴只要22110(0,1)t t t t t >-+⇔-<⇔∈即(0,1)t ∈ ……………10分。
2015杭州二模数学(理)

……………………8 分
(II)当 a 3[1,6] 时, sin C 1 , 当 a 1时, b2 a2 c2 2ac cos B 1 36 2 1 6 于是
1 31 ,∴ b 31 , 2
3 93 6 31 ,从而: sin C , 31 sin C sin π 3 3 3 93 3 ,因为 , 2 31 2
D A G E
C B
PA DH 4 1 2 , PD 2 5 5
4 19 , 3 5 5
P
在 Rt△GHC 中, GC HG2 HC2
GH 2 19 所以 cos GHC . GC 19
所以二面角 A-PD-C 的余弦值为-
A
H D G
2 19 . 19
……………………8 分
1 . 2
π ,即 a2-6a+8=0, 3
根据余弦定理 b2=a2+c2-2accosB,得 (2 7 )2=a2+62-12acos 解得:a=2 或 a=4.
当 a=2 时, SABC ac sin B 2 6 sin 当 a=4 时, SABC
1 1 3 3; 2 2 3 1 1 ac sin B 4 6 sin 6 3 . 2 2 3
2015二模理数答案

长春市普通高中2015届高三质量监测(二)数学(理科)参考答案及评分标准一、选择题(本大题包括12小题,每小题5分,共60分)1. D2. A3. C4. C5. D6. D7. B8. B9. C 10.A 11. C 12. A 简答与提示:1. 【命题意图】本题主要考查集合交集与补集的运算,属于基础题.【试题解析】D 由题意可知{|1Q x x =-≤或2}x >,则{|12}Q x x =-<≤R ð,所以{|02}P Q x x =≤≤R ð. 故选D. 2. 【命题意图】本题考查复数的除法运算,以及复平面上的点与复数的关系,属于基础题.【试题解析】A131255i i i -=--,所以其共轭复数为3155i +. 故选A. 3. 【命题意图】本题考查正态分布的概念,属于基础题,要求学生对统计学原理有全面的认识.【试题解析】C (01)(12)0.5(2)P P P ξξξ==->=≤≤≤≤. 故选C. 4. 【命题意图】本题借助不等式来考查命题逻辑,属于基础题.【试题解析】C 由p 成立,则1a ≤,由q 成立,则1a >,所以p ⌝成立时1a >是q 的充要条件.故选C.5. 【命题意图】本题主要考查线性规划,是书中的原题改编,要求学生有一定的运算能力.【试题解析】D由题意可知,35x y +在(2,1)--处取得最小值,在35(,)22处取得最大值,即35[11,17]x y +∈-.故选D.6. 【命题意图】本题通过正方体的三视图来考查组合体体积的求法,对学生运算求解能力有一定要求.【试题解析】D 该几何体可视为正方体截去两个三棱锥,所以其体积为41138362--=. 故选D. 7. 【命题意图】本题考查向量模的运算.【试题解析】B |2|+==a b 故选B.8. 【命题意图】本题考查学生对茎叶图的认识,通过统计学知识考查程序流程图的认识,是一道综合题.【试题解析】B 由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10. 故选B. 9. 【命题意图】本题主要考查三角函数的图像和性质,属于基础题.【试题解析】C由题意()sin(2)6f x x π=+,将其图像向右平移ϕ(0)ϕ>个单位后解析式为()sin[2()]6f x x πϕ=-+,则26k πϕπ-=,即212k ππϕ=+()k ∈N ,所以ϕ的最小值为12π. 故选C.10. 【命题意图】本题借助基本不等式考查点到直线的距离,属于中档题.【试题解析】A 由直线与圆相切可知||m n +=1mn m n =++,由2()2m n mn +≤可知211()4m n m n ++≤+,解得(,2[222,)m n +∈-∞-++∞. 故选A. 11. 【命题意图】本题主要考查双曲线的几何性质,结合着较大的运算量,属于难题.【试题解析】C 由题可知,过I 、III 象限的渐近线的倾斜角为θ,则tan b a θ=,222tan 2aba bθ=-,因此△OAB 的面积可以表示为3222112tan 227a b a a a a b θ⋅⋅==-,解得34b a =,则54e =. 故选C.12. 【命题意图】本题是最近热点的复杂数列问题,属于难题.【试题解析】A 设(2)n n n b nS n a =++,有14b =,28b =,则4n b n =, 即(2)4n n n b nS n a n =++=当2n ≥时,1122(1)(1)01n n n n S S a a nn ---++-+=- 所以12(1)11n n n n a a n n -++=-,即121n n a a n n -⋅=-,所以{}n a n是以12为公比,1为首项的等比数列,所以11()2n n a n -=,12n n na -=. 故选A.二、填空题(本大题包括4小题,每小题5分,共20分)13. 6014.4915.83π16. 19(2,)8简答与提示:13. 【命题意图】本题主要考查二项式定理的有关知识,属于基础题.【试题解析】由题意可知常数项为2246(2)(60C x =. 14. 【命题意图】本题考查定积分的几何意义及微积分基本定理,属于基础题.【试题解析】由题意322023a a x ==⎰,所以49a =. 15. 【命题意图】球的内接几何体问题是高考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.【试题解析】由题意,面积最小的截面是以AB为直径,可求得3AB =,进而截面面积的最小值为283ππ=. 16. 【命题意图】本题主要考查数形结合以及函数的零点与交点的相关问题,需要学生对图像进行理解,对学生的能力提出很高要求,属于难题.【试题解析】由题意可知()f x 是周期为4的偶函数,对称轴为直线2x =. 若()F x 恰有4个零点,有(1)(1)(3)(3)g f g f >⎧⎨<⎩,解得19(2,)8a ∈.三、解答题(本大题必做题5小题,三选一选1小题,共70分)17. (本小题满分12分)【命题意图】本小题主要考查两角和的正切公式,以及同角三角函数的应用,并借助正弦定理考查边角关系的运算,对考生的化归与转化能力有较高要求.【试题解析】解:(1) +,tan tan()A B C C A B π+=∴=-+ (3分)tan 2,tan 3,tan 1,4A B C C π==∴=∴= (6分)(2)因为tan 3B =sin 3sin 3cos cos BB B B⇒=⇒=,而22sin cos 1B B +=,且B 为锐角,可求得sin B =.(9分)所以在△ABC中,由正弦定理得,sin sin AB AC B C =⨯=. (12分)18. (本小题满分12分)【命题意图】本小题主要考查统计与概率的相关知识、离散型随机变量的分布列以及数学期望的求法. 本题主要考查数据处理能力.【试题解析】(1)由图可知0.035a =,0.025b =. (4分)(2) 利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人. (6分) 从中取出三人,并计算三人所获得代金券的总和X , 则X 的所有可能取值为:150,200,250,300.363101(150)6C P X C ===, 21643101(200)2C C P X C ===,126433(250)10C C P X C ===,343101(300)30C P X C ===,(10分) 且1131150200250300210621030EX =⨯+⨯+⨯+⨯=.(12分)19. (本小题满分12分)【命题意图】本小题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用. 本小题对考生的空间想象能力与运算求解能力有较高要求. 【试题解析】解:(1) 取PB 中点N ,连结MN 、AN ,M 是PC 中点,1//,22MN BC MN BC ∴==, 又//BC AD ,//,MN AD MN AD ∴=,∴四边形ADMN 为平行四边形 ,AP AD AB AD ⊥⊥,AD ∴⊥平面PAB ,AD AN ∴⊥,AN MN ∴⊥ AP AB =,AN PB ∴⊥,AN ∴⊥平面PBC ,AN ⊂平面ADM ,∴平面ADM ⊥平面PBC .(6分) (2) 存在符合条件的λ.以A 为原点,AB 方向为x 轴,AD 方向为y 轴,AP 方向为z 轴,建立空间直角坐标系A xyz -,设(2,,0)E t ,(0,0,2)P ,(0,2,0)D ,(2,0,0)B从而(0,2,2)PD =-,(2,2,0)DE t =-,则平面PDE 的法向量为1(2,2,2)n t =-, 又平面DEB 即为xAy 平面,其法向量2(0,0,1)n =,则1212122cos ,3||||(2n n n n n n ⋅<>===⋅,解得3t =或1t =,进而3λ=或13λ=.(12分)20. (本小题满分12分)【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法,椭圆方程的求法、直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.【试题解析】解:(1) 已知11(||||||)||||22ABC A S AB AC BC r BC y ∆=++⋅=⋅,且||2BC =,||3A y r =,其中r 为内切圆半径,化简得:||||4AB AC +=,顶点A 的轨迹是以B C 、为焦点,长轴长为4的椭圆(去掉长轴端点),其中2,1,a c b ===进而其方程为22143x y +=(0)y ≠. (5分)(2) 1232k k k =+,以下进行证明:当直线PQ 斜率存在时,设直线:(1)PQ y k x =-且11(,)P x y ,22(,)Q x y ,(4,)H m联立22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩可得2122834k x x k +=+,212241234k x x k -=+. (8分)由题意:13mk =,1214y m k x -=-,2324y m k x -=-.11212312()(4)()(4)(4)(4)y m x y m x k k x x --+--+=--21212121212882(5)()2424224()1636363m k kx x m k x x mk m mk x x x x k ++-+++====-+++当直线PQ 斜率不存在时,33(1,),(1,)22P Q -,231332222333m m m k k k -++=+== 综上可得1232k k k =+. (12分)21. (本小题满分12分) 【命题意图】本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值以及函数零点的情况. 本小题对考生的逻辑推理能力与运算求解有较高要求.【试题解析】解:(1) 对()f x 求导得:1()ln(1)1axf x a x b x-'=-++-+,根据条件知(0)0f '=,所以101b b -=⇒=. (3分)(2) 由(1)得()(1)ln(1)f x ax x x =-+-,01x ≤≤1()ln(1)11axf x a x x-'=-++-+ 22(1)(1)21()1(1)(1)a a x ax ax a f x x x x -+--++''=-+=-+++.① 当12a ≤-时,由于01x ≤≤,有221()()0(1)a a x a f x x ++''=-≥+,于是()f x '在[0,1]上单调递增,从而()(0)0f x f ''≥=,因此()f x 在[0,1]上单调递增,即()(0)0f x f ≥=而且仅有(0)0f =;②当0a ≥时,由于01x ≤≤,有221()0(1)ax a f x x ++''=-<+,于是()f x '在[0,1]上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,1]上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =;③当102a -<<时,令21min{1,}a m a+=-,当0x m ≤≤时,221()()0(1)a a x a f x x ++''=-≤+,于是()f x '在[0,]m 上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,]m 上单调递减, 即()(0)0f x f ≤=而且仅有(0)0f =.综上可知,所求实数a 的取值范围是1(,]2-∞-. (8分)(3) 对要证明的不等式等价变形如下:2110000100010000.41000.55210001100111()()(1)(1)100001000100001000e e ++<<⇔+<<+ 所以可以考虑证明:对于任意的正整数n ,不等式215211(1)(1)n n e n n+++<<+恒成立. 并且继续作如下等价变形2152112111(1)(1)()ln(1)1()ln(1)52n n e n n n n n n+++<<+⇔++<<++ 211(1)ln(1)0()5111(1)ln(1)0()2p n n n q n n n ⎧++-<⎪⎪⇔⎨⎪++->⎪⎩对于()p 相当于(2)中21(,0)52a =-∈-,12m =情形,有()f x 在1[0,]2上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =.取1x n =,当2n ≥时,211(1)ln(1)05n n n++-<成立;当1n =时,277(1)ln 21ln 210.710555+-=-<⨯-<.从而对于任意正整数n 都有211(1)ln(1)05n n n ++-<成立.对于()q 相当于(2)中12a =-情形,对于任意x ∈[0,1],恒有()0f x ≥而且仅有(0)0f =. 取1x n=,得:对于任意正整数n 都有111(1)ln(1)02n n n++->成立.因此对于任意正整数n ,不等式215211(1)(1)n n e n n+++<<+恒成立. 这样依据不等式215211(1)(1)n n e n n+++<<+,再令10000n =利用左边,令1000n = 利用右边,即可得到10000.41000.5100011001()()100001000e <<成立. (12分) 22. (本小题满分10分)【命题意图】本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形 相似等内容.本小题重点考查考生对平面几何推理能力.【试题解析】解:(1) 由题意可知,EPC APC ∠=∠,PEB PAC ∠=∠,则△PED ∽△PAC ,则PE PD PA PC =,又PE ED PB BD =,则ED PB PDBD PA PC⋅=. (5分) (2) 由EPC APC ∠=∠,PEB PAC ∠=∠,可得CDE ECD ∠=∠, 在△ECD 中,30CED ∠=,可知75PCE ∠=. (10分)23. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、利用直线的参数方程的几何意义求解直线与曲线交点的距离等内容. 本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求.【试题解析】解:(1) 对于曲线1C 有1x y +=,对于曲线2C 有2214x y +=.(5分) (2) 显然曲线1C :1x y +=为直线,则其参数方程可写为21x y ⎧=⎪⎪⎨⎪=-⎪⎩(t 为参数)与曲线2C :2214x y +=联立,可知0∆>,所以1C 与2C 存在两个交点,由125t t +=,1285t t =,得21||5d t t =-==. (10分) 24. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及到绝对值不等式及 不等式证明等内容. 本小题重点考查考生的化归与转化思想.【试题解析】解:(1) 当3a =时,174,213()5,22341,2x x f x x x x ⎧-≤⎪⎪⎪=<<⎨⎪⎪-≥⎪⎩,所以()7f x >的解集为{|0x x <或2}x >.(5分)(2) ()|21||2||212||1|f x x a x a x a x a a a =-+-+≥-+-+=-+, 由()3f x ≥恒成立,有|1|3a a -+≥,解得2a ≥ 所以a 的取值范围是[)2,+∞.(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年东北三省四城市联考暨沈阳市高三质量监测(二)数 学(理科)沈阳命题:沈阳市第四中学 孙玉才 沈阳市第二十中学 金行宝沈阳市第九中学 付一博 沈阳市第一二0中学 潘 戈 沈阳市回民中学 庞红全 沈阳市第二十八中学 陶 慧 沈阳主审:沈阳市教育研究院 王恩宾本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22题~第24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.注意事项:1. 答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条码粘贴在答题卡指定区域.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动用橡皮擦干净后,再选涂其他答案标号.第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答,在本试题卷上作答无效.3. 考试结束后,考生将答题卡交回.第Ⅰ卷一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 已知集合{11}A x x =-≤≤,2{20}B x x x =-≤,则A B =I ( ) (A ) [1,0]- (B ) ]2,1[ (C ) [0,1] (D ) (,1][2,)-∞+∞U2. 设复数1z i =+(i 是虚数单位),则22z z+=( ) (A )1i + (B )1i - (C )1i -- (D )1i -+3. 已知a ρ=1,b ρ=2,且a ρ)(b a ρρ-⊥,则向量a ρ与向量b ρ的夹角为( )(A )6π (B )4π (C ) 3π (D )23π4. 已知△ABC 中,内角A ,B ,C 的对边分别为,,a b c ,若222a b c bc =+-,4bc =,则△ABC 的面积为( ) (A )12(B )1 (C )3 (D )25. 已知{}2,0,1,3,4a ∈-,{}1,2b ∈,则函数 2()(2)f x a x b =-+为增函数的概率是( ) (A )25 (B )35 (C )12 (D )3106. 阅读如图所示的程序框图,运行相应的程序. 若输出的S 为1112,则判断框中填写的内容可以是( ) (A )6n = (B )6n < (C )6n ≤ (D )8n ≤7. 如图,网格纸上小正方形的边长为1,粗线画出的是某多 面体的三视图,则该多面体的体积为( ) (A )323 (B )64 (C )3233(D ) 643 8. 已知直线22(1)y x =-与抛物线:C x y 42=交于B A ,两点,点),1(m M -,若0=⋅MB MA ,则实数=m ( ) (A )2 (B )22(C )21 (D )09. 对定义在[0,1]上,并且同时满足以下两个条件的函数()f x 称为M 函数:① 对任意的[0,1]x ∈,恒有()0f x ≥;② 当12120,0,1x x x x ≥≥+≤时,总有1212()()()f x x f x f x +≥+成立,则下列函数不是M 函数的是( )(A )2()f x x = (B )()21xf x =- (C )2()ln(1)f x x =+ (D )2()1f x x =+10. 在平面直角坐标系中,若(,)P x y 满足44021005220x y x y x y -+≤⎧⎪+-≤⎨⎪-+≥⎩,则当xy 取得最大值时,点P 的坐标是( )(A )(4,2) (B )(2,2) (C )(2,6) (D )5(,5)211. 已知双曲线22221(0,0)x y a b a b-=>>与函数(0)y x x =≥的图象交于点P . 若函数y x =在点P 处的切线过双曲线左焦点(1,0)F -,则双曲线的离心率是( )(A )512+(B ) 522+ (C )312+ (D )3212. 若对,[0,)x y ∀∈+∞,不等式2242x y x y ax ee +---≤++恒成立,则实数a 的最大值是( ) (A )14 (B )1 (C )2 (D )12第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上) 13. 函数13sin cos 22y x x =+([0,]2x π∈)的单调递增区间是__________. 14. 612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为 .15. 已知定义在R 上的偶函数()f x 在[0,)+∞单调递增,且(1)0f = ,则不等式(2)0f x -≥的解集是 .16. 同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为a ,球的半径为R .设两个正三棱锥的侧面与底面所成的角分别为α、β,则tan()αβ+的值是 .三.解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17. (本小题满分12分)已知数列{}n a 中,11a =,其前n 项的和为n S ,且满足2221n n n S a S =-(2)n ≥. (Ⅰ) 求证:数列1n S ⎧⎫⎨⎬⎩⎭是等差数列;(Ⅱ) 证明:当2n ≥时,1231113 (232)n S S S S n ++++<.18. (本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠DAB =60o,PD ⊥平面ABCD ,PD =AD =1,点,E F 分别为AB 和PD 中点.(Ⅰ)求证:直线AF //平面PEC ; (Ⅱ)求PC 与平面PAB 所成角的正弦值.19. (本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:学生 1号 2号 3号 4号 5号 甲班 6 5 7 9 8 乙班48977(Ⅰ)从统计数据看,甲乙两个班哪个班成绩更稳定(用数据说明)?(Ⅱ) 若把上表数据作为学生投篮命中率,规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X 和Y ,试求X 和Y 的分布列和数学期望.FEBDCAP20.(本小题满分12分)已知椭圆C :22221(0)x y a b a b +=>>的上顶点为(0,1),且离心率为32.(Ⅰ) 求椭圆C 的方程;(Ⅱ)证明:过椭圆1C :22221(0)x y m n m n+=>>上一点00(,)Q x y 的切线方程为00221x x y ym n+=; (Ⅲ)从圆2216x y +=上一点P 向椭圆C 引两条切线,切点分别为,A B ,当直线AB 分别与x 轴、y 轴交于M 、N 两点时,求MN 的最小值.21.(本小题满分12分)若定义在R 上的函数()f x 满足222(1)()2(0)2x f f x e x f x -'=⋅+-, 21()()(1)24x g x f x a x a =-+-+,∈a R.(Ⅰ)求函数()f x 解析式;(Ⅱ)求函数()g x 单调区间;(Ⅲ)若x 、y 、m 满足||||-≤-x m y m ,则称x 比y 更接近m .当2a ≥且1x ≥时,试比较e x和1x e a -+哪个更接近ln x ,并说明理由.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲 如图所示,AB 为圆O 的直径,BC ,CD 为 圆O 的切线,B ,D 为切点. (Ⅰ)求证: OC AD //;(Ⅱ)若圆O 的半径为2,求OC AD ⋅的值.23.(本小题满分10分)选修4-4:坐标系与参数方程已知在直角坐标系xOy 中,圆C 的参数方程为⎩⎨⎧+-=+=θθsin 24cos 23y x (θ为参数).(Ⅰ)以原点为极点、x 轴正半轴为极轴建立极坐标系,求圆C 的极坐标方程; (Ⅱ)已知(2,0),(0,2)A B -,圆C 上任意一点),(y x M ,求△ABM 面积的最大值.24.(本小题满分10分)选修4-5:不等式选讲设函数()222f x x x =+--. (Ⅰ)求不等式2)(>x f 的解集; (Ⅱ)若R ∈∀x ,27()2f x t t ≥-恒成立,求实数t 的取值范围.2015年东北三省四城市联考暨沈阳市高三质量监测(二)数学(理科)参考答案与评分标准说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一.选择题(1)C ;(2)A ;(3)B ;(4)C ;(5)B ;(6)C ;(7)D ;(8)B ; (9)D ;(10)D ;(11) A ;(12)D . 二.填空题 (13)[0,]6π;(14)52-;(15) (,1][3,)-∞+∞U ;(16)433R a -.三.解答题(17)解:(Ⅰ)当2n ≥时,21221nn n n S S S S --=-, …………………2分112n n n n S S S S ---=.1112n n S S --=, 从而⎭⎬⎫⎩⎨⎧n S 1构成以1为首项,2为公差的等差数列. ………………………………6分 (Ⅱ)由(1)可知,111(1)221n n n S S =+-⨯=-,121n S n ∴=-. ………8分 当2n ≥时,11111111()(21)(22)2(1)21n S n n n n n n n n n=<=⋅=-----. ……10分 从而123111111111313...1(1)2322231222n S S S S n n n n ++++<+-+-++-<-<-L . …12分(18)解:(Ⅰ)证明:作FM ∥CD 交PC 于M . ∵点F 为PD 中点,∴CD FM 21=. …………2分 ∵21=k ,∴FM AB AE ==21, ∴AEMF 为平行四边形,∴AF ∥EM , ……4分 ∵AF PEC EM PEC ⊄⊂平面,平面,∴直线AF //平面PEC . ……………6分 (Ⅱ)60DAB ∠=oQ ,DE DC ∴⊥. 如图所示,建立坐标系,则P (0,0,1),C (0,1,0),E (32,0,0), A (32,12-,0),31(,,0)22B , ∴31,,122AP ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,()0,1,0AB =u u u r . …8分设平面PAB 的一个法向量为(),,n x y z =r.∵0n AB ⋅=r u u u r ,0n AP ⋅=r u u u r ,∴⎪⎩⎪⎨⎧==++-02123y z y x ,取1x =,则32z =, ∴平面PAB 的一个法向量为3(1,0,)2n =r . …………………………10分 设向量n PC θr u u u r 与所成角为,∵(0,1,1)PC =-u u u r ,∴3422cos 14724n PCn PCθ-⋅===-⨯r u u u rr u u u r , MFEBACDPFEBACDyzx P∴PC 平面PAB 所成角的正弦值为4214. .…………………………12分 (19)解:(Ⅰ)两个班数据的平均值都为7, ……………………1分甲班的方差22222216-7+-7+-7+-7+-7=25s =()(5)(7)(9)(8), …………3分 乙班的方差2222222-7+-7+-7+-7+-714=55s =(4)(8)(9)(7)(7), …………5分 因为2212s s <,甲班的方差较小,所以甲班的成绩比较稳定. ………………6分 (Ⅱ)X 可能取0,1,2211(0)525P X ==⨯=,31211(1)52522P X ==⨯+⨯=,313(2)5210P X ==⨯=,所以X 分布列为:X0 1 2 P15 12 310 数学期望11311012521010EX =⨯+⨯+⨯=. …………………………………9分Y 可能取0,1,2313(0)5525P Y ==⨯=,342114(1)555525P Y ==⨯+⨯=,248(2)5525P Y ==⨯=,所以Y 分布列为:Y0 1 2 P325 1425 825数学期望314860122525255EY =⨯+⨯+⨯=. …………………………12分 (20)解:(Ⅰ)1b =Q ,3=2c e a =, 2,1a b ∴==,∴椭圆C 方程为2214x y +=. ………………………………………2分(Ⅱ)法一:椭圆1C :22221x y m n +=,当0y >时,221x y n m=-,故22211nxy mx m '=-⋅-,∴当00y >时,200022220002111x nn n k x x y mm m y x n m =-⋅=-=-⋅-. ……………4分 切线方程为()200020x n y y x x m y -=-⋅-,222222220000n x x m y y m y n x m n +=+=,00221x x y ym n +=. …………………………6分 同理可证,00y <时,切线方程也为00221x x y ym n +=.当0=0y 时,切线方程为x m =±满足00221x x y ym n+=.综上,过椭圆上一点00(,)Q x y 的切线方程为00221x x y ym n+=. ……………………7分解法2. 当斜率存在时,设切线方程为y kx t =+,联立方程:22221x y mn y kx t ⎧+=⎪⎨⎪=+⎩可得222222()n x m kx t m n ++=,化简可得: 22222222()2()0n m k x m ktx m t n +++-=,①由题可得:42222222244()()0m k t m n m k t n ∆=-+-=, ……………………4分 化简可得:2222t m k n =+,①式只有一个根,记作0x ,220222m kt m kx n m k t=-=-+,0x 为切点的横坐标,切点的纵坐标200n y kx t t =+=,所以2020x m ky n =-,所以2020n x k m y =-,所以切线方程为:2000020()()n x y y k x x x x m y -=-=--,化简得:00221x x y ym n+=. …………………………… 6分 当切线斜率不存在时,切线为x m =±,也符合方程00221x x y ym n+=,综上:22221x y m n +=在点00(,)x y 处的切线方程为00221x x y ym n+=.(其它解法可酌情给分) ………………………… 7分(Ⅲ)设点P (,)p p x y 为圆2216x y +=上一点,,PA PB 是椭圆2214x y +=的切线,切点1122(,),(,)A x y B x y ,过点A 的椭圆的切线为1114x xy y +=,过点B 的椭圆的切线为2214x xy y +=. Q 两切线都过P 点,12121,144p p p p x x x x y y y y ∴+=+=.∴切点弦AB 所在直线方程为14p p xx yy +=. …………………… 9分1(0)p M y ∴,,4(,0)pN x ,2222222161161=16p pp p p p x y MN x y x y ⎛⎫+∴=++⋅ ⎪ ⎪⎝⎭222222221125=171617216161616p pp pppp p x y x y y x y x ⎛⎫⎛⎫ ⎪++⋅≥+⋅⋅= ⎪ ⎪ ⎪⎝⎭⎝⎭. 当且仅当222216p p ppx y y x =,即226416,55P P x y ==时取等,54MN ∴≥,MN ∴的最小值为54. ……………………………………12分(21)(本小题满分12分) 解:(Ⅰ)22'()'(1)22(0)x f x f e x f -=+-,所以'(1)'(1)22(0)f f f =+-,即(0)1f =.又2(1)(0)2f f e -'=⋅,所以2'(1)2f e =, 所以22()2xf x ex x =+-. ……………………………………4分(Ⅱ)22()2xf x ex x =-+Q ,222111()()(1)(1)(1)2444x x x g x f x a x a e x x x a x a e a x ∴=-+-+=+--+-+=--.……………5分()x g x e a '∴=-,①当0a ≤时,()0g x '>,函数 在R 上单调递增; .……………6分 ②当0a >时,由()0xg x e a '=-=得ln x a =, ∴(),ln x a ∈-∞时,()0g x '<, ()g x 单调递减;()ln ,x a ∈+∞时,()0g x '>,()g x 单调递增.综上,当0a ≤时,函数()g x 的单调递增区间为(,)-∞+∞;当0a >时,函数()g x 的单调递增区间为()ln ,a +∞,单调递减区间为(),ln a -∞. .……………8分 (Ⅲ)解:设1()ln ,()ln x ep x x q x e a x x-=-=+-, Q 21'()0e p x x x=--<,∴()p x 在[1,)x ∈+∞上为减函数,又()0p e =, ∴当1x e ≤≤时,()0p x ≥,当x e >时,()0p x <.Q 11'()x q x e x -=-,121''()0x q x e x -=+>,∴'()q x 在[1,)x ∈+∞上为增函数,又'(1)0q =,∴[1,)x ∈+∞时,'()0q x ≥,∴()q x 在[1,)x ∈+∞上为增函数,)(x g∴()(1)20q x q a ≥=+>.①当1x e ≤≤时,1|()||()|()()x e p x q x p x q x e a x--=-=--, 设1()x e m x e a x -=--,则12'()0x em x e x-=--<,∴()m x 在[1,)x ∈+∞上为减函数,∴()(1)1m x m e a ≤=--,Q 2a ≥,∴()0m x <,∴|()||()|p x q x <,∴e x比1x e -+a 更接近ln x . ②当x e>时,11|()||()|()()2ln 2ln x x ep x q x p x q x x e a x e a x---=--=-+--<--,设1()2ln x n x x e a -=--,则12'()x n x e x -=-,122''()0x n x e x-=--<,∴'()n x 在x e >时为减函数,∴12'()'()0e n x n e e e -<=-<,∴()n x 在x e >时为减函数,∴1()()20e n x n e a e -<=--<, ∴|()||()|p x q x <,∴e x 比1x e -+a 更接近ln x . 综上:在2,1a x ≥≥时,e x比1x e -+a 更接近ln x . …………………………… 12分(22) 解: (1)连接CD CB OD BD ,,,Θ是圆O 的两条切线,OC BD ⊥∴,ο90=∠+∠∴DOC ODB ,又AB Θ为圆O 的直径,DB AD ⊥∴,ο90=∠+∠∴ODB ADO ODA OAD ∠=∠∴,DOC OAD ∠=∠∴,即得证,……5分(2)OD AO =∴,DOC DAO ∠=∠∴,Rt ∴△BAD ∽△COD ,8AD OC AB OD ⋅=⋅=. ………………………………………………………… 10分(23)解:(1)圆C 的参数方程为⎩⎨⎧+-=+=θθsin 24cos 23y x (θ为参数)所以普通方程为4)4()3(22=++-y x …………………………………………2分∴圆C 的极坐标方程:021sin 8cos 62=++-θρθρρ …………………5分(2)点),(y x M 到直线AB :02=+-y x 的距离为 ………………………6分2|9sin 2cos 2|+-=θθd………………………7分△ABM 的面积|9)4sin(22||9sin 2cos 2|||21+-=+-=⨯⨯=θπθθd AB S………………………9分 所以△ABM 面积的最大值为229+ ………………………10分(24) 解:(1)4,1()3,124,2x x f x x x x x --<-⎧⎪=-≤<⎨⎪+≥⎩, ………………………2分当1,42,6,6x x x x <---><-∴<- 当2212,32,,233x x x x -≤<>>∴<< 当2,42,2,2x x x x ≥+>>-∴≥综上所述 2|63x x x ⎧⎫><-⎨⎬⎩⎭或 . ………………………5分 (2)易得min ()(1)3f x f =-=-,若R ∈∀x ,t t x f 211)(2-≥恒成立, 则只需22min 73()32760222f x t t t t t =-≥-⇒-+≤⇒≤≤, 综上所述322t ≤≤.………………………10分。
