《完全平方公式》(第1课时)示范公开课教学PPT课件【部编北师大版七年级数学下册】
合集下载
1.6完全平方公式(第一课时)课件

首尾两项是这两项的平方和
右边:三项式
中间项是加上这两项的积的两倍
你能用字母表示吗?
(a+b) 2= a2+2ab+b2
(a+b) 2=a2+2ab+b2
语言叙述: 两项和的平方,等于这两项的平方和,
再加上这两项积的2倍.
活动探究一
你能用图1-7解释这一公式吗?
(a+b) 2=a2+2ab+b2
b ab b²
七年级下学期北师大版
第一章 整式的乘除
1.6 完全平方公式(第1课时)
实验初中 贾莲香
温故知新
1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个
多项式的每一项,再把所得的积相加.
(a+b) (m+n) = am +an +bm +bn
活动探究一
1.先计算,再观察下列算式及其运算结果, 你有什么发现?
(4) (x+y)2 =x2 ++2 xy +y2 错
2. 指出下列各式ຫໍສະໝຸດ 的错误,并加以改正:(1) (2a−1)2=2a2−2a+1; =(2a)2-2×2a×1+12
(2) (2a+1)2==44aa22-+41a;+1 =(2a)2+2×2a×1+12 =4a2+4a+1
(3) (a−1)2=a2−2a−1.
2.注意:项数、符号、字母及其指数;
注意:1.项数:积的项数为三;
2.符号:特别是(a-b)2= a2 - 2ab+b2;
3.字母:不要漏写;
作业
1. 教材26页习题1.11 第1、2题
右边:三项式
中间项是加上这两项的积的两倍
你能用字母表示吗?
(a+b) 2= a2+2ab+b2
(a+b) 2=a2+2ab+b2
语言叙述: 两项和的平方,等于这两项的平方和,
再加上这两项积的2倍.
活动探究一
你能用图1-7解释这一公式吗?
(a+b) 2=a2+2ab+b2
b ab b²
七年级下学期北师大版
第一章 整式的乘除
1.6 完全平方公式(第1课时)
实验初中 贾莲香
温故知新
1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个
多项式的每一项,再把所得的积相加.
(a+b) (m+n) = am +an +bm +bn
活动探究一
1.先计算,再观察下列算式及其运算结果, 你有什么发现?
(4) (x+y)2 =x2 ++2 xy +y2 错
2. 指出下列各式ຫໍສະໝຸດ 的错误,并加以改正:(1) (2a−1)2=2a2−2a+1; =(2a)2-2×2a×1+12
(2) (2a+1)2==44aa22-+41a;+1 =(2a)2+2×2a×1+12 =4a2+4a+1
(3) (a−1)2=a2−2a−1.
2.注意:项数、符号、字母及其指数;
注意:1.项数:积的项数为三;
2.符号:特别是(a-b)2= a2 - 2ab+b2;
3.字母:不要漏写;
作业
1. 教材26页习题1.11 第1、2题
1.6完全平方公式课件数学北师大版七年级下册

=
2
30 +2×30× +
2
=
感悟新知
知1-练
2-1. 运用完全平方公式进行简便计算:
(1)1022;
解:原式=(100+2)2=10 000+400+ 4=10 404;
(2)99.82;
原式=(100-0.2)2 =10 000-40+ 0.04=9 960.04;
感悟新知
知1-练
阴影部分面积的关系,可以验证的乘法公式是
②
_______.(填序号)
①(a+b)(a-b)=a2-b2;
② (a-b )2 = a2-2ab+b2;
③(a+b)2=a2+2ab+b2;
④(a+b)2=(a-b)2+4ab.
感悟新知
知识点 3 利用乘法公式进行整式的混合运算
知3-讲
1. 当两个三项式相乘时,先利用添括号使原式变成符合乘
感悟新知
知1-练
1-2. 计算:
(1)(2y-1)2;
解:原式=4y2-4y+1;
(2)(3a+2b)2;
原式=9a2+12ab+4b2;
(3)(-x+2y)2;
原式=x2-4xy+4y2;
(4)(-2xy-1)2.
原式=4x2y2+4xy+1.
感悟新知
知1-练
例2 计算:(1)9992;(2) 2.
=-(4x2+12xy+9y2)
若两项都相同或都相反,
=-4x2-12xy-9y2.
则用完全平方公式计算.
感悟新知
知1-练
1-1. [中考·怀化] 下列计算正确的是( C )
2
30 +2×30× +
2
=
感悟新知
知1-练
2-1. 运用完全平方公式进行简便计算:
(1)1022;
解:原式=(100+2)2=10 000+400+ 4=10 404;
(2)99.82;
原式=(100-0.2)2 =10 000-40+ 0.04=9 960.04;
感悟新知
知1-练
阴影部分面积的关系,可以验证的乘法公式是
②
_______.(填序号)
①(a+b)(a-b)=a2-b2;
② (a-b )2 = a2-2ab+b2;
③(a+b)2=a2+2ab+b2;
④(a+b)2=(a-b)2+4ab.
感悟新知
知识点 3 利用乘法公式进行整式的混合运算
知3-讲
1. 当两个三项式相乘时,先利用添括号使原式变成符合乘
感悟新知
知1-练
1-2. 计算:
(1)(2y-1)2;
解:原式=4y2-4y+1;
(2)(3a+2b)2;
原式=9a2+12ab+4b2;
(3)(-x+2y)2;
原式=x2-4xy+4y2;
(4)(-2xy-1)2.
原式=4x2y2+4xy+1.
感悟新知
知1-练
例2 计算:(1)9992;(2) 2.
=-(4x2+12xy+9y2)
若两项都相同或都相反,
=-4x2-12xy-9y2.
则用完全平方公式计算.
感悟新知
知1-练
1-1. [中考·怀化] 下列计算正确的是( C )
北师大版七年级数学下册第一章《完全平方公式1》公开课课件

(1) 你能用多项式的乘法法则来说明它成立吗?
(2) 小颖写出了如下的算式: (a−b)2= [a+(−b)]2
她是怎么想的? 你能继续做下去吗?
推证 (a+b)2 =(a+b)(a+b)=a2+ab+ ab+b2
=a2+2ab+b2;
利用两数和的
(a−b)2= [a+(−b)]2
完全平方公式 推证公式
何 解
左边是 二项式 (两数和(差)) 的平方; 释: a a2 ab
右边是 两数的平方和 加上(减去) 这两数乘积的两倍.
a
b
(a−b)2 = a2−2ab+b2
a−b
b
语言表述: 两数和(差) 的平方
等于
用自己的语 言叙述上面
的公式
a−b (a−b)2 b(a−b)
a
这两数的平方和
b
ab
加(a上−b)(2减=去a2) −这ab两−数b(a乘−b积) 的= 两a2−倍2a.b+b2 .
P34---35 读一读.
纠 错练习
指出下列各式中的错误,并加以改正: (1) (2a−1)2=2a2−2a+1; (2) (2a+1)2=4a2 +1; (3) (a−1)2=a2−2a−1. 解: (1) 第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2 ; 应改为: (2a−1)2= (2a)2−2•2a•1+1;
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/292021/7/292021/7/292021/7/29
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
北师大版数学七年级下册《完全平方公式(第一课时)》课件
探索推广题
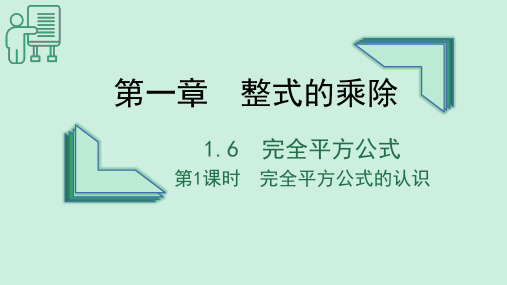
如图的三角形可解释(a+b)n的展开式的各项系数,此三角
形称为“杨辉三角”.
其中(a+b)0=1, (a+b)1=a+b, (a+b)2=a2+2ab+b2, (a+b)3=a3+3a2b+3ab2+b3, 根据“杨辉三角”计算(a+b)4.
解:原式=a4+4a3b+6a2b2+4ab3+b4
ZYT
探究新知
问题1 (a-b)2=?你是怎么做的呢?
方法一:(a-b)2
方法二:(a-b)2
=(a-b)(a-b)
=[a+(-b)][a+(-b)]
=a2-2ab+b2
=a2+2a(-b)+(-b)2
=a2-2ab+b2 问题2 根据你发现的规律,你能写出下列式子的答案吗?
(a-b)2= a2-2ab+b2 .
为另一组”.
ZYT
典例精析
例3 已知x-y=6,xy=-8.求: (1) x2+y2的值; (2)(x+y)2的值.
解:(1)因为x-y=6,xy=-8, (x-y)2=x2+y2-2xy,
所以x2+y2=(x-y)2+2xy =36-16=20;
(2)因为x2+y2=20,xy=-8,
所以(x+y)2=x2+y2+2xy =20-16=4.
小结:本题要熟练掌握完 全平方公式的变式: x2+y2=(x-y)2+2xy =(x+y)2-2xy, (x-y)2=(x+y)2-4xy.
ZYT
巩固练习
(1)已知x+y=10,xy=24,则x2+y2=__5_2__
北师大版七年级下 1.6完全平方公式 (第1课时) 教学课件

理由:(-a-b)2=(-a)2-2·(-a) ·b+b2=a2+2ab+b2=(a+b)2 (b-a)2=b2-2ba+a2=a2-2ab+b2=(a-b)2 (a-b)2=a2-b2不一定相等. 只有当b=0或a=b时,(a-b)2=a2-b2.
知识讲解
判一判:在下列多项式的乘法中,能用完全平方公式计
=4x2 -12x +9;
(2)(4x+5y)2=(4x)2+2 • 4x•5y+(5y)2 =16x2+40xy+25y2;
(3)(mn-a)2 = (mn)2-2mna+a2 =m2n2-2amn+a2
知识讲解
思考? (a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗? (a-b)2与a2-b2相等吗? 为什么?
想一想:这些计算结果有什么规律和特点?
新课导入
根据你发现的规律,计算下列式子: (a+b)2= a2+2ab+b2 ;(a-b)2= a2-2ab+b2 . 证明:
知识讲解
一、完全平方公式:
(a+b)2= a2+2ab+b2 , (a-b)2= a2-2ab+b2 .
两个数的和(或差)的平方,等于它们的平方 和,加上(或减去)它们的积的2倍.这两个公式叫 做(乘法的)完全平方公式.
第 一章 整式的乘除
第一章 整式的乘除
1.6 完全平方公式
第1课时
学习目标
1.理解并掌握完全平方公式的推导过程、结 构特点;(重点) 2.会运用公式进行简单的运算.(难点)
复习旧知
知识讲解
判一判:在下列多项式的乘法中,能用完全平方公式计
=4x2 -12x +9;
(2)(4x+5y)2=(4x)2+2 • 4x•5y+(5y)2 =16x2+40xy+25y2;
(3)(mn-a)2 = (mn)2-2mna+a2 =m2n2-2amn+a2
知识讲解
思考? (a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗? (a-b)2与a2-b2相等吗? 为什么?
想一想:这些计算结果有什么规律和特点?
新课导入
根据你发现的规律,计算下列式子: (a+b)2= a2+2ab+b2 ;(a-b)2= a2-2ab+b2 . 证明:
知识讲解
一、完全平方公式:
(a+b)2= a2+2ab+b2 , (a-b)2= a2-2ab+b2 .
两个数的和(或差)的平方,等于它们的平方 和,加上(或减去)它们的积的2倍.这两个公式叫 做(乘法的)完全平方公式.
第 一章 整式的乘除
第一章 整式的乘除
1.6 完全平方公式
第1课时
学习目标
1.理解并掌握完全平方公式的推导过程、结 构特点;(重点) 2.会运用公式进行简单的运算.(难点)
复习旧知
初中数学《完全平方公式_公开课课件-ppt【北师大版】1

初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
本节课你的收获是什么? 注意完全平方公式和平方差公式不同:
形式不同. 完全平方公式的结果 是三项, 结果不同: 即 (a b)2=a2 2ab+b2;
(1) 1012 (2)(49 4)2
5
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
计算: 1.(a+b+c)2 2.(x+2y-3)(x+2y+3)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
(1) (a+b)2与(-a-b)2相等吗? (2) (a-b)2与(b-a)2相等吗? (3) (a-b)2与a2-b2相等吗?
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
=10000+400+9=10 409
(2) 1992 =(200-1)2 =2002-2200+12 =40000400+1=39601
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
(4)(a b)2 (-2ab) a2 b2
下列计算是否正确?如不正确,应怎样改正?
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
本节课你的收获是什么? 注意完全平方公式和平方差公式不同:
形式不同. 完全平方公式的结果 是三项, 结果不同: 即 (a b)2=a2 2ab+b2;
(1) 1012 (2)(49 4)2
5
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
计算: 1.(a+b+c)2 2.(x+2y-3)(x+2y+3)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
(1) (a+b)2与(-a-b)2相等吗? (2) (a-b)2与(b-a)2相等吗? (3) (a-b)2与a2-b2相等吗?
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
=10000+400+9=10 409
(2) 1992 =(200-1)2 =2002-2200+12 =40000400+1=39601
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
初中数学 《完全 平方公 式》ppt 北师大 版1-精 品课件 ppt(实 用版)
(4)(a b)2 (-2ab) a2 b2
下列计算是否正确?如不正确,应怎样改正?
北师大数学七下课件课题:完全平方公式课件

• 导学:对问题1,同学们在着手求解时,思考数a= ,数b= ,然后代入 公式计算;对问题2,在填空时,要结合公式的数形特征,在理解的基础 上,正确填写。 设计的理由:依据应用迁移原理和重在基础的目的,设计了问题1;为加 深学生应用公式时对两数a、b及整个公式的结构特征的理解,设计了问 题2。力求学生在运用中,小中见大,粗中见细,细中见巧,深刻理解完 全平方公式。
• 设计的理由:根据由特殊到一般的认识规律,设计问题1、2;根据培养学生的逻辑推理能力,设计了 问题3,使学生在提升思维的过程中,经历由感性认识上升到理性认识的过程,实现思维认识的飞跃。
注重“数 形”体会
• • • •
三、合作探究 1、计算下列各题: 1 2 (1)(3m+n) (2)(x- 2 )2 注意:在此处引导学生结合公式的“数形”来理解 题目中的“数形”,体会运用公式的关键处。 • 2、填空:(1)x2+4+ =( )2 • (2)4x2+9y2+ =( )2
• 六、作业与反思:略
• 设计的理由:针对学生在学习中的易错之 处,让学生反思;针对学生在学习中的疑 难点,让学生反思;针对学生在学习中的 好经验、好想法,让学生反思;针对教师 在教学中的不足,教师自己反思。
教学流程: 一、复习导入 1、回顾平方差公式,多项式的乘法法则。 2、运用平方差公式解题的关键之处是什么? 3、运用多项式乘法法则,计算下列各题。同学们从 “数”、“形”上发现什么规律? (1)(a+2)2;(2)(a+4)2 设计的理由:根据知识的相互联系和问题驱原则,在此 处设计了三个问题。力求学生运用已熟悉的知识和已积 累的知识经验,解决新问题,总结新规律1 1、计算:(1)( x-2y)2 (2)、(2x+ y)2 2 5 2、总结: (1)本节课学习的知识及学习收获。 (2)运用公式步骤,关键注意的事项。 导学:总结学习收获,一可总结探究知识方面的收获;二可总结运用知 识方面的收获;三可总结思维技巧方面的收获;四可总结思维创新的收 获。 设计的理由:在此处设计基础题是进一步强化基础训练,做到熟能生巧, 在此处设计了总结的两个问题,目的是促进学生自然地形成知识结构, 积累经验,提高自主总结能力,凸显学生学习过程中的“主体”地位。
• 设计的理由:根据由特殊到一般的认识规律,设计问题1、2;根据培养学生的逻辑推理能力,设计了 问题3,使学生在提升思维的过程中,经历由感性认识上升到理性认识的过程,实现思维认识的飞跃。
注重“数 形”体会
• • • •
三、合作探究 1、计算下列各题: 1 2 (1)(3m+n) (2)(x- 2 )2 注意:在此处引导学生结合公式的“数形”来理解 题目中的“数形”,体会运用公式的关键处。 • 2、填空:(1)x2+4+ =( )2 • (2)4x2+9y2+ =( )2
• 六、作业与反思:略
• 设计的理由:针对学生在学习中的易错之 处,让学生反思;针对学生在学习中的疑 难点,让学生反思;针对学生在学习中的 好经验、好想法,让学生反思;针对教师 在教学中的不足,教师自己反思。
教学流程: 一、复习导入 1、回顾平方差公式,多项式的乘法法则。 2、运用平方差公式解题的关键之处是什么? 3、运用多项式乘法法则,计算下列各题。同学们从 “数”、“形”上发现什么规律? (1)(a+2)2;(2)(a+4)2 设计的理由:根据知识的相互联系和问题驱原则,在此 处设计了三个问题。力求学生运用已熟悉的知识和已积 累的知识经验,解决新问题,总结新规律1 1、计算:(1)( x-2y)2 (2)、(2x+ y)2 2 5 2、总结: (1)本节课学习的知识及学习收获。 (2)运用公式步骤,关键注意的事项。 导学:总结学习收获,一可总结探究知识方面的收获;二可总结运用知 识方面的收获;三可总结思维技巧方面的收获;四可总结思维创新的收 获。 设计的理由:在此处设计基础题是进一步强化基础训练,做到熟能生巧, 在此处设计了总结的两个问题,目的是促进学生自然地形成知识结构, 积累经验,提高自主总结能力,凸显学生学习过程中的“主体”地位。
初中数学《完全平方公式》ppt北师大版1

解: (1)原式=3a(x2+2xy+y2)
=3a(x+y)2; (2)原式=(a+b)2-2·(a+b) ·6+62
=(a+b-6)2.
解疑点拨
反馈训练
1.下列四个多项式中,能因式分解的是( B )
A.a2+1
B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( B ) A.4xy(x-y)-x3 B.-x(x-2y)2
▪
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
▪
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
反馈训练
3.若关于x的多项式x2-8x+m2是完全平方式,则m的 值为___±__4______ .
4.分解因式:(1)4x2+4x+1;(2)
1 3
x2-2x+3.
小聪和小明的解答过程如下:
小聪:
小明:
×
×
他们做对了吗?若错误,请你帮忙纠正过来.
课堂小结
公式
a2±2ab+b2=(a±b)2
完全平方
公式分解
因
式
特点
(1)要求多项式有三项. (2)其中两项同号,且都可以写 成某数或式的平方,另一项则是这 两数或式的乘积的2倍,符号可正 可负. (3)等于这两个数的和或差的平 方.
=3a(x+y)2; (2)原式=(a+b)2-2·(a+b) ·6+62
=(a+b-6)2.
解疑点拨
反馈训练
1.下列四个多项式中,能因式分解的是( B )
A.a2+1
B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( B ) A.4xy(x-y)-x3 B.-x(x-2y)2
▪
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
▪
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
反馈训练
3.若关于x的多项式x2-8x+m2是完全平方式,则m的 值为___±__4______ .
4.分解因式:(1)4x2+4x+1;(2)
1 3
x2-2x+3.
小聪和小明的解答过程如下:
小聪:
小明:
×
×
他们做对了吗?若错误,请你帮忙纠正过来.
课堂小结
公式
a2±2ab+b2=(a±b)2
完全平方
公式分解
因
式
特点
(1)要求多项式有三项. (2)其中两项同号,且都可以写 成某数或式的平方,另一项则是这 两数或式的乘积的2倍,符号可正 可负. (3)等于这两个数的和或差的平 方.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=4x2-12x+9
=16x2-40xy+25y2
(3)(mn−a)2 =(mn)2-2mna+a2 =m2n2-2mna+a2
典型例题
例2.运用完全平方公式计算:
(1)(4m n)2 ;
(2)(y
1 2
)2.
分析:使用完全平方公式与平方差公式的使用一样,先把要计算
的式子与完全平方公式对照,明确哪个是a,哪个是b.
(1) ( x 6)2 ( x )2 2 6 x ( 6 )2
(2) (2m n)2 ( 2m )2 ( 2 2m n) n2
探究新知
几何解析:你能根据图1和图2的面积说明完全平方公式吗?
探究新知
图1大正方形的边长为(a+b),面积就是(a b),2 同时,大正方形 可以分成图中①②③④四个部分,它们的面积分别为 b2,ab,ab,a2 , 因此,整个面积为 a2 ab ab b2 a2 2ab b2 ,即说 明(a b)2 a2 2ab .b2
北师大版·统编教材七年级数学下册
第一章整式的乘除
1.6 完全平方公式
学习目标
1.掌握完全平方公式,能利用完全平方公式进行运算; 2.理解公式的推导过程,了解公式的几何背景.
复习巩固
你能列出下列代数式吗?
(1)两数和的平方;(a b)2 (2)两数差的平方; (a b)2
你能计算出他们的结果吗?
(a b)2 (a b)(a b) a2 2ab b2 (a b)2 (a b)(a b) a2 2ab b2 (3)根据乘方的定义,我们知道:a2 a a,那么(a b)2 应该写 成什么样的形式呢?(a b)2的运算结果有什么规律?
探究新知
(1)计算下列多项式的积,你能发现什么规律?
; -4c2)2
随堂练习
3.利用完全平方公式计算: (1)(5-a)2; (2)(-3m-4n)2; (3)(-3a+b)2. 解:(1)(5-a)2=25-10a+a2; (2)(-3m-4n)2=9m2+24mn+16n2; (3)(-3a+b)2=9a2-6ab+b2.
① (p 1)2 (p 1)(p 1) _p_2___2_p___1 ② (m 2)2 __m__2___4_m___4___ ③ (p 1)2 (p 1)(p 1) _p_2___2_p___1
④ (m 2)2 __m__2___4_m___4____
结果中都有两个数的平方和,而①②中间项2p=2·p·1,4m=2·m·2, 恰好是两个数乘积的2倍;
分析:先根据两平方项确定出这两个数,再根据完全平方公式确 定m的值. 解:∵36x2+(m+1)xy+25y2=(6x)2+(m+1)xy+(5y)2, ∴(m+1)xy=±2·6x·5y,∴m+1=±60,∴m=59或-61.
典型例题
例4.(1)下列等式能成立的是( C ).
A.(a-b)2=a2-ab+b2
(1)中可把4m看成a,n看成b;
(2)中可把y看成a, 看成b.
典型例题
解:(1)(4m n)2 (4m)2 2( 4m) n n2 16m2 8mn n2
(2)(y 1)2 2
y2 2 y 1 (1)2 22
y2 y 1 4
典型例题
例3.如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
随堂练习
1.(1)计算 (a b)2 (a b)2 ,其结果为( A)
A. 4ab
B. 2ab
C. 2a2
D. 2b2
(2)如果 x2 2ax 1是完全平方公式,则a的值为(C )
A.1
B.1
C. 1
D.0
ቤተ መጻሕፍቲ ባይዱ
随堂练习
(3) a2b4 2ab2 1 等于( A )
A.(ab2 1)2
B.(ab2 1)2
类似地可由图2说明(a b)2 a2 2ab .b2
典型例题
例1.用完全平方公式计算: (1) (2x−3)2 ; (2) (4x-5y)2 ;
(3) (mn−a)2
分析:找准与公式中a,b对应因式,代入公式计算.
解:
(1)(2x−3)2
(2)(4x-5y)2
= (2x)2-2(2x)(3)+ (-3)2 =(4x)2-2(4x)(5y)+ (5y)2
C. (a2b2 1)2
D.(a2b 1)2
(4) 2xy x2 y2 等于( D )
A. (x y)2
B. (x y)2
C. (x y)2
D. (x y)2
随堂练习
2.(1)(3x+2y)2-(3x-2y)2= 24xy ; (2)(3a2-2a+1)(3a2+2a+1)= 9a4+2a2+1 (3)( 9a4 )-24a2c2+( 16c4 )=( 3a2
A )=
25x2 5xy 1 y2 成立.
A.5x 1 y 2
4
B.5x
1 2
y
C.5x 1 y D.5x 1 y
2
2
(4)(5x2-4y2)(-5x2+4y2)运算的结果是( B ).
A.-25x4-16y4
B.-25x4+40x2y2-16y2
C.25x4-16y4
D.25x4-40x2y2+16y2
①与③,②与④中间项符号相反.
探究新知
; (2)推广计算: (a b)2 _____________ (a b)2 _____________
得到结果:
(a b)2 (a b)(a b) a2 ab ab b2 a2 2ab b2 (a b)2 (a b)(a b) a2 ab ab b2 a2 2ab b2
(a b)2 a2 2ab b2 (a b)2 a2 2ab b2
即:两个数的和(或差)的平方,等于它们的平方和,加 上(或减去)它们的积的2倍.
探究新知
(3)进一步挖掘公式的结构特征 ①公式左边是一个二项式的完全平方. ②公式的右边是一个二次三项式,分别是二项式中每一项的平方及 两项乘积的2倍(首平方,尾平方,乘积的两倍放中央,中间符号同前 方).
B.(a+3b)2=a2+9b2
C.(a+b)2=a2+2ab+b2
D.(x+9)(x-9)=x2-9
(2)(a+3b)2-(3a+b)2计算的结果是( C ).
A.8(a-b)2
B.8(a+b)2
C.8b2-8a2
D.8a2-8b2
典型例题
(3)在括号内选入适当的代数式使等式
5x
1 2
y
·(
