画法几何及工程制图解题指导

工程制图考试攻略

d' b' X
b d
c'
e'
n'
a' p'
m'
O n ap m
e
MN ABC
c
平面P ABC
12
二、基本体及其截交
（一）平面立体 1、棱柱体 3、4、5、6 2、棱锥体
平面立体的棱线与平面的截交点（二）曲面立体
1、圆柱体：3种 2、圆锥体：5种 3、圆球：1种
13
三、立体相交
1、平面立体与平面立体相交参与相交的立体的棱线与另一个立体的贯穿点同坡屋面
点,可以直接求出.
2'
3'
利用面上取
6' 5' 4'
点的方法， 7'
求棱面上的
几个点.
注意画出未
被截切的棱
I
线和两截切 7
平面之间的交线.
1 6
3 24
5
VII
例14：求带缺口正四棱台的H，W
投影
1"
2"
3" 5"
6" 4" 7"
II III
IV
VI
V
39
圆柱截交线
圆柱截交线
截平面位置
所求
20
例4 作直线使与直线L 平行，并与两交叉直线ⅠⅡ、ⅢⅣ相交。
1' 3'
X 2' 3
2
解题分析3：1.两次换面将ⅠⅡ(或ⅢⅣ)变为
投影面垂直线；
L' 2.过直线的积聚投影作直线∥L 的
投影l，则该直线必与ⅠⅡ、ⅢⅣ

画法几何与工程制图

画法几何及工程制图（辅导教案）绪论§0—1 基本概念一、工程图在生产建设和科学研究工程中，对于已有的或想象中的空间体（如地面、建筑物、机器等）的形状、大小、位置和其它有关部门资料，很难用语言和文字表达清楚，因而需要在平面上（例如图纸上）用图形表达出来。

这种在平面上表达工程物体的图，称为工程图。

工程图常用的有以下几种：1．透视图2．轴测图3．正投影图4．标高投影图二、画法几何当研究空间物体在平面上如何用图形来表达时，因空间物体的形状、大小和相互位置等不相同，不便以个别物体来逐一研究，并且为了使得研究时易于正确、深刻和完全，以及所得结论能广泛地应用于所有物体起见，特采用几何学中将空间物体综合概括成抽象的点、线、面等几何形体的方法，先研究这些几何形体在平面上如何用图形来表达，以及如何通过作图来解决它们的几何问题。

这种研究在片面上用图形来表示空间几何形体和运用几何图来解决它们的几何问题的一门学科，称为画法几何。

例如：正方体6个面组成每个面由无数条线组成每条线由无数个点组三、工程制图把工程上具体的物体，视为由几何形体所组成，根据画法几何的理论，研究它们在平面上用图形来表达的问题，而形成工程图。

在工程图中，除了有表达物体形状的线条以为，还要应用国家制图标准规定的一些表达方法和符号，注以必要的尺寸和文字说明，使得工程图能完善、明确和清晰地表达出物体的形状、大小和位置，以及其它必要的资料（例如：物体的名称、材料的种类和规格，生产方法等）。

研究绘制工程图的这门学科，称为工程制图。

注意：如将工程图比喻为工程界的一种语言，则画法几何便是这种语言的语法。

§0—2画法几何及工程制图课程的目的、任务、要求一、目的培养学生绘图、读图和图解的能力，通过这几方面的实践，培养学生的空间想象能力二、任务1．研究正投影的基本理论2．培养绘制和阅读工程图的能力3．研究常用的图解方法，培养图解能力4．通过绘图、读图和图解的实践，培养空间想象能力5．培养认真、细致、一丝不苟的工作作风6．培养用图形软件绘制图样的初步能力三、应达到的要求1．掌握正投影的基本理论和作图方法2．确使用绘图工具，掌握绘图的技巧和方法，又快又好地作出符合国家标准的工程图，并能正确地阅读一般的工程图纸。

画法几何及工程制图解题指导

选择：选择合适的解题方法并尝试解答
验证：验证答案是否正确如有错误重新思考解题方法
总结：总结解题方法和经验以便下次遇到类似题目时能
够快速解答
解题步骤
分析：分析已知条件和未知量之间的关系找出解题的关键点
画图：根据题意画出相应的图形包括已知图形和未知图形
审题：仔细阅读题目理解题意明确已知条件和未知量
解题步骤： . 利用勾股定理求解三角形边长 b. 利用三角形面积公式求解三角形面积
. 利用勾股定理求解三角形边长
b. 利用三角形面积公式求解三角形面积
解题技巧：注意勾股定理的应用以及三角形面积公式的灵活运用。
单击此处输入你的项正文文字是您思想的提炼请尽量言简赅的意阐述你的观点。
题目四解析
题目类型：平面几何问题
单击此处输入你的项正文文字是您思想的提炼,言简的阐述观点。
解题步骤： . 确定已知条件 b. 画出图形 c. 利用几何定理求解
. 确定已知条件 b. 画出图形
解题技巧： c . 利用几何定理求解 . 注意图形的完整性和准确性 b . 利用辅助线简化问题 c. 灵活运用几何定理和公式
. 注意图形的完整性和准确性 b. 利用辅助线简化问题
答案解析： c . 灵活运用几何定理和公式 . 详细解答过程 b . 答案验证 c . 总结解题方法和技巧
. 详细解答过程 b. 答案验证 c. 总结解题方法和技巧
常见问题及解决方法
问题：无法理解题目要求解决方法：仔细阅读题目理解题目要求明确解题目标解决方法：仔细阅读题目理解题目要求明确解题目标

画法几何及工程制图第七版部分习题解题ppt课件

4'
作出两圆柱偏
3''
2'' 1''
交的相贯线的投影
5''
4''
y
4
3
y
2 5
1
可编辑课件PPT
13
作出圆柱与圆锥正交的相贯线的投影。
可编辑课件PPT
14
作出旋钮上球面与圆柱面相贯线的投影。
可编辑课件PPT
15
作出1/4环面穿圆柱孔后相贯线的投影。
可编辑课件PPT
16
作出物体上相贯线的投
b'
b"
a （b）
（c）
可编辑课件PPT
（A） C
3
B
作出组合回转体的水平投影，以及表面上A、B、C三点的三
面投影。
球
圆柱环
b
c （b） a
c a
圆柱
b
（a）
c
可编辑课件PPT
4
完成正四棱锥被截切后的三面投影。
可编辑课件PPT
5
完成球体被截切后的三面投影。作连一接特般各殊点
可编辑课件PPT
习题解答
可编辑课件PPT
1
作出五棱锥的水平投影，以及它表面上Ａ、Ｂ、Ｃ点的三面投影。
1'
1"
2"
2'
a"
（a'）
s"
s'
5'
5"
c"
c'
3'
b'
b"
3"
4'

画法几何工程制图常见习题例子解答课件

画法几何及建筑工程制
返回
画法几何工程制图常见习题例子解答
2-13.将立面图该画成全剖面，不应有的线打“X”。
画法几何及建筑工程制
1-1
1
1
点击此处查看立体图
15页
画法几何工程制图常见习题例子解答
画法几何及建筑工程制
返回画法几何工程制图常见习题例子解答
2-14.将立面图该画成适当的剖面。
画法几何及建筑工程制
画法几何及建筑工程制
1-1
1 1
1
点击此处查看立体图
17页
画法几何工程制图常见习题例子解答
画法几何及建筑工程制
返回画法几何工程制图常见习题例子解答
2-20. 补画剖面图漏画的线。
画法几何及建筑工程制
点击此处查看立体图
18页
画法几何工程制图常见习题例子解答
画法几何及建筑工程制
（1）
返回画法几何工程制图常见习题例子解答
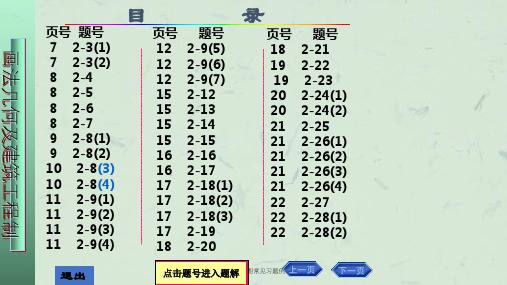
2-8.根据组合体轴测图，画三面视图，并标注尺寸。（4）比例1：1
10画页法几何工程制图常见习题例子解答
2-9.已知两面视图，补画所缺的视图，并标注尺寸。（比例1：1，从图中量取）。
（1）
画法几何及建筑工程制
点击此处查看立体图
1画1法页几何工程制图常见习题例子解答
画法几何及建筑工程制
返回
画法几何工程制图常见习题例子解答
返回
画法几何工程制图常见习题例子解答
画法几何及建筑工程制
2-26.画出指定位置的移出断面。
(1)
1
23
443 1
2
1-1
2-2
3-3
4-4
点击此处查看立体图
21页

画法几何及工程制图解题指导(1-5)精编版

1’
d’
b
m
ΔZ
a
α
c 1
2020/3/20
d
8
2—3（4）已知ΔABC平面对V面的倾角β1=300，作出该三角形的水平投影（bc//X轴）。
b’ m’
a’ 300
1’ c’
bm
c
a
2020/3/20
解不唯一
9
分析：ΔABC是铅垂面，与ΔABC平
2-4（4）已知平面ABC平行于平面DEF，且相距20mm , 求平面DEF的水平投影。
38
P29 5-1（2）作出五棱锥的水平投影，以及它表面上A、B、C点的三面投影。
2020/3/20
39
P29 5-1(4)作出圆锥的水平投影，以及它表面上A、B、C点的三面投影
b’ a’
(c )’
b’’ a’’ c’’
(c)
a
b
2020/3/20
40
P30 5-2(1)作出球体的侧面投影，以及它表面上A、B、C点的三面投影
P1
P2
2020/3/20
56
P385-10（2）作出圆柱与圆锥正交的相贯线的投影。
2020/3/20
57
P39 5-11（1）作出旋钮上球面与圆柱面相贯线的投影。
2020/3/20
58
P395-11（2）作出1/4环面穿圆柱孔后相贯线的投影。
2020/3/20
59
P40 5-12（1）作出物体上相贯线的投影。
o
c
b
2020/3/20
此题有2解
45mm
3
1-8（4）线段CM是等腰ΔABC的高，点A在H面上，B在V面上，求作三

画法几何与工程制图

画法几何及工程制图（辅导教案）绪论§0—1 基本概念一、工程图在生产建设和科学研究工程中，对于已有的或想象中的空间体（如地面、建筑物、机器等）的形状、大小、位置和其它有关部门资料，很难用语言和文字表达清楚，因而需要在平面上（例如图纸上）用图形表达出来。

这种在平面上表达工程物体的图，称为工程图。

工程图常用的有以下几种：1．透视图2．轴测图3．正投影图4．标高投影图二、画法几何当研究空间物体在平面上如何用图形来表达时，因空间物体的形状、大小和相互位置等不相同，不便以个别物体来逐一研究，并且为了使得研究时易于正确、深刻和完全，以及所得结论能广泛地应用于所有物体起见，特采用几何学中将空间物体综合概括成抽象的点、线、面等几何形体的方法，先研究这些几何形体在平面上如何用图形来表达，以及如何通过作图来解决它们的几何问题。

这种研究在片面上用图形来表示空间几何形体和运用几何图来解决它们的几何问题的一门学科，称为画法几何。

例如：正方体6个面组成每个面由无数条线组成每条线由无数个点组三、工程制图把工程上具体的物体，视为由几何形体所组成，根据画法几何的理论，研究它们在平面上用图形来表达的问题，而形成工程图。

在工程图中，除了有表达物体形状的线条以为，还要应用国家制图标准规定的一些表达方法和符号，注以必要的尺寸和文字说明，使得工程图能完善、明确和清晰地表达出物体的形状、大小和位置，以及其它必要的资料（例如：物体的名称、材料的种类和规格，生产方法等）。

研究绘制工程图的这门学科，称为工程制图。

注意：如将工程图比喻为工程界的一种语言，则画法几何便是这种语言的语法。

§0—2画法几何及工程制图课程的目的、任务、要求一、目的培养学生绘图、读图和图解的能力，通过这几方面的实践，培养学生的空间想象能力二、任务1．研究正投影的基本理论2．培养绘制和阅读工程图的能力3．研究常用的图解方法，培养图解能力4．通过绘图、读图和图解的实践，培养空间想象能力5．培养认真、细致、一丝不苟的工作作风6．培养用图形软件绘制图样的初步能力三、应达到的要求1．掌握正投影的基本理论和作图方法2．确使用绘图工具，掌握绘图的技巧和方法，又快又好地作出符合国家标准的工程图，并能正确地阅读一般的工程图纸。

画法几何及工程制图解题指导页PPT文档共119页文档

Thank you
文家。汉族，东晋浔阳柴桑人（今江西九江）。曾做过几年小官，后辞官回家，从此隐居，田园生活是陶渊明诗的主要题材，相关作品有《饮酒》、《归园田居》、《桃花源记》、《五柳先生传》、《归去来兮辞》等。
1
0
、
倚
南
窗
以
寄
傲
，
审
容
膝
之
易
安
。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
画法几何及工程制图解题指导页PPT 文档

、
露
凝
无
游
氛
，
天
高
风
景
澈
。
7、翩翩新来燕，双双入我庐，先巢故尚在，相将还旧居。
8
、
吁
嗟
身
后
名
，
于
我
若
浮
烟
。
9、陶渊明（约 365年 —427年），字元亮，（又一说名潜，字渊明）号五柳先生，私谥“靖节”，东晋末期南朝宋初期诗人、文学家、辞赋家、散

画法几何与工程制图

画法几何及工程制图（辅导教案）绪论§0—1 基本概念一、工程图在生产建设和科学研究工程中，对于已有的或想象中的空间体（如地面、建筑物、机器等）的形状、大小、位置和其它有关部门资料，很难用语言和文字表达清楚，因而需要在平面上（例如图纸上）用图形表达出来。

这种在平面上表达工程物体的图，称为工程图。

工程图常用的有以下几种：1．透视图2．轴测图3．正投影图4．标高投影图二、画法几何当研究空间物体在平面上如何用图形来表达时，因空间物体的形状、大小和相互位置等不相同，不便以个别物体来逐一研究，并且为了使得研究时易于正确、深刻和完全，以及所得结论能广泛地应用于所有物体起见，特采用几何学中将空间物体综合概括成抽象的点、线、面等几何形体的方法，先研究这些几何形体在平面上如何用图形来表达，以及如何通过作图来解决它们的几何问题。

这种研究在片面上用图形来表示空间几何形体和运用几何图来解决它们的几何问题的一门学科，称为画法几何。

例如：正方体6个面组成每个面由无数条线组成每条线由无数个点组三、工程制图把工程上具体的物体，视为由几何形体所组成，根据画法几何的理论，研究它们在平面上用图形来表达的问题，而形成工程图。

在工程图中，除了有表达物体形状的线条以为，还要应用国家制图标准规定的一些表达方法和符号，注以必要的尺寸和文字说明，使得工程图能完善、明确和清晰地表达出物体的形状、大小和位置，以及其它必要的资料（例如：物体的名称、材料的种类和规格，生产方法等）。

研究绘制工程图的这门学科，称为工程制图。

注意：如将工程图比喻为工程界的一种语言，则画法几何便是这种语言的语法。

§0—2画法几何及工程制图课程的目的、任务、要求一、目的培养学生绘图、读图和图解的能力，通过这几方面的实践，培养学生的空间想象能力二、任务1．研究正投影的基本理论2．培养绘制和阅读工程图的能力3．研究常用的图解方法，培养图解能力4．通过绘图、读图和图解的实践，培养空间想象能力5．培养认真、细致、一丝不苟的工作作风6．培养用图形软件绘制图样的初步能力三、应达到的要求1．掌握正投影的基本理论和作图方法2．确使用绘图工具，掌握绘图的技巧和方法，又快又好地作出符合国家标准的工程图，并能正确地阅读一般的工程图纸。

画法几何及工程制图解题指导

29.07.2021
.
61
P40-2
29.07.2021
.
62
P415-13（1）作出圆柱与圆环偏交的相贯线的投影。
29.07.2021
.
63
P41 5-13 （2）作出圆锥与球面偏交的相贯线的投影。
29.07.2021
.
64
P42 514（1）作出圆锥与圆柱斜交的相贯线的投影。
分析：到A、B两点距离相等的点的轨迹是中垂面。
a’ a
b’ m’
m b
29.07.2021
.
15
2-8（4）已知ΔABC垂直ΔDEF，作出ΔABC的水平投影。
l’
e’
b’ m’
分析：1、两平面
k’ 垂直，过其中一
c’ 个平面内一点向
d’ f’ a’
另一平面所作垂
a e
线一定在该平面内；
2、用面上求点的
ΔZ
a’
1’
d’
b
m
ΔZ
a
α
c 1
29.07.2021
.d
8
2—3（4）已知ΔABC平面对V面的倾角β1=300，作出该三角形的水平投影（bc//X轴）。
b’ m’
a’ 300
1’ c’
bm
c
29.07.2021
a
解不唯一
.
9
分析：ΔABC是铅垂面，与ΔABC平
2-4（4）已知平面ABC平行于平面DEF，且相距20mm , 求平面DEF的水平投影。
d
.
此时无解
30
H V1
c’ a’
a a1’ b1’

建筑画法几何及工程制图(辅导教案)

建筑画法几何及工程制图（辅导教案）绪论§0—1 基本概念一、工程图在生产建设和科学研究工程中，对于已有的或想象中的空间体（如地面、建筑物、机器等）的形状、大小、位置和其它有关部门资料，很难用语言和文字表达清楚，因而需要在平面上（例如图纸上）用图形表达出来。

这种在平面上表达工程物体的图，称为工程图。

工程图常用的有以下几种：1．透视图2．轴测图3．正投影图4．标高投影图二、画法几何当研究空间物体在平面上如何用图形来表达时，因空间物体的形状、大小和相互位置等不相同，不便以个别物体来逐一研究，并且为了使得研究时易于正确、深刻和完全，以及所得结论能广泛地应用于所有物体起见，特采用几何学中将空间物体综合概括成抽象的点、线、面等几何形体的方法，先研究这些几何形体在平面上如何用图形来表达，以及如何通过作图来解决它们的几何问题。

这种研究在片面上用图形来表示空间几何形体和运用几何图来解决它们的几何问题的一门学科，称为画法几何。

例如：正方体6个面组成每个面由无数条线组成每条线由无数个点组三、工程制图把工程上具体的物体，视为由几何形体所组成，根据画法几何的理论，研究它们在平面上用图形来表达的问题，而形成工程图。

在工程图中，除了有表达物体形状的线条以为，还要应用国家制图标准规定的一些表达方法和符号，注以必要的尺寸和文字说明，使得工程图能完善、明确和清晰地表达出物体的形状、大小和位置，以及其它必要的资料（例如：物体的名称、材料的种类和规格，生产方法等）。

研究绘制工程图的这门学科，称为工程制图。

注意：如将工程图比喻为工程界的一种语言，则画法几何便是这种语言的语法。

§0—2画法几何及工程制图课程的目的、任务、要求一、目的培养学生绘图、读图和图解的能力，通过这几方面的实践，培养学生的空间想象能力二、任务1．研究正投影的基本理论2．培养绘制和阅读工程图的能力3．研究常用的图解方法，培养图解能力4．通过绘图、读图和图解的实践，培养空间想象能力5．培养认真、细致、一丝不苟的工作作风6．培养用图形软件绘制图样的初步能力三、应达到的要求1．掌握正投影的基本理论和作图方法2．确使用绘图工具，掌握绘图的技巧和方法，又快又好地作出符合国家标准的工程图，并能正确地阅读一般的工程图纸。

画法几何与工程制图.

画法几何与工程制图
说明：1.一律用铅笔答题；
2.要求作图准确，线形分明，图面整洁。

一、改正下面图中表面粗糙度代号标注方法上的错误，将正确的表面粗糙度代
号标注在空白图中
二、根据给出的左视图、俯视图，画组合体的主视图中的相贯线（要画出图中的虚线）
三、本题有两小题
1、已知轴和孔的尺寸公差带代号，试在装配图中注写出配合尺寸。

2、试说明：Φ20是。

K是代号。

h是代号。

7和6是。

该配合是制配合。

四、（每处1分，共19分）
标注下面物体的尺寸。

（尺寸数值从图中1：1量取，并取整数）。

画法几何及工程制图解题指导(1-5)

尺寸标注与技术要求
注意使用规范的语言和符号，确保技术要求的准确性和一致性。
根据实际情况，对关键部分或特殊要求进行强调或补充说明。
感谢您的观看
THANKS
其他表达方法
局部放大图
对机件某一部分进行放大，以更清晰地表达细节结构。局部放大图应标注放大比例和范围。
简化画法
为了简化绘图过程，可以采用一些简化画法，如折线表示均布孔、小平面表示凹槽等。
规定画法
根据国家标准或行业规范，采用统一的规定画法来表示某些特定结构，如螺纹、齿轮等。
05
装配达细节特征，通过剖面图、局部放大图等手段清晰表达
03
零件的细节部分。
零件图的绘制与识读
• 标注尺寸、公差和技术要求，确保生产和检验的要求。
零件图的绘制与识读
01
识读方法
02
了解零件的名称、用途和材料。
03
分析零件的结构和形状，理解其制造和加工过程。
04
注意查看尺寸标注和技术要求，确保满足设计和加工要求。
剖视图与断面图
剖视图
通过剖切机件，去除某些部分，以显示内部结构。剖视图中应标注剖切符号和投影方向。
断面图
仅显示机件某一截面的图形，常用于表达机件的横截面形状。断面图应标注断面名称和投影方向。
注意事项
在剖视图和断面图中，应避免出现不完整要素、假想投影轮廓线和漏线。同时，应合理选择剖切位置，以清晰表达机件内部结构。
机件的表达方法
视图的选择与使用
主视图的选择
选择能反映机件主要形状特征的方向作为主视图的投影方向，通常选择正对着机件前后方向进行投影。
其他视图的选择
根据需要选择俯视图、左视图、右视图、仰视图等，以全面、清晰地表达机件的结构。

大学课程画法几何及工程制图解题指导

是AB与中垂面的交
b d
m
点。
2020/5/23
第二章结束返回目录
c
21
第三章投影变换
2020/5/23
22
3-1（1）求直线AB对H、V面的倾角、及其实长。
直线实长
2020/5/23
a
b
b’
a’ ZA
Y
YA
B
a
ZA
a1’
ZB
b 直线实长
ZB
b1’
23
3-1（3）过点C作直线AB的垂线CD。
n
’
a’
c’
a
c n m
m a
c
n b
b
与正垂面垂直的是正平线，由此可延伸，与铅垂面垂直的是水平线，与侧垂面垂
直的是侧平线。
2020/5/23
15
2—8（3）求作与AB两点等距离的轨迹。
分析：到A、B两点距离相等的点的轨迹是中垂面。
a’
a
b’
m
’
m b
2020/5/23
16
2-8（4）已知ΔABC垂直ΔDEF，作出ΔABC的水平投影。
’
k
a
’
’
n
c
’
n
b
’
k
c
a
m
2020/5/23
28
b
d
’
k
’
m
’
’
Va
H’
c
’
【补充题4】求交叉两直线AB 和CD的距离。
kc
d
b c1
c2
m
’
k1
k2
a
H V1
a1

工程制图画法几何考试不挂必看

b′
水平投影.
X
O
YW
b e
a
还可换成〔…与OX
c
或OY轴相交〕
YH
两
直
线
E
e′
的垂
A
D
B
c′
a′ b′
直问
C
c′
题
e(d)( c)
a b
X
a
H
e(d)( c)
b
AB垂直于AC,且AB平行于H面,那么有ab ac
二.平面局部
1.各种位置平面的投影; 2.平面上取点和直线; 3.平面上的最大斜度线和平面倾角的求解; 4.完成平面的投影;
平面上的最大斜度线⊥平面上的平行线目的求α,β,γ
平面上作一水平线(先作它的正面投影)
α
作该水平线的垂线(对H面的最大斜度线)
这条垂线的α=平面的α
平面上作一正平线(先作它的水平投影)
β
作该正平线的垂线(对V面的最大斜度线)
这条垂线的β=平面的β
平面上作一侧平线(先作它的V或H投影)
复习题3.直线AB延长后经过O点,并与V面成30°角,求直线AB的H、V投影。
a′
X a
b′
30°
0
b
3.两直线的相对位置:平行、相交、穿插
⑴两直线平行时,其同面投影均平行; ⑵两直线相交时,其交点要满足点的投影规律; ⑶两直线不满足平行及相交的条件时,必定为两直线穿插; ⑷相互垂直的两直线,假设其中一直线是投影面的平行线时,那么在该投影面上,两直线的投影相互垂直! (直角投影定律)
1.直线与平面、平面与平面平行 2.直线与平面、平面与平面相交
1.直线与平面、平面与平面平行小结

画法几何与工程制图

画法几何及工程制图（辅导教案）绪论§0—1 基本概念一、工程图在生产建设和科学研究工程中，对于已有的或想象中的空间体（如地面、建筑物、机器等）的形状、大小、位置和其它有关部门资料，很难用语言和文字表达清楚，因而需要在平面上（例如图纸上）用图形表达出来。

这种在平面上表达工程物体的图，称为工程图。

工程图常用的有以下几种：1．透视图2．轴测图3．正投影图4．标高投影图二、画法几何当研究空间物体在平面上如何用图形来表达时，因空间物体的形状、大小和相互位置等不相同，不便以个别物体来逐一研究，并且为了使得研究时易于正确、深刻和完全，以及所得结论能广泛地应用于所有物体起见，特采用几何学中将空间物体综合概括成抽象的点、线、面等几何形体的方法，先研究这些几何形体在平面上如何用图形来表达，以及如何通过作图来解决它们的几何问题。

这种研究在片面上用图形来表示空间几何形体和运用几何图来解决它们的几何问题的一门学科，称为画法几何。

例如：正方体6个面组成每个面由无数条线组成每条线由无数个点组三、工程制图把工程上具体的物体，视为由几何形体所组成，根据画法几何的理论，研究它们在平面上用图形来表达的问题，而形成工程图。

在工程图中，除了有表达物体形状的线条以为，还要应用国家制图标准规定的一些表达方法和符号，注以必要的尺寸和文字说明，使得工程图能完善、明确和清晰地表达出物体的形状、大小和位置，以及其它必要的资料（例如：物体的名称、材料的种类和规格，生产方法等）。

研究绘制工程图的这门学科，称为工程制图。

注意：如将工程图比喻为工程界的一种语言，则画法几何便是这种语言的语法。

§0—2画法几何及工程制图课程的目的、任务、要求一、目的培养学生绘图、读图和图解的能力，通过这几方面的实践，培养学生的空间想象能力二、任务1．研究正投影的基本理论2．培养绘制和阅读工程图的能力3．研究常用的图解方法，培养图解能力4．通过绘图、读图和图解的实践，培养空间想象能力5．培养认真、细致、一丝不苟的工作作风6．培养用图形软件绘制图样的初步能力三、应达到的要求1．掌握正投影的基本理论和作图方法2．确使用绘图工具，掌握绘图的技巧和方法，又快又好地作出符合国家标准的工程图，并能正确地阅读一般的工程图纸。

画法几何及工程制图3

图6—16§6.3 垂直关系一、直线与平面垂直几何条件：如果一直线垂直于平面上的两条相交直线，则此直线垂直于该平面。

反之，如果一直线垂直于一平面，则此直线垂直于该平面上的一切直线。

平面上的水平线和正平线为两条相交直线，这样，我们可以利用直角投影原理作一直线垂直于一平面，或判定一直线是否垂直一平面。

（图6—18）。

图5—13例1 试求点K到△ABC平面的距离（图6—19）作图步骤作垂线→求交点（垂足）→完成距离投影→求实长图6—19例2 试过A点作一条直线，使其与直线BC 垂直相交（图6—20）分析：过A 点与直线BC 垂直的线有无数条，形成一轨迹（集合），这个轨迹就是过点A 与BC 垂直的平面。

所求直线必在此平面内，就是该平面与直线BC 的交点和点A 的连线。

作图步骤: 过A 点作直线BC 的垂面→求交点（垂足）K →连AK 图6—20二、平面与平面垂直几何条件：如果一直线垂直于一平面，则通过此直线的所有平面都垂直于该平面。

反之，如果两平面互相垂直，则自第一个平面上的任意一点向第二个平面所作的垂线，一定在第一个平面上。

（图6—21）图5—15 图5—16图6—21 图6—22例 3 试过直线EF 作一平面垂直于平面ABCD(图6—22) 例 4 试过直线EF 作一平面垂直于平面ABCD(图6—23)图5—17图6—23§6.3 点、线、面综合题及其解法点、线、面综合题是指在解题过程中需要综合运用前面点、线、面，特别是直线、平面相对位置的基本概念和作图方法。

要解决点、线、面综合问题，首先要熟练掌握基本作图方法。

如：●直角三角形法求实长、倾角；●直角投影法则；●平面内定点、定线；●过直线外（或上）一点作直线的垂面；●过平面外（或内）一点作平面的垂线；●过平面外一点作该平面的平行面；●定比关系应用；●求交点、交线；●换面法的基本应用。

其次，要善于挖掘、利用已知的和隐含的条件。

如等腰三角形、等边三角形、长方形、正方形、菱形等隐含的相等、平分、垂直条件。