鲁教版五四制七年级数学上册第一章三角形1认识三角形第3课时同步测试(解析版)
初中数学鲁教版(五四制)七年级上册第一章 三角形1 认识三角形-章节测试习题(68)

章节测试题1.【答题】在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B,则∠B=______度.【答案】60【分析】先整理得到∠A+∠C=2∠B,再利用三角形的内角和等于180°列出方程求解即可.【解答】解:∵∠B﹣∠A=∠C﹣∠B,∴∠A+∠C=2∠B,又∵∠A+∠C+∠B=180°,∴3∠B=180°,∴∠B=60°.故答案为:60.2.【答题】在Rt△ABC中,∠C=90°,∠A=70°,则∠B=______.【答案】20°【分析】本题考查了三角形的内角和定理.【解答】∵Rt△ABC中,∠C=90°,∴∠A+∠B=90°,∵∠A=70°,∴∠B=90°-70°=20°,故答案为:20°.3.【答题】△ABC中,∠C=90°,∠A∶∠B=1∶2,则∠A=______度.【答案】30【分析】本题考查了三角形的内角和定理.【解答】∵△ABC中,∠C=90°,∴∠A+∠B=90°,又∵∠A:∠B=1:2,∴∠B=2∠A,∴∠A+2∠A=90°,∴∠A=30°,故答案为:30.4.【答题】在△ABC中,∠A+∠B=∠C,∠B=2∠A,则∠C=______,∠A=______【答案】90° 30°【分析】本题考查了三角形的内角和定理.【解答】解:∵∠A+∠B+∠C=180°,∠A+∠B=∠C,∴∠C=90°,∠A+∠B=90°.∵∠B=2∠A,∴3∠A=90°,∴∠A=30°.故答案为:90°,30°.5.【答题】已知,在△ABC中,∠A=80°,那么∠B=∠C=______度.【答案】50【分析】本题考查了三角形的内角和定理.【解答】又故答案为:50.6.【答题】在△ABC中,AD是角平分线,若∠B=50º,∠C=70º,则∠ADC=______.【答案】80º【分析】本题考查了三角形的内角和定理、三角形的角平分线.【解答】如图,∵△ABC中,∠B=50º,∠C=70º,∴∠BAC=60°,∵AD平分∠BAC,∴∠DAC=30°,∴∠ADC=180°-70°-30°=80°.故答案为:80°.7.【答题】在△ABC中,∠C=90°,∠A=60°,则∠B=______°.【答案】30【分析】本题考查了三角形的内角和定理.【解答】解:∠B=90°-∠A=90°-60°=30°.故答案为:30.8.【答题】在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理______.【答案】三角形的内角和是180°【分析】本题考查了三角形的内角和定理.【解答】根据折叠的性质,折叠前后的两个角相等,即∠A=∠1,∠B=∠2,∠C=∠3,根据把三角形的三个角转化为一个平角∠1+∠2+∠3=180°,可得∠A+∠B+∠C=180°,因此这个定理为:三角形的内角和是180°.故答案为:三角形的内角和是180°.9.【答题】一个三角形的三个内角之比为1∶2∶3,则三角形是______三角形【答案】直角【分析】本题考查了三角形的内角和定理.【解答】设三角形三内角度数分别为x,2x,3x,根据三角形的内角和为180°得:x+2x+3x=180°,即6x=180°,解得:x=30°,可得三角形三内角分别为30°,60°,90°,则三角形是直角三角形.故答案为:直角.10.【答题】在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为______度.【答案】60【分析】【解答】解:∵三角形是直角三角形,一个锐角等于30°,∴另一个锐角为90°﹣30°=60°.故答案为:60.11.【答题】在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=______.【答案】100°【分析】本题考查了三角形的内角和定理.【解答】①,②,①−②得,解得故答案为:12.【答题】直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为______.【答案】65°和25°【分析】本题考查了三角形的内角和定理.【解答】设这两个锐角的度数分别为x,y,根据题意得,解得故答案为:13.【答题】Rt△ABC中,∠C=90°,∠A=35°30′,则∠B=______.【答案】54.5°【分析】本题考查了三角形的内角和定理.【解答】Rt△ABC中,∵∠C=90°,∠A=35°30′,∴∠B=90°−∠A=90°−35°30′=54°30′=54.5°.故答案为:54.5°.14.【答题】已知,在△ABC中,AD是BC边上的高线,且∠ABC=25°,∠ACD =55°,则∠BAC=______.【答案】100°或30°【分析】本题考查了三角形的内角和定理.【解答】如图,有两种情况,当∠ACD=55°时,∠BAC=∠ACD-∠ABC=55°-25°=30°;当∠AC′D=55°时,∠BAC′=180°-∠ABC-∠AC′B=180°-25°-55°=100°;综上,∠BAC为:100°或30°,故答案为:100°或30°.15.【答题】在△ABC中,∠C=2(∠A+∠B),则∠C=______.【答案】120°【分析】本题考查了三角形的内角和定理.【解答】:∵∠A+∠B=180°-∠C,∠C=2(∠A+∠B),∴∠C=2(180°-∠C),∴∠C=120°.16.【答题】在△ABC中,∠B=50°,∠C=60°,则∠A的度数是______度.【答案】70【分析】本题考查了三角形的内角和定理.【解答】∠B=50°,∠C=60°,∠A+∠B+∠C=180°,.17.【答题】一个三角形的三个内角的度数比是1∶6∶5,最大的一个内角是______度,按角分,它是一个______角三角形.【答案】90 直角【分析】本题考查了三角形的内角和定理.【解答】设这个三角形的最小内角为x,则另外两个角分别为6x、5x,根据三角形的内角和定理可得x+6x+5x=180,解得x=15,∴这个三角形的最大内角为15×6=90°,这个三角形是直角三角形.18.【答题】已知三角形三个内角的度数比是2:3:4,则这个三角形中最大角的度数是______.【答案】80°【分析】本题考查了三角形的内角和定理.【解答】根据三角形的内角和定理,设三个内角分别为2x,3x,4x,可得2x+3x+4x=180°,解得x=20°,因此最大内角的度数为:80°.故答案为:80°.19.【答题】在△ABC中,∠A:∠B:∠C=2:3:4,则∠A=______度【答案】40【分析】本题考查了三角形的内角和定理.【解答】设∠A、∠B、∠C的度数分别为2x、3x、4x,则2x+3x+4x=180°,解得x=20°∴2x=40°,故答案为:40.20.【答题】若一个三角形的三个内角度数之比为4∶3∶2,则这个三角形的最大内角为______度.【答案】80【分析】本题考查了三角形的内角和定理.【解答】根据三角形的内角和是180°,再根据三角形的三个内角之比为4:3:2即可求出这个三角形的最大内角为:180°×=80°.。
鲁教五四制七年级数学上《第1章三角形》单元测试含答案

《第1章三角形》一、选择题:1.全等形都相同的是()A.形状 B.大小 C.边数和角度D.形状和大小2.如图,△ABC≌△DEF,AC∥DF,则∠C的对应角为()A.∠F B.∠AGE C.∠AEF D.∠D3.如图,AB=AD,BC=CD,点E在AC上,则全等三角形共有()A.1对B.2对C.3对D.4对4.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于()A.8 B.7 C.6 D.55.在△ABC和△FED中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件()A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,则①△ABE≌△ACF;②△BOF≌△COE;③点O在∠BAC 的角平分线上,其中正确的结论是()A.3个B.2个C.1个D.0个7.根据下列已知条件,能唯一画出△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=68.下列说法正确的是()A.三角形的三个外角的和是180°B.三角形的一个外角大于任何一个内角C.有两边和它们的夹角对应相等的两个三角形全等D.如果两个三角形不全等,那么这两个三角形的面积一定不相等9.下列各组条件中,能判定△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EFC.AB=DE,BC=EF,△ABC的周长=△DEF的周长D.∠A=∠D,∠B=∠E,∠C=∠F二、填空题10.如果△ABC≌△DEF,若AB=DE,∠B=50°,∠C=70°,则∠D=______.11.如图,△ABC≌△CDA,则对应边是______,对应角是______.12.如图,AB与CD交与O,AC=BD,∠C=∠D,又因为∠______=∠______,所以△AOD≌△BOC,理由是______.13.如图所示,已知∠A=90°,BD是∠ABC的平分线,AC=10,DC=6,则D点到BC的距离是______.14.△ABC中,∠BAC:∠ACB:∠ABC=4:3:2,且△ABC≌△DEF,则∠DEF=______度.三、证明题15.如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.16.如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE.17.如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.《第1章三角形》参考答案一、选择题:1.全等形都相同的是()A.形状 B.大小 C.边数和角度D.形状和大小【解答】解:∵全等形能够完全重合,∴全等形的形状与大小完全相同.故选D.2.如图,△ABC≌△DEF,AC∥DF,则∠C的对应角为()A.∠F B.∠AGE C.∠AEF D.∠D【解答】解”∵AC∥DF,∴∠D=∠BAC;∵△ABC≌△DEF,∴△ABC与△DEF的对应角相等;又∠C是△ABC的一个内角,∴∠C的对应角应△DEF的一个内角;A、∠AGE不是△DEF的一个内角,不符合题意;B、∠AEF不是△DEF的一个内角,不符合题意;C、∠D与∠BAC是对应角,不符合题意;故选A.3.如图,AB=AD,BC=CD,点E在AC上,则全等三角形共有()A.1对B.2对C.3对D.4对【解答】解:∵AB=AD,BC=CD,AC=AC,∴△ABC≌△ADC(SSS),∴∠ACB=∠ACD,∴△BCE≌△DCE(SAS),∴BE=DE,∴△ABE≌△ADE(SSS).∴全等三角形共有3对.故选C.4.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于()A.8 B.7 C.6 D.5【解答】解:∵AB∥FC,∴∠ADE=∠F.又∵DE=EF,∠AED=∠CEF,∴△ADE≌△CFE.∴AD=CF=8.∴BD=AB﹣AD=15﹣8=7.故选B.5.在△ABC和△FED中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件()A.AB=ED B.AB=FD C.AC=FD D.∠A=∠F【解答】解:∵∠C=∠D,∠B=∠E,说明:点C与D,B与E,A与F是对应顶点,AC的对应边应是FD,根据三角形全等的判定,当AC=FD时,有△ABC≌△FED.故选C.6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,则①△ABE≌△ACF;②△BOF≌△COE;③点O在∠BAC 的角平分线上,其中正确的结论是()A.3个B.2个C.1个D.0个【解答】解:①∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°,在△ABE和△ACF中,,∴△ABE≌△ACF;②∵△ABE≌△ACF,∴AE=AF,又∵AB=AC,∴AB﹣AF=AC﹣AE,即BF=CE,在△BOF和△COE中,,∴△BOF≌△COE;③连接AO,∵△BOF≌△COE,∴OB=OC,在△ABO和△ACO中,,∴△ABO≌△ACO,∴∠BAO=∠CAO,∴点O在∠BAC的角平分线上.故选A.7.根据下列已知条件,能唯一画出△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6【解答】解:A、因为AB+BC<AC,所以这三边不能构成三角形;B、因为∠A不是已知两边的夹角,无法确定其他角的度数与边的长度;C、已知两角可得到第三个角的度数,已知一边,则可以根据ASA来画一个三角形;D、只有一个角和一个边无法根据此作出一个三角形.故选C.8.下列说法正确的是()A.三角形的三个外角的和是180°B.三角形的一个外角大于任何一个内角C.有两边和它们的夹角对应相等的两个三角形全等D.如果两个三角形不全等,那么这两个三角形的面积一定不相等【解答】解:A、三角形的三个外角的和是360°,错误;B、三角形的一个外角大于任何与它不相邻的一个内角,错误;C、有两边和它们的夹角对应相等的两个三角形全等,正确;D、如果两个三角形不全等,那么这两个三角形的面积不一定不相等,错误;故选C.9.下列各组条件中,能判定△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EFC.AB=DE,BC=EF,△ABC的周长=△DEF的周长D.∠A=∠D,∠B=∠E,∠C=∠F【解答】解:A、满足SSA,不能判定全等;B、AC=EF不是对应边,不能判定全等;C、符合SSS,能判定全等;D、满足AAA,不能判定全等.故选C.二、填空题10.如果△ABC≌△DEF,若AB=DE,∠B=50°,∠C=70°,则∠D= 60°.【解答】解:∵△DEF≌△ABC,∠B=50°,∠C=70°,∴∠D=∠A=180°﹣∠B﹣∠C=60°.故答案为:60°11.如图,△ABC≌△CDA,则对应边是AB=CD,AD=BC,AC=AC ,对应角是∠D=∠B,∠DAC=∠BCA,∠DCA=∠CAB .【解答】解:∵△ABC≌△CDA,∴AB=CD,AD=BC,AC=AC,∠D=∠B,∠DAC=∠BCA,∠DCA=∠CAB,故答案为:AB=CD,AD=BC,AC=AC;∠D=∠B,∠DAC=∠BCA,∠DCA=∠CAB.12.如图,AB与CD交与O,AC=BD,∠C=∠D,又因为∠AOC =∠BOD ,所以△AOD≌△BOC,理由是AAS .【解答】解:AB与CD交与O,AC=BD,∠C=∠D,又因为∠AOC=∠BOD,所以△AOD≌△BOC,理由是AAS,故答案为:AOC;BOD;AAS13.如图所示,已知∠A=90°,BD是∠ABC的平分线,AC=10,DC=6,则D点到BC的距离是 4 .【解答】解:∵已知∠A=90°,BD是∠ABC的平分线,DE⊥BC,∴∠A=∠DEB=90°,∠ABD=∠EBD.∵BD=BD,∴△ABD≌△EBD.(AAS)∴DE=AD.∵AC=10,DC=6,∴AD=4.∴DE=4.即D点到BC的距离是4.故填4.14.△ABC中,∠BAC:∠ACB:∠ABC=4:3:2,且△ABC≌△DEF,则∠DEF= 40 度.【解答】解:设∠BAC为4x,则∠ACB为3x,∠ABC为2x∵∠BAC+∠ACB+∠ABC=180°∴4x+3x+2x=180,解得x=20∴∠ABC=2x=40°∵△ABC≌△DEF∴∠DEF=∠ABC=40°.故填40.三、证明题15.如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.【解答】解:∵D、E是AB、AC的中点,∴AD=AB,AE=AC,∵AB=AC,∴AD=AE.在△ABE与△ACD中,,∴△ABE≌△ACD(SAS).16.如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE.【解答】证明:∵∠EAB=∠DAC,∴∠EAB+∠BAC=∠DAC+∠BAC.∴∠EAC=∠DAB.又∵AC=AB、AE=AD,∴△EAC≌△DAB.∴BD=CE.17.如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.【解答】证明:∵∠EAC=∠DAB,∴∠EAC+∠CAD=∠DAB+∠CAD,即∠EAD=∠CAB,在△EAD和△CAB中,,∴△EAD≌△CAB(SAS),∴∠D=∠B.。
鲁教版五四制七年级数学上册第一章三角形3探索三角形全等的条件第3课时同步测试(解析版)

知能提升作业(七)第3课时(30分钟 50分)一、选择题(每小题4分,共12分)1.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )(A)∠BCA=∠F (B)∠B=∠E(C)BC∥EF (D)∠A=∠EDF2.如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )(A)∠B=60°(B)∠BAC=90°(C)BD=CD (D)∠B=45°3.如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( )(A)AB=AC (B)DB=DC (C)∠ADB=∠ADC (D)∠B=∠C二、填空题(每小题4分,共12分)4.如图所示,点D,E分别在线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,则需要添加的条件是________(只需一个即可,图中不能再添加其他点或线).5.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC,能得出△ABD≌△ACD的序号是________.6.如图,△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPE=______度.三、解答题(共26分)7.(8分)如图,CE=CB,CD=CA,∠DCA=∠ECB,说明:DE=AB.8.(8分)如图,点E,F分别是AD上的两点,AB∥CD,AB=CD,AF=DE.问:线段CE,BF有什么数量关系和位置关系?并说明理由.【拓展延伸】9.(10分)如图,已知△ABC中,延长AC边上的中线BE到G,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连接AF,AG.(1)补全图形.(2)AF与AG的大小关系如何?试说明理由.(3)F,A,G三点的位置关系如何?试说明理由.答案解析1.【解析】选B.已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可由“SAS”得三角形全等.2.【解析】选C.在△ABD和△ACD中,AD=AD,∠ADB=∠ADC =90°,BD=CD,故△ABD≌△ACD(SAS).3.【解析】选B.在△ABD和△ACD中,已知∠1=∠2,且AD=AD即一边一角,此时只需再添加一角或一边(已知角的另一夹边),故A,C,D均可得△ABD≌△ACD.4.【解析】若利用SAS判定时,则需要添加AC=AB;若利用AAS判定时,则需要添加∠B=∠C,若利用ASA判定时,则需要添加∠AEB=∠ADC.答案不惟一.答案:∠AEB=∠ADC(答案不惟一)5.【解析】①BD=DC,AB=AC,AD=AD是公共边,根据SSS可判定两三角形全等,因此①可以;②∠B=∠C,∠BAD=∠CAD,根据AAS可判定两三角形全等,因此②可以;③∠B=∠C,BD=DC,两三角形中相等的对应元素是SSA和ASS.因此③不能判定两三角形全等;④∠ADB=∠ADC,BD=DC,根据SAS可判定两三角形全等.因此④可以.故正确答案为①②④.答案:①②④6.【解析】因为AB=AC,∠A=40°,所以∠DBP=∠ECP=70°,又因为BP=CE,BD=CP,所以△DBP≌△PCE,所以∠BDP=∠CPE.又因为∠DBP=70°,所以∠DPB+∠BDP=110°,所以∠DPE=180°-(∠DPB+∠EPC)=180°-(∠DPB+∠BDP)=70°.答案:707.【解析】因为∠DCA=∠ECB,所以∠DCE=∠ACB.又CD=CA,CE=CB,所以△CDE≌△CAB,所以DE=AB.8.【解析】数量关系是BF=CE;位置关系是BF∥CE.理由:因为AB∥CD,所以∠A=∠D.因为AB=CD,AF=DE,所以△ABF≌△DCE.所以BF=CE,∠BFA=∠CED,所以BF∥CE.【归纳整合】在证明三角形全等的题目中,给出的条件有些不能直接利用.这就需要我们认真审题和读图,善于把隐藏的条件找出来.例如,给出了平行就间接告诉了角的关系,再有如图(1)中,若已知AB=CD ,则隐藏着AC=BD ;图(2)中,若已知∠AOB=∠COD ,则隐藏着∠AOC=∠BOD.9.【解析】(1)如图.(2)AF=AG.理由:因为D 是AB 的中点,所以AD=BD ,在△ADF 和△BDC 中,{AD =BD,∠FDA =∠CDB,FD =CD,所以△ADF ≌△BDC(SAS),所以AF=BC.同理可知AG=BC ,所以AF=AG.(3)点F ,A ,G 在同一条直线上,且所在直线与BC 平行.理由:因为△ADF ≌△BDC ,所以∠FAB=∠CBA ,所以AF ∥BC ,同理可知:AG ∥BC ,所以F ,A ,G 三点共线,且所在直线与BC 平行.初中数学试卷桑水出品。
初中数学鲁教版(五四制)七年级上册第一章 三角形1 认识三角形-章节测试习题(34)

章节测试题1.【答题】若等腰三角形有两条边的长为5和7,则此等腰三角形的周长为()A. 12B. 17C. 19D. 17或19【答案】D【分析】根据三角形的三边关系进行判断.【解答】解:当等腰三角形的腰为5时,三边为5,5,7,5+5=10>7,此等腰三角形的周长5+5+7=17;当等腰三角形的腰为7时,三边为5,7,7,三边关系成立,周长为5+7+7=19.选D.2.【答题】已知三角形的三边长分别是3,8,x,若x的值为偶数,则x的值有()A. 6个B. 5个C. 4个D. 3个【答案】D【分析】根据三角形的三边关系进行判断.【解答】∵8-3<x<8+3,∴5<x<11,∴符合条件的偶数有:6,8,10共3个.选D.3.【答题】若三条线段中a=3,b=5,c为奇数,那么由a、b、c为边组成的三角形共有()A. 1个B. 3个C. 无数多个D. 无法确定【答案】B【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】根据三角形的三边关系,得5−3<c<5+3,2<c<8.又c是奇数,则c=3或5或7.选B.4.【答题】下列各组线段中,能构成三角形的是()A. 2,3,5B. 3,4,5C. 3,4,10D. 2,5,8【答案】B【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】A.2+3=5,故不能构成三角形,选项错误;B.3+4=7>5,故能构成三角形,选项正确;D.2+5=7<8,故不能构成三角形,选项错误;C.3+4=7<10,故不能构成三角形,选项错误.选B.5.【答题】已知三角形两边的长分别是5和9,则此三角形第三边的长可能是()A. 5B. 10C. 15D. 20【答案】B【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】由三角形的三边关系,得9-5<第三边<9+5,则4<第三边<14,因此,只有B选项符合.选B.6.【答题】已知等腰三角形的一边等于3,一边等于6,那么它的周长等于()A. 12B. 12或15C. 15D. 15或18【答案】C【分析】根据三角形的三边关系进行判断.【解答】解:当3为腰,6为底时,∵3+3=6,∴不能构成三角形;当腰为6时,∵3+6>6,∴能构成三角形,∴等腰三角形的周长为:6+6+3=15,选C.7.【答题】在平面内,线段AC=5cm,BC=3cm,线段AB长度不可能的是()A. 2cmB. 8cmC. 5cmD. 9cm【答案】D【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】若点A,B,C三点共线,则AC=2cm或8cm;若三点不共线,则根据三角形的三边关系,应满足大于2cm而小于8cm.则2cm⩽Ac⩽8cm.选D.8.【答题】下列各组长度的线段能构成三角形的是()A. 1,2,4B. 4,5,9C. 4,6,8D. 5,5,11【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】A选项,∵1+2<4,∴A选项中的线段不能构成三角形;B选项,∵4+5=9,∴B选项中的线段不能构成三角形;C选项,∵4+6>8,∴C选项中的线段能构成三角形;D选项,∵5+5<11,∴D选项中的线段不能构成三角形;选C.9.【答题】三角形两边长分别为3和5,若第三边的长为偶数,则这个三角形的周长可能是()A. 10或12B. 10或14C. 12或14D. 14或16【答案】C【分析】根据三角形的三边关系进行判断.【解答】解:设三角形第三边的长为a,∵三角形的两边长分别为3和5,∴5﹣3<a<5+3,即2<a<8,∵a为偶数,∴a=4或a=6,当a=4时,这个三角形的周长=3+4+5=12;当a=6时,这个三角形的周长=3+5+6=14.综上所述,这个三角形的周长可能是12或14.选C.10.【答题】已知三角形两边长分别为7、11,那么第三边的长可以是()A. 2B. 3C. 4D. 5【答案】D【分析】根据三角形的三边关系进行判断.【解答】设第三边长为x,由题意得:11﹣7<x<11+7,解得:4<x<18,选D.11.【答题】以下列各组数据为边长,能构成三角形的是()A. 4,4,8B. 2,4,7C. 4,8,8D. 2,2,7【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】解:∵4+4=8,故以4,4,8为边长,不能构成三角形;∵2+4<7,故以2,4,7为边长,不能构成三角形;∵4,8,8中,任意两边之和大于第三边,故以4,8,8为边长,能构成三角形;∵2+2<7,故以2,2,7为边长,不能构成三角形;选C.12.【答题】有3cm,3cm,6cm,6cm,12cm,12cm的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为()A. 1B. 2C. 3D. 4【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】根据等腰三角形的性质和三边关系可得:3,6,6,和3,12,12,和6,12,12,三组可以构成等腰直角三角形,选C.13.【答题】已知是△ABC的三条边长,化简的结果为()A. B. C. 0 D.【答案】C【分析】根据三角形的三边关系进行判断化简即可.【解答】∵a、b、c为△ABC的三条边长,∴a+b−c>0,c−a−b<0,∴原式=a+b−c+(c−a−b)=a+b−c+c−a−b=0.选C.14.【答题】已知三角形两边长分别为4和6,则该三角形第三边的长可能是()A. 2B. 9C. 10D. 12【答案】B【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】设第三边的长为x,∵三角形两边的长分别是4和6,∴6−4<x<6+4,即2<x<10.选B.15.【答题】下列各组数中,不可能成为一个三角形三边长的是().A. ,,B. ,,C. ,,D. ,,【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】根据三角形任意两边的和大于第三边,可知A.2+3=5>4,能组成三角形;B.5+7>7,能组成三角形;C.5+6=11<12,不能够组成三角形;D.6+8=14>10,能组成三角形.选A.16.【答题】若一个三角形的两边长分别为3和7,且第三边长为整数,则这样的三角形共有()A. 2个B. 3个C. 4个D. 5个【答案】D【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】设第三边为a,根据三角形的三边关系,得:7-3<a<3+7,即4<a<10,∵a为整数,∴a可取5、6、7、8、9,即符合条件的三角形关于5个,选D.17.【答题】一个等腰三角形的一边长为4cm,另一边长为8cm,则该等腰三角形的周长是()A. 16cmB. 20cmC. 16cm或20cmD. 不能确定【答案】B【分析】根据三角形的三边关系进行判断.【解答】解:∵4+4=8,0<4<8+8=16,∴腰长不能为4,只能为8,∴等腰三角形的周长=4+8+8=20cm.选B.18.【答题】以下列各组线段的长为边,能组成三角形的是()A. 2cm,4cm,10cmB. 2cm,2cm,4cmC. 2cm,3cm,4cmD. 1cm,2cm,3cm【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】解:A.∵2+4<10,故2cm,4cm,10cm不能构成三角形;B.∵2+2=4,故2cm,2cm,4cm不能构成三角形;C.∵2+3>4,故2cm,3cm,4cm能构成三角形;D.∵1+2=3,故1cm,2cm,3cm不能构成三角形;选C.19.【答题】下列长度的三条线段首尾连接不能组成三角形的是()A. 2,3,5B. 5,5,5C. 6,6,8D. 7,8,9【答案】A【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】解:A.3+2=5,不能组成三角形;B.5+5>5,能组成三角形;C.6+6>8,能够组成三角形;D.7+8>9,能组成三角形.选A.20.【答题】下列长度的三条线段能组成三角形的是()A. 1,2,3B. 4,5,10C. 8,15,20D. 5,8,15【答案】C【分析】根据三角形的三边关系进行判断,若任意两边之和大于第三边,则能组成三角形.【解答】解:由1,2,3可得,1+2=3,故不能组成三角形;由4,5,10可得,4+5<10,故不能组成三角形;由8,15,20可得,8+15>20,故能组成三角形;由5,8,15可得,5+8<15,故不能组成三角形;选C.。
第一章三角形单元测试卷(含解析)
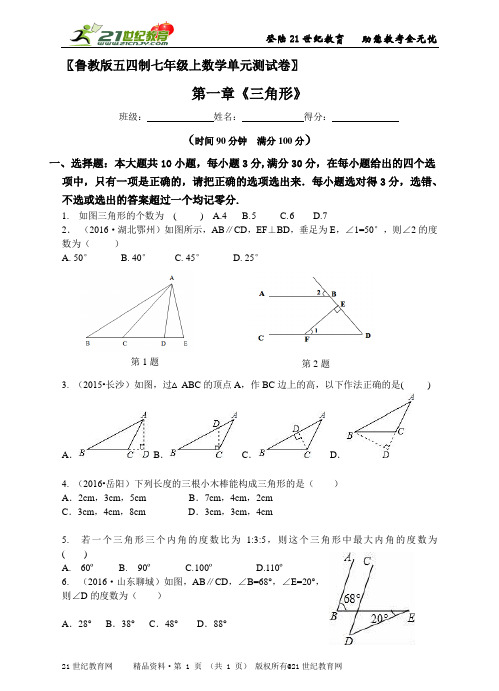
〖鲁教版五四制七年级上数学单元测试卷〗第一章《三角形》班级:姓名:得分:(时间90分钟满分100分)一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.1.如图三角形的个数为() A.4 B. 5 C. 6 D.72.(2016·湖北鄂州)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为()A. 50°B. 40°C. 45°D. 25°第1题第2题3. (2015•长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.4. (2016•岳阳)下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cmC.3cm,4cm,8cm D.3cm,3cm,4cm5.若一个三角形三个内角的度数比为1:3:5,则这个三角形中最大内角的度数为()A. 60ºB. 90ºC. 100ºD.110º6.(2016·山东聊城)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为()A.28°B.38°C.48°D.88°7. 根据下列条件,不能唯一画出△ABC 的是( )A. AB=12,BC=7,CA=8B. AB=20,BC=30,∠A=50ºC. AB=9, ∠A=60º ,AC=15D. ∠A=50º,∠B=40º,AB=238. (2015•绵阳)如图,在△ABC 中,∠B 、∠C 的平分线BE ,CD 相交于点F ,∠ABC=42°,∠A=60°,则∠BFC=( )A . 118°B . 119°C . 120°D . 121°9. 如图,A 点和B 点之间有一池塘,已知OB=OC ,AC=BD ,若能米尺测出CD=10米,就能知道AB 的距离,它根据( ) A. SAS B. SSS C. ASA D. AAS10. (2015•宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD 是一个筝形,其中AD=CD ,AB=CB ,詹姆斯在探究筝形的性质时,得到如下结论: ①AC ⊥BD ;②AO=CO=21AC ;③△ABD ≌△CBD ,其中正确的结论有( )A . 0个B . 1个C . 2个D . 3个二、填空题(本大题共4小题,每小题4分,满分16分)11. (2015•江苏盐城)如图,在△ABC 与△ADC 中,已知AD=AB ,在不添加任何辅助线的前提下,要使△ABC ≌△ADC ,只需再添加的一个条件可以是 .12. 小明家的椅子坏了, 小明在学校学习了鲁教版五四制七上数学第一章《三角形》的知识后,正在家里帮爸爸妈妈修理椅子,请你告诉大家聪明的小明应用的数学原理: 。
初中数学鲁教版(五四制)七年级上册第一章 三角形1 认识三角形-章节测试习题(52)

章节测试题1.【题文】如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,求∠DCN 的度数.【答案】30°【分析】本题考查了平行线的性质,角平分线定义的应用,解本题的关键是求出∠ECA的度数.【解答】解:∵AB//CD,∴∠B=∠BCE=180°,∠BCD=∠B,∵∠B=60°,∴∠BCE=120°,∠BCD=60°,∵CM平分∠BCE,∴∠ECM=∠BCE=60°,∵∠MCN=90°,∴∠DCN=180°-60°-90°=30°.2.【题文】如图AB//CD,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD 于点F.(1)求证:∠1+∠2=90°;(2)如果∠EDF=30°,那么∠BFC等于多少度?【答案】(1)见解答;(2)120°.【分析】本题考查了角平分线的性质以及平行线的性质.解题的关键是掌握角平分线定义和平行线性质的灵活运用.【解答】(1)证明:∵AB∥CD,∴∠ABD+∠BDC=180°,∵BE、DE分别平分∠ABD、∠BDC,∴∠1=∠ABD,∠2=∠BDC,∴∠1+∠2=(∠ABD+∠BDC)=90°,(2)解:∵DE平分∠BDC,BF平分∠ABD,∴∠2=∠EDF=30°,∠1=∠FBD,又∵∠1+∠2=90°,∴∠1=60°,∵AB∥CD,∴∠BFC=180°-∠1=180°-60°=120°.3.【题文】如图,已知△ABC中,点D、E分别在边AB、AC上,点F在CD上.(1)若∠AED=∠ACB,∠DEF=∠B,求证:EF//AB;(2)若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,试求△ABC的面积.【答案】(1)见解答;(2)16【分析】本题考查了平行线判定和性质、三角形中线.【解答】(1)证明:∵∠AED=∠ACB,∴DE∥BC.∴∠ADE=∠B.又∵∠DEF=∠B,∴∠ADE=∠DEF,∴EF∥AB.(2)解:∵点F是DC的中点,∴设S△DEF=S△CEF=x,∵点E是AC的中点,∴S△ADE=S△CDE=2x,∵点D是AB的中点,∴S△BDC=4x,S△BDF=2x,∴S四边形BDEF=3x.∵S四边形BDEF=6,∴3x=6,∴x=2,∴S△ABC=8x=16.4.【题文】如图,AD为△ABC的中线,BE为△ABD的中线.△ABC 的面积为40,BD=5,则E到边BC的距离为多少.【答案】4【分析】本题考查三角形的中线.【解答】解:过E作边BC的垂线,F为垂足,则EF为所求的E到边BC的距离,∵AD是△ABC的中线,∴S△ABD=S△ACD=S△ABC∵BE.是△ABD的中线,∴S△ABE=S△BDE=S△ABD∴S△BDE=S△ABC==10,∴,即,,到边的距离为.5.【答题】三角形的三条高所在的直线相交于一点,此点在()A. 三角形的内部B. 三角形的外部C. 三角形的边上D. 不能确定【答案】D【分析】本题考查了三角形的高.【解答】锐角三角形三条高所在直线的交点在三角形内部,直角三角形三条高所在直线的交点在直角顶点,钝角三角形三条高所在直线的交点在三角形外部,选D.6.【答题】三角形一边上的中线把原三角形一定分成两个()A. 形状相同的三角形B. 面积相等的三角形C. 周长相等的三角形D. 直角三角形【答案】B【分析】本题考查了三角形的中线.【解答】三角形一边上的中线把原三角形分成两个面积相等的三角形.选B. 7.【答题】如图,AE是△ABC的中线,已知EC=4,DE=2,则BD的长为()A. 2B. 3C. 4D. 6【答案】A【分析】本题考查了三角形的中线.【解答】∵AE是△ABC的中线,EC=4,∴BE=EC=4,∵DE=2,∴BD=BE-DE=4-2=2.选A.8.【答题】下列说法不正确的是()A. △ABC的中线AD平分边BCB. △ABC的角平分线BE平分∠ABCC. △ABC的高CF垂直ABD. 直角△ABC只有一条高【答案】D【分析】本题考查了三角形的高、中线与角平分线.【解答】A、∵AD是△ABC的中线,∴D是BC的中点,即AD平分边BC,故此选项正确;B、∵BE是△ABC的角平分线,∴BE平分∠ABC,故此选项正确;C、∵CF是△ABC的高,∴CF⊥AB,故此选项正确;D、直角△ABC有三条高,其中两条是直角边,一条在三角形内部,故此选项错误.选D.9.【答题】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有()①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高.A. 1个B. 2个C. 3个D. 4个【答案】B【分析】本题考查了三角形的高、中线与角平分线.【解答】①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.选B.10.【答题】如图,∠1=∠2,∠3=∠4,则下列结论正确的有()①AD平分∠BAE;②AF平分∠EAC;③AE平分∠DAF;④AF平分∠BAC;⑤AE 平分∠BAC.A. 4个B. 3个C. 2个D. 1个【答案】C【分析】本题考查了三角形的角平分线.【解答】AD不一定平分∠BAE,①错误;AF不一定平分∠EAC,②错误;∵∠1=∠2,∴AE平分∠DAF,③正确;∵∠1=∠2,∠3=∠4,∴∠1+∠3=∠2+∠4,即∠BAE=∠CAE,∴AE平分∠BAC,⑤正确,选C.11.【答题】如图,△ABC中BC边上的高线是______,△BCE中BC边上的高线是______,以CF为高线的三角形有______.【答案】AD;BE;△ABC,△BCF,△AFC【分析】本题考查了三角形的高.【解答】如图,△ABC中BC边上的高是AD;△BCE中BC边上的高是BE;△ACD中CD边上的高是AD;以CF为高线的三角形有△ABC,△BCF,△AFC.故答案为:AD,BE,△ABC,△BCF,△AFC.12.【答题】如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC=______.【答案】40°【分析】本题考查了三角形的角平分线.【解答】∵BD是∠ABC的角平分线,∠ABC=80°,∴∠DBC=∠ABD=∠ABC=×80°=40°.故答案为:40°.13.【答题】AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,△ABD与△ACD的周长之差为______.【答案】2cm【分析】本题考查了三角形的中线.【解答】∵AD是△ABC中BC边上的中线,∴BD=DC=BC,∴△ABD和△ADC的周长的差=(AB+BC+AD)-(AC+BC+AD)=AB-AC=5-3=2(cm).故答案为:2cm.14.【题文】如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.【答案】AD不是△ABC的角平分线【分析】本题考查了三角形的角平分线.【解答】根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD 满足①,但点D不在BC边上,故不满足②.∴,AD不是△ABC的角平分线.15.【题文】如图,△ABC的边BC上的高为AF,AC边上的高为BG,中线为AD.已知AF=6,BC=10,BG=5.(1)求△ABC的面积;(2)求AC的长;(3)试说明△ABD和△ACD的面积相等.【答案】(1)30(2)12(3)见解答.【分析】本题考查了三角形的高、中线.【解答】(1)∵△ABC的边BC上的高为AF,AF=6,BC=10,∴△ABC的面积为BC·AF=×10×6=30.(2)∵AC边上的高为BG,BG=5,∴△ABC的面积为AC·BG=30,即AC×5=30,∴AC=12.(3)∵△ABC的中线为AD,∴BD=CD.∵△ABD以BD为底,△ACD以CD为底,而且等高,∴S△ABD=S△ACD.16.【题文】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度.(1)在图中画出平移后的△A′B′C′;(2)若连接AA′、CC′,则这两条线段的关系是______;(3)利用格点作直线MN,将△ABC分成面积相等的三角形.【答案】见解答.【分析】(1)首先确定A、B、C三点平移后的位置,再顺次连接即可;(2)根据平移的性质:对应点连线平行且相等可得AA′=CC′,AA′∥CC′;(3)根据三角形的中线平分三角形的面积可得MN就是△ABC中线所在直线,因此根据网格图可得AC的中点位置,再画直线即可.【解答】解:(1)如图所示,△A′B′C′即为所求;(2)连接AA′,CC′,根据平移的性质可得AA′=CC′,AA′∥CC′,故答案为:平行且相等;(3)如图所示,直线MN即为所求.①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.17.【题文】在等腰三角形ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为18和15两部分,求这个等腰三角形的底边长.【答案】12或10.【分析】不确定是哪一部分的长是18或15,则需要分类讨论,分18是腰长与腰长一半和15是腰长与腰长一半两种情况.【解答】解:根据题意,①当18是腰长与腰长一半时,AC+AC=18,解得AC=12,∴底边长=15﹣×12=9;②当15是腰长与腰长一半时,AC+AC=15,解得AC=10,∴底边长=18﹣×10=13.∴底边长等于12或10.18.【题文】如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.【答案】∠BAD=40°,∠AOC=115°.【分析】先根据直角三角形的两个锐角互余,求得再根据角平分线的定义,求得最后根据三角形内角和定理,求得中的度数.【解答】∵AD是高,中,∴△ABC中,∵AE,CF是角平分线,∴△AOC中,19.【题文】如图,已知∠ABC=∠ADC,BF,DE是∠ABC,∠ADC的角平分线,∠1=∠2,试说明:DC∥AB.【答案】证明见解答.【分析】先利用角平分线定义得到∠3=∠ADC,∠2=∠ABC,而∠ABC=∠ADC,则∠3=∠2,加上∠1=∠2,则∠1=∠3,于是可根据平行线的判定得到DC∥AB.【解答】证明:∵DE、BF分别是∠ABC,∠ADC的角平分线,∴∠3=∠ADC,∠2=∠ABC,∵∠ABC=∠ADC,∴∠3=∠2,∵∠1=∠2,∴∠1=∠3,∴DC∥AB.20.【题文】若等腰三角形一腰上的中线分周长为12cm和15cm两部分,求这个等腰三角形的底边和腰的长.【答案】三角形三边的长分别为8,8,11或10,10,7.【分析】设腰长为x,底边长为y,根据等腰三角形一腰上的中线将这个等腰三角形的周长分为6cm或9cm两部分,列方程解得即可.【解答】解:在三角形ABC中,AB=AC,BD是中线,设AB=x,BC=y.(1)当AB+AD=12时,则,解得,∴三角形三边的长为8,8,11;(2)当AB+AD=15时,则,解得,∴三角形三边的长为10,10,7;经检验,两种情况均符合三角形的三边关系.三角形三边的长分别为8,8,11或10,10,7.。
鲁教版五四制七年级数学上册第一章三角形3探索三角形全等的条件第1课时同步测试(解析版)

知能提升作业(五)3 探索三角形全等的条件第1课时(30分钟 50分)一、选择题(每小题4分,共12分)1.下列说法中,正确的是( )(A)三个角对应相等的两个三角形全等(B)周长和一边对应相等的两个三角形全等(C)三条边对应相等的两个三角形全等(D)面积和一边对应相等的两个三角形全等2.如图所示,AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中的全等三角形有( )(A)4对(B)3对(C)2对(D)1对3.如果△ABC的三边长分别为5,12,13,△DEF的三边长分别为5,3m-n,2m+n,且这两个三角形全等,则mn的值为( )(A)15 (B)10(C)10或15 (D)有无数个二、填空题(每小题4分,共12分)4.如图,已知AB=AD,那么添加下列一个条件后,能利用“SSS”判定△ABC≌△ADC的是______.5.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是________.6.如图所示的方格中,∠1+∠2+∠3=________度.三、解答题(共26分)7.(8分)已知:如图,AB=AC,AD=AE,BD=CE.试说明∠BAC=∠DAE.8.(8分)如图,已知AB=DC,DB=AC.(1)试说明∠ABD=∠DCA.注:说理过程要求给出每一步结论成立的依据.(2)在(1)的说明过程中,需要作辅助线,它的意图是什么?【拓展延伸】9.(10分)有一块三角形的厚铁板如图,根据实际生产需要,工人师傅要把∠MAN平分,现在他手中只有一把尺子和一根细绳,你能帮他想个办法吗?并说明你的设计理由.答案解析1.【解析】选C.A 项,三个角相等不能判定两个三角形全等,故错误;B 项,不能用周长和一边对应相等来判断三角形全等,故错误;C 项,三角形可利用SSS 证明两个三角形全等,故正确;D 项,不能用面积和一边对应相等来判断三角形全等,故错误.故选C.2.【解析】选B.由DA=BC ,CD=AB ,AC=CA 得△ADC ≌△CBA ;由DA=BC ,AE=CF ,DE=BF ,得△ADE ≌△CBF ;因为AE=CF ,所以AF=CE ,又由于BF=DE ,AB=CD ,所以△ABF ≌△CDE.3.【解析】选C.由题意知,m ,n 应满足:{3m −n =12,2m +n =13或{3m −n =13,2m +n =12, 分别解得{m =5n =3或{m =5n =2, 所以mn=15或10.4.【解析】因为AB=AD(已知),AC=AC(公共边),要利用“SSS ”判定△ABC ≌△ADC ,可添加条件CB=CD.答案:CB=CD5.【解析】在△ABC和△ADC中,AB=AD,CB=CD,AC=AC,所以△ABC≌△ADC,所以∠D=∠B=30°,∠BAC=∠DAC=23°,所以∠ACD=180°-∠D-∠DAC=180°- 30°-23°=127°.答案:127°6.【解析】如图,根据网格结构可知,在△ABC与△EDA中,{AB=ED,BC=DA,AC=EA,所以△ABC≌△EDA(SSS),所以∠1=∠DAE,所以∠1+∠3=∠DAE+∠3=90°.又因为AD=DF,AD⊥DF,所以△ADF是等腰直角三角形,所以∠2=45°,所以∠1+∠2+∠3=90°+45°=135°.答案:1357.【解析】在△ABD和△ACE中,因为AB=AC,AD=AE,BD=CE,所以△ABD≌△ACE(SSS),所以∠BAD=∠CAE,所以∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.8.【解析】(1)连接AD,因为{AB=DC(已知), DB=AC(已知), AD=AD(公共边),所以△ABD≌△DCA(SSS),所以∠ABD=∠DCA(全等三角形的对应角相等).(2)作辅助线的意图:构造全等三角形.9.【解析】能,如图所示,用绳子的一定长度在AM和AN上截取AB=AC,再选取适当长度(不小于BC)的绳子,将其对折,得绳子的中点D点,把绳子确定的端点固定在B,C两点,拽住绳子的中点D,向外拉直BD和CD,确定出D点在板材上的位置,过A,D两点画射线AD,则AD 平分∠MAN.理由如下:在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,所以△ABD≌△ACD(SSS),所以∠MAD=∠NAD.初中数学试卷。
鲁教版(五四制)数学七年级上册第一章《三角形》1.2图形的全等同步练习(含答案)

初中数学鲁教版七年级上册第一章《三角形》1.2图形的全等同步练习学校:___________姓名:___________班级:___________得分:___________一、选择题(本大题共10小题,共30分)1.在下列每组图形中,是全等形的是()。
A. B. C. D.2.下列说法:①能够重合的两个图形一定是全等图形;②两个全等图形的面积一定相等;③两个面积相等的图形一定是全等图形;④两个周长相等的图形一定是全等图形。
这些说法中正确的是()。
A.①②B.②③④C.①②④D.①②③④3.如图,将边长分别为10cm和4cm的矩形纸片沿着虚线剪成两个全等的梯形纸片.裁剪线与矩形较长边所夹的锐角是45°,则梯形纸片中较短的底边长为()。
A.2cmB.2.5cmC.3cmD.3.5cm4.下列说法不正确的是()。
A.如果两个图形全等,那么它们的形状和大小一定相同B.面积相等的两个图形是全等图形C.图形全等,只与形状、大小有关,而与它们的位置无关D.全等三角形的对应边相等,对应角相等5.下列说法正确的是()。
①用一张像纸冲洗出来的10张1寸像片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等,⑤周长相等的两个三角形全等.A.1个B.2个C.3个D.4个6.如图,已知方格纸中是4个相同的小正方形,则∠1+∠2的度数为()。
A.30°B.45°C.60°D.90°7.下图所示的图形分割成两个全等的图形,正确的是()。
A. B. C. D.(示例图形)8.如图,△ABC与△CDA是全等三角形,则一定是一组对应边的是()。
A.AB和DCB.AC和CAC.AD和CBD.AD和DC9.如果两个图形全等,那么这两个图形必定是()。
A.形状大小均相同B.形状相同,但大小不同C.大小相同,但形状不同D.形状大小均不相同10.有一张三角形纸片ABC,已知∠B=∠C=α,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知能提升作业(三)
第3课时
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.不一定在三角形内部的线段是( )
(A)三角形的角平分线
(B)三角形的中线
(C)三角形的高
(D)以上三种线段均有可能在三角形外部
2.如图,AD是△ABC的中线,已知△ABD的周长比△ACD的周
长大6cm,则AB与AC的差为( )
(A)2 cm (B)3 cm
(C)6 cm (D)12 cm
3.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD= 30°,则∠C的度数是( )
(A)70°(B)80°(C)100°(D)110°
二、填空题(每小题4分,共12分)
4.如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=
80°,则∠DBC=________°.
5.如图,已知在三角形ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,则∠DBC 的度数是________.
6.如图,AD是△ABC的中线,△ABC的面积为100cm2,则△ABD的面积是________.
三、解答题(共26分)
7.(8分)在△ABC中,AB=AC,AC上的中线BD把△ABC的周长分为24和18两部分,求三角形三边的长.
8.(8分)如图,已知△ABC的高AD,角平分线AE,∠B=26°,∠ACD=56°,求∠AED的度数.
【拓展延伸】
9.(10分)已知:如图,BD ,CD 分别为∠EBC 和∠FCB 的平分
线.
(1)若∠A=80°,求∠D 的度数.
(2)试探究∠D 和∠A 的关系.
答案解析
1.【解析】选C.①锐角三角形的三条高都在三角形的内部,垂足在相应顶点的对边上;②直角三角形直角边上的高与另一直角边重合,还有一条高在三角形内部,垂足在直角的顶点或斜边上;③钝角三角形中,夹钝角两边上的高在三角形的外部,另一条高在三角形的内部,垂足在相应顶点对边的延长线上或在钝角的对边上.三角形的中线和角平分线一定在三角形内部.
2.【解析】选C.因为AD 是△ABC 的中线,所以BD=DC ,所以△ABD 的周长比△ACD 的周长大6cm ,即AB 与AC 的差为6cm.
3.【解析】选B.AD 平分∠BAC ,∠BAD=30°,
所以∠BAC=60°,
所以∠C=180°-60°-40°=80°.
4.【解析】因为BD 是∠ABC 的角平分线,∠ABC=80°,
所以∠DBC=∠ABD=12∠ABC=12
×80°=40°. 答案:40
5.【解析】因为∠C=∠ABC=2∠A ,
则∠C+∠ABC+∠A=5∠A=180°,
所以∠A=36°,
则∠C=∠ABC=2∠A=72°.
又BD 是AC 边上的高,则∠DBC=90°-∠C=18°.
答案:18°
6.【解析】如图所示,过点A 作AE ⊥BC 于E ,则S △ABC =12BC ·AE , S △ABD =12·BD ·AE.
因为AD 是△ABC 的中线,
所以BD=12BC ,S △ABD =12S △ABC =50cm 2
.
答案:50cm 2
7.【解析】如图,设AB=AC=a ,
BC=b ,
则有a+1
2a=24且12a+b=18,
或a+1
2a=18且12a+b=24,
得到a=16,b=10或a=12,b=18,
这时三角形的三边长分别为16,16,10或12,12
,18. 它们都能构成三角形.
8.【解析】因为∠ACD=56°,
所以∠ACB=124°.
又∠B=26°,
所以∠BAC=30°.
又因为AE 平分∠BAC ,
所以∠BAE=15°,
所以∠AEB=180°-∠B-∠BAE=139°,
则∠AED=41°.
9.【解析】(1)因为∠A=80°,
所以∠ABC+∠ACB=100°.
又因为∠ABC+∠EBC=180°,
∠ACB+∠FCB=180°,
所以∠ABC+∠EBC+∠ACB+∠FCB=360°, 故∠EBC+∠FCB=260°.
又BD ,CD 分别是∠EBC 和∠FCB 的平分线,
所以∠DBC=12∠EBC ,∠DCB=12
∠FCB , 所以∠DBC+∠DCB=12
(∠EBC+∠FCB)=130°, 所以∠D=180°-130°=50°.
(2)∠D=90°-12
∠A. 理由如下:
∠D=180°-(∠DBC+∠DCB)
=180°-12
(∠EBC+∠FCB) =180°-12
(180°-∠ABC+180°-∠ACB) =180°-12
(360°-∠ABC-∠ACB) =180°-180°+12∠ABC+12
∠ACB =12(∠ABC+∠ACB)=12
(180°-∠A) =90°-12
∠A. 初中数学试卷
桑水出品。
