2020年中考数学二轮专项冲刺——二次函数(真题汇编)学生版
2020年中考数学试题分类汇编之13二次函数(试题+详细答案)

2020年中考数学试题分类汇编之13二次函数一、选择题1.(2020安徽)(4分)如图,ABC ∆和DEF ∆都是边长为2的等边三角形,它们的边BC ,EF 在同一条直线l 上,点C ,E 重合.现将ABC ∆在直线l 向右移动,直至点B 与F 重合时停止移动.在此过程中,设点C 移动的距离为x ,两个三角形重叠部分的面积为y ,则y 随x 变化的函数图象大致为( )A .B .C .D .2.(2020福建)已知()111,P x y ,()222,P x y 是抛物线22y ax ax =-上的点,下列命题正确的是( )A. 若12|1||1|->-x x ,则12y y >B. 若12|1||1|->-x x ,则12y y <C. 若12|1||1|-=-x x ,则12y y =D. 若12y y =,则12x x =3.(2020陕西)在平面直角坐标系中,将抛物线y =x 2﹣(m ﹣1)x +m (m >1)沿y 轴向下平移3个单位.则平移后得到的抛物线的顶点一定在( ) A .第一象限B .第二象限C .第三象限D .第四象限4.(2020哈尔滨)(3分)将抛物线2y x =向上平移3个单位长度,再向右平移5个单位长度,所得到的拋物线为( ) A .2(3)5y x =++ B .2(3)5y x =-+ C .2(5)3y x =++ D .2(5)3y x =-+5.(2020杭州)(3分)设函数y =a (x ﹣h )2+k (a ,h ,k 是实数,a ≠0),当x =1时,y =1;当x =8时,y =8,( ) A .若h =4,则a <0 B .若h =5,则a >0C .若h =6,则a <0D .若h =7,则a >06.(2020杭州)(3分)在平面直角坐标系中,已知函数y 1=x 2+ax +1,y 2=x 2+bx +2,y 3=x 2+cx +4,其中a ,b ,c 是正实数,且满足b 2=ac .设函数y 1,y 2,y 3的图象与x 轴的交点个数分别为M 1,M 2,M 3,( ) A .若M 1=2,M 2=2,则M 3=0 B .若M 1=1,M 2=0,则M 3=0 C .若M 1=0,M 2=2,则M 3=0D .若M 1=0,M 2=0,则M 3=07.(2020天津)已知抛物线2y ax bx c =++(a ,b ,c 是常数0a ≠,1c >)经过点()2,0,其对称轴是直线12x =.有下列结论: ①0abc >①关于x 的方程2ax bx c a ++=有两个不等的实数根; ①12a <-. 其中,正确结论的个数是( ) A .0B .1C .2D .38.(2020河北)如图,现要在抛物线(4)y x x =-上找点(,)P a b ,针对b 的不同取值,所找点P 的个数,三人的说法如下, 甲:若5b =,则点P 的个数为0; 乙:若4b =,则点P 的个数为1; 丙:若3b =,则点P 的个数为1. 下列判断正确的是( )A. 乙错,丙对B. 甲和乙都错C. 乙对,丙错D. 甲错,丙对9.(2020江西)在平面直角坐标系中,点O 为坐标原点,抛物线223y x x =--与y 轴交于点A ,与x 轴正半轴交于点B ,连接AB ,将Rt OAB ∆向右上方平移,得到'''Rt O A B ∆,且点'O ,'A 落在抛物线的对称轴上,点'B 落在抛物线上,则直线''A B 的表达式为( ) A .y x = B .1y x =+ C .12y x =+D .2y x =+ 10.(2020四川绵阳)三孔桥横截面的三个孔都是呈抛物线形,两小孔形状、大小完全相同。
2020年初三数学中考压轴题综合训练:《二次函数》含答案

2020年初三数学中考压轴题综合训练:《二次函数》1.已知抛物线的顶点A(﹣1,4),且经过点B(﹣2,3),与x轴分别交于C,D两点.(1)求直线OB和该抛物线的解析式;(2)如图1,点M是抛物线上的一个动点,且在直线OB的上方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;(3)如图2,AE∥x轴交x轴于点E,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G,当点P运动时,求tan∠PCD+tan∠PDC的值.解:(1)设直线OB的解析式为y=kx,∵B(﹣2,3),∴﹣2k=3,∴k=﹣,∴直线OB的解析式为y=﹣x,∵抛物线的顶点为A(﹣1,4),∴设抛物线对应的函数表达式为y=a(x+1)2+4.将B(﹣2,3)代入y=a(x+1)2+4,得:3=a+4,解得:a=﹣1,∴抛物线对应的函数表达式为y=﹣(x+1)2+4,即y=﹣x2﹣2x+3.(2)设M(t,﹣t2﹣2t+3),MN=s,则N的横坐标为t﹣s,纵坐标为﹣(t﹣s),∵,∴x1=﹣2,x2=,∵点M是直线OB的上方抛物线上的点,∴﹣2<t<,∵MN∥x轴,∴﹣t2﹣2t+3=﹣(t﹣s),∴s=﹣t+2=﹣,∵﹣2<t<,∴当t=﹣时,MN的最大值为;(3)解:过点P作PQ∥y轴交x轴于Q,设P(t,﹣t2﹣2t+3),则PQ=﹣t2﹣2t+3,CQ=t+3,DQ=1﹣t,∴tan∠PCD+tan∠PDC=,=,=,=1﹣t+t+3,=4.2.如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点B,与y轴交点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴交于另一点A.如图1,点P为抛物线上任意一点.过点P作PM⊥x轴交BC于M.(1)求抛物线的解析式;(2)当△PCM是直角三角形时,求P点坐标;(3)如图2,作P点关于直线BC的对称点P′,作直线P′M与抛物线交于EF,设抛物线对称轴与x轴交点为Q,当直线P′M经过点Q时,请你直接写出EF的长.解:(1)∵直线y=﹣x+2与x轴交于点B,与y轴交点C,∴B(4,0),C(0,2),∴把B(4,0),C(0,2)代入y=﹣x2+bx+c得,,解得,,∴抛物线的解析式为:y=﹣+2;(2)∵PM⊥x轴交BC于M.BC不平行x轴,∴∠PMC≠90°,当∠CPM=90°时,PC∥x轴,则P点的纵坐标为2,∵y=﹣+2的对称轴为x=1,∴P点的横坐标为:2,此时P(2,2);当∠PCM=90°时,设P(m,),则M(m,﹣m+2),由PC2+CM2=PM2得,=,解得,m=0(与C的横坐标相同,舍去),或m=﹣6,此时P(﹣6,﹣10);综上,P点的坐标为(2,2)或(﹣6,﹣10);(3)作Q点关于直线BC的对称点K,QK与BC相交于点N,再过K作KL⊥x轴于点L,如图所示,则根据题意可知,KL与BC的交点为M,P点在KM上,P'在QM上,∵y=﹣+2,∴抛物线的对称轴为x=1,∴Q(1,0),∴BQ=4﹣1=3,∵∠QBN=∠CBO,∠QNB=∠COB=90°,∴△BQN∽△BCO,∴,即,∴QN=,∴QK=2QN=,∠BQN=∠KQL,∠BNQ=∠KLQ=90°,∴△BQN∽△KQL,∴,即,∴QL=,∴OL=1+,∴M(,),设QM的解析式为:y=kx+b(k≠0),则,∴,∴直线QM的解析式为:y=,联立方程组,解得,,或,∴E(,),F(,),∴EF=.3.如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),且直线BC的解析式为y=x﹣2,作垂直于x轴的直线x=m,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).(1)求抛物线的解析式;(2)若△CEF是以CE为腰的等腰三角形,求m的值;(3)点P为y轴左侧抛物线上的一点,过点P作PM⊥BC交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.解:(1)∵直线BC的解析式为y=x﹣2,∴C(0,﹣2),B(4,0),将A(﹣1,0),B(4,0)代入y=ax2+bx﹣2,得,解得,,∴y=x﹣2;(2)∵∴,=,,若以C为顶点,则CE2=CF2,∴,解得:m1=2,m2=4(舍去),若以E为顶点,则EC2=EF2,∴=,解得:m3=4﹣,m4=4+(舍去),综合以上得m=2或m=4﹣.(3)①∵AC=,BC=2,∴AC2+BC2=25=AB2,∴当点P与点A重合时,点M与点C重合,此时P1(﹣1,0),②如图,当△BPM∽△ABC时,过点M作HR∥x轴,作PH⊥HR于点H,BR⊥HR于点R,∵∠PMB=∠PHM=∠BRM=90°,∴∠BMR=∠MPH,∴△PHM∽△MRB,∴又∵AB∥HR,∴∠ABC=∠BMR,∴tan∠BMR=tan∠ABC=,令BR=a,MR=2a,又∵∠ABC=∠BMR,∴tan∠BMR=tan∠ABC=,∴,∴PH=4a,HM=2a,PQ=3a,∴HR=4a,∴P(4﹣4a,3a),又∵点P在抛物线上,将P(4﹣4a,3a)代入y=x﹣2得:(4﹣4a)﹣2=3a,∴a(8a﹣13)=0,a 1=0(舍),a2=.∴.∴符合条件的点P为P1(﹣1,0)或.4.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.(1)求b,c的值:(2)如图1,点P是第一象限抛物线上一动点,过点P作x轴的垂线1,交BC于点H.当△PHC为等腰三角形时,求点P的坐标;(3)如图2,抛物线顶点为E.已知直线y=kx﹣k+3与二次函数图象相交于M、N两点,求证:无论k为何值,△EMN恒为直角三角形.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),∴,解得:,∴b=2,c=3;(2)∵抛物线的函数表达式为:y=﹣x2+2x+3,∴C(0,3),设直线BC的解析式为y=kx+3,将点B(3,0)代入y=kx+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3,设点P(x,﹣x2+2x+3),则点H(x,﹣x+3),①如图1,过点C作CM⊥PH于点M,则CM=x,PH=﹣x2+3x,当CP=CH时,PM=MH,∠MCH=∠MCP,∵OB=OC,∴∠OBC=45°,∵CM∥OB,∴∠MCH=∠OBC=45°,∴∠PCH=90°,∴MC=PH=(﹣x2+3x),即x=(﹣x2+3x),解得:x1=0(舍去),x2=1,∴P(1,4);②如图2,当PC=PH时,∵PH∥OC,∴∠PHC=∠OCB=45°,∴∠CPH=90°,∴点P的纵坐标为3,∴﹣x2+2x+3=3,解得:x=2或x=0(舍去),∴P(2,3);③当CH=PH时,如图3,∵B(3,0),C(0,3),∴BC==3.∵HF∥OC,∴,∴,解得:x=3﹣,∴P(3﹣,4﹣2).综合以上可得,点P的坐标为(1,4)或(2,3)或(3﹣,4﹣2).(3)∵函数表达式为:y =﹣x 2+2x +3=﹣(x ﹣1)2+4, ∴点E (1,4);设点M 、N 的坐标为(x 1,y 1),(x 2,y 2),∴MN 2=(x 1﹣x 2)2+(y 1﹣y 2)2,ME 2=(x 1﹣1)2+(y 1﹣4)2,NE 2=(x 2﹣1)2+(y 2﹣4)2,∵ME 2+NE 2=(x 1﹣1)2+(y 1﹣4)2+(x 2﹣1)2+(y 2﹣4)2=x 12+x 22﹣2(x 1+x 2)+2+y 12+y 22﹣8(y 1+y 2)+32=x 12+x 22﹣2x 1x 2+2﹣4+y 12+y 22﹣2y 1•y 2+18﹣48+32 ═(x 1﹣x 2)2+(y 1﹣y 2)2, ∴MN 2=ME 2+NE 2, ∴∠MEN =90°, 故EM ⊥EN ,即:△EMN 恒为直角三角形.5.如图1所示,已知直线y =kx +m 与抛物线y =ax 2+bx +c 分别交于x 轴和y 轴上同一点,交点分别是点B (6,0)和点C (0,6),且抛物线的对称轴为直线x =4; (1)试确定抛物线的解析式;(2)在抛物线的对称轴上是否存在点P ,使△PBC 是直角三角形?若存在请直接写出P 点坐标,不存在请说明理由;(3)如图2,点Q 是线段BC 上一点,且CQ =,点M 是y 轴上一个动点,求△AQM的最小周长.解:(1)∵抛物线y=ax2+bx+c与x轴交于点A、B两点,对称轴为直线x=4,∴点A的坐标为(2,0).∵抛物线y=ax2+bx+c过点A(2,0),B(6,0),C(0,6),∴,解得a=,b=﹣4,c=6.∴抛物线的解析式为:y=;(2)设P(4,y),∵B(6,0),C(0,6),∴BC2=62+62=72,PB2=22+y2,PC2=42+(y﹣6)2,当∠PBC=90°时,BC2+PB2=PC2,∴72+22+y2=42+(y﹣6)2,解得:y=﹣2,∴P(4,﹣2);当∠PCB=90°时,PC2+BC2=PB2,∴42+(y﹣6)2+72=22+y2,解得:y=10,∴P(4,10);当∠BPC=90°时,PC2+PB2=BC2.∴42+(y﹣6)2+22+y2=72,解得:y=3.∴P(4,3+)或P(4,3﹣).综合以上可得点P的坐标为(4,﹣2)或(4,10)或(4,3+)或P(4,3﹣).(3)过点Q作QH⊥y轴于点H,∵B(6,0),C(0,6),∴OB=6,OC=6,∴∠OCB=45°,∴∠CQH=∠HCQ=45°,∵CQ=,∴CH=QH=,∴OH=6﹣,∴点Q的坐标为(,),在x轴上取点G(﹣2,0),连接QG交y轴于点M,则此时△AQM的周长最小,∴AQ==,QG==,∴AQ+QG=,∴△AQM的最小周长为4.6.如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=﹣x+3的图象与y轴、x轴的交点,点B在二次函数y=x2+bx+c的图象上,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.(1)试求b、c的值,并写出该二次函数表达式;(2)动点P沿线段AD从A到D,同时动点Q沿线段CA从C到A都以每秒1个单位的速度运动,问:①当P运动过程中能否存在PQ⊥AC?如果不存在请说明理由;如果存在请说明点的位置?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?解:(1)由y=﹣x+3,令x=0,得y=3,所以点A(0,3);令y=0,得x=4,所以点C(4,0),∵△ABC是以BC为底边的等腰三角形,∴B点坐标为(﹣4,0),又∵四边形ABCD是平行四边形,∴D点坐标为(8,3),将点B(﹣4,0)、点D(8,3)代入二次函数y=x2+bx+c,∴,解得:,故该二次函数解析式为:y=x2﹣x﹣3.(2)∵OA=3,OB=4,∴AC=5.①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,∵PQ⊥AC,∴∠AQP=∠AOC=90°,∠PAQ=∠ACO,∴△APQ∽△CAO,∴,即,解得:t=.即当点P运动到距离A点个单位长度处,有PQ⊥AC.②∵S四边形PDCQ +S△APQ=S△ACD,且S△ACD=×8×3=12,∴当△APQ的面积最大时,四边形PDCQ的面积最小,当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽△CAO可得:,解得:h=(5﹣t),∴S△APQ=t×(5﹣t)=(﹣t2+5t)=﹣(t﹣)2+,∴当t=时,S△APQ 达到最大值,此时S四边形PDCQ=12﹣=,故当点P运动到距离点A个单位处时,四边形PDCQ面积最小,最小值为.7.如图,抛物线y=﹣x2+bx+c过点x轴上的A(﹣1,0)和B点,交y轴于点C,点P是该抛物线上第一象限内的一动点,且CO=3AO.(1)抛物线的解析式为:y=﹣x2+2x+3 ;(2)过点P作PD∥y轴交直线BC于点D,求点P在运动的过程中线段PD长度的最大值;(3)若sin∠BCP=,在对称轴左侧的抛物线上是否存在点Q,使∠QBC=∠PBC?若存在,请求出点Q的坐标,若不存在,请说明理由.解:(1)∵A(﹣1,0),∴OA=1,又∵CO=3AO,∴OC=3,∴C(0,3),把A,C两点的坐标代入y=﹣x2+bx+c得,,解得:,∴抛物线的解析式为y=﹣x2+2x+3,故答案为:y=﹣x2+2x+3.(2)由﹣x2+2x+3=0,得B(3,0),设直线BC的解析式为y=kx+b,将点B(3,0),C(0,3)代入得,,解得:,∴直线BC的解析式为y=﹣x+3,设点P(x,﹣x2+2x+3),则D(x,﹣x+3)(0<x<3),∴PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x=.∴当时,PD有最大值.(3)存在.∵,点P在第一象限,∴∠BCP=45°,∵B(3,0),C(0,3),∴OC=OB,∴△BOC是等腰直角三角形,∴∠OBC=∠OCB=45°,∴∠BCP=∠OCB=45°,∴CP∥OB,∴P(2,3),设BQ与y轴交于点G,在△CPB和△CGB中:2,∴△CPB≌△CGB(ASA),∴CG=CP=2,∴OG=1,∴点G(0,1),设直线BQ:y=kx+1,将点B(3,0)代入y=kx+1,∴,∴直线BQ:,联立直线BQ和二次函数解析式,解得:或(舍去),∴Q(,).8.如图,以D为顶点的抛物线y=ax2+2x+c交x轴于点A,B(6,0),交y轴于点C(0,6).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.解:(1)将B(6,0),C(0,6)代入y=ax2+2x+c,得:,解得:,∴抛物线的解析式为y=﹣x2+2x+6.(2)当y=0时,﹣x2+2x+6=0,解得:x1=﹣2,x2=6,∴点A的坐标为(﹣2,0).∵点B的坐标为(6,0),点C的坐标为(0,6),∴直线BC的解析式为y=﹣x+6.如图1,作O关于BC的对称点O′,则点O′的坐标为(6,6).∵O与O′关于直线BC对称,∴PO=PO′,∴PO+PA的最小值=PO′+PA=AO′═=10.设直线AO′的解析式为y=kx+m,将A(﹣2,0),Q′(6,6)代入y=kx+m,得:,解得:,∴直线AO′的解析式为y=x+.联立直线AO′和直线BC的解析式成方程组,得:,解得:,∴点P的坐标为(,).(3)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,∴点D的坐标为(2,8).又∵点C的坐标为(0,6),点B的坐标为(6,0),∴CD=2,BC═=6,BD═=4,∴CD2+BC2=BD2,∴∠BCD=90°.∵点A的坐标(﹣2,0),点C的坐标为(0,6),∴OA=2,OC=6,∴==2,.又∵∠AOC=∠DCB=90°,∴△AOC∽△DCB,∴当Q的坐标为(0,0)时,△AQC∽△DCB.如图2,连接AC,过点C作CQ⊥AC,交x轴与点Q.∵△ACQ为直角三角形,CO⊥AQ,∴△ACQ∽△AOC.又∵△AOC∽△DCB,∴△ACQ∽DCB,∴,即,∴AQ=20,∴点Q的坐标为(18,0).综上所述:当Q的坐标为(0,0)或(18,0)时,以A,C,Q为顶点的三角形与△BCD 相似.9.如图,抛物线L:y=ax2﹣2ax+a+k(a,k为常数且a>0)经过点C(﹣1,0),顶点为M,经过点P(0,a+4)的直线m与x轴平行,且m与L交于点A,B(B在A的右侧),与L的对称轴交于点F,直线n:y=ax+c经过点C.(1)用a表示k及点M的坐标;(2)BP﹣AP的值是否是定值?若是,请求出这个定值;若不是,请说明理由;(3)当直线n经过点B时,求a的值及点A,B的坐标;(4)当a=1时,设△ABC的外心为点N,则:①求点N的坐标;②若点Q在L的对称轴上,其纵坐标为b,且满足∠AQB<∠ACB,直接写出b的取值范围.解:(1)把点C(﹣1,0)代入L,得0=a×(1﹣)2﹣2a×(﹣1)+a+k,∴k=﹣4a.又L:y=ax2﹣2ax+a+k=a(x﹣1)2﹣4a,∴顶点M(1,﹣4a).(2)是定值.根据图象,由抛物线的轴对称性,可知BF=AF,又QL的对称轴为x=1,故PF=1,∴由图象可得,BP﹣AP=(BF+PF)﹣(AF﹣PF),=BF+PF﹣AF+PF=2PF=2.(3)当直线n经过点B时,有ax+a=a(x﹣1)2﹣4a,化简得,ax2﹣3ax﹣4a=0,∵a>0,∴x2﹣3x﹣4=0,解得:x1=﹣1,x2=4,∵B在A的右侧,对称轴为x=1,∴B(4,a+4),A(﹣2,a+4),把点B代入直线n,得a+4=4a+a,解得a=1,∴A(﹣2,5),B(4,5).(4)①根据抛物线的轴对称性可知,L的对称轴x=1就是AB的垂直平分线,故△ABC的外心N就在直线x=1上,则有AN=CN.∴设N(1,c),由(3)可知A(﹣2,5),及C(﹣1,0),∴(﹣2﹣1)2+(5﹣c)2=(﹣1﹣1)2+(0﹣c)2,即32+(5﹣c)2=22+c2,解得c=3.∴N(1,3).②或b.如图,对于点Q(1,b),若∠AQB=∠ACB,根据同弧所对的圆周角相等,可得点Q为x=1与⊙N的交点,由(4)①得,⊙N的半径为r=NC=(﹣1﹣1)2+(0﹣3)2=,则b=﹣(r﹣c)=﹣(﹣3)=3﹣;设点Q关于直线AB的对称点为Q'(1,d),若∠AQ'B=∠ACB,则d=FQ'+5=FQ+5=(5+|3﹣|)+5=+7.综上,若点Q满足∠AQB<∠ACB,则有b或b.10.如图1,抛物线y=﹣x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,(1)直接写出抛物线和直线AB的函数表达式.(2)当点C是DE的中点时,求出m的值,并判定四边形ODEB的形状(不要求证明).(3)在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a <90°),连接D′A、D′B,求D′A+D′B的最小值.解:(1)将点B、A的坐标代入抛物线y=﹣x2+bx+c得,,解得:,∴抛物线的函数表达式为y=﹣.设直线AB的解析式为y=kx+b,∴,解得:,∴直线AB的解析式为y=﹣x+4;(2)∵过点D(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点E,∴E(m,),C(m,﹣m+4).∴EC==.∵点C是DE的中点,∴.解得:m=2,m=4(舍去).∴ED=OB=4,∴四边形ODEB为矩形.(3)如图,由(2)可知D(2,0),在y轴上取一点M′使得OM′=1,连接AM′,在AM′上取一点D′使得OD′=OD.∵OD′=2,OM′•OB=1×4=4,∴OD′2=OM′•OB,∴,∵∠BOD′=∠M′OD′,∴△M′OD′∽△D′OB,∴.∴.∴D′A+D′B=D′A+M′D′=AM′,此时D′A+D′B最小(两点间线段最短,A、M′、D′共线时),∴D′A+D′B的最小值=AM′==.11.如图,抛物线y=ax2+bx+c与x轴交于点A和点B,与y轴交于点C,且OA=2,OB=OC =6,点D是抛物线的顶点,过点D作x轴的垂线,垂足为E.(1)求抛物线的解析式及点D的坐标;(2)连接BD,若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标:(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请求出点Q的坐标.解:(1)∵OA=2,OB=OC=6,∴A(﹣2,0),B(6,0),C(0,6),∴可设抛物线解析式为y=a(x+2)(x﹣6),把C点的坐标代入可得6=﹣12a,解得a=.∴抛物线解析式为y=(x+2)(x﹣6)=﹣x2+2x+6;∴D(2,8);(2)如图1,过F作FG⊥x轴于点G,设F(x,﹣x2+2x+6),则FG=|﹣x2+2x+6|,∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FBG∽△BDE,∴.∵B(6,0),D(2,8),∴E(2,0),BE=4,DE=8,OB=6,∴BG=6﹣x,∴,当点F在x轴上方时,有,解得x=﹣1或x=6(舍去),此时F点的坐标为(﹣1,),当点F在x轴下方时,有,解得x=﹣3或x=6(舍去),此时F点的坐标为(﹣3,),综上可知F点的坐标为(﹣1,)或(﹣3,);(3)如图2,设对角线MN、PQ交于点O′,∵点M、N关于抛物线对称轴对称,且四边形MPNQ为正方形,∴点P为抛物线对称轴与x轴的交点,点Q在抛物线的对称轴上,QO′=MO′=PO′=NO′,PQ⊥MN,设Q(2,2n),则M坐标为(2﹣n,n),∵点M在抛物线y=﹣x2+2x+6的图象上.∴n=﹣(2﹣n)2+2(2﹣n)+6,解得n=﹣1+或n=﹣1﹣,∴满足条件的点Q有两个,其坐标分别为(2,﹣2+2)或(2,﹣2﹣2).12.如图,直线y=x﹣4与x轴,y轴交于点B,C,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线经过B,C,与x轴交于另一点A.(1)求抛物线的解析式;(2)点E从A点出发,在线段AB上以每秒3个单位的速度向B点运动,同时点F从B 点出发,在线段BC上以每秒1个单位的速度向C点运动,当其中一个点到达终点时,另一个点将停止运动.设△EBF的面积为S,点E运动的时间为t.①求S与t的函数关系式,并求出S有最大值时点F的坐标;②点E,F在运动过程中,若△EBF为直角三角形,求t的值.解:(1)∵直线y=x﹣4与x轴,y轴交于点B,C,∴x=0时,y=﹣4,y=0时,x=4,∴B(4,0),C(0,﹣4).∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,∴A点坐标为(﹣2,0),∴,解得:.∴抛物线的解析式为.(2)由题意得,BF=t,BE=6﹣3t,①作FH⊥x轴,如图,∵B(4,0),C(0,﹣4).∴OB=OC=4,∴,∵FH∥BC,∴△BHF∽△BOC,∴,∴.解得:HF=.∴=.当S有最大值时,t=1,此时点F的坐标为().②∵OB=OC,∴∠OBC=45°,若∠BEF=90°,则cos∠EBF=,解得:t=.若∠EFB=90°,则cos∠EFB=.解得:t=.综合以上可得,若△EBF 为直角三角形,t 的值为或.13.如图,在直角坐标系中,y =ax 2﹣4ax +3a 与x 轴交于A 、B 两点(A 点在B 点左),与y 轴交于C 点.(1)若△ABC 的面积为,求抛物线的解析式;(2)已知点P 为B 点右侧抛物线上一点,连PC ,PB 交y 轴于D 点,若∠BCP =2∠ABC ,求的值;(3)若P 为对称轴右侧抛物线上的动点,PA 交y 轴于E 点,判断的值是否为定值,说明理由.解:(1)∵y =ax 2﹣4ax +3a 与x 轴交于A 、B 两点,∴ax 2+4 ax +3a =0,解得x 1=1,x 2=3,∴A (1,0),B (3,0),当x =0,y =3a ,∴OC =﹣3a ,∵S △ABC =, ∴, 解得a =﹣,∴抛物线的解析式为y =﹣;(2)如图,过B 点作BM ⊥x 轴交CP 于M ,过点C 作CF ⊥BM 于点F ,∵AB∥CF,∴∠ABC=∠BCF,∵∠BCP=2∠ABC,∴∠ABC=∠BCF=∠FCM,∵CF=CF,∴△CBF≌△CMF(ASA),∴BF=FM,∴M(3,6a),又∵C(0,3a),设CP解析式y=mx﹣3m,∴8a=m×2,∴m=4a,∴y=4ax﹣12a,∴,解得:x1=3,x2=5,∴P(5,8a),∴直线BP的解析式为y=4ax﹣12a,∴D(0,﹣12a),∵OC=|3a|,OD=|﹣12a|,∴;(3)∵A(1,0),∴设PA的解析式y=k1x﹣k1,∴∴ax2﹣(4a+k1)x+3a+k1=0,∴(ax﹣3a﹣k1)(x﹣1)=0,解得,x=1或x=,∴x p=3+,∵B(3,0),∴设PB的解析式y=k2x﹣3k2,∴,∴ax2﹣(4a+k2)x+3a+3k2=0,∴(ax﹣a﹣k2)(x﹣3)=0,∴x p=1+.又∵EC=﹣k1﹣3 a,DE=﹣3k2﹣3 a,∴==.14.如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点点A(0,1)、点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.解:(1)将A (0,1),B (9,10)代入函数解析式,得, 解得,∴抛物线的解析式y =x 2﹣2x +1;(2)∵AC ∥x 轴,A (0,1), ∴x 2﹣2x +1=1,解得x 1=6,x 2=0(舍),即C 点坐标为(6,1),∵点A (0,1),点B (9,10),∴直线AB 的解析式为y =x +1,设P (m ,m 2﹣2m +1),∴E (m ,m +1),∴PE =m +1﹣(m 2﹣2m +1)=﹣m 2+3m .∵AC ⊥PE ,AC =6,∴S 四边形AECP =S △AEC +S △APC =AC •EF +AC •PF =AC •(EF +PF )=AC •EP =×6×(﹣m 2+3m )=﹣m 2+9m =﹣(m ﹣)2+,∵0<m <6,∴当m =时,四边形AECP 的面积最大,此时P (,﹣);(3)∵y =x 2﹣2x +1=(x ﹣3)2﹣2,∴P (3,﹣2).∴PF=y F﹣y p=3,CF=x F﹣x C=3,∴PF=CF,∴∠PCF=45°,同理可得∠EAF=45°,∴∠PCF=∠EAF,∴在直线AC上存在满足条件得点Q,设Q(t,1)且AB=9,AC=6,CP=3,∵以C,P,Q为顶点的三角形与△ABC相似,①当△CPQ∽△ABC时,,即,解得t=4,∴Q(4,1);②当△CQP∽△ABC时,,即,解得t=﹣3,∴Q(﹣3,1).综上所述:当点P为抛物线的顶点时,在直线AC上存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,Q点的坐标为(4,1)或(﹣3,1).15.已知抛物线y=ax2+bx+3与x轴交于点A(3,0),B(1,0),与y轴交于点C.(1)求抛物线的解析式;(2)如图1,若点P为抛物线的对称轴上一点,连接BP,CP,当四边形BOCP的周长最小时,求点P的坐标;(3)如图2,点D为抛物线的顶点,在线段CD上是否存在点M(不与点C重合),使得△AMO与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(3,0),B(1,0),∴,解得:,∴抛物线的解析式为y=x2﹣4x+3;(2)∵抛物线的解析式为y=x2﹣4x+3,∴令x=0,y=3,∴C(0,3).∴OC+OB=3+1=4,∴当四边形BOCP的周长最小时,则CP+BP最小,如图1,连接AC,与对称轴的交点即为所求的点P,设直线AC的解析式为y=kx+b,∴,解得:.∴直线AC的解析式为y=﹣x+3,∵抛物线的对称轴为x==2,∴x=2时,y=﹣2+3=1,∴P(2,1).(3)∵抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点D的坐标为(2,﹣1),又∵C(0,3),∴直线CD为y=﹣2x+3,OC=3,∵A(3,0),∴AB=2,∠BAC=∠OCA=45°,∴AC=3,∴.∵∠ABC=90°+∠OCB,∴∠ABC为钝角,若△AMO与△ABC相似,显然∠ABC=∠OMA,则在线段CD上存在点M使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,①若点M在x轴上方时,如图2,当∠AOM=∠CAB=45°时,△ABC∽△OMA,设M(a,﹣2a+3),∴a=﹣2a+3,解得a=1,∴M(1,1).此时OM=,OA=3,∴,∴.则△ABC∽△OMA.②若点M在x轴下方,如图3,∵M在线段CD上,∴∠AOM≠45°,∴∠OAM=∠BAC=45°,∴M(2,﹣1),此时点M与点D重合,AM=,OA=3,∴.则△ABC∽△AMO.综合以上可得,在线段CD上存在点M(不与点C重合),使得△AMO与△ABC相似,此时点M的坐标为(1,1)或(2,﹣1).16.如图,一次函数y=﹣x+2的图象与坐标轴交于A、B两点,点C的坐标为(﹣1,0),二次函数y=ax2+bx+c的图象经过A、B、C三点.(1)求二次函数的解析式;(2)如图1,已知点D(1,n)在抛物线上,作射线BD,点Q为线段AB上一点,过点Q 作QM⊥y轴于点M,作QN⊥BD于点M,过Q作QP∥y轴交抛物线于点P,当QM与QN的积最大时,求线段PG的长;(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足∠APE=∠ABO,求S.△OBE解:(1)一次函数y=﹣x+2的图象与坐标轴交于A、B两点,则点A、B的坐标分别为:(0,2)、(4,0),则抛物线的表达式为:y=a(x﹣4)(x+1)=a(x2﹣3x﹣4),即﹣4a=2,解得:a=﹣,则抛物线的表达式为:y=﹣x2+x+2;(2)点D(1,3),点B(4,0),则BD所在的函数表达式为:y=﹣x+4;即直线BD的倾斜角为45°,则∠QGN=45°,QN=QG,设点Q(m,﹣m+2),则点G(m,﹣m+4),QM•QN=m×(﹣m+4+m﹣2)=(﹣m2+2m),当m=2时,QM与QN的积最大,则点P(2,3);(3)设:∠APE=∠ABO=∠α,则tan;①当PE在AP下方时,如图1,由点A(0,2)、P(2,3)知,AP=,设AP与y轴的夹角为β,则tanβ=2,过点H作MH⊥PA交PA的延长线于点M,设:MA=x,则MH=2x,tan∠APH===tanα=,解得:x=,则AH=x=,则点H(0,),设直线PH的表达式为:y=kx+b,∴,解得:,∴直线PH的解析式为y=x+,联立抛物线的解析式和直线的解析式:,解得:x=2(舍去)或﹣,∴点E(﹣,﹣),∴==.②当PE在AP上方时,如图2,过点P作PM⊥y轴交于点M,交抛物线于点E,∵tan∠APM=.tan∠ABO=,∴∠APM=∠ABO,∵PE∥x轴,∴E点的纵坐标为3,将y=3代入抛物线解析式求得x=1,∴E(1,3),∴=6.综上可得△OBE的面积为或6.17.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.(1)求抛物线对应的二次函数的表达式;(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.解:(1)∵A(﹣1,0),B(3,0).代入y=﹣x2+bx+c,得,解得b=2,c=3.∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;(2)如图1,设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F.∴PE⊥CD,PE=PA.由y=﹣x2+2x+3,得对称轴为直线x=1,C(0,3)、D(1,4).∴DF=4﹣3=1,CF=1,∴DF=CF,∴△DCF为等腰直角三角形.∴∠CDF=45°,∴∠EDP=∠EPD=45°,∴DE=EP,∴△DEP为等腰三角形.设P(1,m),∴EP2=(4﹣m)2.在△APQ中,∠PQA=90°,∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2∴(4﹣m)2=[1﹣(﹣1)]2+m2.整理,得m2+8m﹣8=0解得,m=﹣4±2.∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).(3)存在点M,使得△DCM∽△BQC.如图2,连结CQ、CB、CM,∵C(0,3),OB=3,∠COB=90°,∴△COB为等腰直角三角形,∴∠CBQ=45°,BC=3.由(2)可知,∠CDM=45°,CD=,∴∠CBQ=∠CDM.∴△DCM与△BQC相似有两种情况.当时,∴,解得DM=.∴QM=DQ﹣DM=4﹣=.∴M(1,).1当时,∴,解得DM=3,∴QM=DQ﹣DM=4﹣3=1.∴M(1,1).2综上,点M的坐标为或(1,1).18.如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0)、B(3,0)(点A在点B的左边),与y轴交于点C,过点C作CD∥x轴,交抛物线于点D,过点D作DE∥y轴,交直线BC 于点E,点P在抛物线上,过点P作PQ∥y轴交直线CE于点Q,连结PB,设点P的横坐标为m,PQ的长为d.(1)求抛物线对应的函数表达式;(2)求直线BC的函数表达式;(3)当0<m<4时,求d关于m的函数关系式;(4)当△PQB是等腰三角形时,直接写出m的值.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(1,0)、B(3,0),∴解得:∴抛物线解析式为:y=﹣x2+4x﹣3;(2)∵抛物线y=﹣x2+4x﹣3与y轴交于点C,∴点C(0,﹣3)设直线BC解析式为:y=kx﹣3,∴0=3k﹣3∴k=1,∴直线BC解析式为:y=x﹣3;(3)∵设点P的横坐标为m,PQ∥y轴,∴点P(m,﹣m2+4m﹣3),点Q(m,m﹣3),当0<m<3时,PQ=d=﹣m2+4m﹣3﹣(m﹣3)=﹣m2+3m,当3≤m<4时,PQ=d=(m﹣3)﹣(﹣m2+4m﹣3)=m2﹣3m;(4)B(3,0),点C(0,﹣3),∴OB=OC=3,∴∠OCB=∠OBC=45°,∵PQ∥OC,∴∠PQB=45°,若BP=PQ,∴∠PQB=∠PBQ=45°,∴∠BPQ=90°,即点P与点A重合,∴m=1,若BP=QB,∴∠BQP=∠BPQ=45°,∴∠QBP=90°,∴BP解析式为:y=﹣x+3,∴解得:,∴点P(2,1)∴m=2;若PQ=QB,∴(3﹣m)2+(m﹣3﹣0)2=(﹣m2+3m)2,或(3﹣m)2+(m﹣3﹣0)2=(m2﹣3m)2,∴m=±,综上所述:m=1或2或±.19.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y 轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点P为直线BD上方抛物线上一点,若S=3,请求出点P的坐标.△PBD(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+n,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD =S△PQD+S△PQB,∴S△PBD=×PQ×(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△ABD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).20.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)在x轴上找一点E,使△EDC的周长最小,求符合条件的E点坐标;(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出PB2的值;若不存在,请说明理由.解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),将点B、C的坐标代入二次函数表达式得:,解得:,故函数的表达式为:y=﹣x2+2x+3,(2)如图1,作点C关于x轴的对称点C′,连接CD′交x轴于点E,此时EC+ED为最小,则△EDC的周长最小,抛物线的顶点D坐标为(1,4),点C′(0,﹣3),将C′、D的坐标代入一次函数表达式并解得:∴直线C′D的表达式为:y=7x﹣3,当y=0时,x=,故点E(,0),(3)①当点P在x轴上方时,如图2,∵OB=OC=3,则∠OCB=45°=∠APB,过点B作BH⊥AP于点H,设PH=BH=a,则PB=PA=a,由勾股定理得:AB2=AH2+BH2,16=a2+(a﹣a)2,解得:a2=8+4,则PB2=2a2=16+8.②当点P在x轴下方时,同理可得.综合以上可得,PB2的值为16+8.。
2020年九年级数学中考二轮复习:《二次函数综合》压轴题专题训练(含答案)

《二次函数综合》压轴题专题训练1.定义:关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”.例如:y=(x﹣1)2﹣2的“同轴对称抛物线”为y=﹣(x﹣1)2+2.(1)满足什么条件的抛物线与其“同轴对称抛物线”的顶点重合:.(2)求抛物线y=﹣x2+x+1的“同轴对称抛物线”.(3)如图,在平面直角坐标系中,点B是抛物线L:y=ax2﹣4ax+1上一点,点B的横坐标为1,过点B作x轴的垂线,交抛物线L的“同轴对称抛物线”于点C,分别作点B、C关于抛物线对称轴对称的点B′、C′,连接BC、CC′、B′C′、BB′,设四边形BB′C′C的面积为S(S>0).①当四边形BB′C′C为正方形时,求a的值.②当抛物线L与其“同轴对称抛物线”围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出a的取值范围.2.已知抛物线C:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛1物线C:y=x2.2(1)直接写出抛物线C的解析式;1与x轴交于A,B两点,点A在点B的左侧,点P(,t)(2)如图1,已知抛物线C1在抛物线C上,QB⊥PB交抛物线于点Q.求点Q的坐标;1上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛(3)已知点E,M在抛物线C2物线C只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段2NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为.3.如图1,抛物线y=x2+bx+c过点A(4,﹣1),B(0,﹣),点C为直线AB下方抛物线上一动点,M为抛物线顶点,抛物线对称轴与直线AB交于点N.(1)求抛物线的表达式与顶点M的坐标;(2)在直线AB上是否存在点D,使得以C,D,M,N为顶点的四边形是平行四边形,若存在,请求出D点坐标;(3)在y轴上是否存在点Q,使∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.4.如图,已知抛物线y=ax2+bx+c与x轴的交点为A(﹣1,0),B(2,0)且与y轴交于点C,OA=OC.(1)求该抛物线的表达式;(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由;(3)已知点P时直线y=x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q 为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.5.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).(1)求抛物线的解析式;(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.①求S与m之间的函数关系式,并写出自变量m的取值范围;②当S取得最值时,求点P的坐标.(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.6.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y 轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;=3,请求出点P的坐标.(2)如图2,点P为直线BD上方抛物线上一点,若S△PBD(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.7.已知抛物线交x轴于A,B两点(A在B右边),A(3,0),B(1,0)交y轴于C点,C(0,3),连接AC;(1)求抛物线的解析式;(2)P为抛物线上的一点,作PE⊥CA于E点,且CE=3PE,求P点坐标;(3)将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,过H作直线MH,NH,当MH⊥NH时,求MN恒过的定点坐标.:y=(x﹣1)2+k(k>0)经过y轴上的点A,顶点为B.抛物线8.如图,已知抛物线l1l:y=(x﹣h)2+2﹣h(h≥2)的顶点为D,直线y=﹣x+b经过A,B,D三点,两抛物2线交于点C.(1)求b的值和点B的坐标;(2)设点C的横坐标为m,探究m与h之间的数量关系;(3)当△ABC是直角三角形时,求h的值.9.综合与探究.如图1,抛物线y=x2﹣x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).(1)求A,B,C三点的坐标及直线BE的解析式.(2)如图2,过点A作BE的平行线交抛物线于点D,点P是抛物线上位于线段AD下方的一个动点,连接PA,PD,求OAPD面积的最大值.(3)若(2)中的点P为抛物线上一动点,在x轴上是否存在点Q,使得以A,D,P,Q 为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C(0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.11.如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.(1)求抛物线的解析式;(2)点D是抛物线顶点,求△ACD的面积;(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S=,求△APE面积的最大值和此动点P的坐标.△ABE12.图①,抛物线y=﹣2x2+bx+c过A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC.(1)求该抛物线的表达式和对称轴;(2)点D是抛物线对称轴上一动点,当△BCD是以BC为直角边的直角三角形时,求所有符合条件的点D的坐标;(3)如图2,将抛物线在BC上方的图象沿BC折叠后与y轴交与点E,求点E的坐标.13.已知,抛物线y=ax2,其中a>0.(1)如图1,若点A、B是此抛物线上两点,且分属于y轴两侧,连接AB与y轴相交于点C,且∠AOB=90°.求证:CO=;(2)如图2,若点A是此抛物线上一点,过点A的直线恰好与此抛物线仅有一个交点,且与y轴交于点B,与x轴相交于点C.求证:AC=BC.14.如图,抛物线y=ax2﹣x+c与x轴交于A,B两点,与y轴交于C点,连结AC,已知B(1﹣,0),且抛物线经过点D(2,﹣2).(1)求抛物线的解析式;(2)若点E是抛物线上位于x轴下方的一点,且S△ACE =S△ABC,求E的坐标;(3)若点P是y轴上一点,以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标.15.如图,在平面直角坐标系中,直线y=﹣x+4分别与x轴、y轴相交于点B、C,经过点B、C的抛物线y=﹣+bx+c与x轴的另一个交点为A.(1)求出抛物线表达式,并求出点A坐标.(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.参考答案1.解:(1)∵“同轴对称抛物线”的顶点重合,∴顶点关于x轴对称且重合,∴顶点在x轴上,故答案为:顶点在x轴上;(2)∵y=﹣x2+x+1=﹣(x﹣1)2+,∴“同轴对称抛物线”的顶点坐标为(1,﹣),∴y=(x﹣1)2﹣;(3)①由题可知,B(1,1﹣3a),∴C(1,3a﹣1),∵抛物线y=ax2﹣4ax+1的对称轴为x=2,∴B'(3,1﹣3a),C'(3,3a﹣1),∴BB'=CC'=2,∴BC=2﹣6a或BC=6a﹣2,∴2﹣6a=2或6a﹣2=2,∴a=0(舍去)或a=;②函数的对称轴为x=2,函数L的顶点坐标为(2,1﹣4a),∵L与“同轴对称抛物线”是关于x轴对称的,所以整数点也是对称的出现,∵抛物线L与其“同轴对称抛物线”围成的封闭区域内,在x轴上的整数点可以是3个或5个,∴L与x轴围城的区域的整数点为4个或3个;当a>0时,当x=1时,﹣2≤1﹣3a<﹣1,∴<a≤1,当x=2时,1﹣4a<﹣2,∴a>,∴<a≤1;当a<0时,当x=2时,1﹣4a≤2,∴a≥﹣,当x=﹣1时,5a+1<0,∴a<﹣,∴﹣≤a<﹣;综上所述:<a≤1或﹣≤a<﹣.2.解:(1)由已知可知,抛物线C:y=x2向右平移1个单位长度,再向下平移4个单位2:y=ax2+bx+c,长度得到抛物线C1:y=(x﹣1)2﹣4,∴抛物线C1故答案为y=(x﹣1)2﹣4;(2)∵y=(x﹣1)2﹣4,令y=0,(x﹣1)2﹣4=0,解得x=3或x=﹣1,∴A(﹣1,0),B(3,0),上,∵点P(,t)在抛物线C1∴t=(﹣1)2﹣4,解得t=﹣,∴P(,﹣),设Q(t,t2﹣2t﹣3),过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,∵BQ⊥BP,∴∠QBN+∠MBP=∠QBN+∠MQN=90°,∴∠BQN=∠PBM,∴△BNQ∽△QMP,∴=,∴=,∴t=﹣或t=3,∵Q点在第二象限,∴t=﹣,∴Q(﹣,);(3)∵点M与N在y=x2上,∴M(m,m2),N(n,n2)∵EM∥x轴,∴E(﹣m,m2),设MD的解析式为y=kx+b,∴m2=km+b,∴b=m2﹣km,∴y=kx+m2﹣km,∵直线MD与抛物线y=x2只有一个交点,∴kx+m2﹣km=x2,∴△=k2﹣4(m2+km)=0,∴k=2m,∴直线MD的解析式为y=2mx﹣m2,∵NE=DE,∴D(﹣2m﹣n,2m2﹣n2),∴2m2﹣n2=2m(﹣2m﹣n)﹣m2,整理得,n2﹣2mn﹣7m2=0,∴n=(1±2)m,故答案为n=(1±2)m.3.解:(1)将点A(4,﹣1),B(0,﹣)代入抛物线y=x2+bx+c,得,解得,∴y=x2﹣x﹣,∴M点的坐标为(1,﹣4);(2)设直线AB的表达式为y=mx+n,∴,解得,∴y=x﹣;当x=1时,y=﹣3,∴N(1,﹣3),∴MN=1;①若MN为平行四边形的一边时,则有CD∥MN,且CD=MN,设C(t,t2﹣t﹣),则D(t,t﹣),∴CD=t﹣﹣(t2﹣t﹣)=1,∴t=3或t=1(舍去),∴D(3,﹣);②若MN为平行四边形的对角线,设D(t,t﹣),则C(2﹣t,﹣t﹣),将点C代入抛物线解析式得,(2﹣t)2﹣(2﹣t)﹣=﹣t﹣,∴t=﹣1或t=1(舍去),∴D(﹣1,﹣);综上所述:符合条件的D点坐标为(3,﹣)或(﹣1,﹣);(3)在对称轴上取点P(1,﹣1),∴PA=PM=3,∠APM=90°,以P为圆心,PA为半径作圆交y轴于点Q,∴∠AQM=∠APM=45°,作PE⊥y轴交于点E,∴PE=1,∵PQ=3,∴EQ==2,∴Q点坐标为(0,﹣1+2)或(0,﹣1﹣2).4.解:(1)∵点A (﹣1,0)∴OA =1,∵OA =OC =1,且点C 在y 轴负半轴,∴点C (0,﹣1)∵抛物线y =ax 2+bx +c 与x 轴的交点为A (﹣1,0),B (2,0)且与y 轴交于点C , ∴ 解得:∴抛物线的表达式为:y =x 2﹣x ﹣1;(2)∵点C 关于x 轴的对称点为C 1,∴C 1(0,1),∵点B (2,0),点C 1(0,1),∴直线BC 1的解析式为:y =﹣x +1,∴设点M 坐标为(m ,﹣m +1)∴MF =m ,ME =﹣m +1,∴矩形MFOE 的面积=MF ×ME =m ×(﹣m +1)=﹣m 2+m =﹣(m ﹣1)2+, ∴当m =1时,矩形MFOE 的最大面积为,此时点M 的坐标为(1,),即点M 为线段C 1B 中点时,S 矩形MFOE 最大;(3)由题意,C (0,﹣1),C 1(0,1),以C 、C 1、P 、Q 为顶点的四边形为平行四边形,分以下两种情况:①C 1C 为边,则C 1C ∥PQ ,C 1C =PQ ,设P (m ,m +1),Q (m ,m 2﹣m ﹣1),∴|(m 2﹣m ﹣1)﹣(m +1)|=2,解得:m 1=4,m 2=﹣2,m 3=2,m 4=0(舍),P 1(4,3),Q 1(4,5);P 2(﹣2,0),Q 2(﹣2,2);P 3(2,2),Q 3(2,0) ②C 1C 为对角线,∵C 1C 与PQ 互相平分,C 1C 的中点为(0,0),∴PQ 的中点为(0,0),设P (m ,m 2﹣m +1),则Q (﹣m ,m 2+m ﹣1) ∴(m +1)+(m 2+m ﹣1)=0,解得:m 1=0(舍去),m 2=﹣2,∴P 4(﹣2,0),Q 4(2,0);综上所述,点P 和点Q 的坐标为:P 1(4,3),Q 1(4,5)或P 2(﹣2,0),Q 2(﹣2,2)或P 3(2,2),Q 3(2,0)或P 4(﹣2,0),Q 4(2,0).5.解:(1)∵直线x =1是抛物线的对称轴,且点C 的坐标为(0,3),∴c =3,﹣=1,∴b =2,∴抛物线的解析式为:y =﹣x 2+2x +3;(2)①∵y =﹣x 2+2x +3=﹣(x ﹣1)2+4,∴点M (1,4),∵抛物线的解析式为:y =﹣x 2+2x +3与x 轴相交于A ,B 两点(点A 位于点B 的左侧), ∴0=﹣x 2+2x +3∴x 1=3,x 2=﹣1,∴点A (﹣1,0),点B (3,0),∵点M (1,4),点B (3,0)∴直线BM 解析式为y =﹣2x +6,∵点P 在直线BM 上,且PD ⊥x 轴于点D ,PD =m ,∴点P (3﹣,m ),∴S △PCD =×PD ×OD =m ×(3﹣)=﹣m 2+m ,∵点P 在线段BM 上,且点M (1,4),点B (3,0),∴0<m ≤4∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4)②∵S=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,S有最大值为,∴点P(,3)∵0<m≤4时,S没有最小值,综上所述:当m=3时,S有最大值为,此时点P(,3);(3)存在,若PC=PD=m时,∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6);若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,∴m3=﹣2﹣2(舍去),m4=﹣2+2,∴点P(4﹣,﹣2+2);若DC=PC时,∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,∴m5=0(舍去),m6=6(舍去)综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.6.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+b,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD =S△PQD+S△PQB,∴S△PBD=(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△AMD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).7.解:(1)∵抛物线过A(3,0),B(1,0),∴可设抛物线的解析式为y=a(x﹣3)(x﹣1)(a≠0),把c(0,3)代入,得3a=3,∴a=1,∴抛物线的解析式是y=(x﹣3)(x﹣1)=x2﹣4x+3,即y=x2﹣4x+3;(2)过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,如图1,∵A(3,0),C(0,3),∴OA=OC=3,∴∠OAC=45°,∵FG∥OA,∴∠CEF=45°,∴CF=EF=CE,∵PE⊥CA,∴∠PEG=45°,∴PG=EG=PE,∵CE=3PE,∴EF=3FG,设EF=3m,则PG=EG=m,FG=4m,∴DG=OF=OC﹣CF=3﹣3m,PD=PG+DG=3﹣2m,∴P(4m,3﹣2m),把P(4m,3﹣2m)代入y=x2﹣4x+3中得,3﹣2m=16m2﹣16m+3,∴m=,或m=0(舍去),∴P(,);(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线y=x2﹣4x+3的顶点为(2,﹣1),∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,∴H(2,0),由题意知,点H是新抛物线的顶点,∴新抛物线的解析式为y=(x﹣2)2,设M(m,(m﹣2)2),N(n,(n﹣2)2),过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,则MK=(m﹣2)2,KH=2﹣m,HL=n﹣2,NL=(n﹣2)2,∵MH⊥NH,∴∠MHK+∠HMK=∠MHK+∠NHL=90°,∴∠HMK=∠NHL,∵∠MKH=∠HLN=90°,∴△KHM∽△LNH,∴,,∴,∴,设直线MN的解析式为:y=kx+b(k≠0),则,∴,∴直线MN的解析式为:,当x=2时,y=﹣(m2﹣4m+3)=m2﹣4m+4﹣m2+4m﹣3=1,∴MN恒过的定点(2,1).8.解:(1)∵y=(x﹣1)2+k(k>0)经过y轴上的点A,顶点为B,∴A(0,1+k),B(1,k),∵y=(x﹣h)2+2﹣h(h≥2)的顶点为D,∴D(h,2﹣h),∵直线y=﹣x+b经过A,D,∴,∴,∴b的值为2,点B的坐标为(1,1);:y=(x﹣1)2+1,(2)由(1)知,抛物线l1∵点C的横坐标为m,两抛物线交于点C.∴(m﹣1)2+1=(m﹣h)2﹣h+2,整理得2mh﹣2m=h2﹣h∵h≥2∴m==;(3)当AC⊥AB时,则直线AC解析式为:y=x+2,∴∴(舍去),,∴点C坐标为(3,5),∴3=∴h=6;当BC⊥AB时,则直线BC解析式为:y=x,∴∴(舍去),∴点C坐标为(2,2),∴2=∴h=4;9.解:(1)令y=0,则x2﹣x﹣2=0,解得x=4或x=﹣1,∴A(﹣1,0),B(4,0),令x=0,则y=﹣2,∴C(0,﹣2),设直线BE的解析式为y=kx+b,将B(4,0)、E(0,2)代入得,,解得:,∴y=﹣x+2;(2)由题意可设AD的解析式为y=﹣x+m,将A(﹣1,0)代入,得到m=﹣,∴y=﹣x﹣,联立,解得:,,∴D(3,﹣2),过点P作PF⊥x轴于点F,交AD于点N,过点D作DG⊥x轴于点G.∴S△APD =S△APN+S△DPN=PN•AF+PN•FG=PN(AF+FG)=PN•AG=×4PN=2PN,设P(a,﹣a2﹣a﹣2),则N(a,﹣a﹣),∴PN=﹣a2+a+,∴S△APD=﹣a2+2a+3=﹣(a﹣1)2+4,∵﹣1<0,﹣1<a<3,∴当a=1时,△APD的面积最大,最大值为4;(3)存在;①当PD与AQ为平行四边形的对边时,∵AQ∥PD,AQ在x轴上,∴P(0,﹣2),∴PD=3,∴AQ=3,∵A(﹣1,0),∴Q(2,0)或Q(﹣4,0);②当PD与AQ为平行四边形的对角线时,PD与AQ的中点在x轴上,∴P点的纵坐标为2,∴P(,2)或P(,2),∴PD的中点为(,0)或(,0),∵Q点与A点关于PD的中点对称,∴Q(,0)或Q(,0);综上所述:点Q的坐标为(2,0)或(﹣4,0)或(,0)或(,0).10.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,又∵抛物线对称轴为直线x =﹣=2,∴x =2时,y =﹣3×2+3=﹣3,故,点M 的坐标为(2,﹣3);(3))∵OB =OC =3,OB ⊥OC ,∴△BOC 是等腰直角三角形,∵EF ∥y 轴,直线BC 的解析式为y =﹣x +3,∴△DEF 只要是直角三角形即可与△BOC 相似,∵D (2,1),A (1,0),B (3,0),∴点D 垂直平分AB 且到点AB 的距离等于AB ,∴△ABD 是等腰直角三角形,∴∠ADB =90°,如图,①点F 是直角顶点时,点F 的纵坐标与点D 的纵坐标相同,是1,∴x 2﹣4x +3=1,整理得x 2﹣4x +2=0,解得x =2±, 当x =2﹣时,y =﹣(2﹣)+3=1+, 当x =2+时,y =﹣(2+)+3=1﹣, ∴点E 1(2﹣,1+)E 2(2+,1﹣), ②点D 是直角顶点时,联立, 解得,,当x =1时,y =﹣1+3=2,当x =4时,y =﹣4+3=﹣1,∴点E 3(1,2),E 4(4,﹣1),综上所述,存在点E 1(2﹣,1+)或E 2(2+,1﹣)或E 3(1,2)或E 4(4,﹣1),使以D 、E 、F 为顶点的三角形与△BCO 相似.11.解:(1)∵抛物线y =ax 2+2ax +c (a ≠0)与x 轴交于点A ,B (1,0)两点,与y 轴交于点C ,且OA =OC ,∴a +2a +c =0,点C 的坐标为(0,c ),∴点A 的坐标为(c ,0),∴ac 2+2ac +c =0, ∴, 解得,或,∵函数图象开口向上,∴a >0,∴a =1,c =﹣3,∴抛物线的解析式为y =x 2+2x ﹣3;(2)∵y =x 2+2x ﹣3=(x +1)2﹣4,抛物线与与y 轴交于点C ,顶点为D ,OA =OC ,抛物线y =ax 2+2ax +c (a ≠0)与x 轴交于点A ,B (1,0)两点,∴点D 的坐标为(﹣1,﹣4),点C 的坐标为(0,﹣3),点A 的坐标为(﹣3,0), 连接OD ,如右图1所示,由图可知:S △ACD =S △OAD +S △OCD ﹣S △OAC==3;(3)∵A(﹣3,0),点B(1,0),∴AB=4,设点E的纵坐标为t,t<0,∵S△ABE=,∴=,得t=,把y=﹣代入y=x2+2x﹣3,得﹣=x2+2x﹣3,解得,x1=,x2=,∵点E在y轴的右侧,∴点E(,﹣),设直线AE的解析式为y=mx+n(m≠0),∴,得,∴直线AE的解析式为y=﹣x﹣1,过点P作y轴的平行线交AC于点G,如图2所示,设点P的横坐标为x,则P(x,x2+2x﹣3),点G(x,﹣x﹣1),∴PG=(﹣x﹣1)﹣(x2+2x﹣3)=﹣x2﹣x+2,又∵A(﹣3,0),E(,﹣),∴S△APE =S△APG+S△PEG=(﹣x2﹣x+2)(x+3)+(﹣x2﹣x+2)(﹣x)=(﹣x2﹣x+2)(3+)=(x+)2+,∴当x=﹣时,S取得最大值,最大值是,△APE把x=﹣代入y=x2+2x﹣3,得y=(﹣)2+2×(﹣)﹣3=﹣,∴此时点P的坐标为(﹣,﹣).12.解:(1)∵抛物线y=﹣2x2+bx+c过A(﹣1,0)、B(3,0)两点,∴,得,∴y=﹣2x2+4x+6=﹣2(x﹣1)2+8,∴抛物线的对称轴是直线x=1,即该抛物线的解析式为y=﹣2x2+4x+6,对称轴是直线x=1;(2)分两种情况:设点D的坐标为(1,y)第一种情况是:∠BCD=90°时,则CD2+BC2=BD2,∵点B的坐标为(3,0),抛物线y=﹣2x2+4x+6交y轴于点C,∴点C的坐标为(0,6),∴[12+(y﹣6)2]+(32+62)=(3﹣1)2+y2,解得,y=6.5,∴点D的坐标为(1,6.5);第二种情况:当∠DBC=90°时,BD2+BC2=CD2,即[(3﹣1)2+y2]+(32+62)=12+(6﹣y)2,解得,y=﹣1,∴点D的坐标为(1,﹣1),综上所述,符合条件的点D的坐标为(1,6.5),(1,﹣1);(3)因为点C的坐标为(0,6),点B的坐标为(3,0),设直线BC的解析式为y=kx+6,则3k+6=0,得k=﹣2,即直线BC的解析式为y=﹣2x+6,如右图所示,作点E关于直线BC的对称点E′交BC于点F,过点F作FN⊥y轴于点N,设E(0,m),E′(x,y),则EE′⊥BC,∴∠CFE=∠COB=90°,∴BC==3,∵∠ECF=∠BCO,∴△ECF∽△BCO,∴,即,解得,CF=,又∵∠CNF=∠COB,∠NCF=∠OCB,∴△NCF∽△OCB,∴,即,解得,FN=,∴点F的横坐标为,把x=代入直线BC的解析式,得y=,∴点F的坐标为(,),∵EE′关于直线BC对称,∴点F为EE′的中点,∴,解得,∴E′(,),∵点E′在抛物线y=﹣2x2+4x+6上,∴=﹣2×[]2+4×+6,解得,m1=6,m2=,∴点E的坐标为(0,6)或(0,).13.证明:(1)设A(b,ab2),B(c,ac2),∵∠AOB=90°,∴AB2=AO2+BO2,∴(b﹣c)2+(ab2﹣ac2)2=b2+a2b4+c2+a2c4,﹣2bc﹣2a2b2c2=0,1+a2bc=0,∴bc=﹣,设直线AB的解析式为:y=mx+n,则,解得,∴直线AB的解析式为:y=a(b+c)x﹣abc,当x=0时,y=OC=﹣abc=﹣a•(﹣)=;(2)如图2,过A作AD⊥y轴于D,设直线AB的解析式为:y=kx+b,当y=0时,kx+b=0,∴x=﹣,∴OC=﹣,∵过点A的直线AB恰好与此抛物线仅有一个交点,∴ax2=kx+b,∴ax2﹣kx﹣b=0,△=k2+4ab=0,∴b =﹣,OC =﹣=,∴x =,∵a >0,k >0,∴AD =,∵AD ∥OC , ∴==,∴AB =2BC ,∴AC =BC .14.解:(1)把B (﹣1,0),D (2,﹣2)代入y =ax 2﹣x +c 得, 解得:.故抛物线的解析式为y =x 2﹣x ﹣2;(2)当y =0时,x 2﹣x ﹣2=0,解得x 1=﹣1,x 2=3,∴A (3,0),∴AB =4,当x =0时,y =﹣2,∴C (0,﹣2),∴OC =2,∴S △ABC =×4×2=4,设AC 的解析式为y =kx +b ,把A (3,0),C (0,﹣2)代入y =kx +b 得, 解得.∴y =x ﹣2,如图1,过点E 作x 轴的垂线交直线AC 于点F ,设点F (a ,a ﹣2),点E (a ,a 2﹣a ﹣2),其中﹣1<a <3,∴S △ACE =EF |x A ﹣x C |=|a 2﹣a |=,∵S △ACE =S △ABC ,∴a 2﹣3a =2或﹣a 2+3a =2,解得a 1=(舍去),a 2=,a 3=1,a 4=2, ∴E 1(,),E 2(1,﹣),E 3(2,﹣2);(3)在y =ax 2+bx ﹣2中,当x =0时,y =﹣2,∴C (0,﹣2),∴OC =2,如图2,设P (0,m ),则PC =m +2,OA =3,AC ==,①当PA =CA 时,则OP 1=OC =2,∴P 1(0,2);②当PC =CA =时,即m +2=,∴m =﹣2, ∴P 2(0,﹣2); ③当PC =PA 时,点P 在AC 的垂直平分线上,则△AOC ∽△P 3EC , ∴=,∴P 3C =,∴m =,∴P 3(0,),④当PC =CA =时,m =﹣2﹣,∴P 4(0,﹣2﹣).综上所述,P点的坐标(0,2)或(0,﹣2)或(0,)或(0,﹣2﹣).15.解:(1)由已知可求B(6,0),C(0,4),将点B(6,0),C(0,4)代入y=﹣+bx+c,则有,解得,∴y=﹣x2+x+4,令y=0,则﹣x2+x+4=0,解得x=﹣1或x=6,∴A(﹣1,0);(2)∵点D在抛物线上,且横坐标为3,∴D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;∴E(0,8),F(6,8),∴S△BCD =S梯形ECBF﹣S△CDE﹣S△BFD=(EC+BF)×OB﹣×EC×ED﹣×DF×BF=×(4+8)×6﹣×4×3﹣×3×8=36﹣6﹣12=18;(3)设P(m,﹣m2+m+4),∵PQ垂直于x轴,∴Q(m,0),且∠PQO=90°,∵∠COB=90°,∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,==,∴=,解得m=5或m=﹣1,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=5,∴P(5,4);②△PAQ∽△BCO时,==,∴=,解得m=﹣1或m=,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=,∴P(,);综上所述:P(5,4)或P(,)时,点A、P、Q为顶点的三角形与△BOC相似.。
2020年中考数学压轴解答题10 二次函数与线段关系及最值定值问题(学生版)

备战2020中考数学之解密压轴解答题命题规律专题10 二次函数与线段关系及最值定值问题【类型综述】图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用. 一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【方法揭秘】由勾股定理产生的函数关系,在两种类型的题目中比较常用.类型一,已知“边角边”,至少一边是动态的,求角的对边.如图1,已知点A 的坐标为(3, 4),点B 是x 轴正半轴上的一个动点,设OB =x ,AB =y ,那么我们在直角三角形ABH 中用勾股定理,就可以得到y 关于x 的函数关系式.类型二,图形的翻折.已知矩形OABC 在坐标平面内如图2所示,AB =5,点O 沿直线EF 翻折后,点O 的对应点D 落在AB 边上,设AD =x ,OE =y ,那么在直角三角形AED 中用勾股定理就可以得到y 关于x 的函数关系式.图1 图2【典例分析】【例1】如图①,矩形ABCD 中,2,5,1AB BC BP ===,090MPN ∠=,将MPN ∠绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB (或AD )于点E ,PN 交边AD (或CD )于点F .当PN 旋转至PC 处时,MPN ∠的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D ,此时ABP ∆是否与PCD ∆相似?并说明理由;(2)类比探究:如图③,在旋转过程中,PEPF的值是否为定值?若是,请求出该定值;若不是,请说明理由; (3)拓展延伸:设AE t =时,EPF ∆的面积为S ,试用含t 的代数式表示S ;①在旋转过程中,若1t =时,求对应的EPF ∆的面积; ②在旋转过程中,当EPF ∆的面积为4.2时,求对应的t 的值.【例2】如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG ,DG 上的动点(与端点不重合),且∠DMN =∠DAM ,设AM =x ,DN =y . ①写出y 关于x 的函数解析式,并求出y 的最小值;②是否存在这样的点M ,使△DMN 是等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.【例3】抛物线2(0)y ax bx c a =++≠与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点(0,4)C -.已知(2,0)A -,抛物线的对称轴l 交x 轴于点(1,0)D . (1)求出,,a b c 的值;(2)如图1,连接BC ,点P 是线段BC 下方抛物线上的动点,连接,PB PC .点,M N 分别在y 轴,对称轴l 上,且MN y ⊥轴.连接,AM PN .当PBC ∆的面积最大时,请求出点P 的坐标及此时AM MN NP ++的最小值;(3)如图2,连接AC ,把AOC ∆按照直线y x =对折,对折后的三角形记为A OC ∆'',把A OC ∆''沿着直线BC 的方向平行移动,移动后三角形的记为A O C ∆''''',连接DA '',DC '',在移动过程中,是否存在DA C ∆''''为等腰三角形的情形?若存在,直接写出点C ''的坐标;若不存在,请说明理由.【例4】如图在锐角△ABC 中,BC =6,高AD =4,两动点M 、N 分别在AB 、AC 上滑动(不包含端点),且MN ∥BC,以MN 为边长向下作正方形MPQN,设MN =x,正方形MPQN 与△ABC 公共部分的面积为y . (1)如图(1),当正方形MPQN 的边P 恰好落在BC 边上时,求x 的值;(2)如图(2),当PQ 落△ABC 外部时,求出y 与x 的函数关系式(写出x 的取值范围)并求出x 为何值时y 最大,最大是多少?【例5】如图,抛物线y=12-x2+mx+m(m>0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.【例6】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B 点的坐标为(3,0),与y轴交于点C(0,﹣3).(1)求二次函数解析式;(2)若点Q为抛物线上一点,且S△ABQ=12S△ACQ,求点Q的坐标;(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若HM HNHP⋅=5,求m的值.【变式训练】1.如图,抛物线y =ax 2+4x +c (a ≠0)与反比例函数y =5x的图象相交于点B ,且点B 的横坐标为5,抛物线与y 轴交于点C (0,6),A 是抛物线的顶点,P 和Q 分别是x 轴和y 轴上的两个动点,则AQ +QP +PB 的最小值为_____.2.如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D 是抛物线 y =﹣x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为__________3.己知抛物线2114y x =+具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等,如图,点M 的坐标为(3,3),P 是抛物线2114y x =+上一个动点,则△PMF 周长的最小值是__________.4.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 方向以2/s 的速度向点D 运动,过P 点作PE ∥BC 交AC 于点E ,过E 点作EF ⊥BC 于点F ,设△ABP 的面积为S 1,四边形PDFE 的面积为S 2,则点P 在运动过程中,S 1+S 2的最大值为______.5.在平面直角坐标系中,已知()A 2,4、()P 1,0,B 为y 轴上的动点,以AB 为边构造ABC V ,使点C 在x 轴上,BAC 90.M ∠=o 为BC 的中点,则PM 的最小值为______.6.如图,在平面直角坐标系中,抛物线y=﹣x 2+4x 与x 轴交于点A,点M 是x 轴上方抛物线上一点,过点M 作MP ⊥x 轴于点P,以MP 为对角线作矩形MNPQ,连结NQ,则对角线NQ 的最大值为_________.7.如图,在平面直角坐标系中,过A (-1,0)、B (3,0)两点的抛物线交y 轴于点C,其顶点为点D,设△ACD 的面积为S 1,△ABC 的面积为S 2.小芳经探究发现:S 1︰S 2是一个定值.这个定值为________.8.如图,在平面直角坐标系中,有二次函数23333y x x =--+,顶点为H ,与x 轴交于A 、B 两点(A 在B 左侧),易证点H 、B 关于直线3:33l y x =+对称,且A 在直线l 上.过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,则HN NM MK ++的最小值为________9.如图,抛物线2(0)y ax bx c a =++≠与直线1y x =+相交于(1,0)A -,(4,)B m 两点,且抛物线经过点(5,0)C(1)求抛物线的解析式.(2)点P 是抛物线上的一个动点(不与点A 点B 重合),过点P 作直线PD x ⊥轴于点D ,交直线AB 于点E .当2PE ED =时,求P 点坐标;(3)如图所示,设抛物线与y 轴交于点F ,在抛物线的第一象限内,是否存在一点Q ,使得四边形OFQC 的面积最大?若存在,请求出点Q 的坐标;若不存在,说明理由.10.如图,在矩形ABCD 中,AB=18,AD=12,点M 是边AB 的中点,连结DM,DM 与AC 交于点G ,点E,F 分别是CD 与DG 上的点,连结EF,(1)求证:CG=2AG .(2)若DE=6,当以E,F,D 为顶点的三角形与△CDG 相似时,求EF 的长.(3)若点E 从点D 出发,以每秒2个单位的速度向点C 运动,点F 从点G 出发,以每秒1个单位的速度向点D 运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG 的面积的最小值.11.如图①,抛物线y=a(x 2+2x-3)(a≠0)与x 轴交于点A 和点B,与y 轴交于点C,且OC=OB.(1)直接写出点B 的坐标是( , ),并求抛物线的解析式;(2)设点D 是抛物线的顶点,抛物线的对称轴是直线l,连接BD,线段OC 上的点E 关于直线l 的对称点E'恰好在线段BD 上,求点E 的坐标;(3)若点F 为抛物线第二象限图象上的一个动点,连接BF,CF,当△BCF 的面积是△ABC 面积的一半时,求此时点F 的坐标.12.如图,抛物线y =﹣x 2+mx +2与x 轴交于点A ,B ,与y 轴交于点C ,点A 的坐标为(1,0) (1)求抛物线的解析式(2)在抛物线的对称轴l 上找一点P ,使PA +PC 的值最小,求出点P 的坐标 (3)在第二象限内的抛物线上,是否存在点M ,使△MBC 的面积是△ABC 面积的12?若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线212y x mx n =++交x 轴于A 、B 两点,直线y=kx+b 经过点A,与这条抛物线的对称轴交于点M (1,2),且点M 与抛物线的顶点N 关于x 轴对称.(1)求抛物线的函数关系式;(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;(3)在(2)的条件下,求△AQC面积的最大值.14.如图,抛物线y=﹣12x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式;(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,点A在抛物线y=- x2 + 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB 的长.(2)点P 为线段AB .上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H,点F 为y 轴上一点,当∆PBE 的面积最大时,求PH + HF + 12FO 的最小值. (3)在(2)中,PH+HF+12方FO 取得最小值时,将∆CFH 绕点C 顺时针旋转60°后得到∆CF'H',过点F'作CF'的垂线与直线AB 交于点Q,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.16.已知,二次函数24y x x c =-+的图像与x 轴的一个交点为O(0,0),点P (m,0)是x 轴正半轴上的一个动点.(1)如图1,求二次函数的图像与x 轴另一个交点的坐标; (2)如图2,过点P 作x 轴的垂线交直线33y x =与点C,交二次函数图像于点D, ①当PD=2PC 时,求m 的值;如图3,已知A (3,-3)在二次函数图像上,连结AP,求12AP OP +的最小值;(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.17.如图1,已知抛物线y =ax2+bx +c 经过A(-3,0),B (1,0 ),C (0,3 )三点,其顶点为D,对称轴是直线l , l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求∆PBC 周长的最小值;(3)如图2,若 E 是线段AD 上的一个动点(E 与A, D 不重合),过 E 点作平行于y 轴的直线交抛物线于点 F ,交x 轴于点G ,设点 E 的横坐标为m ,四边形AODF 的面积为S 。
2020年中考数学二轮复习压轴专题:二次函数(解析版)

2020 年中考数学二轮复习压轴专题:《二次函数》1.如图,平面直角坐标系中,点 A、点B 在 x 轴上(点A在点B 的左边),点 C在第一象限,知足∠ ACB为直角,且恰使△OCA∽△ OBC,抛物线y=ax2﹣8ax+12a( a<0)经过A、 B、C三点.(1)求线段OB、OC的长.(2)求点C的坐标及该抛物线的函数关系式;( 3)在x 轴上能否存在点,使△为等腰三角形?若存在,求出全部切合条件的P P BCP点的坐标:若不存在,请说明原因.解:( 1)y=ax2﹣ 8ax+12a=a(x﹣ 6)(x﹣ 2),故 OA=2, OB=6,△ OCA∽△ OBC,则2,即: OC= OA?OB,解得: CO=2;( 2)过点C作CD⊥x轴于点D,△ OCA∽△ OBC,则,设 AC=2x,则BC=2x,而AB=4,故 16=( 2x)2+( 2x)2,解得:x=1,故 AC=2, BC=2,S△ABC=AB× CD=AC× BC,解得: CD=,故 OD=3,故点 C(3,);将点 C的坐标代入抛物线表达式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x﹣4;( 3)设点P( m,0),而点B、 C的坐标分别为:(6,0)、(3,);2222则 BC=12,PB =( m﹣6), PC=( m﹣3)2+3,当BC=PB时,12=(m﹣6)2,解得:m=6;当 BC=PC时,同理可得: m=6(舍去)或0;当 PB=PC时,同理可得: m=4,综上点 P 的坐标为:(6, 0)或( 0, 0)或( 4, 0).2.直线y=﹣x+2与 x 轴交于点A,与 y 轴交于点 B,抛物线y=﹣ x2+bx+c 经过 A、 B 两点.(1)求这个二次函数的表达式;(2)若P是直线AB上方抛物线上一点;①当△ PBA的面积最大时,求点 P 的坐标;②在①的条件下,点 P 对于抛物线对称轴的对称点为Q,在直线 AB上能否存在点 M,使得直线QM与直线BA的夹角是∠QAB的两倍?若存在,直接写出点M的坐标;若不存在,请说明原因.解:( 1)直线y=﹣x+2与 x 轴交于点 A,与 y 轴交于点B,则点 A、 B 的坐标分别为:( 4, 0)、( 0, 2),将点、B 的坐标代入抛物线表达式得:,解得:,A故抛物线的表达式为:y=﹣ x2+x+2;2( 2)①过点P作y轴的平行线交BC于点 N,设 P(m,﹣ m+ m+2),点 N( m,﹣m+2),则:△ PBA的面积 S=2m+2+2PN× OA=×4×(﹣ m+m﹣2)=﹣ m+4m,当 m=2时, S 最大,此时,点 P(2,5);②点 P(2,5),则点 Q(, 5),设点M(a,﹣a+2);(Ⅰ)若:∠QMB QAM QM AM 1=2∠1,则1=1,则( a﹣)2+(a﹣3)2=( a﹣4)2+(﹣a+2)2,解得: a=,M,);故点1((Ⅱ)若∠QMB QAM2= 2∠ 1 ,则∠ QM2B=∠ QM1B, QM1= QM2,作 QH⊥AB于 H,BQ的延伸线交x 轴于点 N,则 tan ∠BAO==,则tan∠QNA=2,故直线QH表达式中的k 为2,设直线QH的表达式为:y=2x+b,将点Q的坐标代入上式并解得:b=2,故直线QH的表达式为:y=2x+2,故H(0,2)与 B 重合,M、M对于21B 对称,∴ M(﹣2,);综上,点M的坐标为:(,)或(﹣,).3.如图已知直线y=x+与抛物线y= ax2+bx+c 订交于 A(﹣1,0), B(4, m)两点,抛物线 y= ax2+bx+c 交 y 轴于点 C(0,﹣),交x轴正半轴于D点,抛物线的极点为M.(1)求抛物线的分析式;(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点 P的坐标;( 3)若点Q为x轴上一动点,点N 在抛物线上且位于其对称轴右边,当△QMN与△ MAD 相像时,求N点的坐标.解:( 1)将点B( 4,m)代入y=x+,∴ m=,将点 A(﹣1,0), B(4,),C(0,﹣)代入y=ax2+bx+c,解得 a=,b=﹣1,c=﹣,∴函数分析式为 y= x2﹣ x﹣;( 2)设P(n,n2﹣n﹣),则经过点 P 且与直线 y= x+垂直的直线分析式为y=﹣2x+n2+n﹣,直线 y=x+与其垂线的交点G(n2+ n﹣,n 2+ n+),∴ GP=(﹣ n2+3n+4),当 n=时, GP最大,此时△ PAB的面积最大,∴P(,),∵AB=,PG=,∴△ PAB的面积=××=;(3)∵M( 1,﹣ 2),A(﹣ 1, 0),D( 3,0),∴ AM=2, AB=4, MD=2,∴△ MAD是等腰直角三角形,∵△ QMN与△ MAD相像,∴△ QMN是等腰直角三角形,设 N(t ,t 2﹣ t ﹣)①如图 1,当MQ⊥QN时,N( 3, 0);②如图 2,当QN⊥MN时,过点N作 NR⊥ x 轴,过点 M作 MS⊥ RN交于点 S,∵QN=MN,∠ QNM=90°,∴△ MNS≌△ NMS( AAS)∴﹣ 1=﹣t 2+ + ,t t ∴ t =±,∴ t >1,∴ t =,∴N(,1﹣);③如图 3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点N作NR∥x轴,与过 M点的垂线分别交于点S、 R;∵QN=MQ,∠MQN=90°,∴△ MQR≌△ QNS( AAS),∴ SQ=QR=2,∴ t +2=1+t 2﹣ t ﹣,∴t =5,∴N(5,6);④如图 4,当MN⊥NQ时,过点M作 MR⊥ x 轴,过点 Q作 QS⊥ x 轴,过点N 作x轴的平行线,与两垂线交于点、;R S∵QN=MN,∠MNQ=90°,∴△ MNR≌△ NQS( AAS),∴ SQ=RN,∴ t 2﹣ t ﹣= t ﹣1,∴ t =2±,∵ t >1,∴ t =2+,∴N(2+, 1+);综上所述: N(3,0)或 N(2+, 1+)或 N(5,6)或 N(,1﹣).4.如图,在平面直角坐标系中,已知矩形ABCD的三个极点B(4,0)、C(8,0)、D(8,8).抛物线的分析式为y= ax2+bx.( 1)如图 1,若抛物线经过A,D两点,直接写出 A 点的坐标(4,8);抛物线的对称轴为直线6;( 2)如图 2:①若抛物线经过A、C两点,求抛物线的表达式.②若点 P 为线段 AB上一动点,过点P 作 PE⊥ AB交 AC于点 E,过点 E 作 EF⊥AD于点 F交抛物线于点G.当线段 EG最长时,求点E的坐标;( 3)若a =﹣ 1,且抛物线与矩形没有公共点,直接写出b的取值范围.ABCD解:( 1)点A的坐标为:( 4, 8);函数的对称轴为:x=(4+8)=6;故答案为:( 4,8); 6;( 2)①将点A、C的坐标代入抛物线表达式并解得:a=﹣,b=4,故抛物线的表达式为:y=﹣x2+4x;②由点 A、 C的坐标得,直线AC的表达式为: y=﹣2x+16;设点 E( x,﹣2x+16),则点 G( x,﹣x2+4x),EG=﹣x2+4x﹣(﹣2x+16)=﹣x2+6x﹣16,当 x=6时, EG由最大值为:2,此时点 E(2,4);( 3)若a=﹣ 1,则抛物线的表达式为:y=﹣ x2+bx,当抛物线过点B和点 D时,抛物线与矩形有一个交点,将点 B的坐标代入抛物线表达式得:0=﹣ 16+4b,解得:b= 4,将点 D的坐标代入抛物线表达式并解得:b=9,故 b 的取值范围为:b<4或 b>9.5.如图,直线y =﹣1 与抛物线y=﹣x2+6 ﹣5 订交于、D两点.抛物线的极点为,连x x A C结 AC.( 1)求A,D两点的坐标;( 2)点P为该抛物线上一动点(与点A、 D不重合),连结 PA、PD.①当点 P 的横坐标为 2 时,求△PAD的面积;②当∠ PDA=∠ CAD时,直接写出点P的坐标.解:( 1)联立方程组,解得,,,∴(1,0),(4,3),A D( 2)①过P 作⊥轴,与订交于点,PE x AD E∵点 P的横坐标为2,∴P(2,3), E(2,1),∴PE=3﹣1=2,∴=3;②过点 D作 DP∥AC,与抛物线交于点P,则∠ PDA=∠ CAD,∵y=﹣ x2+6x﹣5=﹣( x﹣3)2+4,∴ C(3,4),设 AC的分析式为: y= kx+b( k≠0),∵A(1,0),∴,∴,∴AC的分析式为: y =2x﹣2,设 DE的分析式为: y=2x+n,把D(4,3)代入,得3=8+n,∴n=﹣5,∴DE的分析式为: y=2x﹣5,联立方程组,解得,,,∴此时 P(0,﹣5),当 P 点在直线 AD上方时,延伸 DP,与 y 轴交于点 F,过 F 作 FG∥AC ,FG与 AD交于点 G,则∠ FGD=∠ CAD=∠ PDA,∴FG=FD,设 F(0, m),∵ AC的分析式为: y=2x﹣2,∴FG的分析式为: y=2x+m,联立方程组,解得,,∴ G(﹣ m﹣1,﹣ m﹣2),∴FG=,FD=,∵ FG=FD,∴=,∴ m=﹣5或1,∵ F 在 AD上方,∴ m>﹣1,∴ m=1,∴ F(0,1),设 DF的分析式为: y= qx+1( q≠0),把 D(4,3)代入,得4q+1=3,∴ q=,∴DF的分析式为: y= x+1,联立方程组∴,,∴此时P 点的坐标为,综上, P 点的坐标为(0,﹣ 5)或.6.综合与研究如图,抛物线y= ax2+bx+c( a≠0)经过点 A、 B、C,已知点 C(0,4),△ AOC∽△ COB,且,点 P 为抛物线上一点(异于A, B)(1)求抛物线和直线AC的表达式(2)若点P是直线AC上方抛物线上的点,过点P作PF⊥AB,与AC交于点E,垂足为F.当PE= EF时,求点 P 的坐标( 3)若点为x 轴上一动点,能否存在点,使得由,,,四点构成的四边形为平M P B C P M行四边形?若存在,直接写出点P 的坐标;若不存在,请说明原因解:( 1),则OA=4OC=8,故点A(﹣8,0);△ AOC∽△ COB,则△ ABC为直角三角形,2则 CO= OA?OB,解得: OB=2,故点 B(2,0);则抛物线的表达式为:y=a( x﹣2)( x+8),将点 C的坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+4;精选文档666AC的表达式为:y=x+4;由点A、 C的坐标可得直线( 2)设点P( x,﹣x2﹣x+4),则点E( x,x +4),PE= EF,即﹣x2﹣x+4﹣x﹣4=x+4;解得: x=﹣8(舍去)或﹣2,故点 P(﹣2,6);2( 3)设点P(m,n),n=﹣m﹣m+4,点 M(s,0),而点 B、C的坐标分别为:(2,0)、( 0, 4);①当 BC是边时,点 B 向左平移2个单位向上平移 4 个单位获得C,相同点 P( M)向左平移 2 个单位向上平移 4 个单位获得M( P),即 m﹣2= s, n+4=0或 m+2= s, n﹣4=0,解得: m=﹣6或﹣ 3,故点P的坐标为:(﹣6,4)或(﹣ 3,﹣ 4)或(﹣﹣3,﹣ 4);②当BC是对角线时,由中点公式得:2=m+s,n= 4,故点 P(﹣6,4);综上,点 P 的坐标为:(﹣6,4)或(﹣3,﹣4)或(﹣﹣3,﹣4).7.如图 1,抛物线y=x2+mx+4m与 x 轴交于点 A( x1,0)和点 B( x2,0),与 y 轴交于点C,且 x1, x2知足 x12+x22=20,若对称轴在y 轴的右边.(1)求抛物线的分析式.(2)如图 2,若点P为线段AB上的一动点(不与A、B重合),分别以AP、BP为斜边,在直线 AB的同侧作等腰直角三角形△ APM和△ BPN,试确立△ MPN最大时 P 点的坐标.( 3)若P(x1,y1),Q(x2,y2)是抛物线上的两点,当a≤ x1≤ a+2,x2≥时,均有y1≤ y2,求 a 的取值范围.解:( 1)x1+x2=﹣ 2m,x1x2=8m,则 x12+x22=( x1+x2)2﹣2x1x2=20,即(﹣ 2m)2﹣ 16m= 20,解得: m=5(舍去)或﹣1;故抛物线的表达式为:y=x2﹣ x﹣4;(2)令y=0,则x=﹣ 2 或 4,故点A、B的坐标分别为:(﹣ 2,0)、( 4,0),则AB=6;设: AP= a,则 PN=6﹣ a,∠ MPN=180°﹣∠ MPA﹣∠ NPB=90°;S△=×PN× PMMPN=a××(6﹣a)=a(6﹣ a)=﹣( a﹣3)2+;∴当a=3时, S最大,此时△MPNOP=1,故点P(1,0);( 3)函数的对称轴为x=1,如图,x=﹣2.5和 x=对于函数对称轴对称,纵坐标均为,由图象看, a≥﹣且a+2≤,解得:﹣≤ a≤.8.如图,在平面直角坐标系中,矩形ABCD的极点B, C, D 的坐标分别(1,0),(3,0),( 3, 4),以A为极点的抛物线y= ax2+bx+c 过点 C.动点 P 从点 A出发,以每秒个单位的速度沿线段AD向点D 匀速运动,过点P 作PE⊥ x 轴,交对角线AC于点N.设点P运动的时间为t (秒).( 1)求抛物线的分析式;( 2)若PN分△ ACD的面积为1: 2 的两部分,求t的值;( 3)若动点P 从A 出发的同时,点Q 从 C出发,以每秒1 个单位的速度沿线段CD向点D匀速运动,点H为线段PE上一点.若以C,Q,N,H为极点的四边形为菱形,求 t的值.解:( 1)∵四边形ABCD为矩形,且B(1,0), C(3,0), D(3,4),∴ A(1,4),设抛物线的分析式为y=a( x﹣1)2+4,将 C(3,0)代入 y= a(x﹣1)2+4,得 0=4a+4,解得 a=﹣1,∴抛物线的分析式为 y=﹣( x﹣1)2+4=﹣ x2+2x+3;(2)∵PE⊥x轴,DC⊥x轴,∴ PE∥DC,∴△ APN∽△ ADC,∵ PN分△ ACD的面积为1:2的两部分,∴=或,当=时,==,∵AD=2,∴ AP=,∴ t 的值为× 2=;当=时,==,∵ AD=2,∴ AP=,∴ t 的值为× 2=,综上所述,t 的值为或;( 3)如图 2﹣ 1,当CN为菱形的对角线时,点 P,N的横坐标均为,设直线的分析式为y =+ ,AC kx b将 A(1,4), C(3,0)代入 y= kx+b,得,解得,∴直线 AC的表达式为y=﹣2x+6,将点 N的横坐标代入y=﹣2x+6,得,即 EN=4﹣ t ,由菱形 CQNH可得, CQ= NH= t = CH,可得 EH=(4﹣ t )﹣ t =4﹣2t ,∵∴,,在 Rt △CHE中,222∵ CE+EH= CH,∴,解得, t 1=,t2=4(舍);如图 2﹣ 2,当CN为菱形的边时,由菱形 CQHN可得, CQ= CN= t ,在 Rt △CNE中,222∵ NE+CE= CN,∴( 4﹣t)2+( 2﹣t )2= t 2,解得, t 1=20﹣8, t 2=20+8(舍);综上所述,t的值为或.9.如图1,过原点的抛物线与x 轴交于另一点A,抛物线极点 C 的坐标为,其对称轴交 x 轴于点 B.( 1)求抛物线的分析式;( 2)如图2,点D为抛物线上位于第一象限内且在对称轴右边的一个动点,求使△ACD 面积最大时点D的坐标;( 3)在对称轴上能否存在点P,使得点 A对于直线OP的对称点 A'知足以点 O、A、C、A'为极点的四边形为菱形.若存在,恳求出点P的坐标;若不存在,请说明原因.解:( 1)设抛物线分析式为y= a( x﹣ h)2+k,( a≠0)∵极点,∴,又∵图象过原点,∴,解出:,∴,即;( 2)令y= 0,即,解得: x1=0, x2=4,∴ A(4,0),设直线 AC的分析式为y=kx+b,将点 A(4,0),代入,得,精选文档666解得,∴直线AC的分析式为y=﹣x+4,过点D作DF∥ y 轴交AC于点F,设,则,∴,∴=,∴当m=3时, S△ACD有最大值,当 m=3时,,∴;( 3)∵∠CBO=∠CBA= 90°,OB=AB= 2,∴,,∴OA=OC= AC=4,∴△ AOC为等边三角形,①如图 3﹣ 1,当点P在C时,OA=AC=CA'=OA' ,∴四边形 ACA'O是菱形,∴;②作点 C对于 x 轴的对称点 C',当点 A'与点 C'重合时, OC= AC=AA'= OA',∴四边形 OCAA'是菱形,∴点 P是∠ AOA'的角均分线与对称轴的交点,记为P2,∴,∵∠2= 90°,=2,OBP OB22∴ OP=2BP,∵∠2= 90°,=2,OBP OB∴OP2=2BP2,设 BP= x,2∴ OP=2x,2又∵,∴( 2x)2=22 +x2,解得或,∴;综上所述,点P的坐标为或.10.已知二次函数与x轴交于A、B(A在B的左边)与y 轴交于点 C,连接 AC、BC.( 1)如图 1,点P是直线BC上方抛物线上一点,当△ PBC面积最大时,点M、N分别为x、y 轴上的动点,连结PM、PN、 MN,求△ PMN的周长最小值;( 2)如图 2,点C对于x轴的对称点为点E,将抛物线沿射线AE的方向平移获得新的拋物线 y',使得 y'交 x 轴于点 H、B( H在 B 的左边).将△ CHB绕点 H 顺时针旋转90°至△C' HB'.抛物线 y'的对称轴上有一动点 S,坐标系内能否存在一点 K,使得以 O、C'、K、S 为极点的四边形是菱形,若存在,请直接写出点K 的坐标;若不存在,请说明原因.解:( 1)如图 1,A(﹣ 2, 0),B( 8, 0),C( 0, 4),∴直线的分析式为,BC过点 P作 y 轴平行线,交线段BC于点 Q,设,∴=,∵ 0<m< 8,∴ P(4,6).作 P 点对于 y 轴的对称点P1,P 点对于 x 轴的对称点 P2,连结 P1P 2交 x 轴、y 轴分别为 M,,N此时△的周长最小,其周长等于线段P1P2的长;PMN∵ P1(﹣4,6), P2(4,﹣6),∴.( 2)如图 2 中,∵ ( 0,﹣ 4),平移后的抛物线经过,,E E B∴抛物线的分析式为y =﹣x2+bx﹣ 4,把( 8, 0)代入获得b=4,B∴平移后的抛物线的分析式为y=﹣x+4x﹣4=﹣(x﹣2)(x﹣8),令 y=0,获得 x=2或8,∴ H(2,0),∵△ CHB绕点 H顺时针旋转90°至△ C′ HB′,∴C′(6,2),当 OC′= C′ S时,可得菱形 OC′S1 K1,菱形 OC′ S2K2,∵ ′=′==2,OC CS∴可得 S1(5,2﹣), S2(5,2+),∵点 C′向左平移一个单位,向下平移获得 S1,∴点 O向左平移一个单位,向下平移个单位获得K1,∴K1(﹣1,﹣),同法可得K2(﹣1,),当′=时,可得菱形′,菱形′,OC OS OC K3S3OC K4S4同法可得 K3(11,2﹣),K4(11,2+),当 OC′是菱形的对角线时,设2222,S5(5, m),则有 5 +m=1 +(2﹣ m)解得 m=﹣5,∴ S5(5,﹣5),∵点O向右平移5 个单位,向下平移 5 个单位获得S5,∴ C′向上平移 5 个单位,向左平移 5 个单位获得K5,∴ K5(1,7),综上所述,知足条件的点K的坐标为(﹣1,﹣)或(﹣ 1,)或( 11,2﹣)或( 11, 2+)或( 1,7).11.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2( a≠0)与 x 轴交于 A(﹣1,0),B(3,0)两点,与y 轴交于点 C.(1)求该抛物线的分析式;(2)如图①,若点D是抛物线上一个动点,设点D的横坐标为 m(0< m<3),连结 CD、BD、 BC、 AC,当△ BCD的面积等于△ AOC面积的2倍时,求 m的值;( 3)若点N为抛物线对称轴上一点,请在图②中研究抛物线上能否存在点M,使得以 B,C,M,N为极点的四边形是平行四边形?若存在,请直接写出全部知足条件的点M的坐标;若不存在,请说明原因.解:( 1)把(﹣ 1,0),( 3,0)代入y =ax2+bx+2 中,得:,解得:,A B∴抛物线分析式为;( 2)过点D作y轴平行线交BC于点 E,把 x=0代入中,得:y=2,∴ C点坐标是(0,2),又 B(3,0)∴直线的分析式为,BC∵∴∴=,由S =2S 得:△BCD△AOC∴,2整理得: m ﹣ 3m +2= 0解得: m = 1, m = 212∵ 0< m < 3∴ m 的值为 1 或 2;( 3)存在,原因:设:点的坐标为:( , ), =﹣2+x +2,点 ( 1, ),点 ( 3, 0)、 ( 0, 2),M m nnxNsBC①当是平行四边形的边时,BC当点 C 向右平移 3 个单位,向下平移 2 个单位获得 ,B相同点 M ( N )向右平移 3 个单位,向下平移 2 个单位 N ( M ),故: m +3= 1, n ﹣ 2= s 或 m ﹣ 3= 1, n +2= s ,解得: m =﹣ 2 或 4,故点M 坐标为:(﹣ 2,﹣)或(4,﹣);②当BC 为对角线时,由中点公式得:m +1= 3,n +3= 2,解得: m = 2,故点M ( 2,2);综上, M 的坐标为:( 2,2)或(﹣2,)或( 4,).12.已知抛物线 y =ax 2﹣ 2ax +3 与 x 轴交于点 A 、 B ( A 左 B 右),且 AB =4,与 y 轴交于 C 点.( 1)求抛物线的分析式;( 2)如图,证明:对于随意给定的一点 P (0, b )( b > 3),存在过点 P 的一条直线交抛物线于 M 、 N 两点,使得 PM = MN 建立;( 3)将该抛物线在 0≤ x ≤ 4 间的部分记为图象 G ,将图象 G 在直线 y = t 上方的部分沿 y= t 翻折,其他部分保持不变,获得一个新的函数的图象,记这个函数的最大值为,最m小值为 n ,若 m ﹣ n ≤ 6,求 t 的取值范围.解:( 1)抛物线y=ax2﹣ 2ax+3 的对称轴为x=1,又AB=4,由对称性得A(﹣ 1,0)、B ( 3, 0).把 A(﹣1,0)代入 y= ax2﹣2ax+3,得 a+2a+3=0,∴ a=﹣1.∴抛物线的分析式为 y=﹣ x2+2x+3.(2)如图,过M作GH⊥x轴,PG∥x轴,NH∥x轴,由 PM=MN,则△ PMG≌△ NMH( AAS),∴PG=NH, MG=MH.22设 M(m,﹣ m+2m+3),则 N(2m,﹣4m+4m+3),∵ P(0, b), GM= MH,∴y G+y H=2y M,222即 b+(﹣4m+4m+3)=2(﹣ m+2m+3),∴2m= b﹣3,∵ b>3,∴对于 m的方程总有两个不相等的实数根,此即说了然点M、 N存在,并使得PM=MN.证毕;( 3)图象翻折前后如右图所示,其极点分别为D(1,4)、 D′(1,2t ﹣4).①当 D′在点 H(4,﹣5)上方时,2t﹣ 4≥﹣ 5,∴t≥﹣,此时, m= t , n=﹣5,∵ m﹣ n≤6,∴ t +5≤6,∴ t ≤1,∴﹣≤ t ≤1;②当点 D′在点 H(4,﹣5)下方时,同理可得: t <﹣,m=t,n=2t﹣4,由 m﹣n≤6,得 t ﹣(2t ﹣4)≤6,∴ t ≥﹣2,∴﹣2≤t<﹣.综上所述,t的取值范围为:﹣2≤t≤ 1.y 轴交于13.如图,抛物线y= ax2+bx﹣2的对称轴是直线x=1,与x 轴交于A,B两点,与点 C,点A 的坐标为(﹣2,0),点P 为抛物线上的一个动点,过点P 作PD⊥ x 轴于点D,E.交直线BC于点(1)求抛物线分析式;(2)若点P在第一象限内,当OD= 4PE时:①求点 D、 P、 E的坐标;②求四边形 POBE的面积.(3)在( 2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,能否存在这样的点 M和点 N,使得以点 B, D, M,N为极点的四边形是菱形?若存在,直接写出点 N的坐标;若不存在,请说明原因.解:( 1)∵抛物线y= ax2+bx﹣2的对称轴是直线x=1, A(﹣2,0)在抛物线上,∴x =﹣= 1,解得:a=,b=﹣,抛物线分析式为y=x2﹣x﹣2;( 2)令y=x2﹣x﹣2=0,( x﹣4)( x+2)=0,解得: x1=﹣2, x2=4,当 x=0时, y=﹣2,由 B(4,0), C(0,﹣2),得,直线BC的表达式为: y=x﹣2设 D(m,0),∵ DP∥ y 轴,∴ E( m,m﹣2), P( m,m2﹣ m﹣2),∵ OD=4PE,2m﹣2﹣ m+2),∴ m=4( m﹣∴ m=5, m=0(舍去),∴ D(5,0), P(5,),E(5,),∴四边形 POBE的面积= S△OPD﹣ S△EBD=× 5×﹣× 1×=;( 3)存在,设M( n,n ﹣2),①以 BD为对角线,如图1,∵四边形 BNDM是菱形,∴MN垂直均分 BD,∴n=4+,∴M(,),∵M,N对于 x 轴对称,∴N(,﹣);②以BD为边,如图2,∵四边形 BDMN是菱形,∴MN∥BD, MN=BD= MD=1,过 M作 MH⊥ x 轴于 H,222∴ MH+DH= DM,即(n﹣2)2+( n﹣5)2=12,∴n1=4(不合题意), n2=5.6,∴N(4.6,),同理(n ﹣ 2)2+(4﹣)2= 1,n∴ n1=4+(不合题意,舍去),n2=4﹣,∴N(5﹣,﹣),③以 BD为边,如图3,过 M作 MH⊥ x 轴于 H,∴2+2=2,MH BH BM即(n﹣2)2+( n﹣4)2=12,∴ n1=4+, n2=4﹣(不合题意,舍去),∴N(5+,),综上所述,点 N坐标为:()或(,)或( 5﹣,)或(5+,).14.如图,矩形中,为原点,点A 在y轴上,点C在x轴上,点B的坐标为( 4,3),OABC O抛物线y =﹣x2+ +与y轴交于点,与直线AB交于点,与x轴交于,两点.bx c A D C E( 1)求抛物线的表达式;( 2)点P 从点C出发,在线段上以每秒 1 个单位长度的速度向点B运动,与此同时,CB点Q 从点A出发,在线段上以每秒个单位长度的速度向点C运动,当此中一点抵达AC终点时,另一点也停止运动.连结、、,设运动时间为t (秒).DP DQ PQ①当 t 为什么值时,△ DPQ的面积最小?②能否存在某一时辰t ,使△ DPQ为直角三角形?若存在,直接写出t 的值;若不存在,请说明原因.解:( 1)点A( 0, 3),点C( 4, 0),将点 A、 C的坐标代入抛物线表达式,解得:b=,c=3,故抛物线的表达式为:y=﹣x2+x+3;( 2)y=﹣x2+x+3=﹣(x﹣4)(x+2),故点E(﹣2,0);抛物线的对称轴为:x=1,则点 D(2,3),由题意得:点Q(t ,3﹣ t ),点 P(4, t ),①△ DPQ的面积= S△ABC﹣( S△ADQ+S△PQC+S△BPD)=3×4﹣ [2 ×t +2( 3﹣t)+( 5﹣)× t ×]= t 2﹣2t .∵> 0,故△的面积有最小值,此时,t =;DPQ②点( 2, 3),点(t , 3﹣),点(4,),D Q t P t (Ⅰ)当是斜边时,如图1,PQ过点作⊥于点,则=,=2﹣t ,= 4﹣ 2=2,=3﹣,Q QM ABMMQ t MD BD PBt则 tan ∠MQD= tan ∠BDP,即,解得:t=(舍去);(Ⅱ)当 PD为斜边时,过点 Q作 y 轴的平行线交AB于点 N,交过点 P 于 x 轴的平行线于点M,则 ND=2﹣t , QN= t ,MP=4﹣t , QM=3﹣ t ﹣ t =3﹣2t ,同理可得:,解得: t =或;(Ⅲ)当 QD为斜边时,同理可得:故t =;综上, t =或或或.15.如图,已知抛物线y= ax2+bx+3经过点 A(﹣1,0)、B(3,0),且与 y 轴交于点 C,抛物线的极点为D,连结 BD,点 P 是线段 BD上的一个动点(不与B、 D)重合.( 1)求抛物线的分析式,并写出极点D的坐标;( 2)过点P 作⊥轴于点,求△面积的最大值及获得最大值时P点的坐标;PE y E PBE(3)在( 2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断能否存在这样的点 M,使得以点 B, P, M, N为极点的四边形是平行四边若存在,请直接写出点 M 的坐标:若不存在,请说明原因.解:( 1)∵二次函数y= ax2+bx+3经过点 A(﹣1,0)、B(3,0)∴因此二次函数的分析式为:y=﹣ x2+2x+3∵ y=﹣ x2+2x+3=﹣( x﹣1)2+4∴ D的坐标为(1,4);( 2)设BD的分析式为y= kx+b∵过点 B(3,0), D(1,4)∴解得BD的分析式为y=﹣2x+6设 P(m,﹣2m+6),∵ PE⊥y 轴于点 E,∴ PE=m,△ BPE的 PE边上的高 h=﹣2m+6,∴ S =×PE× h= m(﹣2m+6)△BPE2=﹣ m+3m=,∵ a=﹣1<0,∴当 m=时△ BPE的面积获得最大值为,当 m=时, y=﹣2×+6=3,∴ P 的坐标是(,3);2( 3)设点M(s, 0),点N(m,n),n=﹣m+2m+3,①当 BP是边时,点 P 向右平移个单位向下平移 3 个单位获得B,同理点 M( N)向右平移个单位向下平移 3 个单位获得N( M),即 s=m,0± 3=n,解得: s=﹣或或;②当 PB为对角线时,m+s=3+,n=3,解得: s=或,故: M点的坐标为:;;;;;.。
2020年中考数学二轮复习专题 二次函数综合(含答案)
2020年中考数学二轮复习专题 二次函数综合(含答案)一、单选题1.二次函数2,0y ax bx c a =++≠()的图象如图如图所示,若M a b c =+-,42N a b c =+-,2P a b =-.则M N P ,,中,值小于0的数有( )A. 3个B. 2个C. 1个D. 0个2.已知抛物线c bx ax y ++=2的图象如图所示,则下列结论中正确的结论有( ) ①0>abc ;②2=++c b a ;③21<a ; ④1>b A.①②B.②③C.③④D.②④3.从车站向东走400米,再向北走500米到小红家;从车站向北走500米,再向西走200米到小强家,则( )A .小强家在小红家的正东B .小强家在小红家的正西C .小强家在小红家的正南D .小强家在小红家的正北4.如图是二次函数2y ax bx c =++图象的一部分,其对称轴为1x =-,且过点(-3,0).下列说法中说法正确的是( )①0abc <; ②20a b -=;③420a b c <++,④若()15y -, ,25,2y ⎛⎫⎪⎝⎭是抛物线上两点,则12y y >A.①②B.②③C.①②④D.5.梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次性购买种子数量x (单位:千克)之间的函数关系如图所示.下列四种说法: ①一次购买种子数量不超过10千克时,销售价格为5元/千克; ②一次购买30千克种子时,付款金额为100元;③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折: ④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱. 其中正确的个数是( ).A. 1个B. 2个C. 3个D. 4个6.函数b kx y +=的图象如图所示,当y>0时,x 的取值范围是( )A 、 x>1B 、 x>2C 、 x<1D 、 x<27.若二次函数2() 0y ax bx c a =++≠的图象与x 轴有两个交点,坐标分别为()()12,0,,0x x ,且12x x <,图象上有一点00,Mx y ()在x 轴下方,则下列判断正确的是( ) A.0a >B.240b ac -≥C.102x x x <<D.()()01020a x x x x --<.8.已知一次函数b kx y +=,y 随着x 的增大而减小,且0<kb ,则在直角坐标系内它的大致图象是( )9.反比例函数myx=的图象如图所示,下列结论:①常数1m<-;②在每个象限内,y随x的增大而增大;③若点()1,A h-,()2,B k在图象上,则h k<;④若点(),P x y在图象上,则点()',P x y--也在图象上。
2020年中考数学二次函数真题汇编(带答案)

2020年中考数学二次函数真题汇编(名师精选全国真题,值得下载练习)一、单选题1.如图,一段抛物线y=﹣x 2+4(﹣2≤x≤2)为C 1 , 与x 轴交于A 0 , A 1两点,顶点为D 1;将C 1绕点A 1旋转180°得到C 2 , 顶点为D 2;C 1与C 2组成一个新的图象,垂直于y 轴的直线l 与新图象交于点P 1(x 1 , y 1),P 2(x 2 , y 2),与线段D 1D 2交于点P 3(x 3 , y 3),设x 1 , x 2 , x 3均为正数,t=x 1+x 2+x 3 , 则t 的取值范围是( )A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12 【答案】D【解析】【解答】解:翻折后的抛物线的解析式为y=(x ﹣4)2﹣4=x 2﹣8x+12, ∵设x 1 , x 2 , x 3均为正数,∴点P 1(x 1 , y 1),P 2(x 2 , y 2)在第四象限, 根据对称性可知:x 1+x 2=8, ∵2≤x 3≤4,∴10≤x 1+x 2+x 3≤12即10≤t≤12, 故答案为:D .【分析】根据题意可求出翻折后的抛物线的解析式,设x 1 , x 2 , x 3均为正数,可得出点P 1(x 1 , y 1),P 2(x 2 , y 2)在第四象限,根据对称性可求出x 1+x 2=8,由2≤x 3≤4,可得出x 1+x 2+x 3的取值范围,从而得出t 的取值范围。
2.已知,平面直角坐标系中,直线y 1=x+3与抛物线y=-x x 的图象如图,点P 是y 2上的一个动点,则点P 到直线y 1的最短距离为( )A.B.C. D.【答案】D【解析】【解答】解、∵点P 到直线y 1的距离最短, ∴点P 是直线与抛物线相切时的交点。
设直线y 1平移k 个单位长度,则此时的解析式为 =x+3+k , 把 =x+3+k 代入y=-x 2+2x 整理得,-x 2+x-3-k=0,△=b 2-4ac=1-4 (-) (-3-k)=0,解得k=-,即直线y 1向下平移个单位长度与抛物线相切, 把k=-代入解析式解方程组可求得点P 的坐标为(1,);过点P 作PD ⊥直线y 1于点D ,则直线PD 的解析式可设为y 3=-x+b ,把点P (1,)代入可求得b=,即直线PD 的解析式为y 3=-x+,将y 1和y 3的解析式联立解方程组可求得点D 的坐标为(-,);若直线PD与x轴相较于点C,直线y1=x+3与x、y轴分别相较于点A、B,易得点A (-3,0)、B(0,3),∴∠BAC==∠DCA,由勾股定理可得:CD=,CP=,∴PD=CD-CP=。
2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型(含详细解答)

2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型一、基础过关1. (2019宿迁)如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,-3).(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足∠P AB=2∠ACO.求点P的坐标;(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.第1题图2. (2019贺州)如图,在平面直角坐标系中,已知点B的坐标为(-1,0),且OA=OC=4OB,抛物线y =ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P 的坐标及PD的最大值.第2题图二、能力提升1. (2019菏泽)如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,-2),点A 的坐标是(2,0),P 为抛物线上的一个动点,过点P 作PD ⊥x 轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线x =-1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积;(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.第1题图三、满分冲关1. (2019襄阳)如图,在直角坐标系中,直线y =-12x +3与x 轴,y 轴分别交于点B ,点C ,对称轴为x=1的抛物线过B , C 两点,且交x 轴于另一点A ,连接A C.(1)直接写出点A ,点B ,点C 的坐标和抛物线的解析式;(2)已知点P 为第一象限内抛物线上一点,当点P 到直线BC 的距离最大时,求点P 的坐标; (3)抛物线上是否存在一点Q (点C 除外),使以点Q ,A ,B 为顶点的三角形与△ABC 相似?若存在,求出点Q 的坐标;若不存在,请说明理由.第1题图2、(2019滨州)如图①,抛物线y =-18x 2+12x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D .(1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点. ①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离; ②当点P 到直线AD 的距离为524时,求sin ∠P AD 的值.3、(2019金牛区一诊)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点分别为A (-3,0)、B (1,0),与y 轴交于点D (0,3),过顶点C 作CH ⊥x 轴于点H .(1)求抛物线的解析式和顶点C 的坐标;(2)连接AD 、CD ,若点E 为抛物线上一动点(点E 与顶点C 不重合),当△ADE 与△ACD 面积相等时,求点E 的坐标;(3)若点P 为抛物线上一动点(点P 与顶点C 不重合),过点P 向CD 所在的直线作垂线,垂足为点Q ,以P 、C 、Q 为顶点的三角形与△ACH 相似时,求点P 的坐标.第1题图备用图参考答案一、基础过关1. 解:(1)把A (1,0),C (0,-3)代入y =x 2+bx +c 得,⎩⎪⎨⎪⎧1+b +c =0c =-3,解得⎩⎪⎨⎪⎧b =2c =-3, ∴抛物线的函数表达式为y =x 2+2x -3;(2)如解图,作点A 关于y 轴的对称点A ′,连接A ′C ,作AD ⊥A ′C 于点D , ∴点A ′的坐标为(-1,0), 则AA ′=2,OC =3,A ′C =10, ∵S △A ′AC =12AA ′·OC =12A ′C ·AD ,∴AD =AA ′·OC A ′C =3105,在Rt △A ′AD 中,∵A ′D 2+AD 2=A ′A 2, ∴A ′D 2+(3105)2=22.解得A ′D =105(负值已舍去), ∴DC =4105,∴tan ∠ACA ′=AD DC =34. 由对称可得∠ACD =2∠ACO ,则∠P AB =∠ACA ′, 设P (a ,a 2+2a -3),①如解图,当点P 在x 轴的上方时,作P 1H 1⊥x 轴于点H 1, ∴tan ∠P 1AB =P 1H 1AH 1=a 2+2a -31-a =34,解得a 1=1(舍),a 2=-154,把a =-154代入得P (-154,5716);②如解图,当点P 在x 轴的下方时,作P 2H 2⊥x 轴于点H 2, ∴tan ∠P 2AB =P 2H 2AH 2=-a 2-2a +31-a =34,解得a 3=1(舍),a 4=-94,把a =-94代入得P (-94,-3916),综上所述,点P 的坐标为(-154,5716)或(-94,-3916);第1题解图(3)是.设Q (m ,m 2+2m -3),则-3<m <1. 设直线AQ 的解析式为y =k 1x +b 1,把A (1,0),Q (m ,m 2+2m -3),代入解析式解得⎩⎪⎨⎪⎧k 1=m +3b 1=m -3, ∴y =(m +3)x -m -3, 当x =-1时,y =-2m -6, 设直线BQ 的解析式为y =k 2x +b 2,把B (-3,0),Q (m ,m 2+2m -3)代入y =k 2x +b 2,解得⎩⎪⎨⎪⎧k 2=m -1b 2=3m -3,∴y =(m -1)x +3m -3, 当x =-1时,y =2m -2, ∴DM =2m +6,DN =-2m +2, ∴DM +DN =2m +6-2m +2=8. 2. 解:(1)∵B (-1,0), ∴OB =1.又∵OA =OC =4OB , ∴OA =OC =4, ∴A (4,0),C (0,-4);(2)将A 、B 、C 三点坐标代入y =ax 2+bx +c 得,⎩⎪⎨⎪⎧16a +4b +c =0a -b +c =0c =-4,解得⎩⎪⎨⎪⎧a =1b =-3c =-4, ∴抛物线的解析式为y =x 2-3x -4;(3)如解图,过点P 作PE ⊥x 轴交AC 于点E , ∴PE ∥y 轴. ∵OA =OC ,∴∠PED =∠OCA =45°, ∴△DEP 为等腰直角三角形, ∴PD =22PE , ∴当PE 取得最大值时,PD 取得最大值, 易得直线AC 的解析式为y =x -4, 设P (x ,x 2-3x -4),则E (x ,x -4),则PE =(x -4)-(x 2-3x -4)=-x 2+4x =-(x -2)2+4, ∵0<x <4,∴当x =2时,PE 取得最大值,最大值为4, 此时PD 取得最大值,最大值为4×22=22,∴点P 的坐标为(2,-6).第2题解图二、能力提升1. 解:(1)∵抛物线与x 轴交于A ,B 两点,点A 的坐标为(2,0),抛物线的对称轴为直线x =-1, ∴点B 的坐标为(-4,0).∴设抛物线的函数表达式为y =a (x +4)(x -2),将点C (0,-2)代入得-8a =-2,解得a =14.∴抛物线的函数表达式为y =14(x +4)(x -2)=14x 2+12x -2;(2)设点P 的坐标为(x ,14x 2+12x -2),则点D 的坐标为(x ,0),设BC 所在直线的表达式为y =kx +b , 将B (-4,0),C (0,-2)代入得,⎩⎪⎨⎪⎧-4k +b =0b =-2,解得⎩⎪⎨⎪⎧k =-12b =-2, ∴BC 所在直线的表达式为y =-12x -2.∴点E 的坐标为(x ,-12x -2).∴PE =14x 2+x .∵PE =14OD ,∴14x 2+x =-14x ,即14x 2+54x =0, 解得x =-5或x =0(舍). ∴PE =54,BD =1,∴S △PBE =12PE ·BD =12×54×1=58;(3)存在.①当DM =DB =1时,如解图①,过点M 作MF ⊥x 轴于点F , 设M (m ,-12m -2),则MF =-12m -2,DF =-m -5,∵MF 2+DF 2=DM 2,∴(-12m -2)2+(-m -5)2=1,解得m =-285或m =-4(舍去).∴点M 的坐标为(-285,45);第1题解图①②当BD =BM =1时,如解图②,过点M 作x 轴的垂线,垂足为N , ∵DE ⊥x 轴, ∴DE ∥MN ,∴BN ∶BD =BM ∶BE ,∴BN ∶1=1∶BE . ∵E (-5,12),∴DE =12,∴BE =52, ∴BN ∶1=1∶52,解得BN =255. ∴点M 的横坐标为-4-255,将x =-4-255代入y =-12x -2,得y =55,即点M 的坐标为(-4-255,55).综上所述,点M 的坐标为(-285,45)或(-4-255,55).第1题解图②三、满分冲关1. 解:(1)A (-4,0),B (6,0),C (0,3),抛物线的解析式为y =-18x 2+14x +3;【解法提示】令y =-12x +3=0,解得x =6,令x =0,得y =3,∴B (6,0),C (0,3).∵抛物线的对称轴为x =1,且过点B 、A ,∴抛物线与x 轴的另一交点A 坐标为(-4,0),设抛物线的解析式为y =a (x +4)(x -6),将点C (0,3)代入得-24a =3,解得a =-18.∴y =-18(x +4)(x -6)=-18x 2+14x +3(2)如解图①,过点P 作PG ⊥x 轴于点G ,交BC 于点Q ,过点P 作PH ⊥BC 于点H . ∵OC =3,OB =6, ∴BC =OC 2+OB 2=3 5. 又∵∠HQP =∠GQB , ∴∠HPQ =∠CBO , ∴sin ∠HPQ =sin ∠CBO =55. 故点P 到直线BC 的距离最大,即PQ 最大. 设P (m ,-18m 2+14m +3),Q (m ,-12m +3),∴PQ =-18m 2+14m +3-(-12m +3)=-18(m -3)2+98.∵-18<0,∴当m =3时,PQ 有最大值为98.∴P (3,218);第1题解图①(3)存在.由(1)得A (-4,0)、B (6,0)、C (0,3), ∴AB =10,AC =32+42=5. 分为两种情况分类讨论:①当△ABC ∽△AQB 时,如解图②所示. ∴AC AB =ABAQ,∠CAB =∠BAQ . ∴AQ =AB 2AC =1025=20,过点Q 作QD ⊥x 轴,垂足为点D , ∴QD =AQ ·sin ∠BAQ =20×35=12,AD =AQ ·cos ∠BAQ =20×45=16.∴Q (12,-12).第1题解图②②当△ABC ∽△BQA 时,如解图③所示, ∴AB BQ =ACAB,∠CAB =∠ABQ . ∴BQ =AB 2AC=20,过点Q 作QE ⊥x 轴,垂足为E ,同理可得QE =BQ ·sin ∠ABQ =20×35=12,BE =BQ ·cos ∠ABQ =20×45=16, ∴Q (-10,-12).综上所述,点Q 的坐标是(12,-12)或(-10,-12).第1题解图③2、解:(1)抛物线y =-18x 2+12x +4, 令x =0,可得A 点的坐标为(0,4),令y =0,可得B 点的坐标为(-4,0),C 点的坐标为(8,0).易得直线AB 的函数解析式为y =x +4,∵OA =OB ,∴∠BAO =45°.又∵直线AD 由直线AB 逆时针旋转90°而来,∴∠BAD =90°,∴∠OAD =45°,△OAD 为等腰直角三角形,∴OD =OA =4,D (4,0),易得直线AD 的函数解析式为y =-x +4;(2)①如解图①,过点P 作PE ⊥x 轴交AD 于点E ,PF ⊥AD 于点F ,第1题解图①易得△PEF 为等腰直角三角形,∴PF =22PE , ∴当PE 取得最大值时,PF 取得最大值,设P (x ,-18x 2+12x +4), 则E (x ,-x +4),∴PE =-18x 2+12x +4-(-x +4)=-18x 2+32x =-18(x -6)2+92, ∴当x =6时,PE 有最大值92, 此时PF 有最大值924, ∴当x =6时,-18x 2+12x +4=52, ∴当点P 到直线AD 的距离最大时,点P 的坐标为(6,52),最大距离为924; ②如解图②,连接AP ,过点P 作PE ⊥x 轴,交AD 于点E ,PF ⊥AD 于点F ,当点P 到AD 的距离为524时,PF =524, 则此时PE =2PF =52, 将PE =52代入PE =-18(x -6)2+92中, 解得x 1=10,x 2=2,∴此时点P 的坐标为(10,-72)或(2,92), 当点P 的坐标为(2,92)时,AP =22+(92-4)2=172, ∴sin ∠P AD =524172=53434; 当点P 的坐标为(10,-72)时, AP =102+(-72-4)2=252, ∴sin ∠P AD =PF AP =524252=210. 综上,sin ∠P AD 的值是53434或210.3、1. 解:(1)把点A 、B 、D 的坐标分别代入抛物线的解析式中得:⎩⎪⎨⎪⎧a +b +c =09a -3b +c =0c =3,解得⎩⎪⎨⎪⎧a =-1b =-2c =3,∴抛物线的解析式为y =-x 2-2x +3,∴抛物线的对称轴为直线x =-b 2a=-1, ∴点C 的坐标为(-1,4);(2)如解图①,过点C 作CE ∥AD 交抛物线于点E ,交y 轴于点T ,则△ADE 与△ACD 面积相等,直线AD 过点D ,设其解析式为y =mx +3,将点A 的坐标代入得:0=-3m +3,解得m =1,则直线AD 的解析式为y =x +3,∵CE ∥AD ,设直线CE 的解析式为y =x +n ,将点C 的坐标代入上式得:4=-1+n ,解得n =5,则直线CE 的解析式为y =x +5,则点T 的坐标为(0,5),联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +5, 解得x =-1或x =-2(x =-1为点C 的横坐标),即点E 的坐标为(-2,3);在y 轴取一点H ′,使DT =DH ′=2,过点H ′作直线E ′E ″∥AD ,则△ADE ′和△ADE ″都与△ACD 面积相等,同理可得直线E ′E ″的解析式为y =x +1,联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +1, 解得x =-3±172, ∴点E ″、E ′的坐标分别为(-3+172,-1+172)、(-3-172,-1-172), 综上,满足要求的点E 的坐标为(-2,3)或(-3+172,-1+172)或(-3-172,-1-172);第1题解图①(3)如解图②,设点P 的坐标为(m ,n ),则n =-m 2-2m +3,把点C 、D 的坐标代入一次函数的解析式y =kx +b 得:⎩⎪⎨⎪⎧4=-k +b b =3, 解得⎩⎪⎨⎪⎧k =-1b =3, 即直线CD 的解析式为y =-x +3,由(1)得,直线AD 的解析式为y =x +3,∴AD ⊥CD ,而直线PQ ⊥CD ,故直线PQ 的解析式中的k 值与直线AD 的解析式中的k 值相同, 同理可得直线PQ 的解析式为y =x +(n -m ),联立⎩⎪⎨⎪⎧y =-x +3y =x +(n -m ), 解得x =3+m -n 2,即点Q 的坐标为(3+m -n 2,3-m +n 2), 则PQ 2=(m -3+m -n 2)2+(n -3-m +n 2)2=(m +n -3)22=12(m +1)2·m 2, 同理可得:PC 2=(m +1)2[1+(m +1)2],AH =2,CH =4,则AC =25,当△ACH ∽△CPQ 时,PC PQ =AC CH =52, 即4PC 2=5PQ 2,整理得3m 2+16m +16=0,解得m =-4或m =-43, ∴点P 的坐标为(-4,-5)或(-43,359); 当△ACH ∽△PCQ 时,同理可得,点P 的坐标为(-23,359)或(2,-5), 综上所述,点P 的坐标为(-4,-5)或(-43,359)或(-23,359)或(2,-5).第1题解图②。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
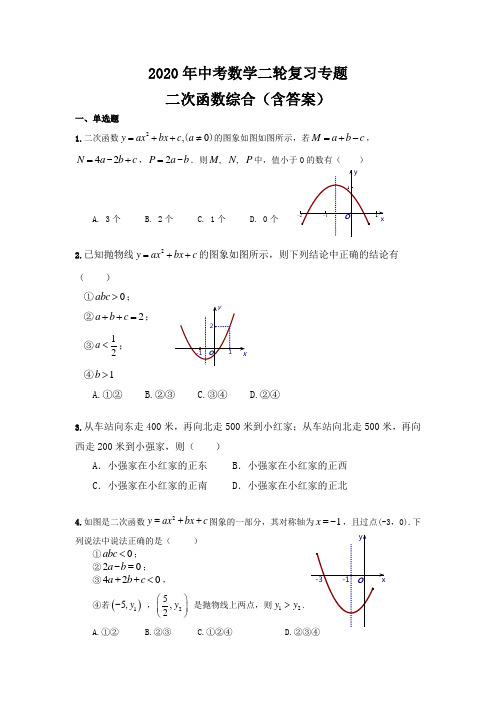
2020年中考数学二轮专项冲刺——二次函数(真题汇编)一、选择题1.(2019年四川省广安市)二次函数y =ax 2+bx +c (a ≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x =1,下列结论:①abc <0②b <c ③3a +c =0④当y >0时,﹣1<x <3,其中正确的结论有( )A .1个B .2个C .3个D .4个 2. (2019年天津市)二次函数c b a c bx ax y ,,(2++=是常数,0≠a )的自变量x 与函数值y的部分对应值如下表:且当x=21-时,与其对应的函数值0>y ,有下列结论:①0>abc ;② - 2和3是关于x 的方程t c bx ax =++2的两个根;③3200<+<n m 。
其中,正确结论的个数是( ) A.0 B.1 C. 2 D.33. (2019年山东省德州市)若函数y =与y =ax 2+bx +c 的图象如图所示,则函数y =kx +b 的大致图象为( )A. B.C. D.4. (2019年山东省济宁市)将抛物线y=x2﹣6x+5向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是()A.y=(x﹣4)2﹣6 B.y=(x﹣1)2﹣3 C.y=(x﹣2)2﹣2 D.y=(x﹣4)2﹣25. (2019年山东省青岛市)已知反比例函数y=的图象如图所示,则二次函数y=ax2﹣2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是()A.B.C.D.6. (2019年四川省资阳市)如图是函数y=x2﹣2x﹣3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是()A.m≥1B.m≤0C.0≤m≤1D.m≥1或m≤07. (2019年河南省)已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则n的值为()A.﹣2 B.﹣4 C.2 D.48. (2019年浙江省衢州市)二次函数y=(x-1)2+3图象的顶点坐标是()A. (1,3)B. (1,-3)C. (-1,3)D. (-1,-3)9. (2019年浙江省温州市)已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是()A.有最大值﹣1,有最小值﹣2 B.有最大值0,有最小值﹣1C.有最大值7,有最小值﹣1 D.有最大值7,有最小值﹣210. (2019年内蒙古赤峰市)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b>0;②a﹣b+c=0;③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;④当x<﹣1或x>3时,y>0.上述结论中正确的是.(填上所有正确结论的序号)11. (2019年甘肃省)如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b >0,③4ac<b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是()A.①②③B.①②④C.②③④D.③④⑤12. (2019年湖北省鄂州市)二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为()A.1个B.2个C.3个D.4个13. (2019年湖北省随州市)如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B 两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论:①abc<0;②a+b+c=0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的有()A. 1个B. 2个C. 3个D. 4个14. (2019年内蒙古呼和浩特市)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.15. (2019年内蒙古通辽市)在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有()A.1个B.2个C.3个D.4个16. (2019年西藏)把函数y=﹣x2的图象,经过怎样的平移变换以后,可以得到函数y =﹣(x﹣1)2+1的图象()A.向左平移1个单位,再向下平移1个单位B.向左平移1个单位,再向上平移1个单位C.向右平移1个单位,再向上平移1个单位D.向右平移1个单位,再向下平移1个单位二、填空题1. (2019年湖北省荆州市)二次函数y=﹣2x2﹣4x+5的最大值是.2. (2019年山东省济宁市)如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B (3,q)两点,则不等式ax2+mx+c>n的解集是.3. (2019年四川省达州市)如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点;②若点M(﹣2,y1)、点N(,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为+.其中正确判断的序号是.4. (2019年广西贺州市)已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①abc<0;②a﹣b+c<0;③3a+c=0;④当﹣1<x<3时,y >0,正确的是(填写序号).5. (2019年甘肃省天水市)二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a﹣b.则M、N的大小关系为M N.(填“>”、“=”或“<”)6. (2019年甘肃省武威市)将二次函数y=x2﹣4x+5化成y=a(x﹣h)2+k的形式为.7. (2019年辽宁省大连市)如图,抛物线y=﹣x2+x+2与x轴相交于A、B两点,与y 轴相交于点C,点D在抛物线上,且CD∥AB.AD与y轴相交于点E,过点E的直线PQ 平行于x轴,与拋物线相交于P,Q两点,则线段PQ的长为.三、解答题1.(2019年安徽省)一次函数y=kx+4与二次函数y=ax2+c的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点.(1)求k,a,c的值;(2)过点A(0,m)(0<m<4)且垂直于y轴的直线与二次函数y=ax2+c的图像相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.2.(2019年北京市)在平面直角坐标系xOy中,抛物线21y ax bxa=+-与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点11(,)2Pa-,(2,2)Q.若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.3.(2019年四川省广安市)如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=kx+n与y轴交于点C,与抛物线y=﹣x2+bx+c 的另一个交点为D,已知A(﹣1,0),D(5,﹣6),P点为抛物线y=﹣x2+bx+c上一动点(不与A、D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.4.(2019年重庆市)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于点A,B (点A在点B的左侧),交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.(1)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+PC的最小值;(2)在(1)中,当MN 取得最大值,HF +FP +PC 取得最小值时,把点P 向上平移个单位得到点Q ,连结AQ ,把△AOQ 绕点O 顺时针旋转一定的角度α(0°<α<360°),得到△A ′OQ ′,其中边A ′Q ′交坐标轴于点G .在旋转过程中,是否存在一点G ,使得∠Q '=∠Q 'OG ?若存在,请直接写出所有满足条件的点Q ′的坐标;若不存在,请说明理由.5.(2019年天津市)已知抛物线c b c bx x y ,(2+-=为常数,0>b )经过点A (-1,0),点M (m ,0)是x 轴正半轴上的点.(I )当b=2时,求抛物线的顶点坐标;(II )点D (b ,D y )在抛物线上,当AM=AD ,m=5时,求b 的值;(III )点Q (21+b ,Q y )在抛物线上,当2AM+2QM 的最小值为4233时,求b 的值.6. (2019年天津市)在平面直角坐标系中,O 为坐标原点,点A (6,0),点B 在y 轴的正半轴上,∠ABO=30°,矩形CODE 的顶点D ,E ,C 分别在OA,AB,OB 上,OD=2. (I )如图①,求点E 的坐标;(II )将矩形CODE 沿x 轴向左平移,得到矩形E D O C '''',点D,O,C,E 的对应点分别为E D O C '''',,,.设t O O =',矩形E D O C ''''与△ABO 重叠部分的面积为s .①如图②,当矩形E D O C ''''与△ABO 重叠部分为五边形时,E C ''、E D ''分别与AB 相交于点M,F ,试用含有t 的式子表示s ,并直接写出t 的范围; ②353≤≤s 时,求t 的取值范围(直接写出结果即可)。
7. (2019年山东省青岛市)已知:如图,在四边形ABCD 中,AB ∥CD ,∠ACB =90°,AB =10cm ,BC =8cm ,OD 垂直平分A C .点P 从点B 出发,沿BA 方向匀速运动,速度为 1cm /s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1cm /s ;当一个点停止运动, 另一个点也停止运动.过点P 作PE ⊥AB ,交BC 于点E ,过点Q 作QF ∥AC ,分别交AD , OD 于点F ,G .连接OP ,EG .设运动时间为t (s )(0<t <5),解答下列问题:(1)当t 为何值时,点E 在∠BAC 的平分线上?(2)设四边形PEGO 的面积为S (cm 2),求S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使四边形PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;(4)连接OE ,OQ ,在运动过程中,是否存在某一时刻t ,使OE ⊥OQ ?若存在,求出t 的值;若不存在,请说明理由.8. (2019年云南省)已知k 是常数,抛物线y =x 2+(k 2+k -6)x +3k 的对称轴是y 轴,并且与x 轴有两个交点. (1)求k 的值:(2)若点P 在抛物线y =x 2+(k 2+k -6)x +3k 上,且P 到y 轴的距离是2,求点P 的坐标.10. (2019年广西贺州市)如图,在平面直角坐标系中,已知点B 的坐标为(﹣1,0),且 OA =OC =4OB ,抛物线y =ax 2+bx +c (a ≠0)图象经过A ,B ,C 三点. (1)求A ,C 两点的坐标; (2)求抛物线的解析式;(3)若点P 是直线AC 下方的抛物线上的一个动点,作PD ⊥AC 于点D ,当PD 的值最大时,求此时点P 的坐标及PD 的最大值.11.(2019年江苏省苏州市)已知矩形ABCD 中,AB =5cm ,点P 为对角线AC 上的一点,且AP =25cm .如图①,动点M 从点A 出发,在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s ),APM ∆的面积为S (cm ²),S 与t 的函数关系如图②所示:(1)直接写出动点M 的运动速度为 /cm s ,BC 的长度为 cm ;(2)如图③,动点M 重新从点A 出发,在矩形边上,按原来的速度和方向匀速运动.同时,另一个动点N 从点D 出发,在矩形边上沿着D C B →→的方向匀速运动,设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C ),动点M 、N 相遇后立即停止运动,记此时APM DPN ∆∆与的面积为()()2212,S cm S cm . ①求动点N 运动速度()/v cm s 的取值范围;②试探究12S S ⋅是否存在最大值.若存在,求出12S S ⋅的最大值并确定运动速度时间x 的值;若不存在,请说明理由.①(图)PBCDAS (cm²)t (s )②图O2.57.512.(2019年江苏省泰州市)如图,在平面直角坐标系xoy 中,二次函数图像的顶点坐标为(4,-3),该图像与x 轴相交于点A 、B ,与y 轴相交于点C ,其中点A 的横坐标为1. (1)求该二次函数的表达式; (2)求tan ∠ABC.13.(2019年江苏省无锡市)已知二次函数42-+=bx ax y (a >0)的图像与x 轴交于A 、B 两点,(A 在B 左侧,且OA <OB ),与y 轴交于点C .D 为顶点,直线AC 交对称轴于点E ,直线BE 交y 轴于点F ,AC :CE =2:1. (1)求C 点坐标,并判断b 的正负性;yxAOC B(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD 与y轴交于点E,连接BC.①若△BCE的面积为8,求二次函数的解析式;②若△BCD为锐角三角形,请直接写出OA的取值范围.xyOx yO14. (2019年陕西省)在平面直角坐标系中,已知抛物线L:y=ax2+(c-a)x+c经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为L′.(1)求抛物线L的表达式;(2)点P在抛物线L′上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB 相似.求符合条件的点P的坐标.15.(2019年浙江省杭州市)设二次函数()()12y x x x x =--(1x 、2x 是实数). ⑴甲求得当0x =时,0y =;当1x =时,0y =,乙求得当12x =时,12y =-.若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由;⑵写出二次函数的对称轴,并求出该函数的最小值(用含1x 、2x 的代数式表示); ⑶已知二次函数的图像经过()0,m ,()1,n 两点(m 、n 是实数),当1201x x <<<时, 求证:1016mn <<.16. (2019年浙江省衢州市)某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y (间)与每间标准房的价格x (元)的数据如下表:x (元) … 190 200 210 220 … y(间)… 65 60 55 50 …(1)根据所给数据在坐标系中描出相应的点,并画出图象。
