《2.1.1 合理推理》课件1-优质公开课-人教B版选修2-2精品
合集下载
高中数学选修1-2《2.1.1合情推理》课件
课前探究学习
课堂讲练互动
活页规范训练
自学导引 归纳推理的概念 由某类事物的部分对象具有某些特征,推出该类事物的 全部对象 都 具有这些特征的推理,或者由个别事实概括出 一般结论的推理.
课前探究学习
课堂讲练互动
活页规范训练
想一想:1.归纳推理的结论一定正确吗? 提示 归纳推理的结论超出了前提所界定的范围,其前提和结 论之间的联系不是必然性的,而是或然性的,结论不一定正 确.
课前探究学习
课堂讲练互动
活页规范训练
所以 a2-a12=-2,即 a22+2a2+1=2, 又 a2>0,所以 a2= 2-1. 同理 a3-a13=-2 2, 即 a23+2 2a3+2=3, 又 a3>0,所以 a3= 3- 2. 可推测 an= n- n-1.
课前探究学习
课堂讲练互动
活页规范训练
课前探究学习
课堂讲练互动
活页规范训练
规律方法 虽然由归纳推理所得到的结论未必是正确的,但它所 具有的由特殊到一般、由具体到抽象的认识过程,对于数学的发 现是十分有用的,观察、实验,对有限的资料作出归纳整理,提 出带有规律性的猜想,是数学研究的基本方法之一.
课前探究学习
课堂讲练互动
活页规范训练
【变式 1】 (1)在数列{an}中,a1=1,an+1=22+anan,n∈N*,猜想 这个数列的通项公式. (2)已知正项数列{an}的前 n 项和 Sn,满足 Sn=12an+a1n(n∈ N*),求出 a1,a2,a3,并推测 an 的表达式. 解 (1)在{an}中,a1=1,a2=22+a1a1=23, a3=2+2aa2 2=24,a4=22+a3a3=25,…, 所以猜想{an}的通项公式 an=n+2 1.
(选修2-2)2.1.1合情推理课件2.24
偶数=奇质数+奇质数
通过更多特例的检验, 从6开始,没有出现反例.
任何一个不小于6 的偶数都等于两个 奇质数的和.
2n p1 p2 (n N , n 3)
大胆猜想:
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体 形势的变化,由个别推知一般.
谚语“瑞雪兆丰年” 物理学中牛顿发现万有引力
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
即是由部分到整体,由个别到一般的推理.
你能举出归纳推理 的例子吗?
观察下列等式
6=3+3, 12=5+7,
8=3+5, 14=3+11,
10=3+7, 16=5+11 归纳出一个规律:
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的 海龟是用肺呼吸的
爬行动 物都是 用肺呼
整 体 蜥蜴是用肺呼吸的
吸的
一般
共 第一个数为2
第二个数为4 第三个数为6
性
第n个 数为2n.
第四个数为8
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
化学中的门捷列夫元素周期表Fra bibliotek天文学中开普勒行星运动定律
歌德巴赫猜想 四色定理 牛顿发现万有引力 门捷列夫发现元素周期律等等
应用归纳推理可以 发现新事实,获得新结论!
归纳推理的过程: 归纳推理的特点:
实验观察
在同一类事物中 (1)从特殊到一般;
通过更多特例的检验, 从6开始,没有出现反例.
任何一个不小于6 的偶数都等于两个 奇质数的和.
2n p1 p2 (n N , n 3)
大胆猜想:
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体 形势的变化,由个别推知一般.
谚语“瑞雪兆丰年” 物理学中牛顿发现万有引力
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
即是由部分到整体,由个别到一般的推理.
你能举出归纳推理 的例子吗?
观察下列等式
6=3+3, 12=5+7,
8=3+5, 14=3+11,
10=3+7, 16=5+11 归纳出一个规律:
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的 海龟是用肺呼吸的
爬行动 物都是 用肺呼
整 体 蜥蜴是用肺呼吸的
吸的
一般
共 第一个数为2
第二个数为4 第三个数为6
性
第n个 数为2n.
第四个数为8
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
化学中的门捷列夫元素周期表Fra bibliotek天文学中开普勒行星运动定律
歌德巴赫猜想 四色定理 牛顿发现万有引力 门捷列夫发现元素周期律等等
应用归纳推理可以 发现新事实,获得新结论!
归纳推理的过程: 归纳推理的特点:
实验观察
在同一类事物中 (1)从特殊到一般;
人教版选修2-2《2.1.1合情推理》课件(共23张PPT)
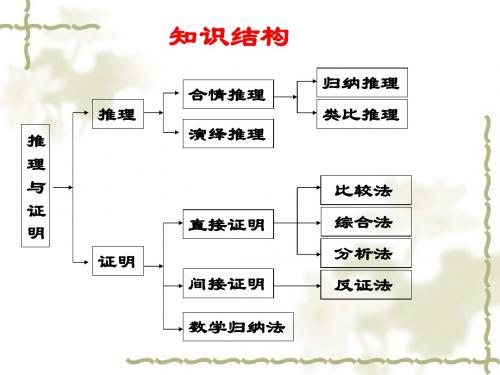
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体
8
6
12
五棱柱
截角正方体
尖顶塔
猜想 F+V-E=2 欧拉公式
多面体 面数(F) 顶点数(V) 棱数(E)
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体86Fra bibliotek12五棱柱
7
10
15
截角正方体 7
10
15
尖顶塔
7.利用等差数列性质类比等比数列性质
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
改写为:10=3+7,20=3+17,30=13+17.
6=3+3, 8=3+5,
10=5+5, 12=5+7, 14=7+7, 16=5+11,
18 =7+11, …,
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征, 推出该类事物的全部对象都具有这些特征 的推理,或者由个别事实概栝出一般结论 的推理,称为归纳推理.(简称;归纳)
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1 当n=2时,a2= 3
2
1
3
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1
人教版高中数学选修2-2课件 2.1.1合情推理

18
规律方法:归纳推理和类比推理的共同点:
可见,归纳推理和类比推理都是根据已有的事实,经 过观察、分析、比较、联想,再进行归纳、推理、类 比,然后提出猜想的推理,我们把它们统称为合情推 理. 通俗地说,合情推理是指“合乎情理”的推理.
19
►变式训练 4.观察下列等式: (1+1)=2×1, (2+1)(2+2)=22×1×3, (3+1)(3+2)(3+3)=23×1×3×5, … 照此规律, 第n个等式可为____________.
24
【易错剖析】三角形中的内角类比到空间中可以是 线面角,也可以是面面角,这里面面角应该合理些; 三角形中的射影定理等式右边是边长与角的余弦值 相乘,类比到空间中,应该是面积与面面角的余弦 值相乘,而不是棱长与角的余弦值相乘.这些类比 的不确定性,要根据实际情况认真分析.
25
20
解析:从给出的规律可看出,左边的连乘式中,连 乘式个数以及每个连乘式中的第一个加数与右边连 乘式中第一个乘数的指数保持一致,其中左边连乘 式中第二个加数从1开始,逐项加1递增,右边连乘 式中从第二个乘数开始,组成以1为首项,2为公差 的等差数列,项数与第几等式保持一致,则照此规 律,第n个等式可为(n+1)(n+2)…(n+n)= 2n×1×3×…×(2n-1). 答案:(n+1)(n+2)…(n+n)=2n×1×3×…×(2n- 1)
21
析疑难 提能 力
22
类比不当致误. 【典例】 如图所示,在△ABC中,射影定理 可表示为a=b·cos C+c·cos B,其中a,b,c分 别为角A,B,C的对边,类比上述定理,写出 对空间四面体性质的猜想.
23
解析:如右图所示,在四面体PABC中,设S1,S2, S3,S分别表示△PAB,△PBC,△PCA,△ABC 的面积,α,β,γ依次表示面PAB,面PBC,面 PCA与底面ABC所成二面角的大小. 我们猜想射影定理类比推理到三维空间,其表现 形式应为S=S1·cos α+S2·cos β+S3·cos γ
规律方法:归纳推理和类比推理的共同点:
可见,归纳推理和类比推理都是根据已有的事实,经 过观察、分析、比较、联想,再进行归纳、推理、类 比,然后提出猜想的推理,我们把它们统称为合情推 理. 通俗地说,合情推理是指“合乎情理”的推理.
19
►变式训练 4.观察下列等式: (1+1)=2×1, (2+1)(2+2)=22×1×3, (3+1)(3+2)(3+3)=23×1×3×5, … 照此规律, 第n个等式可为____________.
24
【易错剖析】三角形中的内角类比到空间中可以是 线面角,也可以是面面角,这里面面角应该合理些; 三角形中的射影定理等式右边是边长与角的余弦值 相乘,类比到空间中,应该是面积与面面角的余弦 值相乘,而不是棱长与角的余弦值相乘.这些类比 的不确定性,要根据实际情况认真分析.
25
20
解析:从给出的规律可看出,左边的连乘式中,连 乘式个数以及每个连乘式中的第一个加数与右边连 乘式中第一个乘数的指数保持一致,其中左边连乘 式中第二个加数从1开始,逐项加1递增,右边连乘 式中从第二个乘数开始,组成以1为首项,2为公差 的等差数列,项数与第几等式保持一致,则照此规 律,第n个等式可为(n+1)(n+2)…(n+n)= 2n×1×3×…×(2n-1). 答案:(n+1)(n+2)…(n+n)=2n×1×3×…×(2n- 1)
21
析疑难 提能 力
22
类比不当致误. 【典例】 如图所示,在△ABC中,射影定理 可表示为a=b·cos C+c·cos B,其中a,b,c分 别为角A,B,C的对边,类比上述定理,写出 对空间四面体性质的猜想.
23
解析:如右图所示,在四面体PABC中,设S1,S2, S3,S分别表示△PAB,△PBC,△PCA,△ABC 的面积,α,β,γ依次表示面PAB,面PBC,面 PCA与底面ABC所成二面角的大小. 我们猜想射影定理类比推理到三维空间,其表现 形式应为S=S1·cos α+S2·cos β+S3·cos γ
人教B版高中数学选修2-2第2章2.1第2课时《演绎推理》ppt课件

平行公理“三条直线 a、b、c,若 a∥b,b∥c,则 a∥c” 中所蕴含的推理规则是________.
[答案] 传递性关系推理
四、完全归纳推理 把所有的情况都考虑在内的演绎推理规则叫做完全归纳推 理. 完全归纳推理有两个规则:一是前提中被判断的对象必须 是该类事物的全部对象;二是前提中的所有判断都必须是真实 的.
• 1.合情推理包括哪两种推理方式? • 2.我们知道金属能够导电,而铁是金属,由此能得
到怎样的结论?
• 答案:1.归纳推理和类比推理.
• 2.铁能够导电.
• 一、演绎推理
• 从一般性的原理出发,推出某个特殊情况下的结论, 我们把这种推理叫做演绎推理.它是从一般到特殊 的推理模式.
• 演绎推理的特点:
设 a>0,b>0,a+b=1.求证:1a+1b+a1b≥8. [证明] 因为 a>0,b>0,a+b=1, ∴1=a+b≥2 ab,即 ab≤12. ∴a1b≥4, ∴1a+1b+a1b=(a+b)1a+1b+a1b≥2 ab·2 a1b+a1b≥4+4 =8,当且仅当 a=b 时等号成立,所以1a+1b+a1b≥8.
当 q≠1 时,Sn=a111--qqn, 从而 Sn·Sn+2-S2n+1=a211-1q-n1q-2 qn+2 -a2111--qqn+212=-a21qn<0. 综上,得 Sn·Sn+2<S2n+1. 故log0.5Sn+2log0.5Sn+2>log0.5Sn+1.
完全归纳推理
36 整除.
求证:当 1≤n≤4 时,f(n)=(2n+7)·3n+9 能被
[证明] 当 n=1 时,f(1)=(2+7)·3+9=36,能被 36 整除; 当 n=2 时,f(2)=(2×2+7)·32+9=108=36×3,能被 36 整除;
【高中数学选修2-2】2.1.1合情推理 精品优选公开课件

:河内塔(Tower of Hanoi)
传说在古老的印度有一座神庙,神庙中有三根针和套在一 根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则, 把圆环从一根针上全部移到另一根针上,第三根针起“过渡” 的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面. 如果有一天,僧侣们将这64个圆环全部移到另一根针上, 那么世界末日就来临了.
第二重境界是“衣带渐宽终不悔,为伊消得人憔悴”。事情是需要去做才能成的,成越大的事业,需要越大的努力和付出,甚至要经受越大的磨难和困苦。这个世间,从来都是“艰难困苦,玉汝于成”;所以无论如何,都要“天行健,君子”。这说的是历经磨难而逐渐成熟、成长,最终豁然贯通、水到渠成。这其中蕴含一个重要道理,就是苏东坡所说的“厚积而薄发”。只有厚积才能薄发,人要做的,就是不断厚积,等待薄发。这就是拿得起的完整路径,也是事业成功的完整过程。 跟佛家学放得下 。佛家是追求出世、讲究清净的,要求能看到《金刚经》所言的“一切有为法,如梦幻泡影”,做到《心经》所言的“照见五蕴皆空”。概括为三个字,就是“放得下”。 什么是“放得下”?且看这个“佛”字——左边一个“人”,右边一个“弗”,弗的意思是“不”,合起来就是“不人”和“人不”。不人就是无人,也就是放下自我,摆脱私心的困缚;人不就是懂得拒绝,也就是放下欲望,超脱对外物的追逐。这两点能做到,就是放得下。
合情推理.
练 .在平面上,设ha,hb,hc是三角形ABC三条边上的高.P为
三们角可形以内得任 到一 结点 论,:P到相p应a三边的p距b 离分p别c 为p1a,pb,pc,我 ha hb hc
试通过类比,写出在空间中的类似结论.
A
B
pbPppac
C
pa pb pc 1 ha hb hc
人教版2017高中数学(选修2-2)2.1.1.1归纳推理PPT课件
2.1 合情推理与演绎推理
-1-
2.1.1 合情推理
-2-
第1课时 归纳推理
-3-
首页
课前预习案
课堂探究案
学 习 目 标 1.了解归纳推理的含义. 2.掌握归纳推理的方法与步骤. 3.能运用归纳推理进行推理.
思 维 脉 络 定义 归纳推理 特点→应用 步骤
首页
课前预习案
课堂探究案
1.归纳推理 (1)归纳推理的定义:由某类事物的部分对象具有某些特征,推出这 类事物的全部对象都具有这些特征的推理,或者由个别事实概括出 一般结论的推理称为归纳推理(简称归纳).简言之,归纳推理是由 部分到整体、由个别到一般的推理. (2)归纳推理的特点:由于归纳推理是根据部分已知的特殊现象推 断未知的一般现象,因而归纳推理具有以下特点: ①所得结论超越了前提所包含的范围; ②所得结论具有猜测性质,准确性需要证明; ③归纳的基础在于观察、实验或经验.
答案: ������ + 1 +
������+1 (������+1) -1
2
������+1
2
(������+1) -1
.
首页
课前预习案
课堂探究案
2.归纳推理的一般步骤 (1)通过观察个别情况发现某些相同性质. (2)从已知的相同性质中推出一个明确表述的一般性命题(猜想). 做一做2 根据给出的数塔猜测123 456×9+7等于 ( ) 1×9+2=11 12×9+3=111 123×9+4=1 111 1 234×9+5=11 111 12 345×9+6=111 111 A.1 111 110 B.1 111 111 C.1 111 112 D.1 111 113 解析:由数塔呈现的规律知,结果是各位都是1的7位数. 答案:B
-1-
2.1.1 合情推理
-2-
第1课时 归纳推理
-3-
首页
课前预习案
课堂探究案
学 习 目 标 1.了解归纳推理的含义. 2.掌握归纳推理的方法与步骤. 3.能运用归纳推理进行推理.
思 维 脉 络 定义 归纳推理 特点→应用 步骤
首页
课前预习案
课堂探究案
1.归纳推理 (1)归纳推理的定义:由某类事物的部分对象具有某些特征,推出这 类事物的全部对象都具有这些特征的推理,或者由个别事实概括出 一般结论的推理称为归纳推理(简称归纳).简言之,归纳推理是由 部分到整体、由个别到一般的推理. (2)归纳推理的特点:由于归纳推理是根据部分已知的特殊现象推 断未知的一般现象,因而归纳推理具有以下特点: ①所得结论超越了前提所包含的范围; ②所得结论具有猜测性质,准确性需要证明; ③归纳的基础在于观察、实验或经验.
答案: ������ + 1 +
������+1 (������+1) -1
2
������+1
2
(������+1) -1
.
首页
课前预习案
课堂探究案
2.归纳推理的一般步骤 (1)通过观察个别情况发现某些相同性质. (2)从已知的相同性质中推出一个明确表述的一般性命题(猜想). 做一做2 根据给出的数塔猜测123 456×9+7等于 ( ) 1×9+2=11 12×9+3=111 123×9+4=1 111 1 234×9+5=11 111 12 345×9+6=111 111 A.1 111 110 B.1 111 111 C.1 111 112 D.1 111 113 解析:由数塔呈现的规律知,结果是各位都是1的7位数. 答案:B
《2.1.1合情推理》课件1-优质公开课-人教A版选修2-2精品
[问题1]
[提示1]
我们熟知的《三国演义》第46回草船借箭中诸
诸葛亮“先生”的推理过程是
葛亮先生的推理过程是怎样的呢?
1.今夜恰有大雾 2.曹操生性多疑 3.北军不善水战 ⇒草船借箭必将成功 弓弩利于远战 4.今夜恰有东风
数学 选修2-2
第二章 推理与证明
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
数学 选修2-2
第二章 推理与证明
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
第二章
推理与证明
数学 选修2-2
第二章 推理与证明
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
2.1 合情推理与演绎推理
2.1.1 合情推理
数学 选修2-2
第二章 推理与证明
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
1 1 1 1 解析: 在四面体中 V=3S1r+3S2r+3S3r+3S4r 1 3V =3(S1+S2+S3+S4)r.∴r= . S1+S2+S3+S4
2.合情推理的过程
观察、分析 从具体问题出发 → → 归纳、类比 → 提出猜想 比较、联想
数学 选修2-2
第二章 推理与证明
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
1.下列哪个平面图形与空间的平行六面体作为类比对象
比较合适的是( A.三角形 C.平行四边形 解析: ) B.梯形 D.矩形
归纳推理
定义 特征 部分对象 具有某些特征, 归纳推理是由 由某类事物的_________ 部分到整体 、 推出该类事物的__________ 全部对象 都具有这些 ____________ 特征的推理,或者由__________ 个别事实 概括出 一般结论 的推理,称为归纳推理 __________ 由____________ 个别到一般 的推理
人教版高中数学选修2-2精品课件:2.1 合情推理与演绎推理课件
2.类比推理的定义:
由两类对象具有某些类似特征,和其 中一类对象的某些已知特征,推出另一类
对象也具有这些特征的推理称为类比推理 (简称类比).
简言之,类比推理是由特殊到特殊的推理.
发明行星三大运动定律的开普勒曾说类比 推理数是学「家自波然利奧亚妙曾的指参出与“者类」比和是自一己个「伟最大好的 引的路老人师,求」解立体几何往往有赖于平面几何的类 比问题.”
第三个芒果是 甜的
例:观察下图,可以发现 1+3=4=22, 1+3+5=9=32, 1+3+5+7=16=42, 1+3+5+7+9=25=52, ……
1+3+…+(2n-1)=n2.
归纳推理的一般步骤:
⑴ 对有限的资料进行观察、分析、 归纳整理;
⑵ 提出带有规律性的结论,即猜想;
⑶ 检验猜想。
2.类比是从一种事物的特殊属性推测另一种事靠,单它却有发 现的功能.
例4 类比平面内直角三角形的勾股定理,试 给出空间 中四面体性质的猜想.
例5 类比平面内直角三角形的勾股定理,试 给出空间中四面体性质的猜想.
直角三角形
3个面两两垂直的四面体
∠C=90° 3个边的长度a,b,c 2条直角边a,b和1条斜边c
具体的材料 观察分析
猜想出一般性的结论
例如: 金受热后体积膨胀, 银受热后体积膨胀, 铜受热后体积膨胀, 铁受热后体积膨胀,
金、银、铜、铁是金属的部分小类对象,它们受热 后分子的凝聚力减弱,分子运动加速,分子彼此 距离加大,从而导致体积膨胀
所以,所有的金属受热后都体积膨胀。
例如: 磨擦双手(S1 )能产生热(P), 敲击石头(S2)能产生热(P) , 锤击铁块(S3)能产生热(P) , 磨擦双手、敲击石头、锤击铁块都是物质运动; 所以,物质运动能产生热。
人教B版选修2-2高中数学2.1.1《合情推理》ppt课件(1)
18 =7+11, …,
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征,
推出该类事物的全部对象都具有这些特征
的推理,或者由个别事实概栝出一般结论
的推理,称为归纳推理.(简称;归纳)
归纳推理的几个特点;
1.归纳是依据特殊现象推断一般现象,因而,由归纳
所得的结论超越了前提所包容的范围.
这就是着名的哥德巴赫猜想。欧拉在6月30日给他的回信中说, 他相信这个猜想是正确的,但他不能证明。叙述如此简单的问 题,连欧拉这样首屈一指的数学家都不能证明,这个猜想便引 起了许多数学家的注意。从提出这个猜想至今,许多数学家都 不断努力想攻克它,但都没有成功。当然曾经有人作了些具体 的验证工作,例如: 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5 = 3 + 7, 12 = 5 + 7, 14 = 7 + 7 = 3 + 11,16 = 5 + 11, 18 = 5 + 13, . . . . 等等。有人对33×108以内且大过6之偶数一 一进行验算,哥德巴赫猜想(a)都成立。但验格的数学证明尚 待数学家的努力。 从此,这道著名的数学难题引起了世界上成千上万数学家的注 意。200年过去了,没有人证明它。哥德巴赫猜想由此成为数 学皇冠上一颗可望不可及的“明珠”。到了20世纪20年代,才 有人开始向它靠近。1920年、挪威数学家布爵用一种古老的筛 选法证明,得出了一个结论:每一个比大的偶数都可以表示为 (99)。这种缩小包围圈的办法很管用,科学家们于是从(9 十9)开始,逐步减少每个数里所含质数因子的个数,直到最 后使每个数里都是一个质数为止,这样就证明了“哥德巴赫”。
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征,
推出该类事物的全部对象都具有这些特征
的推理,或者由个别事实概栝出一般结论
的推理,称为归纳推理.(简称;归纳)
归纳推理的几个特点;
1.归纳是依据特殊现象推断一般现象,因而,由归纳
所得的结论超越了前提所包容的范围.
这就是着名的哥德巴赫猜想。欧拉在6月30日给他的回信中说, 他相信这个猜想是正确的,但他不能证明。叙述如此简单的问 题,连欧拉这样首屈一指的数学家都不能证明,这个猜想便引 起了许多数学家的注意。从提出这个猜想至今,许多数学家都 不断努力想攻克它,但都没有成功。当然曾经有人作了些具体 的验证工作,例如: 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5 = 3 + 7, 12 = 5 + 7, 14 = 7 + 7 = 3 + 11,16 = 5 + 11, 18 = 5 + 13, . . . . 等等。有人对33×108以内且大过6之偶数一 一进行验算,哥德巴赫猜想(a)都成立。但验格的数学证明尚 待数学家的努力。 从此,这道著名的数学难题引起了世界上成千上万数学家的注 意。200年过去了,没有人证明它。哥德巴赫猜想由此成为数 学皇冠上一颗可望不可及的“明珠”。到了20世纪20年代,才 有人开始向它靠近。1920年、挪威数学家布爵用一种古老的筛 选法证明,得出了一个结论:每一个比大的偶数都可以表示为 (99)。这种缩小包围圈的办法很管用,科学家们于是从(9 十9)开始,逐步减少每个数里所含质数因子的个数,直到最 后使每个数里都是一个质数为止,这样就证明了“哥德巴赫”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x (2)已知: f(x)= , 设 f1(x)=f(x), fn(x)=fn-1(fn-1(x))(n>1, 1-x 且 n∈N+),则 f3(x)的表达式为______,猜想 fn(x)(n∈N+)的表 达式为___________________________________.
【思路探究】 (1)观察等式的结构特征, 寻找规律求解. (2)求出 f2(x),f3(x),f4(x),f5(x),寻找规律求解.
《2.1.1 合理推理》课件1
●三维目标 1.知识与技能 了解合情推理的含义, 认识归纳推理的基本方法与步骤, 能利用归纳进行简单的推理应用.
2.过程与方法 通过学生的积极参与,经历归纳推理概念的获得过程, 了解归纳推理的含义.让学生通过欣赏一些伟大猜想产生的 过程,体会如何利用归纳去猜测和发现一些新的结论,培养 学生归纳推理的思维方式. 3.情感、态度与价值观 正确认识合情推理在数学中的重要作用,并体会归纳推 理在日常活动和科学发现中的作用,养成认真观察事物、发 现问题、分析问题、探求新知识的习惯.
合情推理 (1)定义:前提为真时,结论 可能为真 的推理,叫做合 情推理. (2)分类:数学中常用的合情推理有归纳推理 和 类比推
理
.
(3)归纳和类比推理的定义、特征及步骤
数、式中的归纳推理
(2013· 陕西高考)(1)观察下列等式: (1+1)=2×1, (2+1)(2+2)=22×1×3, (3+1)(3+2)(3+3)=23×1×3×5, „„ 照此规律,第 n 个等式可为________.
●重点难点 重点:归纳推理的含义与特点. 难点:归纳推理的应用.
●教学建议 1.关于归纳推理的教学 关于归纳推理的教学,建议教师以学生熟悉的例子为载 体,引导学生进行观察、分析、归纳推理并借助例题具体说 明在数学发现的过程中猜想、归纳的作用,教学中也要让学 生进行简单的归纳推理的练习,培养学生应用这种思维方法 的意识.
【提示】
区别:归纳推理是由特殊到一般的推理;而
类比推理是由个别到个别的推 理或是由特殊 到特殊的推 理.联系:在前提为真时,归纳推理与类比推理的结论都可 真可假.
2.归纳推理和类比推理的结论一定正确吗?
【提示】
归纳推理的结论超出了前提所界定的范围,
其前提和结论之间的联系不是必然性的, 结论不一定正确. 类 比推理是从人们已经掌握了的事物的特征,推测正在被研究 中的事物的特征,所以类比推理的结果具有猜测性,不一定 正确.
【自主解答】 (1)从给出的规律可看出,左边的连乘式 中,连乘式个数以及每个连乘式中的第一个加数与右边连乘 式中第一个乘数的指数保持一致,其中左边连乘式中第二个 加数从 1 开始,逐项加 1 递增,右边连乘式中从第二个乘数 开始,组成以 1 为首项,2 为公差的等差数列,项数与第几 等式保持一致, 则照此规律, 第 n 个等式可为(n+1)(n+2)„(n +n)=2n×1×3ׄ×(2n-1).
【提示】 属于归纳推理.它符合归纳推理的定义特征, 即由部分对象具有某些特征,推出该类事物的全部对象都具 有这些特征的推理.
类比推理
【问题导思】 1.科学家对火星进行研究,发现火星与地球有许多类似 的特征:(1)火星也是绕太阳公转、绕轴自转的行星;(2)有大 气层,在一年中也有季节更替;(3)火星上大部分时间的温度 适合地球上某些已知生物的生存等.请问:科学家由此猜想 到什么?他们使用了什么样的推理?
归纳推理
【问题导思】 1.某同学在一份杂志上看到这样一段话:蛇、鳄鱼、海 龟、蜥蜴都是用肺呼吸的,而蛇、鳄鱼、海龟、蜥蜴都是爬 行动物.所以,所有的爬行动物都是用肺呼吸的.在这段话 中用到了什么推理?
【提示】 归纳推理.
2. 统计学中, 从总体中抽取样本, 然后用样本估计总体, 是否属归纳推理?
推理 (1)定义: 根据一个或几个已知 事实(或假设) 得出一个判 断,这种 思维方式 就是推理. (2)结构:一般由两部分组成,一部分是 已知的事实(或
假设) , 叫做前提; 一部分是由已知 推出的判断, 叫做结论.
(3)分类:推理一般分为 合情推理 与 演绎推理 .
合情推理
【问题导思】 1.归纳推理与类比推理有何区别与联系+2)„(n+n)=2n×1×3ׄ×(2n -1) x x (2) - 1-4x 1-2n 1x
进行数、式中的归纳推理的一般规律 (1)已知等式或不等式进行归纳推理的方法: ①要特别注意所给几个等式 (或不等式) 中项数和次数等 方面的变化规律; ②要特别注意所给几个等式 (或不等式) 中结构形式的特 征; ③提炼出等式(或不等式)的综合特点; ④运用归纳推理得出一般结论.
2.关于类比推理的教学 建议教师在教学中要借助实例充分挖掘两类对象之间的 类似特征,提炼出类比推理的一般过程,概括出类比推理的 含义.教学中也要让学生进行简单的类比推理的练习.
●教学流程
演示结束
1.了解合情推理的含义.(易混点) 课标 2.理解归纳推理和类比推理的含 解读 义,并能利用归纳和类比推理进 行简单的推理.(重点、难点)
【提示】 科学家猜想:火星上也可能有生命存在.他
们使用了类比推理.
2.(1)圆有切线,切线与圆只交于一点,切点到圆心的距 离等于半径.由此结论如何类比到球体? (2)平面内不共线的三点确定一个圆.由此结论如何类比 得到空间的结论? 【提示】 (1)球有切面,切面与球只交于一点,切点到 球心的距离等于半径.(或球有切线,切线与球只交于一点, 切点到球心的距离等于半径.) (2)空间中不共面的四点确定一个球.
x x (2)∵f(x)= ,∴f1(x)= . 1-x 1 -x 又∵fn(x)=fn-1(fn-1(x)), x 1-x x ∴f2(x)=f1(f1(x))= = , x 1-2x 1- 1 -x x f3(x)=f2(f2(x))= = , x 1-4x 1-2× 1-2x x 1-2x
x f4(x)=f3(f3(x))= = , x 1-8x 1-4× 1-4x x f5(x)=f4(f4(x))= = , x 1-16x 1-8× 1-8x x ∴根据前几项可以猜想 fn(x)= n-1 . 1-2 x x 1-8x
