轴向拉伸和压缩习题附标准答案
工程力学轴向拉伸与压缩答案
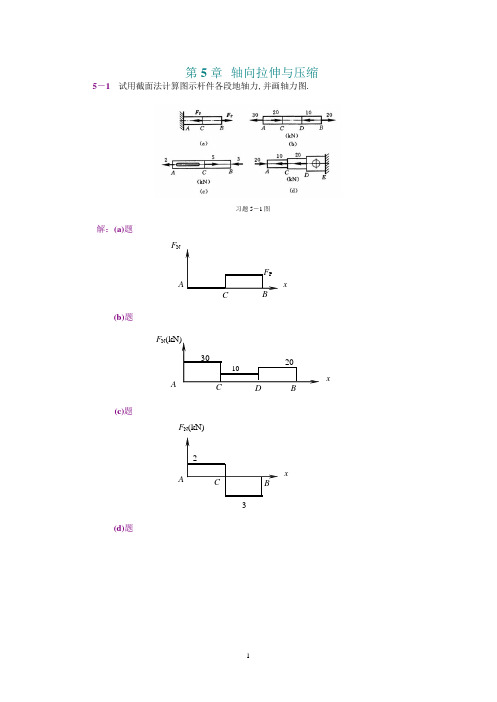
第5 章轴向拉伸与压缩5-1 试用截面法计算图示杆件各段地轴力,并画轴力图.习题5-1 图解:(a)题F Nx(b)题F NxA(c)题F N(kN)x-3(d)题F N-10x5-2 图示之等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成.直杆各部分地直径均为 d =36 mm ,受力如图所示.若不考虑杆地自重,试求 AC 段和 AD 段杆地轴向变形量 Δl AC和 Δl AD习题 5-2 图(F N ) l AB (F N ) l BC解: Δl AC =AB πd 2E s4+BC πd 2 E s 4 150 ×103 × 2000 +100 ×103 ×3000 4 = × = 2.947 mm(F N ) 200 ×103 l π ×362100 ×103 × 2500 × 4 Δl = Δl + CD CD = 2.947 + = 5.286 mm AD AC πd 2 E c4105 ×103 × π ×3625-3 长度 l =1.2 m 、横截面面积为 1.10×l0-3m 2 地铝制圆筒放置在固定地刚性块上;刚性板mC B −6 B 直径 d =15.0mm 地钢杆 BC 悬挂在铝筒顶端地刚性板上;铝制圆筒地轴线与钢杆地轴线重 合.若在钢杆地 C 端施加轴向拉力 F P ,且已知钢和铝地弹性模量分别为 E s =200GPa ,E a =70GPa ;轴向载荷 F P =60kN ,试求钢杆 C 端向下移动地距离.解:u A− u B −F l = P AB E a A a 3(其中 u A = 0)3∴ u =60 ×10 ×1.2 ×10= 0.935 mm B 70 ×10 3 ×1.10 ×10 −3 ×10 6钢杆 C 端地位移为F l60 ×103 × 2.1×103u = u + P BC = 0.935 + = 4.50 m m E s A s200 ×103 × π ×15245-4 螺旋压紧装置如图所示.现已知工件所受地压紧力为 F =4 kN .装置中旋紧螺栓 螺纹地内径 d 1=13.8 mm ;固定螺栓内径 d 2=17.3 mm .两根螺栓材料相同,其许用应力[σ ] =53.0 MPa .试校核各螺栓地强度是否安全.解:∑ M B = 0 ,F A = 2kN ∑ F y = 0 ,F B = 6kN习题 5-4 解图习题 5-4 图 σ = F A = 2000 = A π2000 × 42= 13.37 MPa < [σ ] ,安全. A A d 2 π ×13.8 ×104 σ = F B = 16000= 25.53 MPa <[σ ] ,安全. A B π ×17.32 ×10−645-5 现场施工所用起重机吊环由两根侧臂组成.每一侧臂 AB 和 BC 都由两根矩形截面 杆所组成,A 、B 、C 三处均为铰链连接,如图所示.已知起重载荷 F P =1200 kN ,每根矩形 杆截面尺寸比例 b/h =0.3,材料地许用应力[σ ]=78.5MPa .试设计矩形杆地截面尺寸 b 和 h .4⋅2FF N习题 5-5 图解:由对称性得受力图如习题 5-5 解图所示.∑ F y = 0 ,4F N cos α = F P 习题 5-5 解图F = F P = N 4 cos α 1200 ×103960 = 3.275 ×105 Nσ = F N A= F N 0.3h 2≤ [σ ]9602 + 42025h ≥ F N =0.3[σ ]3.275 ×100.3 × 78.5 ×106= 0.118m b = 0.3h ≥ 0.3 × 0.118 = 0.0354m = 35.4mmh = 118mm ,b = 35.4mm5-6 图示结构中 BC 和 AC 都是圆截面直杆,直径均为 d =20mm ,材料都是 Q235 钢, 其许用应力[σ ]=157MP .试求该结构地许用载荷.B习题 5-6 图习题 5-6 解图∑ F x = 0 , F B = 2F A (1)∑ F y= 0 ,2 F A + 23F B − F P = 0 2(2)1 + 3 F P = F B2(3)F ≤ [σ ] ⋅πd2B43 mdWs由式(1)、(2)得:F ≤ 1 + P2 = 1 + 23 ⋅π d 2 [σ ] 43 ⋅π × 202 ×10−4 ×157 ×106 = 67.4kN 4` (4)F P =2 (1 + 23 ) F A = 2 (1 + 2 3 ) ⋅[σ ]π 24= 90.28kN (5)比较(4)、(5)式,得 [F P ] = 67.4 kN5-7 图示地杆件结构中 1、2 杆为木制,3、4 杆为钢制.已知 1、2 杆地横截面面积A 1=A 2=4000 mm 2,3、4 杆地横截面面积 A 3=A 4=800 mm 2;1、2 杆地许用应力[σ]=20MPa , 3、4 杆地许用应力[σ ]=120 MPa .试求结构地许用载荷[F P ].习题 5-7 图P(a)3(b)解:1. 受力分析:由图(a )有5∑ F y = 0 , F 3 =F P 3 4 4由图(b )由∑ F x = 0 , F 1 = − 5 F 3 = − 3 F P∑ F x = 0 , F 4 = 4 F 3 = 5 43 F P2. 强度计算:5∑ F y = 0 , F 2= − 3F 3 = −F P| F 1 |>| F 2 || F 1 |≤ [σ w ] A 14 F ≤ A [σ ] 3P 1 w F ≤ 3 A [σ ] = 3 × 4000 ×10 −6 × 20 ×10 6 = 60 kN P 4 1 w4F 35F 3 > F 4 , ≤ [σ s ] , A 3F P ≤ [σ ]A 3 3F ≤3 [σ] A 3 ×120 ×10 6 × 800 ×10 −6= 57.6 kN[F P] = 57.6 kNa*5-8 由铝板和钢板组成地复合柱,通过刚性板承受纵向载 荷 F P =38 kN ,其作用线沿着复合柱地轴线方向.试确定:铝板和 钢板横截面上地正应力. 解:此为超静定问题.1. 平衡方程2. 变形协调方程:3. 物性关系方程:F Ns + F Na = F P Δl s = Δl a(1)(2)联立解得⎧F F Ns E s A sE s A s= FNaE a A a(3)习题 5-8 图⎪ Ns = E A E A F P ⎪ ⎨ ⎪F = s s + a E a A a a(压) F NaE A + E A P s s a aσ =F Ns =−E s F P = −E s F P s A E b h + E⋅ 2b h b hE + 2b hE s s 0 a 1 0 s 1 a9 3σ = − 200 ×10 ×385 ×10175MPa (压)= − s 0.03 × 0.05 × 200 ×109 + 2 × 0.02 × 0.05 × 70 ×109σa = F Na A = −b hE E a F P+ 2b hEa 0 s 1 aσ = −175E a E s = −17570 200= −61.25MPa (压)*5-9 铜芯与铝壳组成地复合棒材如图所示,轴向载荷通过两端刚性板加在棒材上. 现已知结构总长减少了 0.24 mm .试求:1.所加轴向载荷地大小; 2. 铜芯横截面上地正应力.习题 5-9 图F NcE A =F NaE A(1)E A E A σ aF = ΔlE c A c , F= ΔlE a A aF Nc + F Na = F P(2)Nc l NalF = F + F = ΔlE c A c + ΔlE a A aP Nc Nal l = Δl E A + E A( c c a a) l= 0.24 ×10−3 ⎧ π 2 =π ⎡ 2 2 ⎤⎫ = ⎨105 ×106 × ×(25 ×10−3 ) + 75 ×106 × × (60 ×10−3 ) − (25 ×10−3 ) ⎬ 30 ×10−3⎩ 4 4 ⎭ = 171 kNF =E c A cNc c c F P + E a A aF =E a A a Na c cF P + E a A a⎧ F Nc E c F P E c F P ⎪σ c = ⎪ A c ⎪ ∴ ⎨= E c A c + E a A a = E c ⋅ πd 2 4 + E a π 2 2 ⋅ (D− d ) 4 ⎪ = F Na ⎪ A a ⎪⎩ = πd 2E c 4E aF Pπ(D 2 − d 2 ) + E a 4 9 32. σ =4 ×105 ×10 ×171×1083.5MPa = c105 ×109 × π × 0.0252 + 70 ×109 × π × (0.062 − 0.025)2σa = σcE a = 83.5 × 70= 55.6MPa E c 105*5-10 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 地正方形,钢和铸铁 各占横截面地一半(b ×2b ).载荷 F P ,通过刚性板沿铅垂方向加在组合柱上.已知钢和铸铁 地弹性模量分别为 E s =196GPa ,E i =98.0GPa .今欲使刚性板保持水平位置,试求加力点地 位置 x =?解:∑ M 0 = 0 , (b ⋅ 2b σ 习题 5-10 图) ⋅( x − b ) = (b ⋅ 2b )σs i( 3 b − x )23∴σ σ s =iE sE i2 x − b = σ i3b − 2 x σ s(1)(2)代入(1)得σ i σ s4 x − 2b = 3b − 2 x5= 98 = 1196 2(2)∴ x = b 65-11 电线杆由钢缆通过旋紧张紧器螺杆稳固.已知钢缆地横截面面积为1×103 mm 2 ,E =200GPa ,[σ ] = 300MPa .欲使电杆有稳固力F R =100kN ,张紧器地螺杆需相对移动多少? 并校核此时钢缆地强度是否安全.F R习题 5-11 图解:(1)设钢缆所受拉力为 F N ,由平衡条件F N cos30°=F RF N =100/ cos30°=115.5kNΔl = F N l = 115.5 ×103 ×10 ×103= 6.67mm EA 200 ×103 ×103× 3 / 2张紧器地螺杆需相对移动 6.67mm .(2)钢缆地应力与强度σ = F N A = 115.5 ×10 103= 115.5MP a < [σ ]所以,强度安全.5-12 图示小车上作用着力 F P =15kN ,它可以在悬架地 AC 梁上移动,设小车对 AC梁地作用可简化为集中力.斜杆 AB 地横截面为圆形(直径 d =20mm),钢质,许用应力 [σ]=160MPa .试校核 AB 杆是否安全.3习题 5-12 图F N ABαF N ACF P习题 5-12 解图解:当小车开到 A 点时,AB 杆地受力最大,此时轴力为 F N A B .(1) 受力分析,确定 AB 杆地轴力 F N A B ,受力图如图 5-12 解图所示, 由平衡方程∑Fy= 0 ,F N AB sin α − F P = 0sin α =解得轴力大小为:0.8 0.82 +1.92F N AB = 38.7kN(2)计算应力σ = F N AB = F N AB = 4 × 38.7 ×10 =123 ×106Pa = 123MPa < [σ ] AB强度安全.A AB πd 2 4π × 202 ×10−65-13 桁架受力及尺寸如图所示.F P =30kN ,材料地抗拉许用应力[σ]+=120MPa , 抗压许用应力[σ]-=60MPa .试设计AC 及AD 杆所需之等边角钢钢号.(提示:利用附录B 型钢表.)F N AC45DAF N ADF PF RA习题 5-13 图习题 5-13 解图解:(1)受力分析,确定 AC 杆和 AD 杆地轴力 F N AC 、 F N AD ,对整体受力分析可得, F R A= F R B = F P 2= 15kN再取节点 A ,受力分析,受力图如图 5-13 解图所示,建立平衡方程D D 3 3 2 4 ∑F y = 0 , − F N AC sin 45 + F R A = 0解得 AC 杆轴力大小为:F N AC = 21.2kN(压)∑ F x = 0 , − F N AC cos 45 + F N AD = 0解得 AD 杆轴力大小为: F N AD = 15kN(拉)(2)强度条件拉杆:A AD = F N AD [σ ]+ = 15 ×10 120 = 125mm 2 压杆:(3)选择钢号A AC = F N AC [σ ]− = 21.2 ×10 60 = 353.3mm 2 拉杆: 20 × 20 × 4压杆: 40 × 40 × 55-14 蒸汽机地气缸如图所示.气缸内径D =560mm ,内压强p =2.5MPa ,活塞杆直径 d =100mm .所有材料地屈服极限σs =300MPa . (1)试求活塞杆地正应力及工作安全系数.(2)若连接气缸和气缸盖地螺栓直径为30mm ,其许用应力[σ]=60MPa ,求连接每个气缸盖 所需地螺栓数.习题 5-14 图解:(1)活塞杆受到地轴力为:⎡π (D 2 F = pA = p − d 2 ) ⎤ = 2.5⎡π (560 −1002 ) ⎤ = 596.12kN N ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ 4 ⎦活塞杆地正应力:σ =F N A 杆596.12 ×103 ) = = 75.9MPa π ×102 / 4 工作安全系数: (2)螺栓数mn = σ s σ= 300 = 3.95 75.93x 3 x y xm = F N = 596.12 ×10 = 14.1 个 A 栓 [σ ]栓 π × 302 / 4 × 60由于圆对称,取m =16个.5-15 图示为硬铝试件,h =200mm ,b =20mm .试验段长度l 0=70mm .在轴向拉力 F P =6kN 作用下,测得试验段伸长Δl 0=0.15mm ,板宽缩短Δb =0.014mm .试计算硬铝地弹 性模量E 和泊松比ν .习题 5-15 图解:(1)计算弹性模量Eε = Δl 0 l 0= 0.15 = 2.143 ×10−3 70σ = F P = 6 ×10 = 150MPa AE = σ = 20 × 2 150 ×106 = 70GPa ε 2.143 ×10−3 (2) 计算泊松比νε = Δb 0 b 0= − 0.014 = −7 ×10−4 20ε ν = y = − 7 ×10−4 = 0.327 ε 2.143 ×10−3上一章返回总目录下一章。
轴向拉伸与压缩第四章答案

思考题四1、 轴向拉伸(或压缩)杆件的外力特点和变形特点是什么?受轴向拉伸和压缩的杆件,其外力特点是:作用在杆件两端的两个力大小相等,方向相反,作用线与杆件的轴线相重合。
其变形特点是:杆件沿轴向伸长或缩短,其横截面变细或变粗。
2、 轴力图上轴力相等的杆件部分应力是否相等?为什么?不相等,因为应力不仅与轴力有关,还与截面积有关。
3、 受轴向拉伸(或压缩)杆件的强度条件是什么?用它可以解决哪些工程计算问题?拉(压)杆的正应力强度条件为A F N=max σ≤[]σ解决三种类型的强度计算问题:①强度校核;②设计截面尺寸;③确定许可载荷。
4、 低碳钢在拉伸实验中可分为几个阶段? 各阶段表现出怎样的力学性能?四个阶段:比例阶段、屈服阶段、强化阶段和局部颈缩阶段。
比例阶段:在试件拉伸的初始阶段,Oa 表现为直线,即σ 与ε 成正比。
屈服阶段:应力在此阶段基本保持不变,而应变却明显增加。
强化阶段:材料恢复了抵抗变形的能力,强化阶段中的最高点d所对应的应力是材料所能承受的最大应力。
局部颈缩阶段:横向尺寸急剧缩小,最后试件在缩颈段被拉断。
5、工程上,如何区分塑性材料和脆性材料?工程上将δ≥5%的材料称为塑性材料,如低碳钢、铝合金、青铜等均为常见的塑性材料。
<5%的材料称为脆性材料,如铸铁、高碳钢、混凝土等均为脆性材料。
6、一般塑性材料的强度指标是什么?脆性材料的强度指标是什么?塑性材料的强度指标是屈服强度;脆性材料的强度指标是抗拉强度。
8、现有低碳钢和铸铁两种材料,试对图4-17结构中的杆选用合适的的材料,并说明理由。
图4-17 思考题8图图4-18 思考题10图 1杆选抗拉强度高的材料,2杆选抗压强度高的材料。
因为1杆受拉力,2杆受压力。
9、胡克定律的两种表述形式是什么?它的适用条件是什么?胡克定律 σ =E ⋅εEA lF l N =∆适用条件是在材料的比例阶段适用。
10、两根材料相同的拉杆,如图4-18所示,试判断它们的绝对变形是否相同?哪根变形大?绝对变形不相同,b)图的拉杆变形大。
轴向拉伸和压缩—思考题

E x x ( y z ) y ( z x ) ( ) x y z
2 E x (1 ) x (1 ) 2 0 (1 ) x (1 ) y
Steel
0.00015 时低碳钢杆、
、
Concrete
的值。
Steel
Steel
210 10 9
E Steel
Concrete
28 10
9
Steel
Concrete
28 10 9 2 9 210 10 15
Concrete
时,胡克定律不成立。因为此时的应变包含两部分:弹性应变(可恢复) ;非弹 性塑性应变(不可恢复) 。
-4-
2-5 弹性模量 E 的物理意义是什么。若低碳钢弹性模量 E Steel 210 GPa ,混凝土 弹性模量 E Concrete 28 GPa ,试求(在弹性变形范围内) (1)在低碳钢杆、混凝土杆两杆横截面上正应力 低碳钢杆、混凝土杆两杆纵向应变
FAC C
FAB B 60
o
y A F x
F F
AB AC
x y
0 : 0 :
AC
h B FAB (a) F y 60 o A
F F
F
cos 60 o 0
sin 60 o F 0
x
C FAC (b)
F F A B 3 F AC 2 F 3 F AC [ t ] A
y0
x x 0 E y x 0 E
第十二章 轴向拉伸与压缩
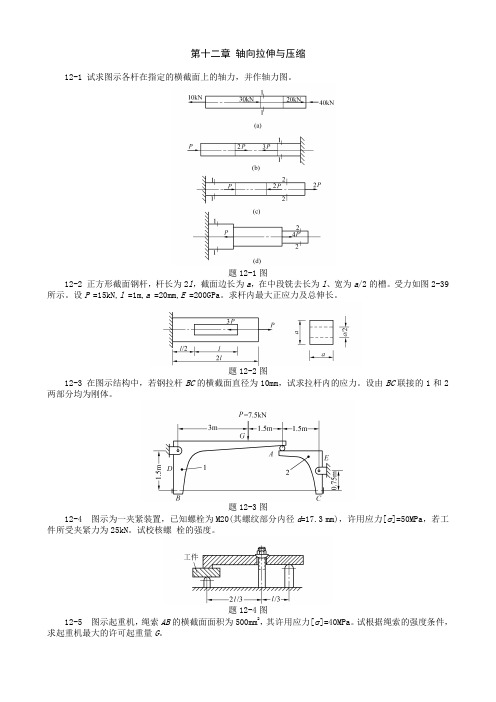
第十二章轴向拉伸与压缩12-1 试求图示各杆在指定的横截面上的轴力,并作轴力图。
题12-1图12-2 正方形截面钢杆,杆长为2l,截面边长为a,在中段铣去长为l、宽为a/2的槽。
受力如图2-39所示。
设P =15kN,l =1m,a =20mm,E =200GPa。
求杆内最大正应力及总伸长。
题12-2图12-3 在图示结构中,若钢拉杆BC的横截面直径为10mm,试求拉杆内的应力。
设由BC联接的1和2两部分均为刚体。
题12-3图12-4 图示为一夹紧装置,已知螺栓为M20(其螺纹部分内径d=17.3 mm),许用应力[ζ]=50MPa,若工件所受夹紧力为25kN。
试校核螺栓的强度。
题12-4图12-5 图示起重机,绳索AB的横截面面积为500mm2,其许用应力[ζ]=40MPa。
试根据绳索的强度条件,求起重机最大的许可起重量G。
题12-5图12-6 设有一起重架如图所示,A、B、C为铰接,杆AB为方形截面木材制成的,P =5kN,许用应力[ζ]=3Mpa ,求杆AB截面每边长度应为多少?题12-6图12-7 蒸汽机的汽缸内的工作压力p=12MPa,汽缸内径D=400mm。
汽缸盖与汽缸用直径d=18mm的螺栓连接。
如螺栓材料的许用应力[ζ]=40MPa,求需要多少个螺栓?见图。
题12-7图题12-8图12-8 某拉伸试验机的结构示意图如图所示。
设试验机的CD杆与试件AB 材料同为低碳钢,其ζp=200MPa,ζs=240MPa,ζb=400MPa。
试验机最大拉力为100 kN。
①用这一试验机作拉断试验时,试样直径最大可达多大?②若设计时取试验机的安全系数n=2,则CD杆的横截面面积为多少?③若试样直径d=10mm,今欲测弹性模量E,则所加载荷最大不能超过多少?12-9 一钢试件如图,E=200GPa,ζP=200GPa,直径d =10cm,在标距l=10 cm之内用放大500倍的引伸仪测量变形,试问:当引伸仪上的读数为伸长25cm时,则试件沿轴线方向的线应变ε、横截面上的应力ζ及所受载荷P各为多少?题12-9图12-10 平板拉伸试件,宽度b=298mm,厚度h=41mm。
工程力学:拉伸压缩 习题与答案

一、单选题1、拉压正应力计算公式s=F/A的适用条件是()。
A.应力小于弹性极限B.应力小于屈服极限C.应力小于比例极限D.外力的合力沿杆轴线正确答案:D2、材料经过冷作硬化后,其比例极限和塑性分别()。
A.提高,提高B.下降,不变C.下降,提高D.提高,下降正确答案:D3、假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为()。
A.大于450MPaB.300MPa£s£450MPaC.450MPaD.小于300MPa正确答案:B4、受轴向拉伸的杆件,其最大切应力与轴线的角度为()。
A.30B.90C.45D.0正确答案:C5、一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的()。
A.应力不同,变形相同B.应力不同,变形不同C.应力相同,变形不同D.应力相同,变形相同正确答案:C6、脆性材料与塑性材料相比,其拉伸性能的最大特点是()。
A.没有明显的屈服阶段和塑性变形B.应力应变关系严格遵守虎克定律C.强度低、对应力集中不敏感D.强度极限比塑性材料高正确答案:A7、现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1, 杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为()。
A.2:1B.1:1C.4:1D.1:2正确答案:C8、在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是()。
A.屈服阶段B.颈缩阶段C.强化阶段D.线弹性阶段正确答案:A9、现有两相互接触的平板,在垂直于板平面的方向上打一直径为d的销孔,使用直径d、许用切应力[τ]、许用挤压应力[sbs]的圆柱形销钉进行固定,两板的厚度均为h, 现分别在两板施加大小相同、方向相反的F,使两板有沿接触面相互错动的倾向,若要销钉不失效破坏,则要满足的条件是()。
(完整版)轴向拉伸、压缩与剪切(例题)

P
FN1 Ptg
P
FN2 cos
(b) 确定许可载荷。由杆1的强度条件得
α
FN2
P
FN1 A1
C
Ptg A1
P 132k N
由杆2的强度条件得
FN 2 A2
P
cos
A2
(c) 确定许可载荷。
P 88 .6k N
杆系的许可载荷必须同时满足1、2杆的强度要求,所以应取上述计算中小的值,
2.62kN.m
1.32kN.m
注释:这里求出的符号为负的轴力只是说明整根活塞杆均受压,而AB段的轴力最大, 为2.62kN。
p.4
例题
例2-2
例题
试计算例2-1中活塞杆在截面1-1和2-2上的应力。设活塞杆的直径d = 10mm。
FN
x
(-)
1.32kN.m
2.62kN.m
解:(a) 截面1-1上的应力。
p.3
例题
例题
例2-1
—双压手铆机如图所示。作用于该手铆机活塞杆上的力分别简化为Pl=2.62kN, P2=1.3kN,P3=1.32kN。试求活塞杆横截面1-1和2-2上的轴力,并画出轴力图。
(d) 轴力图。由于活塞杆受集中力作用,所以在其作用间的截面轴力都为常量, 据此可画出轴力图
FN x
(-)
即许可载荷为[P]=88.6kN p.6
例题
例题
例2-4 图示简易支架,AB和CD杆均为钢杆,弹性模量E = 200 GPa,AB长度为l1 = 2m, 横截面面积分别是A1 = 200 mm2和A2 = 250mm2,P = 10 kN,求节点A的位移。
B
解:(a) 求内力。用截面法求1、2杆的内力
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
轴向拉伸与压缩习题
轴向拉伸与压缩习题一、填空题1.在工程设计中,构件不仅要满足、和稳定性的要求,同时还必须符合经济方面的要求。
2、在式σ=eε中,比例系数e称作材料的拉压_______,相同材料的e值相同;它充分反映某种材料抵抗变形的能力,在其他条件相同时,ea越大,杆件的变形__________。
3、构件工作应力的最高极限叫做__________。
材料能承受的最大应力叫做材料__________。
4、材料抵抗弹性变形能力的指标就是____和_______。
5.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的现象称为。
二、选择题1.轴向弯曲或放大时,直杆横截面上的内力称作轴力,则表示为:()a.fnb.fsfqc.d.fjy2.材料的塑性指标有:()a.σu和δb.σs和ψc.σb和δd.δ和ψ3.截面上的内力大大,()a.与截面的尺寸和形状无关b.与截面的尺寸有关,但与截面的形状无关c.与截面的尺寸无关,但与截面的形状有关d.与截面的尺寸和形状都有关4.等横截面直杆在两个外力的促进作用下出现轴向放大变形时,这对外力所具有的特点一定就是等值、()。
a逆向、共线b反向,过截面形心c方向相对,促进作用线与杆轴线重合d方向相对,沿同一直线促进作用5.一阶梯形杆件受拉力p的作用,其截面1-1,2-2,3-3上的内力分别为n1,n2和n3,三者的关系为()。
an1≠n2n2≠n3bn1=n2n2=n3cn1=n2n2>n3dn1=n2n2<n36.图示阶梯形杆,cd段为铝,横截面面积为a;bc和de段为钢,横截面面积均为2a。
设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3,则其大小次序为()。
aσ1>σ2>σ3bσ2>σ3>σ1cσ3>σ1>σ2dσ2>σ1>σ37.轴向拉伸杆,正应力最大的截面和剪应力最大的截面()a分别是横截面、450斜截面b都是横截面c分别是450斜截面、横截面d都是450斜截面10.由变形公式δl=pl/ea即e=pl/aδl可知,弹性模量()a与载荷、杆长、横截面面积毫无关系b与载荷成正比c与杆长成正比d与横截面面积成正比11.在以下观点,()就是恰当的。
工程力学第5章 轴向拉伸与压缩答案
第5 章轴向拉伸与压缩5-1 试用截面法计算图示杆件各段的轴力,并画轴力图。
习题5-1 图解:(a)题F Nx(b)题F NxA(c)题F N(kN)x-3(d)题F N-10x5-2 图示之等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成。
直杆各部分的直径均为 d =36 mm ,受力如图所示。
若不考虑杆的自重,试求 AC 段和 AD 段杆的轴向变形量 Δl AC和 Δl AD习题 5-2 图(F N ) l AB (F N ) l BC解: Δl AC =AB πd 2E s 4+BC πd 2 E s4 150 ×103 × 2000 +100 ×103 ×3000 4 = × = 2.947 mm(F N ) 200 ×103 l π ×362100 ×103 × 2500 × 4 Δl = Δl + CD CD = 2.947 + = 5.286 mm AD AC πd 2 E c4105 ×103 × π ×3625-3 长度 l =1.2 m 、横截面面积为 1.10×l0-3m 2 的铝制圆筒放置在固定的刚性块上;刚性板m固定刚性板C B −6 B直径 d =15.0mm 的钢杆 BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重 合。
若在钢杆的 C 端施加轴向拉力 F P ,且已知钢和铝的弹性模量分别为 E s =200GPa ,E a =70GPa ;轴向载荷 F P =60kN ,试求钢杆 C 端向下移动的距离。
解:u A− u B −F l = P AB E a A a 3(其中 u A = 0)3∴ u =60 ×10 ×1.2 ×10= 0.935 mm B 70 ×10 3 ×1.10 ×10 −3 ×10 6钢杆 C 端的位移为F l60 ×103 × 2.1×103u = u + P BC = 0.935 + = 4.50 m m E s A s200 ×103 × π 15245-4 螺旋压紧装置如图所示。
第二章轴向拉伸与压缩
第二章轴向拉伸与压缩(王永廉《材料力学》作业参考答案(第1-29题))2012-02-26 00:02:20| 分类:材料力学参答|字号订阅第二章轴向拉伸与压缩(第1-29题)习题2-1试绘制如图2-6所示各杆的轴力图。
图2-6解:由截面法,作出各杆轴力图如图2-7所示图2-7习题2-2 试计算图2-8所示结构中BC杆的轴力。
图2-8 a)解:(a)计算图2-8a中BC杆轴力截取图示研究对象并作受力图,由∑M D=0,即得BC杆轴力=25KN(拉)(b)计算图2-8 b中BC杆轴力图2-8b截取图示研究对象并作受力图,由∑MA=0,即得BC杆轴力=20KN(压)习题2-3在图2-8a中,若杆为直径的圆截面杆,试计算杆横截面上的正应力。
解:杆轴力在习题2-2中已求出,由公式(2-1)即得杆横截面上的正应力(拉)习题2-5图2-10所示钢板受到的轴向拉力,板上有三个对称分布的铆钉圆孔,已知钢板厚度为、宽度为,铆钉孔的直径为,试求钢板危险横截面上的应力(不考虑铆钉孔引起的应力集中)。
解:开孔截面为危险截面,其截面面积由公式(2-1)即得钢板危险横截面上的应力(拉)习题2-6如图2-11a所示,木杆由两段粘结而成。
已知杆的横截面面积A=1000 ,粘结面的方位角θ=45,杆所承受的轴向拉力F=10KN。
试计算粘结面上的正应力和切应力,并作图表示出应力的方向。
解:(1)计算横截面上的应力= = 10MPa(2)计算粘结面上的应力由式(2-2)、式(2-3),得粘结面上的正应力、切应力分别为cos245,=5 MPa45=sin(2*45。
)=5MPa45=其方向如图2-11b所示习题2-8 如图2-8所示,等直杆的横截面积A=40mm2,弹性模量E=200GPa,所受轴向载荷F1=1kN,F2=3kN,试计算杆内的最大正应力与杆的轴向变形。
解:(1)由截面法作出轴力图(2)计算应力由轴力图知,故得杆内的最大正应力(3)计算轴向变形轴力为分段常数,杆的轴向变形应分段计算,得杆的轴向变形习题2-9阶梯杆如图2-13a所示,已知段的横截面面积、段的横截面面积,材料的弹性模量,试计算该阶梯杆的轴向变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章轴向拉伸和压缩
、填空题
1、杆件轴向拉伸或压缩时,其受力特点是:作用于杆件外力的合力的作用线与杆件轴线相_________ .
2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面,并通过截面_____________ .
4、杆件轴向拉伸或压缩时,其横截面上的正应力是___________ 分布的.
7、在轴向拉,压斜截面上,有正应力也有剪应力,在正应力为最大的截面上剪应力为________ .
8杆件轴向拉伸或压缩时,其斜截面上剪应力随截面方位不同而不同,而剪应力的最大值发生在与轴线间的夹角为
________ 的斜截面上.矚慫润厲钐瘗睞枥庑赖。
9、杆件轴向拉伸或压缩时,在平行于杆件轴线的纵向截面上,其应力值为_______ .
10、胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________ 极限.
11、杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力,这说明杆件材料的弹性模量E值越大,其变形就越 ________ 聞創沟燴鐺險爱氇谴净。
12、在国际单位制中,弹性模量E的单位为________ .
13、在应力不超过材料比例极限的范围内,若杆的抗拉(或抗压)刚度越_________ ,则变形就越小.
15、低碳钢试样据拉伸时,在初始阶段应力和应变成___________ 关系,变形是弹性的,而这种弹性变形在卸载后能完全
消失的特征一直要维持到应力为__________ 极限的时候.残骛楼諍锩瀨濟溆塹籟。
16、在低碳钢的应力一应变图上,开始的一段直线与横坐标夹角为a,由此可知其正切tg a在数值上相当于低碳钢的值.酽锕极額閉镇桧猪訣锥。
17、金属拉伸试样在屈服时会表现出明显的__________ 变形,如果金属零件有了这种变形就必然会影响机器正常工作.
彈贸摄尔霁毙攬砖卤庑。
18、金属拉伸试样在进入屈服阶段后,其光滑表面将出现与轴线成_______ 角的系统条纹,此条纹称为__________ .謀养
抟箧飆鐸怼类蒋薔。
19、低碳钢试样拉伸时,在应力-应变曲线上会出现接近水平的锯齿形线段,若试样表面磨光,则在其表面上关键所在可
看到大约与试样轴线成_________ 倾角的条纹,它们是由于材料沿试样的_________ 应力面发生滑移而出现的.厦礴恳蹒骈時
盡继價骚。
20、使材料试样受拉达到强化阶段,然后卸载,在重新加载时,其在弹性范围内所能随的最大荷载将 ________ ,而且
断裂后的延伸率会降低,此即材料的___________现象.茕桢广鳓鯡选块网羈泪。
21、铸铁试样压缩时,其破坏断面的法线与轴线大致成___________ 的倾角.
22、铸铁材料具有_______ 强度高的力学性能,而且耐磨,价廉,故常用于制造机器底座,床身和缸体等.鹅娅尽損鹤惨
歷茏鴛賴。
25、混凝土,石料等脆性材料的抗压强度远高于它的___________ 强度.
债蛏练淨。
26、为了保证构件安全,可靠地工作在工程设计时通常把____________ 应力作为构件实际工作应力的最高限度.籟丛妈羥为贍
27、安全系数取值大于1的目的是为了使工程构件具有足够的____________ 储备.
28、设计构件时,若片面地强调安全而采用过大的__________ ,则不仅浪费材料而且会使所设计的结构物笨重•預頌圣鉉儐
歲龈讶骅籴。
29、正方形截而的低碳钢直拉杆,其轴向向拉力3600N,若许用应力为lOOMpa,由此拉杆横截面边长至少应为_____________ mm.渗釤呛俨匀谔鱉调硯錦。
二、判断题(对论述正确的在括号内画,错误的画X)
1、杆件两端受到等值,反向和共线的外力作用时,一定产生轴向拉伸或压缩变形.()
4、轴力图可显示出杆件各段内横截面上轴力的大小但并不能反映杆件各段变形是伸长还是缩短.()
5、一端固定的杆,受轴向外力的作用,不必求出约束反力即可画内力图.()
6、轴向拉伸或压缩杆件横截面上的内力集度----应力一定正交于横截面.()
9、求轴向拉伸或压缩杆件的轴力时,一般地说,在采用了截面法之后,是不能随意使用力的可传性原理来研究留下部
分的外力平衡的.()铙誅卧泻噦圣骋贶頂廡。
15、材料相同的二拉杆,其横截面面积和所产生的应变相等,但杆件的原始长度不一定相等.()
16、一钢杆和一铝杆若在相同下产生相同的应变,则二杆横截面上的正应力是相等的()
17、弹性模量E值不相同的两根杆件,在产生相同弹性应变的情况下,其弹性模量E值大的杆件的受力必然大.()擁締凤袜备訊顎轮烂蔷。
32、在强度计算时,如果构件的工作和工作应力值大于许用应力很少,而且没有超过5%.则仍可以认为构件的强度是
足够的.()贓熱俣阃歲匱阊邺镓騷。
三、最佳选择题(将最符合题意的一个答案的代号填入括号内)
1、在轴向拉伸或压缩杆件上正应力为零的截面是()
A、横截面 B 、与轴线成一定交角的斜截面
C沿轴线的截面 D 、不存在的
2、在轴向拉伸或压缩杆件横截面上不在此列应力是均布的,而在斜截面上()
A、仅正应力是均布的;
B、正应力,剪应力都是均布的;
C仅剪应力是均布的;D、正应力,剪应力不是均布的;
3、一轴向拉伸或压缩的杆件,设与轴线成45.的斜截面上的剪应力为T,则该截面上的正应力等于()坛搏乡囂忏
蒌鍥铃氈淚。
A 0 ;
B 、1.14 T;
C 、0.707 ;
D 、T;
6、一圆杆受拉,在其弹性变形范围内,将直径增加一倍,则杆的相对变形将变为原来的()倍.
债蛏练淨。
第四章
轴向拉伸和压缩
4
1 1
A ;
B 、
; C 、 1; D 、 2
4
2
7、由两杆铰接而成的三角架(如图所示) ,杆的横截面面积为 处受到铅垂载荷 P 作用时,铅垂杆 AB 和斜杆BC 的变形应分别为
11、两圆杆材料相同,杆I 为阶梯杆,杆n 为等直杆,受到拉力
A 、为杆n 伸长的2倍;
B 、小于杆n 的伸长;
C 为杆n 伸长的2.5 倍;
12、几何尺寸相同的两根杆件,其弹性模量分别为 E 1=180Gpa,E 2=60 Gpa,在弹性变形的范围内两者的轴力相同,这时弹性模量;17、塑性;18、450、滑移线;19、45°、最大剪;20、提高、冷作硬化;21、45°; 22、抗压;23、高;24、
杆的变形情况,可知杆I 的伸长(
)的结论是正确的.買鯛鴯譖昙膚遙闫撷凄。
Pl 4PI EA ,
3EA
、0,旦;
EA
PI PI 2EA‘ 3EA
产生的应变的比值—应力为(
)綾镝鯛駕櫬鹕踪韦辚糴。
1
A 、一
B 、1 ;
C 、2;
D 、3
3
13、一钢和一铝杆的长度,横截面面积均相同,在受到相同的拉力作用时,铝杆的应力和( )
A 钢杆的应力相同,但变形小于钢杆;
B 变形都小于钢杆;
C 钢杆的应力相同,但变形大于钢杆;
D 变形都大于钢杆•
四、图所示支架,AB 为钢杆,横截面积AAEF600mr r t BC 为木杆,横截面积 钢的许用应力[d ]=140Mpa ,木材的许用拉应力[d L ]=8Mpa ,许用压应力[ 求支架的许可载荷.驅踬髏彦浃绥譎饴憂锦。
第四章 轴向拉伸和压缩答案
一、填空题:
D
、等于杆n 的伸长;
1、重合;
2、形心;4、均匀;7、零;8、45°; 9、零;10、比例;11、小;12、Pa;1
3、大;15、正比、比例;16、拉;25、抗拉;26、许用;27、强度;28、安全系数;29、6 ;.猫虿驢绘燈鮒诛髅貺庑。
二、判断题:
1、X;
2、“;
3、“;
4、X;
5、“;
6、2;
7、2;
8、“;
9、X;10、X;11、X;12、X;13、";14、X;
15、";16、X;17、X;32、“.锹籁饗迳琐筆襖鸥娅薔。
三、最佳选择题:
1 —C;
2 —B;
3 —D;
4 —A;
5 —C;
6 —A;
7 —D;
8 —B;
9 —C;10 —B;11 —C;12 —A;13 —C;構氽頑黉碩饨荠龈话骛。
四、[P]=101KN.
第四章轴向拉伸和压缩5。
