初中奥数中环杯竞赛试题3篇-高清打印版
十三届初二中环杯决赛
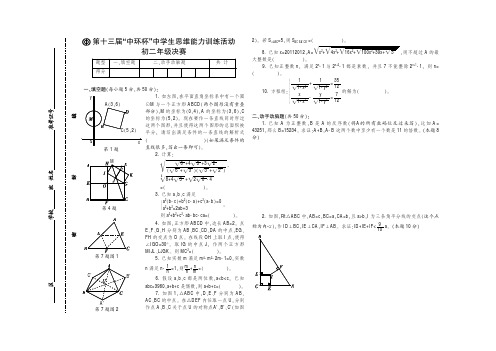
蚁IGO=30毅遥 取 IG 的中点 J袁 作两个正方形
第 7 题图 1
MIJL尧LJGK遥 则 MC2=渊
冤遥
5. 已知实数 m 满足 m4-m2-2m-1=0袁实数
C'
n
满足
n-
1 n
=1袁则
m n
+
n m
=渊
冤遥
B'
6. 假设 a尧b尧c 都是两位数袁a<b <c袁 已知
abc=3960袁a+b+c 是偶数袁则 a+b+c=渊
43251袁那么 B=15234遥 求证院A +B袁A -B 这两个数中至少有一个数是 11 的倍数遥 渊本题 8 分冤
2. 如图袁Rt吟A BC 中袁A B=c袁BC=a袁CA =b袁且 a>b袁I 为三条角平分线的交点渊这个点
称为内心冤袁作 ID彝BC袁IE彝CA 袁IF彝A B遥
求证院ID+IE+IF<
D'
C' 图3
4. 已知 n伊n 的表格中袁每格内都有一盏灯袁开始的时候所有的灯都是关着的遥 每次 操作改变同一行或者同一列的连续 m 盏灯的状态渊原来关着的要打开袁原来开着的要关 上冤遥 若要求最后可以使得所有的灯都打开袁求证院m讦n遥 渊本题 10 分冤
淤 当 琢 满足什么条件时袁图中有且仅有三个等腰三角形渊三边都有 线连接袁无所谓是实线还是虚线袁都可以算为一个三角形冤钥
第十三届野中环杯冶中学生思维能力训练活动 初二年级决赛
题型 一尧填空题 得分
二尧动手动脑题
共计
一尧填空题渊每小题 5 分袁共 50 分冤院
y A 渊3袁6冤
第15届中环杯9年级选拔赛试题

第10题C第十五届“中环杯”中学生思维能力训练活动九年级选拔赛得分:填空题:1.已知α、β是方程x 2-3x +1=0的两个根,则α7+β7的值为。
2.如图,二次函数的解析式为y =k 2-x 2(k >0),A 、D 是二次函数与x 轴的交点,ABCD 为矩形,二次函数的顶点V 在线段BC 上。
若ABCD 的周长为48,则k =。
3.一个三位数abc ,其中的三个数码a 、b 、c 是不同的质数,而且abc 也是一个质数。
满足这些条件的abc 最大为。
4.如图,正六边形ABCDEF 中,GH //AB ,阴影部分面积是整个正六边形面积的16。
AB =2厘米,则GH =厘米。
5.已知f (x )=1x -4x √+3,其定义域为116≤x ≤1。
则f (x )的最大值与最小值之和为。
6.如图,两个同心圆的半径分别为1和2。
阴影部分是一个八边形,这个八边形的八条边都相等。
那么这个八边形的周长为。
7.小明需要将一封信送到大明湖畔27145号大楼内,他记住了这五个数字,但是没有记住它们的顺序。
他将这五个数字随意组合,构成一个五位数。
这个五位数中有且仅有两个数字所在的位置与原数相同(比如27451中的2和7所在的位置与原数相同,符合我们的要求)。
符合要求的五位数有个。
8.一枚标准立方体骰子的任两个相对面上点数之和都为7。
若将27枚相同的标准骰子在桌面上堆叠成3×3×3的立方体,那么,从某个位置望过去最多可以看到个点。
9.已知Rt △ABC 中,∠C 为直角,且sinA 与sinB 是方程(5n +8)x 2-(7n -20)x +120=0的两个根,则整数n =。
10.如图,在梯形ABCD 中,AD //BC ,并且∠ABC +∠CDA =270°,AB ·tan ∠BCD =20,CD =13,则AB 2=。
11.我们用S =24+34+54+74+…+174974表示前2014个质数的四次方之和,那么S 除以240的余数为。
11届中环杯选拔赛七年级

题型一、填空题二、动手动脑题共计得分第十一届“中环杯”小学生思维能力训练活动初一年级选拔赛一、填空题:(每题7分,共56分。
)1.凸十边形的最大外角至少为()度。
2.计算:20111+12+20112+22+20113+32+……+20112010+20102=()。
3.已知代数式ax3+bx+c,当x=0时代数式的值为2,当x=3时代数式的值为-1,则当x=-3时代数式的值为()。
4.若x-1x=4,则x2x4+x2+1的值是()。
5.哥哥对弟弟说:“到21世纪的x2年,我恰好x岁。
”那么,哥哥生于()年。
(x2指代某四位数的年份)6.三角形的三边分别为4、2-3a、7,则a的取值范围是()。
7.已知(x+3)2(x+1)3=A x+1+B(x+1)2+C(x+1)3,则2A+B+C的值等于()。
8.如图,大三角被分成了9个小三角形,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加的和相等。
请想一想,怎样填这些数才能使5个数的和尽可能小一些。
这些五个数的和最小的是()。
二、动手动脑题:(每题11分,共44分。
)1.已知abc=1,求a ab+a+1+b bc+b+1+c ca+c+1的值。
2.下面两个图案都是由8个大小一样的小长方形拼成的,并且第二个图形的总面积(包含中间的小正方形)是121平方厘米。
(1)图形吗?(2)求小长方形的面积。
3.能否将下列数组中的数填入3×3的方格表,每个小方格中填一个数,使得每行、每列、两条对角线上的3个数的乘积都相等?若能,请给出一种填法;若不能,请给予证明。
(1)1,2,3,4,6,9,12,18,24(2)1,2,3,4,6,9,12,18,364.有8个边长为2厘米的等边三角形,4个边长同为2厘米的正方形,如图。
请你选取其中的一些或全部,分别拼出一个六边形和一个九边形。
第一届中环杯竞赛试题

第一届中环杯竞赛试题尊敬的参赛者们,欢迎参加第一届中环杯竞赛。
本次竞赛旨在激发学生的创新思维和解决问题的能力,同时增进对科学、技术、工程和数学(STEM)领域的了解。
以下是本次竞赛的试题内容:一、数学部分1. 计算下列表达式的值:\( \sqrt{25} + \frac{1}{2} \times 4 \)2. 解下列方程:\( 3x - 7 = 2x + 5 \)3. 证明:\( \tan(45^\circ) = 1 \)二、物理部分1. 一个物体从静止开始,以恒定加速度 \( a \) 运动。
如果它在\( t \) 秒内移动了 \( s \) 米,求 \( a \)。
2. 描述并解释牛顿第三定律。
3. 一个质量为 \( m \) 的物体在地球表面受到的重力是 \( F \)。
如果物体被带到月球表面,其重力将如何变化?三、化学部分1. 描述水的化学性质,并解释为什么水是生命之源。
2. 写出下列化学反应的平衡方程式:\( \text{N}_2(g) +3\text{H}_2(g) \rightleftharpoons 2\text{NH}_3(g) \)。
3. 解释什么是氧化还原反应,并给出一个例子。
四、生物部分1. 解释什么是基因突变,并举例说明其可能的影响。
2. 描述细胞分裂的过程,并区分有丝分裂和减数分裂。
3. 阐述生态系统中食物链和食物网的概念及其重要性。
五、编程部分1. 编写一个简单的程序,计算并打印出前 \( n \) 个自然数的和。
2. 解释什么是递归,并给出一个使用递归的算法示例。
3. 描述面向对象编程的基本概念,并给出一个简单的类定义示例。
结束语我们希望本次竞赛能够成为你们展示才华的舞台,同时也希望你们在解题过程中享受学习的乐趣。
预祝各位参赛者取得优异的成绩!第一届中环杯竞赛组委会。
13届中环杯决赛七年级
第十三届“中环杯”中学生思维能力训练活动初一年级决赛一、填空题(每小题5分,共50分):1)2-ab (a+b )-a-b+1=()。
2.已知有一个面积为2013的正方形。
对它做一个外接圆,对外接圆作外切正方形,我们称其为一次操作。
那么,最少要经过()次操作,最大的正方形的面积会超过20130316。
3.把正整数中所有位数上的数字都不大于5的数从小到大排成一列,那么第2013个数是()。
4.已知a =71×39,b =71×32,c =32×39。
则a 2+b 2+c 2√=()。
5.若大于100的正整数n 满足:首尾两个数字相同,且其余数字均与首尾两个数字不同,则这样的n 称为“中环数”。
比如:1381和2442都是“中环数”,而4321和24282不是“中环数”。
则有()个“中环数”小于2013。
6.已知a ,b ,c 满足a 2(b-c )+b 2(c-a )+c 2(a-b )=0a 2+b 2=2ab+3{,则a 2+b 2+c 2-ab-bc-ca =()。
7.已知x x 2-ax +1=1(a 为正整数,且是3的倍数),且x 6-a 3x 3+1x3除以9的余数与20122012…2012n 个2012除以9的余数相同,则n 的最小值是()。
8.数据库中有2013,20132,20133,20134,…,201320130316共20130316个数。
小明编写了一个程序,该程序从数据库中任取2个数代入下式运算:2ab-a-b +1。
将取出的2个数从数据库中移去,再将运算结果写入数据库。
当数据库中只剩下一个数的时候,剩下的那个数是()。
9.已知x 满+1x -1-1+x 2+4x 2-3x ,则x 2-26x=()。
10.已知的正整数m 、n ,满足(m+n )2│(4mn +4),则m-n =()。
二、动手动脑题(共50分):1.已知a 、b 、c 、d 是四个连续正整数,求证:d 2一定是a+b 2+c 3的因数。
第16届中环杯决赛试卷与答案七年级_2861

a
b
最后,这个对称图形的大致形状如图 c 所示(该图只是示意图),为了完成整个图 形,需要_______块等腰梯形
c 【答案】54 二、动手动脑题(本大题共 4 小题,每题 10 分,共 40 分,请写出解题过程): 11. 若非零实数 x, y 满足 x3 xy 2 y 6 y 4 ,求: x y 的最小值 【答案】
第 16 届中环杯七年级决赛
一、填空题(本大题共 10 小题,每题 6 分,共 60 分): 1. 计算:
20142 20152 40282 2 2014 2015 2 2014 4028 2 2015 4028 ________. 22 42 62 1002
2 3 13 ,所以 2 3 13 6 19 。则 242 262 的最大素因数为_____. 3 2 6
【答案】157
6. 如果一个自然数的所有因数中至少有四个是两位数,那么这样的自然数就称为“中环 数”。最小的“中环数”是______. 【答案】48 7. 在一个游戏中,战士身穿盔甲,抵挡来自外界的攻击。如果一个战士的盔甲值为 k , 那么他可以抵挡住
14. 已知 n 是一个正整数,在黑板上写上 n3 个不同的三元有序正整数组 a, b, c ,其中
1 a, b, c n 。接下来,从每个数对中选出最大的数(可能有多个最大的数),将剩余
的数擦去。比如,在数组 1,3, 4 中,擦去 1、3,留下 4;在数组 2, 4, 4 中,擦去 2, 留下 4、4。对这 n3 个数组都进行这样的操作后,求证:黑板上留下数的个数不可能是 一个完全平方数 【证明】略
k k 的外界攻击,我们将 称为他的抵挡值。比如,某个战士 k 10 k 10 40 80% 的外界攻击,这个战士的抵挡值就是 40 10
杯赛真题精选上中下及答案

(中环杯初赛诊断试题第1题)200592005920059999999999999×+个“”个“”个“”的得数的末尾有( )个零。
(第九届中环杯四年级第1题)计算:345345×788+690×105606=( )(第九届中环杯四年级第5题)201×202×203×……×300的结果除以10,所得到的商再除以10……重复这样的操作,在第_____次除以10时,首次出现余数。
计算54÷64×51÷(27÷128×17)(第四届小机灵邀请赛)将6放在一个两位数的右侧,形成的三位数比原来的两位数多294,求原来的两位数八个正整数由小到大排列,从第三个数开始,每个数都是它前面两个数之和,如果第五个数是21,求第八个数是多少?2000×1999-1999×1998+1998×1997-1997×1996+…+4×3-3×2+2×1(第六届“中环杯”小学生思维能力训练活动五年级复赛第一大题填空题第1题)7999.99+799.99+79.99+7.99+8.99+89.99+899.99+8999.9+8999.99=( )(第七届“中环杯”小学生思维能力训练活动五年级初赛第一大题填空题第3题)12+22+32+42+52+…20052+20062的和的末位数是( )。
测试题1.(第五届中环杯复赛)2222×17+3333×4+6666×92. (2008年第八届“春蕾杯”小学数学邀请赛决赛)199772×199911-199771×199912 =3.247×285+247×386+671×253=4.甲乙两数的平均数是30,乙丙两数的平均数是44,甲丙两数的平均数是34。
第十四届“中环杯”九年级数学初赛选拔试题(word版,含答案)

中环杯初中场】第十四届“中环杯”中学生思维能力训练活动初三年级选拔赛试题填空题:1.已知实数a、b满足a3+b3+3ab=1,且ab≠1,则a+b=____________2.已知使得1584x为立方数(立方数就是指某个自然数的立方)的最小正整数为x,而使得xy是1584的倍数的最小正整数为y,则y=__________3.如图,在平行四边形ABCD中,分别在AD、BC上取点E、F,使得=,=。
AC、EF相较于点O,在AB上取点G,使得=,连接GO,并延长交DC于点H,则DH:HC=___________.4.在1,2,3……,2013这2013个自然数中,最多可以取到_____________个数,使得其中任意两个数之和为160的倍数。
5.已知实数x满足方程 + +=3+ ,则x有_______个解。
6.下列数阵中,有__________个完全平方数。
111111...11 (1)2013个1222222...22 (2)2013个2333333...33 (3)2013个3………………999999...99 (9)2013个97.将编号为1-10的10本书放入编号为1-10的10个书架上,要求编号为k的书只能放在编号为k-1或k或k+1的书架上,例如:编号为1的书只能放在编号为1或2的书架上;编号为4的书只能放在编号为3或4或5的书架上;编号为10的书只能放在编号为9或10的书架上。
那么一共有______________种放法。
8.如图,在Rt△ABC中,E为斜边AB的三等分点中靠近B的那个点,∠AEC=45°,则=__________。
9.如图,三角形ABC为等腰直角三角形,在线段BC上取点D,作正方形ADEF,EF与BC.相较于点G。
若BD=4,CG=3,则正方形ADEF的边长为______________。
10.请找到所有的正整数n,使得2n+n1(8n+n),则n=_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中奥数中环杯竞赛试题3篇
初中奥数中环杯竞赛试题篇1
1、甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?
2、甲乙两艘轮船分别从A、B两港同时出发相向而行,甲船每小时行驶18千米,乙船每小时行驶15千米,经过6小时两船在途中相遇。
两地间的水路长多少千米?
3、一辆汽车和一辆摩托车同时分别从相距900千米的甲、乙两地出发,汽车每小时行40千米,摩托车每小时行50千米。
8小时后两车相距多少千米?
4、甲乙两车分别从相距480千米的A、B两城同时出发,相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时。
两车出发后多少小时相遇?
5、王欣和陆亮两人同时从相距2000米的两地相向而行,王欣每分钟行110米,陆亮每分钟行90米。
如果一只狗与王欣同时同向而行,每分钟行500米,遇到陆亮后,立即回头向王欣跑去;遇到王欣后再回头向陆亮跑去。
这样不断来回,直到王欣和陆亮相遇为止,狗共行了多少米?
初中奥数中环杯竞赛试题篇2
1、小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘在家中,爸爸带着文具盒立即骑自行车以每分钟280米的速度去追小明。
爸爸出发几分钟后追上小明?
2、甲、乙、丙三人都从A城到B城,甲每小时行4千米,乙每小时行5千米,丙每小时行6千米,甲出发3小时后乙才出发,恰好三人同时到达B城。
乙出发几小时后丙才出发?
3、四年级同学从学校步行到工厂参观,每分钟行75米,24分钟以后,因有重要事情,派张兵骑车从学校出发去追。
如果他每分钟行225米,那么几分钟后可以追上同学们?
4、两名运动员在环形跑道上练习长跑。
甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙。
环形跑道一周长多少米?如果两人同时同地背向而行,经过多少分钟两人相遇?
5、我骑兵以每小时20千米的速度追击敌兵,当到达某站时,得知敌人已于2小时前逃跑。
已知敌人逃跑的速度是每小时15千米。
我骑兵几小时后可以追上敌人?
初中奥数中环杯竞赛试题篇3
1、一项工程,甲、乙两队合做需12天完成,乙、丙两队合作需15天完成,甲、丙两队合作需20天完成,如果有甲、乙、丙三队合作需几天完成?
2、一项工程,甲单独完成需12天,乙单独完成需9天,若甲先做若干天后乙接着做,共用10天完成,问甲做了几天?
3、做一件工程,甲独做需要12小时完成,乙独做需要18小时完成,甲、乙合做1小时后,然后由甲工作1小时,再由乙工作1小时,两人如此交替工作,完成任务还需要多少小时?
4、加工一批零件,甲、乙合做1小时完成了这批零件的11/60,乙、丙两人接着生产1小时,又完成了全部的3/20,甲、丙又合做2小时完成了1/3,剩下的任务由甲、乙、丙三人合作,还需多少小时完成?
5、一条公路,甲队独修需24天完成,乙队独修需30天完成,甲、乙两队合修若
干天后,乙队停工休息,甲队继续修了12天完成,乙队修了多少天?。
