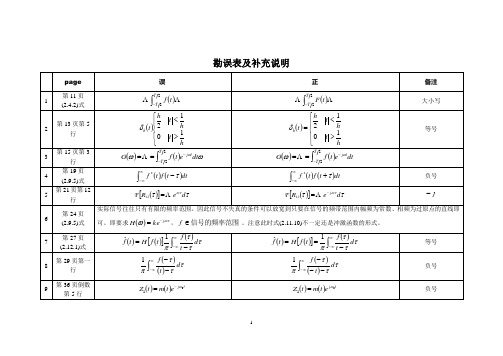
《信号与系统(第三版)习题解析》勘误表
信号与系统(第三版)习题详解1-2章

"!#!
"#%"
"’"’’
!
$"
-%#’
!
$##&$
"
%$’#"
’
!
"%#"%
"#
’"
$!#$
%
%
’
!!!’#1
"##"#
"#"
+%$$
’’
!!
’$1
’
"
’
"#’#""$!#
"",
’"!’-!#$!’$’
"#"#""#
"#"#%"#"#"#-""&
."’"!
’’’’’’$/#’
.
!$%$!$’!$/#
’"""""#
(#/(") ’#$!#!(’) ’
!!$!判定下列信号是否为周期信号(若是周期信号’则确定信号周期,(
"!#"##%2-*3%#$
!
""*3#)2
"#"’*23%#-+()*!#
"%#%
"#$
"##"##/()#0*3
%$
#
""*-2槡#
"#’"#"#
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(5-6章)【圣才出品】

2.脉冲编码调制(PCM) (1)脉冲调制概念 利用脉冲序列对连续信号进行抽样产生的信号称为脉冲幅度调制(PAM)信号。把连 续信号转换成数字(编码)信号进行传输或处理的调制方式称为脉冲编码调制(PCM)。PCM 通信系统的简化框图如图 5-1-2 所示。
图 5-1-2 PCM 通信系统简化框图 (2)PCM 通信特点(见表 5-1-4)
5-2 若系统函数H(jω)=1/(jω+1),激励为周期信号e(t)=sin(t)+sin(3t), 试求响应r(t),画出e(t),r(t)波形,讨论经传输是否引起失真。
解:激励信号 e(t)=sin(t)+sin(3t),则 E(jω)=F[e(t)]=jπ[δ(ω+1)-δ(ω-1)]+jπ[δ(ω+3)-δ(ω-3)]
一、系统函数 H(jω)
当且仅当 H(s)在虚轴上及右半平面无极点时,有 H ( j) H (s) s j ,也即,对于 H(s)在虚轴上有极点的系统,有 H ( j) H (s) s j 。
二、无失真传输 1.定义 系统无失真传输是指响应信号与激励信号相比,只是大小与出现的时间不同,而无波形 上的变化。 设激励信号为 e(t),响应信号为 r(t),则无失真传输的条件是 r(t)=Ke(t-t0), K 为常数,t0 为滞后时间,如图 5-1-1 所示。
6 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台
故响应为:
R( j) = E( j)×H ( j)
=
jπ j +
[ 1
(
+
1)
-
(
-
1)] +
jπ j +
[ 1
(
+
3)
《信号与系统》教材重印勘误

《信号与系统》教材重印勘误P.3 式(1.2.1),最好改为:()10sin(π)20π/2t f t +=P.5 式(1.2.6)和式(1.2.9)之前的空行? P.6 式 0)e 1(1lim d e 1limd )(1lim2-2/04-2/2/23=-===∞→∞→-∞→⎰⎰ττττττττττt t t f P t改为/2/22-4-23/2111lim()d lime d lim(1e )04t P f t t t ττττττττττ-→∞→∞→∞===-=⎰⎰P.18 1.2(3)“而平均功率都为零”改为“而平均功率都为有限值”1.3(4)⎪⎩⎪⎨⎧<<-<<-+=其它01010112)(4k k k k k f 改为 4210()10202k k f k k k -≤≤+<⎧⎪=-<⎨⎪⎩其它 P.29 例2.3.1中,“f 2(t )”改为 “f (t )”P.35 图2.4.1如下修改:P.38 式122-22--12()()*()e ()[()(3)]d e ()()d e()(3)d ()()y t f t f t u u t u t u u t u u t y t y t τττττττττττττ∞-∞∞∞--∞∞==----=---+-=⎰⎰⎰中,最后一行改为:12()()()y t y t y t -=同理,本例解答中:“最后得”后面的12()()()y t y t y t +=也改为12()()()y t y t y t -=P.45 题图2.2中,“f (t )”改为 “f (4-2t )”t0.2 0 4f (t ) 图2.4-1 例2.4-1图1-1t t0.20 1-10.8 f A (t ) f D(a )(b )(c )0 3.2-0.8该脉冲删除P.61 例3.4.2f 22222(2)()()*()e ()*[()(2)]e ()*()e ()*(2)11(1-e )()[1-e ](2)22t t t t t y t f t h t u t u t u t u t u t u t t u t u t ε------==--=--=--改为f 22222(2)()()*()e ()*[()(2)]e ()*()e ()*(2)11(1-e )()[1-e ](2)22t t t t t y t f t h u t u t u t u t u t u t u t t u t u t ------==--=--=--P.76 式j2π-j2πj4π-j4πj6π-j6π-j6π-j2π-j4πj2πj2πj6π1e e e e 2e e 22232111111 e e e e e e 342243()t t t t t tt t t t t tf t +++++=++++=+ 改为j2π-j2πj4π-j4πj6π-j6π-j6π-j4π-j2πj2πj4πj6πe e e e e e 1052222e 2.5e 5e 5e 2().5e e t t t t t tt t t t t tf t +++++++==+++ P.76 式(4.1.1)0011()[cos sin ]c s()22o n n n n n n A f t a n t b n t A n t A ϕ∞∞===+Ω+Ω=+Ω+∑∑改为0011()[cos sin ]cos()22n n n n n n A f t a n t b n t A n t a ϕ∞∞===+Ω+Ω=+Ω+∑∑ P.78 图4.1.3中,字母a~e 适当下移。
勘误表
1. "线性调制"的一种定义是看它是否满足叠加原理(见[1],第 232 页) ,DSB 是线性调制:
m1 (t ) cos ωc t + m2 (t ) cos ωc t = [m1 (t ) + m2 (t )] cos ωc t
46 第 190 页倒 数第 3~5 行 在这个定义下,标准调幅 AM,SSB,2ASK,2PSK 都不是线性调制.但因为它门在实质上是 DSB,所以也可归类于线性调制. 注:对于 AM,用两个基带信号的和做 AM 调制结果虽然也是 AM 信号,但载波分量不是叠加关系 2.还有人将"线性调制"定义为: "调制后信号的频谱为调制信号频谱的平移及线性变换" (见[3],第 27 页) (见 3.因为"线性"一词有"成比例"的意思,故有人也把 FM 叫做线性调制,取 FM 的瞬时频偏同基带调制信号的电压成正比之意. [2],第 138 页)
V P(s1 ) p T s 1
+
∞
=∫
∞
[s1 (τ ) + nw (τ )]s1 (Tb t + τ )dτ
另外请注意其它各处 条件概率的记号
35
第 154 页 (5.3.45)式 第 158 页 (5.4.12)式
V p ( s2 ) p T s 2
P(s1 ) p(VT | s1 ) P(s2 ) p(VT | s2 )
4
33
page 第 147 页倒 数第 2 行
误 滤波器的三分贝单边带宽 B
正 滤波器的等效噪声带宽 B
备注
34 第 152 页 (5.3.27)式
∞ ∞ ∞
= ∫ r (τ )s1 (t Tb + τ )dτ =∫
电子教案《信号与系统》(第三版)信号系统习题解答

《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第8章 z变换、离散时间系统的z域分

(7)
X
z
1 2
n
u
n
u
n
10
z
n
9 n0
1 2
n
z
n
9 n0
1 2z
n
1
1 2z
1 1
10
z 0
2z
X(z)的零、极点分布图如图 8-2-1(g)所示。
(8)
8 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
X
z
n台
1 2
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 8 章 z 变换、离散时间系统的 z 域分析
8.1 复习笔记
从本章开始陆续讨论 Z 变换的定义、性质以及它与拉氏变换、傅氏变换的联系。在此 基础上研究离散时间系统的 z 域分析,给出离散系统的系统函数与频率响应的概念。通过 本章,读者应掌握对于离散时间信号与系统的研究,是先介绍 z 变换,然后引出序列的傅 里叶变换以及离散傅里叶变换(第九章)。
4 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平
台
于实轴的直线映射到 z 平面是负实轴;
(3)在 s 平面上沿虚轴移动对应于 z 平面上沿单位圆周期性旋转,每平移 ωs,则沿
单位圆转一圈。
2.z 变换与拉氏变换表达式
Z
x nT X z zesT X s Z
n
u
n
1 3
n
u
n
z
n
n
(3)
X
z
n
1 3
n
u
n
z
n
n0
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(第4章)【圣才出品】

3.全通函数 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于 jω 轴互为镜像,这种系统函数称为全通函数,此系统则称为全通系统或全通网络。它的幅频特 性是常数。
4.最小相移函数 零点仅位于左半平面或 jω轴的网络函数称为“最小相移函数”,该网络称为“最小相 移网络”。非最小相移函数可以表示为最小相移函数与全通函数的乘积,即非最小相移网络 可以用最小相移网络与全通网络的级联来代替。
(1)部分分式展开法求解
首先将 F(s)展开成部分分式之和的形式,再对各部分分式分别取逆变换后叠加即可
得出 f(t)。
(2)留数定理求解
将拉氏逆变换的积分运算转化为求被积函数 F(s)est 在围线中所有极点的留数之和。
L 1[F (s)] 1 j F (s)estds [F (s)est的留数]
1 s
s2
s 2
,故
7 / 122
圣才电子书 十万种考研考证电子书、题库视频学习平台
L
[1 cos(t)]et
s
1
s (s )2 2
;
(7) L
[t 2
2t]
d2 ds2
1 s
d ds
2 s
2 s3
2 s2
(8) L [2 (t) 3e7t ] 2 3 s7
图 子书、题库视频学习平台
二、系统函数与系统特性 1.系统函数 系统的零状态响应的拉氏变换与激励的拉氏变换之比称为系统函数,即 H(s)=RZS (s)/E(s)。且冲激响应 h(t)↔H(s)。
2.零极点分布
H (s)
(9)e-αtsinh(βt);
(10)cos2(Ωt);
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】

第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节,是整个信号与系统学习的基础。
本章介绍了有关信号与系统的基本概念和术语,给出几种典型的信号和系统的表现形式,讲述了各信号与系统的特点以及信号之间的运算和转换。
通过本章学习,读者应掌握:如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。
一、信号概述
1.信号的概念及分类(见表1-1-1)
表1-1-1信号的概念及分类
2.典型的连续信号(见表1-1-2)
表1-1-2典型的信号及表示形式
3.信号的运算(见表1-1-3)
表1-1-3信号的运算
4.阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号,许多复杂信号皆可由二者或二者的线性组合表示。
具体见表1-1-4及表1-1-5。
(1)单位阶跃信号u(t)
表1-1-4单位阶跃信号u(t)
(2)单位冲激信号δ(t)
表1-1-5单位冲激信号δ(t)表示形式及性质
5.信号的分解
一个一般信号根据不同类型可分解为以下几种分量,具体见表1-1-6。
表1-1-6信号的分解
二、系统
1.系统概念及分类(见表1-1-7)
表1-1-7系统的概念及分类
系统模型如下:
输入信号经过不同系统可得到不同输出信号,具体见表1-1-8。
表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?
(a)
(b)
(c)
(d)
(e)
(f)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信号与系统(第三版)习题解析》勘误表1
谷源涛
2012年3月25日
一、可能影响理解的错误
1、 第12页,第3行“(t −π4)”改为“(t +π4)”,即把减号改成加号
2、 第291页,第10行“=Wal2{[(i −1)⊕j ]+1,t]”改为“=Wal2{[(i −1)⊕j ]+1,t }”,
即最后一个中括号改成大括号
3、 第297页,第7行行末“πA 28δ(ω+1800)”改为“πA 28[δ(ω+1800)”并移至第8行行
首,注意改动是插入方括号
4、 第311页,倒数第6行“cos (ωc T −ωc t )+sin (ωc T −ωc t )”改成“cos (ωc T −ωc t )−
sin (ωc T −ωc t )”,即加号改成减号
5、 第311页,倒数第5行“cos (ωc t )−sin (ωc t )”改成 “cos (ωc t )+sin (ωc t )”,即减号改
成加号
6、 第391页,倒数第4行“DFT[x (n )]=X (k )”改为“DFT[x (n )]=X (k )”,即去掉x 和X 上的
黑体;将“IDFT[X ](k )=x (n )”改为“IDFT[X (k )] =x (n )”,即一方面去掉黑体,另一方面将(k )移到方括号之内
7、 第434页,第7行“0.739”改为“2.825”
8、 第434页,倒数第3行“0.739”改为“2.825”
9、 第455页,倒数第4行“,代价是增大了主瓣宽度和过渡带宽度”删掉
10、 第460页,第9行“在∞有一个四阶零点,”删掉
11、 第469页,第6行“ℒ[KΘ(t )]”改为“ℒ[Kθ(t )]”,即大写Θ改成小写θ,注意花体的ℒ还
用原来的样子
12、 第472页,倒数第3、4行“在PI 控制跟踪阶跃信号稳态误差不为零的情况下,”删掉
13、 第472页,倒数第3行“可以改善”改为“可以提高系统稳定性,改善”
14、 第486页,最后一行,分母“e jw −12”改成“e jω−12”,即把w 改成omega
15、 第521页,第5行“|0
00−100006
23
2−200−3|”改为“[000−100006232−200−3]”,即把绝对值号改为方括号 1 已将本勘误表交给出版社;希望这些问题能在第二次印刷中更正。
二、不影响正确理解的文字错误或遗漏
1、 第4页,倒数第2行,“总结出在:将”改为“总结出:在将”,即交换冒号和“在”的
顺序
2、 第77页,第4行“方便证明本题”改为“方便地证明本题”,即插入“地”字
3、 第127页,倒数第10行“F (−ω)”改为“F (−ω)。
”,即在句末加句号
4、 第163页,题4-1(9),“sin[空格]h ” 改为 “sinh ”,即去掉空格
5、 第213页,第7行行首“其中”顶格,即不缩进;“故为强迫响应”改成“为强迫响应”,
即删除“故”字
6、 第221页,第5行“C 的值”改为“C 的值。
”,即行末加句号
7、 第222页,第4行“所示于是”改为“所示,于是”,即插入逗号
8、 第275页,第4行“灵活性等优点”改为“灵活性好等优点”,即插入“好”字
9、 第356页,倒数第2行“[sin (nω)+sin (n +1)ω]”改为“{sin (nω)+sin [(n +1)ω]}”,
即增加一对方括号,同时把最外侧的方括号改成花括号
10、 第369页,倒数第7行“严格的说”改为“严格地说”
11、 第417页,倒数第2行“DFT 最后取实部”改为“DFT 后取实部”,即删掉“最”字
12、 第458页,第6行两个“=”改成“为”
13、 第478页,倒数第10行“规则(1)”改为“规则(i)”;“规则(2)”改为“规则(ii)”
14、 第478页,倒数第9行“规则(4)”改为“规则(iv)”
15、 第479页,解图11-17(3),横坐标-2处的零点(小圆圈)不应该是空心,应该被横轴压
住(或穿过)
16、 第480页,解图11-19,横坐标14和12处的两个零点(小圆圈)不应该是空心,应该被横轴
压住(或穿过)
三、虽然正确但排版不美观或不标准的地方
1、 第177页,第7行行末的“=”移到第8行行首,且和第10行的等号对齐
2、 第177页,将第10行行末的“{e −at −”移到第11行行首,即保证两个大括号在同一行
3、 第203页,第4行行末的“200399”移到第5行行首
4、 第230页,最后一行“b 、c 、[空格]d[空格]。
”改为“b 、c 、d 。
”,即删掉两个空格
5、 第262页,第4行行末“1
2π[G (ω)∙H (ω)]∗jπδ(ω+ω0)−”移到第5行行首
G(ω+ω0)∙sgn(ω+ω0)+”移到第9行行首
6、第262页,第8行行末“1
2
]+”移到倒数第5行行首,同时在第6行行7、第273页,倒数第6行行末“{δ[ω+2πΔ
T(T+Δ)
末加“∙”表示乘法
8、第278页,最后一行“([空格]其他[空格])”改为“(其他)”,即删掉两个空格
sin(−ω0T−ω0τ+2φ0)+”移至第6行行首
9、第296页,第5行行末“1
2ω0
δ(ω+2200)+”移至第4行行首
10、第297页,第3行行末“π
8
[δ(ω+1800)+”移至第12行行首
11、第297页,第11行行末“πA2
8
[δ(ω+1700)+”移至第16行行首
12、第297页,第15行行末“πA2
8
13、第311页,倒数第2行,“E(s)H(s)=ℒ[e(t)]ℒ[ℎ(t)]”改成“H(s)E(s)=ℒ[ℎ(t)]ℒ[e(t)]”,
注意花体的ℒ还用原来的样子
14、第328页,倒数第9行之上有行空白,请删除
15、第336页,倒数第2行的“表7-29(a)”改为“表7-29-1”;最后一行的“表7-29(b)”改
为“表7-29-2”;同时把两个表的标题也做相应的改动,以便和全书统一
16、第377页,第6行“H(e jω)”改为“H(e jω)”,即去掉e和j的黑体
17、第392页,第5行“题示x(n)序列”改为“题示x(n)序列”,即去掉x上的黑体
18、第394页,请将倒数第1、2行按“=”对齐到倒数第3、4、5行
19、第434页,第3行和倒数第6行(即小标题(1)和(2)所在行)缩进
20、第437页,解图10-13-2(a),图中的“0.016μF”印刷模糊
21、第443页,解图10-17,请将两个子图的标题(a)和(b)对齐
22、第454页,请将倒数第3、4、5行的行首和倒数第6行的等号右侧对齐
23、第480页,第3行应左对齐,即和第4、5行,以及第1行的“若”字对齐
24、第482页,解图11-20,实线或虚线上的箭头(共计10个)略小,看不清楚,建议增大。
