有限差分法
有限差分法
有限差分法finite difference method用差分代替微分，是有限差分法的基本出发点。
是一种微分方程和积分微分方程数值解的方法。
把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
如何根据问题的特点将定解区域作网格剖分；如何把原微分方程离散化为差分方程组以及如何解此代数方程组。
此外为了保证计算过程的可行和计算结果的正确，还需从理论上分析差分方程组的性态，包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。
对于一个微分方程建立的各种差分格式，为了有实用意义，一个基本要求是它们能够任意逼近微分方程，这就是相容性要求。
另外，一个差分格式是否有用，最终要看差分方程的精确解能否任意逼近微分方程的解，这就是收敛性的概念。
此外，还有一个重要的概念必须考虑，即差分格式的稳定性。
因为差分格式的计算过程是逐层推进的，在计算第n＋1层的近似值时要用到第n层的近似值，直到与初始值有关。
前面各层若有舍入误差，必然影响到后面各层的值，如果误差的影响越来越大，以致差分格式的精确解的面貌完全被掩盖，这种格式是不稳定的，相反如果误差的传播是可以控制的，就认为格式是稳定的。
只有在这种情形，差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。
最常用的方法是数值微分法，比如用差商代替微商等。
另一方法叫积分插值法，因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理，一般可以通过积分形式来表示。
此外还可以用待定系数法构造一些精度较高的差分格式。
龙格库塔龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
有限差分法的原理与计算步骤
有限差分法的原理与计算步骤有限差分法（Finite Difference Method）是一种常用的数值计算方法，用于求解偏微分方程的数值解。
其基本原理是将连续的偏微分方程转化为差分方程，通过逼近导数，使用离散的点代替连续的点，从而将问题转化为代数问题。
下面将详细介绍有限差分法的原理和计算步骤：一、基本原理：有限差分法基于Taylor级数展开，通过利用函数在其中一点附近的导数信息来逼近函数在该点处的值。
该方法将连续的偏微分方程转化为差分方程，使用离散的点代替连续的点，从而将问题转化为代数问题。
在有限差分法中，常用的差分逼近方式有前向差分、后向差分和中心差分。
二、计算步骤：1.网格划分：将求解区域划分为有限个离散点，并定义网格上的节点和网格尺寸。
通常使用等距离网格，即每个网格点之间的间距相等。
2.离散化：将偏微分方程中的各个导数项进行逼近，利用差分近似来替代和求解。
一般采用中心差分逼近方式，即通过函数值在两侧点的差来逼近导数。
3.代数方程系统：利用离散化的差分方程，将偏微分方程转化为代数方程系统。
根据问题的边界条件和初值条件，构建代数方程系统的系数矩阵和常数向量。
4. 求解代数方程：利用求解线性方程组的方法求解代数方程系统，常用的方法有直接法（如高斯消元法、LU分解法）和迭代法（如Jacobi迭代法、Gauss-Seidel迭代法）。
求解得到各个离散点的解。
5.后处理：根据求解结果进行后处理，包括结果的插值和可视化。
将离散点的解通过插值方法进行平滑处理，并进行可视化展示，以得到连续的函数解。
三、优缺点：1.直观：有限差分法基于网格划分，易于理解和实现。
2.精度可控：可通过调整网格大小和差分逼近方式来控制计算的精度。
3.广泛适用性：可用于求解各种偏微分方程，适用于不同的边界条件和初值条件。
然而，有限差分法也存在一些缺点：1.精度依赖网格：计算结果的精度受到网格划分的影响，因此需要谨慎选择网格大小。
2.限制条件：有限差分法适用于边界对应点处导数有定义的问题，不适用于奇异点和非线性问题。
有限差分法
两端都要给定边界条件（双程坐标） 。
9
(C) 双曲型方程：适当的边界条件和初始条件，与波动传 播的性质有关 如：一维对流方程
∂u ∂u +c =0 ∂t ∂x u (x ,0) = f (x )
解为 u (x , t ) = f (x − ct ) ，代表一个向右(c > 0 时)或向左 ( c < 0 时)传播的波形。必须在波形传来的一侧提供边界条 件（单程坐标） 。
10
不适定的例子：
utt + u xx = 0 u (x ,0) = u t (x ,0) = 0
拉普拉斯方程＋非闭域边界条件，解为 u (x , t ) ≡ 0 。 然而，若定解条件为 u (x ,0) = 0, ut (x ,0) =
u (x , t ) = 1 sin nx ，解为 n
1 sinh nt sin nx n
(
)
n n um+1 = um −
cτ n n um +1 − um −1 2h
(
)
设计算到第 n 步时的累积误差
n ~n εn = 计算值um − 差分法精确解um m
反之
n ~n um = εn + um m
15
则第 n+1 步的计算值
~n ~ n cτ u n − u n ~ ~ um+1 = um − m +1 m −1 2h cτ n cτ n n n = um − um +1 − um −1 + εn − εm +1 − εn −1 m m 2h 2h n = um+1 + εn +1 m
uin +1 − uin −1 uin+1 − uin +1 − uin −1 − uin−1 −α =0 Lh u = τ h2 ατ 2 ⎛ ∂ 2u ⎞ τ 2 ⎛ ∂ 3u ⎞ Ti = Lh u − Lu (x i , t n ) = 2 ⎜ 2 ⎟ + ⎜ 3 ⎟ − L 截断误差 6 ⎜ ∂t ⎟i h ⎜ ∂t ⎟i ⎝ ⎠ ⎝ ⎠
有限差分法
有限差分法有限差分法是数学领域的一项最新成果，它在某些特定情况下能得到非常好的结果。
所谓有限差分方程就是利用积分和求差公式将差分方程化成为多个等价的偏微分方程组的组合形式，然后再应用最优化方法求解这种方程组，从而得出未知数的近似值。
当已知方程组的每个参数及其变量代入数据计算后的误差时，只要对其进行必要的调整或者修改后，就可获得满意的精度与效率的估计值。
此外，还可以通过有限差分方程的求解来了解其物理背景。
比如说在物体碰撞问题中，两个质点之间距离的测量往往涉及到很复杂的三维几何关系。
即使是一个小的距离误差也会引起很大的误差。
因此，对于碰撞问题中两个质点之间的相互位置误差测量，必须考虑它们之间的三维几何关系，并根据具体问题建立相应的坐标系统。
有限差分方程可以用来描述许多不同类型的实际问题，例如质量、压力、速度、温度、流动、热传导、声音和电磁场等。
但是由于数学模型本身的复杂性，使得有限差分方程在求解上遇到了困难。
因此，人们开始寻找一种更加直观的方法来解决问题。
有限差分法正是基于此原理提出的。
利用有限差分方程求解偏微分方程，我们首先要给出所求解的偏微分方程的数学表达式，这样才能够在有限差分方程的数学模型中寻找解析解。
有限差分方程的解析解，需要借助解析函数的理论来确定。
但是在自然科学和工程技术领域里，对于一般的实际问题，很少会存在着某种数学模型完全适合于所有的具体问题，那么对于任意一个偏微分方程，总是存在着一个解析解。
当把偏微分方程的解析解用适当的坐标表示出来后，有限差分方程的求解就转化为如何寻找与这个解相对应的函数值的问题。
通常，解析函数的形式是比较复杂的，因此需要运用数值方法进行拟合，从而得到符合实际的数学表达式。
然后通过对这个数学表达式的求解来确定所求偏微分方程的解析解。
这种数值求解方法称为数值积分法。
在研究有限元法和边界元法时都可以采用一些简单易行而且计算机可能很容易处理的函数作为边界条件，而这些函数本身又是很容易计算的。
有限差分法
有限差分法有限差分法（Finite Differential Method, FDM ）什么是有限差分法 有限差分法是指用泰勒技术展开式将变量的导数写成变量，在不同时间或空间点值的差分形式的方法。
按时间步长和空间步长将时间和空间区域剖分成若干网格，用未知函数在网格结(节)点上的值所构成的差分近似代替所用偏微分方程中出现的各阶导数，从而把表示变量连续变化关系的偏微分方程离散为有限个代数方程，然后解此线性代数方程组，以求出溶质在各网格结(节)点上不同时刻的浓度。
有限差分法的基本步骤（1）剖分渗流区，确定离散点。
将所研究的水动力弥散区域按某种几何形状(如矩形、任意多边形等)剖分成网络系统。
（2）建立水动力弥散问题的差分方程组。
（3）求解差分方程组。
采用各种迭代法，如点逐次超松驰方法(SOR)、线逐次超松驰方法(LSOR)、迭代的交替方向隐式方法(IADI)及强隐式方法(SID)等。
(1) 现在分别对时间（从0时刻到到期日）和股票价格（S max )为可达到的足够高的股票价格）进行分割，即\triangle S=S_{max}/M,\triangle T/N,这样就分别有N+1个时间段和M+1个股票价格，建立如图(所示的坐标方格，将定解区域网格化，坐标方格上的点（i,j ）对应时刻和股票价格，用变量f i ,j 表示（i,j ）点的期权价格。
2.建立差分格式（1）内含的有限差分方法其步骤可分为以下几步：(1)求前向差分近似:(2) 后向差分格式：(3)将(2),(3)式平均可更加对称地求出的近似，即(4)(2)求用前向差分近似：(5)(3)求(6)(4)将(4),(5),(6)式代入(1)式可得到内含有限差分公式：+ b j f i,j−c j f i,j + 1 = f i + 1,j(7)aj f i,j− 1其中：i=0,1,…，N-1。
j=0,1…，M-1针对看跌期权和看涨期权可分别求出方程的边界条件：看跌期权：看涨期权：(5)利用边界条件和(7)式可以给出M-1个联立方程组：+ b j f N− 1,j + c j f N− 1,j + 1j=1,2…，M-1aj f N− 1,j− 1求解这M-1个联立方程组即可以求出期权价格，但对美式看跌期权时我们必须考虑其提前执行的情况。
微分方程数值求解——有限差分法
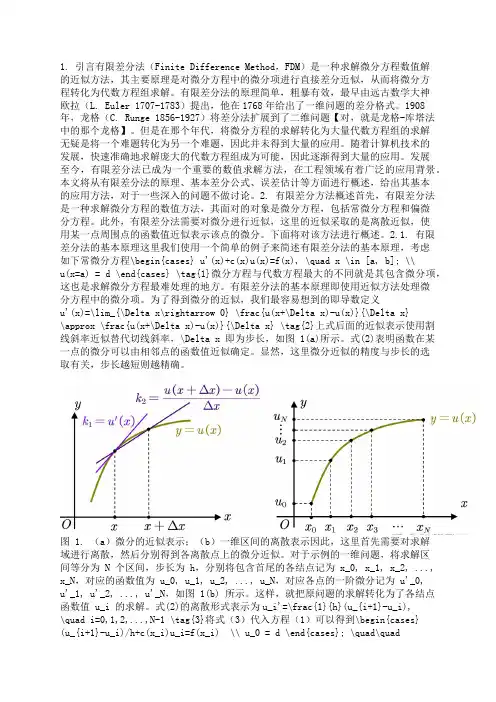
1. 引言有限差分法（Finite Difference Method，FDM）是一种求解微分方程数值解的近似方法，其主要原理是对微分方程中的微分项进行直接差分近似，从而将微分方程转化为代数方程组求解。
有限差分法的原理简单，粗暴有效，最早由远古数学大神欧拉（L. Euler 1707-1783）提出，他在1768年给出了一维问题的差分格式。
1908年，龙格（C. Runge 1856-1927）将差分法扩展到了二维问题【对，就是龙格-库塔法中的那个龙格】。
但是在那个年代，将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题，因此并未得到大量的应用。
随着计算机技术的发展，快速准确地求解庞大的代数方程组成为可能，因此逐渐得到大量的应用。
发展至今，有限差分法已成为一个重要的数值求解方法，在工程领域有着广泛的应用背景。
本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述，给出其基本的应用方法，对于一些深入的问题不做讨论。
2. 有限差分方法概述首先，有限差分法是一种求解微分方程的数值方法，其面对的对象是微分方程，包括常微分方程和偏微分方程。
此外，有限差分法需要对微分进行近似，这里的近似采取的是离散近似，使用某一点周围点的函数值近似表示该点的微分。
下面将对该方法进行概述。
2.1. 有限差分法的基本原理这里我们使用一个简单的例子来简述有限差分法的基本原理，考虑如下常微分方程\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\u(x=a) = d \end{cases} \tag{1}微分方程与代数方程最大的不同就是其包含微分项，这也是求解微分方程最难处理的地方。
有限差分法的基本原理即使用近似方法处理微分方程中的微分项。
为了得到微分的近似，我们最容易想到的即导数定义u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}上式后面的近似表示使用割线斜率近似替代切线斜率，\Delta x 即为步长，如图 1(a)所示。
传热学有限差分法
传热学有限差分法
传热学有限差分法是一种精确且高效的热分析方法。
它利用数学模型对传热过程进行模拟，能够准确地预测温度分布和热传导系数。
这种方法在工程领域被广泛应用，特别是在建筑、航空航天、电子和化学工业等领域。
有限差分法通过将连续的空间离散化为有限个网格，以解决偏微分方程的数值解问题。
在每个网格点上，有限差分法用差分方程近似代替偏微分方程，从而得到一组线性方程组。
然后，通过求解这组线性方程组，可以得到每个网格点的温度值，进而得到整个空间的温度分布。
这种方法具有高效性和精确性，因此在许多实际应用中都得到了广泛的应用。
例如，在建筑行业中，有限差分法可以用来模拟建筑物的热传导过程，从而预测建筑物的能耗和热舒适度。
在航空航天领域，有限差分法可以用来模拟飞机和火箭的热传导过程，从而预测其性能和安全性。
总的来说，传热学有限差分法是一种非常重要的工具，在解决复杂的传热问题时具有广泛的应用前景。
计算流体力学有限差分法
计算流体力学有限差分法流体力学有限差分法(Finite Difference Method，FDM)是一种常用的计算流体力学的方法。
它是基于流体力学基本方程对系统求解压力、速度和位置变化的一种近似数值方法，这些方程可以使用有限差分法求解得到准确结果。
一、流体力学有限差分法的概念1、端点条件：端点条件是差分方程组确定变量的边界条件，主要有边界条件和内部条件。
2、场变量定义：流动的物质可以用速度、压力和密度来描述，这种变量称为场变量。
3、有限差分法：有限差分法试图使描述精度在最小情况下得到一个可以接受的结果。
它将待求解区域划分为若干个小块，并且计算每一个小块上的变量。
4、边界条件：边界条件是用来描述物理事件发生的时候的物理量，如压力、流动量等。
二、流体力学有限差分法的基本步骤1、数学模型：开发有限差分方程，用来描述流体力学问题，这种模型可以由流体力学的基本方程得到。
2、网格划分：将区域网格划分成更小的网格，为了更准确的解决流体力学问题。
3、空间离散：将每一个网格按照有限差分公式空间离散，获得离散的压力方程式。
4、时间离散：在解决大规模动态流体力学问题时，通过一个更小的时间步骤进行求解。
5、求解：用适当的方法和算法求解有限差分方程式，获得求解结果。
三、流体力学有限差分法的优势1、高精度：使用此法，可以获得较高数值精度，从而准确描述流体力学过程。
2、计算效率：该方法可以快速找出有效的解决方案，并且计算效率更高。
3、计算能力：此方法可以处理复杂的物理问题，而且没有太多的硬件限制。
4、收敛性：当求解复杂的物理问题时，有限差分法不太容易出现"收敛"的情况。
5、可靠性：此方法可以快速、准确的求解出可靠的结果，相对于其他求解方法，其精度更高。
四、总结流体力学有限差分法是一种常用的计算流体力学的方法。
它易于实施，并且可以获得较高数值精度，从而准确描述流体力学过程。
处理复杂的物理问题时，它可以提供较快、较准确的结果，更能可靠性和可靠性更好。
有限差分法基本原理
有限差分法的应用领域
流体力学
用于模拟流体在固定或变形网格 上的流动，如计算流体动力学 （CFD）中的数值模拟。
热传导
用于求解热传导方程，模拟热 量在物体中的传播和分布。
波动传播
用于求解波动方程，如地震波 、声波和电磁波的传播。
有限差分法基本原理
CONTENTS 目录
• 引言 • 有限差分法的基本原理 • 有限差分法的实现 • 有限差分法的优缺点 • 有限差分法的改进方向
CHAPTER 01
引言
有限差分法的定义
有限差分法是一种数值计算方法，通 过将连续的物理量离散化为有限个离 散点上的数值，并建立代数方程来近 似描述物理量随时间和空间的变化规 律。
缺点
精度问题
由于有限差分法采用的是离散化的方法， 因此其精度受到网格大小的影响，网格越
小精度越高，但同时也会增加计算量。
数值耗散误差
在模拟非线性问题时，有限差分法可能会 产生数值耗散误差，导致能量的损失或者
非物理振荡。
数值色散误差
在模拟波动性问题时，有限差分法可能会 产生数值色散误差，导致波的传播速度发 生变化。
常用的离散化方法包括均匀网格、非均匀网格、有限元法等，
应根据实际问题选择合适的离散化方法。
差分近似
Hale Waihona Puke 01差分近似公式根据微分方程的性质，构造差分 近似公式，将微分方程转化为差 分方程。
精度分析
02
03
稳定性分析
分析差分近似公式的精度，确定 其与微分方程的误差大小和分布。
分析差分近似公式的数值稳定性， 确保计算过程中误差不会累积放 大。
有限差分法
第四章有限差分方法4.1引言有限差分法：数值求解常微分方程或偏微分方程的方法。
物理学和其他学科领域的许多问题在被分析研究之后, 往往可以归结为常微分方程或偏微分方程的求解问题。
一般说来，处理一个特定的物理问题，除了需要知道它满足的数学方程外，还应当同时知道这个问题的定解条件，然后才能设计出行之有效的计算方法来求解。
有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。
在有限差分方法中，我们放弃了微分方程中独立变量可以取连续值的特征，而关注独立变量离散取值后对应的函数值。
但是从原则上说，这种方法仍然可以达到任意满意的计算精度。
因为方程的连续数值解可以通过减小独立变量离散取值的间格，或者通过离散点上的函数值插值计算来近似得到。
这种方法是随着计算机的诞生和应用而发展起来的。
其计算格式和程序的设计都比较直观和简单，因而，它的实际应用已经构成了计算数学和计算物理的重要组成部分。
有限差分法的具体操作分为两个部分：(1)用差分代替微分方程中的微分，将连续变化的变量离散化，从而得到差分方程组的数学形式； (2)求解差分方程组。
在第一步中，我们通过所谓的网络分割法，将函数定义域分成大量相邻而不重合的子区域。
通常采用的是规则的分割方式。
这样可以便于计算机自动实现和减少计算的复杂性。
网络线划分的交点称为节点。
若与某个节点P 相邻的节点都是定义在场域内的节点，则P 点称为正则节点；反之，若节点P 有处在定义域外的相邻节点，则P 点称为非正则节点。
在第二步中，数值求解的关键就是要应用适当的计算方法，求得特定问题在所有这些节点上的离散近似值。
有限差分法的差分格式：一个函数在x 点上的一阶和二阶微商，可以近似地用它所临近的两点上的函数值的差分来表示。
如对一个单变量函数f(x)，x 为定义在区间[a,b]的连续变量。
以步长h=Δx 将[a,b]区间离散化，我们得到一系列节点x = a , x = x + h , x = x + h = a + 212132Δx , ..., x = x + h = b , 然后求出 f(x)在这些点上的近似值。
有限差分方法
有限差分方法有限差分法是一种用于数值解决常微分方程（ODE）、偏微分方程（PDE）的数学技术。
它将原本的微分方程式转化为差分方程，最终可以用数值计算解决。
作为一门数值分析技术，有限差分方法主要用于计算解决微分方程的参数和状态。
有限差分法的步骤一般分为三个：（1）数学模型的构建，（2）对物理场的离散化，（3）对差分方程进行求解。
首先，我们要建立准确的物理模型，这一步涉及到选取合适的假设和参数，以及采用适当的边界条件和初始条件。
其次，我们要对原方程进行离散处理，使其转化为有限差分方程，从而为求解此类方程打下基础。
最后，我们要设计出一个有效的求解方法，通过用数值计算解决有限差分方程，获得所求解的结果。
有限差分法的优点主要体现在精度和速度上。
首先，它的精度极高，它可以求解出精确的解，而且计算速度也很快，无需复杂的数学推理，就可以较快速度解决问题，大大降低了计算的难度。
其次，有限差分法可以拓展到更多的系统，不限于只能解决二维静止场，而能够解决一般感兴趣的场景。
此外，有限差分技术也可以解决有时限性的问题，例如分析物体的动态特性。
此外，有限差分方法也存在一些缺点，例如边界条件的处理和计算复杂性的增加。
由于差分的求解是基于某些边界条件的，一旦边界条件发生变化，原有的求解方案就会失效。
此外，在进行离散化处理时，随着问题规模的增大，计算复杂性也会随之增加，使得求解较大规模的问题极其困难。
有限差分法已经成为当今解决复杂问题数值计算的重要技术手段。
它在准确性、精度和计算速度方面均具有优势，深受工业界、医学界及数学领域的青睐。
有限差分法的实际应用也正在层出不穷，今后有望在更多的领域得到广泛的应用。
有限差分法推导
有限差分法推导摘要：一、有限差分法简介1.有限差分法的概念2.有限差分法在数值计算中的应用二、有限差分法的推导1.差分法的定义2.有限差分法的推导过程3.有限差分法的性质三、有限差分法的应用1.微分方程的数值解法2.有限差分法在数值积分中的应用四、有限差分法的优缺点1.优点2.缺点正文：一、有限差分法简介有限差分法是一种数值计算方法，通过将连续函数离散化，用差分代替微分，从而实现对微分方程或积分方程的求解。
有限差分法广泛应用于科学、工程和金融领域，例如，在天气预报、海洋学、生物学、经济学等方面都有重要作用。
二、有限差分法的推导1.差分法的定义差分法是一种将函数在某一点上的值与该点附近点的值相减的方法，用于近似计算函数在该点处的导数或变化率。
给定一个函数f(x)，在x=a 处求导，可以得到差分算子Df(a,h)，其中h 为差分步长。
2.有限差分法的推导过程有限差分法是将差分法应用于离散点集，通过有限个差分算子来近似表示函数在某一点的值。
设函数f(x) 在区间[x0, x1] 上可导，离散点集为{x0,x0+h, x0+2h, ..., x1}，有限差分法的表达式为：Df(x0+k h) ≈ (h/(k+1)) * [f(x0+k h) - f(x0+(k-1) h)] (k=1,2,3,...,n-1)3.有限差分法的性质有限差分法具有以下性质：(1) 线性性质：Df(x) + Dg(x) = D(f(x) + g(x))(2) 移位性质：Df(x+h) = Df(x) + h * df(x)/dx(3) 微分性质：Df(x) * (x - x0) = f"(x) * (x - x0) + O(h^2)三、有限差分法的应用1.微分方程的数值解法有限差分法可以用于求解微分方程，例如，对于一阶线性微分方程：df(x)/dx + p(x) * f(x) = q(x)可以用有限差分法将其离散化为一个线性代数方程组，从而求解离散解。
有限差分法
有 限 差 分 法流体运动的控制方程多为偏微分方程，在复杂的情况下不存在解析解。
但是对于一些简单的情况存在解析解，偏微分方程的解析解可用精确的数学表达式表示，该表达式给出了因变量在整个定义域中的连续变化状况。
有限差分法（Finite Difference Method ,FDM ）是数值计算中比较经典的方法，由于其计算格式直观且计算简便，因此被广泛地应用在计算流体力学中。
有限差分法首先将求解区域划分为差分网格，变量信息存储在网格节点上，然后将偏微分方程的导数用差商代替，代入微分方程的边界条件，推导出关于网格节点变量的代数方程组，通过求解代数方程组，获得偏微分方程的近似解。
偏微分方程被包含离散点未知量的代数方程所替代，这个代数方程能求出离散节点处的变量，这种离散方法叫做有限差分法。
2.1有 限 差 分 逼 近2.1.1 有限差分网格 由于有限差分法求解的是网格节点上的未知量值，因此首先介绍有限差分网格。
图2.1 – 1是x-y 平面上的矩形差分网格示意图。
在x 轴方向的网格间距为△x ，在y 轴方向的网格间距为△y ，网格的交点称为节点，计算变量定义在网格节点上。
称△x 和△y 为空间步长，△x 一般不等于△y ，且△x 和△y 也可以不为常数。
取各方向等距离的网格，可以大大简化数学模型推导过程，并且经常会取得更加精确的数值解。
本章作为计算流体力学入门知识，假设沿坐标轴的各个方向网格间距分别相等，但是并不要求各方向的网格间距一致。
例如假设△x 和△y 是定值，但是不要求△x 等于△y 。
在图2.1 - 1中，网格节点在x 方向用i 表示，在y 方向用j 表示。
因此，假如（i ，j ）是点P 在图2.1 – 1中的坐标，那么，点P 右边的第一个点的就可以用（i+1，j ）表示；在P 左边的第一个点的就可以用（i —1，j ）表示；点P 上边的第一个点的就可以用（i ，j+1）表示；点P 下边的第一个点的就可以用（i ，j —1）表示。
有限差分法
u ( x, y )
= ϕ ( x, y )
Γ = ∂Ω
泊松方程的第一类边界条件 泊松方程的第一类边界条件 Dirichlet条件 条件） （Dirichlet条件）为：
其中 Ω 为以 Γ 为边界的有界区域， 为分 Γ Ω 段光滑曲线， U Γ 称为定解区 ϕ 域， f ( x, y ) ， ( x, y ) 分别为 Ω ，Γ 上 的已知连续函数。
τ ah R( xk , t j ) = ut′′ ( xk , t j + θ2τ ) + u′′2 ( xk + θ1h, t j ) = O(τ + h) 2 2 2 x
差分方程的 截断误差
如果一个差分方程的截断误差为 R = O (τ + h ) ，则称差分方程 对 是 q 阶精度，对 x 是 p 阶精度的。显然，截断误差的阶 数越大，差分方程对微分方程的逼近越好。
有限差分法
有限差分法(finite difference method)是一种普遍认为 method)是一种普遍认为 有限差分法(finite 行之有效的处理函数微分的数值方法， 行之有效的处理函数微分的数值方法，科学与工程计算中 常见的偏微分方程和方程组大都可以采用有限差分方法求 本章首先讨论偏微分方程的定解问题， 解。本章首先讨论偏微分方程的定解问题，然后介绍有限 差分法的基本概念、方法和实现过程， 差分法的基本概念、方法和实现过程，重点介绍了求解椭 圆型偏微分方程定解问题的差分方法。 圆型偏微分方程定解问题的差分方法。
∂ 2u ∂ 2u = a2 ∂ t2 ∂ x2 u (x, 0) = ϕ (x) ∂u = ψ (x) ∂ t t=0
t > 0,
有限差分法
有限差分法有限差分法是基于差分原理的一种数值计算法。
其基本思想：将场域离散为许多小网格，应用差分原理，将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题。
1.1 二维泊松方程的差分格式图1-1 有限差分的网格分割二维静电场边值问题：F yx =-=∂∂+∂∂ερϕϕ2222 (1-1) )(s f L =ϕ (1-2)通常将场域分成足够小的正方形网格,网格线之间的距离为h ,节点4,3,2,1,0上的电位分别用3210,,,ϕϕϕϕ和4ϕ表示。
设函数ϕ在0x 处可微，则沿x 方向在0x 处的泰勒公式展开为()()()∑=-+-=nK n K K K 000)(!χχοχχϕϕχ （1-3）将1χχ=和3χ分别代入式（1－3）,得⋅⋅⋅⋅⋅⋅+∂∂+∂∂+∂∂+=03330222001)(!31)(!21)(x h x h x h ϕϕϕϕϕ （1-4）⋅⋅⋅⋅⋅⋅+∂∂-∂∂+∂∂-=03330222003)(!31)(!21)(xh x h x h ϕϕϕϕϕ （1-5）由（1-4）-（1-5）得h2x 31x x 0ϕϕϕ-≈∂∂=)(（1-6）(1-4)+(1-5)得2301x x 22h2x 0ϕϕϕϕ+-≈∂∂=)( （1-7） 同理hy y y 2)(310ϕϕϕ-≈∂∂= （1-8） 2301222)(0hy y y ϕϕϕϕ+-≈∂∂= （1-9） 将式(1-7)、（1-9）代入式（1-1），得到泊松方程的五点差分格式)(414243210204321Fh Fh -+++=⇒=-+++ϕϕϕϕϕϕϕϕϕϕ当场域中,0=ρ得到拉普拉斯方程的五点差分格式)(41044321004321ϕϕϕϕϕϕϕϕϕϕ+++=⇒=-+++1.2 边界条件的离散化处理图1-2 边界条件的离散化处理若场域离散为矩形网格(如图2-2示)，差分格式为：F 2h 1h 1h 1h 10222142222121=+-+++ϕϕϕϕϕ)()()( (1-10) （1）第一类边界条件:给边界离散节点直接赋已知电位值 （2）对称边界条件:合理减小计算场域，差分格式为：)(F h 24124210-++=ϕϕϕϕ (1-11)图1-3 边界条件的离散化处理•12（3）第二类边界条件:边界线与网格线相重合的差分格式：h f f hn 2102010-ϕ=ϕ=ϕ-ϕ≈∂ϕ∂,)((1-12)(4)介质分界面衔接条件 的差分格式)1212(4143210ϕϕϕϕϕ+++++=KKK (1-13)其中b a K εε=1.3 差分方程组的求解方法(1) 高斯——赛德尔迭代法][)(,)(,)(,)(,)(,2k 1j i k j 1i 1k 1j i 1k j 1i 1k j i Fh 41-+++=+++-+-+ϕϕϕϕϕ (1-14)式中：⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅=,2,1,0,2,1,k j i ，• 迭代顺序可按先行后列，或先列后行进行。
有限差分法
有限差分法一、有限差分法的定义有限差分法（Finite Differential Method ）是基于差分原理的一种数值计算法。
其基本思想：将场域离散为许多小网格，应用差分原理，将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题。
二、有限差分法的应用例3.7.1 有一个无限长直的金属槽，截面为正方形，两侧为正方形，两侧面及底板接地，上盖板与侧面绝缘，其上的电位为ϕ=100V, 试用有限差分法计算槽内电位。
（1）用Matlab 中的有限差分法计算槽内电位；（2）对比解析法和数值法的异同点；（3）选取一点，绘制收敛曲线；（4）总的三维电位图；1、根据有限差分公式计算出电位最终近似值为1,12,13,11,22,23,21,32,33,3=7.144=9.823=7.144=18.751=25.002=18.751=42.857=52.680=42.857ϕϕϕϕϕϕϕϕϕ，，，，，，用Matlab有限差分法计算出来结果：（见附录程序一）2、解析法和数值法的异同点解析法数值法定义在分析具体问题的基础上，抽取出一个数学模型，这个数学模型能用若干个解析表达式表示出来，解决了这些表达式，问题也就得以解决。
数值法是用高性能的计算机以数值的、程序的形式解决问题，主要是指有限元法和差分法相同点都是在具体问题的基础上取一个用解析表达式表示的数学模型来解决问题；数值法是在解析法的基础上在不同尺度上进行有限元离散,离散单元尺度不同,进行有限元计算时要满足的连续性条件不同,预测结果的精确度就不同不同点解析法可以计算出精确的数值结果；可以作为近似解和数值解的检验标准；解析法过程可以观察到问题的内在和各个参数对数值结果起的作用。
但是分析过程困难又复杂使其仅能解决很少量的问题。
数值法求解过程简单，普遍性强，用户拥有的弹性大；用户不必具备高度专业化的理论知识就可以用提供的程序解决问题。
但求解结果没有解析法精确。
岩石力学-有限差分法
平衡方程 （运动方程）
新的速度和 位移
应力－应变关系 （本构方程）
新的应力或 力
显式有限差分法计算流程图
显式算法的核心概念是计算“波速”总 是超前于实际波速。
用运动方程求解静力问题，还必须采取 机械衰减方法来获得非惯性静态或准静态解， 通常采用动力松弛分法是求解给定初值和（或）边值问题 的较早数值方法之一。
有限差分法和有限元法都产生一组待解方程组。 1、有限差分基本方程 2、平面问题有限差分方程 3、显式有限差分算法－时间递步法
可以保证在被模拟的物理系统本身是非稳定的 情况下，有限差分数值计算仍有稳定解。对于非线 性材料，物理不稳定的可能性总是存在的。
有限差分方法
n
Δt
（2-2）
空间导数用一阶中心差商近似代替，即
ζ in+1 − ζ in−1 ⎛ ∂ζ ⎞ ⎜ ⎟ ≈ 2Δx ⎝ ∂x ⎠ i
则在 ( xi , t n ) 点的对流方程就可近似地写作
（2-3）
ζ in +1 − ζ in
Δt
+α
ζ in+1 − ζ in−1
2Δx
（1-11）
当然，在某些情况下也可取向前或向后的二阶差商。
9
第一节 差分原理及逼近误差/差分原理 以上是一元函数的差分与差商。多元函数f(x,y,…)的差分与 差商也可以类推。 如一阶向前差商为
Δf f ( x + Δx , y , Λ ) − f ( x , y , Λ ) = , Δx Δx
Δf f ( x, y + Δy , Λ ) − f ( x, y , Λ ) = , Δy Δy ΛΛ
（1-6）
6
第一节 差分原理及逼近误差/差分原理 函数的差分与自变量的差分之比，即为函数对自变量的 差商。 一阶向前差商为 一阶向后差商为
f ( x + Δx) − f ( x) Δy = Δx Δx
（1-7）
f ( x ) − f ( x − Δx ) Δy = Δx Δx
（1-8）
7
第一节 差分原理及逼近误差/差分原理 一阶中心差商为
15
第一节 差分原理及逼近误差/非均匀步长
图1-2 均匀和非均匀网格实例1
16
第一节 差分原理及逼近误差/非均匀步长
图1-3 均匀和非均匀网格实例2
17
第二节 差分方程 差分相应于微分，差商相应于导数。差分和差商是用有限形 式表示的，而微分和导数则是以极限形式表示的。如果将微 分方程中的导数用相应的差商近似代替，就可得到有限形式 的差分方程。现以对流方程为例，列出对应的差分方程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用有限差分法分析电磁场边界问题在一个电磁系统中，电场和磁场的计算对于完成该系统的有效设计师极端重要的。
例如，在系统中，用一种绝缘材料是导体相互隔离是，就要保证电场强度低于绝缘介质的击穿强度。
在磁力开关中，所要求的磁场强弱，应能产生足够大的力来驱动开关。
在发射系统中进行天线的有效设计时，关于天线周围介质中电磁场分布的知识显然有实质性的意义。
为了分析电磁场，我们可以从问题所涉及的数学公式入手。
依据电磁系统的特性，拉普拉斯方程和泊松方程只能适合于描述静态和准静态（低频）运行条件下的情况。
但是，在高频应用中，则必须在时域或频域中求解波动方程，以做到准确地预测电场和磁场，在任何情况下，满足边界条件的一个或多个偏微分方程的解，因此，计算电池系统内部和周围的电场和磁场都是必要的。
对电磁场理论而言，计算电磁场可以为其研究提供进行复杂的数值及解析运算的方法，手段和计算结果；而电磁场理论则为计算电磁场问题提供了电磁规律，数学方程，进而验证计算结果。
常用的计算电磁场边值问题的方法主要有两大类，其每一类又包含若干种方法，第一类是解析法；第二类是数值法。
对于那些具有最简单的边界条件和几何形状规则的（如矩形、圆形等）问题，可用分离变量法和镜像法求电磁场边值问题的解析解（精确解），但是在许多实际问题中往往由于边界条件过于复杂而无法求得解析解。
在这种情况下，一般借助于数值法求解电磁场的数值解。
有限差分法，微分方程和积分微分方程数值解的方法。
基本思想是把连续的定解区域用有限个离散点构成的网络来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
差分运算的基本概念：有限差分法是指用差分来近似取代微分，从而将微分方程离散成为差分方程组。
于是求解边值问题即转换成为求解矩阵方程[5]。
对单元函数()x f而言，取变量x的一个增量x∆=h，则函数()x f的增量可以表示为()x f∆=()hxf+-()x f称为函数()x f的差分或一阶差分。
函数增量还经常表示为()x f∆=⎪⎭⎫⎝⎛+2hxf-⎪⎭⎫⎝⎛-2hxf称为函数()x f 的中心差分或一阶中心差分。
函数一阶差分()x f ∆与自变量增量h 的比值()x f ∆/h 称为一阶差商。
在一阶差分运算中，它常用来近似函数()x f ∆的一阶导数()dx x df /。
函数()x f 的二阶差商定义为()22x x f ∆∆()[]()[]h h x f h h x f ∆-+∆= ()()2h x f h x f ∆-+∆=它常被用来近似函数()x f 的二阶导数()22/dx x f d 。
我们还可以采用类似方法给出二阶以上差分的定义，并用它们来近似函数二阶以上的导数。
但由于二阶以上的倒数在本次研究中没有用到，因此就不在赘述了。
3.1 个相同形式的差分方程。
有限差分法应用 有限差分法基本思想是将场域离散为许多小网格，应用差分原理，将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题[6][7]。
现在，以静电场边值问题为例，说明有限差分法的应用。
f(s)为边界点s 的点函数，二位场域D 和边界L 示于下图中。
yx02413D Lhh有限差分的网格分割通常将场域分成足够小的正方形网格,网格线之间的距离为h ,节点4,3,2,1,0上的电位分别用3210,,,ϕϕϕϕ和4ϕ表示。
设函数ϕ在x 处可微，则沿x 方向在x 处的泰勒公式展开为()()()∑=-+-=nK nKK K 000)(!χχοχχϕϕχ将1χχ=和3χ分别代入上式,得⋅⋅⋅⋅⋅⋅+∂∂+∂∂+∂∂+=03330222001)(!31)(!21)(x h x h x h ϕϕϕϕϕ ⋅⋅⋅⋅⋅⋅+∂∂-∂∂+∂∂-=03330222003)(!31)(!21)(x h x h x h ϕϕϕϕϕ由上式得h x x x 2)(310ϕϕϕ-≈∂∂=2301x x 22h 2x 0ϕϕϕϕ+-≈∂∂=)(同理h y y y 2)(310ϕϕϕ-≈∂∂=2301222)(0h y y y ϕϕϕϕ+-≈∂∂= 得到泊松方程的五点差分格式)(414243210204321Fh Fh -+++=⇒=-+++ϕϕϕϕϕϕϕϕϕϕ当场域中,0=ρ得到拉普拉斯方程的五点差分格式：)(41044321004321ϕϕϕϕϕϕϕϕϕϕ+++=⇒=-+++从这个公式我们可以看出，当我们将一个二维无源区场域剖分为一系列正方形网格时，场域内任何一个节点的电位都等于它周围四个节点电位的算术平均值。
这就是规则正方形网格内某点的电位所满足的拉普拉斯方程的差分格式，或差分方程[8]。
对于场域内的每一个结点，关系式都成立，都可以列出。
分离变量法：具体例题如下：3） 如图所示，有一长方形的导体槽，a = 20，b = 10，设槽的长度为无限长，槽上有一块与槽绝缘的盖板，电位为100V ，其他板电位为零，求槽内的电位分布。
yb解：用有限差分法求金属盒内电位（20x10） （1）在盒内取20×10个离散的电位节点第一步，在场域内部节点上选定电位初始值，为简单起见，可将它们都取为零，记为()01Φ=()02Φ=···=()0200Φ=0，常称为零次解。
第二步，将零次解代入差分方程式（3.2.10），得出诸内部节点电位值的一次解，它们为：()11Φ=()()40002102Φ+++Φ=40000+++=0()12Φ=()()()400220103Φ+Φ++Φ=40000+++=0()120Φ=()140Φ=()160Φ=…=()1200Φ=25其他()1n Φ=0；在求出一次解的200个节点电位值以后，原来零次解中的200个节点电位值将被一次解中的相应电位值所取代，在计算机的内存中不予保留，从而达到了节省存储空间的目的。
第三步，重复上述步骤，令每一个内部节点上的二次解电位值等于该节点周围四个相邻节点（或边界点）一次解电位值的算术平均值，并用二次解电位值冲去内存中的原一次解电位值。
这样迭代一次又一次的继续下去，可望诸节点的电位值变化越来越小，这时可取这些节点上的电位值为该边值问题的数值解，经50次迭代，得到电位分布如下：0 0 0 0 0 0 0 0 0 00 0.0993 0.1089 0.1423 0.1467 0.1778 0.1921 0.1892 0.0920 00 0.1325 0.1448 0.2532 0.3184 0.3977 0.4334 0.3542 0.1537 00 0.1396 0.2420 0.3833 0.5165 0.5671 0.5586 0.3818 0.1796 00 0.1692 0.3943 0.5392 0.6585 0.6773 0.6581 0.4655 0.2314 00 0.2387 0.5355 0.7320 0.8969 1.0173 0.9740 0.6603 0.2704 00 0.3618 0.7712 1.1408 1.4273 1.5196 1.2679 0.7968 0.3287 00 0.5793 1.2419 1.7832 2.0459 2.0252 1.7003 1.1574 0.6089 00 0.9598 1.8628 2.4876 2.8179 2.8438 2.4066 1.7408 0.8674 00 1.3658 2.5222 3.4567 3.9657 3.9424 3.4661 2.4649 1.3123 00 1.9464 3.6736 4.9513 5.5895 5.7230 4.8560 3.5389 1.8705 00 2.7943 5.1636 6.9056 8.0372 7.8414 6.8346 5.0202 2.7216 00 3.8931 7.3130 10.0082 11.0921 11.0886 9.7018 7.1720 3.8510 00 5.5621 10.5944 13.7608 15.6352 15.5737 13.6932 10.2165 5.5458 00 8.2507 14.7118 19.5283 21.9300 21.8742 19.3603 14.6006 7.9489 00 11.3214 20.8403 27.1814 30.3563 30.3316 27.0933 20.7935 11.4501 00 17.5203 30.5113 38.5788 42.3738 42.2936 38.3838 30.3113 17.5032 00 27.7508 44.8055 54.0068 57.9932 57.9459 53.8699 44.8833 27.8587 00 48.6873 67.0168 74.6269 77.5080 77.4550 74.5761 67.0989 48.7180 00 100.0000 100.0000 100.0000 100.0000 100.0000 100.0000 100.0000 100.0000 0由上得出的数值解可以看出，金属盒内点电位分布是越靠中间电位越高，越靠近金属盒顶部电位越高，这是由于金属盒底部和两边的电位都为零，而顶部最高。
由此表明此方法计算出的电位值，符合金属盒内的电位分布情况。
当用解析法求解时：槽内电势满足二维直角坐标系中的拉普拉斯方程及其边界条件:应用分离变量法 , 得到满足方程 ( 1 ) 和边界条件式(2)—式 (4) 的解的形式为()10x10ysin,1ππφn shn A y x n n ∑∞==带入边界条件（3）得100=πn 210ysin1∑∞=n n sh n A π利用三角函数正交性，求得系数n A ，最后可得槽内电位的解析解为： ()10x）1-n 2（10y ）1-n 2（sin ）π1-n 2（2100)12(4,1n πππφsh sh n y x -=∑∞=.解析法的优点是：可将解答表示为已知函数的显式，从而计算出精确的数值结果； 可以作为近似解和数值解的检验标准；在解析过程中和在解的显式中可以观察到问题的内在联系和各个参数对数值结果所起的作用。
但解析法也存在严重缺点，主要是，它仅能解决很少量的问题。
事实上，只有在为数不多的坐标系中才能分离变量，而用积分方程法是往往求不出结果，致使分析过程既困难又复杂。