第六届大学生力学竞赛试题-理论力学
第六届江苏省大学生力学竞赛(专科组)试卷试题答案

参考答案及评分标准第Ⅰ部分(共7题,每题4分)1. 1 0.5 【每 2分】 2. 0Fa 【每 2分】 3. 7.125o 【4分】 4.2Fl EAF EA Fl EA FEA 【每 1分】5. b e f g 【每 1分】 6.零杆见图示1N F F =(拉)【零杆共10根,答对41N 大小1分,表明拉的1分】 7.【剪力图2分,荷载图2分】4kN4kN或第Ⅱ部分(共6题,每题7分)1.由整体0A M ∑=,得/2250kN B F F == 再由杆BD 0C M ∑=,得/2433kN DE F == 故选用能承受500kN 张力的绳①。
【计算5分,结论2分】 2.设重心距AB 线右端D 之距离为C x ,则0.3m i Ci C ix A =∑设板重为W ,由平衡条件可求得:A 处吊杆受力0.9A F W =,B 处吊杆受力0.1B F W =设AB 杆长均为l ,材料弹性模量均为E ,A 杆面积为A A ,B 杆面积为A B ,则0.9A A A AF l Wl l EA EA ∆==,0.1B B B B F l Wll EA EA ∆== AB 边保持水平,则A B l l ∆∆=,计算得9A B A A =,A 、B 杆均为圆截面,故3A Bdd = 【求板重心位置2分,求二杆作用力1分,二杆变形1分,保持AB 水平条件1分,二杆直径比计算2分】3.在C 节点沿CA(图a ),或在节点沿x 、y 方向各作用一个拉力x y F F F ==(图b )以上两种情况均满足题意要求,且各杆内力均为0AD AB CD CB F F F F ====,AC F由各杆所受内力知,AD 、AB 、CD 、CB 均不变形,只有AC 杆沿AC 方向伸长2AC Fll CC EA EA∆''===(图c ) 由小变形,作垂线代替圆弧得C 节点位移至C′,则AC CC l EA'==D 节点有x方向的刚性位移DD CC ''==【主动力3分,其中:作用点位置、主动力方向及大小各1分;各杆内力2分,各节点位移2分】F =A C ′图a图b图c4.图a 33(a)0.098232d W d π==, 图b33(b)(/0.05896d W d ==图c o o 23(c)(cos 60)(sin 60)0.06256d d W d ==图a 22(a)0.7854d A d π==, 图b22(b)0.50A d == 图c o o 2(c)(cos60)(sin60)0.433A d d d ==由[]M W σ=计算梁所能承受的最大弯矩3max max (a)[][]0.0982[]M W W d σσσ===,为圆截面梁由max min MW σ=计算梁所能承受的最大工作应力max 33(b)170.0589M M M W d d σ===,为方截面梁由min min G A γ=计算梁的最轻自重2min (c)0.433G A d γγ==,为矩形截面梁 【max M 2分, max σ2分; 自重最轻3分】5.设材料单位体积重为γ,则实心圆梁自重集度24q D πγ=空心圆管梁 22(1)4q D παγ'=-,0.5dDα== 实心梁 2m a x 34M q l W D σπ== 空心圆管梁 2m a x 344(1)M q l W D σπα'''=='- 由于210.75q q α'=-=,故max 42max 10.8(1)1q q σσαα''===-+ 实心梁 44max45320384384ql ql w EI ED π== 空心圆管梁 44max445320384384(1)q l q l w EI ED πα'''=='- 故max 4max 0.8(1)w q w q α''==- 【/q q '比值1分,二梁max σ各1分,比值1分;二梁max w 各1分,比值1分】6.顺风:θθαθcos )cos(cos -==F F F N y)]sin ()cos(cos )1()sin([θθαθθαθ-⋅-+⋅-⋅--=F d dF y]sin )cos(cos )[sin(θθαθθα⋅--⋅-=F 0=)tan(tan θαθ-=,2αθ=逆风:如右图,帆画在角α′内即可。
第一届至第六届周培源大学生力学竞赛初赛试题及答案

8
第六届周培源全国大学生力学竞赛样题
设飞轮转动惯量为 J ,可在箱内电机驱动下以角加速度 ε 顺时针转动。为说明问题,暂
时设 B 处是铰链。
用动静法,飞轮上作用有力矩
系统对 A 点取矩,有
M s = Joε
(M1
+
M
2
)g
⋅
1 2
(e)如果要两盏灯亮,则是不稳定平衡。在第一象限内,两盏灯亮对应的区域是 EG 和 GF 边表示亮两盏灯的区域(不含 G 点)。
7
第六届周培源全国大学生力学竞赛样题
(f)一盏灯亮对应的区域是 G 点。 最后根据 x 轴和 y 轴的对称性,即可作出整个桌面的亮灯数目区域图。 (本题改写自:陈嘉,《力学与实践》小问题第 29 题,1982,No.3;秦寿珪,《力学与 实践》小问题第 100 题,1985,No.4)
5
第六届周培源全国大学生力学竞赛样题
y
4
5
6
o
x
1
2
3
(3)模特儿在不同区域时会有不同数目的灯亮起来,请在长方形舞台上确定各区域的 边界并画出示意图,然后在该区域内写上亮灯的数目(提示,亮灯的数目有可能为 6、5、4、 3、2、1)。
y
4 H
C5 六
o
E 四
6 三G
五D 四
B Fx
A(x,y)
1
2I
时,如果要求
P
点的速度和加速度,你如何考虑?取 a
= 1m
,l
=
4m ,β
=
1 6
π
,ω
= 1rad/s ,
速度和加速度是多少?
第六届大学生力学竞赛试题-理论力学

第六届⼤学⽣⼒学竞赛试题-理论⼒学湖南省第六届⼤学⽣⼒学竞赛试题——理论⼒学(竞赛时间:180分钟)请将答案写在相应横线上,答案正确给全分,答案不正确给零分。
⼀、综合题(16分)1.长度为l ,重P 为1kN 的匀质板搁在倾⾓为600的V 型⽔渠上,如图所⽰。
板与斜⾯间的摩擦⾓为15o。
试求可以通过该桥⼈的最⼤体重Q= (4分)。
题1.1图题1.2图2.连杆滑块机构中,OA =2l,AB =l,杆OA 在图⽰平⾯内绕O 轴以匀⾓速度0ω转动。
试求当⾓0=?时,AB 杆的⾓速度为(4分)。
3.⼀匀质圆盘半径为R ,质量为m ,放在光滑的⽔平平⾯上。
初始时以匀⾓速度0ω绕盘边缘⼀点A 转动。
当转动到图⽰位置时,突然释放A 点,固定盘边缘上的B 点,再释放B 点。
试求此后圆盘运动的⾓速度为=ω(4分)。
4.图⽰机构,曲柄OA 可绕O 轴定轴转动,AB 杆穿过套筒C ,OC 连线⽔平,其中OA =r ,AB =4r ,OA 曲柄作⽤⼤⼩为M 的顺时针⼒偶,初始时刻曲柄OA 处于铅垂位置,C 为AB 中点,在AB 杆的B 端施加⼀⼒P 可使系统在该位置平衡,为了使⼒P 最⼩,可以改变其⽅向,若不计各处摩擦,试求平衡时⼒P 的最⼩值为(4分)。
密封线ω题1.3图题1.4图⼆、正⽅体边长为a ,⼒12, F F ⼤⼩均为F ,该⼒系对轴CA '之矩为(4分);该⼒系简化可能得到的最⼩主矩为(6分)。
题3图题⼆图题三图三、(4分+4分+7分=15分)图⽰均质轮轴重量为G ,半径为R ,轮轴上⿎轮半径为r ,在⿎轮上缠绕轻质绳经过定滑轮系以重物,各处摩擦因数均为f ,θ⾓已知,试求平衡时重物的最⼤重量0G 。
CAC 'AA四、图⽰平⾯机构中,滑块C 与滚轮A ⽤杆和铰链连接,A 为轮⼼,套筒绕O 轴转动,图⽰瞬时O 在AB 中点,α =60o,BC ⊥AB 。
已知O 、C 在同⼀⽔平线上,AB =20cm ,V A 为常数,且V A =16cm/s ,试求该瞬时AB 杆的⾓速度为(4分),滑块C 的速度⼤⼩为(4分),AB 杆的⾓加速度为(4分),绞B 的加速度⼤⼩为(4分)。
周培源力学竞赛试题与解答)
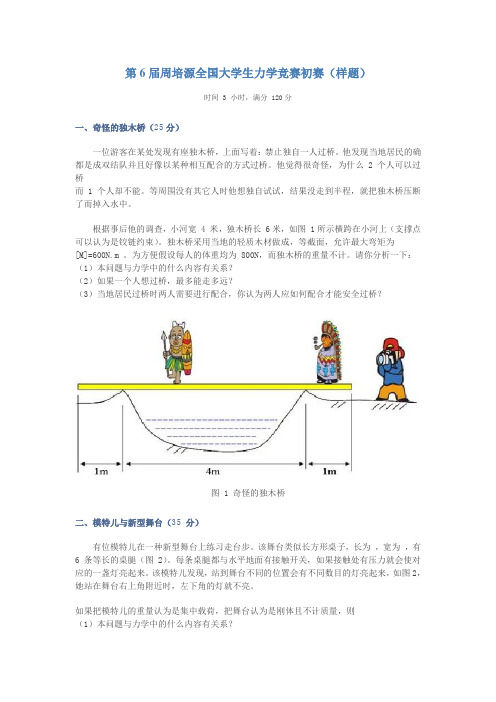
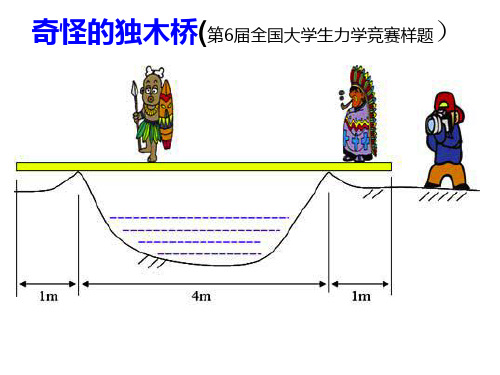
第6届周培源全国大学生力学竞赛初赛(样题)时间 3 小时,满分 120分一、奇怪的独木桥(25分)一位游客在某处发现有座独木桥,上面写着:禁止独自一人过桥。
他发现当地居民的确都是成双结队并且好像以某种相互配合的方式过桥。
他觉得很奇怪,为什么 2 个人可以过桥而 1 个人却不能。
等周围没有其它人时他想独自试试,结果没走到半程,就把独木桥压断了而掉入水中。
根据事后他的调查,小河宽 4 米,独木桥长 6米,如图 1所示横跨在小河上(支撑点可以认为是铰链约束)。
独木桥采用当地的轻质木材做成,等截面,允许最大弯矩为[M]=600N.m 。
为方便假设每人的体重均为 800N,而独木桥的重量不计。
请你分析一下:(1)本问题与力学中的什么内容有关系?(2)如果一个人想过桥,最多能走多远?(3)当地居民过桥时两人需要进行配合,你认为两人应如何配合才能安全过桥?图 1 奇怪的独木桥二、模特儿与新型舞台(35 分)有位模特儿在一种新型舞台上练习走台步。
该舞台类似长方形桌子,长为,宽为,有6 条等长的桌腿(图 2)。
每条桌腿都与水平地面有接触开关,如果接触处有压力就会使对应的一盏灯亮起来。
该模特儿发现,站到舞台不同的位置会有不同数目的灯亮起来,如图2,她站在舞台右上角附近时,左下角的灯就不亮。
如果把模特儿的重量认为是集中载荷,把舞台认为是刚体且不计质量,则(1)本问题与力学中的什么内容有关系?(2)如果模特儿站在舞台的正中央,会有几盏灯亮起来?(3)模特儿在不同区域时会有不同数目的灯亮起来,请在长方形舞台上确定各区域的边界并画出示意图,然后在该区域内写上亮灯的数目(提示,亮灯的数目有可能为 6、5、4、3、2、1)。
图 2 模特儿的新舞台三、魔术师的表演(25分)魔术师要表演一个节目。
其中一个道具是边长为a的不透明立方体箱子,质量为M1;另一个道具是长为L的均质刚性板 AB,质量为 M2 ,可绕光滑的 A铰转动;最后一个道具是半径为R的刚性球,质量为 M3 ,放在刚性的水平面上。
第六届周培源力学竞赛试题

第6届周培源全国大学生力学竞赛初赛(样题)时间3小时,满分120分一、奇怪的独木桥(25分)一位游客在某处发现有座独木桥,上面写着:禁止独自一人过桥。
他发现当地居民的确都是成双结队并且好像以某种相互配合的方式过桥。
他觉得很奇怪,为什么2个人可以过桥而1个人却不能。
等周围没有其它人时他想独自试试,结果没走到半程,就把独木桥压断了而掉入水中。
根据事后他的调查,小河宽4米,独木桥长6米,如图1所示横跨在小河上(支撑点可以认为是铰链约束)。
独木桥采用当地的轻质木材做成,等截面,允许最大弯矩为[]600N mM=⋅。
为方便假设每人的体重均为800N,而独木桥的重量不计。
请你分析一下:(1)本问题与力学中的什么内容有关系?(2)如果一个人想过桥,最多能走多远?(3)当地居民过桥时两人需要进行配合,你认为两人应如何配合才能安全过桥?图1 奇怪的独木桥二、模特儿与新型舞台(35分)2a a 有位模特儿在一种新型舞台上练习走台步。
该舞台类似长方形桌子,长为,宽为,有6条等长的桌腿(图2)。
每条桌腿都与水平地面有接触开关,如果接触处有压力就会使对应的一盏灯亮起来。
该模特儿发现,站到舞台不同的位置会有不同数目的灯亮起来,如图2,她站在舞台右上角附近时,左下角的灯就不亮。
如果把模特儿的重量认为是集中载荷,把舞台认为是刚体且不计质量,则(1)本问题与力学中的什么内容有关系?(2)如果模特儿站在舞台的正中央,会有几盏灯亮起来?(3)模特儿在不同区域时会有不同数目的灯亮起来,请在长方形舞台上确定各区域的边界并画出示意图,然后在该区域内写上亮灯的数目(提示,亮灯的数目有可能为6、5、4、3、2、1)。
aaaa图2 模特儿的新舞台三、魔术师的表演(25分)魔术师要表演一个节目。
其中一个道具是边长为的不透明立方体箱子,质量为a 1M;另一个道具是长为L 的均质刚性板AB ,质量为2M ,可绕光滑的A 铰转动;最后一个道具是半径为R 的刚性球,质量为3M ,放在刚性的水平面上。
奇怪的独木桥(第6届全国大学生力学竞赛样题)
四、跳板跳水(30 分) 举世瞩目的第 29 届北京奥林匹克运动会上,具有“梦之队”之称的中国跳 队获得了跳水比赛8枚金牌中的7枚,囊括了3m跳板跳水的4枚金牌。Duraflex 的 Maxiflex Model B 跳水板是奥林匹克跳水比赛和国际级跳水比赛唯一指定使 用的产品,它的具体尺寸如图所示,其中横截面尺寸为b =0.5m,h =0.05m, 跳板的弹性模量E =70GPa ,比重γ =25kN/m ,a =3.2m,l =1.6m。运动员从 跳板上上跃至距地面最高点后落至跳板端点C,再从跳板上弹起至空中完成动 作后落水。若运动员体重G = 700N,最大弹跳高度H = 0.6m,取g =9.8m/s 。 1. 根据所学知识,建立相应的力学分析模型。 2. 为保证运动员落水安全,运动员从空中落入水中时,在跳板所在平面处, 运动员质心距跳板C端最小距离s应大于0.5m。试求运动员从跳板上跃时所需最 小水平速度(假设水平方向为匀速运动)? 3. 不计跳板质量,将运动员视为刚体时,运动员冲击跳板时,跳板中的最 大动应力为多少? 4. 如运动员为弹性体,定性说明在冲击时跳板中的最大动应力增大还是减 小? 5. 如考虑跳板质量,试计算跳板中的最大动应力。
奇怪的独木桥(第6届全国大学生力学竞赛样题)
奇怪的独木桥(第6届全国大学生力来自竞赛样题)一位游客在某处发现有座独木桥,上写:禁止独自一 人过桥。他发现当地居民的确都是成双结队并且好像以 某种相互配合的方式过桥。他觉得很奇怪,为什么2个人 可以过桥而1个人却不能。等周围没有其它人时他想独自 试试,结果没走到半程,就压断独木桥而掉入水中。 据事后调查,河宽4米,桥长6米,如图示(支撑点可 认为是铰链约束)。桥用轻质木材做成,等截面,允许 最大弯矩为600NmM。 假设人的体重均为800N,而桥重不计。请分析一下: (1)本问题与力学中的什么内容有关系? (2)如果一个人想过桥,最多能走多远? (3)当地居民过桥时两人需要进行配合,你认为两 人应如何配合才能安全过桥?
本科生力学竞赛试题及答案

本科生力学竞赛试题及答案一、选择题(每题3分,共30分)1. 在经典力学中,牛顿第一定律又称为:A. 惯性定律B. 作用力与反作用力定律C. 力与加速度定律D. 万有引力定律答案:A2. 一个物体的质量为2kg,受到10N的力作用,产生的加速度为:A. 5 m/s²B. 10 m/s²C. 20 m/s²D. 4 m/s²答案:A3. 根据胡克定律,弹簧的弹力F与弹簧的形变量x成正比,比例系数k为弹簧的劲度系数。
当弹簧伸长2m时,弹力为100N,则弹簧的劲度系数k为:A. 50 N/mB. 100 N/mC. 200 N/mD. 25 N/m答案:A4. 一个物体从静止开始自由下落,忽略空气阻力,其下落过程中的加速度为:A. 9.8 m/s²B. 0 m/s²C. 2 m/s²D. 19.6 m/s²答案:A5. 在国际单位制中,力的单位是以哪位科学家的名字命名的?A. 牛顿B. 爱因斯坦C. 伽利略D. 阿基米德答案:A6. 一个物体在水平面上做匀速直线运动,其受到的摩擦力为10N,那么推力的大小为:A. 0 NB. 10 NC. 20 ND. 不能确定答案:B7. 根据能量守恒定律,一个物体从高处自由下落到地面,其势能转化为:A. 动能B. 内能C. 电能D. 化学能答案:A8. 在斜面上下滑的物体,其受到的重力分量可以分解为:A. 垂直于斜面的压力B. 沿斜面向下的力C. 垂直于斜面的力D. 沿斜面向下的力和垂直于斜面的力答案:D9. 一个物体在水平面上以恒定的加速度加速运动,其受到的合外力与速度的方向:A. 相反B. 相同C. 不确定D. 垂直答案:B10. 两个物体之间的万有引力与它们的质量乘积成正比,与它们之间的距离的平方成反比。
这个定律是由哪位科学家提出的?A. 牛顿B. 爱因斯坦C. 伽利略D. 阿基米德答案:A二、简答题(每题10分,共40分)11. 什么是动量守恒定律?请举例说明。
理论力学竞赛练习题答案

理论力学竞赛练习题一、基础概念题1. 列出牛顿运动定律的三个基本内容。
2. 简述质点与刚体的区别。
4. 解释力的合成与分解。
5. 简述功和能量的概念及其关系。
二、单选题A. 速度B. 力C. 加速度D. 质量2. 在自由落体运动中,物体的加速度为:A. 0B. 9.8 m/s²C. 5 m/s²D. 10 m/s²A. 惯性与物体的速度有关B. 惯性与物体的质量无关C. 惯性是物体保持静止状态的性质D. 惯性是物体保持匀速直线运动状态的性质三、计算题1. 一物体从静止开始沿直线加速运动,经过10秒后速度达到20 m/s,求物体的加速度。
2. 一质量为2 kg的物体在水平面上受到10 N的力作用,求物体的加速度。
3. 一物体从高度h自由落下,不计空气阻力,求物体落地时的速度。
4. 一物体沿半径为5 m的圆周运动,速度为10 m/s,求物体的向心加速度。
5. 一物体在水平面上受到两个力的作用,其中一个力为30 N,方向向东,另一个力为40 N,方向向北,求物体的合力。
四、应用题1. 一辆汽车以20 m/s的速度行驶,紧急刹车后,加速度为5m/s²,求汽车停止前行驶的距离。
2. 一物体在斜面上受到重力和摩擦力的作用,已知重力为30 N,摩擦力为10 N,求物体的合力。
3. 一质量为1 kg的物体在水平面上受到一个变力的作用,力随时间的变化关系为F=3t²(N),求物体在05秒内的位移。
4. 一物体在半径为10 m的圆形轨道上做匀速圆周运动,速度为5 m/s,求物体在1分钟内转过的角度。
5. 一质量为5 kg的物体在水平面上受到一个恒力的作用,力的大小为20 N,方向与初速度方向成30°角,求物体在5秒内的位移。
五、判断题1. 动能定理表明,物体的动能变化等于所受外力做的功。
()2. 在圆周运动中,物体的速度方向始终沿着半径方向。
()3. 作用力和反作用力大小相等,方向相反,作用在同一直线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(竞赛时间:180分钟)
请将答案写在相应横线上,答案正确给全分,答案不正确给零分。
一、综合题(16分)
1.长度为l ,重P 为1kN 的匀质板搁在倾角为600的V 型水渠上,如图所示。
板与斜面间的摩擦角为15º。
试求可以通过该桥人的最大体重Q= (4分)。
题图 题图
2.连杆滑块机构中,OA =2l,AB =l,杆OA 在图示平面内绕O 轴以匀角速度0ω转动。
试求当角0=ϕ时,AB 杆的角速度为 (4分)。
3.一匀质圆盘半径为R ,质量为m ,放在光滑的水平平面上。
初始时以匀角速度
0ω绕
盘边缘一点A 转动。
当转动到图示位置时,突然释放A 点,固定盘边缘上的B 点,再释放B 点。
试求此后圆盘运动的角速度为=ω (4分)。
4.图示机构,曲柄OA 可绕O 轴定轴转动,AB 杆穿过套筒C ,OC 连线水平,其中OA =r ,AB =4r ,OA 曲柄作用大小为M 的顺时针力偶,初始时刻曲柄OA 处于铅垂位置,C 为AB 中点,在AB 杆的B 端施加一力P 可使系统在该位置平衡,为了使力P 最小,可以改变其方向,若不计各处摩擦,试求平衡时力P
的最小值为 (4分)。
O
ω
题图
题图
二、正方体边长为a ,力12, F F 大小均为F ,该力系对轴CA '之矩为 (4分);该力系简化可能得到的最小主矩为
(6分)。
题3图
题二图
题三图
三、(4分+4分+7分=15分)图示均质轮轴重量为G ,半径为R ,轮轴上鼓轮半径为r ,在鼓轮上缠绕轻质绳经过定滑轮系以重物,各处摩擦因数均为f ,θ角已知,试求平衡时重物的最大重量0G 。
四、图示平面机构中,滑块C 与滚轮A 用杆和铰链连接,A 为轮心,套筒绕O 轴转动,图
C
A C '
A
示瞬时O 在AB 中点,
=60º,BC AB 。
已知O 、C 在同一水平线上,AB =20cm ,V A 为常
数,且V A =16cm/s ,试求该瞬时AB 杆的角速度为
(4分),滑块C 的速度大小为 (4分),AB 杆的角加速度为 (4分),绞B 的加速度大小为 (4分)。
题四图 题五图
五、已知半径为R ,质量为M 的均质球体相对于过球心轴的转动惯量为22
5
MR 。
现将半径
为r ,质量为m 的均质半球体放于光滑的水平和铅垂平面之间,C 为质心轴位置,初始位置如图所示。
今无初速地放开,试求:
(1)初始位置时,质心C 的加速度大小为 (3分); (2)半球体转过90°时,质心C 的速度大小为 (3分); (3)此后半球体继续侧转的最大角度0为
(5分);
(4)侧转角度0时,质心C 与轮心O 的加速度大小比值为 (4分);
(5)侧转角度0时,半球体受水平面约束力大小为
(4分)。
六、均质薄壁圆环质量为m ,半径为r ,均质细杆OA 质量也为m ,长度为r ,圆环与杆固结。
在图示杆处于水平位置时静止释放,圆环在铅直平面内沿水平面作纯滚动,试求 (1)初始圆环角加速度大小为 (3分); (2)初始杆端A 的约束力偶矩为 (3分); (3)运动中圆环的最大角速度为 (5分)。
题6图
C
α
A
V A
O
B
C
O
3r
8
O
七、质量为4m,半径为r的均质圆柱体O放在水平面上。
质量为m的质点A放在柱表面的顶端。
初始时静止,质点在小扰动下自圆柱表面下滑。
(1)若所有接触都是光滑的,则:
质点未脱离圆柱面时的运动轨迹为(4分);
质点脱离柱体的位置角θ(如图所示)满足的方程为
(4分);(2)若水平面粗糙,圆柱滚动,质点A光滑接触圆柱,其未脱离时,轮心O向左位移x 与角θ的关系是(5分)。
题7图
《。
